Abstract
The game ‘Mafia’ is a logic puzzle that has been a top-rated party game played worldwide. Many studies have been dedicated to determining the best character combination to keep players engaged while analyzing the overall death toll. Although it has only two-sided plays, there are multiple combinations of characters in which each character’s rules are different. This paper explores the game’s sophistication using the game refinement theory and motion in mind model while measuring the entertainment of each character’s actions. It then focuses on the dynamics of minority versus majority behaviors during the game process. Computer simulations were conducted to collect the data of each character and assess the entertainment impacts. Moreover, the energy value of each character was computed based on the motion in mind model. The results show that when the number of ‘Mafia’ and the number of ‘Sheriffs’ are equal, the sophistication of each character is maximized. In addition, the data indicates the player engagement in the following order: . Thus, it can be concluded that the actions of the Mafia character are the most complicated and significantly impact the game. It is expected that the results in this study enable game designers to improve each character’s perspective and examine possible enhancements from the viewpoint of entertainment.
1. Introduction
The traditional game theory originated with the idea of the existence of mixed-strategy equilibria a in two-person zero-sum game [1], which has also been shown as a powerful tool in many fields such as political science, sports, psychology, and economics. However, few studies analyze games’ entertainment and sophistication in a mathematical way. Game refinement (GR) theory was proposed earlier by Iida et al. [2] to determine different levels of the game’s sophistication. The GR theory is based on the game outcome uncertainty, with a logistic model constructed as a core framework.
The Mafia game or the Werewolf game is a kind of party game with a high logic, which also can be played on the Internet. A simple version of the Mafia game contains two groups with three kinds of characters: (1) Mafia and Citizens, and (2) Mafia, Sheriffs and Citizens. The game alternates between day and night round by round; players in different roles have their own functions. The game was suitable for analyzing the sophistication and energy exchange between players and the game itself since it is a multiplayer game.
In this paper, our main objective is to find the best combinations of character setting by applying the GR theory to each play aspect of the game. Based on the result, the energy exchange of each character with the game is analyzed. The paper organization is as follows. Section 2 provides an overview of the Mafia game and some related works. The fundamentals of GR theory and its application to the Mafia game are given in Section 3. Then, the simulations and evaluation of the results are provided in Section 4. Section 5 provides the energy analysis and its assessment. Finally, Section 6 concludes the study.
2. Related Works
In this section, a brief sketch of the Mafia game is given, and an overview of research development with the game is presented.
2.1. The Mafia Game
The Mafia game is a party game and can be played both offline and online on the Internet. The moderator divides the players into two secret teams: the Mafias and the Citizens. Then, the moderator sends the identity cards to each player. The Mafias’ goal is to kill all of the Citizens before being discovered. The Citizens’ goal is to identify the Mafias and vote to lynch them—the game cycles between day and night.
During the night in the game, everyone closes their eyes except the Mafias. The Mafias will silently decide which player they want to kill and signal their choice to the judge. Once they have made their choice, the judge asks everyone to open their eyes and announces who was killed. Then everyone is free to say or do anything to guess who the Mafias are and vote to lynch someone they suspect. That player reveals their identity, and if there are any surviving Mafias, the night begins again. The standard edition Mafia game contains “Judge”, “Mafias”, “Sheriffs”, and “Citizens”. The game is based on the “kill all the Citizens and Sheriffs, or all the Mafias” rule. The actions of each character are provided as follows:
- Judge: The judge has to guide the course of the game, and not participate with any team. The game begins at night. Firstly, everyone needs to close their eyes, except for the judge and the Mafias. The judge will let the Mafias know who the teammates are and identify the player they want to kill. Then, let the Mafias close their eyes, tell the Sheriffs to open eyes to realize teammates, and verify players. During the daytime, the judge tells everyone to open their eyes and declare the player dead based on the results of the Mafia killings at night. After this, players will be directed to speak in order and point out the players they suspect of being a Mafia by the judge. Finally, the player is instructed to vote, noting that the player with the most votes will be declared out of the referendum by the judge. After the progress above, the judge will conduct the second night.
- Mafias: The Mafias’ goal is to kill all the players of the Citizen camp. Hence, they will disguise themselves as much as possible and mislead other players during the daytime. On the first night, guided by the judge, they identify their teammates and use hand signals to tell the judge which player they want to kill. In offline game conditions, the Mafias communicate by using gestures that do not make a sound. In the online game, voice communication is possible. On the first night, they make a random choice of players to kill. On the subsequent nights, they choose the player most likely to know their identity to kill (Sheriffs or Citizens), depending on the daytime situation, to ensure victory for the Mafias. Since the simple version of the Mafia game does not have a role that prevents players from being killed, the Mafias will succeed in killing players.
- Citizens: The Citizens’ goal is to help the Sheriff to win the game for the Citizen camp. The Citizens will close their eyes at night without any extra information. During the daytime, they will be guided by the judge to speak by pointing out the players they suspect of being Mafias. They vote to lynch the players they think are Mafias based on their analysis of the game situation. They vote by telling the judge the player number. All players will participate in the voting.
- Sheriffs: The Sheriffs’ goal is the same as the Citizen’s. During the night, they will verify the true identity of other players, guided by a judge. During the daytime, they will inform other players of their verification results when they are speaking. They will convince other players of their identity as much as possible, to guide other players to vote the Mafias out of the game.
2.2. Research Development on Mafia Game
Norhaidi et al. [3] had conducted a study with a focus on the use of the Mafia game in linguistic classrooms based on self-reporting and a set of semi-structured interviews administered to 137 undergraduate students and 12 facilitators. The findings revealed that learners participated and mitigated anxiety in learning English since the game required interrogate and team-driven decision-making. However, careful consideration of the level of linguistic ability relative to the game implementation as an instructional tool can be learner-specific. Meanwhile, Conner and Baxter [4] reported on the implementation of student-centered applied-learning activity using the game Werewolf (a similar variant of the Mafia game with additional roles or characters), where learners engaged with symbolic interaction theory and analyzed everyday life experiences. Such an implementation aimed to incorporate more active learning approaches to social theory by outlining an applied-learning activity based on the role-playing game Werewolf as an alternative pedagogical tool that demonstrated heightened understanding of the underlying concepts.
From the perspective of natural language processing and automating AI negotiation, complex negotiation involves an uncooperative situation requiring an agent’s ability to hide information and infer intention from communication between AI agents [5]. Such a feat had been achieved by designing the protocol between agents, which was analyzed from the agent communication in the game Werewolf. This situation includes features such as the absence of objectivity, reasoning, and persuasion which were derived from the lack of objectivity, along with modeling of others’ self from the viewpoint of others. In a study, a non-human agent that can play the game Werewolf (i.e., AI wolf) was constructed by Hirata et al. [6]. Another study by Nagayama et al. [7] involves analyzing in-game conversation logs where cooperation between werewolves via measure of the number of “whispers” (werewolves’ private chat) and its influence on the percentage of winning. The study found that the winning percentage of werewolves is higher when two werewolves have established frequent dialogue or a high number of whispers occurred. In addition, an -Nash equilibrium analysis of the “stealth werewolf” strategy is proposed by Bi and Tanaka [8]. The results show that it is not an optimal choice, but only a suboptimal choice in a disadvantageous situation for the werewolf players.
Recently, Chang [9] proposed a simulator that can simulate various characters’ actions more realistically by adding a weight of credibility, which changes continuously as the game progresses and clearly distinguishes the identity of each player. In addition, the study also analyzed the simulation to find the best combination solution dynamically as the change of the total number of players relative to two theories: (1) a simple asymptotic formula for the Mafia-winning chance, and (2) game refinement (GR) theory. Since deceptive games such as the Mafia game require development of strategies (deceivers draw in unknown bystanders and bystanders detecting falsehoods), a study by Ibraheem et al. [10] developed a computational classifier to identify Mafias from text-based role-playing behaviors of the characters with up to 70% accuracy. The study’s finding suggests that understanding the systematic features that define honest and deceptive players advances the ability to automate the detection of online deceit and grasp group dynamics in real-world collaboration.
From the information science perspective, manipulating and exploiting the game rules and settings change the complexity of the Mafia game which, ultimately, could also influence its entertainment impact. However, limited studies were conducted to quantify and determine these criteria while maintaining the relative balance of ‘chance’ and ‘skill’ in the game itself. Analyzing game sophistication via the GR theory has been successfully applied for such purposes to various board games [11] and sports games [12,13]. However, focusing on psychology research between an informed minority and uninformed majority, the Mafia game provides different dynamics of interactions between multiple players that pose unique challenges themselves [14]. In addition, Braverman et al. [15] analyzed the minority players in the Mafia game as a subgroup should be how large and strong for dominating the game. From the macro-level analysis and application of Nash equilibrium, Xiong et al. [16] found that the optimal combinations of characters directly influenced the sophistication of the Mafia game.
A study on combinatorics game theory can be found in [17]. The author studied the Mafia game using the combinatorics research method of vertex coverage and Nash equilibrium theory. Our study is to analyze the behavior of majority and minority players to find the optimal combination of players through the overall game entertainment assessment. We expect our analysis results to be consistent with the results of combinatorics analysis. Bi and Tanaka [8] conducted a method to analyze the game Werewolf from the perspective of both camps (Werewolf or non-werewolf) in the game. It used the CRF+ algorithm to calculate the -Nash equilibrium and improved the hash function, which is proposed by Braverman et al. [15]. The CFR+ algorithm is studied by Bowling et al. [18], which can handle significant games analysis. The algorithm is originally a variant of the counterfactual regret minimization algorithm, which was proposed by Zinkevich et al. [19].
Nevertheless, such a situation assumed that the behaviors of each character were always optimal, but in reality, they were not always optimal. As such, this study attempts to focus on each character’s actions and assess their entertainment impact by applying the game refinement theory and motion in mind model [20]. Our objective is to find the combinations of players that maximize the expected entertainment of the game through the analysis of minority versus majority behaviors of the Mafia game players. Moreover, we intend to assess such entertainment aspects of the Mafia game from the game designer’s perspective by analyzing the relationship among them. To achieve this goal, we decided to use the GR theory as our assessment methodology, which has been successfully adopted in many previous studies as a foundation for entertainment assessment.
3. Assessment Methodology
Game refinement (GR) theory was proposed earlier to determine different levels of sophistication of games. Furthermore, it was proposed based on the concept of game progress and game information progress [2]. It bridges a gap between board games and sports games [21]. The game progress model of the GR theory will be introduced in Section 3.1. Then, the method for applying the GR theory in the Mafia game is provided in Section 3.2.
3.1. Game Progress Model and Game Refinement Theory
Generally, some games are score-limited, others are time-limited. Hence, there are two factors for calculating the scoring rate in the game. One is the goal in the game; another is the time or steps to achieve the goal. The game progress represents the degree of certainty of a game’s result in time or steps (t). By observing the whole situation of a game, the overall game is regarded as linear progress. Hence, the game progress will be given as a linear function of the amount of uncertainty solving as given by (1), where parameter n (where ) is the number of possible options and and . However, during the in-game time, the game’s result is always uncertain. The result of the game is unknown until it is finished. As such, it is reasonable to render the game progress exponential where (2) gives a realistic model of the game progress model.
In the game progress model, n is the rate of action that contributes to the goal of the game, and the is the percentage of game goal completion. Then, the acceleration of game information progress (rate of uncertainty solving) is obtained by deriving (2) twice by solving it at , (3) is obtained. According to (3), game progress is happening in our minds. Since the physics of information in the brain is still unknown, the acceleration of information progress is likely subject to physics’s forces and laws. The physics of information in the brain may not be seen directly or indirectly by us. However, we do feel tension, anxiety, excitement and other emotions when we are playing games. Similarly, we can find similar ideas in a famous psychological study which is called flow theory and proposed by Csikszentmihalyi [22]. Our study is trying to keep the bridge from psychology to physics in mind. We can also find more details about similar work from [20]. In the game progress model, the acceleration of velocity implies the difference in the rate of acquired information during game progress. A measure of game refinement () is obtained as the root square of the second derivative. For a game with branching factor B and game length D (i.e., a board game, approximated by utilizing an efficient algorithm in a MIN/MAX tree search structure), the can be approximated as in (4).
In the game refinement theory, the various games can be represented through the game progress model, where there are two kinds of progress models: the game speed or scoring rate. At the same time, another one is game information progress that focuses on the game outcome. Several games are sophisticated by applying the GR measure (Table 1), where is the branching factor or total goals, and the is the game length or total shot attempts, respectively. The table shows that these games have similar GR measures (). It indicated that these games have similar game sophistication, quantified by the game refinement theory. In this condition, players enjoy the same level of engagement among various types of games. Similarly, game refinement theory can also be applied to a non-game context that had successfully been evaluated in the hotel loyalty programs [23]. Many previous works have shown that the players enjoy the game most when the GR measure is located in the “zone” of . This is the result of realistic observation combined with mathematical theory analysis. An analysis of popularity research of an arcade game which is named Jump & Jump can also explain this condition [24]. Since the Mafia game is a kind of party and deceptive game, it is expected that the Mafia game could potentially be analyzed using the GR theory.

Table 1.
GR measure of several sophisticated games [25].
3.2. Game-Refinement Theory in the Mafia Game
In order to analyze the Mafia game according to the possible actions, we need to first clarify the actions of each character in the game (four characters in the Mafia game: Judge, Mafias, Citizens, Sheriffs). After introducing the character’s action in detail in Section 2.1, a simple description will be shown as follows:
- Judge: Hosts the game, not participating with any team.
- Mafias: Kills one character (except the Mafia) every night and pretends to be a player during the daytime.
- Citizens: Votes to lynch someone during the daytime.
- Sheriffs: Each night, the Sheriff can discover the real identity of a player (except the Sheriff).
From the actions of each character in the game, it can be observed that there are a number of different ways the Mafias can kill the Citizens. They can kill the Citizen at night, or induce other players to lynch someone during the daytime. The Citizens take into account the statements of the others and the results of each round, then choose the player they believe to be guilty to lynch them. Therefore, to analyze the sophistication of each character, the value for B can be defined differently in (4) for each character.
- Mafias: Let be the sum of the and , where indicates the average number of killing actions at night, and indicates the number of players who are lynched by voting with Mafias during the daytime.
- Citizens: Let be the average number of Mafias who are lynched by Citizen voting.
- Sheriffs: Let be the average number of Mafias with their identity confirmed by the Sheriffs and then be lynched by voting.
To assess the entertainment of this game, the branching factor (B) analyzed above is regarded as the contribution to the game goal in the game progress for each character. Then, D in (4) is the average of the sum of all the actions, during the life of each character in this game. Thus, the final form of game refinement measures in the Mafia game is given by function (5).
3.3. Motion in Mind Model
The notion of “motion” in game-playing relies on the rate of the information representing the “progress” of the gaming process, constituting the speed or “velocity” of the game, defined as the success rate (v) [20]. In contrast, the challenge or difficulty of reaching such a success rate would constitute the weight or “mass” of a game that can be generally defined as the difficulty rate (). In the context of games, given one part of m and one part of v, the fundamental assumptions of zero-sum game-playing condition where gain or loss utility of one player is exactly balanced by the losses or gains of the utility of its opponent [27,28].
In this study, the focus is shifted towards the potential energy () and momentum () in the game, where the former is defined as the game playing potential or the expected game information required to finish a game, while the latter refers to the competitive balance of a game involving the degree of challenge needed (m) and effort given (v) to drive the game progression. Since and , it can be observed that . This implies that momentum is maximized when [20]. With respect to the study conducted on player satisfaction model by Xiaohan et al. [29], the reward system (N) was incorporated to better represent the motion in mind model, given by (6) and (7) for the and , respectively.
4. Experiment Results and Its Analysis
In this section, simulation design with AI and its results of data analysis are shown.
4.1. Simulation Setup and Analysis
The simulation was conducted to imitate real human behaviors such as in-group cooperation and competition using a simulator engine that considers preset actions of each character adopted by AI agents. Each action is generated randomly for each character, and some actions use weighting for specific cases. For example, on the first night, the Sheriffs and the Mafias will randomly select players to check and kill, respectively. We will perform this random behavior in our simulation program. For the probability of the Sheriffs checking into the Mafias and the Mafias killing the Sheriffs, we will add a random number as a weight parameter (correct probability) to the checking function and killing function to affect the return value of these functions. We only show the main process of the simulator in the following algorithm, so the random function is not mentioned in the algorithm. For each character’s behavior, their condition is shown as follows:
- Sheriff (S): Generally, after the Sheriffs discovered that a player’s identity is “Mafia”, there is a high probability that they will vote for the player in the next voting, and induce other Citizens to vote for this player. Therefore, we set a parameter to indicate the possibility of exposing the identity of Mafias.
- Mafia (M): The Mafias kill the Citizens randomly except that one of them has been exposed by any sheriff. At this time, the Sheriff that revealed them would be their target.
- Citizen (C): Because all the Citizens do not know the identity of each player, there is no guarantee that all Citizens will believe the Sheriff’s speech. Therefore, we set a parameter for each Citizen to indicate that possibility of believing in the Sheriff.
Based on the probabilities of each character’s action, the model can imitate the “identity hiding” behavior of a real player in the game; thus, making the simulator close to reality helps us analyze each character’s sophistication. Hence, we create a program to simulate the Mafia game by using C++ for collecting the action data. The process of the simulator is shown in Algorithm 1, where it describes the overall process of the simulator. In general, the process first starts with the Mafias choosing the player to kill which then the identity of all players is checked by the Sheriff. Then, the players’ discussion is simulated by voting function to decide which player will be lynched out. Finally, the game continues if the number of Mafias is smaller than the total number of the Sheriff and Citizens (), or one Mafia still exists ().
| Algorithm 1: Mafia simulation |
 |
Each of the functions was as follows. The MafiaKilling(C,S) function involves the Mafias randomly selecting the target to kill. If the Mafia feels that the Sheriff is marking them, the priority is given to targeting the Sheriff. In the SheriffChecking() function, only the Sheriff can check the identity of the players. First, they choose a random target to check the identity, and a threshold value determines the possibility of exposing the identity of the Mafia. This threshold is generated by a random number used as a correct probability and depends on the remaining number of each character (proportions of players). If they identify the Mafia, the Mafia will be marked.
In voting, the SheriffVoting() function determines if there is any Mafia marked by the Sheriffs. If there is, then a priority vote is given to that Mafia while persuading other players to vote together. If there is no marked Mafias, they will randomly select a player to vote instead. Meanwhile, the MafiaVoting() function involves voting a player randomly. For the CitizenVoting() function, the voting is determined based on their judgment of other players. This condition is determined by using a threshold value, where they will mark a player as a Mafia when over the threshold while choosing a random target to vote when under the threshold. The Citizens’ judgment is based on the threshold value. Similarly, the thresholds here are similar to those of the Sheriffs. However, since the proportions of players in their eyes are not the same as the number in the Sheriffs’ eyes, or the correct probability is different, the judgments among Citizens are also different. For the JudgeStatistics(V) function, the judge finds the player who accumulated the most votes and shows the result. Then, the player who accumulated the most votes will be out of the game, given by the Lynch(V) function.
4.2. Results Analysis of
A total of 648 combinations of each game character were simulated, in which the game was run 10,000 times to ensure the result reliability. Table 2 showed ten sets of data to observe the trend of our data. From the table, ‘S’, ‘C’, ‘M’ showed the number of players for “Sheriff”, “Citizen”, and “Mafia”, respectively. In addition, “” and “” represented the number of wins in their respective roles (Citizen and Mafia) for 10,000 games. Here, it can be noted that, when the number of Mafias is greater than one-fifth of the total number, the Mafias will win overwhelmingly. The average number of actions, the average number of effective actions, and the GR measure for each combination will be shown for each character. According to the Table 2, it can be noted that for each character, as the number of players increases, that more changes will happen while decreasing the GR value (for instance, the parameter and ).

Table 2.
GR measure of Mafia characters based on various settings.
For the Sheriffs and the Mafias, because they were constrained by each other when the number of players is small, the players can choose fewer operations, resulting in a more considerable GR value (For instance, the parameter and ). In contrast, for the Citizens, due to the high randomness of the actions, if the player number is large, the effective actions will be small, resulting in a long game and a lower GR measure (For instance, the parameter and ).
For finding the best choice combination, the GR measure of each character was assessed. Most previous works found that is the ‘zone’ value in various games that provide a balance between skill and chance [2]. In other words, the game is the most engaged in this context. Ideally, all the assessment of GR values in this study should conform to this ‘zone’ value. However, it is hard to achieve because of their mutual restraint. Alternatively, its variance from 0.07 could help us select the best combination to indicate relative closeness to the ‘zone’ value. From the simulation results, when the number of Mafias is equal to the number of the Sheriffs, each character’s average sophistication is the highest. However, considering the most balanced case of all results, the parameters of and were the most appropriate choices.
4.3. Result Analysis of
With the GR measure among various characters, further analysis is conducted to determine the players’ potential energy using the potential energy () measure of the motion in the mind model. Although the rules of the Mafia game constitute three or more characters, the game is essentially still two-sided. As such, the energy for each character is defined as (8)–(10), where the results are given in Table 3. From the table, ‘S’, ‘C’, ‘M’ showed the number of players for “Sheriff”, “Citizen”, and “Mafia”, respectively. In addition, “” and “” represented the number of wins in their respective character (Citizen and Mafia) for the 10,000 game run.

Table 3.
Potential energy of Mafia characters based on various settings.
5. Discussion
Various games considered in this study constitute three distinct sports landscapes: mind (or m-sports; e.g., board games or abstract games such as Go, Shogi, and Chess), physical (or p-sports; e.g., Basketball, Soccer, Table Tennis, and Badminton), and electronic (or e-sports; e.g., DoTA and action games), as depicted in Figure 1 (adapted with permission from Xiaohan et al. [29]). Since N values were related to the reward ratio for a player in the game-playing process, in the context of this study, the N value is determined as (v is the game speed defined by the ratio of ).
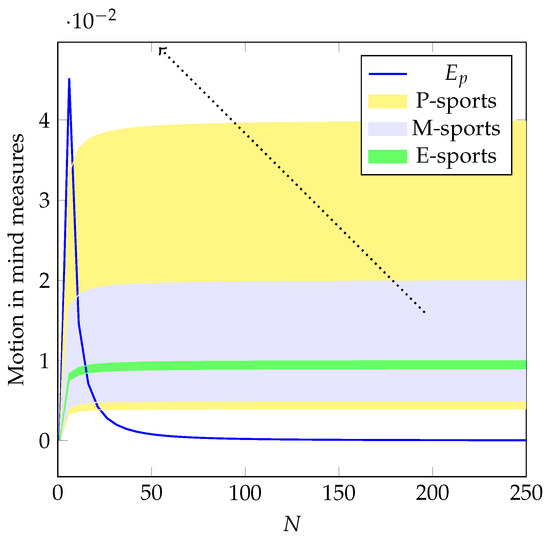
Figure 1.
The convergence of p-sports, m-sports, and e-sports based on the a indicators, relative to the physics in mind measures.
The energy changes of each character in the Mafia game had been given in Figure 2, where the x-axis is the N value and the y-axis is the variance of the energy. It can be observed that the for Sheriffs and Mafia, while for the Citizen. This situation describes that Mafia and Sheriffs always remain hidden in the game (minority) but represent a compelling character. Depending on their roles, they often have to complete their tasks in secret (such as identifying their partner or avoiding being a target of lynching). Therefore, according to their N value, Sheriffs and Mafia are required to be more competitive and typically dealing with a more stable condition (lower range of N values). In addition, compared to Mafia, Sheriffs could not directly control the game results based on their role but can help Citizens, making them need more energy when N is small. In contrast, Citizens have a larger range of N values; thus, reflecting their unstable condition and relying on high ability, motivation, and effort, but less competitive than the other two characters. Thus, ranking the engagement experience, the order was . As for the rank of game effort, the order was .
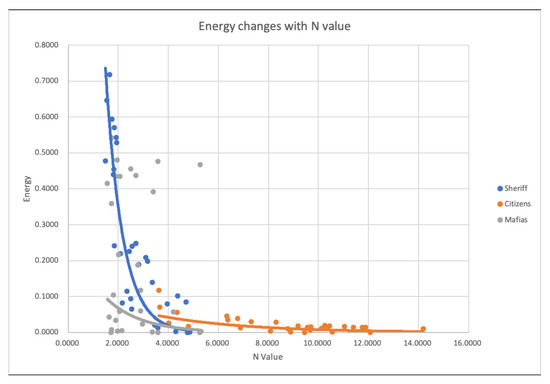
Figure 2.
Energy changes of each character.
When observing the change in player number (Figure 3), it was found that, as the player number increases, the energy decreases, which reflects that players would need less energy to play the game. This condition describes that, as the number of players increases, the game ‘pressure’ for each character in the Mafia game will not be as much since the thrill of engagement occurred less often and was less evident due to their being rarely suspected or targeted. The further analysis reflected that an increase in the proportion of Mafia decreases the energy of Mafia, as shown in Figure 4. This condition means that the game will be easier when the number of Mafia increases. In contrast, when the proportion of Sheriff increases, their energy increases, which shows that it is more difficult to be engaged when a larger proportion of the player is the Sheriff. For Citizens, no direct impact was observed when its proportion changed due to less functionality being expected from the Citizen role (given that this is the most straightforward character to play and they usually cannot know a substantial amount other characters’ details), which does not change the energy. As such, they were stable in any of the settings.
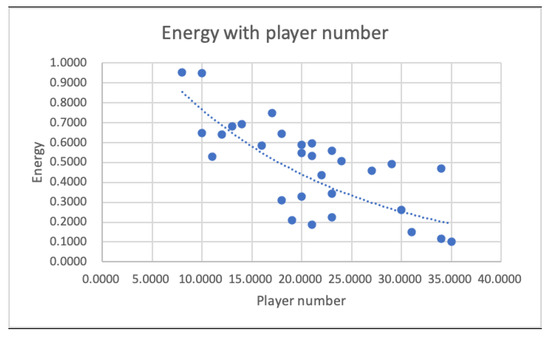
Figure 3.
Energy changes with player number.
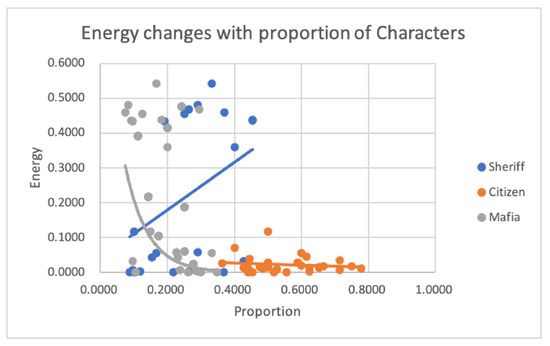
Figure 4.
Energy changes with the proportion of characters.
6. Conclusions
This study proposed methods to analyze the sophistication of character roles in the Mafia game using the GR theory, while expanding the analysis to its game-playing experience using the motion in mind model via the reward ratio to determine their potential energy. Typical analysis of such a game involves determination of the best character combination by analyzing the overall death toll [16]. This study is interested in observing how the combinations of characters affect the game-playing experience and impact the overall expected entertainment which originates from the mutual restraint between the characters. A total of 6,480,000 game runs were analyzed from the simulator of the Mafia game implemented using the C++ program.
Based on the analysis of the GR value, several entertainment character combinations in the Mafia game were identified, which helps balance the game experience in terms of ability and chance while providing enough sophistication to be entertaining when using any of the characters. Analysis from the energy in mind perspective, the relationship between reward ratio (N) and proportion of character roles was also explored. The N value and the value of the character’s proportion affect the player’s experience of playing Mafia and Sheriff, while Citizens always have a stable engagement experience.
The study potentially describes dynamics of minority versus majority behaviors in a party game setting of the Mafia game, which had been analyzed by theoretical quantification methods of GR value and motion in the mind model. Nevertheless, this study does not claim that such a method could perfectly describe players’ actual behaviors in game-playing settings but rather estimate the possibility of such behaviors and approximate the entertainment expectation from it. In addition, the game designer can also improve the character roles and functionality in the minority or majority group to enhance the game-playing experience, while improving its entertainment aspects. Therefore, future studies could be conducted to compare, on a large scale, how the current simulation results hold against actual human behaviors while further verifying the effectiveness of this quantification method. Similarly, such a quantification method could also be adapted to determine the educational potential of the Mafia game, which had been previously suggested to be an essential tool that was useful in such endeavors.
Author Contributions
Conceptualization, H.R., X.K., M.N.A.K. and H.I.; data curation, H.R. and X.K.; formal analysis, H.R., X.K., M.N.A.K. and H.I.; funding acquisition, H.I.; investigation, H.R. and X.K.; methodology, H.R., X.K., M.N.A.K. and H.I.; project administration, H.I.; resources, H.I.; software, H.R. and X.K.; supervision, H.I.; validation, H.R., X.K., M.N.A.K. and H.I.; visualization, H.R., X.K., M.N.A.K. and H.I.; writing—original draft, H.R., X.K., M.N.A.K. and H.I.; writing—review and editing, H.R., X.K., M.N.A.K. and H.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by a grant from the Japan Society for the Promotion of Science, in the framework of the Grant-in-Aid for Challenging Exploratory Research (Grant Number: 19K22893).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here https://www.kaggle.com/nolanbconaway/rollercoaster-tycoon-rides/ (accessed on 1 January 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roger, B.M. Game Theory: Analysis of Conflict; The President and Fellows of Harvard College: Cambridge, MA, USA, 1991. [Google Scholar]
- Iida, H.; Takahara, K.; Nagashima, J.; Kajihara, Y.; Hashimoto, T. An application of game-refinement theory to Mah Jong. In Proceedings of the International Conference on Entertainment Computing, Eindhoven, The Netherlands, 1–3 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 333–338. [Google Scholar]
- Norhaidi, W.M.S.W.; Romly, R.; Abdullah, A.N.S. Lowering Anxiety Among Low Proficiency ESL Learners using the Mafia Game. Int. J. Innov. Technol. Explor. Eng. 2019, 752, 67–73. [Google Scholar]
- Conner, C.T.; Baxter, N.M. Are you a Werewolf? Teaching Symbolic Interaction Theory Through Game Play. Teach. Sociol. 2022, 50, 17–27. [Google Scholar] [CrossRef]
- Osawa, H.; Otsuki, T.; Aranha, C.; Toriumi, F. Negotiation in hidden identity: Designing protocol for werewolf game. In Proceedings of the International Workshop on Agent-Based Complex Automated Negotiation, Macau, China, 10–13 August 2019; Springer: Singapore, 2019; pp. 87–102. [Google Scholar]
- Hirata, Y.; Inaba, M.; Takahashi, K.; Toriumi, F.; Osawa, H.; Katagami, D.; Shinoda, K. Werewolf Game Modeling Using Action Probabilities Based on Play Log Analysis. In Computers and Games; Plaat, A., Kosters, W., van den Herik, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 103–114. [Google Scholar]
- Nagayama, S.; Abe, J.; Oya, K.; Sakamoto, K.; Shibuki, H.; Mori, T.; Kando, N. Strategies for an autonomous agent playing the “werewolf game” as a stealth werewolf. In Proceedings of the 1st International Workshop of AI Werewolf and Dialog System (AIWolfDial2019), Tokyo, Japan, 29 October 2019; pp. 20–24. [Google Scholar]
- Bi, X.; Tanaka, T. Human-Side Strategies in the Werewolf Game Against the Stealth Werewolf Strategy. In Computers and Games; Plaat, A., Kosters, W., van den Herik, J., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 93–102. [Google Scholar]
- Chang, Q. A Simulator for Analyzing the Balance of Mafia Game. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Information Systems (ICAIIS), Dalian, China, 20–22 March 2020; pp. 622–627. [Google Scholar]
- Ibraheem, S.; Gates, V.; DeNero, J.; Griffiths, T. Investigating the Behavior of Malicious Actors Through the Game of Mafia. In Proceedings of the 42th Annual Meeting of the Cognitive Science Society-Developing a Mind: Learning in Humans, Animals, and Machines (CogSci. 2020), Virtual, 29 July–1 August 2020. [Google Scholar]
- Iida, H.; Takeshita, N.; Yoshimura, J. A metric for entertainment of boardgames: Its implication for evolution of chess variants. In Entertainment Computing; Springer: Berlin/Heidelberg, Germany, 2003; pp. 65–72. [Google Scholar]
- Nossal, N.; Iida, H. Game refinement theory and its application to score limit games. In Proceedings of the 2014 IEEE Games Media Entertainment, Toronto, ON, Canada, 22–24 October 2014; pp. 1–3. [Google Scholar]
- Sutiono, A.P.; Ramadan, R.; Jarukasetporn, P.; Takeuchi, J.; Purwarianti, A.; Iida, H. A Mathematical Model of Game Refinement and Its Applications to Sports Games. EAI Endorsed Trans. Creative Technol. 2015, 2. [Google Scholar] [CrossRef]
- Yao, E. A theoretical study of mafia games. arXiv 2008, arXiv:0804.0071. [Google Scholar]
- Braverman, M.; Etesami, O.; Mossel, E. Mafia: A theoretical study of players and coalitions in a partial information environment. Ann. Appl. Probab. 2008, 18, 825–846. [Google Scholar] [CrossRef]
- Xiong, S.; Li, W.; Mao, X.; Iida, H. Mafia Game Setting Research Using Game Refinement Measurement. In Proceedings of the 2017 International Conference on Advances in Computer Entertainment, London, UK, 14–16 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10714, pp. 830–846. [Google Scholar]
- Valla, T. Combinatorial Games Theory. Ph.D. Thesis, Computer Science Institute of Charles University, Prague, Czech Republic, 2012. [Google Scholar]
- Bowling, M.; Burch, N.; Johanson, M.; Tammelin, O. Heads-up limit hold’em poker is solved. Science 2015, 347, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Zinkevich, M.; Johanson, M.; Bowling, M.; Piccione, C. Regret Minimization in Games with Incomplete Information. In Advances in Neural Information Processing Systems; Platt, J., Koller, D., Singer, Y., Roweis, S., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2008; Volume 20. [Google Scholar]
- Iida, H.; Khalid, M.N.A. Using games to study law of motions in mind. IEEE Access 2020, 8, 138701–138709. [Google Scholar] [CrossRef]
- Sutiono, A.P.; Purwarianti, A.; Iida, H. A mathematical model of game refinement. In Proceedings of the International Conference on Intelligent Technologies for Interactive Entertainment, Chicago, IL, USA, 9–11 July 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 148–151. [Google Scholar]
- Csikszentmihalyi, M. Beyond Boredom and Anxiety; Jossey-Bass: Hoboken, NJ, USA, 2000. [Google Scholar]
- Zuo, L.; Xiong, S.; Iida, H. An analysis of hotel loyalty program with a focus on the tiers and points system. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 507–512. [Google Scholar]
- Ri, H.; Akmal Khalid, M.N.; Iida, H. Analysis of Jump amp; Jump Game and its Possible Enhancement. In Proceedings of the 2020 International Conference on Advanced Information Technologies (ICAIT), Yangon, Myanmar, 4–5 November 2020; pp. 82–87. [Google Scholar] [CrossRef]
- Xiong, S.; Zuo, L.; Iida, H. Quantifying engagement of electronic sports game. Adv. Soc. Behav. Sci. 2014, 5, 37–42. [Google Scholar]
- Cincotti, A.; Iida, H.; Yoshimura, J. Refinement and complexity in the evolution of chess. In Information Sciences 2007; World Scientific: Singapore, 2007; pp. 650–654. [Google Scholar]
- Macrae, N. John von Neumann: The Scientific Genius Who Pioneered the Modern Computer, Game Theory, Nuclear Deterrence, and Much More; Plunkett Lake Press: Lexington, MA, USA, 2019. [Google Scholar]
- Khalid, M.N.A.; Iida, H. Objectivity and Subjectivity in Games: Understanding Engagement and Addiction Mechanism. IEEE Access 2021, 9, 65187–65205. [Google Scholar] [CrossRef]
- Xiaohan, K.; Khalid, M.N.A.; Iida, H. Player Satisfaction Model and its Implication to Cultural Change. IEEE Access 2020, 8, 184375–184382. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).