Neural Vocoding for Singing and Speaking Voices with the Multi-Band Excited WaveNet
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
2. Materials and Methods
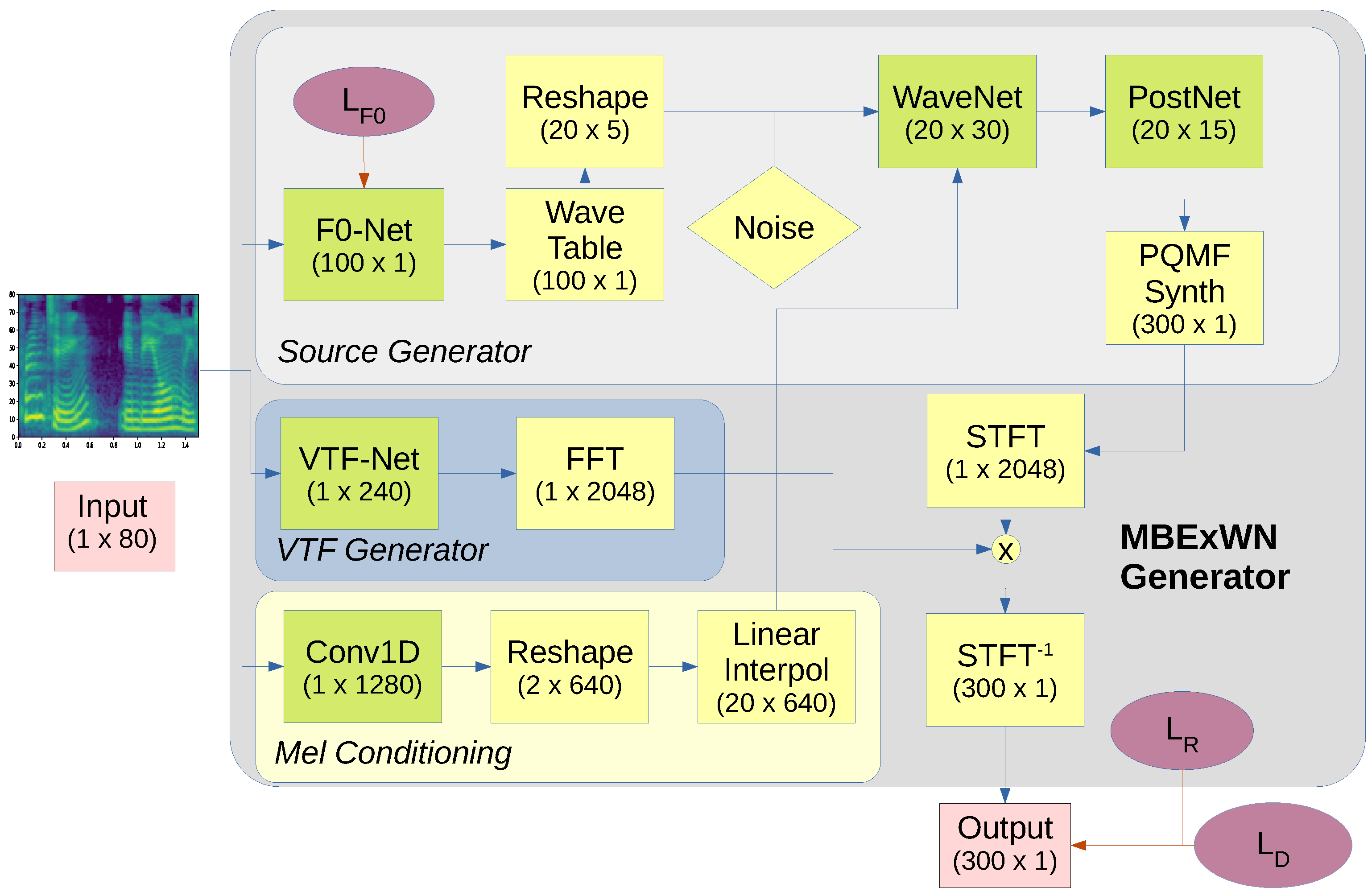
2.1. Model Topology
- Conv1D:
- The classic one-dimensional convolutional layer.
- Conv1D-UP:
- A Conv1D layer followed by a reshape operator. Conv1D-UP is used to perform upsampling using sub-pixel convolution and is initialized with checkerboard free initialization following [42].
- LinConv1D-UP:
- A Conv1D-Up layer with fixed, pre-computed weights followed by a reshape operation. The weights are pre-computed such that the layer performs upsampling by means of linear interpolation.
2.1.1. VTF Generation
2.1.2. Excitation Generation
2.1.3. The PQMF Synthesis Filter
2.2. Loss Functions
2.3. Signal Adaptive Data Normalization
- Derive an appropriate pair of gain sequences from the sequence of log amplitude mel spectra, .
- Shift the log amplitude mel spectrum by means of −.
- Apply the neural vocoder on the normalized mel spectrogram; and
- Multiply the generated signal by means of .
Estimation of Normalization Gain Contours from the Log Amplitude Mel Spectrogram
3. Results
- An objective evaluation of the adaptive normalization strategy has been added.
- Training the vocoder with random gain augmentation has been added as an alternative strategy to avoid problems with gain variations during inference.
- A new voice model trained jointly on singing and speech database has been added to study the effect of increasing diversity in the training set.
- To not overcharge the perceptual tests the single singer and single speaker MBExWN models are no longer used in the test.
- Training parameters have been changed slightly to use smaller and longer batches.
- Two bugs in the implementation of the reconstruction loss have been fixed, and the set of resolutions used for the reconstruction loss has been adapted slightly.
3.1. Databases and Annotations
3.2. Evaluation
3.2.1. Training
3.2.2. Evaluation of the Adaptive Normalization Strategy
3.2.3. Ablation Study
- Default
- The configuration as displayed in Figure 1 using 13 wavetables as described in Section 2.1.2.
- Default-2S
- Default configuration using only two sinusoids as shown in Equation (7) instead of the 13 wavetables. This should validate the use of the wavetable.
- WT+PQMF
- Default configuration with a PQMF analysis filter replacing the reshape operator after the wavetable.
- NO VTF
- Default configuration without the VTF Generator using the output of the PQMF synthesis filter as the output signal.
- NO PQMF
- Default configuration with the PQMF synthesis filter is replaced by a reshape operator.
3.3. Perceptual Tests
3.4. Computational Complexity
4. Discussion
Demonstration Material
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNN | Deep neural network |
| MBExWN | Multi_band Excited WaveNet |
| PQMF | pseudo quadrature mirror filterbank |
| VTF | vocal tract filter |
Appendix A. Model Topology
Appendix A.1. VTF-Net
| Layer | Filter Size | # Filters | Activation |
|---|---|---|---|
| Conv1D | 3 | 400 | leaky ReLU |
| Conv1D | 1 | 600 | leaky ReLU |
| Conv1D | 1 | 400 | leaky ReLU |
| Conv1D | 1 | 400 | leaky ReLU |
| Conv1D | 1 | 240 | - |
Appendix A.2. F0-Net
| Layer | Filter Size | # Output Features | Up-Sampling | Activation |
|---|---|---|---|---|
| Conv1D | 3 | 150 | leaky ReLU | |
| Conv1D-Up | 3 | 150 | 2 | leaky ReLU |
| Conv1D | 5 | 150 | leaky ReLU | |
| Conv1D | 3 | 120 | leaky ReLU | |
| Conv1D-Up | 3 | 120 | 5 | leaky ReLU |
| Conv1D | 1 | 120 | leaky ReLU | |
| Conv1D-Up | 3 | 100 | 5 | leaky ReLU |
| Conv1D | 1 | 100 | leaky ReLU | |
| Conv1D | 3 | 50 | leaky ReLU | |
| LinConv1D-Up | 2 | fast sigmoid |
Appendix B. Adaptive Normalization
| Normalization | Average | ||||
|---|---|---|---|---|---|
| norm_M(3, 1) | |||||
| norm_M(2, 1) | |||||
| norm_M(3, 3) | |||||
| norm_M(1, 3) | |||||
| norm_M(1, 2) | |||||
| norm_M(1, 1) | |||||
| norm_M(2, 2) | |||||
| norm_M(10, 3) | |||||
| norm_P(1, 3) | |||||
| norm_P(1, 1) | |||||
| norm_P(3, 1) | |||||
| norm_P(3, 3) | |||||
| norm_P(10, 3) | |||||
| rand_att(0.1) | |||||
| rand_att(0.01) | |||||
| rand_att(0.5) | |||||
| rand_att(1) | |||||
| norm_M(1, 0) | |||||
| norm_P(1, 0) |
| Normalization | Average | ||||
|---|---|---|---|---|---|
| norm_M(3, 1) | |||||
| norm_M(1, 2) | |||||
| norm_M(2, 1) | |||||
| norm_M(3, 3) | |||||
| norm_M(1, 1) | |||||
| norm_M(1, 3) | |||||
| norm_M(10, 3) | |||||
| norm_M(2, 2) | |||||
| rand_att(0.01) | |||||
| rand_att(0.1) | |||||
| norm_M(1, 0) | |||||
| norm_P(1, 0) | |||||
| norm_P(1, 1) | |||||
| rand_att(0.5) | |||||
| norm_P(3, 1) | |||||
| norm_P(1, 3) | |||||
| norm_P(10, 3) | |||||
| rand_att(1) | |||||
| norm_P(3, 3) |
Appendix C. The Effect of the VTF Generator

References
- Dudley, H. Remaking Speech. J. Acoust. Soc. Am. 1939, 11, 169–177. [Google Scholar] [CrossRef]
- Flanagan, J.L.; Golden, R.M. Phase Vocoder. Bell Syst. Tech. J. 1966, 45, 1493–1509. [Google Scholar] [CrossRef]
- McAulay, R.J.; Quatieri, T.F. Speech Analysis-Synthesis Based on a Sinusoidal Representation. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 744–754. [Google Scholar] [CrossRef] [Green Version]
- Moulines, E.; Charpentier, F. Pitch-Synchronous Waveform Processing Techniques for Text-to-Speech Synthesis Using Diphones. Speech Commun. 1990, 9, 453–467. [Google Scholar] [CrossRef]
- Quatieri, T.F.; McAulay, R.J. Shape Invariant Time-Scale and Pitch Modification of Speech. IEEE Trans. Signal Process. 1992, 40, 497–510. [Google Scholar] [CrossRef]
- Kawahara, H.; Masuda-Katsuse, I.; de Cheveigné, A. Restructuring Speech Representations Using a Pitch-Adaptive Time-Frequency Smoothing and an Instantaneous-Frequency-Based F0extraction: Possible Role of a Repetitive Structure in Sounds. Speech Commun. 1999, 27, 187–208. [Google Scholar] [CrossRef]
- Kawahara, H.; Morise, M.; Takahashi, T.; Nisimura, R.; Irino, T.; Banno, H. TANDEM-STRAIGHT: A temporally stable power spectral representation for periodic signals and applications to interference-free spectrum, F0, and aperiodicity estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2008), Las Vegas, USA, 30 March–4 April 2008; pp. 3933–3936. [Google Scholar]
- Zen, H.; Tokuda, K.; Black, A.W. Statistical Parametric Speech Synthesis. Speech Commun. 2009, 51, 1039–1064. [Google Scholar] [CrossRef]
- Röbel, A. Shape-Invariant Speech Transformation with the Phase Vocoder. In Proceedings of the International Conference on Spoken Language Processing (INTERSPEECH 2010), Makuhari, Japan, 26–30 September 2010; pp. 2146–2149. [Google Scholar]
- Degottex, G.; Lanchantin, P.; Roebel, A.; Rodet, X. Mixed Source Model and Its Adapted Vocal-Tract Filter Estimate for Voice Transformation and Synthesis. Speech Commun. 2013, 55, 278–294. [Google Scholar] [CrossRef]
- Morise, M.; Yokomori, F.; Ozawa, K. WORLD: A Vocoder-Based High-Quality Speech Synthesis System for Real-Time Applications. IEICE Trans Inf. Syst. 2016, 99, 1877–1884. [Google Scholar] [CrossRef] [Green Version]
- Markel, J.D.; Gray, A.H. Linear Prediction of Speech; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Fant, G. The Source Filter Concept in Voice Production. STL-QPSR Dept Speech Music Hear. KTH 1981, 22, 21–37. [Google Scholar]
- Rothenberg, M. Acoustic interaction between the glottal source and the vocal tract. In Vocal Fold Physiology; Stevens, K.N., Hirano, M., Eds.; University of Tokyo Press: Tokyo, Japan, 1981; pp. 305–323. [Google Scholar]
- Titze, I.R. Nonlinear Source–Filter Coupling in Phonation: Theory. J. Acoust. Soc. Am. 2008, 123, 1902–1915. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, J.; Pang, R.; Weiss, R.J.; Schuster, M.; Jaitly, N.; Yang, Z.; Chen, Z.; Zhang, Y.; Wang, Y.; Skerrv-Ryan, R.; et al. Natural TTS synthesis by conditioning wavenet on MEL spectrogram predictions. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2018), Calgary, AB, Canada, 15–20 April 2018; pp. 4779–4783. [Google Scholar] [CrossRef] [Green Version]
- van den Oord, A.; Li, Y.; Babuschkin, I.; Simonyan, K.; Vinyals, O.; Kavukcuoglu, K.; van den Driessche, G.; Lockhart, E.; Cobo, L.C.; Stimberg, F.; et al. Parallel WaveNet: Fast High-Fidelity Speech Synthesis. arXiv 2017, arXiv:1711.10433. [Google Scholar]
- Prenger, R.; Valle, R.; Catanzaro, B. Waveglow: A flow-based generative network for speech synthesis. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3617–3621. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Takaki, S.; Yamagishi, J. Neural Source-Filter Waveform Models for Statistical Parametric Speech Synthesis. IEEEACM Trans. Audio Speech Lang. Process. 2020, 28, 402–415. [Google Scholar] [CrossRef]
- Yamamoto, R.; Song, E.; Kim, J.M. Parallel wavegan: A fast waveform generation model based on generative adversarial networks with multi-resolution spectrogram. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2020), Barcelona, Spain, 4–8 May 2020; pp. 6199–6203. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Yang, S.; Liu, K.; Fang, P.; Chen, W.; Xie, L. Multi-band melgan: Faster waveform generation for high-quality text-to-speech. In Proceedings of the 2021 IEEE Spoken Language Technology Workshop (SLT 2021), Shenzhen, China, 19–22 January 2021; pp. 492–498. [Google Scholar] [CrossRef]
- Lorenzo-Trueba, J.; Drugman, T.; Latorre, J.; Merritt, T.; Putrycz, B.; Barra-Chicote, R.; Moinet, A.; Aggarwal, V. Towards Achieving Robust Universal Neural Vocoding. In Proceedings of the 20th Annual Conference of the International Speech Communication Association (INTERSPEECH 2019), Graz, Austria, 15–19 September 2019; pp. 181–185. [Google Scholar] [CrossRef] [Green Version]
- Jang, W.; Lim, D.; Yoon, J. Universal MelGAN: A Robust Neural Vocoder for High-Fidelity Waveform Generation in Multiple Domains. arXiv 2021, arXiv:2011.09631. [Google Scholar]
- Jiao, Y.; Gabryś, A.; Tinchev, G.; Putrycz, B.; Korzekwa, D.; Klimkov, V. Universal neural vocoding with parallel wavenet. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2021), Toronto, ON, Canada, 6–11 June 2021; pp. 6044–6048. [Google Scholar] [CrossRef]
- Ping, W.; Peng, K.; Gibiansky, A.; Arik, S.O.; Kannan, A.; Narang, S.; Raiman, J.; Miller, J. Deep Voice 3: Scaling Text-to-Speech with Convolutional Sequence Learning. arXiv 2018, arXiv:1710.07654. [Google Scholar]
- Zhang, J.X.; Ling, Z.H.; Dai, L.R. Non-Parallel Sequence-to-Sequence Voice Conversion with Disentangled Linguistic and Speaker Representations. IEEEACM Trans. Audio Speech Lang. Process. 2020, 28, 540–552. [Google Scholar] [CrossRef]
- Qian, K.; Zhang, Y.; Chang, S.; Yang, X.; Hasegawa-Johnson, M. AutoVC: Zero-shot voice style transfer with only autoencoder loss. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 5210–5219. [Google Scholar]
- Qian, K.; Zhang, Y.; Chang, S.; Hasegawa-Johnson, M.; Cox, D. Unsupervised speech decomposition via triple Information Bottleneck. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 7836–7846. [Google Scholar]
- Benaroya, L.; Obin, N.; Roebel, A. Beyond Voice Identity Conversion: Manipulating Voice Attributes by Adversarial Learning of Structured Disentangled Representations. arXiv 2021, arXiv:2107.12346. [Google Scholar]
- Desler, A. ‘Il Novello Orfeo’ Farinelli: Vocal Profile, Aesthetics, Rhetoric. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2014. [Google Scholar]
- Lample, G.; Zeghidour, N.; Usunier, N.; Bordes, A.; Denoyer, L.; Ranzato, M. Fader Networks:Manipulating Images by Sliding Attributes. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5967–5976. [Google Scholar]
- He, Z.; Zuo, W.; Kan, M.; Shan, S.; Chen, X. AttGAN: Facial Attribute Editing by Only Changing What You Want. IEEE Trans. Image Process. 2019, 28, 5464–5478. [Google Scholar] [CrossRef] [Green Version]
- Collins, E.; Bala, R.; Price, B.; Susstrunk, S. Editing in style: Uncovering the local semantics of GANs. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5770–5779. [Google Scholar] [CrossRef]
- Engel, J.; Hantrakul, L.; Gu, C.; Roberts, A. DDSP: Differentiable Digital Signal Processing. arXiv 2020, arXiv:2001.04643. [Google Scholar]
- Engel, J.; Hantrakul, L.; Gu, C.; Roberts, A. DDSP Software. Available online: https://github.com/magenta/ddsp (accessed on 22 December 2021).
- Serra, X.J.; Smith, J.O. Spectral Modeling Synthesis: A Sound Analysis/Synthesis System Based on a Deterministic plus Stochastic Decomposition. Comput. Music J. 1990, 14, 12–24. [Google Scholar] [CrossRef]
- Song, E.; Byun, K.; Kang, H.G. ExcitNet vocoder: A neural excitation model for parametric speech synthesis systems. In Proceedings of the 2019 IEEE 27th European Signal Processing Conference (EUSIPCO), Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Juvela, L.; Bollepalli, B.; Tsiaras, V.; Alku, P. GlotNet—A Raw Waveform Model for the Glottal Excitation in Statistical Parametric Speech Synthesis. IEEEACM Trans. Audio Speech Lang. Process. 2019, 27, 1019–1030. [Google Scholar] [CrossRef]
- Juvela, L.; Bollepalli, B.; Yamagishi, J.; Alku, P. GELP: GAN-excited liner prediction for speech synthesis from mel-spectrogram. In Proceedings of the International Speech Communication Association (Interspeech 2019), Graz, Austria, 15–19 September 2019; pp. 694–698. [Google Scholar]
- Oh, S.; Lim, H.; Byun, K.; Hwang, M.J.; Song, E.; Kang, H.G. ExcitGlow: Improving a WaveGlow-based Neural Vocoder with Linear Prediction Analysis. In Proceedings of the IEEE 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 831–836. [Google Scholar]
- Roebel, A.; Bous, F. Towards Universal Neural Vocoding with a Multi-band Excited WaveNet. arXiv 2021, arXiv:2110.03329. [Google Scholar]
- Aitken, A.; Ledig, C.; Theis, L.; Caballero, J.; Wang, Z.; Shi, W. Checkerboard Artifact Free Sub-Pixel Convolution: A Note on Sub-Pixel Convolution, Resize Convolution and Convolution Resize. arXiv 2017, arXiv:1707.02937. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2234–2242. [Google Scholar]
- Van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A generative model for raw audio. In Proceedings of the 9th ISCA Speech Synthesis Workshop, Sunnyvale, CA, USA, 13–15 September 2016; p. 125. [Google Scholar]
- Smith, J.O. Spectral Audio Signal Processing. 2011. Available online: https://ccrma.stanford.edu/~jos/sasp (accessed on 10 May 2021).
- Röbel, A.; Villavicencio, F.; Rodet, X. On Cepstral and All-Pole Based Spectral Envelope Modeling with Unknown Model Order. Pattern Recognit. Lett. Spec. Issue Adv. Pattern Recognit. Speech Audio Process. 2007, 28, 1343–1350. [Google Scholar] [CrossRef]
- Smith, J.O. Introduction to Digital Filters with Audio Applications. 2007. Available online: https://ccrma.stanford.edu/~jos/filters/filters.html (accessed on 10 May 2021).
- Yu, C.; Lu, H.; Hu, N.; Yu, M.; Weng, C.; Xu, K.; Liu, P.; Tuo, D.; Kang, S.; Lei, G. DurIAN: Duration Informed Attention Network for Speech Synthesis. In Proceedings of the 21st Annual Conference of the International Speech Communication Association (INTERSPEECH 2020), Shanghai, China, 25–29 October 2020; pp. 2027–2031. [Google Scholar]
- Lin, Y.P.; Vaidyanathan, P. A Kaiser Window Approach for the Design of Prototype Filters of Cosine Modulated Filterbanks. IEEE Signal Process. Lett. 1998, 5, 132–134. [Google Scholar] [CrossRef] [Green Version]
- Shanker, M.; Hu, M.Y.; Hung, M.S. Effect of Data Standardization on Neural Network Training. Omega 1996, 24, 385–397. [Google Scholar] [CrossRef]
- McFee, B. Librosa—Librosa 0.8.1 Documentation. 2021. Available online: https://librosa.org/doc/latest/index.html#id1 (accessed on 5 October 2021).
- Griffin, D.; Lim, J. Signal Estimation from Modified Short-Time Fourier Transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ito, K.; Johnson, L. The LJ Speech Dataset. 2017. Available online: https://keithito.com/LJ-Speech-Dataset (accessed on 10 May 2021).
- Yamagishi, J.; Veaux, C.; MacDonald, K. CSTR VCTK Corpus: English Multi-Speaker Corpus for CSTR Voice Cloning Toolkit (Version 0.92). 2019. Available online: https://datashare.ed.ac.uk/handle/10283/3443 (accessed on 5 October 2021). [CrossRef]
- Pirker, G.; Wohlmayr, M.; Petrik, S.; Pernkopf, F. A Pitch Tracking Corpus with Evaluation on Multipitch Tracking Scenario. In Proceedings of the 12th Annual Conference of the International Speech Communication Association (INTERSPEECH 2011), Florence, Italy, 27–31 August 2011; pp. 1509–1512. [Google Scholar]
- Le Moine, C.; Obin, N. Att-HACK: An Expressive Speech Database with Social Attitudes. In Proceedings of the 10th International Conference on Speech Prosody, Tokyo, Japan, 25–28 May 2020. [Google Scholar]
- Grammalidis, N.; Dimitropoulos, K.; Tsalakanidou, F.; Kitsikidis, A.; Roussel, P.; Denby, B.; Chawah, P.; Buchman, L.; Dupont, S.; Laraba, S.; et al. The I-treasures intangible cultural heritage dDataset. In Proceedings of the 3rd International Symposium on Movement and Computing, Thessaloniki, Greece, 5–6 July 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Duan, Z.; Fang, H.; Li, B.; Sim, K.C.; Wang, Y. The NUS sung and spoken lyrics corpus: A quantitative comparison of singing and speech. In Proceedings of the 2013 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference, Kaohsiung, Taiwan, 29 October–1 November 2013; pp. 1–9. [Google Scholar]
- Tsirulnik, L.; Dubnov, S. Singing voice database. In Proceedings of the International Conference on Speech and Computer, Istanbul, Turkey, 20–25 August 2019; pp. 501–509. [Google Scholar]
- Koguchi, J.; Takamichi, S.; Morise, M. PJS: Phoneme-balanced Japanese singing-voice corpus. In Proceedings of the 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Auckland, New Zealand, 7–10 December 2020; pp. 487–491. [Google Scholar]
- Tamaru, H.; Takamichi, S.; Tanji, N.; Saruwatari, H. JVS-MuSiC: Japanese Multispeaker Singing-Voice Corpus. arXiv 2020, arXiv:2001.07044. [Google Scholar]
- Ogawa, I.; Morise, M. Tohoku Kiritan Singing Database: A Singing Database for Statistical Parametric Singing Synthesis Using Japanese Pop Songs. Acoust. Sci. Technol. 2021, 42, 140–145. [Google Scholar] [CrossRef]
- Zen, H.; Dang, V.; Clark, R.; Zhang, Y.; Weiss, R.J.; Jia, Y.; Chen, Z.; Wu, Y. LibriTTS: A Corpus Derived from LibriSpeech for Text-to-Speech. arXiv 2019, arXiv:1904.02882. [Google Scholar]
- Ardaillon, L.; Roebel, A. Fully-Convolutional Network for Pitch Estimation of Speech Signals. In Proceedings of the 20th Annual Conference of the International Speech Communication Association (INTERSPEECH 2019), Graz, Austria, 15–19 September 2019; pp. 2005–2009. [Google Scholar] [CrossRef] [Green Version]
- Roebel, A. SuperVP Software. 2015. Available online: http://anasynth.ircam.fr/home/english/software/supervp (accessed on 31 January 2021).
- Huber, S.; Roebel, A. On glottal source shape parameter transformation using a novel deterministic and stochastic speech analysis and synthesis system. In Proceedings of the 16th Annual Conference of the International Speech Communication Association (Interspeech 2015), Dresden, Germany, 6–10 September 2015. [Google Scholar] [CrossRef]
- Rafii, Z.; Liutkus, A.; Stöter, F.R.; Mimilakis, S.; Bittner, R. The MUSDB18 Corpus for Music Separation. 2017. Available online: https://sigsep.github.io/datasets/musdb.html (accessed on 31 January 2021).
- Roebel, A.; Bous, F. MBExWN_Vocoder. 2022. Available online: https://github.com/roebel/MBExWN_Vocoder (accessed on 8 February 2022).
- Yoneyama, R.; Wu, Y.C.; Toda, T. Unified Source-Filter GAN: Unified Source-filter Network Based On Factorization of Quasi-Periodic Parallel WaveGAN. arXiv 2021, arXiv:2104.04668. [Google Scholar]

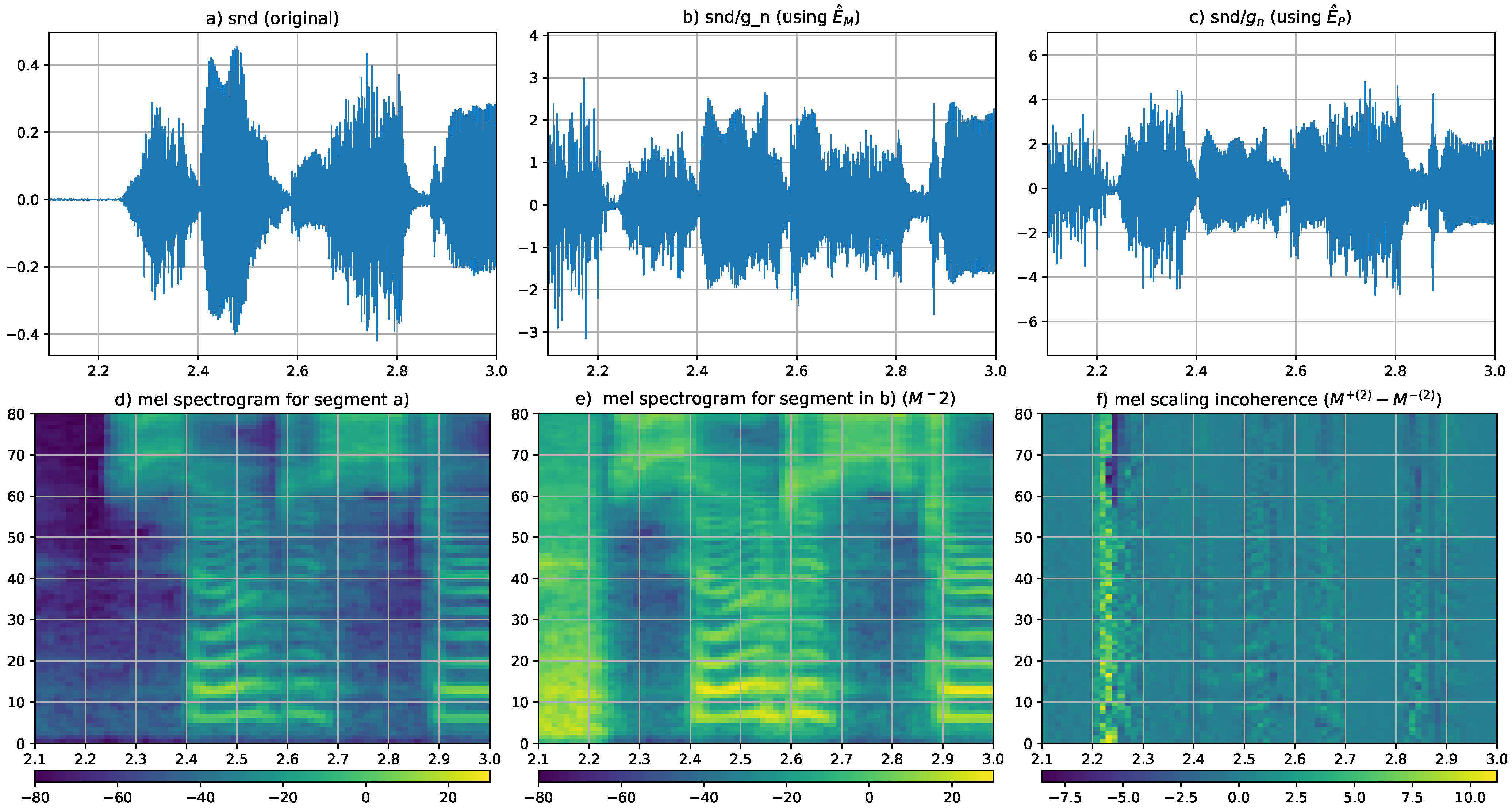

| Diff Measure/Iteration | ||||||
|---|---|---|---|---|---|---|
| Normalization using Equation (17) | ||||||
| [dB] | 1.14 | 0.59 | 0.43 | 0.36 | 0.31 | 0.28 |
| [dB] | 21.70 | 11.15 | 7.23 | 6.03 | 5.56 | 4.91 |
| Normalization using Equation (16) | ||||||
| [dB] | 1.18 | 0.63 | 0.47 | 0.39 | 0.34 | 0.30 |
| [dB] | 20.86 | 8.98 | 6.49 | 5.55 | 4.88 | 4.50 |
| MBExWN Configuration | Mel Error [dB] |
|---|---|
| Default | |
| WT+PQMF | |
| Default-2S | |
| No PQMF | |
| No VTF |
| Data\Model | HREF | MW-SP-FD | MW-SI-FD | MW-VO-FD | MW-VO-FR |
|---|---|---|---|---|---|
| SP | 96 (1.7) | 86 (5.0) | - | 82 (5.9) | 62 (7.4) |
| SI | 95 (1.8) | - | 82 (6.1) | 91 (3.3) | 80 (6.0) |
| Data\Model | HREF | MW-SP-FD | MW-VO-FD | UMG-LJ+LT-FD | MMG-LJ-FD |
|---|---|---|---|---|---|
| LJ | 94 (1.9) | 85 (4.3) | 82 (5.2) | - | 86 (4.1) |
| UMG(LJ) | 93 (3.7) | 86 (6.8) | 77 (11.4) | 80 (10.6) | - |
| UMG(others) | 94 (2.2) | 78 (6.4) | 74 (7.5) | 81 (6.3) | - |
| Data\Model | HREF | MW-SI-FD | MW-VO-FD | MMG-DI-FD |
|---|---|---|---|---|
| DI | 94 (2.7) | 83 (8.4) | 86 (6.2) | 85 (5.5) |
| Pop(MusDB) | 93 (2.7) | 73 (8.3) | 79 (8.1) | - |
| Rough | 96 (2.7) | 60 (12.7) | 68 (11.3) | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roebel, A.; Bous, F. Neural Vocoding for Singing and Speaking Voices with the Multi-Band Excited WaveNet. Information 2022, 13, 103. https://doi.org/10.3390/info13030103
Roebel A, Bous F. Neural Vocoding for Singing and Speaking Voices with the Multi-Band Excited WaveNet. Information. 2022; 13(3):103. https://doi.org/10.3390/info13030103
Chicago/Turabian StyleRoebel, Axel, and Frederik Bous. 2022. "Neural Vocoding for Singing and Speaking Voices with the Multi-Band Excited WaveNet" Information 13, no. 3: 103. https://doi.org/10.3390/info13030103
APA StyleRoebel, A., & Bous, F. (2022). Neural Vocoding for Singing and Speaking Voices with the Multi-Band Excited WaveNet. Information, 13(3), 103. https://doi.org/10.3390/info13030103






