Tuberculosis Bacteria Detection and Counting in Fluorescence Microscopy Images Using a Multi-Stage Deep Learning Pipeline
Abstract
1. Introduction
- We describe a fast method for extracting a new representation of microscopic slides, which enhances the differentiation of bacteria from their background;
- We describe a novel method for the detection of salient, that is, bacteria-containing regions within microscopic slides, which uses cycle-consistent generative adversarial networks to synthesise slides with bounding box annotations;
- We introduce a transfer learning-trained convolutional neural network-based refinement of the list of salient regions detected in the previous step;
- We propose a convolutional neural network-based method for counting bacteria, which appear in highly variable ways, in image patches, using regression as a means of increasing the robustness of the count.
2. Related Work
3. Proposed Method
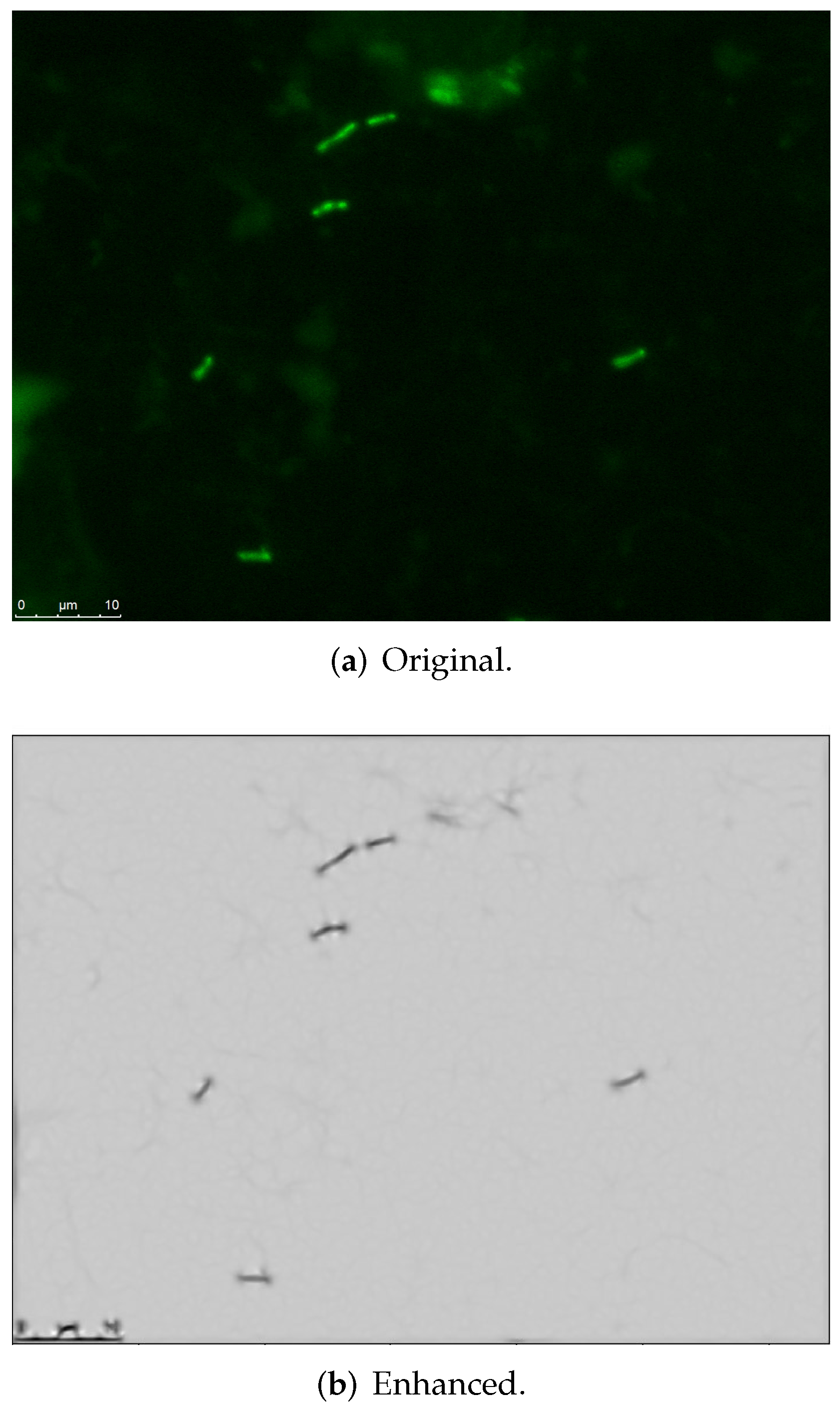
3.1. Image Processing-Based Enhanced Representation Extraction
3.2. Semantic Segmentation Using Cycle-Consistent Adversarial Networks
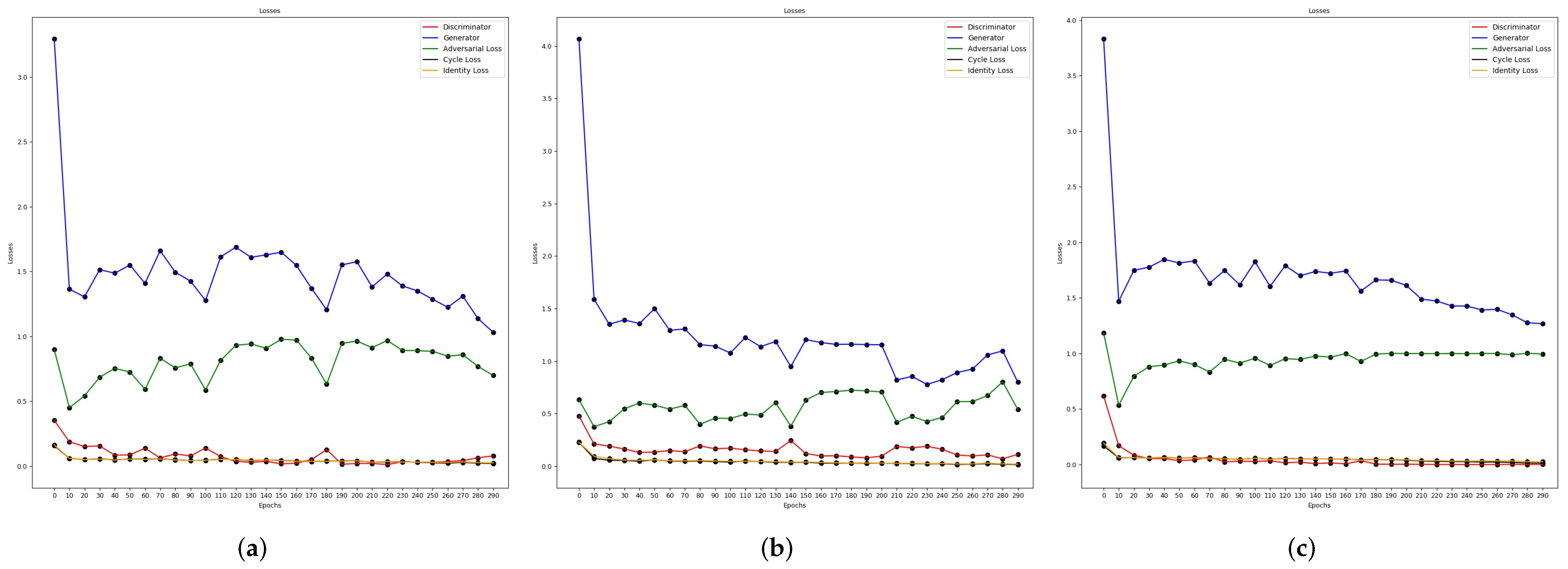
Training the Cycle-Gan
3.3. Extracting Salient Patches from Synthetically Labelled Images
3.4. Classifying Cropped Patches
3.5. Counting Bacteria
4. Experimental Evaluation
4.1. Data Acquisition
4.2. Results
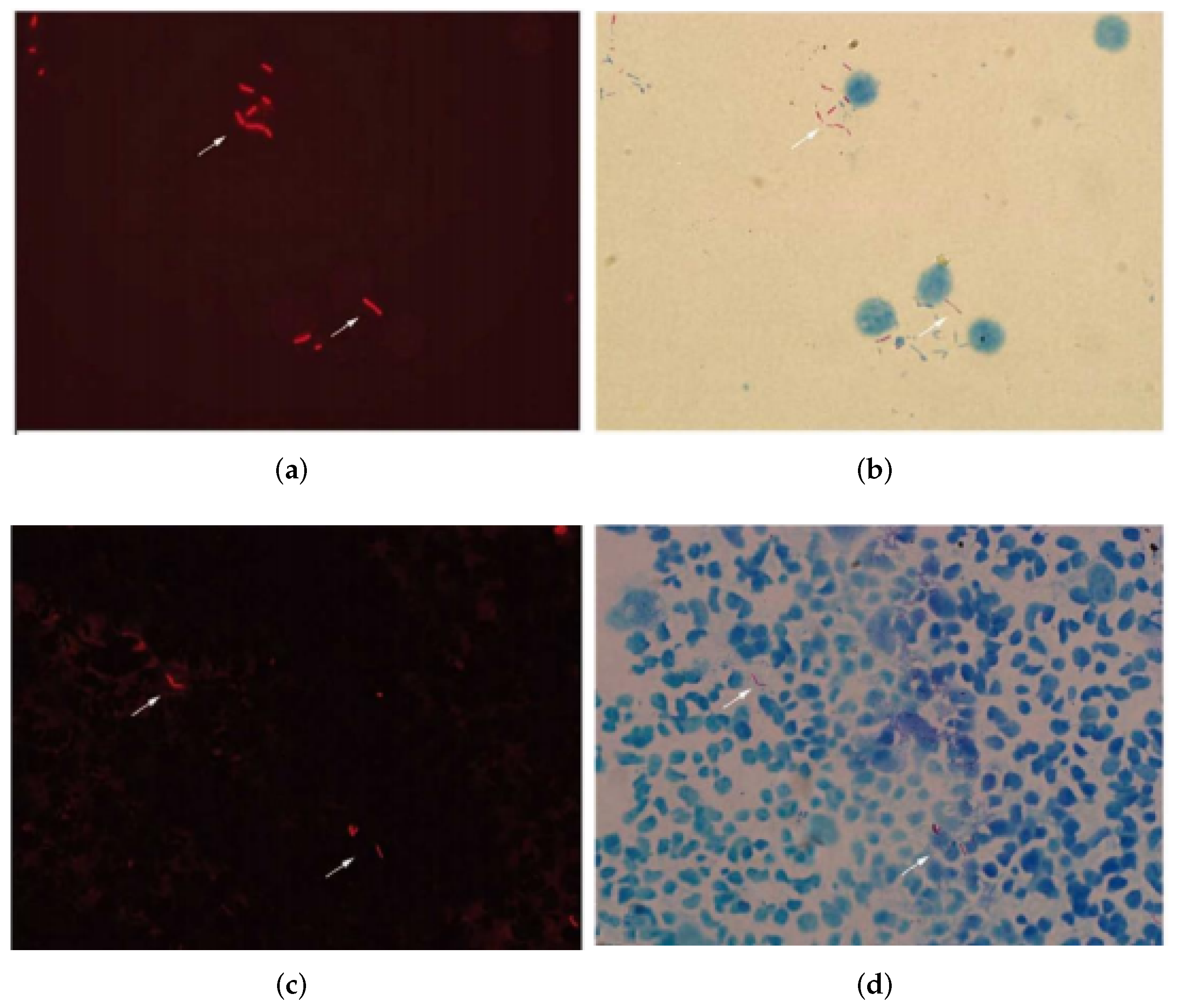
4.2.1. Semantic Segmentation Using Cycle-Gan
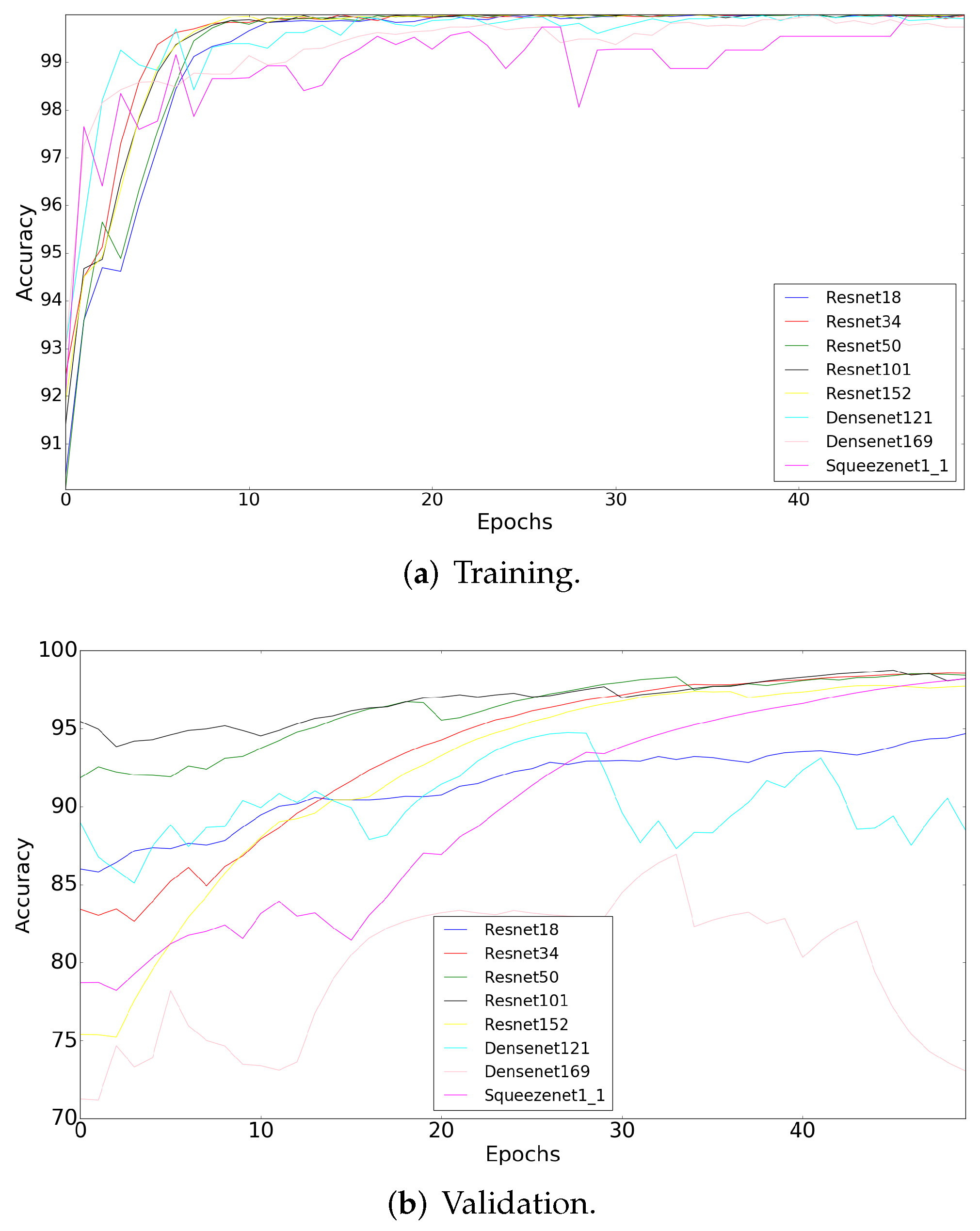
4.2.2. Deep Learning-Based Patch Classification
4.3. Bacterial Count
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daley, C.L. The global fight against tuberculosis. Thorac. Surg. Clin. 2019, 29, 19–25. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Tuberculosis Report; Technical Report; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Zignol, M.; Cabibbe, A.M.; Dean, A.S.; Glaziou, P.; Alikhanova, N.; Ama, C.; Andres, S.; Barbova, A.; Borbe-Reyes, A.; Chin, D.P. Genetic sequencing for surveillance of drug resistance in tuberculosis in highly endemic countries: A multi-country population-based surveillance study. Lancet Infect. Dis. 2018, 18, 675–683. [Google Scholar] [CrossRef]
- Gele, A.A.; Bjune, G.; Abebe, F. Pastoralism and delay in diagnosis of TB in Ethiopia. Lancet Infect. Dis. 2009, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Peter, J.G.; van Zyl-Smit, R.N.; Denkinger, C.M.; Pai, M. Diagnosis of TB: State of the art. Eur. Respir. Monogr. 2012, 58, 123–143. [Google Scholar]
- Hailemariam, M.; Azerefegne, E. Evaluation of Laboratory Professionals on AFB Smear Reading at Hawassa District Health Institutions, Southern Ethiopia. Int. J. Res. Stud. Microbiol. Biotechnol. 2018, 4, 12–19. [Google Scholar]
- Lin, P.L.; Flynn, J.L. The end of the binary era: Revisiting the spectrum of tuberculosis. J. Immunol. 2018, 201, 2541–2548. [Google Scholar] [CrossRef]
- Mehta, P.K.; Raj, A.; Singh, N.; Khuller, G.K. Diagnosis of extrapulmonary tuberculosis by PCR. FEMS Immunol. Med. Microbiol. 2012, 66, 20–36. [Google Scholar] [CrossRef]
- Toman, K. Toman’s Tuberculosis: Case Detection, Treatment and Monitoring. Questions and Answers; World Health Organization: Geneva, Switzerland, 2004. [Google Scholar]
- Aldridge, B.B.; Fernandez-Suarez, M.; Heller, D.; Ambravaneswaran, V.; Irimia, D.; Toner, M.; Fortune, S.M. Asymmetry and Aging of Mycobacterial Cells Lead to Variable Growth and Antibiotic Susceptibility. Science 2012, 335, 100–104. [Google Scholar] [CrossRef]
- Lipworth, S.; Hammond, R.J.; Baron, V.O.; Hu, Y.; Coates, A.; Gillespie, S.H. Defining dormancy in mycobacterial disease. Tuberculosis 2016, 99, 131–142. [Google Scholar] [CrossRef]
- Vente, D.; Arandjelović, O.; Baron, V.O.; Dombay, E.; Gillespie, S.H. Using Machine Learning for Automatic Estimation of M. Smegmatis Cell Count from Fluorescence Microscopy Images. Int. Workshop Health Intell. 2019, 843, 57–68. [Google Scholar] [CrossRef]
- Sloan, D.J.; Mwandumba, H.C.; Garton, N.J.; Khoo, S.H.; Butterworth, A.E.; Allain, T.J.; Heyderman, R.S.; Corbett, E.L.; Barer, M.R.; Davies, G.R. Pharmacodynamic modeling of bacillary elimination rates and detection of bacterial lipid bodies in sputum to predict and understand outcomes in treatment of pulmonary tuberculosis. Clin. Infect. Dis. 2015, 61, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Costa Filho, C.F.F.; Costa, M.G.F.; Júnior, A.K. Autofocus functions for tuberculosis diagnosis with conventional sputum smear microscopy. Curr. Microsc. Contrib. Adv. Sci. Technol. 2012, 1, 13–20. [Google Scholar]
- Steingart, K.R.; Henry, M.; Ng, V.; Hopewell, P.C.; Ramsay, A.; Cunningham, J.; Urbanczik, R.; Perkins, M.; Aziz, M.A.; Pai, M. Fluorescence versus conventional sputum smear microscopy for tuberculosis: A systematic review. Lancet Infect. Dis. 2006, 9, 570–581. [Google Scholar] [CrossRef]
- Zou, Y.; Bu, H.; Guo, L.; Liu, Y.; He, J.; Feng, X. Staining with two observational methods for the diagnosis of tuberculous meningitis. Exp. Ther. Med. 2016, 12, 3934–3940. [Google Scholar] [CrossRef] [PubMed]
- Shea, Y.R.; Davis, J.L.; Huang, L.; Kovacs, J.A.; Masur, H.; Mulindwa, F.; Opus, S.; Chow, Y.; Murray, P.R. High sensitivity and specificity of acid-fast microscopy for diagnosis of pulmonary tuberculosis in an African population with a high prevalence of human immunodeficiency virus. J. Clin. Microbiol. 2009, 47, 1553–1555. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar]
- Suleymanova, I.; Balassa, T.; Tripathi, S.; Molnar, C.; Saarma, M.; Sidorova, Y.; Horvath, P. A deep convolutional neural network approach for astrocyte detection. Sci. Rep. 2018, 8, 12878. [Google Scholar] [CrossRef]
- Panicker, R.O.; Kalmady, K.S.; Rajan, J.; Sabu, M.K. Automatic detection of tuberculosis bacilli from microscopic sputum smear images using deep learning methods. Biocybern. Biomed. Eng. 2018, 38, 691–699. [Google Scholar] [CrossRef]
- Sotaquira, M.; Rueda, L.; Narvaez, R. Detection and quantification of bacilli and clusters present in sputum smear samples: A novel algorithm for pulmonary tuberculosis diagnosis. In Proceedings of the International Conference on Digital Image Processing, Bangkok, Thailand, 7–9 March 2009; pp. 117–121. [Google Scholar]
- Mithra, K.; Emmanuel, W.S. FHDT: Fuzzy and Hyco-entropy-based decision tree classifier for tuberculosis diagnosis from sputum images. Sādhanā 2018, 43, 1–15. [Google Scholar] [CrossRef]
- Daniel Chaves Viquez, K.; Arandjelovic, O.; Blaikie, A.; Ae Hwang, I. Synthesising wider field images from narrow-field retinal video acquired using a low-cost direct ophthalmoscope (Arclight) attached to a smartphone. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 90–98. [Google Scholar]
- Rudzki, M. Vessel detection method based on eigenvalues of the hessian matrix and its applicability to airway tree segmentation. In Proceedings of the 11th International PhD Workshop OWD, Wisla, Poland, 17–20 October 2009; pp. 100–105. [Google Scholar]
- Chi, Y.; Xiong, Z.; Chang, Q.; Li, C.; Sheng, H. Improving Hessian matrix detector for SURF. IEICE Trans. Inf. Syst. 2011, 94, 921–925. [Google Scholar] [CrossRef]
- Dzyubak, O.P.; Ritman, E.L. Automation of hessian-based tubularity measure response function in 3D biomedical images. IEICE Trans. Inf. Syst. 2011, 2011, 920401. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.C.S.; Radhika, Y. Optimized maximum principal curvatures based segmentation of blood vessels from retinal images. Biomed. Res. 2019, 30, 203–206. [Google Scholar] [CrossRef]
- Ghiass, R.S.; Arandjelovic, O.; Bendada, H.; Maldague, X. Vesselness features and the inverse compositional AAM for robust face recognition using thermal IR. In Proceedings of the Twenty-Seventh AAAI Conference on Artificial Intelligence, Washington, DC, USA, 14–18 July 2013. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Wang, S. Generative Adversarial Networks (GAN): A Gentle Introduction. In Tutorial on GAN in LIN395C: Research in Computational Linguistics; University of Texas at Austin: Austin, TX, USA, 2017. [Google Scholar]
- Magister, L.C.; Arandjelović, O. Generative Image Inpainting for Retinal Images using Generative Adversarial Networks. In Proceedings of the 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Mexico City, Mexico, 1–5 November 2021; pp. 2835–2838. [Google Scholar]
- Hjelm, R.D.; Jacob, A.P.; Che, T.; Trischler, A.; Cho, K.; Bengio, Y. Boundary-seeking generative adversarial networks. arXiv 2017, arXiv:1702.08431. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Arandjelović, O. Hallucinating optimal high-dimensional subspaces. Pattern Recognit. 2014, 47, 2662–2672. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Li, C.; Wand, M. Precomputed real-time texture synthesis with markovian generative adversarial networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 702–716. [Google Scholar]
- Zachariou, M.; Dimitriou, N.; Arandjelović, O. Visual reconstruction of ancient coins using cycle-consistent generative adversarial networks. Science 2020, 2, 52. [Google Scholar] [CrossRef]
- Gadermayr, M.; Gupta, L.; Klinkhammer, B.M.; Boor, P.; Merhof, D. Unsupervisedly training GANs for segmenting digital pathology with automatically generated annotations. arXiv 2018, arXiv:1805.10059. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Zhuang, J.; Tang, T.; Ding, Y.; Tatikonda, S.C.; Dvornek, N.; Papademetris, X.; Duncan, J. Adabelief optimizer: Adapting stepsizes by the belief in observed gradients. Adv. Neural Inf. Process. Syst. 2020, 33, 18795–18806. [Google Scholar]
- Yue, X.; Dimitriou, N.; Arandjelovic, O. Colorectal cancer outcome prediction from H&E whole slide images using machine learning and automatically inferred phenotype profiles. arXiv 2019, arXiv:1902.03582. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- He, D.; Xia, Y.; Qin, T.; Wang, L.; Yu, N.; Liu, T.Y.; Ma, W.Y. Dual learning for machine translation. Adv. Neural Inf. Process. Syst. 2016, 29, 820–828. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Cooper, J.; Um, I.H.; Arandjelović, O.; Harrison, D.J. Hoechst Is All You Need: Lymphocyte Classification with Deep Learning. arXiv 2021, arXiv:2107.04388. [Google Scholar]
- Newell, A. A Tutorial on Speech Understanding Systems. Speech Recognit. 1975, 29, 4–54. [Google Scholar]
- Beykikhoshk, A.; Arandjelović, O.; Phung, D.; Venkatesh, S. Overcoming data scarcity of Twitter: Using tweets as bootstrap with application to autism-related topic content analysis. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 25–28 August 2015; pp. 1354–1361. [Google Scholar]
- Guindon, B.; Zhang, Y. Application of the dice coefficient to accuracy assessment of object-based image classification. Can. J. Remote. Sens. 2017, 43, 48–61. [Google Scholar] [CrossRef]
- Veropoulos, K.; Learmonth, G.; Campbell, C.; Knight, B.; Simpson, J. Automated identification of tubercle bacilli in sputum: A preliminary investigation. Can. J. Remote Sens. 1999, 21, 277–282. [Google Scholar]
- Forero, M.G.; Sroubek, F.; Cristóbal, G. Identification of tuberculosis bacteria based on shape and color. Real-Time Imaging 2004, 10, 251–262. [Google Scholar] [CrossRef]
- Kant, S.; Srivastava, M.M. Towards automated tuberculosis detection using deep learning. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Bangalore, India, 18–21 November 2018; pp. 1250–1253. [Google Scholar]
- Zhai, Y.; Liu, Y.; Zhou, D.; Liu, S. Automatic identification of mycobacterium tuberculosis from ZN-stained sputum smear: Algorithm and system design. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Tianjin, China, 14–18 December 2010; pp. 41–46. [Google Scholar]
- Ghosh, P.; Bhattacharjee, D.; Nasipuri, M. A hybrid approach to diagnosis of tuberculosis from sputum. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques, Chennai, India, 3–5 March 2016; pp. 771–776. [Google Scholar]




| Layer | Kernel Size | Strides | Padding |
|---|---|---|---|
| Layer 1 | 3 × 3 | 2 | 3 |
| Layer 2 | 3 × 3 | 1 | 1 |
| Layer 3 | 3 × 3 | 1 | 1 |
| Layer 4 | 3 × 3 | 3 | 1 |
| Layer 5 | 3 × 3 | 2 | 1 |
| Model | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| ResNet18 | 97.28% | 0.974 | 0.949 | 0.961 |
| ResNet34 | 99.35% | 0.970 | 0.951 | 0.960 |
| ResNet50 | 99.74% | 0.990 | 0.967 | 0.960 |
| ResNet101 | 99.61% | 0.983 | 0.958 | 0.970 |
| ResNet152 | 99.48% | 0.980 | 0.954 | 0.967 |
| DenseNet121 | 95.20% | 0.952 | 0.928 | 0.939 |
| DenseNet169 | 88.41% | 0.900 | 0.849 | 0.874 |
| SqueezeNet | 99.38% | 0.980 | 0.958 | 0.969 |
| Model | Test Count (Ground Truth ) | MSE | Training MAE | R |
|---|---|---|---|---|
| ResNet18 | 394 | 0.0054 | 0.0345 | 0.006439 |
| ResNet34 | 407 | 0.0444 | 0.0457 | 0.006506 |
| ResNet50 | 414 | 0.0457 | 0.0425 | 0.006523 |
| ResNet101 | 431 | 0.0253 | 0.0236 | 0.000656 |
| ResNet152 | 496 | 0.0231 | 0.0201 | 0.000095 |
| DenseNet121 | 575 | 0.0104 | 0.0603 | 0.000345 |
| DenseNet169 | 667 | 0.0086 | 0.0406 | 0.000356 |
| SqueezeNet1_1 | 404 | 0.0082 | 0.0227 | 0.006571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zachariou, M.; Arandjelović, O.; Sabiiti, W.; Mtafya, B.; Sloan, D. Tuberculosis Bacteria Detection and Counting in Fluorescence Microscopy Images Using a Multi-Stage Deep Learning Pipeline. Information 2022, 13, 96. https://doi.org/10.3390/info13020096
Zachariou M, Arandjelović O, Sabiiti W, Mtafya B, Sloan D. Tuberculosis Bacteria Detection and Counting in Fluorescence Microscopy Images Using a Multi-Stage Deep Learning Pipeline. Information. 2022; 13(2):96. https://doi.org/10.3390/info13020096
Chicago/Turabian StyleZachariou, Marios, Ognjen Arandjelović, Wilber Sabiiti, Bariki Mtafya, and Derek Sloan. 2022. "Tuberculosis Bacteria Detection and Counting in Fluorescence Microscopy Images Using a Multi-Stage Deep Learning Pipeline" Information 13, no. 2: 96. https://doi.org/10.3390/info13020096
APA StyleZachariou, M., Arandjelović, O., Sabiiti, W., Mtafya, B., & Sloan, D. (2022). Tuberculosis Bacteria Detection and Counting in Fluorescence Microscopy Images Using a Multi-Stage Deep Learning Pipeline. Information, 13(2), 96. https://doi.org/10.3390/info13020096







