Abstract
This paper presents the fsmpy Python library for the implementation of any type of measures and comparisons of different types of fuzzy sets, as well as other important and useful utilities and algorithms. In this paper, we analyze the motivation behind its implementation, the design principles followed, the implemented modules of the library and its capabilities, considering intuitionistic fuzzy sets as the case study. Lastly, some examples of its application to widely used pattern recognition, medical diagnosis and image segmentation are presented.
1. Introduction
Fuzzy Sets (FSs) were initially introduced in 1965 by Zadeh [1], with a number of new orders of FSs being introduced over the years and many successful applications in various fields. With the introduction of intuitionistic fuzzy sets (IFSs) by Antanassov [2], a generalization of the traditional mathematical framework of FSs, they found application in image segmentation [3,4] and preprocessing [5], decision making [6,7,8] and pattern recognition [9].
The main characteristic of IFSs are the expression of the degree of membership (membership value–belongingness) and the degree of non-membership (non-membership value–non-belongingness) for elements of a universe through functions. A notable notion in the literature is that of vague sets, proposed by Gau and Buehrer [10], which, as pointed out by Bustince and Burillo [11], are identified as IFSs. Other extensions of IFS theory were proposed, such as intuitionistic trapezoidal fuzzy multi-numbers [12] or fuzzy soft expert sets [13] defining basic union operations.
With the introduction of IFS theory and their application to the aforementioned fields, appropriate measures that compare the information carried by two IFSs needed to be defined. Consequently, many studies in the literature proposed different types of measures, with the most notable types being that of a distance [14,15,16] and similarity [17,18,19], with the literature having a greater focus on the latter. This can also be highlighted by the reviews conducted through the years, for example [20,21,22], showing a great interest in the field and the need for the definition of appropriate measures.
From the above, the recognition of the importance of this field and the studies that were conducted for the definition of such measures should be highlighted. With the continuing growth of the field and the proposition of even more measures, along with the research that depends on such measures, the development of a library that implements those measures, as well as the general application of the IFSs theory, becomes very important. There are many examples in the literature that show the growth a field can experience through the release of such a library (following the open-source paradigm), with some famous examples being those of Tensorflow [23] and PyTorch [24] for deep learning, or OpenCV [25] for computer vision.
There are numerous libraries and tools available in the literature, with each one focusing on different parts of the FS theory. Fuzzy-rough-learn [26] builds upon the scikit-learn [27] library to allow the user to apply machine learning with fuzzy rough sets, providing numerous preprocessors, classifiers, data descriptors and other functionalities. Fuzzycreator [28] implements some useful tools for the generation of fuzzy sets from the data, their visualization, the representation of fuzzy sets (Interval/General Type 2 and other) and the calculation of different types of membership values. Despite this, the number of implemented measures and types of measures are very small, and, to date, the toolkit itself has not received any important updates. Lastly, S. Topal et al. [29,30] presented a Python tool on Bipolar Neutrosophic Matrices that helps with the operations of such matrices, which can also be applied on fuzzy matrices.
Despite the useful tools existing in the literature, there are not any available that focus extensively on the implementation of fuzzy measures, an important aspect of FS theory and its application in other disciplines. Therefore, this paper introduces fsmpy, a Python library that follows the open-source paradigm and both functional and object-oriented programming, exploiting the performance of the NumPy [31] library. Fsmpy implements both distance and similarity measures that have been proposed in the literature. The library also provides utility functions and objects for the application of other required processes in classification problems, such as an estimator compatible with the well-known library scikit-learn. The library aims to facilitate in the practical application of FS measures and their extension and application in other fields.
2. Design Overview
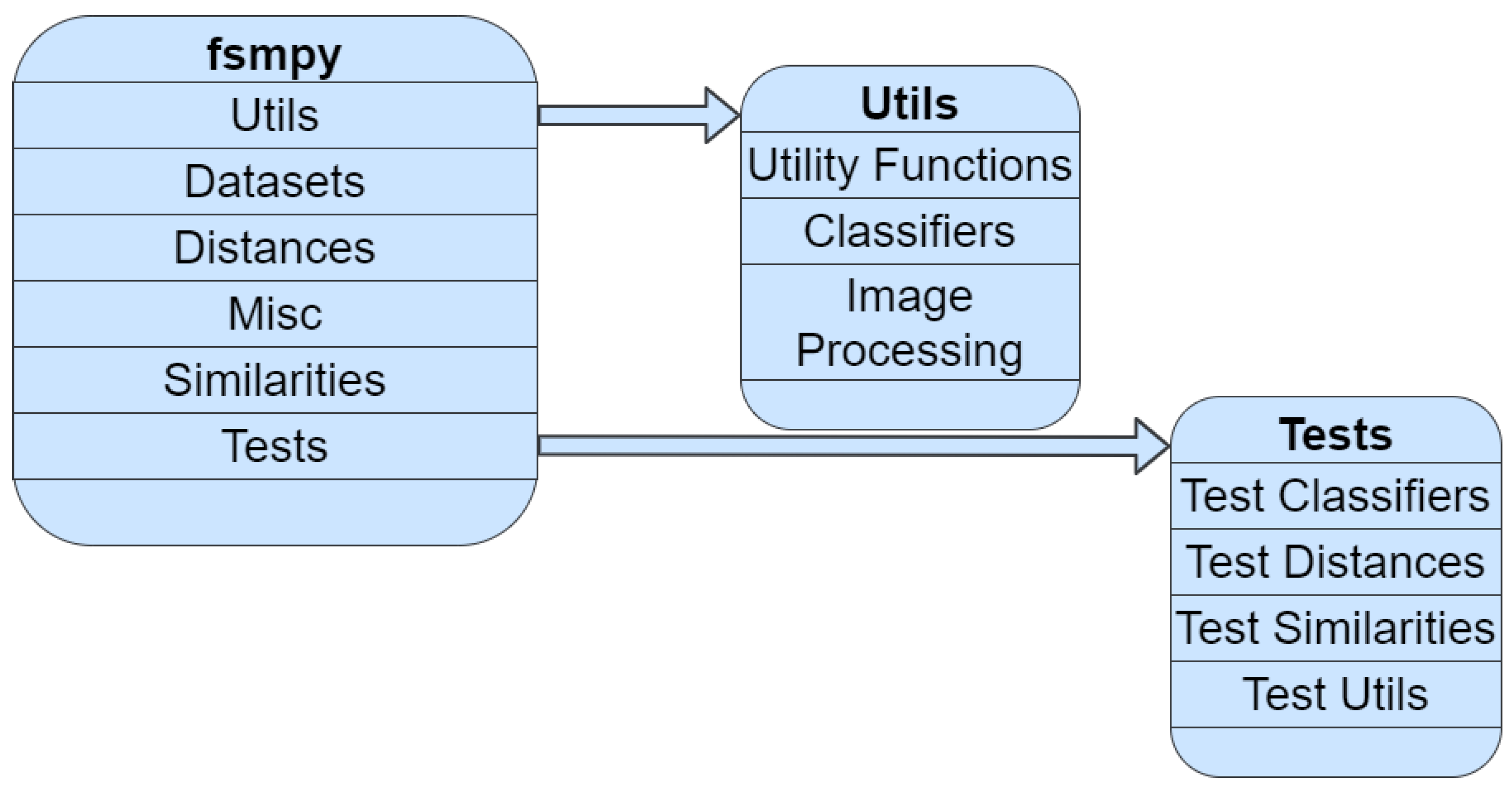
In this section, we demonstrate the overall architecture of fsmpy, which is divided into three modules: the Main, Utils and Tests modules. For better presentation, Figure 1 shows an outline of the library’s modules and sub-packages.
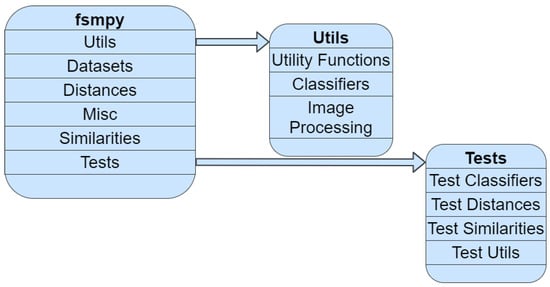
Figure 1.
Library outline with its modules and sub-packages.
2.1. Main Module
The main module consists of the distances, similarities and miscellaneous measures, the datasets and the sets files. The measures files contain all the measures that were analyzed in the comparative study conducted by G.A. Papakostas et al. [20], with some additional similarities from studies [32,33,34,35,36,37,38]. For now, the miscellaneous measures consist of the Fuzzy Divergence, proposed by J. Fan and W. Xie [39], and the Index of Fuzziness proposed by T. Chaira and A. Ray [3].
For the representation of an FS or IFS, the fuzzy set and intuitionistic fuzzy set objects were implemented, which are extensively used in the library for any process requiring them. As for the datasets module, it contains data from a medical diagnosis dataset, which is commonly used in the literature for the comparison of the performance of a proposed IFS measure. Of course, with the continuous work conducted on the library, more measures, types of measures and fuzzy sets and datasets will be added.
In Table 1, Table 2 and Table 3, we show the main features of the methods that are implemented in the library. The first two columns refer to the name of the authors of each function and the corresponding name of the method that implements it. The third column shows the parameters, other than the two fuzzy sets A and B, required by the functions in order to calculate the corresponding measure. The types of these parameters are analyzed in the documentation. In the fourth column, we show the name of the function that the authors use in the original paper to mathematically describe the functions.

Table 1.
Features of similarity methods applied.

Table 2.
Features of distance methods applied.

Table 3.
Features of miscellaneous methods applied.
2.2. Utils Module
In this module, some very useful tools were implemented, including a classifier object, that included classifiers for several classification tasks. To date, a text classifier has been developed, which follows the methodology proposed by P. Intarapaiboon [54]. Furthermore, in this module, a function for the calculation of the degree of confidence is provided, a widely used performance index factor proposed by A. Hatzimichailidis et al. [55].
As Python has already become a very popular and widely used programming language in the scientific field, the development of novel IFS measures is being undertaken. For this reason, the proposed library provides a function that performs the appropriate checks to validate if a similarity measure, , satisfies the following defined properties:
- ;
- ;
- .
with and being two IFSs.
2.3. Tests Module
The majority of the proposed measures in the literature present the results obtained from their application in specific examples. By using those examples and results, appropriate test functions were implemented that verify the correct implementation of the corresponding measure.
3. Applications
In this section, the application of the proposed library is presented in different fields, specifically: medical diagnosis, text classification and image segmentation. The examples used in all the applications presented in the following subsections are widely used in the literature, to showcase the performance of a fuzzy measure. Through those examples, the usability of the library is highlighted.
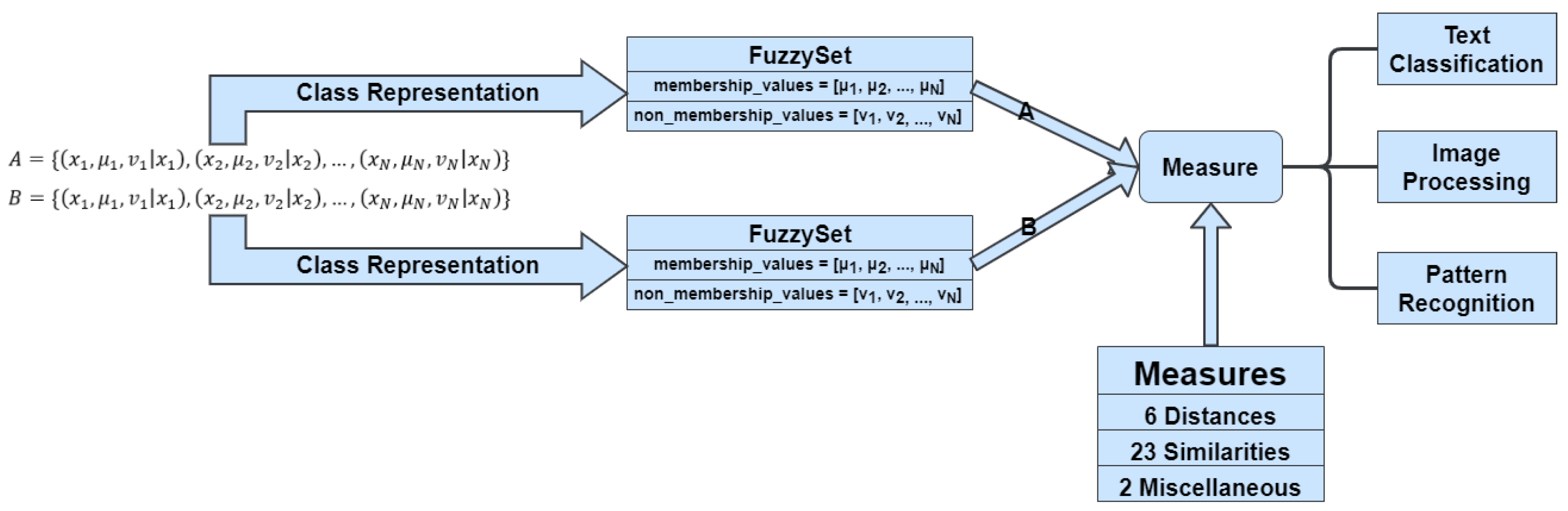
Figure 2 shows a high-level process diagram of the library, highlighting the representation of the fuzzy sets inside the library, while also showing when and where the fuzzy measures can be applied.
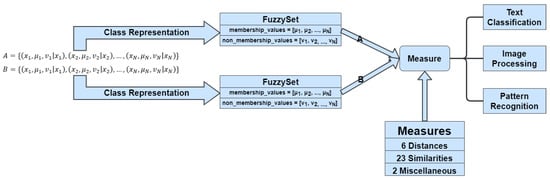
Figure 2.
High-level process diagram of the fsmpy library.
3.1. Medical Diagnosis
The application of IFSs in medical diagnosis has been considered by quite a few studies in the literature. In this application example, the data used in many studies was utilized. The data consist of a set of 4 patients (), 6 diagnoses () and 5 symptoms (). The sets are defined as follows:
- ;
- ;
- .
The aforementioned data are represented using the IFS theory, with a membership and non-membership value representing each characteristic of a diagnosis and each symptom of a patient. Table 4 shows the characteristics of each diagnosis and Table 5 shows each patient’s symptoms, where each element consists of the membership and non-membership values of the corresponding case as .

Table 4.
Symptom characteristics for each diagnosis.

Table 5.
Symptom characteristics for each patient.
To find the correct diagnosis for each patient, the fuzzy measure between the sets of a patient’s symptoms and that of a diagnosis’ characteristics has to be calculated. Depending on the type of measure that is applied, the correct diagnosis is determined according to the minimum distance or the maximum similarity between the two sets.
In general, to classify a sample set to a specific class, given the class patterns, the presented library provides a function. This function allows the user to classify a sample set by using a single line of the code, with its parameters being the patterns of each class, the sample’s patterns, the measure to be used, its parameters and if the measure provided is a distance or not.
Therefore, by using the aforementioned function, we classified each patient’s symptoms to their corresponding diagnosis, with Table 6 showing the results. As the aim of this study was not to compare the measures that were included in the library; however, to showcase its usability, we used the Euclidean distance between two IFSs, proposed by Atanassov [2]. Along with the predicted diagnosis, the degree of confidence was also provided (rounded to two decimals). Algorithm 1 shows the pseudo-code steps that are followed to classify each patient’s symptoms and to obtain the degree of confidence of each prediction.

Table 6.
Predicted diagnosis for each patient’s symptoms along with the degree of confidence of each prediction.
3.2. Text Classification
Text classification using IFS theory was also considered by a few studies. In this example, two popular news datasets [56] (BBC and BBCSport) were used, constructed from a total of 2225 news articles, belonging to 5 topical areas.
As mentioned in the previous section, the text classification classifier follows the methodology proposed by P. Intarapaiboon [54], and so the same preprocessing steps are applied to the datasets as well. Thus, 9635 words are obtained for each article, with the BBCSport dataset containing 737 articles on 5 areas and each article is represented by the frequency of 4613 words. For the sake of space and simplicity, the similarity measure used for the classification process is the one proposed by Z. Liang and P. Shi [47], and the membership and non-membership weights ( and ) were set to 1.
Thus, similar results to the ones in [54] were obtained (Table 7). With the classifier object that is provided by fsmpy, the user can easily use it for text classification and choose any measure provided by the library (or a personally developed one). Additionally, as mentioned in Section 2.2, by following the estimator implementation of the scikit-learn library, the user can easily connect the classifier object with the grid search algorithm provided by the aforementioned library, to find the best parameters for any chosen measure. To highlight this feature, we applied the grid search over a fixed set of parameter values, obtaining better results.
| Algorithm 1. Pseudo-code of the classification algorithm implemented in fsmpy. |
| Input: class_patterns, sample_pattern, measure_caller, is_distance = True, return_confidence = False, **kwargs Output: prediction[confidence_degree] |
| measures = [] |
| for class_pattern in class_patterns do |
| measure = measure_caller(sample_pattern, class_pattern, **kwargs) |
| measure = measure * (is_distance == True ? 1: −1) |
| measures.append(measure) |
| end for |
| prediction = index_of_min(measures) |
| min_measure = measures[prediction] |
| other_measures = measures.remove_at(prediction) |
| if return_confidence == True then |
| return prediction, confidence_degree(min_measure, other_measures) |
| else |
| return prediction |
| end if |

Table 7.
Parameter optimization.
3.3. Image Segmentation
Another common application of IFSs is in image segmentation. The implemented algorithm follows the methodology proposed by T. Chaira [3] (and extended by I. Vlachos and G. Sergiadis [16]), which aims to minimize the fuzzy divergence between the calculated fuzzy set of the segmented image (for a threshold value, ) and the ideally segmented image (membership values equal to 1).
The proposed library provides a number of grayscale images that are widely used in the literature, for example the rice image, along with the corresponding ground truth segmented image for result evaluation. Figure 3 shows the results after applying the segmentation algorithm with different distance and similarity measures.

Figure 3.
Segmentation results on the rice image. (a) Original image; (b) ground truth segmentation; (c) fuzzy divergence; (d) Liang and Shi’s similarity measure and (e) Vlachos Sergiadis’ intuitionistic counterpart.
Again, the aim of the result’s showcase is not to compare the performance of the implemented measures, but to present the library’s usability and features. Therefore, to segment a given image, , the user only needs to call the function provided by the utils module. This function takes as its parameters the image to be segmented, the measure to be calculated, the measure’s parameters (if needed) and if the measure provided is a distance measure or not.
4. Availability
Fsmpy will be available at https://github.com/MachineLearningVisionRG/fsmpy (accessed on 19 January 2022), under the 3-Clause BSD license. Along with the source code, examples of the use of the above applications are available, as well as the basic usage examples. With the introduction and release of this library, we hope the scientific community not only make use of the provided functionality and measures, but also contribute to the library by extending and improving its functionalities and adding more intuitionistic fuzzy measures.
5. Conclusions
In this study, we presented a novel Python library named fsmpy, for comparing the fuzzy sets of different types. The library provides the implementation of a number of different distances, the similarity and other types of measures, along with other useful tools required for their implementation and application. By following the implementation designs of other libraries, fmpy becomes fast, easy to use and easy to interconnect with other libraries, such as scikit-learn and NumPy.
Compared to other available toolkits and libraries, fsmpy implements a large number of different fuzzy measures. Moreover, it provides tools for their application in different classification problems and their interconnection with other libraries. It is the first library to present very simple functionalities for different applications (medical diagnosis, text classification and image segmentation). With the open-source paradigm, the library can be extended with additional measures, types of measures and types of FSs, as well as more datasets, classifiers and membership value calculation functions.
At this point, some of the library’s limitations should be discussed. Firstly, there are some tests for the validation of the correct implementation of a measure that fail. This is currently being addressed with a high priority, but can also be attributed to the typographic errors in the publication of the original measure. Similarly, the results obtained in the image segmentation application are not exactly the same as the ones presented in [16]. Secondly, a very small number of types of fuzzy sets and miscellaneous functions are implemented, and only one evaluation dataset is provided (medical diagnosis). Lastly, when compared to the Fuzzycreator library (a very similar one), fsmpy currently lacks of any visualization functionalities and implements only one membership calculation function.
As for the future works, the aims focus on solving the aforementioned limitations, as well as the following aspects:
- Implementation of additional measures (distance, similarity and other types), classifiers and membership value calculation functions.
- Further study of the implemented measures and their tests.
- Additional tools useful for the development of novel measures (such as the testing of theorems).
- Extension of library application and utility functions.
Author Contributions
Conceptualization, G.A.P. and G.K.S.; methodology, G.K.S. and K.D.A.; software, G.K.S., K.D.A. and N.D.; validation, G.K.S., K.D.A. and N.D.; investigation, G.K.S. and K.D.A.; writing—original draft preparation, G.K.S. and K.D.A.; writing—review and editing, G.K.S. and G.A.P.; visualization, G.K.S.; supervision, G.A.P.; project administration, G.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the MPhil program “Advanced Technologies in Informatics and Computers”, hosted by the Department of Computer Science, International Hellenic University, Kavala, Greece.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Chaira, T.; Ray, A.K. Threshold Selection Using Fuzzy Set Theory. Pattern Recognit. Lett. 2004, 25, 865–874. [Google Scholar] [CrossRef]
- Bouchet, A.; Montes, S.; Ballarin, V.; Díaz, I. Intuitionistic Fuzzy Set and Fuzzy Mathematical Morphology Applied to Color Leukocytes Segmentation. SIViP 2020, 14, 557–564. [Google Scholar] [CrossRef]
- Chaira, T. Intuitionistic Fuzzy Approach for Enhancement of Low Contrast Mammogram Images. Int. J. Imaging Syst. Technol. 2020, 30, 1162–1172. [Google Scholar] [CrossRef]
- Pei, Z.; Zheng, L. A Novel Approach to Multi-Attribute Decision Making Based on Intuitionistic Fuzzy Sets. Expert Syst. Appl. 2012, 39, 2560–2566. [Google Scholar] [CrossRef]
- Stanujkić, D.; Karabašević, D. An Extension of the WASPAS Method for Decision-Making Problems with Intuitionistic Fuzzy Numbers: A Case of Website Evaluation. Oper. Res. Eng. Sci. Theor. Appl. 2019, 1, 29–39. [Google Scholar] [CrossRef]
- Şahïn, M.; Uluçay, V. Fuzzy Soft Expert Graphs with Application. Asian J. Math. Comput. Res. 2019, 26, 216–229. [Google Scholar]
- Baccour, L.; Kanoun, S.; Märgner, V.; Alimi, A. An Application of Intuitionistic Fuzzy Information for Handwritten Arabic Word Recognition. In Proceedings of the 12th International Conference on IFSs (NIFS08), Sofia, Bulgaria, 17–18 May 2008. [Google Scholar]
- Gau, W.-L.; Buehrer, D.J. Vague Sets. IEEE Trans. Syst. Man. Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague Sets Are Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Uluçay, V.; Deli, I.; Şahin, M. Intuitionistic Trapezoidal Fuzzy Multi-Numbers and Its Application to Multi-Criteria Decision-Making Problems. Complex Intell. Syst. 2019, 5, 65–78. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R. Fuzzy Soft Expert Set and Its Application. AM 2014, 05, 1349–1368. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distances between Intuitionistic Fuzzy Sets and/or Interval-Valued Fuzzy Sets Based on the Hausdorff Metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic Fuzzy Information—Applications to Pattern Recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Hong, D.H.; Kim, C. A Note on Similarity Measures between Vague Sets and between Elements. Inf. Sci. 1999, 115, 83–96. [Google Scholar] [CrossRef]
- Dengfeng, L.; Chuntian, C. New Similarity Measures of Intuitionistic Fuzzy Sets and Application to Pattern Recognitions. Pattern Recognit. Lett. 2002, 23, 221–225. [Google Scholar] [CrossRef]
- Mitchell, H.B. On the Dengfeng–Chuntian Similarity Measure and Its Application to Pattern Recognition. Pattern Recognit. Lett. 2003, 24, 3101–3104. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Hatzimichailidis, A.G.; Kaburlasos, V.G. Distance and Similarity Measures between Intuitionistic Fuzzy Sets: A Comparative Analysis from a Pattern Recognition Point of View. Pattern Recognit. Lett. 2013, 34, 1609–1622. [Google Scholar] [CrossRef]
- Atanassov, K.T. Review and New Results on Intuitionistic Fuzzy Sets. Int. J. Bioautomation 2016, 20, S17–S26. [Google Scholar]
- Kahraman, C.; Oztaysi, B.; Onar, S.C.; Otay, I. A Literature Review on the Extensions of Intuitionistic Fuzzy Sets. In Proceedings of the Developments of Artificial Intelligence Technologies in Computation and Robotics, Cologne, Germany, 18–21 August 2020; World Scientific: Cologne, Germany, 2020; pp. 199–207. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Naveenkumar, M.; Vadivel, A. OpenCV for Computer Vision Applications. In Proceedings of the National Conference on Big Data and Cloud Computing (NCBDC’15), Jeju Island, Korea, 9–11 February 2015; pp. 52–56. [Google Scholar]
- Lenz, O.U.; Peralta, D.; Cornelis, C. Fuzzy-Rough-Learn 0.1: A Python Library for Machine Learning with Fuzzy Rough Sets. In Rough Sets; Bello, R., Miao, D., Falcon, R., Nakata, M., Rosete, A., Ciucci, D., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12179, pp. 491–499. ISBN 978-3-030-52704-4. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar]
- McCulloch, J. Fuzzycreator: A Python-Based Toolkit for Automatically Generating and Analysing Data-Driven Fuzzy Sets. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9 July 2017; pp. 1–6. [Google Scholar]
- Topal, S.; Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F. A Python Tool for Implementations on Bipolar Neutrosophic Matrices; Zenodo: Genève, Switzerland, 2019. [Google Scholar] [CrossRef]
- Broumi, S.; Topal, S.; Bakali, A.; Talea, M.; Smarandache, F. A Novel Python Toolbox for Single and Interval-Valued Neutrosophic Matrices: In Advances in Logistics, Operations, and Management Science; Abdel-Basset, M., Smarandache, F., Eds.; IGI Global: Hershey, PA, USA, 2020; pp. 281–330. ISBN 978-1-79982-555-5. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.; Jiang, Y.; Fu, J. Monotonic Similarity Measures between Intuitionistic Fuzzy Sets and Their Relationship with Entropy and Inclusion Measure. Inf. Sci. 2015, 316, 348–369. [Google Scholar] [CrossRef]
- Iancu, I. Intuitionistic Fuzzy Similarity Measures Based on Frank T-Norms Family. Pattern Recognit. Lett. 2014, 42, 128–136. [Google Scholar] [CrossRef]
- Muthukumar, P.; Sai Sundara Krishnan, G. A Similarity Measure of Intuitionistic Fuzzy Soft Sets and Its Application in Medical Diagnosis. Appl. Soft Comput. 2016, 41, 148–156. [Google Scholar] [CrossRef]
- Nguyen, H. A Novel Similarity/Dissimilarity Measure for Intuitionistic Fuzzy Sets and Its Application in Pattern Recognition. Expert Syst. Appl. 2016, 45, 97–107. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xue, A. A Novel Similarity Measure on Intuitionistic Fuzzy Sets with Its Applications. Appl. Intell. 2015, 42, 252–261. [Google Scholar] [CrossRef]
- Chen, S.-M.; Cheng, S.-H.; Lan, T.-C. A Novel Similarity Measure between Intuitionistic Fuzzy Sets Based on the Centroid Points of Transformed Fuzzy Numbers with Applications to Pattern Recognition. Inf. Sci. 2016, 343–344, 15–40. [Google Scholar] [CrossRef]
- Intarapaiboon, P. A Hierarchy-Based Similarity Measure for Intuitionistic Fuzzy Sets. Soft Comput. 2016, 20, 1909–1919. [Google Scholar] [CrossRef]
- Fan, J.; Xie, W. Distance Measure and Induced Fuzzy Entropy. Fuzzy Sets Syst. 1999, 104, 305–314. [Google Scholar] [CrossRef]
- Shyi-Ming Chen Measures of Similarity between Vague Sets. Fuzzy Sets Syst. 1995, 74, 217–223. [CrossRef]
- Shyi-Ming Chen Similarity Measures between Vague Sets and between Elements. IEEE Trans. Syst. Man Cybern. B 1997, 27, 153–158. [CrossRef] [PubMed]
- Hung, W.-L.; Yang, M.-S. Similarity Measures of Intuitionistic Fuzzy Sets Based on Hausdorff Distance. Pattern Recognit. Lett. 2004, 25, 1603–1611. [Google Scholar] [CrossRef]
- Hung, W.-L.; Yang, M.-S. On the J-Divergence of Intuitionistic Fuzzy Sets with Its Application to Pattern Recognition. Inf. Sci. 2008, 178, 1641–1650. [Google Scholar] [CrossRef]
- Hung, W.-L.; Yang, M.-S. On Similarity Measures between Intuitionistic Fuzzy Sets. Int. J. Intell. Syst. 2008, 23, 364–383. [Google Scholar] [CrossRef]
- Hung, W.-L.; Yang, M.-S. Similarity Measures of Intuitionistic Fuzzy Sets Based on Lp Metric. Int. J. Approx. Reason. 2007, 46, 120–136. [Google Scholar] [CrossRef]
- Hwang, C.-M.; Yang, M.-S. Modified Cosine Similarity Measure between Intuitionistic Fuzzy Sets. In Artificial Intelligence and Computational Intelligence; Lei, J., Wang, F.L., Deng, H., Miao, D., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7530, pp. 285–293. ISBN 978-3-642-33477-1. [Google Scholar]
- Liang, Z.; Shi, P. Similarity Measures on Intuitionistic Fuzzy Sets. Pattern Recognit. Lett. 2003, 24, 2687–2693. [Google Scholar] [CrossRef]
- Liu, H.-W. New Similarity Measures between Intuitionistic Fuzzy Sets and between Elements. Math. Comput. Model. 2005, 42, 61–70. [Google Scholar] [CrossRef]
- Julian, P.; Hung, K.-C.; Lin, S.-J. On the Mitchell Similarity Measure and Its Application to Pattern Recognition. Pattern Recognit. Lett. 2012, 33, 1219–1223. [Google Scholar] [CrossRef]
- Ye, J. Cosine Similarity Measures for Intuitionistic Fuzzy Sets and Their Applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H. Similarity Measures on Three Kinds of Fuzzy Sets. Pattern Recognit. Lett. 2006, 27, 1307–1317. [Google Scholar] [CrossRef]
- Wang, W.; Xin, X. Distance Measure between Intuitionistic Fuzzy Sets. Pattern Recognit. Lett. 2005, 26, 2063–2069. [Google Scholar] [CrossRef]
- Yang, Y.; Chiclana, F. Consistency of 2D and 3D Distances of Intuitionistic Fuzzy Sets. Expert Syst. Appl. 2012, 39, 8665–8670. [Google Scholar] [CrossRef]
- Intarapaiboon, P. Text Classification Using Similarity Measures on Intuitionistic Fuzzy Sets. ScienceAsia 2016, 42, 52. [Google Scholar] [CrossRef][Green Version]
- Hatzimichailidis, A.G.; Papakostas, G.A.; Kaburlasos, V.G. A Novel Distance Measure of Intuitionistic Fuzzy Sets and Its Application to Pattern Recognition Problems. Int. J. Intell. Syst. 2012, 27, 396–409. [Google Scholar] [CrossRef]
- Greene, D.; Cunningham, P. Producing Accurate Interpretable Clusters from High-Dimensional Data. In Knowledge Discovery in Databases: PKDD 2005; Jorge, A.M., Torgo, L., Brazdil, P., Camacho, R., Gama, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3721, pp. 486–494. ISBN 978-3-540-29244-9. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).