Realizing Mathematics of Arrays Operations as Custom Architecture Hardware-Software Co-Design Solutions
Abstract
1. Introduction
2. Mathematics of Arrays Principles and Application
2.1. Why a New Theory of Arrays?
Existing array theories and compiler optimizations on array loops, are proper subsets of MoA. All of NumPy’s array and tensor operations can be formulated in MoA. In MoA one algorithm, thus, one circuit, describes the Hadamard Product, Matrix Product, Kronecker Product, and Reductions(Contractions) versus four. Consequently less circuitry, power, and energy.
2.2. The Simplicity of MoA: Shapes and the Psi Function
Scalar operations are at the heart of computation, , and in general for n-d arrays, , where f is an arbitrary scalar function.
That is, indexing distributes over scalar operations, or in compiler optimization terms, loop fusion.
This means, with an array’s shape, , generate an array of indices, . Then, using that array as an argument to Psi, the original array ξ, is returned.
2.3. Why MoA Inner and Outer Products?
2.4. Examples: MM, KP and, HP
General Algorithms: Kronecker: FFT and Wavelets
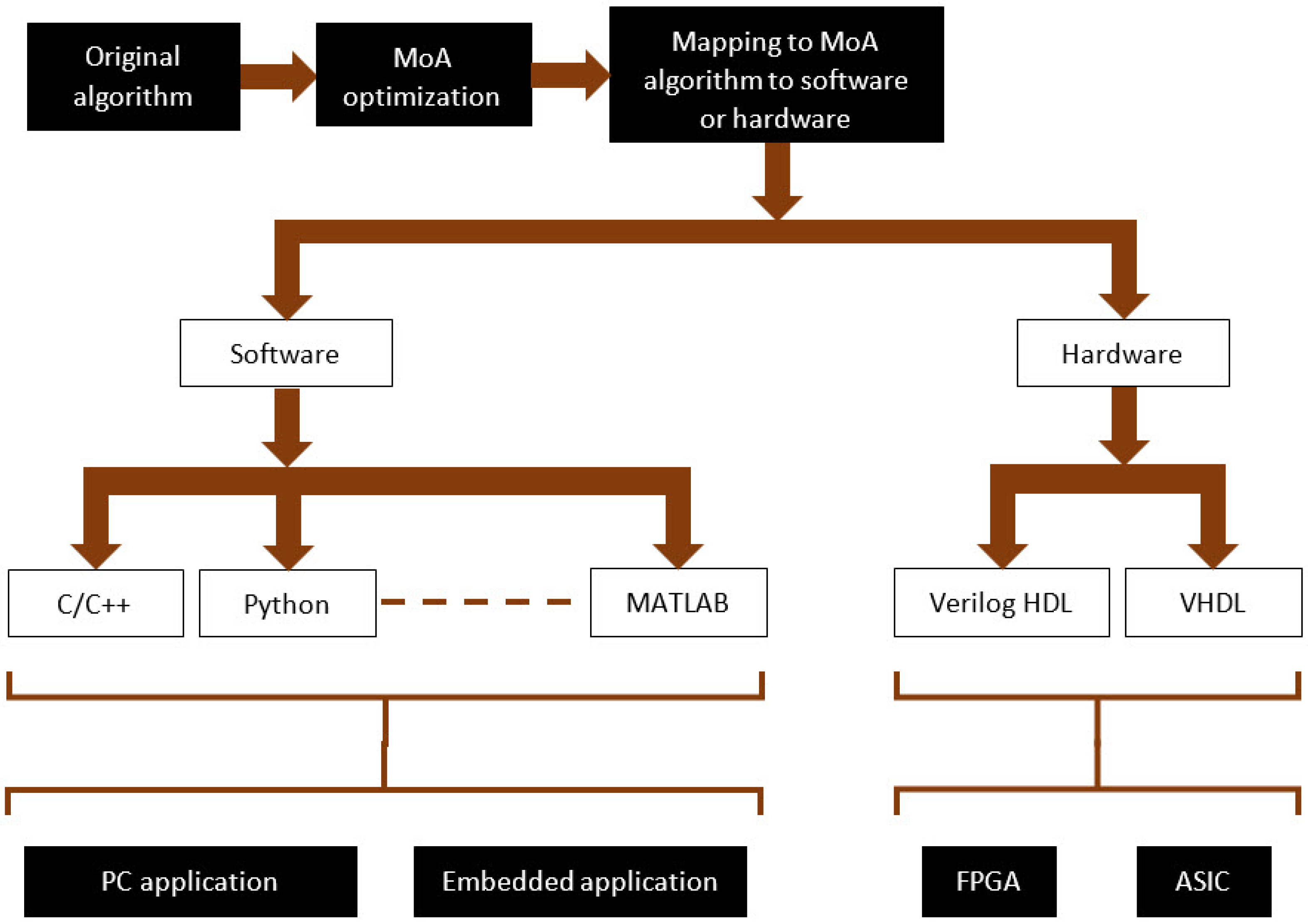
3. Digital Systems Design Using Field Programmable Gate Array and Application Specific Integrated Circuit Technologies
- 1.
- Software programmed processor. A standard processor architecture based on the CPU, GPU or TPU would be used (or created as a custom architecture processor) with the aim to run a suitable software program. This could target a PC application or an embedded (system) application. The selection of the processor and overall system would need to be based on the target application, whether it is aimed at general-purpose or application-specific needs. The ability to initially program and then re-program the system operation multiple times by changing the software program would be an integral part of the system functionality. Typically, C and C++ programs are created. Whilst predefined processor architectures may be suitable for many applications, it may be necessary to consider modifying an available processor architecture to improve performance. For example, in ref. [40], ten reasons for optimizing a processor are presented.
- 2.
- Field Programmable Gate Array (FPGA). The FPGA is a programmable device that consists of programmable hardware and programmable interconnect. This allows a digital system design to be developed and programmed (configured) into memory within the FPGA that controls the programmable parts of the device. Devices available today allow for designs to be created as hardware only designs or hardware-software co-designs where one or more processors can be embedded into the device. Typically, Verilog HDL and VHDL (VHSIC (Very High Speed Integrated Circuit) HDL) are used to describe the hardware (logic and memory), and C and C++ programs are created to run on the embedded processor(s). This allows for low-cost entry into digital system design and fast design prototyping as well as for creating the final system where applicable.
- 3.
- Application Specific Integrated Circuit (ASIC). Here, the designer creates an IC design to implement the required circuits functions. This allows for the most efficient design to be created (circuitry used, performance and power consumption), but would be a high cost approach where low volumes are produced. However, the ASIC approach becomes cost effective when high volume production is considered. Typically, Verilog HDL and VHDL are used to describe the digital hardware (logic and memory). Either one HDL only or both HDLs may be utilized in a design project for describing both the design modules and simulation testfixture modules.
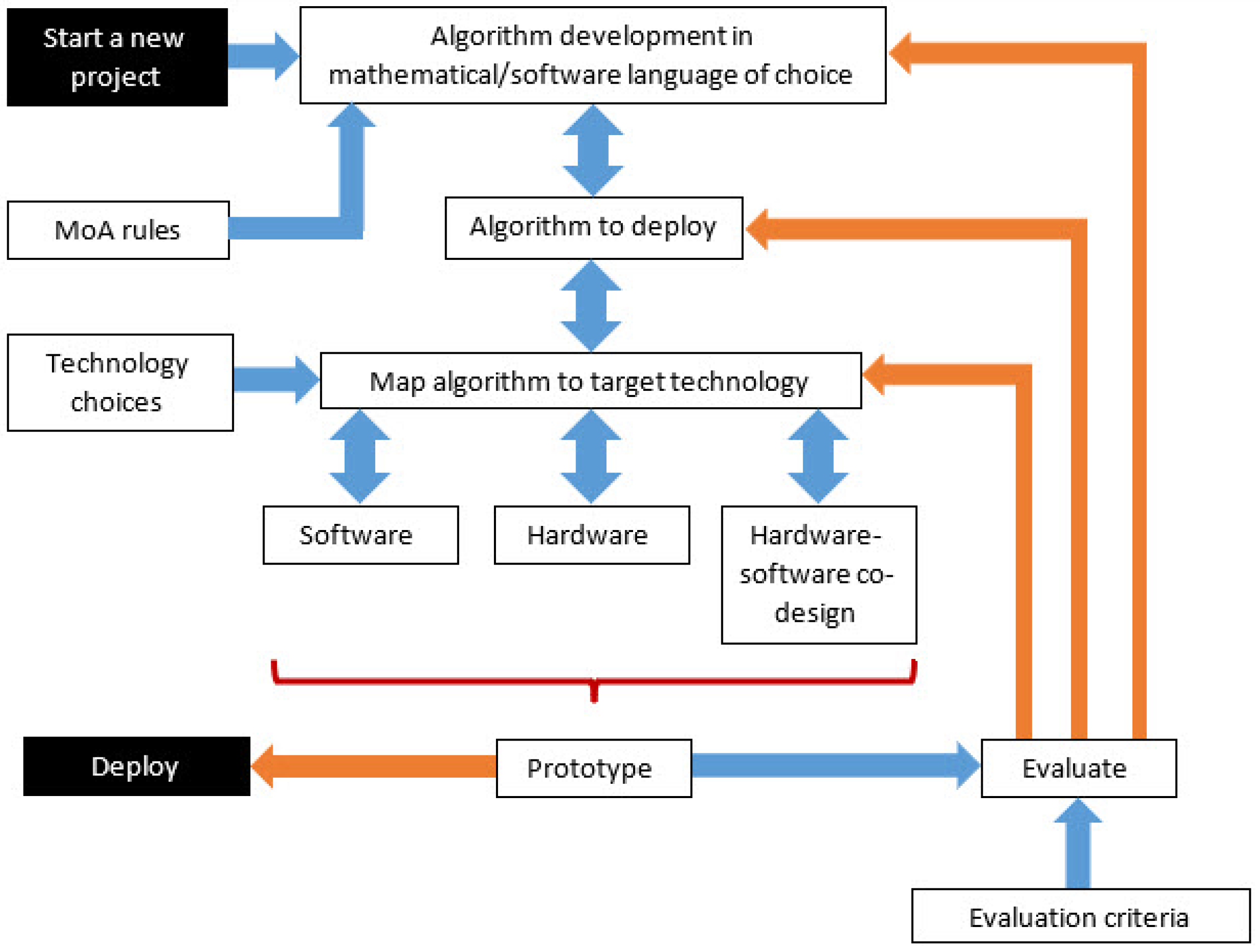
4. Mapping MoA Algorithms to Software and Hardware
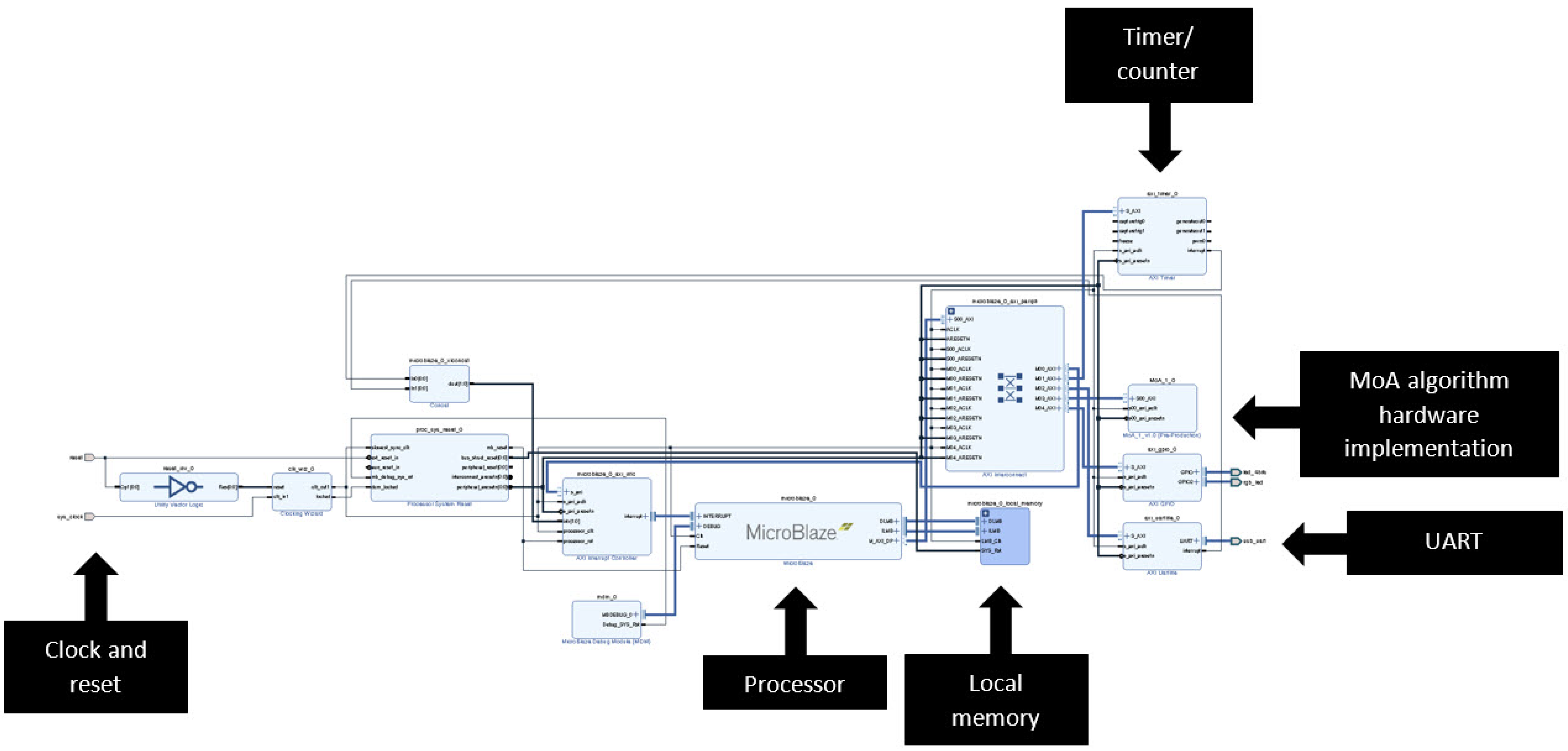
5. Case Study Design
- Matrix multiplication (np.matmul).
- Element-by-element multiplication, the Hadamard Product (np.multiply).
- Tensor Outer Product (np.outer).
- Kronecker Product (np.kron).
5.1. Python with NumPy
5.2. MoA Definitions
- NumPy’s definition of Hadamard Product, np.multiply, is simply MoA’s definition of scalar operations on n-d arrays, e.g., product. In MoA:
- NumPy’s definition of outer product, np.outer is defined in MoA as follows and is simply a reshaping of MoA’s shape to NumPy’s, in this case to :
- NumPy’s definition of the Kronecker Product, np.kron, is the same as MoA. However, like the matrix multiplication, accesses all arrays contiguously, then at the end permutes them to their reshaped locations. This is particularly important with multiple Kronecker Products [28].
5.3. Small Example of Psi Reduction to DNF, ONF, and Generic Program
- (1)
- Psi Reduce to DNF:
- (a)
- Get the Shape:By definition, shapes must be conformable. So the shape of must be equivalent to the shape of b and the shapes of a and b must be the same.
- (b)
- Get the Components: Here the Psi function is used because layout of the arrays does not matter. Psi Reduction is applied based on the definitions to compose the indices to it’s DNF, or semantic normal form, the least amount of computation AND memory needed to perform the operations. With the shape we have the bounds of indices i and j:Now use the Psi function to Psi Reduce to the DNF:In order to turn the DNF to ONF, layout of the arrays in memory is needed. Assume a and b are layout in row major order. A family of gamma functions, i.e., layout functions that map indices to their offset in memory exist. For this example is used. Gamma takes an index and a shape.
- (2)
- Get the ONF:rav is a function that flattens an array based on layout. Bracket notation is now used to illustrate the building phase of design:This is the ONF.
- (3)
- Generic Program:Finally, using standard notation for the generic program letting C to denote the result, and A and B to denote a and b.This is the Generic Program and illustrates the process of going from a high level mathematical specification in NumPy formulated in MoA, Psi Reduced to the DNF, ONF and finally to a generic program.
5.4. Returning to the Python Example
Example
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ASIC | Application Specific Integrated Circuit |
| CPU | Central Processing Unit |
| CR | Church-Rosser |
| DGEMM | Double-precision, GEneral Matrix-matrix Multiplication |
| DL | Deep Learning |
| DMA | Direct Memory Access |
| DNF | Denotational Normal Form |
| FFT | Fast Fourier Transform |
| FPGA | Field Programmable Gate Array |
| GEMM | GEneral Matrix-matrix Multiplication |
| GPU | Graphics Processing Unit |
| HDL | Hardware Description Language |
| HP | Hadamard Product |
| IP | Intellectual Property |
| ISR(s) | Interrupt Service Routine(s) |
| KP | Kronecker Product |
| KR | Khatri-Rao |
| LU | LU Decomposition |
| ML | Machine Learning |
| MM | Matrix Multiplication |
| MoA | Mathematics of Arrays |
| ONF | Operational Normal Form |
| OS(es) | Operating System(s) |
| PC | Personal Computer |
| PIM | Processing in Memory |
| QR | QR Decomposition |
| RISC | Reduced Instruction Set Computer |
| RMA | Remote Memory Access |
| RNN(s) | Recurrent Neural Network(s) |
| RTOS | Real-Time Operating System |
| TPU | Tensor Processing Unit |
| UART | Universal Asynchronous Receiver Transmitter |
| USB | Universal Serial Bus |
| VHDL | VHSIC (Very High Speed Integrated Circuit) HDL |
References
- Google. TensorFlow. 2022. Available online: https://www.tensorflow.org (accessed on 1 September 2022).
- Ahmad Shawahna, S.M.S.; El-Maleh, A. FPGA-Based Accelerators of Deep Learning Networks for Learning and Classification: A Review. IEEE Access 2018, 7, 7823–7859. [Google Scholar] [CrossRef]
- Intel Corporation. Intel(C) Core(TM) Processor Family. 2022. Available online: https://www.intel.co.uk/content/www/uk/en/products/details/processors/core.html (accessed on 1 September 2022).
- NVIDIA Corporation. NVIDIA Technologies. 2022. Available online: https://www.nvidia.com/en-us/technologies/ (accessed on 1 September 2022).
- Google. Cloud TPU. 2022. Available online: https://cloud.google.com/tpu/ (accessed on 1 September 2022).
- Advanced Micro Devices, Inc. FPGAs & 3D ICs. 2022. Available online: https://www.xilinx.com/products/silicon-devices/fpga.html (accessed on 1 September 2022).
- Arm Limited. Whitepaper: Lowering the barriers to entry for ASICs. 2022. Available online: https://community.arm.com/designstart/b/blog/posts/whitepaper-lowering-the-barriers-to-entry-for-asics (accessed on 1 September 2022).
- Mullin, L.M.R. A Mathematics of Arrays. Ph.D. Thesis, Syracuse University, Syracuse, NY, USA, 1988. [Google Scholar]
- Python. 2022. Available online: https://www.python.org/ (accessed on 1 September 2022).
- ISO/IEC 9899:2018; Information Technology—Programming Languages—C. International Organization for Standardization (ISO): Geneva, Switzerland, 2022. Available online: https://www.iso.org/standard/74528.html (accessed on 1 September 2022).
- Institute of Electrical and Electronics Engineers (IEEE). 1364-2005—IEEE Standard for Verilog Hardware Description Language. 2022. Available online: https://ieeexplore.ieee.org/document/1620780 (accessed on 1 September 2022).
- Xilinx. Artix 7. 2022. Available online: https://www.xilinx.com/products/silicon-devices/fpga/artix-7.html (accessed on 1 September 2022).
- Wolfe, M. Performant, Portable, and Productive Parallel Programming with Standard Languages. Comput. Sci. Eng. 2021, 23, 39–45. [Google Scholar] [CrossRef]
- Thomas, S.; Mullin, L.; Świrydowicz, K.; Khan, R. Threaded Multi-Core GEMM with MoA and Cache-Blocking. In Proceedings of the 2021 World Congress in Computer Science, CSCE’21, Las Vegas, NV, USA, 26–29 July 2021. [Google Scholar]
- Thomas, S.; Mullin, L.; Świrydowicz, K. Improving the Performance of DGEMM with MoA and Cache-Blocking. In Proceedings of the Array 2021, ACM, Online, 20–26 June 2021. [Google Scholar]
- NumPy. NumPy. 2022. Available online: https://numpy.org/ (accessed on 1 September 2022).
- Xilinx. MicroBlaze Soft Processor Core. 2022. Available online: https://www.xilinx.com/products/design-tools/microblaze.html (accessed on 1 September 2022).
- Hunt, H.B.; Mullin, L.R.; Rosenkrantz, D.J.; Raynolds, J.E. A Transformation–Based Approach for the Design of Parallel/Distributed Scientific Software: The FFT. arXiv 2008, arXiv:cs.SE/0811.2535. [Google Scholar]
- Mullin, L.; Phan, W. A Transformational Approach to Scientific Software: The Mathematics of Arrays (MoA) FFT with OpenACC. In Proceedings of the OpenACC Summit 2021, Remote Event, 14–15 September 2021. [Google Scholar]
- Mullin, L.; Thibault, S. A Reduction Semantics for Array Expressions: The Psi Compiler; Technical Report, CSC-94-05; University Missouri-Rolla: Rolla, MO, USA, 1994. [Google Scholar]
- Ostrouchov, C.; Mullin, L. PythonMoA. Available online: https://labs.quansight.org/blog/2019/04/python-moa-tensor-compiler/ (accessed on 1 September 2022).
- Gibbons, J. (Ed.) Proceedings of the 6th ACM SIGPLAN International Workshop on Libraries, Languages and Compilers for Array Programming, ARRAY@PLDI 2019, Phoenix, AZ, USA, June 22, 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Chetioui, B.; Abusdal, O.; Haveraaen, M.; Järvi, J.; Mullin, L. Padding in the Mathematics of Arrays. In Proceedings of the 8th ACM SIGPLAN International Workshop on Libraries, Languages and Compilers for Array Programming, Virtual Event, 21 June 2021. [Google Scholar]
- Chetioui, B.; Larney, M.K.; Jarvi, J.; Haveraaen, M.; Mullin, L. P3 Problem and Magnolia Language: Specializing Array Computations for Emerging Architectures. Front. Comput. Sci. Sect. Softw. 2022. to appear. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, F. On the Kronecker Products and Their Applications. J. Appl. Math. 2013, 2013, 296185. [Google Scholar] [CrossRef]
- Acar, A.; Anandkumar, A.; Mullin, L.; Rusitschka, S.; Tresp, V. Tensor Computing for Internet of Things (Dagstuhl Perspectives Workshop 16152). Dagstuhl Rep. 2016, 6, 57–79. [Google Scholar] [CrossRef]
- Thakker, U.; Beu, J.G.; Gope, D.; Zhou, C.; Fedorov, I.; Dasika, G.; Mattina, M. Compressing RNNs for IoT devices by 15-38x using Kronecker Products. arXiv 2019, arXiv:1906.02876. [Google Scholar]
- Mullin, L.R.; Raynolds, J.E. Scalable, Portable, Verifiable Kronecker Products on Multi-scale Computers. In Constraint Programming and Decision Making; Ceberio, M., Kreinovich, V., Eds.; Springer: Cham, Switzerland, 2014; Volume 539, pp. 111–129. [Google Scholar] [CrossRef]
- Gustafson, J.; Mullin, L. Tensors Come of Age: Why the AI Revolution Will Help HPC. arXiv 2017, arXiv:1709.09108. [Google Scholar]
- Mullin, L.R. A uniform way of reasoning about array-based computation in radar: Algebraically connecting the hardware/software boundary. Digit. Signal Process. 2005, 15, 466–520. [Google Scholar] [CrossRef]
- Mullin, L.R.; Raynolds, J.E. Conformal Computing: Algebraically connecting the hardware/software boundary using a uniform approach to high-performance computation for software and hardware applications. arXiv 2008, arXiv:0803.2386. [Google Scholar]
- Chetioui, B.; Mullin, L.; Abusdal, O.; Haveraaen, M.; Järvi, J.; Macià, S. Finite difference methods fengshui: Alignment through a mathematics of arrays. In Proceedings of the 6th ACM SIGPLAN International Workshop on Libraries, Languages and Compilers for Array Programming, Phoenix, AZ, USA, 22 June 2019. [Google Scholar]
- Berkling, K. Arrays and the Lambda Calculus; Technical Report 93; SU-CIS-90-22; Syracuse University: Syracuse, NY, USA, 1990. [Google Scholar]
- Iverson, K.E. A Programming Language; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1962. [Google Scholar] [CrossRef]
- Abrams, P.S. An APL Machine. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1970. [Google Scholar]
- Grout, I.; Mullin, L. Hardware Considerations for Tensor Implementation and Analysis Using the Field Programmable Gate Array. Electronics 2018, 7, 320. [Google Scholar] [CrossRef]
- Grout, I.; Mullin, L. Realization of the Kronecker Product in VHDL using Multi-Dimensional Arrays. In Proceedings of the 2019 7th International Electrical Engineering Congress (iEECON), Cha-am, Thailand, 6–8 March 2019. [Google Scholar] [CrossRef]
- Mullin, L.M.R.; Jenkins, M.A. Effective data parallel computation using the Psi calculus. Concurr. Pract. Exp. 1996, 8, 499–515. [Google Scholar] [CrossRef]
- Anandkumar, A. Role of Tensors in Machine Learning. Available online: https://developer.download.nvidia.com/video/gputechconf/gtc/2019/presentation/s9733-role-of-tensors-in-machine-learning.pdf (accessed on 1 September 2022).
- Cadence Design Systems, Inc. Ten Reasons to Optimize a Processor. 2022. Available online: https://ip.cadence.com/uploads/770/TIP_WP_10Reasons_Customize_FINAL-pdf (accessed on 1 September 2022).

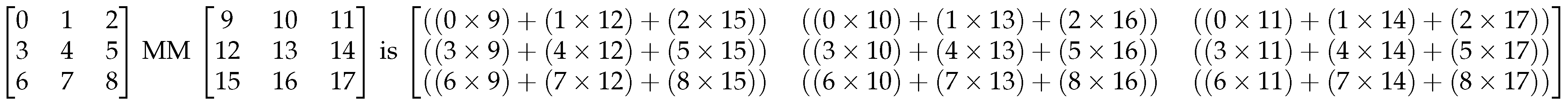





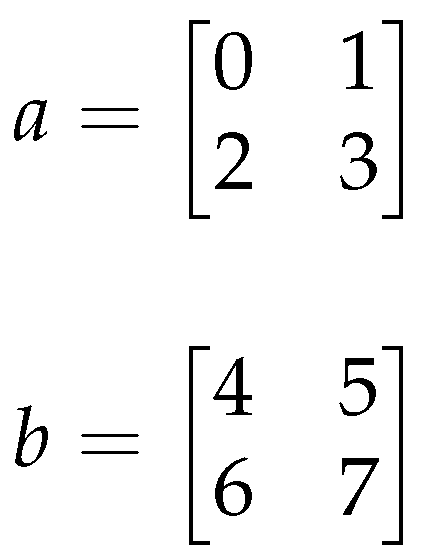


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grout, I.A.; Mullin, L. Realizing Mathematics of Arrays Operations as Custom Architecture Hardware-Software Co-Design Solutions. Information 2022, 13, 528. https://doi.org/10.3390/info13110528
Grout IA, Mullin L. Realizing Mathematics of Arrays Operations as Custom Architecture Hardware-Software Co-Design Solutions. Information. 2022; 13(11):528. https://doi.org/10.3390/info13110528
Chicago/Turabian StyleGrout, Ian Andrew, and Lenore Mullin. 2022. "Realizing Mathematics of Arrays Operations as Custom Architecture Hardware-Software Co-Design Solutions" Information 13, no. 11: 528. https://doi.org/10.3390/info13110528
APA StyleGrout, I. A., & Mullin, L. (2022). Realizing Mathematics of Arrays Operations as Custom Architecture Hardware-Software Co-Design Solutions. Information, 13(11), 528. https://doi.org/10.3390/info13110528






