A Blockchain-Based Secure Multi-Party Computation Scheme with Multi-Key Fully Homomorphic Proxy Re-Encryption

Abstract

At present, secure multi-party computing is an effective solution for organizations and institutions that want to derive greater value and benefit from the collaborative computing of their data. Most current secure multi-party computing solutions use encryption schemes that are not resistant to quantum attacks, which is a security risk in today’s quickly growing quantum computing, and, when obtaining results, the result querier needs to collect the private keys of multiple data owners to jointly decrypt them, or there needs to be an interaction between the data owner and the querier during the decryption process. Based on the NTRU cryptosystem, which is resistant to quantum computing attacks and has a simple and easy-to-implement structure, and combined with multi-key fully homomorphic encryption (MKFHE) and proxy re-encryption, this paper proposes a secure multi-party computing scheme based on NTRU-type multi-key fully homomorphic proxy re-encryption in the blockchain environment, using the blockchain as trusted storage and a trusted execution environment to provide data security for multi-party computing. The scheme meets the requirements of being verifiable, conspiracy-proof, individually decryptable by the querier, and resistant to quantum attacks.

1. Introduction

With the rapid development of communication technology and the steady advancement of global information, data information owned by organizations or individuals can generate great value and wealth through communication and integration. To make full use of the value of data to obtain greater benefits, data interaction, and sharing, information integration and utilization between different institutions and organizations have become urgent needs, among which collecting data from all parties for collaborative computing is a typical scenario. Participants want to protect the security of data, protect the privacy of all parties, and ensure the fairness of computing in the process of data collection and use. The proposal and development of secure multi-party computation (SMPC) [1] provide an effective solution and technical support for the above requirements. In order to protect the privacy of all parties and the security of their private data during the use of secure multi-party computation, it is necessary to continuously improve the security of secure multi-party computation solutions. In addition, since the homomorphic encryption algorithm (FHE) [2] can solve the problem of user data privacy protection in cloud computation and big data environments, it is also a research hotspot to combine the homomorphic encryption algorithm with secure multi-party computation.

SMPC refers to the collaborative computation of a function by two or more participants in a collaborative computation, without trusting each other, using data held secretly by each party as the input. The privacy of each participant is protected by requiring each party to have no access to additional information beyond its own secret input and the final result of the computation. Specifically, SMPC protects the privacy of each participant by means of the secret data held by the participants for ${\mathrm{P}}_i,i=1,\dots ,\mathrm{n}$ separate secret inputs held by $x_i,i=1,\dots ,\mathrm{n}$, in order to jointly compute a common function $f$ with the values of $f\left(x_1,x_2,\dots ,x_n\right)=\left(y_1,y_2,\dots ,y_n\right)$. Throughout the computation process, the participant’s ${\mathrm{P}}_i$ cannot learn anything other than the result of the computation and their own secret inputs $\left(x_i,y_i\right)$. The participants are not privy to any information other than the result of the computation and their own secret input.

Fully homomorphic encryption is an encryption algorithm that allows direct manipulation of encrypted data, which has the property that the result of the direct manipulation of the ciphertext is the same as the result of manipulating the plaintext first and then encrypting it, a property that allows it to be applied in outsourced computing scenarios. Multi-key fully homomorphic encryption (MKFHE) was first proposed by A. López-Alt et al. [3], who used a modified NTRU scheme to construct an MFHE scheme. Multi-key fully homomorphic encryption is an encryption method that can process data encrypted and uploaded by multiple different keys, breaking the restriction that homomorphic encryption can only process data encrypted by the same key, but, in the decryption method, the resultant querier needs to collect the private keys of multiple data owners to jointly decrypt the data or interaction between the data owner and the querier is required during the decryption process. To address the above issues, S. Yasuda et al. [4] proposed multi-key homomorphic proxy re-encryption (MKH-PRE). The MKH-PRE scheme allows the data owner to encrypt the data with its own public key for multi-key homomorphic computation, as well as allowing the ciphertext obtained from the homomorphic computation to be proxy re-encrypted, converting the resultant ciphertext into a new ciphertext that can only be decrypted by the resultant querier. The advantage of the NTRU cryptosystem is that it is resistant to quantum attacks, and the NTRU-based scheme is a much easier way to generate secret keys, using only modulo multiplication and modulo inverse operations, with a simple structure that is easy to implement. It can be used not only to construct NTRU-based MKFHEs but also to construct proxy re-encryption schemes that transform ciphertext into data that can be decrypted with a querier key.

1.1. Motivation and Contribution

The encryption schemes used in most current secure multi-party computing schemes are not resistant to quantum attacks, which is currently a security risk with the rapid development of quantum computing, and the SMPC scheme that uses MKFHE cannot be decrypted separately by the querier when obtaining the computation results. Therefore, it is necessary to design a secure multi-party computing scheme that is resistant to quantum attacks and can be decrypted individually by the querier.

The main research contributions of this paper are as follows:

• A secure multi-party computation scheme based on NTRU-type [5] multi-key fully homomorphic encryption proxy re-encryption is proposed. The use of proxy re-encryption solves the problem that the multi-key homomorphic encryption scheme cannot be decrypted separately when the result is obtained, and the data owner can go offline after encrypting the uploaded data and does not have to stay online during secure multi-party computation.
• A scheme combining the blockchain with an NTRU multi-key fully homomorphic encryption agent re-encryption secure multi-party computing scheme is proposed. The decentralized, transparent, and non-tamper characteristics of the blockchain are utilized to achieve the traceability and verifiability of the scheme and prevent collusion of the participants.
• The security proof and comparison with other solutions demonstrate that this secure multi-party computing solution meets the requirements of being independent of trusted third parties, verifiable, privacy-protected, collusion-proof, individually decryptable by the querier, and resistant to quantum attacks.

1.2. Paper Structure

The rest of this paper is organized as follows: Section 2 presents related works. Section 3 describes the scheme model, the steps of the scheme operation, the algorithms involved, and the security model used. Section 4 proves the security of the scheme. Section 5 compares the scheme with other relevant SMPC schemes. The conclusion is provided in Section 6.

2. Related Work

YAO first proposed a two-party secure computation method in [6] using the “millionaire problem”. Goldreich and others extended the two-party computation model to a basic multi-party computation model [7]. Using this as a starting point, the security of SMPC schemes has been a concern. To provide a trusted execution environment for SMPC, some researchers have chosen to perform secure multi-party computing through trusted third parties, such as Wu Y. et al., who constructed a generic server-assisted secure multi-party computing protocol for secure execution of collaborative computing tasks in cloud computing [8]. However, trusted third parties are vulnerable to attacks forming a single point of failure and also have the potential to be complicit with malicious parties.

Researchers found that blockchains can provide a more secure execution environment for SMPC. The open, transparent, and tamper-evident nature of blockchain can provide a means of verification and traceability for SMPC, and the incentive mechanism can effectively prevent complicity from occurring. H. Gao et al., proposed a BFR-MPC scheme in combination with the blockchain [9] that encourages all participants to cooperate through an incentive mechanism and maintains a public reputation system in the scheme, in which honest participants gain more and more benefits while corrupt participants are increasingly punished. Y. Yang et al., proposed Block-SMPC, a blockchain-based SMPC scheme [10], which ensures data integrity and authentication by using the blockchain, introduces a multi-party computer system based on homomorphic encryption, and improves privacy security by separating the authority of homomorphic keys and ciphertexts. Liu et al., proposed a secure multi-party computing protocol, BPLSM, for ubiquitous data privacy protection in combination with blockchain technology [11]. It achieves on-chain signature verification, a guarantee of commitment, the correctness of encrypted values and address hiding, and off-chain combined transaction commitment using the property of Pederson’s additive homomorphism to construct a secure multi-party computation scheme that can sign different messages in combination with the Schnorr protocol.

The secure multi-party computation scheme in the above study improves the security of SMPC with the help of blockchain features, but the scheme cannot be decrypted separately by the querier when obtaining the computation result. In order to meet the requirement of being able to carry out decryption individually, T. Wang et al. [12] proposed a secure, high-performance sharing and multi-party computing model by combining the features of the blockchain, based on a combination of on-chain storage and off-chain storage, and, in this storage environment, data are shared by using proxy re-encryption. However, most of the encryption algorithms involved in the above scheme are based on large integer decomposition or discrete logarithm difficulty problems, which do not have the ability to resist quantum attacks.

To solve these problems, this paper proposes a secure multi-party computing scheme based on a multi-key homomorphic proxy re-encryption scheme and an NTRU-based MKFHE scheme [13,14] with resistance to quantum attacks in the blockchain environment.

3. SMPC Scheme with Multi-Key Fully Homomorphic Proxy Re-Encryption

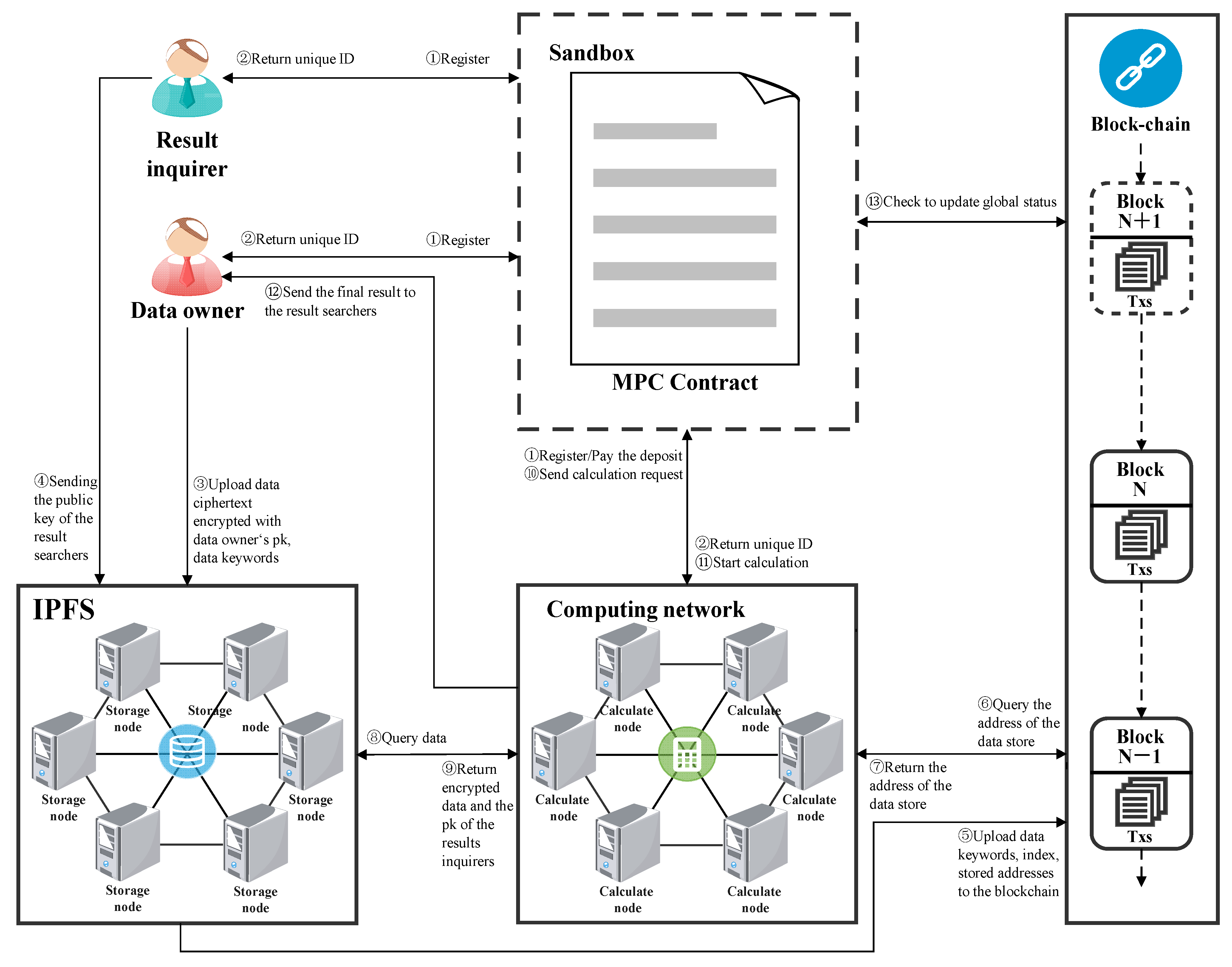
3.1. System Model

The system consists of several components: the data owner, the data querier (in general, the data owner, but possibly also the authorized user), the computation network, the SMPC contract, the InterPlanetary File System (IPFS) [15], and the blockchain. The system architecture is shown in Figure 1. The functions of each part of the system are as follows:

• Data owner

As the data provider of secure multi-party computation, the data owner owns the original data as the input of the computation. To ensure the privacy and data security of all parties, the data must be encrypted by the data owner before being used as the input of the computation.

• Result inquirer

As the receiver of the computation result, the result inquirer is generally the data owner or the authorized user who does not provide the data. With the support of the proxy re-encryption algorithm, the result inquirer can decrypt the encrypted computation result through their own private key and obtain the calculation result.

• Blockchain

The blockchain participates in the process as a trusted storage and execution environment. This scheme provides resistance to quantum attacks through proxy re-encryption to enable the result querier to decrypt the ciphertext result alone. At the same time, open, transparent, and untampered information stored on the blockchain can be verified as proof.

• IPFS

IPFS is used to store encrypted raw data as off-chain storage to save storage space. A Bloom filter [16] generates index values, and then IPFS uploads the data keywords, index values, and storage address to the blockchain. SMPC nodes look up the data storage address on the blockchain and then download the encrypted data from IPFS to local storage for calculation.

• SMPC Contracts

Data owners, data inquirers, and SMPC nodes need to register with the SMPC contract before the calculation begins. Participants (SMPC nodes or users) pay a deposit to the SMPC contract, and the SMPC contract returns a unique ID to the registrant. The data inquirers send their public keys to the SMPC contract, which generates the proxy re-encryption key. The computation function in the contract is agreed upon in advance by the participants of the secure multi-party calculation so that the code can be written and deployed on the blockchain platform to automatically trigger the execution of the agreed computation without human intervention.

• Computing networks

The SMPC computing network undertakes the task of data calculation. It queries the corresponding encrypted data on IPFS as the input and performs the calculation on the encrypted data consistently with the agreed calculation function according to the SMPC contract. The obtained encryption results are sent to each data interrogator after the agent re-encryption operation.

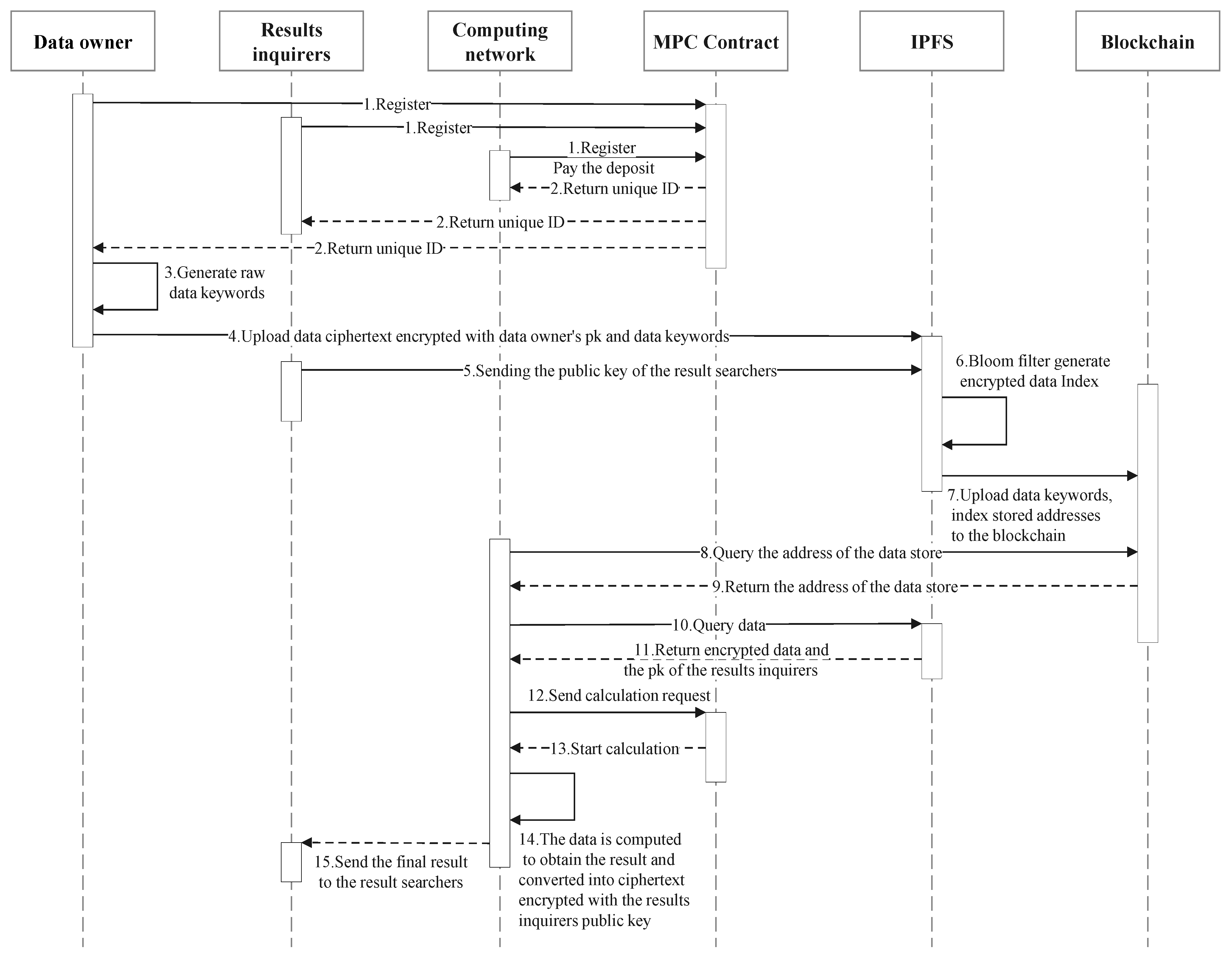
3.2. Program Steps

The steps in the operation of the system are shown in Figure 2.

• Initially, the data owner, the data querier, and the SMPC node register with the SMPC contract, which distributes a unique ID to each registered node, while the SMPC node pays a deposit to the contract.
• The data owner generates keywords for the original data to be involved in the operation and then encrypts the data to be involved in the operation with its own public key and uploads them to IPFS, where a Bloom filter generates the index value of the encrypted data. The data owner uploads the keywords generated from the original data and the storage address of the encrypted data.
• The computing network node interacts with the blockchain by querying keywords, querying the corresponding block to obtain the storage address of the required encrypted information, and obtaining the encrypted data from the IPFS data storage address for calculation.
• The data querier sends its public key to the SMPC contract, and the ciphertext result after the homomorphic calculation is converted into the ciphertext result encrypted by the data querier’s public key through the NTRU proxy re-encryption algorithm. To obtain the final calculation result, the data querier only needs to decrypt the calculation result returned by the computing network with its own private key. The contract is carried out in a sandbox isolation environment, and the blockchain rewards or deducts the deposit based on whether the node is honest or not.
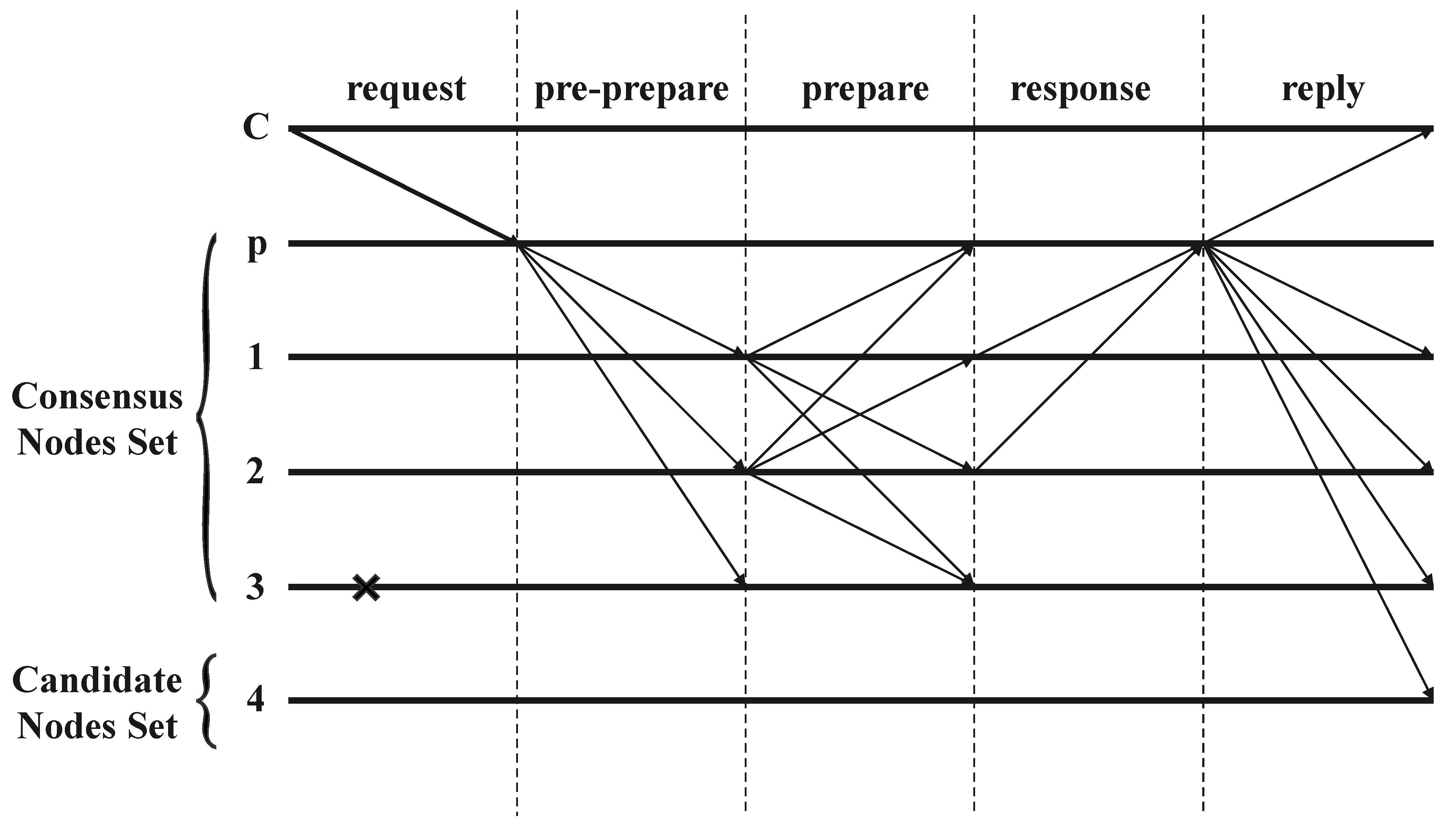
• At the end of the calculation, the blockchain validation node checks whether any dishonest nodes have committed mischief before or after the calculation process. If this does not happen, the deposit of each node will be returned as is; if this happens, the deposit of the honest node will be returned, and the deposit of the dishonest node will be deducted and distributed as a reward to the honest node as a punishment.

In order to enable the nodes in the scheme to reach consensus quickly while ensuring security during the operation, the Score Grouping-practical Byzantine fault-tolerant (SG-PBFT) consensus algorithm, which is based on a modified version of the practical Byzantine fault-tolerant (PBFT) algorithm [17] proposed in the literature [18], is used in the scheme.

The SG-PBFT sets the initial score of N sequential random nodes as 100 points and divides them into a consensus node set and a candidate node set. The consensus node executes the consensus process, while the candidate node does not participate in the consensus process and only receives the consensus results. The primary node is selected by $\mathrm{p}=\mathrm{vmodCN}$. CN represents the agreed number of nodes. When the primary node p is attacked or fails, the view v will be changed, and the recalculated primary node will replace it.

When the nodes reach a consensus, the master node will send the confirmed results to all consensus nodes and update the score of the node. If the result of the node is consistent with the consensus result, one point will be added. Otherwise, five points will be deducted. The m nodes with the lowest score will be removed from the consensus node set and attached to the end of the candidate node set. The m nodes with the highest score in the candidate set will be added to the consensus node set and renumbered.

The SG-PBFT renumbers and adjusts nodes after each agreement is reached. This ensures that the identity of the primary node is hidden and therefore resistant to distributed denial of service (DDoS) attacks. In the SG-PBFT, even if all malicious nodes join together, they can only send no more than 1/3 of the total number of messages. Malicious nodes cannot reach a consensus, therefore the SG-PBFT can resist selective attacks. The SG-PBFT operating process is shown in Figure 3. The “x” on the line indicates that the node is a failed node.

3.3. Algorithm Construction

The algorithms in the scheme are divided into four parts: the initialization algorithm, the key generation algorithm, the multi-key homomorphic encryption algorithm, and the proxy re-encryption algorithm. The operations in the scheme are all performed on the ring $R=\mathbb{Z}\left[\mathrm{X}\right]/{\Phi }_m\left(x\right)$, over which $q$ is a prime number, and ${\mathsf{\Phi }}_m\left(x\right)$ is a partitioned circle polynomial of the degree $n=\phi \left(m\right)$. Let $R_q=R/qR$.

• Initialization algorithm

$\mathrm{Setup}\left(1^{\lambda }\right)\to pp$: Enter the security parameters’ $\lambda$ to generate ring learning with errors (RLWE) [19] with dimension n, the plaintext modulus $p$, the ciphertext modulus $q$, and the ring $R$ distribution over the ring $\psi ,\phi$. Vector $\mathit{\alpha }$ and matrix $\mathit{B}$ are extracted randomly on the uniform distributions $U\left(R_q^d\right)$ and $U\left(R_q^{2\times m}\right)$ of ring R, respectively, and then a common parameter $pp=\left(n,p,q,\psi ,\phi ,\mathit{\alpha },\mathit{B}\right)$ is output.

The public parameter $pp$ is used as the input to the key generation algorithm for the generation of keys by the data owner and the result querier in addition to the generation of the computational key $Evk$ in the multi-key homomorphic encryption algorithm.

• Key generation algorithm

$\mathrm{KeyGen}\left(pp\right)\to \left(p{k}_i,s{k}_i\right)$: Randomly select $u^{\prime },l$ in the distribution $\psi$; it is required that the extracted $u^{\prime }$ is reversible in $R_q$. Calculate $u=p{u}^{\prime }+1\left(\mathrm{mod}q\right)$, $u^{-1}\in R_q$, and let $v=pl{u}^{-1}\left(\mathrm{mod}q\right)$. The error vector $\mathit{\beta }$ is randomly selected from the distribution ${\phi }^d$, and $\mathit{f}=-\mathit{\alpha }u+\mathit{\beta }\left(\mathrm{mod}q\right)$ is calculated. Set $u=\left(u,1\right)\in R_q^{1\times 2}$, randomly select the error vector ${\beta }^{\prime }$ from the distribution ${\phi }^{d^{\prime }}$, and calculate g $=-\mathit{u}\mathit{B}+{\mathit{\beta }}^{\prime }\left(\mathrm{mod}q\right)\in R_q^{n^{\prime }}$. Output the private key $sk=u$ and the public key $pk=\left(v,f\mathit{,}\mathit{g}\right)$.

The data owner and the result querier generate their respective public key $pk$ and private key $sk$ by means of a key generation algorithm.

• Multi-key homomorphic encryption algorithm

The components of the multi-key homomorphic encryption algorithm include the computational key generation algorithm $\mathrm{EvkGen}$, the encryption algorithm $\mathrm{Enc}$, the ciphertext extension algorithm $\mathrm{CtxtExtend}$, and the homomorphic computation algorithm $\mathrm{Eval}$.

$\mathrm{EvkGen}\left(pp,pk,sk\right)\to Evk$: Randomly select $\mathrm{s}$ in the distribution $\phi$, randomly select ${\mathit{r}}_0,{\mathit{\beta }}_0,{\mathit{\beta }}_1$ in the distribution ${\phi }^d$, calculate ${evk}_0=v{r}_0+{\mathit{\beta }}_0+u^{-1}sl\left(\mathrm{mod}q\right)$ and ${evk}_1=s\alpha +{\beta }_1+ul\left(\mathrm{mod}q\right)$, and output the computation key $Evk=[{evk}_0|{evk}_1]$.

The computational key generation algorithm EvkGen generates the computational key $Evk$ using the public parameters, the public key $pk$ of the data owner, and the private key $sk$.

$\mathrm{Enc}\left(pk,m\right)\to c$: Randomly selects $r,\beta$ in the distribution $\phi$, set $\mathsf{\delta }=q/p$, and compute the ciphertext $c=vp+\beta +\mathsf{\delta }m\left(\mathrm{mod}p\right)$.

The data owner uses the encryption algorithm $\mathrm{Enc}$ to encrypt the data they need to participate in the operation and then generates a cipher text and uploads it to IPFS.

$\mathrm{CtxtExtend}\left({\mathit{c}}_1,{\mathit{c}}_2,\dots ,{\mathit{c}}_s\right)\to {\mathit{c}}_i^{*}$: Let the number of ciphertexts involved in this operation be s and ${\mathit{c}}_1=\left(c_1,c_2,\dots ,c_{k_i}\right)\in R_q^{k_i}$. The corresponding user ID set is $\left\{i{d}_{k_1},i{d}_{k_2},\dots ,i{d}_{k_i}\right\},i=1,2,\dots ,s$. Let $k=\max \left(k_1,k_2,\dots ,k_s\right)$ and output the k-dimensional ciphertext ${\mathit{c}}_i^{*}=\left(c_1^{*},c_2^{*},\dots ,c_k^{*}\right)\in R_q^k$ where

$$c_i^{*}=\left\{\begin{array}{c}{c}_j,i=id, 1\le j\le k_i\\ 0, others\end{array}\right.$$

(1)

$\mathrm{Eval}\left({\mathit{c}}_1,{\mathit{c}}_2,Evk\right)$: Calling $\mathrm{CtxtExtend}\left({\mathit{c}}_1,{\mathit{c}}_2\right)$ gives ${\mathit{c}}_1^{*},{\mathit{c}}_2^{*}\in R_q^k$ by calculation. Then homomorphic addition or multiplication is performed.

• $\mathrm{HAdd}\left({\mathit{c}}_1^{*},{\mathit{c}}_2^{*}\right)$: Compute and output the ciphertext $\mathit{c}={\mathit{c}}_1^{*}+{\mathit{c}}_2^{*}\left(\mathrm{mod}q\right)$.
• $\mathrm{HMult}\left({\mathit{c}}_1^{*},{\mathit{c}}_2^{*},\mathrm{evk}\right)$: Calculate ${\mathit{c}}^{\prime }=p/q\times {\mathit{c}}_1^{*}\otimes {\mathit{c}}_2^{*}\left(\mathrm{mod}q\right)$ and output the ciphertext $\mathit{c}=\mathrm{Reline}\left({\mathit{c}}^{\prime },\mathrm{evk}\right)\in R_q^k$.

• Proxy re-encryption algorithm

Proxy re-encryption algorithms include the re-encryption key generation algorithm $\mathrm{RKGen}$, the re-encryption algorithm $\mathrm{ReEnc}$, and the re-encrypted ciphertext decryption algorithm $\mathrm{PRDec}$. The algorithms are used to re-encrypt the ciphertext after the homomorphic encryption calculation into a ciphertext that can be decrypted by the resultant querier’s private key.

$\mathrm{RKGen}\left(s{k}_i,p{k}_j\right)\to r{k}_{i\to j}$: Select $p{k}_j$ from ${\mathit{h}}_j$and let ${\mathit{H}}_j=\mathit{B}+{\mathit{\beta }}_2^T\otimes {\mathit{h}}_j,$ where ${\mathit{\beta }}_2=\left(0\parallel 1\right)\in {\mathbb{Z}}^2$. Select $X_i$, $n^{\prime }\ge 2\log q+2\mathsf{\lambda }$, from ${\left\{0,1\right\}}^{n^{\prime }\times d}$ and compute and output $r{k}_{i\to j}=R{K}_{i\to j}={\mathit{H}}_j,{\mathit{X}}_i+\left(\begin{array}{c}\mathbf{0}\\ u_i\mathit{l}\end{array}\right)\left(\mathrm{mod}q\right)\in R_q^{2\times h}$.

$\mathrm{ReEnc}\left(r{k}_{1\to j},\dots ,r{k}_{k\to j},c\right)\to c^{\prime }$: Let $\mathbf{c}=\left(c_1,\dots ,c_k\right)$ and calculate and output $c^{\prime }={\displaystyle \sum }_{i=1}^{k}R{K}_{i\to j}{u}^{-1}\left(c_i\right)\left(\mathrm{mod}q\right)\in R_q^2$.

$\mathrm{PRDec}\left(s{k}_j,c^{\prime }\right)\to \mathrm{m}$: Let ${\mathit{u}}_j=\left(u_j,1\right)$ and compute and output $\mathrm{m}=\lfloor \left(p/q\right)\langle {\mathit{u}}_j,c^{\prime }\rangle \rceil \left(\mathrm{mod}p\right)$.

3.4. Security Model

The scheme uses the definition of security from the literature [5] for the MKH-PRE scheme. The definition designs an IND-CPA security game between a challenger and an adversary $\mathcal{A}$. The re-encryption process is represented using a directed acyclic graph, such that $D$ is the set of edges in the re-encryption graph. During the game, the adversary can initiate an interrogation of the challenger about the re-encryption key generation based on the re-encryption graph. The formal definition of a secure game is as follows:

• Preparation phase

The challenger sends the generated public parameters $\mathrm{Setup}\left(1^{\lambda }\right)\to pp$ to the adversary $\mathcal{A}$.

Generate honest keys. The number of honest keys received by the challenger from $\mathcal{A}$ is $N_{\mathrm{h}}$, and the challenger generates $\left(p{k}_i,s{k}_i\right),i=1,\dots ,N_{\mathrm{h}}$ and sends the $p{k}_i$ to $\mathcal{A}$. Let ${\chi }_{\mathrm{h}}$ be the set of honest public keys.

Generate non-honest keys. The number of non-honest keys received by the challenger from $\mathcal{A}$ is $N_d$, and the challenger generates $\left(p{k}_i,s{k}_i\right),i=1,\dots ,N_d$ and sends the $p{k}_i$ to $\mathcal{A}$. Let ${\chi }_d$ be the set of non-honest public keys.

• Inquiry phase

The adversary can initiate a polynomial inquiry of any order.

Generate the re-encryption key. $\mathcal{A}$ sends $\left(i,j\right)$ to the challenger. If $i, j\in {\chi }_{\mathrm{h}}$, and there is a directed acyclic graph $E=\left({\chi }_{\mathrm{h}},D\cup \left(i,j\right)\right)$, then the challenger adds $\left(i,j\right)$ to $D$ and sends the generated re-encryption key for i to j $\mathrm{RKGen}\left(s{k}_i,p{k}_j\right)\to r{k}_{i\to j}$ to $\mathcal{A}$; otherwise, $\perp$ is returned.

Re-encryption. $\mathcal{A}$ sends $\left(i,j,c\right)$ to the challenger. If $i,j\in {\chi }_d$, and $=c^{\prime }$, the challenger returns $\perp$. Otherwise, the challenger sends a ciphertext re-encrypted with the j’s public key $c_j$ sent to $\mathcal{A}$; otherwise, $\perp$ is returned.

• Challenge phase.

The plaintext space is $M$. Take $m_0,m_1\in M$, and $i^{\prime }\in N_{\mathrm{h}}$. $\mathcal{A}$ sends $\left(i^{\prime },m_0,m_1\right)$ to the challenger, who chooses a random bit $b\in \left\{0,1\right\}$, generates $c^{\prime }$ by $\mathrm{Enc}\left(p{k}_{i^{\prime }},m_b\right)$, and returns it to $\mathcal{A}$. $\mathcal{A}$ can only initiate a challenging inquiry once.

• Judgment phase.

$\mathcal{A}$ outputs one bit $b^{\prime }\in \left\{0,1\right\}$. In this game, the advantage of adversary $\mathcal{A}$ is defined as

$${\mathrm{Adv}}_{\mathrm{MKH}-\mathrm{PRE},\mathcal{A}}^{\mathrm{ind}-\mathrm{cpa}}\left(\mathsf{\lambda }\right)=\mid \mathrm{Pr}\left[b^{\prime }=b\right]-\frac{1}{2}\mid$$

(2)

If, for any probabilistic polynomial time adversary $\mathcal{A}$ there is

$${\mathrm{Adv}}_{\mathrm{MKH}-\mathrm{PRE},\mathcal{A}}^{\mathrm{ind}-\mathrm{cpa}}\left(\mathsf{\lambda }\right)=\mathrm{negl}\left(\mathsf{\lambda }\right)$$

(3)

then, the scheme is IND-CPA safe.

4. Proof of Safety

Here, we demonstrate the safety of the MKH-PRE scheme. If the RLWE assumption, the decisional small polynomial ratio (DSPR) [20] assumption, and the cyclic safety assumption are difficult, then the MKHE scheme in this paper is IND-CPA safe.

The security of the PRE process is considered below. Here, we demonstrate the security of the PRE process through an IND-CPA security game between a challenger and an adversary $\mathcal{A}$. $\mathcal{A}$ is an adversary in arbitrary probabilistic polynomial time, which has access to the re-encryption key generation and evolution $\mathrm{RKGen}$ and the re-encryption oracle machine $\mathrm{ReEnc}$ and can only initiate queries for generating re-encryption keys based on the re-encryption graph. Consider the following set of security games:

Game 0. The IND-CPA safe game was defined in the previous section. Assuming ${\chi }_{\mathrm{h}}=\left\{1,\dots ,N\right\}$, ${\chi }_{\mathrm{b}}=\left\{N+1,\dots ,M\right\}$. According to the topological order determined by the re-encryption graph, if $i<j$, then there are no edges from $i$ to $j$, i.e., $\mathcal{A}$ can only be initiated in the $i>j$ case of a re-encryption key$r{k}_{i\to j}$ of the query.

Divide Game k, $k=1,\dots ,N$, into two categories, Game. 1 k and Game. 2 k.

Game. 1 k. When $\mathcal{A}$ initiates a query to generate an honest key, for all $i<k$, the challenger randomly draws $v_i$ and ${\mathit{g}}_i$ in the uniform distributions $R_q$ and $R_q^{n^{\prime }}$, respectively, to generate the public key; for all $k<i\le N$, the challenger generates the public key by $\mathrm{KeyGen}\left(pp\right)\to \left(v_i,{\mathit{g}}_i\right)$. The rest of the operation is the same as Game. 2 k-1.

Game. 2 k. When A initiates the query to generate the re-encryption key, the challenger generates the re-encryption key $r{k}_{i\to j}$ by drawing a random matrix from $R_q^{2\times n^{\text{’}}}$ for all $j<i\le k$; for $k<i,j\le N$, the challenger generates the re-encryption key by $\mathrm{RKGen}\left(s{k}_i,p{k}_j\right)\to r{k}_{i\to j}$. The rest of the operation is the same as Game. 2 k.

Game End. When $\mathcal{A}$ initiates a challenge query, the challenger generates the ciphertext $c$ through random sampling, and the rest of the operation is the same as Game. 2 N.

The strengths of $\mathcal{A}$ in each game are assessed separately as follows:

Because Game 0 is an IND-CPA safe game of the original MKH-PRE scheme,

$${\mathrm{Adv}}_{\mathrm{MKH}-\mathrm{PRE},\mathcal{A}}^{\mathrm{ind}-\mathrm{cpa}}\left(\mathsf{\lambda }\right)={\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}0}\left(\mathsf{\lambda }\right)$$

(4)

In Game. 1 k, the re-encryption key $r{k}_{k\to i}$ generated by the challenger satisfies $r{k}_{k\to i}=R{K}_{k\to i}={\mathit{H}}_i,{\mathit{X}}_k+\left(\begin{array}{c}\mathbf{0}\\ u_k\mathit{l}\end{array}\right)\left(\mathrm{mod}q\right)$ when $i<k$, where ${\mathit{X}}_k$ is randomly selected in the uniform distribution of ${\left\{0,1\right\}}^{n^{\prime }\times d}$ and $n^{\prime }\ge 2\log q+2\mathsf{\lambda }$. Since ${\mathit{h}}_i$ and $\mathit{B}$ are randomly selected from the uniform distribution when $i<k$, ${\mathit{H}}_i=\mathit{B}+{\mathit{\beta }}_2^T\otimes {\mathit{h}}_i$ is also subject to the uniform distribution. According to the residual hash lemma, H and X are subject to uniform distributions, so ${\mathit{H}}_i$ and ${\mathit{X}}_k$ are statistically indistinguishable from a matrix randomly drawn from a uniform distribution. The results show that $r{k}_{k\to i}$ is statistically indistinguishable from the random matrix extracted from the uniform distribution, meaning that Game. 1 k and Game. 2 k are statistically indistinguishable. Therefore, there is

$$\left|{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.1k}\left(\mathsf{\lambda }\right)\right.\left.-{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.2k}\left(\mathsf{\lambda }\right)\right|=\mathrm{negl}\left(\mathsf{\lambda }\right)$$

(5)

Adversary $\mathcal{A}$ constructs a PPT algorithm $\mathcal{Q}$ to distinguish the RLWE distribution from the uniform distribution, and the sample $\mathit{x}\in R^2$ input to $\mathcal{Q}$ comes from the RLWE distribution or one of the uniform distributions.

• Preparation phase

$\mathcal{Q}$ calculates $\overline{\mathit{B}}=\left(x_1^{\mathrm{T}}\parallel \dots \parallel x_{n^{\prime }}^{\mathrm{T}}\right)$ and randomly extracts $v_k,{\mathit{g}}_k$ from the uniform distribution $R_q,R_q^{n^{\prime }}$. Q sends $\mathit{B}=\overline{\mathit{B}}+\left(\begin{array}{c}\mathbf{0}\\ d_k\end{array}\right)$ to $\mathcal{A}$.

Generate honest keys

When $\mathcal{A}$ initiates an honest key generation query, the response of $\mathcal{Q}$ is as follows:

When $i<k$, $\mathcal{Q}$ randomly selects $v_i,{\mathit{g}}_i$ from the uniform distribution $R_q,R_q^{n^{\prime }}$ and lets $p{k}_i=\left(v_i,{\mathit{g}}_i\right)$.

When $i=k$, $\mathcal{Q}$ lets $p{k}_i=\left(v_k,{\mathit{g}}_k\right)$.

When $i>k$, $\mathcal{Q}$ generates the public key by $\mathrm{KeyGen}\left(pp\right)\to \left(p{k}_i,s{k}_i\right)$.

Finally, $\mathcal{Q}$ sends $p{k}_i$, $i\in \left\{1,\dots ,k\right\}$ to $\mathcal{A}$.

Generate dishonest keys

When $\mathcal{A}$ initiates a generate dishonest keys query, $\mathcal{Q}$ calculates $\mathrm{KeyGen}\left(\mathit{B}\right)\to \left(p{k}_i,s{k}_i\right)$ and sends $\left(p{k}_i,s{k}_i\right)$ to $\mathcal{A}$.

• Inquiry phase.

Generate re-encryption keys

When $\mathcal{A}$ initiates a generate re-encryption key query $\left(i,j\right)$, if $i,j<k$, then $\mathcal{Q}$ returns $R{K}_{i\to j}\in R_q^{2\times h}$ randomly selected from the uniform distribution; if $i,j>k$, then $\mathcal{Q}$ returns $\mathrm{RKGen}\left(s{k}_i,p{k}_j\right)\to R{K}_{i\to j}$.

Re-encryption

When $\mathcal{A}$ initiates a re-encryption query $\left(i_1,\dots ,i_s,j,c\right)$, $\mathcal{Q}$ returns $\mathrm{ReEnc}\left(R{K}_{i_1\to j},\dots ,R{K}_{i_s\to j},\mathrm{c}\right)\to {\mathrm{c}}_j$ to $\mathcal{A}$.

• Challenge phase.

$m_0,m_1\in M$, and $i^{\prime }\in N_{\mathrm{h}}$ are selected. $\mathcal{A}$ starts the query $\left(i^{\prime },m_0,m_1\right)$, and $\mathcal{Q}$ randomly selects a bit $b\in \left\{0,1\right\}$, generating $c^{\prime }$ by $\mathrm{Enc}\left(p{k}_{i^{\prime }},m_b\right)$ and returning it to $\mathcal{A}$.

• Judgment phase.

$\mathcal{A}$ ceases the query and outputs bits$b^{’}\in \left\{0,1\right\}$. Then, Q outputs 1 if $b=b^{\prime }$, or 0 otherwise.

If the RLWE distribution is entered in $\mathcal{Q}$, then $\mathcal{Q}$ simulates Game. 2 k−1. The first rows of $\overline{\mathit{B}}$ and ${\mathit{g}}_k$ are both random quantities that obey a uniform distribution, so $\mathit{B}$ also obeys a uniform distribution. In addition, the distributions of ${\mathit{g}}_k\approx -(f||1)\mathit{B}$ are the same as in the actual game. In the previous game, $r{k}_{i\to j}$ was replaced by a randomly selected matrix from a uniform distribution, where $\mathit{B}$ simulates Game. 2 k-1. If the uniform distribution is entered in $\mathcal{Q}$, then $\mathit{B}$ simulates Game.1 k. From the above analysis, the RLWE assumption, and the DSPR assumption, it follows that:

$$\left|{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.2k-1}\left(\mathsf{\lambda }\right)\right.\left.-{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.1k}\left(\mathsf{\lambda }\right)\right|=\mathrm{negl}\left(\mathsf{\lambda }\right)$$

(6)

The ciphertext in Game End is drawn randomly from a uniform distribution; in Game. 2 N, all public keys are replaced in the previous games with vectors drawn randomly from a uniform distribution, and the polynomial drawn randomly from a uniform distribution is statistically indistinguishable from the ciphertext output by the encryption algorithm under the RLWE assumption; therefore, Game. 2 N is statistically indistinguishable from Game End.

$$\left|{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.2N}\left(\mathsf{\lambda }\right)\right.\left.-{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}\mathrm{End}}\left(\mathsf{\lambda }\right)\right|=\mathrm{negl}\left(\mathsf{\lambda }\right)$$

(7)

The advantages of $\mathcal{Q}$ in Game End are:

$${\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}\mathrm{End}}\left(\mathsf{\lambda }\right)=\mathrm{negl}\left(\mathsf{\lambda }\right)$$

(8)

Based on the above analysis, it can be concluded that

$$\begin{array}{ll}({\mathrm{Adv}}_{\mathrm{MKH}-\mathrm{PRE},\mathcal{A}}^{\mathrm{ind}-\mathrm{cpa}}\left(\mathsf{\lambda }\right)& \\ & \le {\displaystyle \sum }_{k=1}^N\left|{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.2k-1}\left(\mathsf{\lambda }\right)\right.\left.-{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.1k}\left(\mathsf{\lambda }\right)\right|+\left|{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}.2N}\left(\mathsf{\lambda }\right)\right.\left.-{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}\mathrm{End}}\left(\mathsf{\lambda }\right)\right|\\ & +{\mathrm{Adv}}_{\mathcal{A}}^{\mathrm{Game}\mathrm{End}}\left(\mathsf{\lambda }\right)=\mathrm{negl}\left(\mathsf{\lambda }\right)\end{array}$$

(9)

Therefore, the solution in this paper is IND-CPA safe.

5. Comparison of Programs

Constructed by Y. Wu et al., to address the problem of secure execution of collaborative computing tasks in cloud computing, a generic server-assisted secure multi-party computing protocol [8] was proposed without complicity between the server and client; however, the scheme also relies on the participation of trusted third parties, cannot prevent complicity, and does not have a reliable means of verification of the computing process. To make the scheme verifiable, researchers have used the properties of the blockchain to add verifiability to the scheme while providing privacy protection by introducing the blockchain in the scheme construction. Examples include H. Gao et al.’s blockchain-based BFR-MPC scheme [9], Y. Yang et al.’s SMPC scheme Block-SMPC [10], and Liu et al.’s BPLSM [11], a secure multi-party computing protocol for ubiquitous data privacy protection combined with the blockchain technology. The above schemes make improvements to the scheme via the blockchain but require joint decryption by multiple querying parties when obtaining the results. T. Wang et al. [12] proposed a sharing and multi-party computation mode scheme in combination with the blockchain, using proxy re-encryption for data sharing so that querying parties can carry out decryption individually, but none of the encryption methods used in the above schemes are resistant to quantum attacks.

This scheme performs multi-party secure computation on the blockchain and pays a deposit during the computation of a transaction via a smart contract to prevent complicity between participants. The NTRU-based scheme design provides the scheme with resistance to quantum attacks. The decryption of ciphertext results by the result querier alone is achieved through proxy re-encryption, and the data owner can go offline after uploading the data and public key. The specific performance comparison is shown in

Table 1. Performance comparison of this paper with other SMPC solutions.

Literature	Not Relying on Trusted Third Parties	Verifiable	Privacy	Anti-Conspiracy	Individual Decryption Available to Enquirers	Resistant to Quantum Attacks
[8]	×	×	√	×	×	×
[9]	√	√	√	√	×	×
[10]	√	√	√	√	×	×
[11]	√	√	√	-	×	×
[12]	√	√	√	-	√	×
This paper	√	√	√	√	√	√

In the table, “√” means that the scheme can meet this requirement, “×” means that the scheme cannot meet this requirement, and “-” means that the literature does not describe whether the scheme can meet this requirement.

. As can be seen from the table, the scheme can meet the requirements of not relying on trusted third parties, being verifiable, having privacy protection, being anti-complicity, being individually decryptable by the querier, and being resistant to quantum attacks.

6. Conclusions

In this paper, to solve the problem that the encryption schemes used in most current secure multi-party computation schemes are not resistant to quantum attacks, and the secure multi-party computation schemes constructed via MKFHE cannot be decrypted by the result querier alone when the result is obtained, an NTRU-type multi-key fully homomorphic proxy re-encryption secure multi-party computation scheme in the blockchain environment was proposed. By designing a multi-key fully homomorphic encryption algorithm and a proxy re-encryption algorithm under the NTRU cryptosystem, the scheme meets the requirements of individual decryption by the querier, offline access by the data owner after uploading encrypted data, and resistance to quantum attacks. At the same time, the decentralized, immutable, open, and transparent nature of the blockchain provides a trusted execution environment for the scheme, providing a traceable and verifiable means of data. The blockchain’s incentives encourage honest cooperation between the various computing participants and prevent complicity.

The security of the scheme is based on the RLWE problem and the DSPR assumption, which is not a standard cryptographic assumption. Although there is no efficient way to break the DSPR assumption for the small-modulus case, it can be assumed that the DSPR assumption is secure, but this issue needs attention. Therefore, how to construct a secure multi-party computation scheme with NTRU-type multi-key fully homomorphic proxy re-encryption whose security depends only on the RLWE problem requires further research. In addition, how to apply the scheme proposed in this paper in the actual multi-party computation scenario is also an important research direction.