Detecting Cyber Attacks in Smart Grids Using Semi-Supervised Anomaly Detection and Deep Representation Learning
Abstract
:1. Introduction
2. Related Work
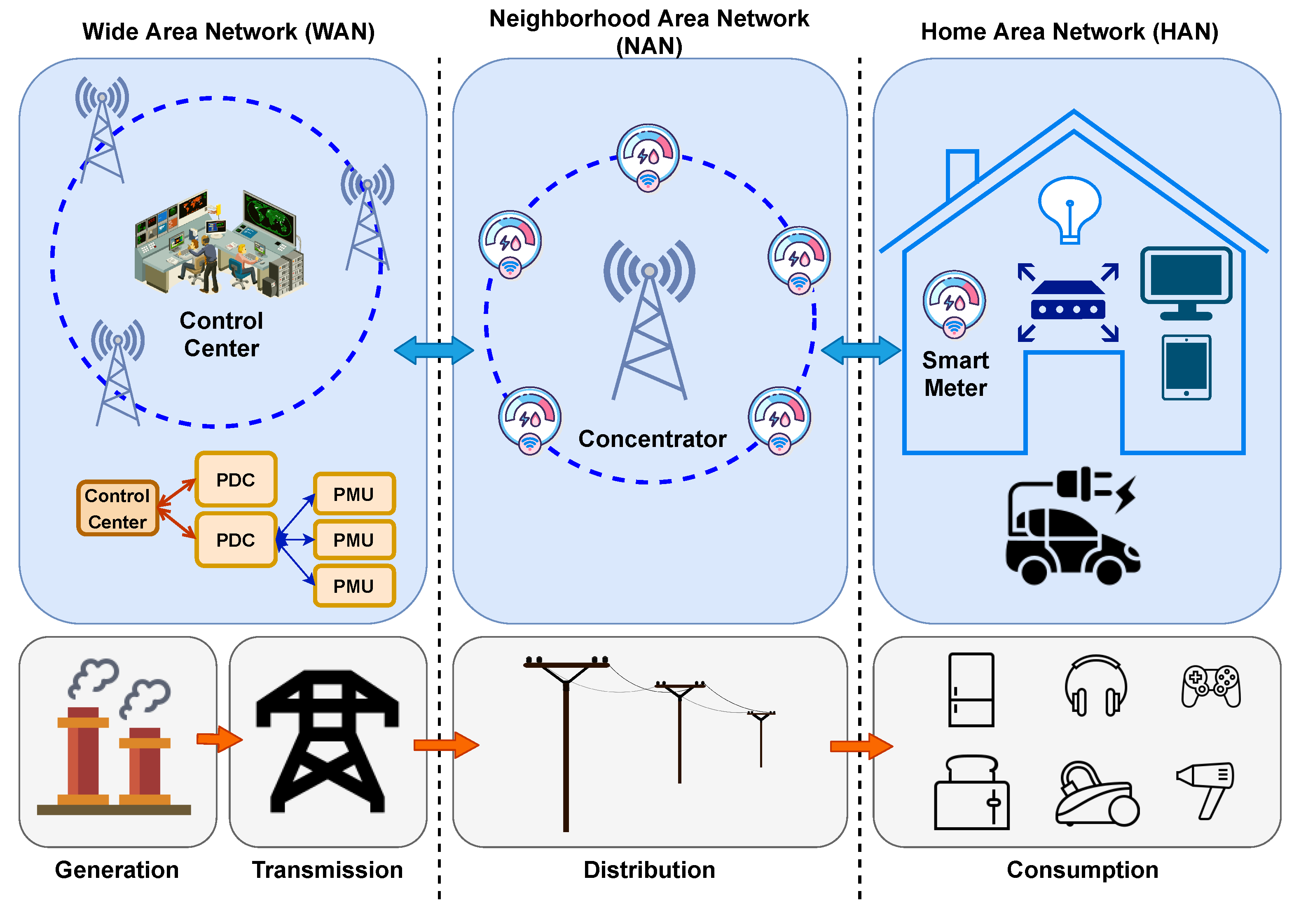
3. Power System Framework and Cyber Attack Datasets
- No event: Normal readings.
- Short-circuit fault: A single line-to-ground fault occurred and can specifically be found by reading the percentage range in data.
- Line maintenance: Operators toggle one or more IEDs to perform maintenance on certain parts of the power system and its components.
- Remote tripping command injection attack: Attackers can send commands that toggle IEDs to switch breakers when they can penetrate to the system.
- Relay setting change attack: Attackers change settings, such as disabling primary functions of the settings, causing the IEDs not to toggle the breakers whenever a valid fault or command occurs.
- Data injection attack: Attackers change the PMU measurements such as voltage, current and sequence components to mimic a valid fault causing the breakers to be switched off.
4. Methodology
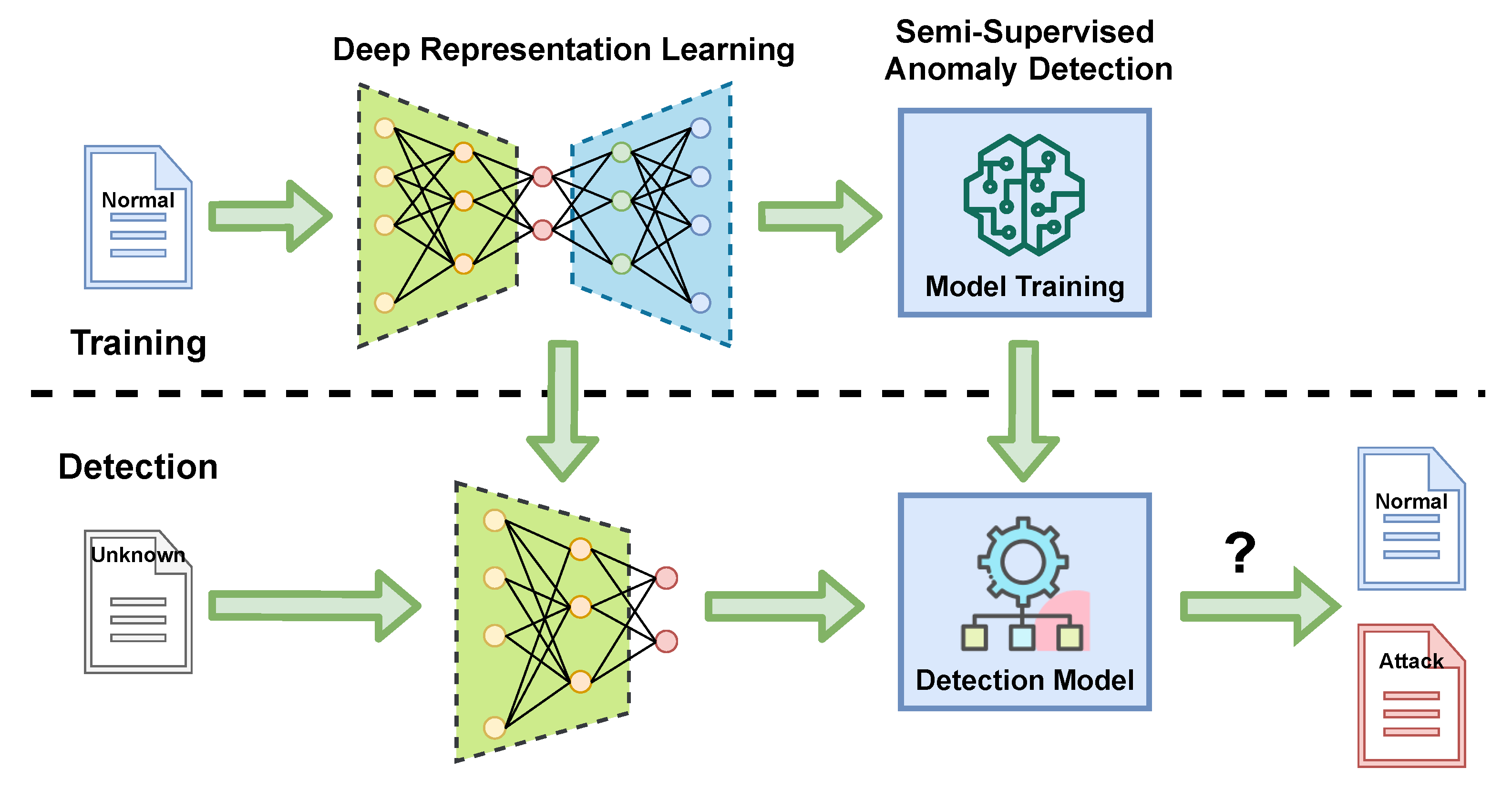
4.1. Overview of the Proposed Method
4.2. Feature Extraction
4.2.1. Deep Representation Learning with DAE
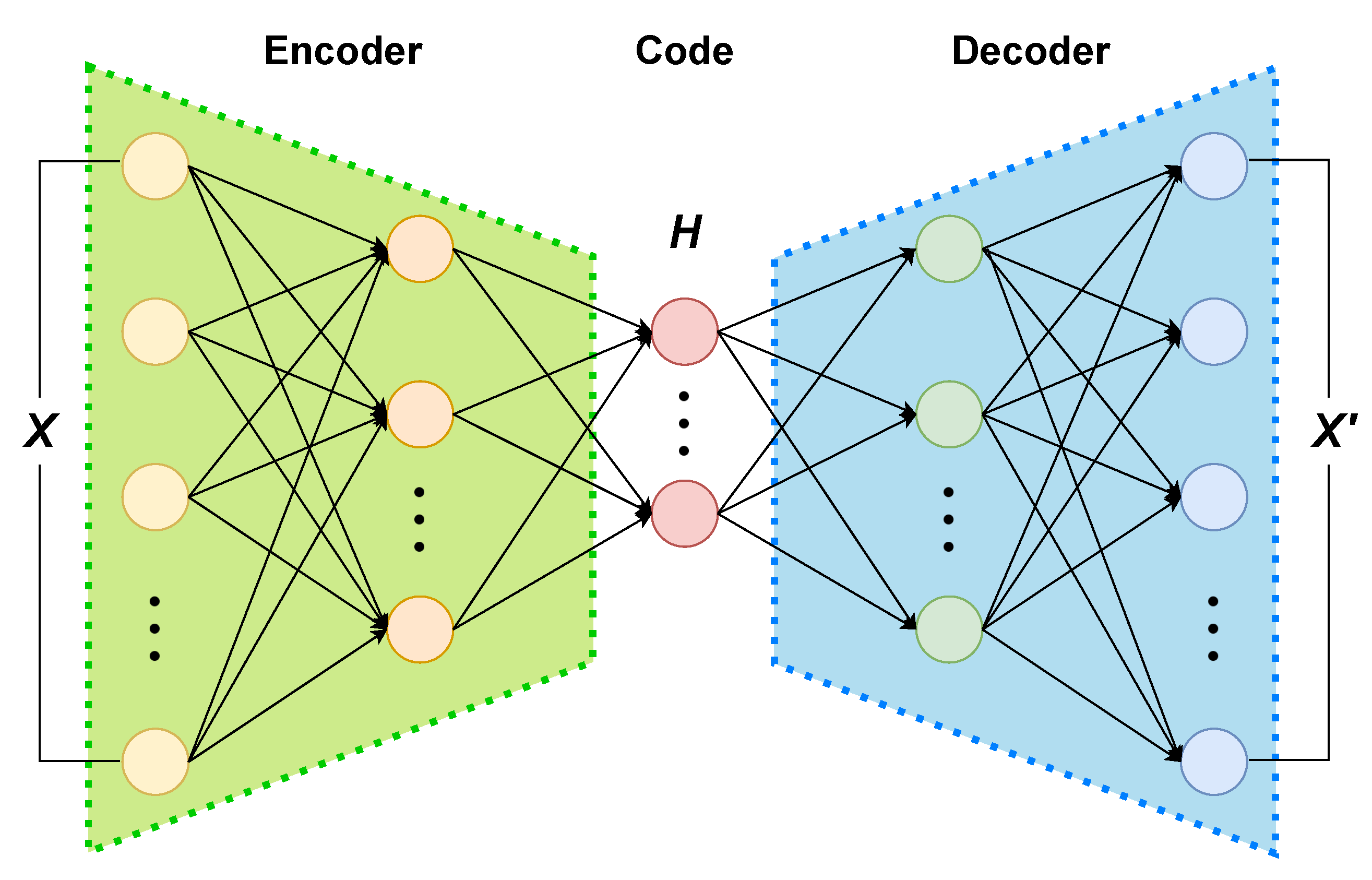
4.2.2. PCA
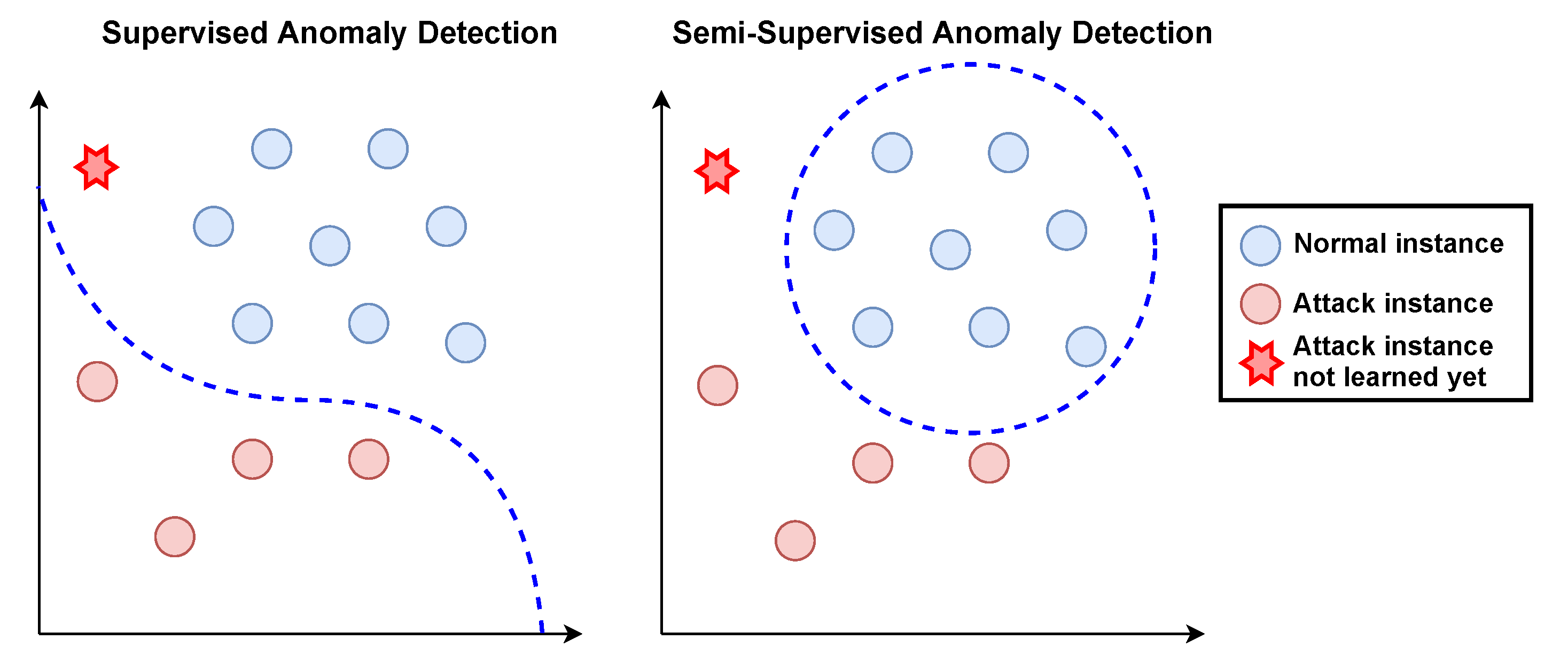
4.3. Semi-Supervised Anomaly Detection Algorithms
4.3.1. Linear Models
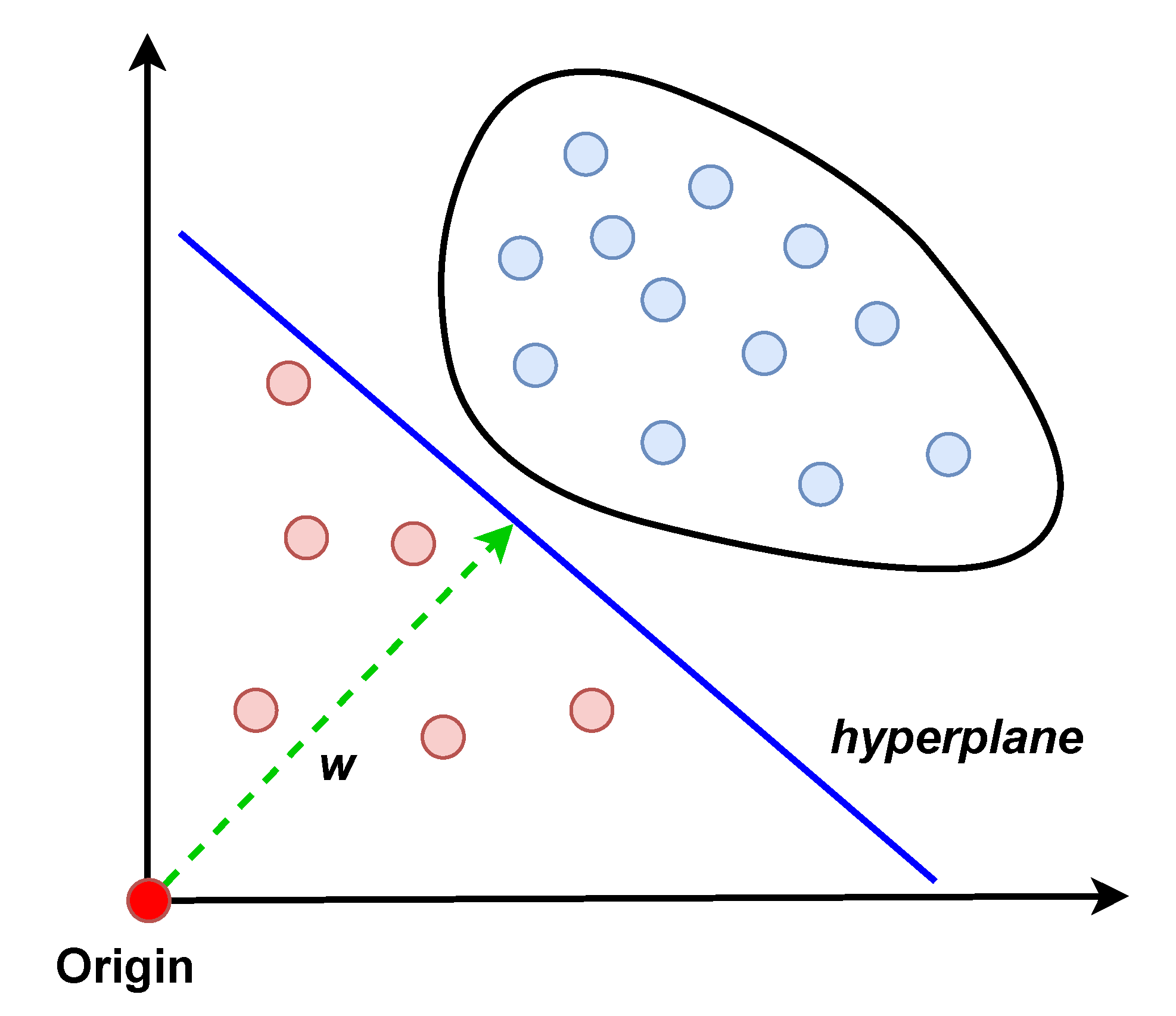
- One-class SVM (OCSVM): OCSVM was proposed in [29] as a semi-supervised version of the popular supervised learning algorithm, SVM. SVM finds a hyperplane to separate the data of two classes with the maximum margin. OCSVM needs to find the hyperplane with only normal data. In [29], the data are mapped into a high-dimensional space first. A hyperplane is then constructed to separate all normal instances from the origin with the maximum margin, which serves as the boundary to separate normal and abnormal instances. The working principle of OCSVM is illustrated in Figure 6. OCSVM solves a quadratic minimization problem to find the hyperplane, which is shown in Equation (5), where w is the normal vector of the hyperplane, is the distance from the hyperplane to the origin, are the separation errors for penalization, is the mapping function to map an instance into a high-dimensional space, and . is an important parameter for OCSVM which controls the number of training instances to be used as support vectors and the fraction of anomalies:
4.3.2. Proximity-Based Methods
- Histogram-based outlier score (HBOS): In [30], HBOS was proposed as a fast outlier detection method with a computational complexity of , which has been applied for problems involving a large amount of data such as network anomaly detection [31]. For each feature of the dataset, HBOS constructs a univariate histogram first. The frequency of occurrence of the values is used by HBOS for a categorical feature. Numerical features can be dealt with by two different methods:
- −
- The static method, which separates the range of feature values into k equal-width intervals—he number of instances falling in the interval is the height of the corresponding bin;
- −
- The dynamic method, which sorts the instances based on the feature values, where a fixed amount of successive values is then grouped into a bin—the width of the bin is determined by the feature values of the instances.
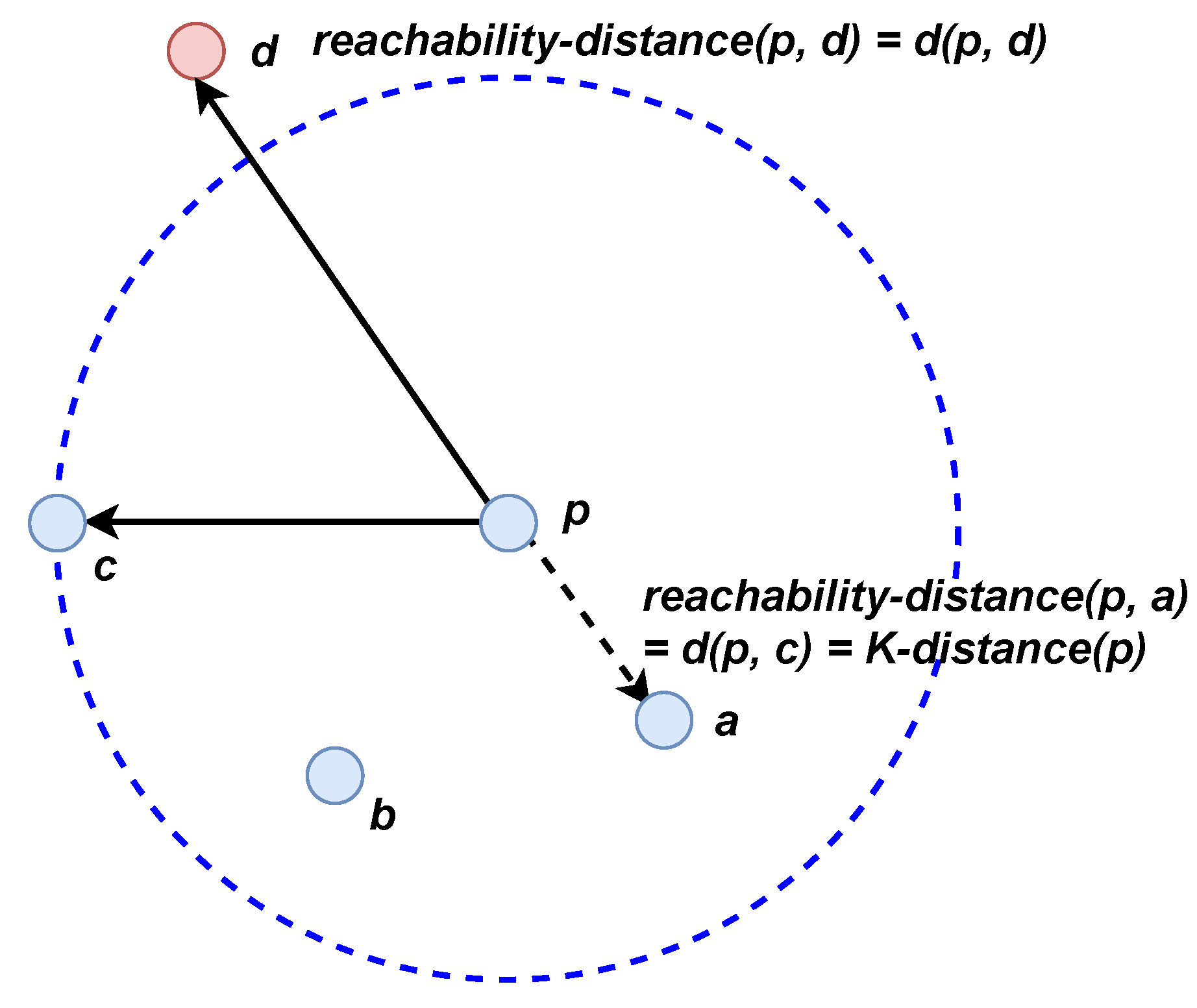
- Local outlier factor (LOF): LOF is a popular density-based outlier detection algorithm which estimates the abnormality of an instance according to its deviation with respect to its local neighbors [32]. The algorithm first defines the local locality of an instance p as its K nearest neighbors, , and the K- of p as the distance between p and its K-th nearest neighbor. The reachability distance between p and any other instance q is then calculated as the distance between p and q but at least K-. Figure 7 shows an example for determining the reachability distance where K equals 3. In Figure 7, the reachability distances of instances a to c are the same which equal to K-, i.e., . Since the instance d is not one of p’s K nearest neighbors, its reachability distance equals the real distance between p and d:
- Clustering-based local outlier factor (CBLOF): the LOF algorithm has a high computational complexity of . CBLOF was proposed by He et al. [33] as an efficient method with a computational complexity of . CBLOF first applies the Squeezer algorithm [34] to partition the input data into clusters, which are then divided into two groups of large cluster (LC) and small cluster (SC) based on a parameter b. Supposing that the clusters are ordered based on their sizes as , b separates the clusters as and , which is determined by satisfying the conditions in Equations (11) and (12) where and are two numeric parameters and is the size of the dataset. Equation (11) is derived based on the fact that a large portion of instances are normal so that they should be in the LC group, while Equation (12) means that clusters in the LC and SC groups should have significant differences in cluster size:The CBLOF score of p is defined as
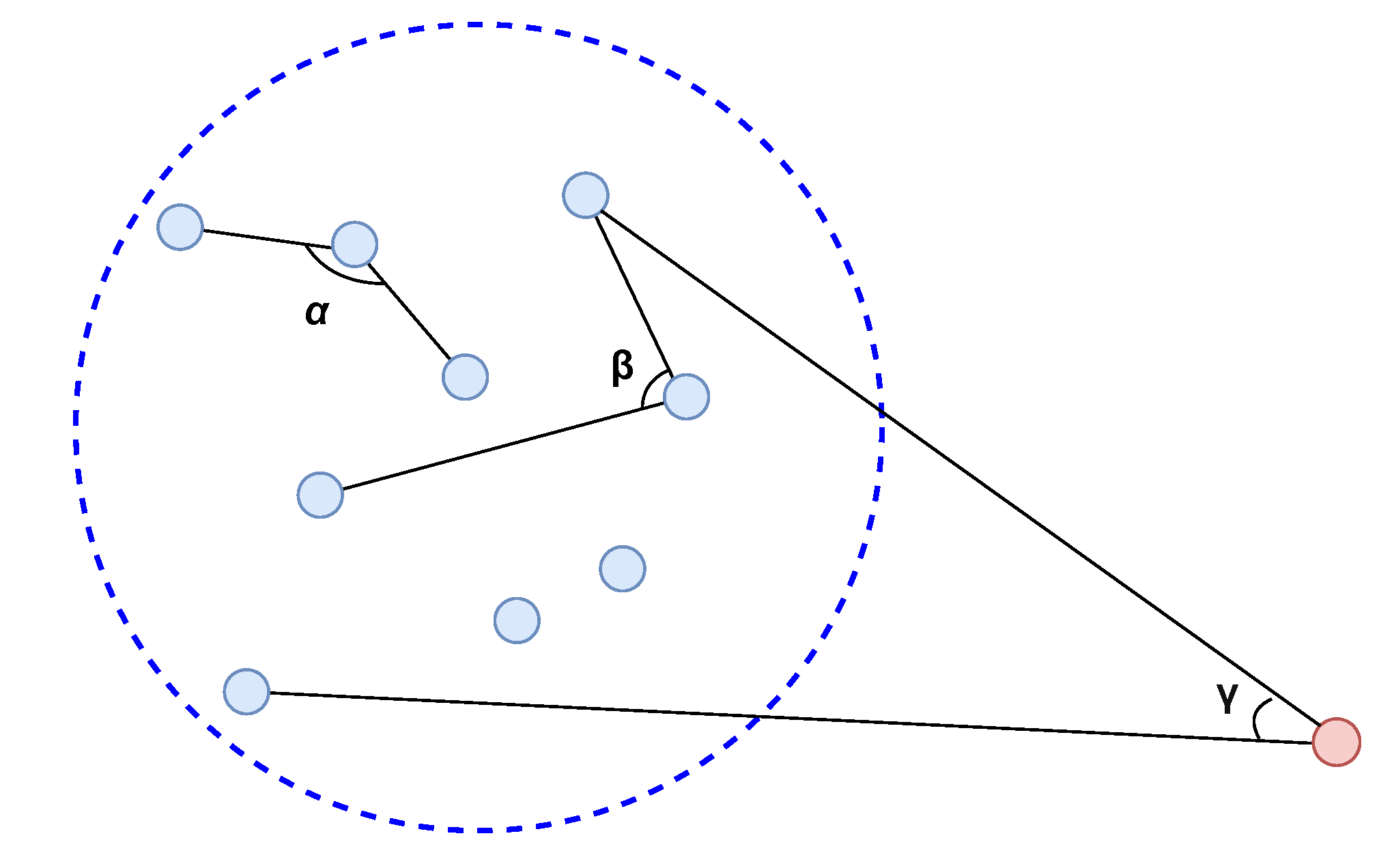
- Angle-based outlier detector (ABOD): ABOD was proposed in [35] as a proximity-based method to detect outliers in high-dimension data, which primarily relies on the angle between a pair of distance vectors instead of the distance. This is due to the fact that the distances may be quantitatively meaningless in high-dimensional space [36,37]. Figure 8 shows the working principle of ABOD. As a normal instance is generally located within a dense cluster with other normal instances, the variance of angles between its distance vectors is large as the angles vary in a wide range. On the other hand, an anomaly is generally located far from the cluster so that most of the angles between its distance vectors are small, leading to a low variance of angles. Since the computation of all angles for an instance has high complexity, an approximate method was proposed in [35] called FastABOD, which only calculates the angles of pairs within an instance’s K nearest neighbors.
- K-nearest-neighbor outlier detection (KNNOD): KNNOD was proposed in [38] as a simple but efficient proximity-based method for outlier detection. The information of an unknown instance’s K nearest neighbors is used by KNNOD to evaluate its abnormality. The anomaly score of the unknown instance is calculated as the distance of the instance to its K-th nearest neighbor, where the distance can be calculated based on any norm such as Euclidean distance ( norm) or Manhattan distance ( norm). A larger distance indicates a higher abnormality unknown instance. The average distance or the median distance to an unknown instance’s K nearest neighbors can also be used as the anomaly score, as proposed in [39].
4.3.3. Ensembles
- Feature bagging: Lazarevic and Kumar proposed feature bagging in [40] as an ensemble-based approach for outlier detection in high-dimensional and noisy data. Multiple-base outlier detection algorithms are combined in feature bagging and a randomly selected feature subset is used to train each base algorithm. The anomaly score of an unknown instance is determined by calculating the combination of the outputs of all base algorithms. LOF was used as the base outlier detection algorithm in [40].
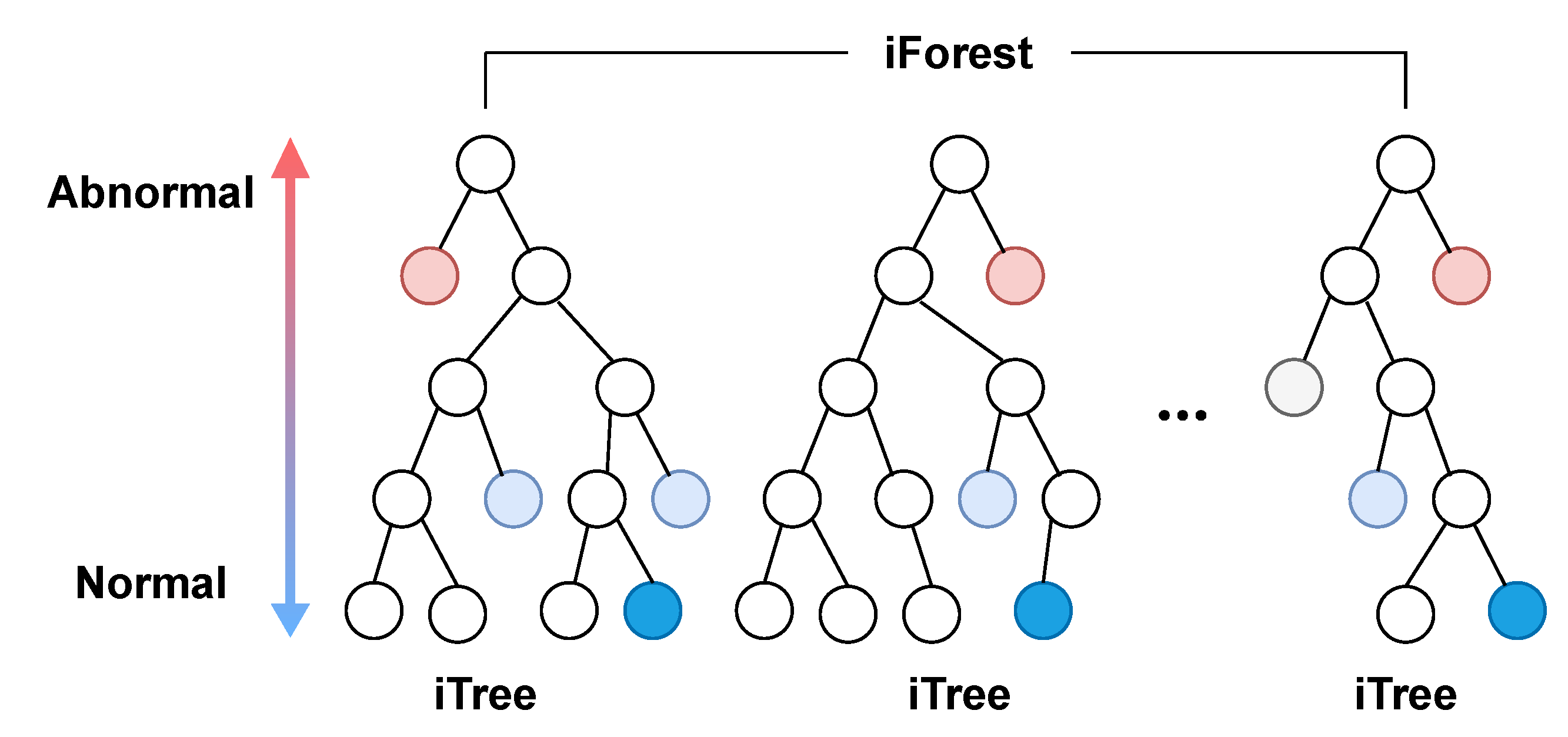
- Isolation forest (iForest): iForest was proposed by Liu et al. [41] for anomaly detection, which is an ensemble of binary search trees (BSTs) called isolation trees (iTrees). iTrees are built by randomly selected data subsets, features and split values. There are two types of nodes in an iTree: internal nodes with two children and leaf nodes without children. The rationale behind iForest is that abnormal instances are more likely to be isolated from other instances in early tree partitioning. Thus, the abnormality of an instance, p, is corresponding to the path length, , from the root node to the leaf node including p, which is illustrated in Figure 9. The average path length of all leaf node terminations can be estimated as the unsuccessful searches in BST, as shown in Equation (14):
5. Performance Evaluation and Results
5.1. Experiments and Performance Metrics
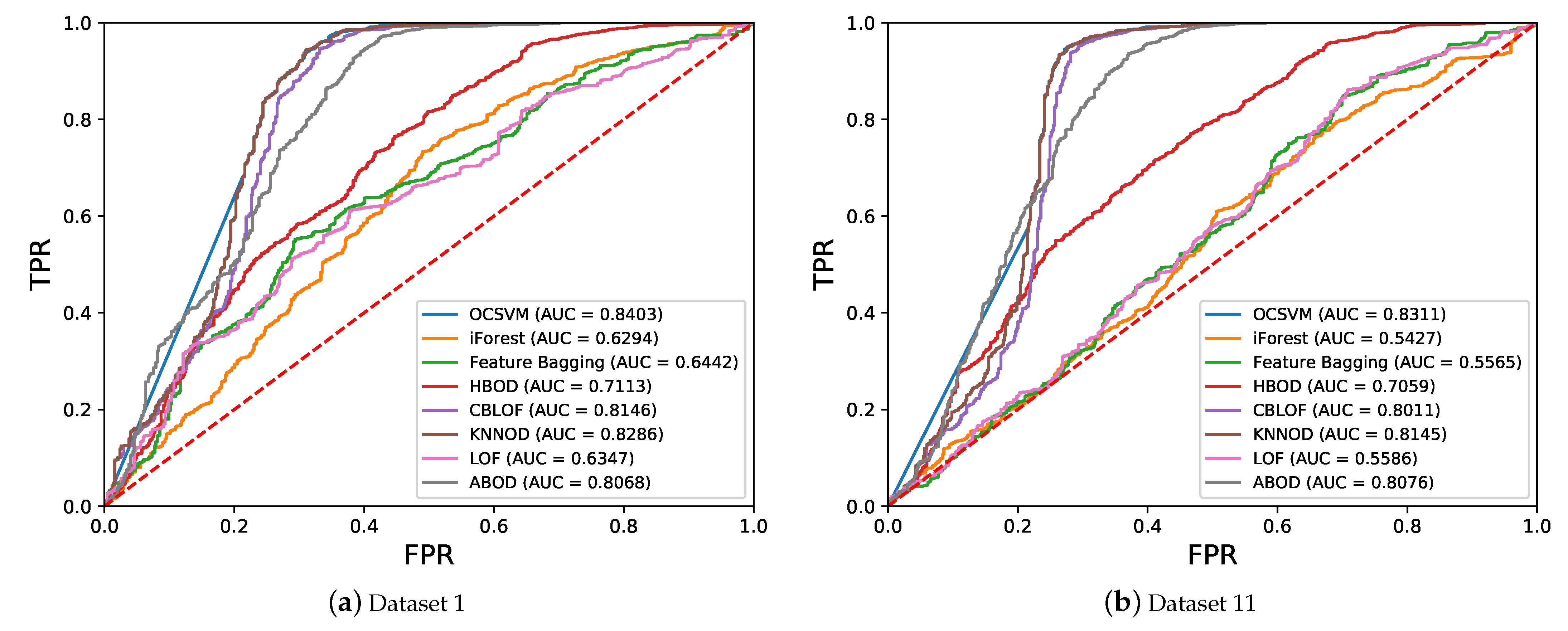
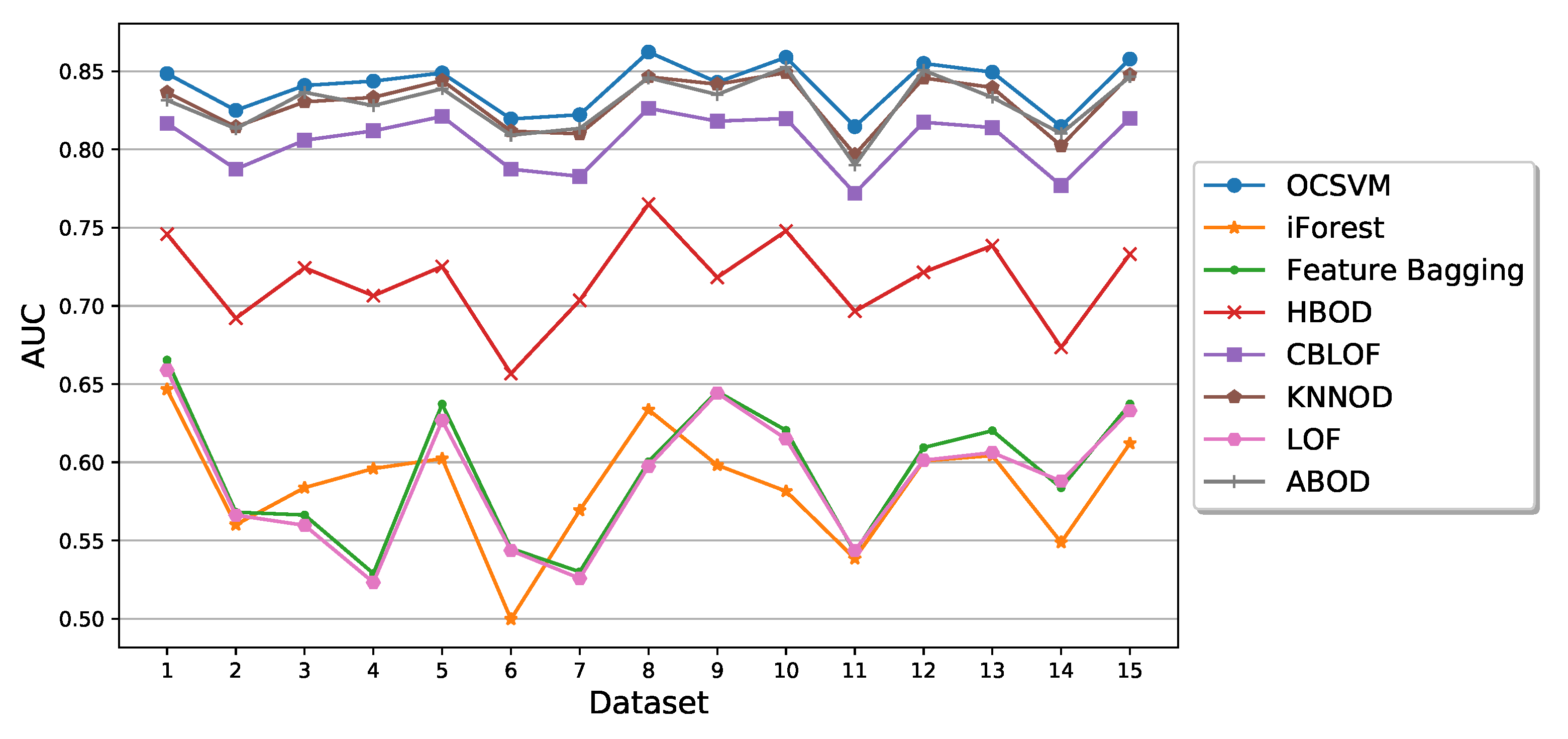
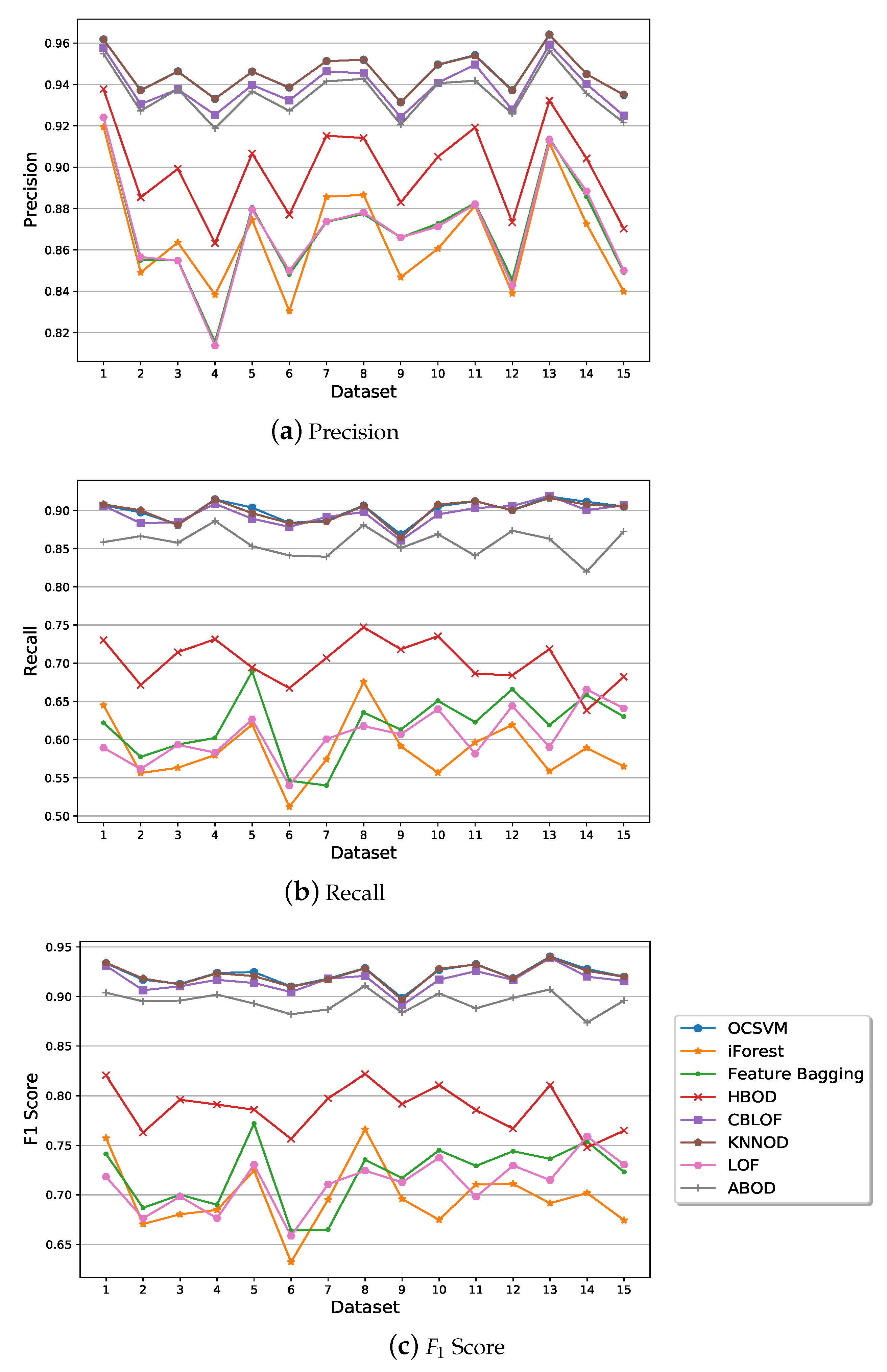
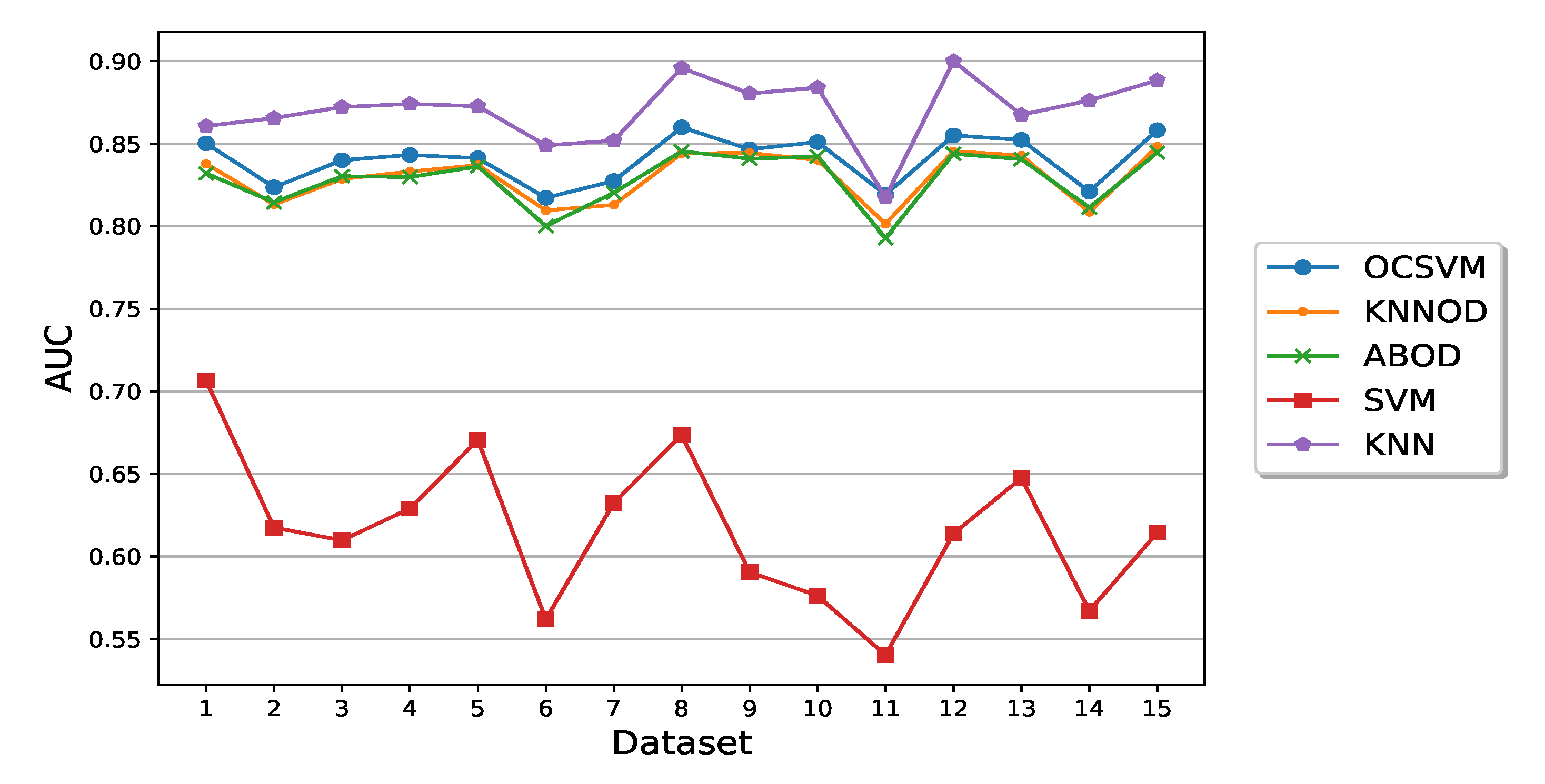
5.2. Performance of Semi-Supervised Anomaly Detection Algorithms
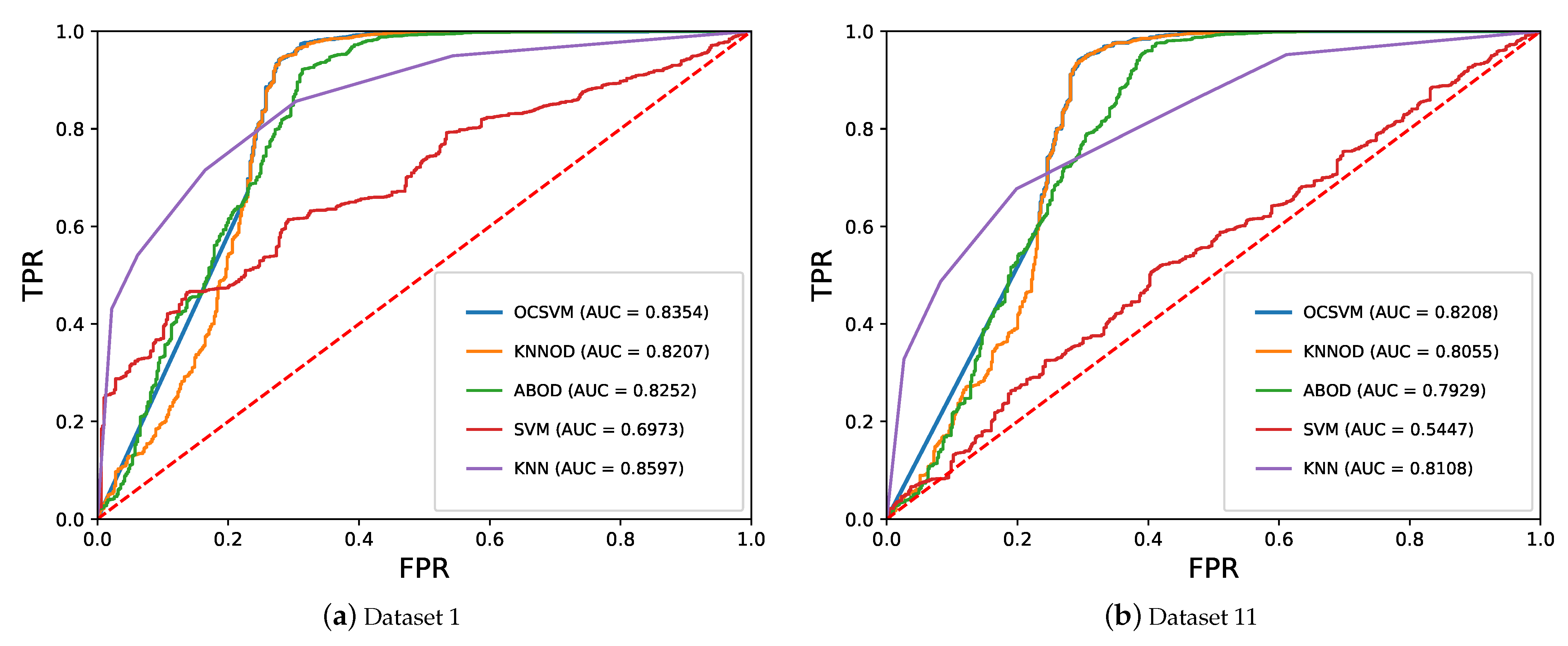
5.3. Performance Comparison of Semi-Supervised and Supervised Algorithms
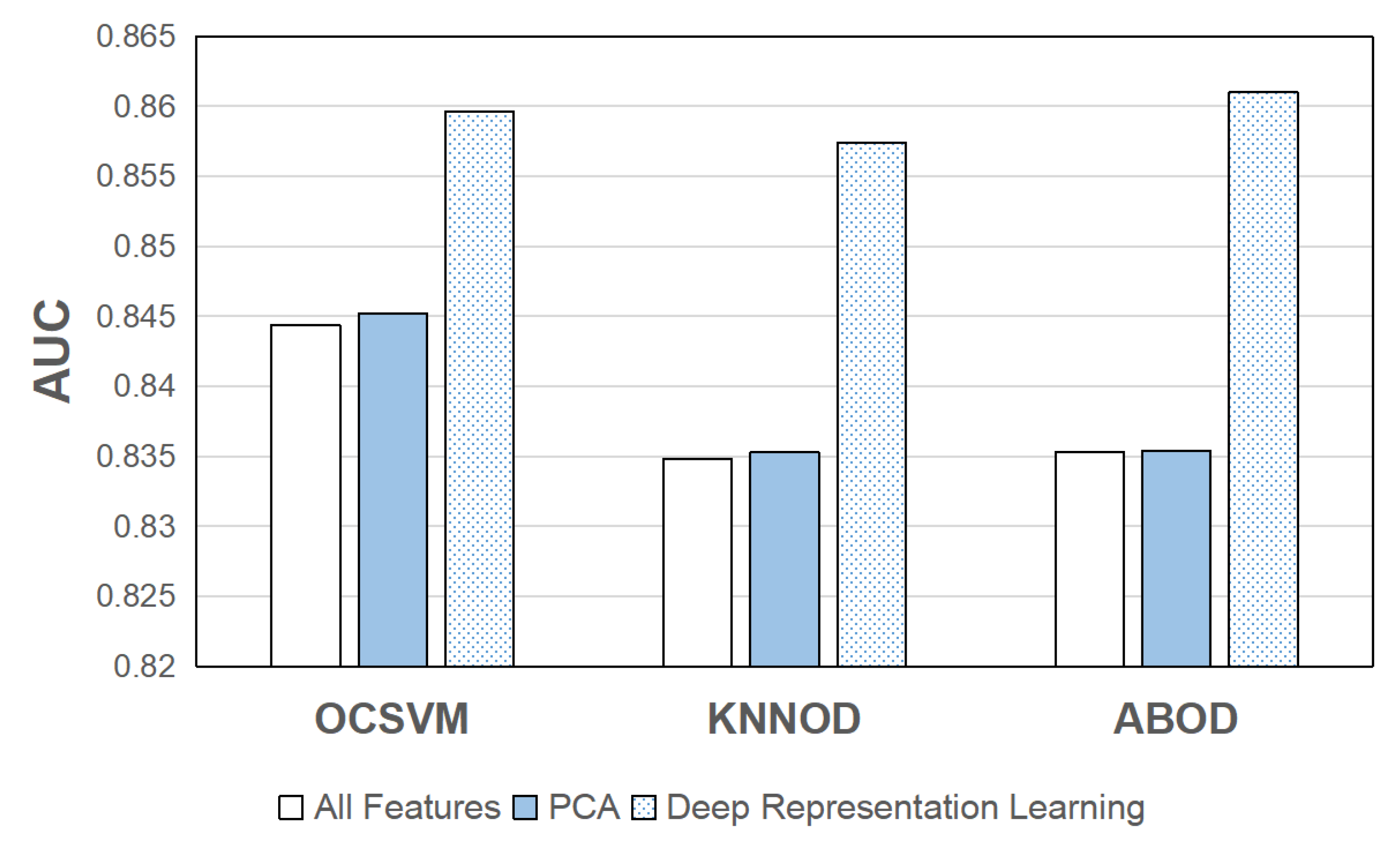
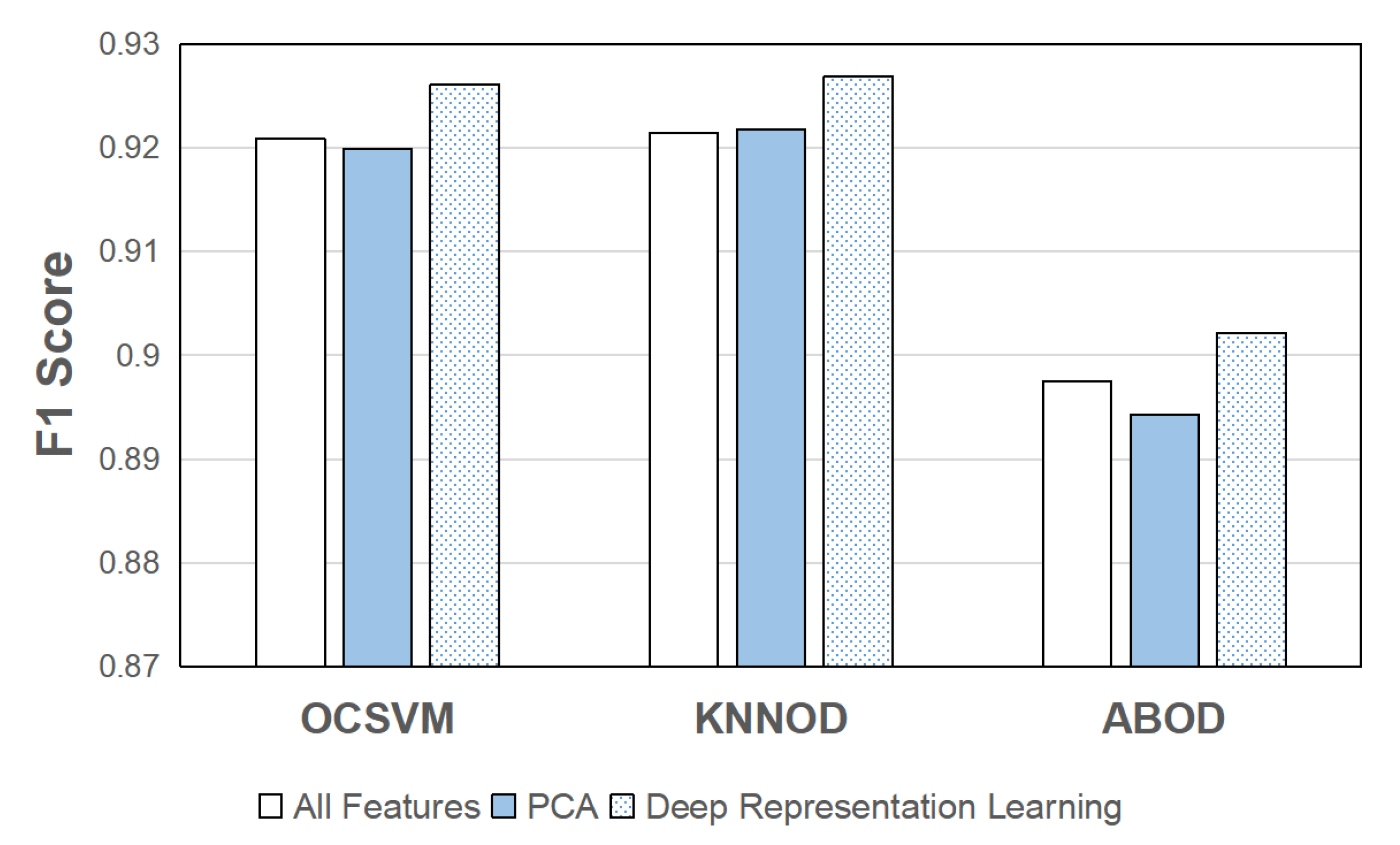
5.4. Performance Improvement with Deep Representation Learning
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inform. 2011, 7, 529–539. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980. [Google Scholar] [CrossRef]
- Dileep, G. A survey on smart grid technologies and applications. Renew. Energy 2020, 146, 2589–2625. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, Y.; Gjessing, S.; Yuen, C.; Xie, S.; Guizani, M. Cognitive radio based hierarchical communications infrastructure for smart grid. IEEE Netw. 2011, 25, 6–14. [Google Scholar] [CrossRef]
- Flick, T.; Morehouse, J. Securing the Smart Grid: Next Generation Power Grid Security; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Hink, R.C.B.; Beaver, J.M.; Buckner, M.A.; Morris, T.; Adhikari, U.; Pan, S. Machine learning for power system disturbance and cyber-attack discrimination. In Proceedings of the 2014 7th International Symposium on Resilient Control Systems (ISRCS), Denver, CO, USA, 19–21 August 2014; pp. 1–8. [Google Scholar]
- Salmon, D.; Zeller, M.; Guzmán, A.; Mynam, V.; Donolo, M. Mitigating the aurora vulnerability with existing technology. In Proceedings of the 36th Annual Western Protection Relay Conference, Spokane, WA, USA, 20–22 October 2009. [Google Scholar]
- Karnouskos, S. Stuxnet worm impact on industrial cyber-physical system security. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4490–4494. [Google Scholar]
- Alert, I.C. Cyber-Attack against Ukrainian Critical Infrastructure; Tech. Rep. ICS Alert (IR-ALERT-H-16-056-01); The Cybersecurity and Infrastructure Security Agency: Washington, DC, USA, 2016.
- Ashok, A.; Govindarasu, M.; Wang, J. Cyber-physical attack-resilient wide-area monitoring, protection, and control for the power grid. Proc. IEEE 2017, 105, 1389–1407. [Google Scholar] [CrossRef]
- Blair, S.; Burt, G.; Gordon, N.; Orr, P. Wide area protection and fault location: Review and evaluation of PMU-based methods. In Proceedings of the 14th International Conference on Developments in Power System Protection, Belfast, UK, 12–15 March 2018. [Google Scholar]
- Kim, T.T.; Poor, H.V. Strategic protection against data injection attacks on power grids. IEEE Trans. Smart Grid 2011, 2, 326–333. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Vural, F.T.Y.; Kulkarni, S.R.; Poor, H.V. Sparse attack construction and state estimation in the smart grid: Centralized and distributed models. IEEE J. Sel. Areas Commun. 2013, 31, 1306–1318. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.Y.; Yang, S.; McCann, J.A.; Lin, J.; Yang, X. Detection of false data injection attacks in smart-grid systems. IEEE Commun. Mag. 2015, 53, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Rawat, D.B.; Bajracharya, C. Detection of false data injection attacks in smart grid communication systems. IEEE Signal Process. Lett. 2015, 22, 1652–1656. [Google Scholar] [CrossRef]
- Huang, Y.; Tang, J.; Cheng, Y.; Li, H.; Campbell, K.A.; Han, Z. Real-time detection of false data injection in smart grid networks: An adaptive CUSUM method and analysis. IEEE Syst. J. 2016, 10, 532–543. [Google Scholar] [CrossRef] [Green Version]
- Ozay, M.; Esnaola, I.; Vural, F.T.Y.; Kulkarni, S.R.; Poor, H.V. Machine learning methods for attack detection in the smart grid. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1773–1786. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Tang, B.; He, H. Detection of false data attacks in smart grid with supervised learning. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1395–1402. [Google Scholar]
- Singh, V.K.; Govindarasu, M. Decision tree based anomaly detection for remedial action scheme in smart grid using pmu data. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Wang, D.; Wang, X.; Zhang, Y.; Jin, L. Detection of power grid disturbances and cyber-attacks based on machine learning. J. Inf. Secur. Appl. 2019, 46, 42–52. [Google Scholar] [CrossRef]
- Sakhnini, J.; Karimipour, H.; Dehghantanha, A. Smart grid cyber attacks detection using supervised learning and heuristic feature selection. In Proceedings of the 2019 IEEE 7th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2019; pp. 108–112. [Google Scholar]
- Esmalifalak, M.; Liu, L.; Nguyen, N.; Zheng, R.; Han, Z. Detecting stealthy false data injection using machine learning in smart grid. IEEE Syst. J. 2014, 11, 1644–1652. [Google Scholar] [CrossRef]
- Ahmed, S.; Lee, Y.; Hyun, S.H.; Koo, I. Unsupervised machine learning-based detection of covert data integrity assault in smart grid networks utilizing isolation forest. IEEE Trans. Inf. Forensics Secur. 2019, 14, 2765–2777. [Google Scholar] [CrossRef]
- Maglaras, L.A.; Jiang, J. Intrusion detection in SCADA systems using machine learning techniques. In Proceedings of the 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 626–631. [Google Scholar]
- Maglaras, L.A.; Jiang, J. Ocsvm model combined with k-means recursive clustering for intrusion detection in scada systems. In Proceedings of the 10th International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness, Rhodes, Greece, 18–20 August 2014; pp. 133–134. [Google Scholar]
- Song, F.; Guo, Z.; Mei, D. Feature selection using principal component analysis. In Proceedings of the 2010 International Conference on System Science, Engineering Design and Manufacturing Informatization, Yichang, China, 12–14 November 2010; Volume 1, pp. 27–30. [Google Scholar]
- Oh, M.; Zhang, L. DeepMicro: Deep representation learning for disease prediction based on microbiome data. Sci. Rep. 2020, 10, 6026. [Google Scholar]
- Aggarwal, C.C. An introduction to outlier analysis. In Outlier Analysis; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–34. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.J.; Shawe-Taylor, J.; Platt, J.C. Support vector method for novelty detection. NIPS 1999, 12, 582–588. [Google Scholar]
- Goldstein, M.; Dengel, A. Histogram-based outlier score (hbos): A fast unsupervised anomaly detection algorithm. In Proceedings of the 35th Annual German Conference on Artificial Intelligence, Saarbrücken, Germany, 24–27 September 2012; pp. 59–63. [Google Scholar]
- Paulauskas, N.; Baskys, A. Application of Histogram-Based Outlier Scores to Detect Computer Network Anomalies. Electronics 2019, 8, 1251. [Google Scholar] [CrossRef] [Green Version]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- He, Z.; Xu, X.; Deng, S. Discovering cluster-based local outliers. Pattern Recognit. Lett. 2003, 24, 1641–1650. [Google Scholar] [CrossRef]
- He, Z.; Xu, X.; Deng, S. Squeezer: An efficient algorithm for clustering categorical data. J. Comput. Sci. Technol. 2002, 17, 611–624. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Schubert, M.; Zimek, A. Angle-based outlier detection in high-dimensional data. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 444–452. [Google Scholar]
- Hinneburg, A.; Aggarwal, C.C.; Keim, D.A. What is the nearest neighbor in high dimensional spaces? In Proceedings of the 26th International Conference on Very Large Databases, Cairo, Egypt, 10–14 September 2000; pp. 506–515. [Google Scholar]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In Proceedings of the International Conference on Database Theory (ICDT), London, UK, 4–6 January 2001; pp. 420–434. [Google Scholar]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 427–438. [Google Scholar]
- Angiulli, F.; Pizzuti, C. Fast outlier detection in high dimensional spaces. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery (PKDD), Helsinki, Finland, 19–23 August 2002; pp. 15–27. [Google Scholar]
- Lazarevic, A.; Kumar, V. Feature bagging for outlier detection. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 22–24 August 2005; pp. 157–166. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Zhao, Y.; Nasrullah, Z.; Li, Z. Pyod: A python toolbox for scalable outlier detection. arXiv 2019, arXiv:1901.01588. [Google Scholar]
- Coffin, M.; Sukhatme, S. Receiver operating characteristic studies and measurement errors. Biometrics 1997, 53, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Perkins, N.J.; Schisterman, E.F. The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve. Am. J. Epidemiol. 2006, 163, 670–675. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Mao, Z. A dynamic ensemble outlier detection model based on an adaptive k-nearest neighbor rule. Inf. Fusion 2020, 63, 30–40. [Google Scholar] [CrossRef]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Asian Conference on Computer Vision (ACCV), Perth, Australia, 2–6 December 2018; pp. 622–637. [Google Scholar]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep learning for anomaly detection: A review. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]


| Scenario No. | Description of Event | Event Type |
|---|---|---|
| 1–6 | Short-circuit fault | Natural |
| 13, 14 | Line maintenance | Natural |
| 7–12 | Data injection | Attack |
| 15–20 | Remote tripping command injection | Attack |
| 21–30, 35–40 | Relay setting change | Attack |
| 41 | Normal readings | No Event |
| Features (No.) | Description |
|---|---|
| PA1:VH-PA3:VH (1–3) | Phase A–Phase C Voltage Phase Angle |
| PM1:V-PM3:V (4–6) | Phase A–Phase C Voltage Magnitude |
| PA4:IH-PA6:IH (7–9) | Phase A–Phase C Current Phase Angle |
| PM4:I-PM6:I (10–12) | Phase A–Phase C Current Magnitude |
| PA7:VH-PA9:VH (13–15) | Pos.–Neg.–Zero Voltage Phase Angle |
| PM7:V-PM9:V (16–18) | Pos.–Neg.–Zero Voltage Magnitude |
| PA10:VH-PA12:VH (19–21) | Pos.–Neg.–Zero Current Phase Angle |
| PM10:V-PM12:V (21–24) | Pos.–Neg.–Zero Current Magnitude |
| F (25) | Frequency for Relays |
| DF (26) | Frequency Delta (dF/dt) for Relays |
| PA:Z (27) | Appearance Impedance for Relays |
| PA:ZH (28) | Appearance Impedance Angle for Relays |
| S (29) | Status Flag for Relays |
| Algorithm | Parameters |
|---|---|
| OCSVM | RBF kernel, degree = 3, |
| HBOS | # of Bins = 50 |
| LOF | |
| CBLOF | # of Clusters = 50, , |
| ABOD | |
| KNNOD | |
| Feature bagging | # of base learners = 10, base learner = LOF |
| iForest | # of iTrees = 100 |
| KNN | |
| SVM | RBF kernel, degree = 3, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, R.; Rasband, C.; Zheng, J.; Longoria, R. Detecting Cyber Attacks in Smart Grids Using Semi-Supervised Anomaly Detection and Deep Representation Learning. Information 2021, 12, 328. https://doi.org/10.3390/info12080328
Qi R, Rasband C, Zheng J, Longoria R. Detecting Cyber Attacks in Smart Grids Using Semi-Supervised Anomaly Detection and Deep Representation Learning. Information. 2021; 12(8):328. https://doi.org/10.3390/info12080328
Chicago/Turabian StyleQi, Ruobin, Craig Rasband, Jun Zheng, and Raul Longoria. 2021. "Detecting Cyber Attacks in Smart Grids Using Semi-Supervised Anomaly Detection and Deep Representation Learning" Information 12, no. 8: 328. https://doi.org/10.3390/info12080328
APA StyleQi, R., Rasband, C., Zheng, J., & Longoria, R. (2021). Detecting Cyber Attacks in Smart Grids Using Semi-Supervised Anomaly Detection and Deep Representation Learning. Information, 12(8), 328. https://doi.org/10.3390/info12080328







