Integer-Wise Functional Bootstrapping on TFHE: Applications in Secure Integer Arithmetics ^†

Abstract

TFHE is a fast fully homomorphic encryption scheme proposed by Chillotti et al. in Asiacrypt’ 2018. Integer-wise TFHE is a generalized version of TFHE that can encrypt the plaintext of an integer that was implicitly presented by Chillotti et al., and Bourse et al. presented the actual form of the scheme in CRYPTO’ 2018. However, Bourse et al.’s scheme provides only homomorphic integer additions and homomorphic evaluations of a sign function. In this paper, we construct a technique for operating any 1-variable function in only one bootstrapping of the integer-wise TFHE. For applications of the scheme, we also construct a useful homomorphic evaluation of several integer arithmetics: division, equality test, and multiplication between integer and binary numbers. Our implementation results show that our homomorphic division is approximately $3.4$ times faster than any existing work and that its run time is less than 1 second for 4-bit integer inputs.

1. Introduction

Gentry first proposed a fully homomorphic encryption (FHE) construction in 2009 [1,2], and a variety of new features and hardness assumptions for FHE schemes [3,4,5,6,7,8,9,10,11,12,13] have been considered. The FHE performs computations on encrypted data without decryption of the data.

One notable application is secure computation in order to protect the secrecy of data against computation servers. An example of secure computation services is privacy-preserving machine learning as a service (MLaaS) [14,15]. In such a service, users want to hide sensitive data (e.g., genomic, anamnesis data, etc.) from the server and the server does not want to provide its cognitive models to users. FHE should be a fundamental component of secure multi-party computation (MPC). However, most applications are constructed without FHE operations because the MPC may require FHE operations many times and the run time of the operations would be substantial due to the inefficiency of FHE schemes.

Most FHE schemes consist of bit-wise or integer-wise encryption operations; the plaintext space is ${\mathbb{Z}}_2$ in bit-wise encryption, and the plaintext space is ${\mathbb{Z}}_p$ for some $p>2$ in integer-wise encryption [16,17,18]. Some schemes have been executed via integer arithmetics, but bit-wise integer addition and multiplication are not practical even though the bit-wise integer comparison algorithm is efficient [19]. In particular, the full adder algorithm has to execute homomorphic multiplication l times for an l-bit length integer. Thus, homomorphic integer multiplication based on the full adder must execute approximately $l^2$ [18] operations.

On the other hand, integer-wise FHE schemes can efficiently perform addition and multiplication because the construction of those calculations in a homomorphic manner is merely integer addition and multiplication. Recent studies [14,15,20,21] on secure MLaaS used integer-wise homomorphic encryption. Secure integer-wise comparison [22] and integer-wise division [23] have recently been proposed; however, arithmetic operations such as division are remain impractical. The design of efficient algorithms for basic arithmetic operations is an open issue required to reduce computational costs of the operations.

HElib [24], HEAAN [25], PALISADE [26], SEAL [27], and TFHE [6,7,8] are open-source implementations of homomorphic encryption. TFHE is a variant of the FHEW scheme [28] in which the bootstrapping procedure can be performed in less than 0.1 seconds, which is a major bottleneck of FHE. TFHE successfully improved the overall performance of arithmetic operations, although TFHE does not explicitly provide integer-wise arithmetics. Moreover, the number of bootstrapping operations required is equal to the number of bits. Bourse et al. [14] modified TFHE to enable integer-wise encryption, which only supports homomorphic integer addition and homomorphic evaluation of the sign function.

Contribution

In this paper, we present an approach where an arbitrary function is executed during a bootstrap procedure in the integer-wise TFHE scheme with a generalization of the constant variable “test vector” in the bootstrapping. Our bootstrapping procedure is applicable to homomorphic operations of fundamental arithmetics, where specific settings of the value of test vector are given: We propose the homomorphic equality test (Eq, Algorithm 6) and its variant, which test the equality between a ciphertext and a plaintext (ConstEq, Algorithm 7); the homomorphic multiplication between an integer and a binary number (MultbyBin, Algorithm 8); and homomorphic division, where the dividend is a ciphertext and the divisor is a constant plaintext (DivbyConst, Algorithm 9). Based on these building blocks, we propose a homomorphic algorithm for integer division (Div, Algorithm 10). Our implementation of Divruns approximately $3.4$ times faster than the fastest existing work. We also generalize the Divalgorithm to a homomorphic evaluation of an any 2-variable function.

2. Preliminaries

2.1. Notation

We write the security parameter as $\lambda$. We denote by $\mathbb{T}$ the torus of real numbers modulo 1, $\mathbb{R}/\mathbb{Z}$. For any ring $\mathcal{R}$, polynomials of the variable X with coefficients in $\mathcal{R}$ are denoted by $\mathcal{R}\left[X\right]$. We define ${\mathbb{R}}_N\left[X\right]:=\mathbb{R}\left[X\right]/(X^N+1)$, ${\mathbb{Z}}_N\left[X\right]:=\mathbb{Z}\left[X\right]/(X^N+1)$, and their quotient ${\mathbb{T}}_N\left[X\right]:={\mathbb{R}}_N\left[X\right]/{\mathbb{Z}}_N\left[X\right]$, which are the ring of polynomials of variable X with quotient $X^N+1$ and real coefficients modulo 1. Let $\mathbb{B}:=\{0,1\}$ be a set, and we write vectors in bold. We write $\mathbf{s}\stackrel{\$}{\leftarrow }\mathcal{S}$ when $\mathbf{s}$ is uniformly random sampled from $\mathcal{S}$. We denote by $\mathcal{U}\left(\mathcal{S}\right)$ the uniform distribution over the set $\mathcal{S}$, and we denote by $e\leftarrow \chi$ the process of sampling e according to the distribution $\chi$.

2.2. Background of TFHE

2.2.1. Learning with Errors

The learning with errors (LWE) problem is a computational problem introduced by Regev [29]. We use the torus variant of LWE, as in [6,30]. Let $n\in \mathbb{N}$, and let $\chi$ be a statistical distribution on $\mathbb{R}$. The torus LWE distribution for a fixed uniformly random secret vector $\mathbf{s}\stackrel{\$}{\leftarrow }{\mathbb{B}}^n$ is defined as follows:

$${\mathrm{LWE}}_{n,\mathbf{s},\chi }:=\left\{(\mathbf{a},b)\right|\mathbf{a}\stackrel{\$}{\leftarrow }{\mathbb{T}}^n,e\leftarrow \chi ,b=\mathbf{a}·\mathbf{s}+e\in \mathbb{T}\}.$$

The search-LWE problem is to find the secret vector $\mathbf{s}$ from LWE samples ${\left\{({\mathbf{a}}_i,{\mathbf{a}}_i·\mathbf{s}+e_i)\right\}}_{i=1}^m$ sampled from ${\mathrm{LWE}}_{n,\mathbf{s},\chi }$. The decision-LWE problem is to distinguish whether samples ${\left\{({\mathbf{a}}_i,\mathbf{s}·{\mathbf{a}}_i+e_i)\right\}}_{i=1}^m$ are drawn from ${\mathrm{LWE}}_{n,\mathbf{s},\chi }$ or $\mathcal{U}\left({\mathbb{T}}^{n+1}\right)$.

TFHE uses a sub-Gaussian distribution for the error distribution. A distribution ${\chi }_{\sigma }$ over $\mathbb{R}$ such that $\forall t\in \mathbb{R},E\left(e^{tX}\right)\le e^{{\sigma }^2{t}^2/2}$ is called $\sigma$-sub-Gaussian. Let Y and Z be independent random variables that are $\sigma$- and ${\sigma }^{\prime }$-sub-Gaussian, respectively. Then, for all k, $l\in \mathbb{R}$, $k·Y+l·Z$ is $\sqrt{k^2{\sigma }^2+l^2{{\sigma }^{\prime }}^2}$-sub-Gaussian.

2.2.2. Bit-Wise LWEEncryption

We briefly explain bit-wise Regev’s encryption [29], which is a building block of the (bit-wise) TFHE. Let $m\in \mathbb{B}$ be a plaintext. The encryption scheme works as follows:

• $\mathrm{Setup}\left(\lambda \right)$: Let the security parameter be $\lambda$. Select and fix public parameters $n=n\left(\lambda \right)$, $\sigma =\sigma \left(\lambda \right)$; then, $\mathrm{Setup}\left(\lambda \right)$ samples a secret key $\mathbf{s}\stackrel{\$}{\leftarrow }{\mathbb{B}}^n$ and outputs it.
• $\mathrm{Enc}(\mathbf{s},m)$: a uniformly random vector $\mathbf{a}\stackrel{\$}{\leftarrow }{\mathbb{T}}^n$ and a noise $e\leftarrow {\mathcal{D}}_{{\mathbb{T}}_N\left[X\right],\sigma }$ are sampled, where ${\mathcal{D}}_{{\mathbb{T}}_N\left[X\right],\sigma }$ is the Gaussian distribution over ${\mathbb{T}}_N\left[X\right]$ with a standard deviation $\sigma$. Then, the algorithm outputs a ciphertext $(\mathbf{a},b)$, where

  $$\begin{array}{c}\hfill b=\mathbf{a}·\mathbf{s}+e+m/2.\end{array}$$

  (1)
• $\mathrm{Dec}(\mathbf{s},(\mathbf{a},b\left)\right)$: The decryption algorithm returns $\lceil 2(b-\mathbf{a}·\mathbf{s})\rfloor$. It outputs plaintext correctly if the size of noise e is bounded as

  $$\begin{array}{c}\hfill \left|e\right|<1/4,\end{array}$$

  (2)
  Since $2(b-\mathbf{a}·\mathbf{s})=2e+m$, $\left|2e\right|<\frac{1}{2}$, thus $\lceil 2(b-\mathbf{a}·\mathbf{s})\rfloor =m$.

We explain later in Section 2.4 that this scheme can be extended to integer-wise encryptions.

2.2.3. Torus LWE(TLWE)

The General-LWEproblem (GLWE) proposed by Brakerski, Gentry, and Vaikuntanathan [31] is a general problem that includes the LWE problem, and the Ring-LWE problem proposed by Lyubashevsky, Peikert, and Regev in [32]. TLWE is a torus analogue of the GLWE problem. Let k be a positive integer, N be a power of 2, and $\chi$ be a probability distribution over ${\mathbb{R}}_N\left[X\right]$. A TLWE secret key $\overline{\mathbf{s}}$ is a vector of k polynomials over ${\mathbb{Z}}_N\left[X\right]$ with binary coefficients, denoted as $\overline{\mathbf{s}}\in {\mathbb{B}}_N{\left[X\right]}^k$. Given a polynomial message $\mu \in {\mathbb{T}}_N\left[X\right]$, a “fresh” TLWE ciphertext of $\mu$ under the key $\overline{\mathbf{s}}$ is a TLWE sample $(\overline{\mathbf{a}},\overline{b})\in {\mathbb{T}}_N{\left[X\right]}^k\times {\mathbb{T}}_N\left[X\right]$, where $\overline{\mathbf{a}}\leftarrow {\mathbb{T}}_N{\left[X\right]}^k$ and $\overline{b}=\overline{\mathbf{s}}·\overline{\mathbf{a}}+\mu +e$, where $e\leftarrow \chi$.

Let $(\overline{\mathbf{a}},\overline{b})$ be a TLWE ciphertext of a polynomial message $\mu \in {\mathbb{T}}_N\left[X\right]$ under a TLWE key $\overline{\mathbf{s}}\in {\mathbb{B}}_N{\left[X\right]}^k$. Notice that the coefficients of the TLWE sample is an LWE ciphertext of the constant term of the polynomial message $\mu$. We define the function SampleExtract that simply extracts the coefficients vector of the TLWE sample, and we denote the vector of coefficients of a polynomial $a\in {\mathbb{T}}_N\left(X\right)$ by $\mathrm{coefs}\left(a\right(X\left)\right)$. Then, we can obtain the extracted LWE ciphertext as $({\mathbf{a}}^{\prime },b^{\prime }):=\mathrm{SampleExtract}\left((\overline{\mathbf{a}},\overline{b})\right)$, where ${\mathbf{a}}^{\prime }=(\mathrm{coefs}\left({\overline{a}}_1(1/X)\right)$, …, $\mathrm{coefs}\left({\overline{a}}_k(1/X)\right))$ and $b^{\prime }$ is the constant term of the polynomial $\overline{b}$. This is the ciphertext encrypted with an extracted key ${\mathbf{s}}^{\prime }:=\mathrm{KeyExtract}\left(\overline{s}\right)$ $:=(\mathrm{coefs}\left({\overline{s}}_1\left(X\right)\right),\dots ,\mathrm{coefs}\left({\overline{s}}_k\left(X\right)\right))\in {\mathbb{Z}}^{kN}$.

As mentioned before, TLWE includes the LWE problem and the Ring-LWE problem. When $N>1$ is large and $k=1$, TLWE is the (binary-secret) Ring-LWE. Conversely, when $N=1$ and k is large, TLWE is the (binary-secret) LWE. Note that, in the TFHE library [33], $N=1024$ and $k=1$ by default; thus, TLWE is simply a Ring-LWE in the library, i.e., we can simple consider the TLWE samples as Ring-LWE samples $(a,b)\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$ in this paper.

2.2.4. TGSW

TGSW is a generalized variant of the GSW FHE scheme proposed by Gentry, Sahai, and Waters [10]. TGSW can be regarded as the matrix extension of TLWEbecause GSW is the matrix extension of LWE. Each row of a TGSW sample is a TLWE sample. As with TFHE [6], an external product ⊡ that maps $⊡:\mathrm{TGSW}\times \mathrm{TLWE}\to \mathrm{TLWE}$ can be defined. The product of the TGSW ciphertext of a polynomial message ${\mu }_{\mathrm{TGSW}}\in {\mathbb{T}}_N\left[X\right]$ and the TLWE ciphertext of a polynomial message ${\mu }_{\mathrm{TLWE}}\in T_N\left[X\right]$ becomes a TLWE ciphertext of a polynomial message $({\mu }_{\mathrm{TGSW}}·{\mu }_{\mathrm{TLWE}})\in T_N\left[X\right]$. We refer the readers to [6] for more details.

2.3. Overview of TFHE Bootstrapping

We refer to the bootstrapping procedure of the TFHE in [6]. We present the bootstrapping algorithm in Algorithm  1. As we mentioned before, in the default settings of the TFHE library [33], the dimension of the TLWE sample is set as $k=1$. This means that the TLWE sample is simply the Ring-LWEsample $(\overline{a},\overline{b})\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$. In the rest of this paper, we set $k=1$: we also consider the TLWE sample to be the Ring-LWEsample $(a,b)\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$.

Algorithm 1: TFHE bootstrapping [6] for binary arithmetics.

Input: An LWE sample $(\mathbf{a},b)\in {\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{in}}\right)$whose plaintext $m_{\mathrm{in}}\in \{0,1\}$, a constant $m_{\mathrm{set}}\in \{0,1\}$, a    bootstrapping key ${\mathrm{BK}}_{\mathbf{s}\to {\mathbf{s}}^{″},\alpha }$, and a keyswitching key ${\mathrm{KS}}_{{\mathbf{s}}^{\prime }\to \mathbf{s},\gamma }$, where ${\mathbf{s}}^{\prime }=\mathrm{KeyExtract}\left({\mathbf{s}}^{″}\right)$. Output: An LWE sample ${\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{out}}\right)$, where $m_{\mathrm{out}}=m_{\mathrm{in}}·m_{\mathrm{set}}$. 1 $\mu :=\frac{m_{\mathrm{set}}}{2}\in \mathbb{T}$, ${\mu }^{\prime }=\frac{\mu }{2}\in \mathbb{T}$ 2 $\overline{b}:=\lceil 2Nb\rfloor$, $\overline{a_i}:=\lceil 2N{a}_i\rfloor$ for each $i\in [1,n]$ 3 testv $:=(1+X+\dots +X^{N-1})·X^{\frac{N}{2}}·{\mu }^{\prime }\in {\mathbb{T}}_N\left[X\right]$ 4 $\mathrm{ACC}\leftarrow X^{\overline{b}}·(\mathbf{0},\mathrm{testv})\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$ 5 for $i=1$ to n do $\mathrm{ACC}\leftarrow [\mathbf{h}+(X^{-{\overline{a}}_i}-1)·{\mathrm{BK}}_i]⊡\mathrm{ACC}$ $\phantom{(}$                            //$\phantom{(}$$\mathrm{ACC}=\mathrm{TLWE}(X^{(\overline{b}-\overline{a}s)}·testv)=\mathrm{TLWE}(X^{(m_{\mathrm{in}}N+e)}·testv)$$\phantom{(}$ 6 $\mathbf{u}:=(\mathbf{0},{\mu }^{\prime })+\mathrm{SampleExtract}\left(\mathrm{ACC}\right)$       //  $\phantom{(}$$\mathrm{msg}\left(\mathrm{SampleExtract}\left(\mathrm{ACC}\right)\right)={\mu }^{\prime }(m_{\mathrm{in}}=1)$, $-{\mu }^{\prime }(m_{\mathrm{in}}=0)$$\phantom{(}$ 7  return  ${\mathrm{KeySwitch}}_{\mathrm{KS}}\left(\mathbf{u}\right)$

2.3.1. Input

The input for the bootstrapping is an LWE ciphertext of message binary message $m_{\mathrm{in}}\in \mathbb{B}$, $(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$, where $b=\mathbf{a}·\mathbf{s}+e+\frac{m_{\mathrm{in}}}{2}$. The noise e is sampled according to the distribution such that $\left|e\right|<\frac{1}{4}$ to satisfy the condition for correct decryption of the LWE encryption.

2.3.2. Rounding

After the rounding operation in line 2, we obtain an rounded LWE ciphertext $(\overline{\mathbf{a}},\overline{b})\in {\mathbb{Z}}_{2N}^n\times {\mathbb{Z}}_{2N}$, where

$$\begin{array}{cc}\hfill \overline{b}-\overline{\mathbf{a}}·\mathbf{s}& =\lceil 2Nb\rfloor -\sum _{i=1}^n\lceil 2N{a}_i\rfloor s_i=2Nb+{\xi }_0-\sum _{i=1}^n(2N{a}_i+{\xi }_i)s_i\hfill \\ \hfill & =2N\left(e+m_{\mathrm{in}}/2\right)+e_{\mathrm{ACC}},\hfill \end{array}$$

(3)

and $e_{\mathrm{ACC}}:={\xi }_0-{\sum }_{i=1}^n{\xi }_i{s}_i$ and ${\xi }_0,\dots {\xi }_n$ are rounding errors that are uniformly distributed over $(-\frac{1}{2},\frac{1}{2})$. Note that $e_{\mathrm{ACC}}=0$ when the coefficients $(\mathbf{a},b)$ are in $\frac{1}{2N}\mathbb{Z}/\mathbb{Z}$; thus, we can ignore $e_{\mathrm{ACC}}$ when we use the default parameter setting in the TFHE library of $N=1024$.

2.3.3. BlindRotate

At the line 4, $\mathrm{ACC}$ is a trivial TLWE ciphertext $(0,X^{\overline{b}}·\mathrm{testv})\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$; thus, ${\parallel \mathrm{Error}\left({\mathrm{ACC}}_1\right)\parallel }_{\infty }=0$. After the loop in line 5, from [6] (Theorem 4.6), we have

$$\begin{array}{cc}\hfill {∥\mathrm{Error}\left({\mathrm{ACC}}_n\right)∥}_{\infty }& \le 2n(k+1)lN\beta {\alpha }_{\mathrm{BK}}+n(1+kN)ϵ,\hfill \end{array}$$

(4)

where $\beta =B_g/2$ and $ϵ=1/2B_g^l$ are the precision parameters of the gadget decomposition, $l\in \mathbb{N}$, $B_g\in \mathbb{N}$, and ${\alpha }_{\mathrm{BK}}$ is a error size ratio of the bootstrapping key BK. After the loop in line 5, the message of ACC becomes a polynomial $X^{\overline{b}-\overline{\mathbf{a}}\mathbf{s}}·\mathrm{testv}$. From (3) and $e_{\mathrm{ACC}}=0$, we have $\psi \left((\overline{\mathbf{a}},\overline{b})\right):=\overline{b}-\overline{\mathbf{a}}·\mathbf{s}=2N\left(e+m_{\mathrm{in}}/2\right).$ Notice that

$$X^{\overline{b}-\overline{\mathbf{a}}·\mathbf{s}}·\mathrm{testv}=X^{\overline{b}-\overline{\mathbf{a}}·\mathbf{s}+\frac{N}{2}}·(1+X^{-1}+\dots +X^{-(N-1)})·{\mu }^{\prime },$$

where $\overline{b}-\overline{\mathbf{a}}·\mathbf{s}+\frac{N}{2}=2Ne+\frac{N}{2}+N{m}_{\mathrm{in}}$, and from (2), we obtain $0<2Ne+\frac{N}{2}<N$. Therefore, we have the following facts:

$$\begin{array}{cc}\hfill \overline{b}-\overline{\mathbf{a}}·\mathbf{s}+\frac{N}{2}& \in \left\{\begin{array}{cc}[0,N)\hfill & (m_{\mathrm{in}}=0),\hfill \\ [N,2N)\hfill & (m_{\mathrm{in}}=1),\hfill \end{array}\right.\hfill \\ \mathrm{the\; constant\; term\; of}\hfill X^{\overline{b}-\overline{\mathbf{a}}·\mathbf{s}}·\mathrm{testv}& =\left\{\begin{array}{cc}{\mu }^{\prime }\hfill & (m_{\mathrm{in}}=0),\hfill \\ -{\mu }^{\prime }\hfill & (m_{\mathrm{in}}=1).\hfill \end{array}\right.\hfill \end{array}$$

Note that, here, we used the fact that $X^{-i}\equiv -X^{N+i}$, which follows the definition $X^N+1\equiv 0$.

2.3.4. Extract

The output of SampleExtract in line 6 is simply the coefficients vector of the TLWE sample over the torus $({\mathbf{a}}^{\prime },b^{\prime }):=(\mathrm{coefs}\left(a^{\prime \prime }\left(X\right)\right),b_0^{\prime \prime })\in {\mathbb{T}}^N\times \mathbb{T}$, where $\mathrm{coefs}\left(a^{″}\left(X\right)\right)$ is a coefficient vector of $a^{″}\in {\mathbb{T}}_N\left(X\right)$ and $b_0^{″}\in \mathbb{T}$ is a constant term of the polynomial $b^{″}\in {\mathbb{T}}_N\left(X\right)$. The message of the extracted sample $\mathrm{msg}\left(({\mathbf{a}}^{\prime },b^{\prime })\right)$ is the constant term of the polynomial $(X^{\overline{b}-\overline{\mathbf{a}}·\mathbf{s}}·\mathrm{testv})$. The message is ${\mu }^{\prime }$ if $m_{\mathrm{in}}=0$ and $-{\mu }^{\prime }$ if $m_{\mathrm{in}}=1$. Therefore,

$$\begin{array}{c}\hfill \mathrm{msg}\left(\mathbf{u}\right)={\mu }^{\prime }+\mathrm{msg}(\mathrm{SampleExtract}\left(\mathrm{ACC}\right)=\left\{\begin{array}{cc}2{\mu }^{\prime }(=\mu )\hfill & (m_{\mathrm{in}}=0),\hfill \\ 0\hfill & (m_{\mathrm{in}}=1);\hfill \end{array}\right.\end{array}$$

i.e., $\mathrm{msg}\left(\mathbf{u}\right)=\mu ·(1-m_{\mathrm{in}})$. The size of the error of $({\mathbf{a}}^{\prime },b^{\prime })$ remains ${∥\mathrm{Error}\left(\mathrm{ACC}\right)∥}_{\infty }$ since SampleExtract adds no extra noise.

2.3.5. KeySwitch

The output of KeySwitchin line 7 is a TLWE sample $(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$ of a message $\frac{m_{\mathrm{out}}}{2}\in \mathbb{T}$, with the secret key $\mathbf{s}$. We write this TLWE ciphertext as ${\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{out}}\right)$ for simplicity of the notation. The KeySwitchprocedure is the same as that in [6]. We refer to KeySwitch in Algorithm 2 for completeness of this paper. The keyswitching key is defined as ${\mathrm{KS}}_{{\mathbf{s}}^{\prime }\to \mathbf{s},\gamma ,t}$, where ${\mathrm{KS}}_{i,j}\in {\mathrm{LWE}}_{\mathbf{s},\gamma }(s_i^{\prime }·2^{-j})$ for $i\in [1,N]$ and $j\in [1,t]$. Here, $\gamma \in \mathbb{R}$ is a parameter that decides the size of the noise of the key switching key, which satisfies ${∥\mathrm{Error}\left({\mathrm{KS}}_{i,j}\right)∥}_{\infty }\le \gamma$, and $t\in \mathbb{N}$ is a parameter that decides the precision. From [6] (Lemma 4.3), we obtain

$$\begin{array}{cc}\hfill {\psi }_{\mathbf{s}}(\mathbf{a},b)& ={\psi }_{\mathbf{s}}(\mathbf{0},b^{\prime })-\sum _{i=1}^N\sum _{j=1}^t{a}_{i,j}^{\prime }{\phi }_{\mathbf{s}}\left({\mathrm{KS}}_{i,j}\right),\hfill \\ \hfill & ={\psi }_{{\mathbf{s}}^{\prime }}({\mathbf{a}}^{\prime },b^{\prime })-\sum _{i=1}^N\sum _{j=1}^t{a}_{i,j}^{\prime }\mathrm{Error}\left({\mathrm{KS}}_{i,j}\right)+\sum _{i=1}^N(a_i^{\prime }-{\overline{a}}_i^{\prime })s_i^{\prime }.\hfill \end{array}$$

Therefore, we have the bound on the size of the noise as follows:

$$\begin{array}{cc}\hfill {∥\mathrm{Error}(\mathbf{a},b)∥}_{\infty }& \le {∥\mathrm{Error}\left(\mathrm{ACC}\right)∥}_{\infty }+Nt\gamma +N{2}^{-(t+1)},\hfill \\ \hfill & \le 2n(k+1)lN\beta {\alpha }_{\mathrm{BK}}+n(1+kN)ϵ+Nt\gamma +N{2}^{-(t+1)},\hfill \end{array}$$

where the second inequality follows from (4). The bootstrapping outputs a “fresh” LWE ciphertext when the parameters satisfy the following:

$$2n(k+1)lN\beta {\alpha }_{\mathrm{BK}}+n(1+kN)ϵ+Nt\gamma +N{2}^{-(t+1)}<1/4.$$

(5)

Algorithm 2: KeySwitch.

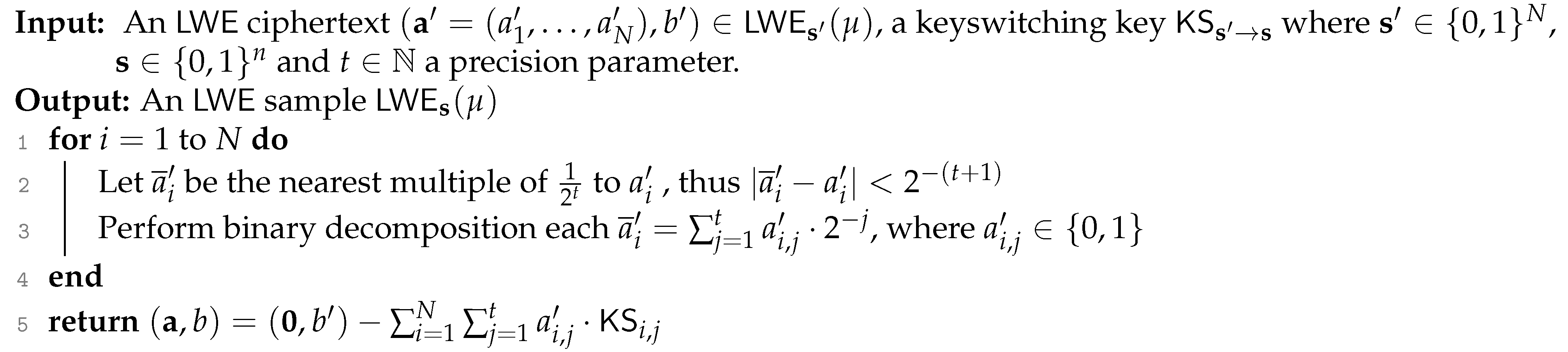This upper bound follows from (2).

2.4. Integer-Wise LWE Encryption

We use a integer-extended variant of Regev’s encryption following the scheme proposed by Bourse et al. in [14]. Let $\tau \in \mathbb{N}$, the message $m\in \{-\tau ,\dots ,\tau -1\}$. The integer-wise LWE encryption works as follows:

• $\mathrm{Setup}\left(\lambda \right)$: On a input security parameter $\lambda$, $n=n\left(\lambda \right)$ and $\sigma =\sigma \left(\lambda \right)$ are fixed; a secret key $\mathbf{s}\stackrel{\$}{\leftarrow }{\mathbb{B}}^n$ is output.
• $\mathrm{Enc}(\mathbf{s},m)$: A uniformly random vector $\mathbf{a}\stackrel{\$}{\leftarrow }{\mathbb{T}}^n$ and a noise $e\leftarrow {\mathcal{D}}_{{\mathbb{T}}_N\left[X\right],\sigma }$ are sampled, where ${\mathcal{D}}_{{\mathbb{T}}_N\left[X\right],\sigma }$ is a Gaussian distribution over ${\mathbb{T}}_N\left[X\right]$ with a standard deviation $\sigma$. A ciphertext $(\mathbf{a},b)$ is output, where

  $$b=\mathbf{a}·\mathbf{s}+e+\frac{m}{2\tau }.$$

  (6)
• $\mathrm{Dec}(\mathbf{s},(\mathbf{a},b\left)\right)$: The decryption algorithm returns $\lceil (b-\mathbf{a}·\mathbf{s})·2\tau \rfloor$. The decryption works correctly if the size noise $\left|e\right|$ is small enough, i.e.,

  $$\begin{array}{cc}\hfill \left|e\right|& <1/4\tau ,\hfill \end{array}$$

  (7)
  Since $\left(b-\mathbf{a}·\mathbf{s}\right)·2\tau =\left(e+\frac{m}{2\tau }\right)·2\tau =m+2\tau e$ and $\left|2\tau e\right|<\frac{1}{2}$ holds from (7).

3. Integer-Wise General Functional Bootstrapping

We modify TFHE to a variant that can encrypt the plaintext of an integer and perform any 1-variable function in only one bootstrapping. We highlight this section as follows:

• We present our general bootstrapping in Algorithm 3 of Section 3.1, which is built upon the integer-wise LWE encryption Section 2.4.
• Our key technique to construct the general bootstrapping is generalizing the setting of the coefficients of the test vector, which is used in the BlindRotate part of the bootstrapping procedure, in Algorithm 4.
• We also discuss the possible security issue that arose after our modification in Section 3.2.

3.1. General Functional Bootstrapping

We present our bootstrapping scheme in Algorithm 3. Our bootstrapping is different from that of Chillotti et al.’s Algorithm 1 in the setting of the test vector used in the BlindRotatepart. Our bootstrapping procedure is constructed over the integer-wise LWE encryption described in Section 2.4, where homomorphic evaluation is performed in an integer-wise manner. We summarize in Table 1 how the input ciphertext is converted line by line for clarity.

Table 1. Overview of the bootstrapping scheme.

	Ctxt	Ptxt	Noise (or Its Bound)
	$(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$	$\frac{m_{\mathrm{in}}}{2\tau }$	$e\in \mathbb{T}$
$\stackrel{\mathrm{Round}}{\to }$	$(\overline{\mathbf{a}},\overline{b})\in {\mathbb{Z}}_{2N}^n\times {\mathbb{Z}}_{2N}$	$2N\left(\frac{m_{\mathrm{in}}}{2\tau }\right)$	$2Ne$
$\stackrel{\mathrm{BlindRotate}}{\to }$	$(a^{\prime \prime },b^{\prime \prime })\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$	$X^{\overline{b}-\overline{\mathbf{a}}\mathbf{s}}·\mathrm{testv}$	${∥\mathrm{Error}\left(\mathrm{ACC}\right)∥}_{\infty }$
$\stackrel{\mathrm{SampleExtract}}{\to }$	$({\mathbf{a}}^{\prime },b^{\prime })\in {\mathbb{T}}^N\times \mathbb{T}$	$\frac{m_{\mathrm{out}}}{2\tau }$	${∥\mathrm{Error}\left(\mathrm{ACC}\right)∥}_{\infty }$
$\stackrel{\mathrm{KeySwitch}}{\to }$	$(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$	$\frac{m_{\mathrm{out}}}{2\tau }$	${∥\mathrm{Error}\left(\mathrm{ACC}\right)∥}_{\infty }\begin{array}{c}\hfill break\end{array}+N(t\gamma +2^{-(t+1)})$

Algorithm 3: General functional bootstrapping.

Input: A ciphertext $C_{m_{\mathrm{in}}}:=$ An LWE sample $(\mathbf{a},b)\in {\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{in}}\right)$, such that its plaintext $m_{\mathrm{in}}\in \{-\tau ,\dots ,\tau -1\}$, a    bootstrapping key ${\mathrm{BK}}_{\mathbf{s}\to {\mathbf{s}}^{″},\alpha }$, a keyswitching key ${\mathrm{KS}}_{{\mathbf{s}}^{\prime }\to \mathbf{s},\gamma }$, where ${\mathbf{s}}^{\prime }=\mathrm{KeyExtract}\left({\mathbf{s}}^{″}\right)$, a constant function     $f:\{0,\dots ,\tau -1\}\to \{-\tau ,\dots ,\tau -1\}$, and a set of coefficients $\{{\mu }_0,\dots ,{\mu }_{N-1}\}$ of the test vector that.     corresponds to the function f Output: An LWE sample ${\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{out}}\right):=\mathrm{Bootstrap}(C_{m_{\mathrm{in}}},f)$, where $$\begin{array}{c}\hfill m_{\mathrm{out}}=f^{\prime }(m_{\mathrm{in}}):=\{\begin{array}{cc}f\left(m_{\mathrm{in}}\right)\hfill & (m_{\mathrm{in}}\in \{0,\dots ,\tau -1\left\}\right),\hfill \\ -f(\tau +m_{\mathrm{in}})\hfill & (m_{\mathrm{in}}\in \{-\tau ,\dots ,-1\left\}\right).\hfill \end{array}\end{array}$$ (8) 1 $\overline{b}:=\lceil 2Nb\rfloor$, $\overline{a_i}:=\lceil 2N{a}_i\rfloor$ for each $i\in [1,n]$ 2  Set the test vector as $$\mathrm{testv}:={\mu }_0+{\mu }_1{X}^{-1}+\dots +{\mu }_{N-1}{X}^{-(N-1)}\in {\mathbb{T}}_N\left[X\right].$$ (9) 3 $\mathrm{ACC}\leftarrow X^{\overline{b}}·(0,\mathrm{testv})\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$ 4 for $i=1$ to n do $\mathrm{ACC}\leftarrow [\mathbf{h}+(X^{-{\overline{a}}_i}-1)·{\mathrm{BK}}_i]⊡\mathrm{ACC}$  $\phantom{(}$ 5 $\mathbf{u}:=\mathrm{SampleExtract}\left(\mathrm{ACC}\right)$ 6 return  ${\mathrm{KeySwitch}}_{\mathrm{KS}}\left(\mathbf{u}\right)$

3.1.1. Input

The input for our bootstrapping scheme is an LWE ciphertext $(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$ of an integer message $m_{\mathrm{in}}\in \{-\tau ,\dots ,\tau -1\}$, where $b=\mathbf{a}·\mathbf{s}+e+m_{\mathrm{in}}/2\tau$. The noise e is sampled according to the distribution such that (7) holds to satisfy the condition for correct decryption of the LWE encryption.

3.1.2. Rounding (Line 1)

The output of the rounding is an rounded LWE ciphertext $(\overline{\mathbf{a}},\overline{b})\in {\mathbb{Z}}_{2N}^n\times {\mathbb{Z}}_{2N}$. Similar to (3), we have

$$\begin{array}{cc}\hfill \overline{b}-\overline{\mathbf{a}}\mathbf{s}& =2N\left(e+m_{\mathrm{in}}/2\tau \right)+e_{\mathrm{ACC}}.\hfill \end{array}$$

(10)

Concretely, we obtain $e_{\mathrm{ACC}}=0$ when $N=1024$, as we mentioned in Section 2.3.

3.1.3. BlindRotate (Line 3 to Line 4)

At line 3, the $\mathrm{ACC}$ is a trivial (noiseless) TLWE sample $(0,X^{\overline{b}}·\mathrm{testv})\in {\mathbb{T}}_N\left[X\right]\times {\mathbb{T}}_N\left[X\right]$. After the iteration in line 4, the message of ACC becomes a polynomial $X^{\overline{b}-\overline{\mathbf{a}}\mathbf{s}}·\mathrm{testv}$. Since $e_{\mathrm{ACC}}=0$ and from (10), we have $\psi \left((\overline{\mathbf{a}},\overline{b})\right):=\overline{b}-\overline{\mathbf{a}}\mathbf{s}=2N\left(e+\frac{m_{\mathrm{in}}}{2\tau }\right)$. Thus, we obtain from (7) that

$$-\frac{N}{2\tau }<2Ne<\frac{N}{2\tau }.$$

(11)

Note that we define the test vector in general form $\mathrm{testv}:={\mu }_0+{\mu }_1{X}^{-1}+\dots +{\mu }_{N-1}{X}^{-(N-1)}\in {\mathbb{T}}_N\left[X\right]$, which is the core modification of our scheme. In the following, we explain how to set the value of the $\mathrm{testv}$ coefficients for a homomorphic evaluation of the arbitrary input function f in one bootstrapping. We summarize the setting in Algorithm 4 and show its illustration in Figure 1.

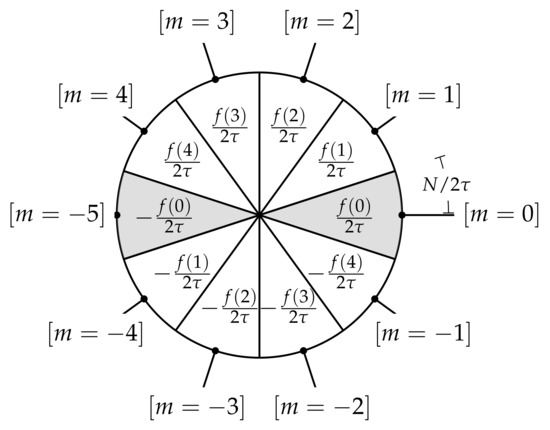
Figure 1. Illustration of the “slices” for the integer-wise LWEencryption and bootstrapping procedure when $\tau =5$.

• When $m_{\mathrm{in}}=0$, we have $\psi \left((\overline{\mathbf{a}},\overline{b})\right)=2Ne$ and $(\overline{\mathbf{a}},\overline{b})\in \{-\lfloor \frac{N}{2\tau }\rfloor ,\dots ,\lfloor \frac{N}{2\tau }\rfloor \}$. Thus, the constant term of the polynomial

  $$\begin{array}{cc}\hfill X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·\mathrm{testv}& =X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·({\mu }_0+{\mu }_1{X}^{-1}+\dots +{\mu }_{N-1}{X}^{-(N-1)})\hfill \\ \hfill & =X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·(\dots -{\mu }_{N-1}{X}^1+{\mu }_0+{\mu }_1{X}^{-1}\dots )\hfill \end{array}$$

  is in

  $${\mathcal{M}}_0:=\{-{\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,-{\mu }_{N-1},{\mu }_0,{\mu }_1,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\}.$$
  We define the value of all elements $\mu \in {\mathcal{M}}_0$ as $\mu :=\frac{f\left(0\right)}{2\tau }\in \mathbb{T}$. Note that, since $X^N+1\equiv 0$, we now have $X^{-i}\equiv -X^{N-i}$ or, equivalently, $X^i\equiv -X^{-(N-i)}$. Similar to this case, when $m_{\mathrm{in}}=-\tau$, the constant term of the polynomial $X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·\mathrm{testv}$ is in $\{{\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor }$, …, ${\mu }_{N-1}$, $-{\mu }_0$, $-{\mu }_1$, …, $-{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\}$$:={\mathcal{M}}_{-\tau }$. The elements of this set are the sign inversions of the elements of the set ${\mathcal{M}}_0$. Therefore, $\mu \in {\mathcal{M}}_{-\tau }$ are already defined as $\mu :=\frac{-f\left(0\right)}{2\tau }\in \mathbb{T}$.
• When $m_{\mathrm{in}}\in \{1,\dots ,\tau -1\}$, we have $\psi \left((\overline{\mathbf{a}},\overline{b})\right)=2N\left(e+\frac{m_{\mathrm{in}}}{2\tau }\right)$. From (11), we have $\frac{N}{2\tau }$ < $\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }$<$\psi \left((\overline{\mathbf{a}},\overline{b})\right)$<$\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }$ < N. Thus, we obtain $\psi \left((\overline{\mathbf{a}},\overline{b})\right)\in \left\{⌈\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }⌉,\dots ,⌊\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }⌋\right\},$ and the constant term of the polynomial $X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·\mathrm{testv}$ is in

  $${\mathcal{M}}_{m_{\mathrm{in}}}:=\{{\mu }_{⌈\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }⌉},\dots ,{\mu }_{⌊\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }⌋}\}.$$
  We define the value of all $\mu \in {\mathcal{M}}_{m_{\mathrm{in}}}$ as $\mu :=\frac{f\left(m_{\mathrm{in}}\right)}{2\tau }\in \mathbb{T}$. Similarly, when $m_{\mathrm{in}}\in \{-(\tau -1),\dots ,-1\}$, we have $-N$ < $\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }$ < $\psi \left((\overline{\mathbf{a}},\overline{b})\right)$ < $\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }$ < $-\frac{N}{2\tau }$. Thus, $\psi \left((\overline{\mathbf{a}},\overline{b})\right)\in$$\left\{⌈\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }⌉\right.$,…, $\left.⌊\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }⌋\right\}$, and the constant term of the polynomial $X^{\psi \left((\overline{\mathbf{a}},\overline{b})\right)}·\mathrm{testv}$ is in $\{-{\mu }_{N+⌈\left(m_{\mathrm{in}}-\frac{1}{2}\right)\frac{N}{\tau }⌉}$, …, $-{\mu }_{N+⌊\left(m_{\mathrm{in}}+\frac{1}{2}\right)\frac{N}{\tau }⌋}\}$. These values are the sign inversions of the previously defined $\mu \in {\mathcal{M}}_{m_{\mathrm{in}}}$ for $m_{\mathrm{in}}\in \{1,\dots ,\tau -1\}$.

Algorithm 4: Our setting of the test vector coefficients defined in (9).

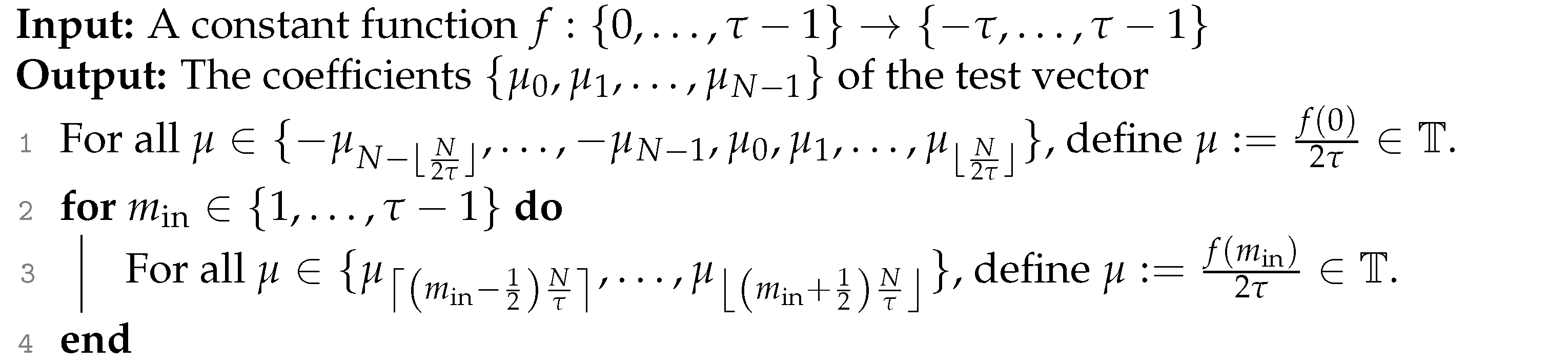3.1.4. Extract (Line 5)

The message of the output $\mathbf{u}:=\mathrm{SampleExtract}\left(\mathrm{ACC}\right)$ in line 5, denoted as $\mathrm{msg}\left(({\mathbf{a}}^{\prime },b^{\prime })\right)$, is the constant term of ($X^{\overline{b}-\overline{\mathbf{a}}\mathbf{s}}·\mathrm{testv}$). By our construction of BlindRotate, it is the coefficient $\mu =\frac{m_{\mathrm{out}}}{2\tau }=\frac{f^{\prime }\left(m_{\mathrm{in}}\right)}{2\tau }\in \mathbb{T}$, where $f^{\prime }$ is defined in (8).

3.1.5. KeySwitch (Line 7)

Our scheme uses the same KeySwitchprocedure as the original TFHE, which is mentioned in Section 2.3.5. The output ${\mathrm{KeySwitch}}_{\mathrm{KS}}\left(\mathbf{u}\right)$ of line 6 is a TLWE sample denoted as $(\mathbf{a},b)\in {\mathbb{T}}^n\times \mathbb{T}$. The sample is the encryption of the message $\frac{m_{\mathrm{out}}}{2\tau }\in \mathbb{T}$ with the secret key $\mathbf{s}$. We denote this TLWE ciphertext as ${\mathrm{LWE}}_{\mathbf{s}}\left(m_{\mathrm{out}}\right)$ for simplicity of the notation. Only the difference from the original bit-wise TFHE is the upper bound of (5): From (7), we need to choose the parameters that satisfy the upper bound

$$2n(k+1)lN\beta {\alpha }_{\mathrm{BK}}+n(1+kN)ϵ+Nt\gamma +N{2}^{-(t+1)}<1/4\tau ,$$

(12)

so that we can obtain a “fresh” LWE sample after the bootstrapping with overwhelming probability.

3.2. Security

The security of our scheme largely relies on the original TFHE scheme because we only modify the test vector, and it changes only the bound of the size of noise given in (12). Although the noise bound of TFHE is fixed to $1/4$, as in (5), that of our scheme is $1/4\tau$. Therefore, when we use the larger plaintext space, the bound becomes lower. This means that we need to use the TLWE sample with smaller noise if the bound (12) does not hold. Conversely, we select the security parameters and $\tau$ that satisfy (12); then, the security of our scheme relies solely on the original TFHE scheme. We use the same security parameters and noise as those in the original TFHE scheme and choose a value of $\tau$ that satisfies (12) in our experiments in Section 5. Notably, the bound in (12) is independent of the input function f; therefore, our scheme can run arbitrary functions with the same parameters and running time.

4. Applications

We present several basic applications of our integer-wise general TFHE bootstrapping procedure (Algorithm 3):

• $C_{\mathrm{sign}\left(a\right)}=\mathrm{Sign}\left(C_a\right)$: Homomorphic evaluation of the sign function over a ciphertext (Algorithm 5)
• $C_{(a=b)}=\mathrm{Eq}(C_a,C_b)$: Homomorphic evaluation of the equality test (Algorithm 6)
• $C_{(a=b)}=\mathrm{ConstEq}(C_a,b)$: Homomorphic evaluation of the equality test with a plaintext (Algorithm 7)
• $C_{a·b}=\mathrm{MultbyBin}(C_a,C_b)$: Homomorphic evaluation of multiplication by a binary number (Algorithm 8)
• $C_{⌊a/d⌋}=\mathrm{DivbyConst}(C_a,d)$: Homomorphic evaluation of division by a plaintext (Algorithm 9)
• $C_{⌊a/d⌋}=\mathrm{Div}(C_a,C_d)$: Homomorphic evaluation of division (Algorithm 10)

The function $\mathrm{Sign}\left(\right)$, which is the homomorphic algorithm of sign, was already presented by Bourse et al. in [14]. For clarity, we describe $\mathrm{Sign}\left(\right)$ performed in our scheme to show that our general Bootstrapping schemes includes the sign function. Additionally, the integer-wise TFHE proposed by Bourse et al. [14] can evaluate only $\mathrm{Sign}\left(\right)$ bootstrapping; it does not support the homomorphic multiplication of integer ciphertexts.

We show Eqand ConstEqin Section 4.2, MultbyBinin Section 4.3, and DivbyConstin Section 4.4. We propose Divin Section 4.5 using DivbyConst, ConstEq, and MultbyBinas building blocks. We also generalize the Divfunction to the homomorphic algorithm that evaluates any 2-variable function in Section 4.5.

Algorithm 5:$\mathrm{Sign}\left(C_{m_{\mathrm{in}}}\right)$: Homomorphic sign evaluation in our bootstrapping scheme.

Input: A ciphertext $C_{m_{\mathrm{in}}}$, where $m_{\mathrm{in}}\in \{-\tau ,\dots ,\tau -1\}$. Output: $C_{m_{\mathrm{out}}}:=\mathrm{Sign}\left(C_{m_{\mathrm{in}}}\right)$, where ${\displaystyle m_{\mathrm{out}}=\{\begin{array}{cc}-1\hfill & (m_{\mathrm{in}}\in \{-\tau +1,\dots ,-1\}),\hfill \\ 0\hfill & (m_{\mathrm{in}}\in \{-\tau ,0\}),\hfill \\ 1\hfill & (m_{\mathrm{in}}\in \{1,\dots ,\tau -1\}).\hfill \end{array}}$   1 return $\mathrm{Bootstrap}(C_{m_{\mathrm{in}}},f_{\mathrm{sign}})$, where $f_{\mathrm{sign}}\left(x\right):=1$ if $x\in \{1,\dots ,\tau -1\}$, 0 if $x=0$.

Algorithm 6:$\mathrm{Eq}(C_{m_1},C_{m_2})$: Equality test.

Input: Two ciphertexts $C_{m_1}$ and $C_{m_2}$, where $m_1,m_2\in \{0,\dots ,\tau -1\}$. Output: $C_{m_{\mathrm{out}}}:=\mathrm{Eq}(C_{m_1},C_{m_2})$, where ${\displaystyle m_{\mathrm{out}}=\{\begin{array}{cc}\tau \left(\mathtt{true}\right)\hfill & \mathrm{if}{m}_1=m_2,\hfill \\ 0 \left(\mathtt{false}\right)\hfill & \mathrm{otherwise}.\hfill \end{array}}$   1 return $\mathrm{Bootstrap}(C_{m_1}-C_{m_2},f_{\mathrm{ztest}})$, where $f_{\mathrm{ztest}}\left(x\right):=\tau$ if $x=0$, $f_{\mathrm{ztest}}\left(x\right):=0$ otherwise.

Algorithm 7:$\mathrm{ConstEq}(C_{m_1},m_2)$: Equality test with a constant

Input: A ciphertext $C_{m_1}$ and plaintext $m_2$, where $m_1,m_2\in \{0,\dots ,\tau -1\}$. Output: $C_{m_{\mathrm{out}}}:=\mathrm{ConstEq}(C_{m_1},m_2)$, where ${\displaystyle m_{\mathrm{out}}=\{\begin{array}{cc}\tau \left(\mathtt{true}\right)\hfill & \mathrm{if}{m}_1=m_2,\hfill \\ 0 \left(\mathtt{false}\right)\hfill & \mathrm{otherwise}.\hfill \end{array}}$ 1    Encode $m_2\in \{0,\dots ,\tau -1\}$ to ${\nu }_{m_2}:=\frac{m_2}{2\tau }\in \mathbb{T}$.   2 return $\mathrm{Bootstrap}(C_{m_1}-(\mathbf{0},{\nu }_{m_2}),f_{\mathrm{ztest}})$, where $f_{\mathrm{ztest}}\left(x\right):=\tau$ if $x=0$, $f_{\mathrm{ztest}}\left(x\right):=0$ otherwise.

4.1. Homomorphic Evaluation of the Sign Function: $\mathrm{Sign}\left(\right)$

Algorithm 5 shows that our algorithms homomorphically evaluate the sign function. This algorithm is constructed using Bootstrap with an input function $f_{sign}$. Specifically, we “express” $f_{sign}$ by defining the coefficients ${\mu }_0,\dots ,{\mu }_{N-1}\in \mathbb{T}$ of test vector using Algorithm 4, as follows:

$$\left\{\begin{array}{cc}{\mu }_0,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\hfill & :=0,\hfill \\ {\mu }_{\lfloor \frac{N}{2\tau }\rfloor +1},\dots ,{\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor -1}\hfill & :=\frac{1}{2\tau },\hfill \\ {\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,{\mu }_{N-1}\hfill & :=0.\hfill \end{array}\right.$$

We illustrate the setting of the test vector coefficients in Figure 2. We can confirm from (8) that $m_{\mathrm{out}}=f^{\prime }\left(m_{\mathrm{in}}\right)=f_{sign}\left(m_{\mathrm{in}}\right)=1$ for $m_{\mathrm{in}}\in \{1,\dots ,\tau -1\}$, $m_{\mathrm{out}}=f^{\prime }\left(m_{\mathrm{in}}\right)=-f_{sign}(B+m_{\mathrm{in}})=-1$ for $m_{\mathrm{in}}\in \{-\tau +1,\dots ,-1\}$, $m_{\mathrm{out}}=f^{\prime }\left(m_{\mathrm{in}}\right)=0$ for $m_{\mathrm{in}}=0$, and $m_{\mathrm{out}}=f^{\prime }\left(m_{\mathrm{in}}\right)=-f_{sign}(B+m_{\mathrm{in}})=0$ for $m_{\mathrm{in}}=-\tau$. Note that the plaintext of the output with $m_{\mathrm{in}}=-\tau$ is the same as that with $m_{\mathrm{in}}=0$.

Algorithm 8:$\mathrm{MultbyBin}(C_{m_{\mathrm{int}}},C_{m_{\mathrm{bin}}})$: Homomorphic multiplication by binary number

Input: Ciphertexts $C_{m_{\mathrm{int}}},C_{m_{\mathrm{bin}}}$, where $m_{\mathrm{int}}\in \{0,\dots ,\tau -1\}$, $m_{\mathrm{bin}}\in \{\tau \left(\mathtt{true}\right),0\left(\mathtt{false}\right)\}$. Output: ${\displaystyle C_{m_{\mathrm{out}}}:=\mathrm{MultbyBin}(C_{m_{\mathrm{int}}},C_{m_{\mathrm{bin}}})=\{\begin{array}{cc}{C}_{m_{\mathrm{int}}}\hfill & (m_{\mathrm{bin}}=\tau \left(\mathtt{true}\right)),\hfill \\ C_0\hfill & (m_{\mathrm{bin}}=0\left(\mathtt{false}\right)).\hfill \end{array}}$ 1 $C_{\mathrm{tmp}}=\mathrm{Bootstrap}(C_{m_{\mathrm{int}}}+C_{m_{\mathrm{bin}}}+(\mathbf{0},\frac{\tau }{2\tau }),f_{\mathrm{id}})$   //$\phantom{(}$${\displaystyle C_{\mathrm{tmp}}=\{\begin{array}{cc}{C}_{m_{\mathrm{int}}}\hfill & (m_{\mathrm{bin}}=\tau \left(\mathtt{true}\right)),\hfill \\ C_{-m_{\mathrm{int}}}\hfill & (m_{\mathrm{bin}}=0\left(\mathtt{false}\right)).\hfill \end{array}}$$\phantom{(}$ 2 return  $\mathrm{Bootstrap}(C_{m_{\mathrm{int}}}+C_{\mathrm{tmp}},f_{\mathrm{half}})$   //$\phantom{(}$${\displaystyle C_{m_{\mathrm{int}}}+C_{\mathrm{tmp}}=\{\begin{array}{cc}2·C_{m_{\mathrm{int}}}\hfill & (m_{\mathrm{bin}}=\tau \left(\mathtt{true}\right)),\hfill \\ C_0\hfill & (m_{\mathrm{bin}}=0\left(\mathtt{false}\right)).\hfill \end{array}}$$\phantom{(}$

Algorithm 9:$\mathrm{DivbyConst}(C_{m_{\mathrm{in}}},m_d)$: Homomorphic division by a constant

Input: A ciphertext $C_{m_{\mathrm{in}}}$, where $m_{\mathrm{in}}\in \{0,\dots ,\tau -1\}$, and a constant plaintext $m_d\in \{1,\dots ,\tau -1\}$. Output: $C_{m_{\mathrm{out}}}:=\mathrm{DivbyConst}(C_{m_{\mathrm{in}}},m_d):=C_{⌊m_{\mathrm{in}}/m_d⌋}$   1 return $\mathrm{Bootstrap}(C_{m_{\mathrm{in}}},f_{\mathrm{div},m_d})$

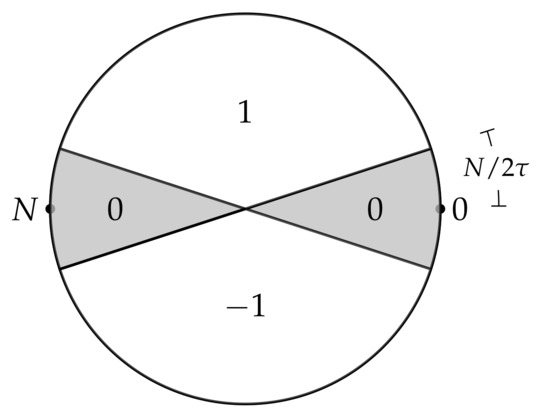
Figure 2. Illustration of the slices for the test vector coefficients of sign bootstrapping (when $\tau =5$).

Algorithm 10:$\mathrm{Div}(C_{m_{\mathrm{in}}},C_{m_d})$: Homomorphic division.

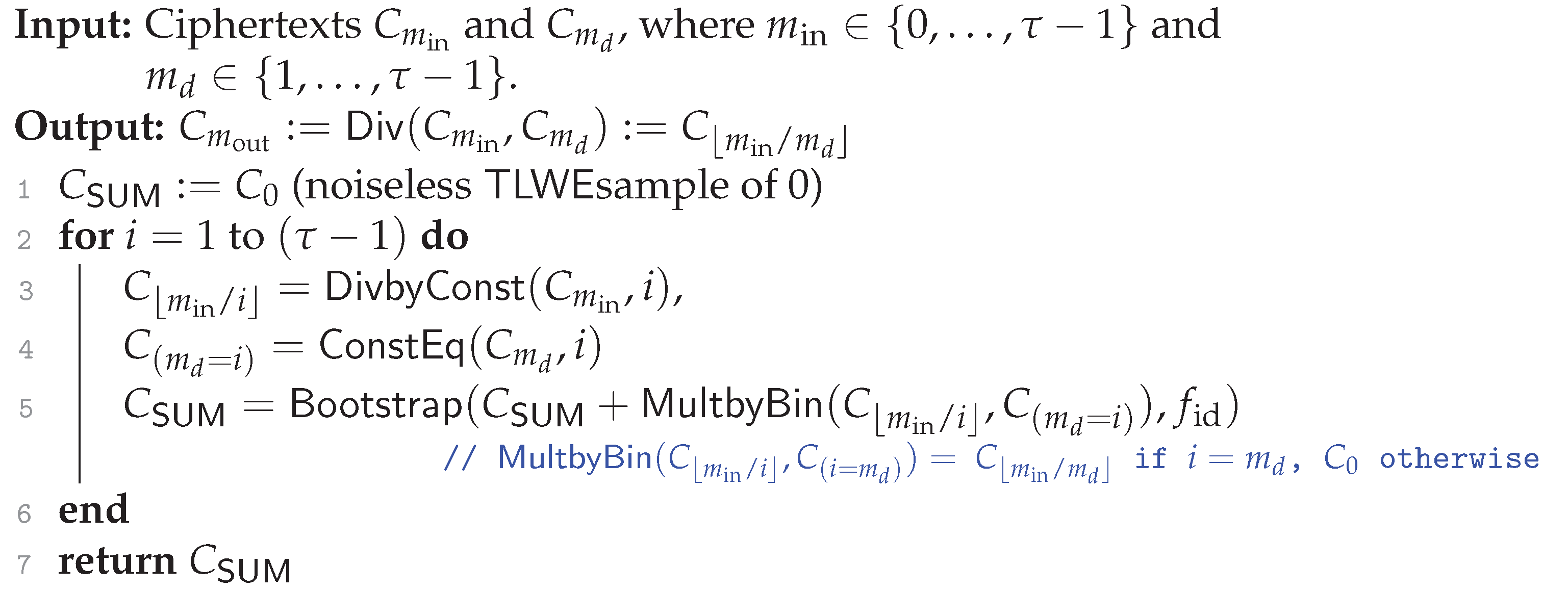4.2. Homomorphic Equality Test: $\mathrm{Eq}\left(\right)$ and $\mathrm{ConstEq}\left(\right)$

For clarity, we present that our bootstrapping scheme includes the homomorphic equality test. This concept is similar to the homomorphic comparison on TFHE proposed by Bourse et al. in [34]. Note that we require the input plaintext space to be in $\{0,\dots ,\tau -1\}$ (or in $\{-\tau ,\dots ,-1\}$), for our equality tests Algorithms 6 and 7. This restriction is required since, if we allowed $m_1$ and $m_2$ to be in $\{-\tau ,\dots ,\tau -1\}$, we would have $m_2-m_1=\tau$ and would obtain the trueoutput when $m_2=\tau +m_1$, although $m_1\ne m_2$.

Some previous integer-wise homomorphic equality tests were performed based on Fermat’s little theorem [35] in other FHE schemes, such as HElib. For example, in HElib (i.e., in the BGV FHE scheme [31]), the plaintext space was ${\mathbb{Z}}_p$ for some prime number modulus p, and the equality test was constructed using the fact

$$\begin{array}{c}\hfill {(x-y)}^{p-1}\equiv \left\{\begin{array}{cc}1modp\hfill & (x-y\neg \equiv 0)\hfill \\ 0modp\hfill & (x-y\equiv 0).\hfill \end{array}\right.\end{array}$$

However, this approach is not efficient because it calls for homomorphic multiplication many ($\approx log\left(p\right)$) times, and thus, some additional bootstrapping are required in order to reduce the increase in noise caused by the homomorphic multiplication. Our homomorphic equality test is efficient because it calls only one bootstrapping procedure.

Algorithm 6 shows $\mathrm{Eq}(·,·)$, the equality test between two ciphertexts. The algorithm is based on the integer-wise “zero test” bootstrapping with the function $f_{\mathrm{ztest}}$, where $f_{\mathrm{ztest}}\left(x\right):=\tau$ if $x=0$, 0 otherwise. Concretely, we define the test vector coefficients ${\mu }_0,\dots ,{\mu }_{N-1}\in \mathbb{T}$ that correspond to $f_{\mathrm{ztest}}$, based on Algorithm 4, as follows:

$$\left\{\begin{array}{cc}{\mu }_0,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\hfill & :=\frac{\tau }{2\tau }=\frac{1}{2},\hfill \\ {\mu }_{\lfloor \frac{N}{2\tau }\rfloor +1},\dots ,{\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor -1}\hfill & :=0,\hfill \\ {\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,{\mu }_{N-1}\hfill & :=\frac{-\tau }{2\tau }=-\frac{1}{2}.\hfill \end{array}\right.$$

We show the illustration of the setting of the coefficients of the test vector in Figure 3.

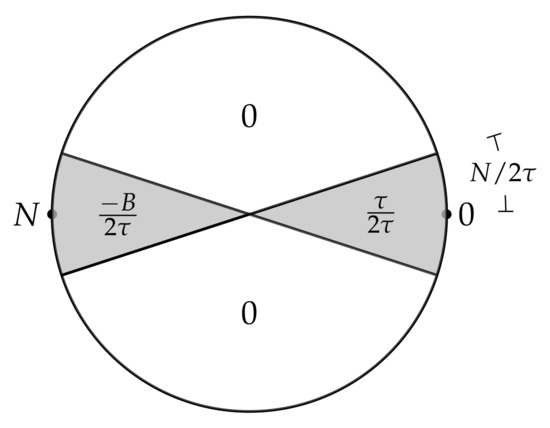
Figure 3. Illustration of the slices for the test vector coefficients of equality test bootstrapping (when $\tau =5$).

Algorithm 7 shows the variant that is performed between a ciphertext and a plaintext. Notice that the second argument of the algorithm is a plaintext $m_1$, which is then encoded as a trivial $(0,{\nu }_{m_1})$ LWE ciphertext in line 1.

4.3. Homomorphic Multiplication by a Binary Number: $\mathrm{MultbyBin}\left(\right)$

Algorithm 8 shows the algorithm used to homomorphically evaluate the multiplication by a binary number (MultbyBin). As mentioned before, integer-wise TFHE cannot perform homomorphic multiplication between integer ciphertexts. MultbyBinhomomorphically multiplies an integer ciphertext by a ciphertext of a binary message. MultbyBinis called as a module in the homomorphic division Div, which we describe later in Algorithm 10. Figure 4 illustrates how the MultbyBinworks. Note that we need restrictions for MultbyBin: (1) $\tau$ to be an odd number and (2) $m_{\mathrm{in}}\in \{0,\dots ,\tau -1\}$. We explained these restrictions later in this subsection.

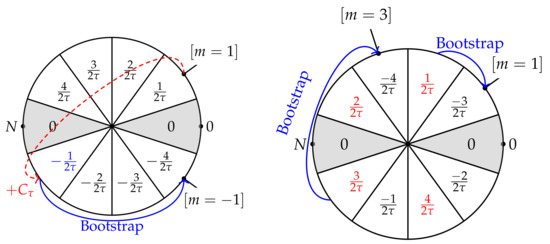
Figure 4. Illustration of MultbyBinwhen $(m_{\mathrm{int}},m_{\mathrm{bin}})=(1,0)$. The left figure illustrates the procedure in line 1, and the right figure illustrates the procedure in line 2.

We define two functions $f_{\mathrm{id}}$ and $f_{\mathrm{half}}$ to be used as inputs of Bootstrapto construct MultbyBin. The function $f_{\mathrm{id}}:\{0,\dots ,\tau -1\}\to \{0,\dots ,\tau -1\}$ is an identity function defined as $f_{\mathrm{id}}\left(x\right):=x$. Based on Algorithm 4, we define the test vector coefficients ${\mu }_0,\dots ,{\mu }_{N-1}\in \mathbb{T}$ for $f_{\mathrm{id}}$ as follows:

$$\left\{\begin{array}{cc}{\mu }_0,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{id}}\left(0\right)}{2\tau }=0,\hfill \\ {\mu }_{\lfloor \frac{(2i-1)N}{2\tau }\rfloor +1},\dots ,{\mu }_{\lfloor \frac{(2i+1)N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{id}}\left(i\right)}{2\tau }=\frac{i}{2\tau },for i=1,\dots ,\tau -1,\hfill \\ {\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,{\mu }_{N-1}\hfill & :=\frac{-f_{\mathrm{id}}\left(0\right)}{2\tau }=0.\hfill \end{array}\right.$$

The function $f_{\mathrm{half}}$ is defined as

$$f_{\mathrm{half}}\left(x\right):=\left\{\begin{array}{cc}\frac{x}{2}\hfill & \left(x\mathrm{is}\mathrm{even}\right),\hfill \\ -\frac{x+1}{2}-\frac{\tau -1}{2}\hfill & \left(x\mathrm{is}\mathrm{odd}\right).\hfill \end{array}\right.$$

For $f_{\mathrm{half}}$, we define the test vector coefficients ${\mu }_0,\dots ,{\mu }_{N-1}\in \mathbb{T}$ based on Algorithm 4, as follows:

$$\left\{\begin{array}{cc}{\mu }_0,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{half}}\left(0\right)}{2\tau }=0,\hfill \\ {\mu }_{\lfloor \frac{(2i-1)N}{2\tau }\rfloor +1},\dots ,{\mu }_{\lfloor \frac{(2i+1)N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{half}}\left(i\right)}{2\tau },fori=1,\dots ,\tau -1,\hfill \\ {\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,{\mu }_{N-1}\hfill & :=\frac{-f_{\mathrm{half}}\left(0\right)}{2\tau }=0.\hfill \end{array}\right.$$

We now explain Algorithm 8. First, in line 1, we homomorphically multiply a ciphertext of a binary message in $\{\tau ,0\}$, $C_{m_{\mathrm{bin}}}$ and a constant $(\mathbf{0},\frac{\tau }{2\tau })$ to $C_{m_{\mathrm{int}}}$. The output of the bootstrapping of the sum with $f_{\mathrm{id}}$ is stored as $C_{\mathrm{tmp}}$.

• If $C_{m_{\mathrm{bin}}}$ is a ciphertext of 0 (which means $\mathtt{false}$), then $C_{m_{\mathrm{bin}}}+(\mathbf{0},\frac{\tau }{2\tau })$ is $C_{\tau }$ (ciphertext of the constant $\tau$). Thus, the phase of $C_{m_{\mathrm{int}}}$ is rotated to a position symmetrical about the origin, as illustrated in Figure 4 by the dashed arrow in the left image. Then, the phase of the ciphertext is rotated to a position symmetrical about the x-axis. After bootstrapping with $f_{\mathrm{id}}$, $C_{\mathrm{tmp}}$ becomes a ciphertext of $-m_{\mathrm{int}}$.
• If $C_{m_{\mathrm{bin}}}$ is a ciphertext of $\tau$ (which means $\mathtt{true}$), then $C_{m_{\mathrm{bin}}}+(\mathbf{0},\frac{\tau }{2\tau })$ is $C_0$ (ciphertext of 0). Thus, $C_{\mathrm{tmp}}$ remains a ciphertext of $m_{\mathrm{int}}$.

Therefore, in line 2, $C_{m_{\mathrm{int}}}+C_{\mathrm{tmp}}=C_{m_{\mathrm{int}}}+C_{m_{\mathrm{int}}}$ when $m_{\mathrm{bin}}=\tau$, and $C_{m_{\mathrm{int}}}+C_{\mathrm{tmp}}=C_0$ when $m_{\mathrm{bin}}=0$. After bootstrapping with $f_{\mathrm{half}}$, $C_{m_{\mathrm{int}}}+C_{m_{\mathrm{int}}}$ is converted to $C_{m_{\mathrm{int}}}$, and $C_0$ remains $C_0$, as illustrated in Figure 4. Finally, we obtain $C_{m_{\mathrm{out}}}=C_{m_{\mathrm{int}}}$ when $m_{\mathrm{bin}}=\tau$ and $C_0$ when $m_{\mathrm{bin}}=0$.

As noted before, we need to restrict $\tau$ to odd values. If $\tau$ is even, when $m_{\mathrm{int}}=\frac{\tau }{2}$ and $m_{\mathrm{bin}}=\tau$, the ciphertext in line 2 $C_{m_{\mathrm{int}}}+C_{\mathrm{tmp}}=C_{m_{\mathrm{int}}}+C_{m_{\mathrm{int}}}$ is converted to $C_0$, but we require it to remain as $C_{\frac{\tau }{2}}$. Therefore, $\tau$ needs to be an odd number to homomorphically evaluate the division by 2 with the function $\mathrm{Bootstrap}(·,f_{\mathrm{half}})$. Additionally, we require the input $m_{\mathrm{int}}$ to be in $\{0,\dots ,\tau -1\}$ because we cannot perform multiplication with binary values on negative plaintext $m_{\mathrm{int}}\in \{-\tau +1,\dots ,-1\}$ with MultbyBin. (Although we can perform binary multiplication on $m_{\mathrm{int}}=-\tau$ or $\tau$, which is equivalent to $m_{\mathrm{int}}=0$, we omit $-\tau$ from the input plaintext space, for simplicity.) For $m_{\mathrm{int}}\in \{-\tau +1,\dots ,-1\}$,

• if $m_{\mathrm{bin}}=\tau$ (which means $\mathtt{true}$), the message of $C_{\mathrm{tmp}}$ in line 1 is $-(\tau +m_{\mathrm{int}})$, and the output becomes $m_{\mathrm{out}}=0$ because $C_{\mathrm{tmp}}+C_{m_{\mathrm{bin}}}=C_{\tau }$ for all $m_{\mathrm{int}}\in \{-B+1,\dots ,-1\}$ while $m_{\mathrm{bin}}=\tau \left(\mathtt{true}\right)$.
• If $m_{\mathrm{bin}}=0$ (which means $\mathtt{false}$), in line 1, the message of $C_{\mathrm{tmp}}$ is $\tau -m_{\mathrm{int}}$ and the output is $m_{\mathrm{out}}=-\tau +m_{\mathrm{int}}$.

Therefore, for negative inputs $m_{\mathrm{int}}\in \{-\tau +1,\dots ,-1\}$, $\mathrm{MultbyBin}$ does not work as multiplication with binary values; thus, we need the restriction.

4.4. Homomorphic Division by a Constant: $\mathrm{DivbyConst}$

Algorithm 9 shows that DivbyConsthomomorphically evaluates “division by a constant”. DivbyConsttakes a ciphertext $C_{m_{\mathrm{in}}}$ and a plaintext $m_d$ as inputs, and it outputs a ciphertext of $C_{⌊m_{\mathrm{in}}/m_d⌋}$. Note that we need to restrict $m_{\mathrm{in}}\in \{0,\dots ,\tau -1\}$ and $m_d\in \{1,\dots ,\tau -1\}$.

Bit-wise integer division by 2 on TFHE was proposed in [7]. The algorithm was constructed based on a right shift over the bits; therefore, it only supports a power of two dividend. Homomorphic division by a (not only 2) constant was proposed in [23] based on HElib. This algorithm uses polynomial interpolation, which needs to homomorphically calculate all powers of the ciphertexts $\{C_a,C_a^2,C_a^3,\dots ,C_a^{p-1}\}$, where p is the modulus of the plaintext space ${\mathbb{Z}}_p$. Thus, it is not efficient since many ($p-1$) homomorphic multiplications are needed for a homomorphic polynomial interpolation. Contrary to that, our homomorphic division by a constant on the integer-wise TFHE is efficient because it needs only one bootstrapping.

The function $f_{\mathrm{div},d}:\{0,\dots ,\tau -1\}\to \{0,\dots ,\tau -1\}$ is defined as $f_{\mathrm{div},d}\left(x\right):=⌊x/d⌋$ for a constant $d\in \{1,\dots ,\tau -1\}$. We define the test vector coefficients for $f_{\mathrm{div},d}$ based on Algorithm 4, as follows:

$$\left\{\begin{array}{cc}{\mu }_0,\dots ,{\mu }_{\lfloor \frac{N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{div},d}\left(0\right)}{2\tau }=0,\hfill \\ {\mu }_{\lfloor \frac{(2i-1)N}{2\tau }\rfloor +1},\dots ,{\mu }_{\lfloor \frac{(2i+1)N}{2\tau }\rfloor }\hfill & :=\frac{f_{\mathrm{div},d}\left(i\right)}{2\tau }=\frac{⌊i/d⌋}{2\tau },\mathrm{for} i=1,\dots ,\tau -1,\hfill \\ {\mu }_{N-\lfloor \frac{N}{2\tau }\rfloor },\dots ,{\mu }_{N-1}\hfill & :=\frac{-f_{\mathrm{div},d}\left(0\right)}{2\tau }=0.\hfill \end{array}\right.$$

(13)

Note that we need to have a set of $\{{\mu }_0,\dots ,{\mu }_{N-1}\}$ for all $d\in \{0,\dots ,\tau -1\}$: we need to store $NB$ values in $\mathbb{T}$ before starting the algorithm. Additionally, we need the restriction $m_{\mathrm{in}}\in \{0,\dots ,\tau -1\}$ since we cannot perform divisions for $m_{\mathrm{in}}\in \{-\tau ,\dots ,-1\}$, as the output $m_{\mathrm{out}}$ becomes $-⌊(\tau -m_{\mathrm{in}})/m_d⌋$.

4.5. Homomorphic Division: $\mathrm{Div}\left(\right)$

As a final application, we construct a homomorphic division Divin Algorithm 10. It calls DivbyConst, ConstEq, and MultbyBinas subalgorithms. As these subalgorithms need the restriction $m_{\mathrm{in}}\in \{0,\dots ,\tau -1\}$, Divalso follows this restriction.

We now explain Div. First, in line 1, we set a $C_{\mathrm{SUM}}=C_0=(\mathbf{0},0)$ as a trivial TLWE ciphertext of a message 0. In the iteration on line 2 and 6, we obtain a ciphertext of $\lceil a/i\rfloor$, denoted as $C_{\lceil a/i\rfloor }$ with DivbyConst, and then, we test if $i=d$ with ConstEq, where d is the plaintext of the input $C_d$. The output is the ciphertext of the Boolean value of the test result $C_{(d=i)}$. Second, in line 5, we have

$$\mathrm{MultbyBin}(C_{\lfloor a/i\rfloor },C_{(i=d)})=\left\{\begin{array}{cc}{C}_{\lfloor a/d\rfloor }\hfill & (i=d),\hfill \\ C_0\hfill & \left(\mathrm{otherwise}\right).\hfill \end{array}\right.$$

Therefore, after this loop, we have $C_{\mathrm{SUM}}=C_0+\dots +C_{\lfloor a/d\rfloor }+\dots +C_0=C_{\lfloor a/d\rfloor }$.

Generalization to a Two-Variable Function: $\mathrm{Func}\left(\right)$

We now generalize Divto any two-variable function $\mathrm{Func}(C_{m_1},C_{m_2})$, in Algorithm 11. The algorithm takes the following inputs: two ciphertexts $C_{m_1}$ and $C_{m_2}$; a two-variable function $f(x,y)$; and sets of test vector coefficients $\{{\mu }_{0,y},\dots ,{\mu }_{N-1,y}\}$, which corresponds to a one-variable function $f_y\left(x\right):=f(x,y)$ for all fixed $y\in \{0,\dots ,\tau -1\}$. The output of the algorithm is a ciphertext $C_{f(m_1,m_2)}$. This algorithm generalizes Divby generalizing the DivbyConstto $\mathrm{Bootstrap}(C_{m_{\mathrm{in}}},f_y)$, which is the homomorphic evaluation of a general one-variable function $f_y\left(x\right):=f(x,y)$ over a ciphertext $C_x$.

5. Results of Homomorphic Division

In this section, we present the implementation results of Div. We implemented our bootstrapping procedure and Divby modifying the TFHE library [33]. The parameter values are the same as the defaults of the TFHE library:

• The degree of the polynomials in the ring: $N=1024$.
• The dimensions of the LWE and TLWE: $n=500$ and $k=1$.
• Decomposition basis and length of TGSWciphertexts: $B_g=2^{10}$ and $l=2$.
• Decomposition basis and length of KeySwitch: $2^l$ and $t=8$.
• Standard deviation of the noise of the key-switching keys KS: ${\sigma }_{\mathrm{KS}}=2.44·{10}^{-5}$.
• Standard deviation of the noise of the bootstrapping keys BK: ${\sigma }_{\mathrm{BK}}=7.18·{10}^{-9}$.

These choices of parameters achieve at least 128-bit security [6]. A single bootstrapping procedure takes approximately 10 msec on our PC with a $3.4$-GHz Intel Core i5 CPU. We implemented Divfor a 4-bit integer, which is the same target as that of existing work on homomorphic division algorithms [16,17,18,23]. Thus, we set $B=17$ to encrypt 4-bit integers.

Table 2 shows our results, including the values taken from the existing works on homomorphic division. We ran Div (Algorithm 10) 1000 times and took the average. Our method is approximately $3.4$ times faster than the fastest method ([23]) shown in the table while achieving a higher level of security ($\lambda >128$) than that of existing methods. For a fair comparison, we also implemented the “non-restorative division algorithm” on the original (bit-wise) TFHE library with the same parameters. The non-restorative division algorithm is a classic bit-wise algorithm for integer division that is used in previous works [16,17,18]. We can confirm from Table 2 that our method is approximately $2.2$ times faster than non-restorative division. In the asymptotic analysis, as shown in the “Complexity” column of the table, our division algorithm and that of [23] take exponential time. Thus, our algorithm and that of [23] are asymptotically slower than other works based on the bit-wise non-restorative division algorithm. The main bottle necks of our algorithm and that in [23] are the exhaustive loop of line 2–6 in Algorithm 10, similar to the part in [23]. However, while the method of [23] needs an $O\left(2^{2l}\right)$ calculation, our algorithm is quadratically faster: it takes a smaller $O\left(2^l\right)$ calculation. This is due to that our bootstrapping being able to evaluate any one-variable function without extra computational costs over the original TFHE, and in contrast, the bootstrapping in [23] needs an $O\left(2^l\right)$ calculation for homomorphic evaluation of the general one-variable function.

Table 2. Results: comparison with existing homomorphic division implementations. We abbreviate the non-restoring division method as NRD. The “Complexity” column shows the asymptotic complexity for a one-bit-length integer input.

Method	FHE lib.	Type	Bits (l)	Time [sec]	Complexity	Security $\mathit{\lambda }$
[17]	HElib	Bit-wise	4	67.94	$O\left(l^2\right)$	>128
[18]	HElib	Bit-wise	4	14.63	$O\left(l^2\right)$	>128
[16]	HElib	Bit-wise	4	7.74	$O\left(l^2\right)$	>80
[23]	HElib	Integer-wise	4	3.15	$O\left(2^{2l}\right)$	>80
Ours (Div)	TFHE	Integer-wise	4	0.93	$O\left(2^l\right)$	>128
NRD	TFHE	Bit-wise	4	2.05	$O\left(l^2\right)$	>128

Algorithm 11:$\mathrm{Func}(C_{m_1},C_{m_2},f(·,·))$: Homomorphic evaluation of a 2-variable function $f(x,y)$

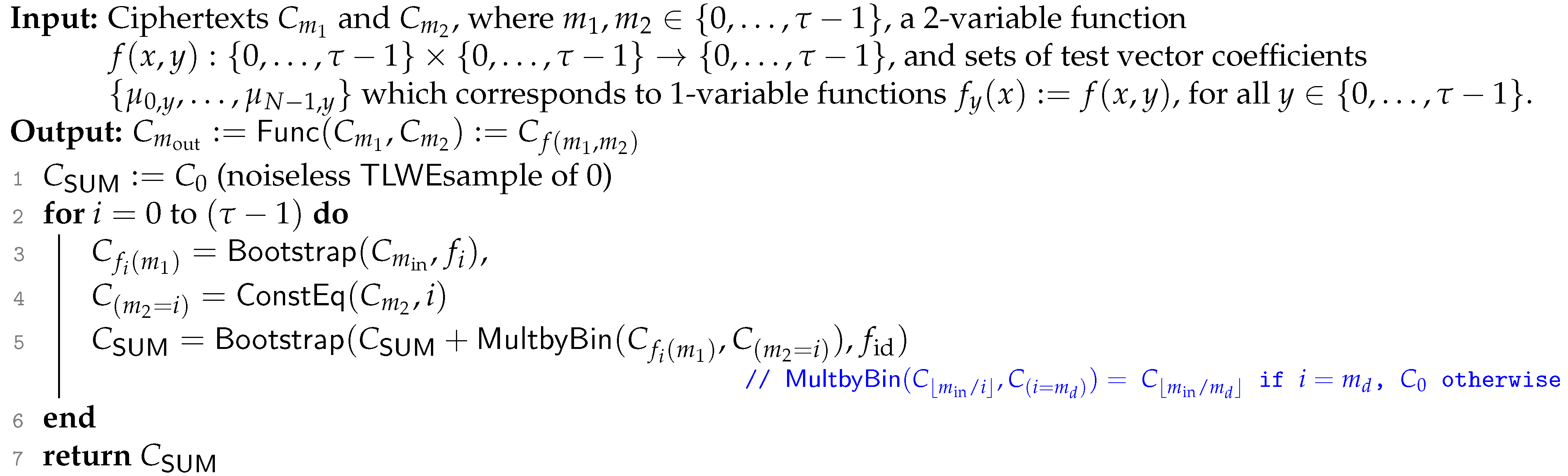We show in Table 3 the breakdown of the run time of our Div, which was completed in 930 msec in total. The run time for each of MultbyBin, ConstEq, DivbyConst, and $\mathrm{Bootstrap}(·,f_{\mathrm{id}})$ in line 5 of Algorithm 10 are shown in the table. The run times of these subalgorithms account for almost the entire run time. As the single bootstrapping takes approximately 10 msec on our PC, the cost of these functions is dominated by the run time of bootstrapping, i.e., our functions entail minimal additional costs.

Table 3. A breakdown of the run time of our Div  (Algorithm 10).

Functions	# of Bootstrap	Time [msec]	# of Calls	Mean [msec]
$\mathrm{MultbyBin}$ (line 5)	2	346.0 (37.2%)	$\tau -1=16$	21.6
$\mathrm{ConstEq}$ (line 4)	1	174.8 (18.8%)	$\tau -1=16$	10.9
$\mathrm{DivbyConst}$ (line 3)	1	175.8 (18.9%)	$\tau -1=16$	11.0
$\mathrm{Bootstrap}(·,f_{\mathrm{id}})$ (line 5)	1	173.9 (18.7%)	$\tau -1=16$	10.9

Limitations of Correctness

In the parameter setting of this section, the final standard deviation of the noise after bootstrapping is $\sigma =0.00961$, as in [6]. The probability of decryption failure, i.e., the probability of the standard deviation of noise after bootstrapping is larger than $1/16$ and is bounded by $erf(1/16\sqrt{2}\sigma )<2^{-32}$. The condition suffices for the bit-wise TFHE scheme. However, for our scheme, decryption fails if the size of the noise after bootstrapping is larger than $1/4\tau$, as shown in (12). The probability of decryption error is bounded by $erf(1/4\tau \sqrt{2}\sigma )<2^{-4.06}$ for our scheme. This upper bound appears large, but we empirically observed in our experiment that the decryption error rate is approximately $0.08\%$ (4 decryption errors in 5000 bootstrappings). In other words, there is a trade-off between the size of the plaintext space $\tau$ and the decryption error rate. For 5-bit integers, i.e., when $B=33$, the upper bound of the decryption failure probability rapidly increases to approximately $30\%$. Thus, for the parameter setting in this section, our scheme is practical only for $\le 4$-bit integer input. Notably, although the decryption failure rate of our scheme increases as $\tau$ increases, the security of the scheme is not affected because $\tau$ is independent of the standard deviation $\sigma$ of the noise [14].

6. Conclusions

We proposed a technique for performing arbitrary 1-variable functions with only one bootstrapping procedure using the integer-wise variant of TFHE. The core modification is to generalize the test vector used in the bootstrapping and the concrete setting of the values of the test vector coefficients. Based on this general functional bootstrapping procedure, we extended the functionality of the integer-wise TFHE scheme to construct several basic applications, such as homomorphic equality testing, multiplication by a binary number, and a division algorithm. We implemented our homomorphic division algorithm and showed that it can be performed in less than 1 second, which is approximately $3.4$ times faster than the fastest division algorithm. However, as a limitation, our scheme is practical only for ≤4-bit integer inputs, when we use the default parameters of TFHE library. In order to use our scheme for larger integer inputs, we need to use a smaller error rate.

Efficient algorithms for basic arithmetic operations are needed to increase the options for optimizing high-level secure computation applications. We believe our bootstrapping scheme can be used to develop a wide variety of homomorphic calculation algorithms.