Abstract
The electric grid is becoming increasingly cyber-physical with the addition of smart technologies, new communication interfaces, and automated grid-support functions. Because of this, it is no longer sufficient to only study the physical system dynamics, but the cyber system must also be monitored as well to examine cyber-physical interactions and effects on the overall system. To address this gap for both operational and security needs, cyber-physical situational awareness is needed to monitor the system to detect any faults or malicious activity. Techniques and models to understand the physical system (the power system operation) exist, but methods to study the cyber system are needed, which can assist in understanding how the network traffic and changes to network conditions affect applications such as data analysis, intrusion detection systems (IDS), and anomaly detection. In this paper, we examine and develop models of data flows in communication networks of cyber-physical systems (CPSs) and explore how network calculus can be utilized to develop those models for CPSs, with a focus on anomaly and intrusion detection. This provides a foundation for methods to examine how changes to behavior in the CPS can be modeled and for investigating cyber effects in CPSs in anomaly detection applications.
1. Introduction
The electric grid has been rapidly evolving into a cyber-physical system (CPS) with the addition of smart grid technologies and advancements which have significantly improved grid operations with greater situational awareness and fast, automated control. Grid operators are now considering using distributed energy resources (DER) to provide distribution voltage regulation rather than installing costly voltage regulation hardware. In utilizing DERs for voltage regulation, operators have the difficult decision of selecting the best operating mode and settings for the DER []. Additional concerns such as any lack of in-field measurements can be addressed in a variety of ways, such as by using a real-time digital twin, as in [], to effectively provide state estimation pseudo-measurements that can be used to optimize DER operations for distribution voltage regulation.
However, these modernization efforts also include new access interfaces, third-party software, and internet-based communications that broaden the grid’s attack surface [,,]. If not protected or defended against adequately, cyber attacks and other malicious disturbances can cause detrimental, cascading impact to the grid []. The 2003 Northeast Blackout demonstrated the critical need for situational awareness across utility systems and improvements in state estimation techniques []. Moreover, as cyber attacks increase in frequency and sophistication, this situational awareness can no longer be limited to the physical system dynamics and needs to be extended to the communications network connecting devices in the system as well [].
To mitigate the serious consequences of malicious grid disturbances, an important first step is obtaining situational awareness into the cyber and physical states of the system and their interactions. As mentioned, it no longer suffices to only monitor the physical system (e.g., power system measurements) to achieve full situational awareness of the grid. Conversely, applying cybersecurity tools, such as intrusion detection systems (IDS), that only process cyber data, such as network traffic, is not enough to thwart adversaries from harming the grid, as is shown in []. Even within IDS technologies there are a large variety of techniques and methods, using various types of data and features to analyze behavior and detect compromises to system security. These may include analysis of network traffic or host-based solutions that analyze changes to specific devices, and can also be broken out into behavioral methods that examine if system behavior has changed from normal conditions, or signature-based techniques which look for specific indicators of known exploits or attacks [].
With all these techniques available, when designing detection algorithms it is still important to be able to connect what is being measured for the detection algorithm to the behavior of the CPS. In this manner, we can evaluate performance in detecting compromise when comparing different techniques and strategies for observing changes to system behavior, as well as examine any fundamental limitations that may arise. In a CPS, the features of interest that can inform whether the system is in normal or abnormal conditions may be physical or cyber signals, and so approaches that model the behavior of both the cyber and physical components of the system are needed. One way to examine how well the cyber and physical behavior of a CPS can be measured is through the concept of cyber-physical observability, which is the ability to determine both cyber and physical system states from system measurements in finite time, which can be a crucial requirement for any IDS to be able to detect anomalies and changes to behavior in a CPS and defend against cyber attacks.
In [], Jacobs et al. developed an approach to define cyber-physical observability by combining physical observability algorithms with graph-theoretic network observability methods. Specifically, a combined cyber-physical directed graph was developed with both physical grid and communication infrastructure components, and both network and physical (e.g., phasor measurement unit (PMU) placement algorithms) observability methods were applied to arrive at the cyber-physical observability definition. To expand on this work and apply it to informing cyber-physical IDS placement in DER systems, this paper will develop the necessary network models to represent data flows for grid communication traffic and examine how these models can be used to examine features used in anomaly and intrusion detection []. The insights provided by examining features of the network traffic could then be combined with physical system monitoring and the resultant physical measures to detect cyber-physical compromise.
This paper’s contribution is in examining the usage of network calculus to model the impact and behavior of network communications in a CPS for anomaly and intrusion detection applications. This type of modeling provides a method to connect features of interest which can be measured in communications traffic to the observable effects of anomalies in the system, and the ability to represent cyber attacks that affect the communications capabilities of the cyber network in the CPS. Additionally, while this work concentrates on data flows for the purpose of examining the ability to detect deviations in CPS behavior due to anomalies in the CPS, this work can also be useful more generally when studying both network and physical system behavior in CPS.
In this paper, background on network modeling and properties, as well as a review of related approaches, are provided in Section 2 and network calculus concepts and their application for modeling data flows in a communication network are discussed in Section 3. The developed network modeling approach is demonstrated with the IEEE 13-bus use case in Section 4. Finally, conclusions are provided in Section 5.
2. Network Communications in a Cyber-Physical System: Properties and Related Work
Cyber-physical systems combine physical process dynamics with computation such as from software and communications; this integration enables comprehensive modeling, design, and analysis for the entire system []. Since the electric grid is increasingly more connected in cyberspace, as networking and computing devices are used to provided added functionality through smart grid technologies and other advancements, it is important to understand the intricacies and interactions between the cyber and physical components of the system [,,].
This can be done in many ways; one useful framework to utilize is that of applying directed graphs to represent the influences and connections between components of the system. This gives a picture of how all the pieces fit together, but mechanisms to model those interactions directly are still needed. In a power system, the modeling of the physical process can be done using established methods and tools from linear systems analysis. In the process of modeling the communications network behavior, there are several important characteristics to consider, such as the fact that modern networks are packet-switched, which results in various characteristics for the dynamic behavior of the system. Furthermore, the dynamics of each node in the communications network needs to be appropriately modeled, which is often done by representing a device in the communications network as a first-in first-out (FIFO) queue, while another approach is to examine the bounding behavior on how data flows through the network. These approaches, coming from the well-studied fields of queueing theory and network calculus, help us to develop analytical models of the network traffic [,]. Although these two approaches do differ, they are related to each other, as is shown in [,]. For example, in [] the Lindley recursion principle, which is an important result in queueing theory, is connected to results from network calculus to better understand how network calculus deals with queues and how these two approaches are connected.
Furthermore, for the problems of studying anomaly detection or intrusion detection in CPSs, especially for cybersecurity applications, it is also important to be able to represent the propagation of effects to the system due to such anomalous behavior and how this impacts the performance and security of the CPS. In [], a hybrid process calculus is developed to connect the logical behavior of the connected components of a CPS with the underlying process dynamics. These methods use the language of transition systems to describe the logical interactions of components, while the physical system is typically represented by either continuous-time differential equations or discrete time difference equations. This framework was used develop a method for studying cyber-physical attacks in CPS in [], and to provide a way to examine the impact to the CPS from cyber-physical attacks. This area of related work, which has a background in formal methods, concentrates on the problems of model verification and model checking, and providing ways to ensure the CPS meets its operational requirements. The modeling of how data flows through the communications network, and how features of interest for anomaly detection applications can be modeled, is not represented here as the connections of components is represented logically using labeled transition systems.
The detection of cyber-physical attacks in power networks was studied in [], where such attacks are represented as additional input signals to linear descriptor systems used to represent the power network. A variation of that work that focused on distributed detection of attacks can be found in []. In these papers, both limitations and requirements are provided to determine whether it is possible to detect attacks and algorithms were developed for detection. However, this work did not model data flows in the communications network that may be useful for attack detection on the cyber side of the CPS, such as measuring the amount of traffic going through the network, and is limited to the type of attacks that inject signals into the state or measurement equations of the dynamical system being studied rather than studying attacks that may affect the communications capabilities of the cyber components in the CPS.
In a paper by Burmester et al., the modeling of security in CPSs is explored, where the author’s focus on developing a framework for examining effects from an adversary’s behavior (controlled by a threat model) that encompasses the cyber and physical aspects of the CPS []. The author’s proposed methods for a high level threat model and leveraged traditional Byzantine paradigms to capture adversarial behavior in CPSs as state transitions that are connected to vulnerabilities in the threat model. In [], Akella et al. examined the security of information flows in CPS, and did so using event-based logics and security models for the underlying processes and their execution traces to analyze whether important security properties, such as confidentiality, are maintained. This area of work concentrates on capturing vulnerability risk and ensuring that the CPS does not transition into unsafe or insecure states, and so is powerful in capturing the vulnerabilities in CPSs but does not aim to model physical or cyber effects and behaviors in the CPS.
Prior work studying the integration of heterogenous components in a CPS include a paper by Sztipanovits et al. that investigates CPS integration and discuss challenges due to the heterogeneity of components and interactions []. Their paper proposes a passivity-based design approach in studying the composition of heterogeneous systems, with their main focus being the stability of the system. The use-case for the paper focuses on unmanned air vehicles (UAV) and the CPS integration is focused on the control aspects of the cyber and physical systems and demonstrating how the stability of networked control systems in CPS can be decoupled from timing uncertainties from network and platform effects. This is done by ensuring that uncertainty in the network communications (such as potential data loss or delays) do not inject energy into the system and thus violate passivity assumptions, but does not deal with system performance other than guaranteeing system stability.
Lastly, stochastic network calculus has been applied before to the problem of analyzing power supply reliability with varying renewable energy configurations in the paper by Wang et al. []. In that work, the ability to characterize arrival and service curves in a queueing system using network calculus is extended for the purpose of modeling the energy flows from different renewable energy resources rather than for the application of modeling the communication network itself.
All in all, although there is a great deal of work that has been completed in studying the communication network of CPSs, few works dive into capturing the communication system dynamic behavior as a result of cyber-physical events. Most of the literature focuses on adversarial models and vulnerabilities, which are critical research topics for securing CPSs. In our paper, we aim to add to that body of work by utilizing network calculus to capture detailed impact and deviations in behavior to the cyber-side of a CPS to inform anomaly detection and other security applications.
3. Modeling Data Flows: Network Calculus
Network calculus is an approach to modeling communications networks that allows us to compute deterministic bounds on data flows. This provides a mechanism to study network behavior, but also gives several straightforward ways to directly connect these models with measures of network performance such as latency. There are a variety of ways this may be useful in practice. One example is providing bounds on how much delay is observed in a control network, which can be combined with control system requirements on acceptable delay, or in other words showing that we are within the delay margin for the control system.
This contrasts with approaches such as queueing theory, which uses data structures known as queues to examine the behavior of the communications network, and a good reference for the topic can be found in []. Here we utilize network calculus due to how well the parameters of these models map directly to features that are relevant for examining performance for IDSs. We provide some background here, but for further details, see [,] for good introductions to the topic.
3.1. Preliminaries
Network calculus is a paradigm for modeling network behavior that applies the mathematics of min-plus and max-plus algebra to calculate the performance bounds for network data flows. This allows a systematic approach to be applied that mirrors that of conventional linear systems theory, where systems can be studied by their input–output behavior, and can be combined together in series or parallel to obtain bounds on the data flows in entire networks.
In network calculus, a specific algebra called min-plus (max-plus) algebra is used which replaces the addition operation with the infimum (supremum) operation, as shown in (1), and multiplication is defined to be the standard addition +. Note that is a subset of the reals in union with .
This gives the algebraic structure (, ∧, +). It can be shown that these operations still satisfy algebraic properties such as associativity, closure, existence of neutral and zero elements, commutativity, distributivity, and idempotency, see [] for details.
With the operations ∧ and +, we can compute bounds on the performance for data flows in network calculus. However, before we are able to concatenate systems together we need another important operation: Convolution. This will be defined over a set of functions that are called wide sense increasing, which is defined in (2). In other words, this class of functions is such that for any time s greater or equal to a starting time t, the value of the function . This class of functions may seem restrictive, but is useful in practice to describe the properties of bits flowing through a network, and how many bits have been transmitted or received over time. Furthermore, this make it easier to define and use operations like convolution, which in min-plus algebra, is defined as shown in (3). A dual operation of convolution, min-plus deconvolution, can also be defined as in (4).
Min-plus convolution and deconvolution are needed in network calculus to connect the performance bounds of multiple systems (or sub-systems). For instance, when calculating overall system performance of a network by combining the values for each node in the network. These are also used to measure the horizontal and vertical distances, or deviations, between two curves, as seen in (5) and (6).
These operations assist in calculating the performance measures of the network, which are defined using functions in network calculus called arrival and service curves. As mentioned above, these are built using cumulative functions which describe the wide-sense increasing amount of bits that have been transmitted across a system, over some time interval . These can be generically labeled for some system as for the input and for the output, as shown in Figure 1.
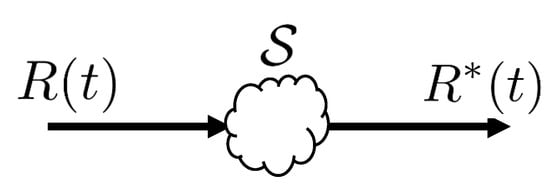
Figure 1.
Relationship between input of system and its output .
These types of functions can be used to define and characterize data arrival and service curves, which give upper and lower bounds on the transmission of data in the network. Arrival curves give upper bounds on the data arrival times, while service curves give the minimum rate of transmission of information.
Formally, the function is an arrival curve if it satisfies the requirements of (7), which states that during any time interval , the flow of information is limited by the function as an upper bound.
One of the most common arrival curves used, both for its ease of use and for its good representation of network dynamics and beneficial mathematical characteristics, is the affine arrival curve, as seen in (8). This curve allows both for bursts in data flows, represented by the parameter b, and limits overall traffic volume to the rate r bits per second. This is the arrival curve we will use later on in Section 4.1.
Service curves are similar to arrival curves in that they give performance guarantees for data flows, but is instead a lower bound on the minimum amount of data that are output by a system. This must satisfy the requirement of (9), which states that the difference in the number of output bits between times and t must exceed the minimum service amount, defined by the rate r.
A common service curve is the rate-latency service curve, which is a simplified approximation for a generalized processor sharing node, and models data being served at rate R, but there is a possible delay for each bit by an amount of time up to time T. This is a useful model to represent data that may need to wait in a queue before being scheduled to be processed and forwarded. There are more advanced models that can be used to describe nodes, such as generalized processor sharing (GPS) nodes, which include dealing with priority scheduling and multiple data flows, are not considered in this initial work. For modeling and related background on such models, see [].
This modeling approach gives several straightforward measures of network performance that can be examined and utilized using the curves we have just defined, such as backlog and virtual delay. Since backlog is a measure of how many bits are inside a system at time t, it can be defined as the difference between the number of bits input to the system and the number of bits output, as shown in (11).
Similarly, the virtual delay of system can be computed as the distance in time until the output equals the input, as shown in (12). Throughout this paper, we will use the terms delay and latency interchangeably, and are referring to (12) in whenever these terms are mentioned.
There are several bounds on data flows through a system that are important, and help to define how deviations in performance impact the entire data flow. We will present and note these results here, but for details on the derivations see [,].
Bounds on backlog and delay in a system can be given that use the vertical and horizontal deviations between the arrival and service curves of a node, or set of nodes, as given in (5) and (6). In one use case, any violation of these bounds would show anomalous behavior that could warrant further examination, for maintenance or showing denial-of-service like conditions. Furthermore, these are useful for calculating the backlog and delay over entire data flows using the arrival and service curves of the concatenated nodes over that entire path.
So far, the modeling shown has been developed for systems sending one bit at a time, or bit-by-bit systems. This can be adjusted to account for packetization, such as seen in modern communications networks, by shaping the output of each node to fit the required curve shape. However, the approach is still the same so for the purpose of simplicity we have left out packetization, as well as priority queueing and scheduling for multiple data flows for this paper. See [] for further details on how those considerations are handled in network calculus models.
3.2. Connecting the Pieces
We now have the pieces to build up a representation of how data flows in the communications network. Although established power system analysis and state estimation techniques help to give insight into the power system performance, adding in network calculus modeling will help to examine the behavior of the communications network in the CPS and get a more complete picture of the overall system.
To accomplish this, we first need to take into consideration the types of data flows that will be present; these are defined by which nodes in the network need to talk to each other. Consider an exemplar power system with connected DERs, typically this would involve a control center, distribution and transmission power system, aggregators, and the DERs. Control centers can have direct communication with the distribution and power system, the DERs, and the aggregator (especially if the DERs are not utility-owned) for communicating control set-points, querying system state, etc. Smart technologies including smart inverters, used to convert direct current to alternating current power for DERs such as solar photovoltaic (PV) systems, may also be included in the communication network. Therefore, some example communications are:
- Communications from an aggregator or control center to the DERs, which could include changes to control settings;
- Reporting of system state and status back to an aggregator, which is useful for situational awareness and monitoring of system state;
- Other data flows in the network.
To build up and analyze each of these data flows, as well as the aggregate whole of the network behavior, we will need to characterize the starting locations and destinations, which will give us candidate paths that must be traversed for data to travel. Routing and scheduling considerations are not considered in this paper for simplicity, but will be added in the future.
For this work, we will use the simple example network shown in Figure 2, that is associated with the IEEE 13-bus system with added DERs, shown in Figure 3. DERs are added to nodes 645, 634, 684, 675, and 680. Each of these DERs are assumed to have communication back to the utility network (e.g., via smart meters, smart inverters), and a small representative communications network was developed to connect these DERs back to a utility control network. Here, we assume that all inverters are communicating back to a central server located in another location in the utility network. More information on the DERs and their configuration can be found in Section 4.
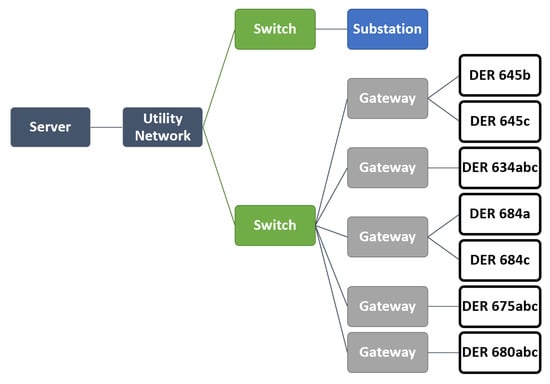
Figure 2.
Representative network structure for IEEE 13-bus test system with extensive distributed energy resource (DER) usage, derived from [].
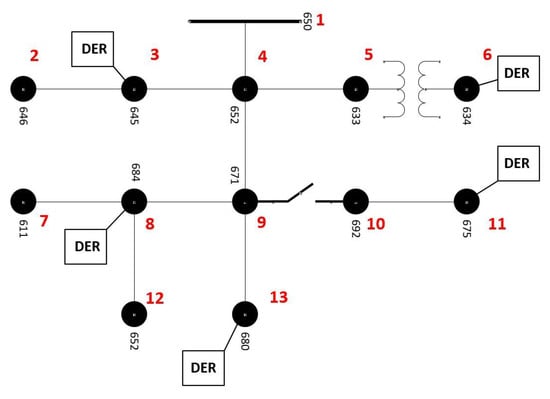
Figure 3.
IEEE 13-bus Test Feeder with added DER locations.
We will utilize the affine arrival and rate-latency service curves, from (7) and (9), to build our model of network data flows. The network parameters for bit rates will be defined as in Table 1. These parameters are setup as shown here for illustrative purposes. The values used for the data rates in this network are determined so as to be similar to the nominal data rate of 10 megabits per second (Mb/s) of Ethernet, as found in the IEEE 802.3 standard [], while having slightly lower data rates for some of the devices to represent variations in equipment. Note that this is illustrative only, and that these values also incorporate timing considerations and data rates for the device characteristics themselves and their ability to process traffic, which would need to be represented in practice. The delay for each individual node will be set to 0.1 s except for the utility network, which will have a delay of s since there are multiple hops internal to that node that have been abstracted away. For simplicity, we will set the burstiness parameter kB of (7) in this paper for all nodes. We will assume that all the DERs have similar characteristics in respect to their network connectivity and will, therefore, be modeled with the same data rates and for all 7 inverters. We have also defined an extra server internal to the utility network to act as an endpoint for communications to and from the DERs, and act as an aggregator or as a high-level controller for the system.

Table 1.
Parameters for Data Flow Model.
We can utilize the models for each data node, and by combining multiple systems in series, we can calculate the arrival and service curves that would result from the arrival and service curves of each node.
To demonstrate how nodes can be connected together, a subset of the network is shown in Figure 4. Here, we can compute the output service curve as shown in (15), giving us our minimal level of service.
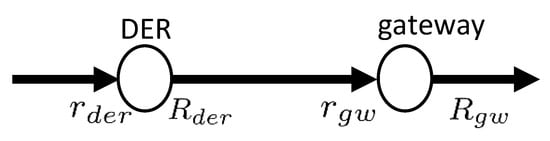
Figure 4.
Simple concatenation of network nodes.
Similarly, the output arrival curve of a system can be recomputed using (16), which allows us to derive a new arrival curve for the next node in the network. By performing this operation at each node, we can derive new bounds for the arrival curve for an entire data flow.
As noted previously, all this can be used to calculate performance measures for the network. Recall that b is a parameter that accounts for bursts in the arrival curves, r is the upper limit for the rate of traffic allowed, and R is the rate for the service rate of the output service curve. (17) shows how the delay for a data flow can be calculated over multiple nodes.
This can be repeated and generalized for n nodes, by performing the same operation with an aggregated parts of the path.
4. IEEE 13-Bus Use Case
To demonstrate how the network communications modeling presented in this paper can be incorporated in the analysis of a CPS, the scenarios mentioned next in Section 4.1 will be run on the IEEE 13 node feeder where a representative network structure was developed and shown in Figure 2. Table 2 shows the kVA rating for these inverter additions, the point of common coupling (PCC), and the phase configuration. Note that the PCC is given in the inverter name by the bus number that the inverter is attached to, and the phase configuration is given by the letters accompanying the bus number (phases a, b, and/or c).

Table 2.
Sizes for Inverters added to IEEE 13-Bus Test Feeder.
Considering both the IEEE 13-bus feeder and the communications network shown in Figure 2, we can utilize the approach developed in [] to develop a directed graph of the entire CPS with both the communications network and the power system. This is shown in Figure 5, and shows how the physical system interacts with the communications network. Any communication assisted control schemes applied to this CPS would require data flows through the data network, which can be modeled as done in this paper. Note that each node in Figure 5 is either a device in the communications network or a bus in the connected power system (in this case, the IEEE 13-bus feeder), while the directed edges show the connections that allow each node to interact. Importantly, the cyber side of the CPS is connected to the physical system through actuation and sensing links.
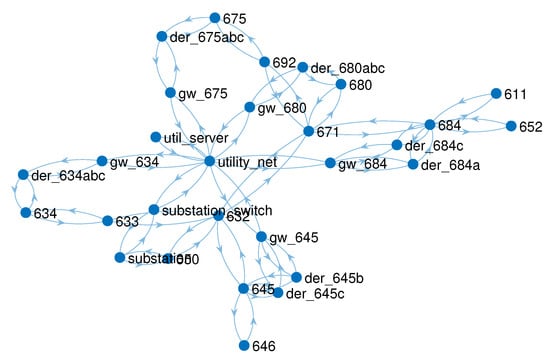
Figure 5.
Directed Graph of Cyber-Physical System with Example Communications Network and IEEE 13-bus Test Feeder.
4.1. Scenarios
To show that this methodology is useful for studying dynamic network behavior, it is important to show that we can also represent changes to the network and have these changes affect the output of our analysis. This is done by applying the following scenarios:
- Denial-Of-Service (DOS) - Gateway overloaded or processing slowed;
- Change in control settings, which does not impact network performance but does impact the power system.
Note that the results here are only meant to be illustrative, and are not exhaustive. These scenarios were chosen to demonstrate how changes to behavior in both the power system and in the communications network can be observed and shown through the approach developed here. In practice, it would be important to consider that the parameters of the network model will need to be matched to the actual values of the equipment used, giving rates for how well data can be transmitted and processed. This step is not examined here, as we are merely applying a simplistic model as an exemplar system to show how this methodology can be applied in practice.
In the first scenario, we will examine a scenario that is developed to represent a DOS scenario. Such a scenario can come about by a variety of ways, including by bombarding a device with an excessive amount of traffic, by system misconfiguration, or by having some processing power diverted for unauthorized processes. This will result in the traffic through this gateway being slowed, which in terms of the network calculus models being studied here can be represented by modifying either the service data rate R or the delay T.
For both cases, this scenario is performed by adjusting one of the gateways at the DER sites, specifically gateway 645 as seen in Figure 2. For the first disruption where we are examining a DOS scenario, we will increase the processing delay on that node to s instead of milliseconds in the normal case, creating a slowdown to one tenth of the normal speed for the processing of traffic at that node. Note that in terms of the network calculus models being utilized in this work, this will affect the service curve by delaying its output as it routes traffic to its destination. In the rate-latency model for the service curve for a network node, the data are output at a rate R after some delay T, so in this scenario this disruption will be represented by an increase in T, as we are only increasing the delay and are assuming the rate R is unaffected. Increasing T will affect the overall time it takes for bits to traverse the network when they flow through that node. This impact in route times can be observed by applying Equation (17) to the data flows in our system, which is shown in Table 3 for a possible set of routes chosen consisting of the DERs to the utility server. Here, recall that our base parameters are kB, and R is as shown in Table 1.

Table 3.
Route times for DERs to utility server.
Here we see that the impact to gateway 645 is affecting the communication times for the two DERs that must communicate through that gateway, but not the other routes. Likewise, the backlog of traffic at each node can be calculated using (11), and the bounds for the overall backlog along a network data flow can be calculated using (6) and (13). If we apply (11) for our scenario to calculate the backlog at each node in the system, we will see the results shown in Table 4.

Table 4.
Backlog for nodes.
In this scenario, there is an additional backlog of bits at the gateway that was disrupted by this scenario, but the backlogs for other nodes are not affected. This is because this value tells us the difference between the arrival and service curves, and in this case we are examining each node separately, so these values are the max number of bits that are still being processed at each node. A simple increase in the delay at gateway 645 from 100 milliseconds to 1 s increases the backlog at that node by 150%, a rather significant increase that will affect any data flows passing through that node, and the overall performance of the communications network. As shown here in this simple simulation, this setup allows us to easily connect a disruption in the service at an individual node to the effects observed in the network traffic and its behavior.
For DOS scenarios where there may be a misconfiguration or some other cause creating a complete drop in traffic, this modeling approach can represent the effects by setting the processing delay T to a very large value, effectively stopping traffic passing through that node in the network. Note that these results match our intuition but the process used to get to these results is scalable and usable in larger, more complex networks as well. This enables more complete analysis of how communications behavior in CPSs may be affected in various conditions, and how this will affect the CPS overall.
Anomalies in the data network are not the only place where issues arise in CPS, as there are also scenarios that are very hard to detect solely from traffic. One such scenario would be an insider threat where there is no large change to network traffic but the control settings of devices, such as DERs, are modified. This can result in anomalous behavior that is not modeled in the communications network, so if we are going to comprehensively model the entire CPS we need to include the physical behavior as well. It is here that we can see the benefit of including both the physical system and the communications network as graphs that are combined and interconnected. Furthermore, for distributed CPS where information about the physical system is transmitted through the communications network we can leverage information from the network model in studying important properties for algorithms that are based on the values of physical system states. A scenario is shown here where the control settings for some of the inverters are changed to disrupt the system, but the communications network is unmodified. Three different experiments noted as baseline (BL), Volt-Var (VV), and attacked Volt-Var (AVV) were performed. Figure 6 show the average feeder voltages for each experiment.
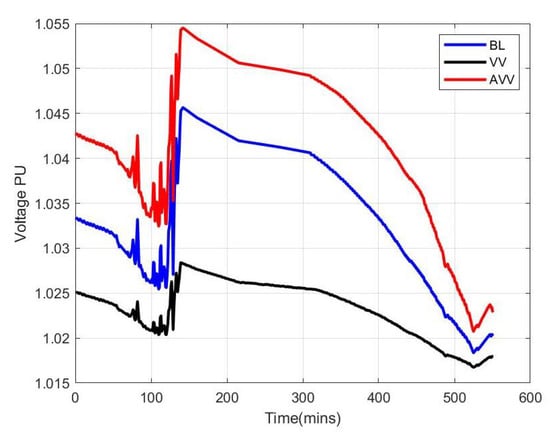
Figure 6.
Voltage Per Unit across IEEE 13-bus Test Feeder for Baseline, Volt-Var controlled, and Attacked Volt-Var Scenarios.
The BL experiment was configured to purposely be well over 1 pu, to highlight the need for voltage regulation which was communication enabled. The VV experiment used the default 1547–2018 set-points; with the voltage points = 0.5%, 0.95%, 0.98%, 1.02%, 1.05%, 1.5% and Var points = 0.44% 0.44%, 0%, 0%, −0.44%, −0.44% []. The AVV experiment used the same voltage points in the VV experiment, however the Var points were flipped, such that Var points = −0.44% −0.44%, 0%, 0%, 0.44%, 0.44%. Inverters 3 and 6 were selected during the AVV experiment to be configured with the AVV curve, while the other inverters had the non-effected VV curve. Figure 6, shows the 3 experiments.
The VV experiment reduced the overall system voltage below the BL voltage. The AVV experiment raised the average system voltage above the BL average system voltage and for longer than an hour, above the ANSI C84.1 Range A voltage limits []. Note that this scenario does not impact the network communications, and so would not be represented in the network model. This helps to demonstrate how there are cases where either the cyber or physical information in the network may not be descriptive for examining IDS performance, but by utilizing both information about the network communications and the physical system we can build a more comprehensive picture of the overall behavior of the CPS. Thus, as we can see, anomaly detection applications in CPS, the usage of features of interest from both the network communications and from the underlying physical system will be important. By providing methods to model and study the combined cyber-physical behavior utilizing the communication models developed in this work and with power system modeling we can achieve a much better picture of the system dynamics and response to anomalies and system disruptions.
5. Conclusions
In this work, we have examined how network calculus can be utilized to develop models for data flows in a CPS and have discussed how these data flows can be useful in studying anomalies in network behavior. This provides a few ways to connect the features that an IDS may study for detection of cyber intrusions with analytical models of a network, providing a solid foundation to use when studying cyber effects in CPSs.
Specifically, we focused on the electric grid and the application of a cyber-physical IDS where changes in both cyber and physical systems need to be monitored. It is no longer sufficient to only focus on physical system situational awareness in the grid (e.g., power system states); cyber-physical situational awareness is required for maintaining continued system operation and control, as well as security. Thus, by modeling the grid data flows using network calculus, a rigorous and detailed approach is achieved to better analyze and understand the grid’s cyber-physical interactions and behavior.
Future work will extend this research to incorporate more sophisticated characteristics of cyber systems, such as packetization, priority queueing and scheduling, and lossy systems (e.g., dropped packets). In addition, a more complete set of cybersecurity scenarios will be examined for anomaly detection, dealing with more complex behaviors and disruptions. Furthermore, this work can be used as a foundation for studying IDS placement approaches to detect deviations in both cyber and physical parts of a CPS (beyond the electric grid). Most IDS solutions focus on detecting signatures of malicious activity in the communications network, and, as mentioned, situational awareness tools and state estimation in power systems only examine the physical state of the system. By examining both, a hybrid cyber-physical IDS could potentially improve detection performance in the CPS and provide mechanisms to formulate suitable response.
Author Contributions
Conceptualization, N.J., S.H.-M. and A.S.; Formal analysis, N.J., S.H.-M. and A.S.; Investigation, N.J., S.H.-M. and A.S.; Methodology, N.J., S.H.-M. and A.S.; Project administration, S.H.-M.; Software, N.J. and A.S.; Supervision, S.H.-M.; Validation, N.J. and A.S.; Visualization, N.J., S.H.-M. and A.S.; Writing—original draft, N.J., S.H.-M. and A.S.; Writing—review & editing, N.J., S.H.-M. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the U.S. Department of Energy (DOE) Solar Energy Technologies Office (SETO) project #34234. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government. SAND2021-7215J.
Acknowledgments
We would like to acknowledge and thank our other team members and colleagues Adrian Chavez, Christian Birk Jones, and Brian Wright, for all the helpful discussions and feedback.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Summers, A.; Johnson, J.; Darbali-Zamora, R.; Hansen, C.; Anandan, J.; Showalter, C. A Comparison of DER Voltage Regulation Technologies Using Real-Time Simulations. Energies 2020, 13, 3562. [Google Scholar] [CrossRef]
- Darbali-Zamora, R.; Johnson, J.; Summers, A.; Jones, C.B.; Hansen, C.; Showalter, C. State Estimation-Based Distributed Energy Resource Optimization for Distribution Voltage Regulation in Telemetry-Sparse Environments Using a Real-Time Digital Twin. Energies 2021, 14, 774. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Xiang, Y.; Ten, C. Power System Reliability Evaluation with SCADA Cybersecurity Considerations. IEEE Trans. Smart Grid 2015, 6, 1707–1721. [Google Scholar] [CrossRef]
- Zonouz, S.; Rogers, K.M.; Berthier, R.; Bobba, R.B.; Sanders, W.H.; Overbye, T.J. SCPSE: Security-Oriented Cyber-Physical State Estimation for Power Grid Critical Infrastructures. IEEE Trans. Smart Grid 2012, 3, 1790–1799. [Google Scholar] [CrossRef]
- Lai, C.; Jacobs, N.; Hossain-McKenzie, S.; Cordeiro, P.; Onunkwo, I.; Johnson, J. Cyber Security Primer for DER Vendors, Aggregators, and Grid Operators; Sandia Report SAND2017-13113; Sandia National Laboratories: Albuquerque, NM, USA, 2017.
- Case, D.U. Analysis of the Cyber Attack on the Ukrainian Power Grid; Electricity Information Sharing and Analysis Center (E-ISAC): Washington, DC, USA, 2016; Volume 388. [Google Scholar]
- Hemsley, K.E.; Fisher, E. History of Industrial Control System Cyber Incidents; Idaho National Laboratory: Idaho Falls, ID, USA, 2018. [Google Scholar]
- U.S.-Canada Power System Outage Task Force. Final Report on the August 14, 2003 Blackout in the United States and Canada: Causes and Recommendations; U.S.-Canada Power System Outage Task Force: Ottawa, ON, Canada, 2004. [Google Scholar]
- Chavez, A.; Lai, C.; Jacobs, N.; Hossain-McKenzie, S.; Jones, C.B.; Johnson, J.; Summers, A. Hybrid Intrusion Detection System Design for Distributed Energy Resource Systems. In Proceedings of the 2019 IEEE CyberPELS (CyberPELS), Knoxville, TN, USA, 29 April–1 May 2019; pp. 1–6. [Google Scholar]
- Lai, C.; Chavez, A.; Jones, C.B.; Jacobs, N.; Hossain-McKenzie, S.; Johnson, J.; Summers, A. Review of Intrusion Detection Methods and Tools for Distributed Energy Resources; Sandia Technical Report SAND2021-1737; Sandia National Laboratories: Albuquerque, NM, USA, 2021.
- Jacobs, N.; Hossain-McKenzie, S.; Summers, A.; Jones, C.B.; Wright, B.; Chavez, A. Cyber-Physical Observability for the Electric Grid. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar]
- Shi, J.; Wan, J.; Yan, H.; Suo, H. A survey of Cyber-Physical Systems. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 9–11 November 2011; pp. 1–6. [Google Scholar]
- Khaitan, S.K.; McCalley, J.D. Cyber physical system approach for design of power grids: A survey. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Shahid, A. Cyber-physical modeling and control of smart grids—A new paradigm. In Proceedings of the 2016 IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Yu, X.; Xue, Y. Smart Grids: A Cyber-Physical Systems Perspective. Proc. IEEE 2016, 104, 1058–1070. [Google Scholar] [CrossRef]
- Bertsekas, D.; Gallager, R. Data Networks, 2nd ed.; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1992. [Google Scholar]
- Le Boudec, J.Y.; Thiran, P. Network Calculus: A Theory of Deterministic Queuing Systems for the Internet; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Jiang, Y. Network calculus and queueing theory: Two sides of one coin: Invited paper. In Proceedings of the VALUETOOLS ’09: Proceedings of the Fourth International ICST Conference on Performance Evaluation Methodologies and Tools, Pisa, Italy, 20–22 October 2009. [Google Scholar]
- Pandit, K.; Schmitt, J.; Steinmetz, R. Network calculus meets queueing theory—A simulation based approach to bounded queues. In Proceedings of the Twelfth IEEE International Workshop on Quality of Service (IWQOS 2004), Montreal, QC, Canada, 9 June 2004; pp. 114–120. [Google Scholar] [CrossRef]
- Lanotte, R.; Merro, M. A Calculus of Cyber-Physical Systems. arXiv 2016, arXiv:1612.00484. [Google Scholar]
- Lanotte, R.; Merro, M.; Muradore, R.; Viganò, L. A Formal Approach to Cyber-Physical Attacks. In Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA, USA, 21–25 August 2017; pp. 436–450. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dörfler, F.; Bullo, F. Cyber-physical attacks in power networks: Models, fundamental limitations and monitor design. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 2195–2201. [Google Scholar] [CrossRef]
- Dörfler, F.; Pasqualetti, F.; Bullo, F. Distributed detection of cyber-physical attacks in power networks: A waveform relaxation approach. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 1486–1491. [Google Scholar] [CrossRef]
- Burmester, M.; Magkos, E.; Chrissikopoulos, V. Modeling security in cyber-physical systems. Int. J. Crit. Infrastruct. Prot. 2012, 5, 118–126. [Google Scholar] [CrossRef]
- Akella, R.; Tang, H.; McMillin, B.M. Analysis of information flow security in cyber-physical systems. Int. J. Crit. Infrastruct. Prot. 2010, 3, 157–173. [Google Scholar] [CrossRef]
- Sztipanovits, J.; Koutsoukos, X.; Karsai, G.; Kottenstette, N.; Antsaklis, P.; Gupta, V.; Goodwine, B.; Baras, J.; Wang, S. Toward a Science of Cyber–Physical System Integration. Proc. IEEE 2012, 100, 29–44. [Google Scholar] [CrossRef]
- Wang, K.; Ciucu, F.; Lin, C.; Low, S.H. A Stochastic Power Network Calculus for Integrating Renewable Energy Sources into the Power Grid. IEEE J. Sel. Areas Commun. 2012, 30, 1037–1048. [Google Scholar] [CrossRef]
- Van Bemten, A.; Kellerer, W. Network Calculus: A Comprehensive Guide; Technical Report No. 201603; Technical University of Munich: Munich, Germany, 2016. [Google Scholar] [CrossRef]
- IEEE Standard for Ethernet. IEEE Std 802.3-2018 (Revision of IEEE Std 802.3-2015); IEEE: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- NEMA. American National Standard for Electric Power Systems and Equipment-Voltage Rating (60 Hz); National Electrical Manufacturers Association: Rosslyn, VA, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).