On the Distributed Construction of Stable Networks in Polylogarithmic Parallel Time
Abstract
1. Introduction
Our Approach
2. Materials and Methods
2.1. The Model
2.2. Problem Definitions
- k-Children Spanning Tree: The goal is to construct a spanning tree where each individual element has at most children.
- -Regular Network: A spanning network where for any where , elements with degree form a clique and all others have a degree of at least l and at most k.
2.3. Experimental Setup
3. Results
3.1. Polylogarithmic Time Protocols for k-Children Spanning Trees
| Algorithm 1k-Slot protocol |
| :
|
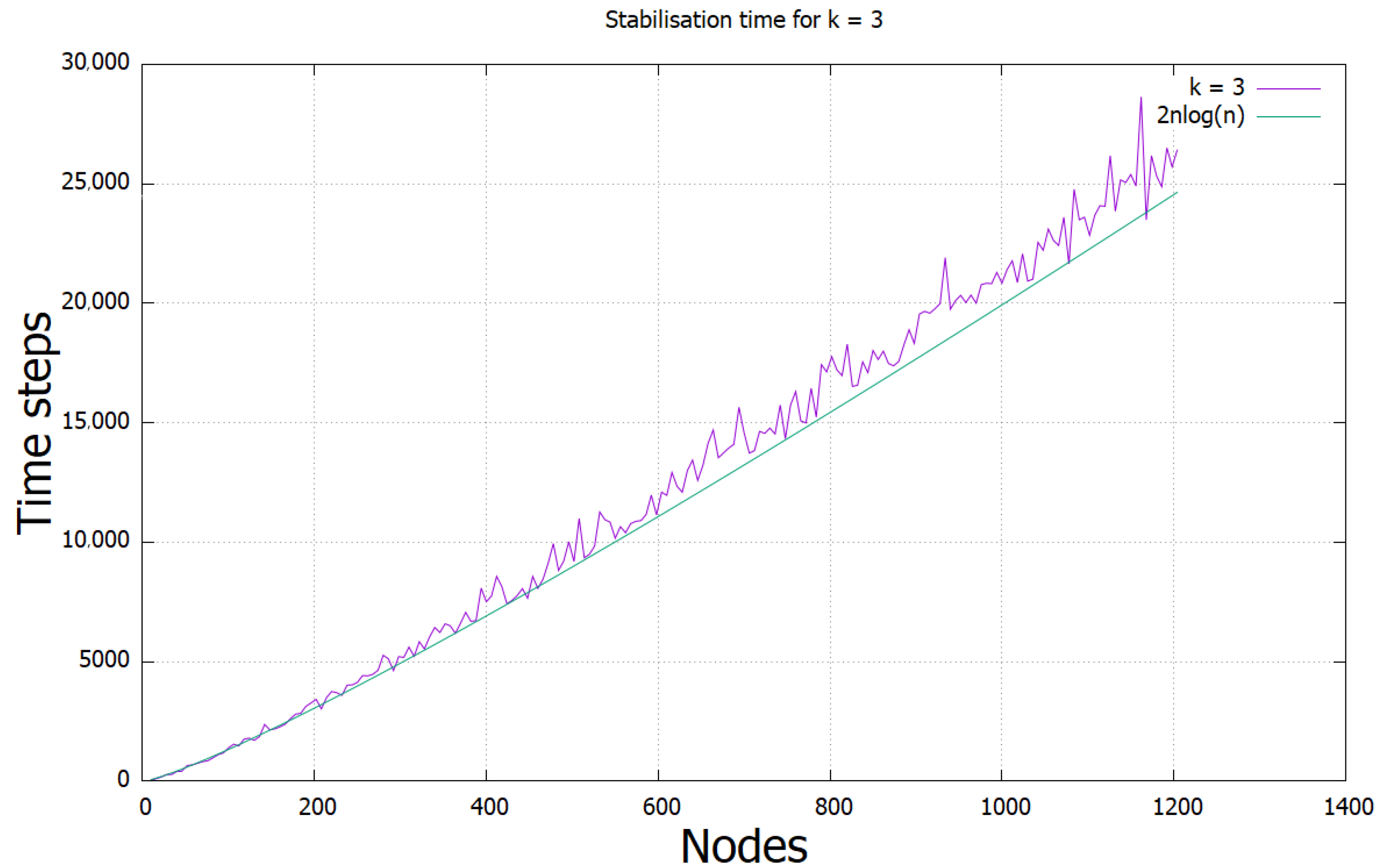
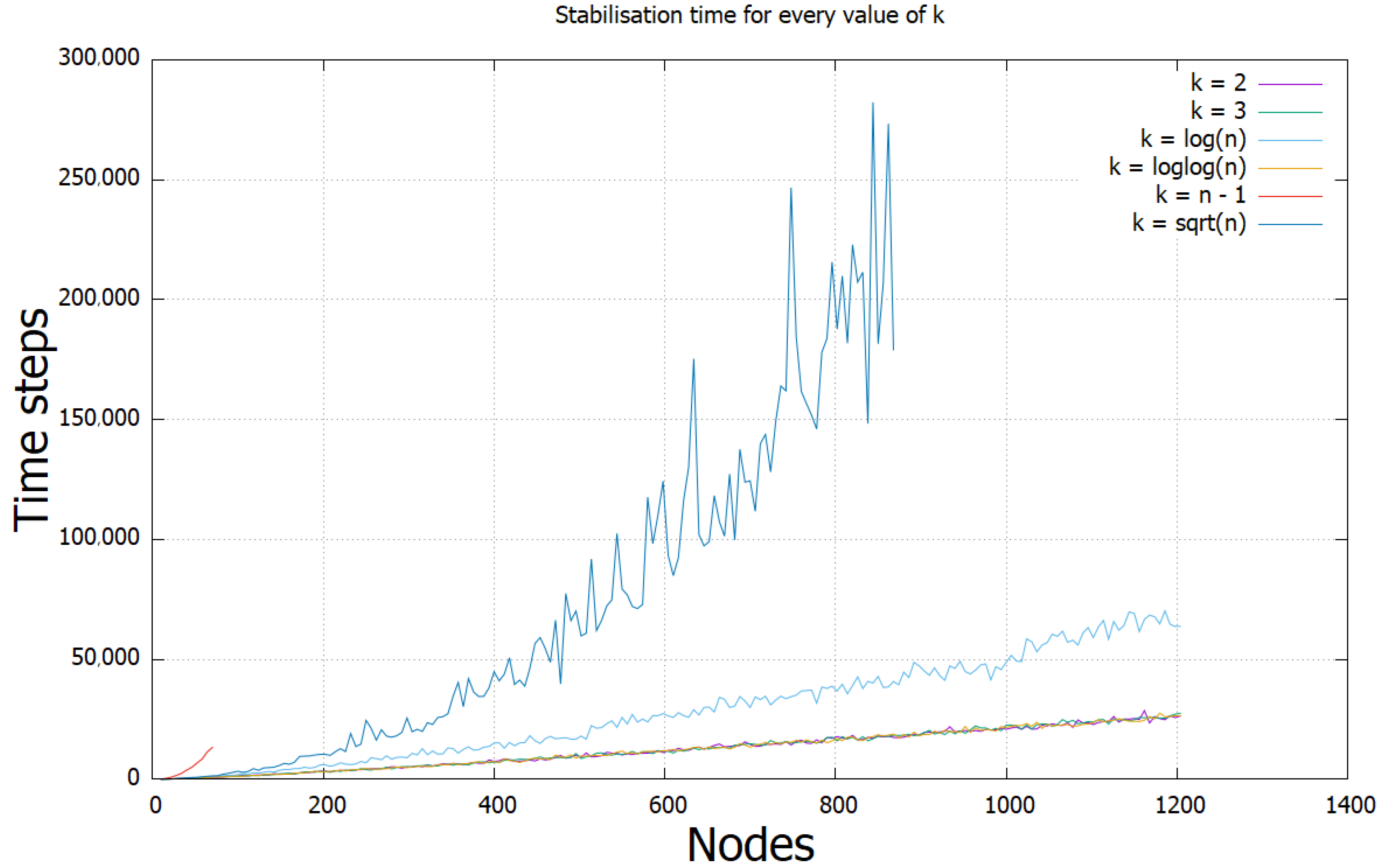
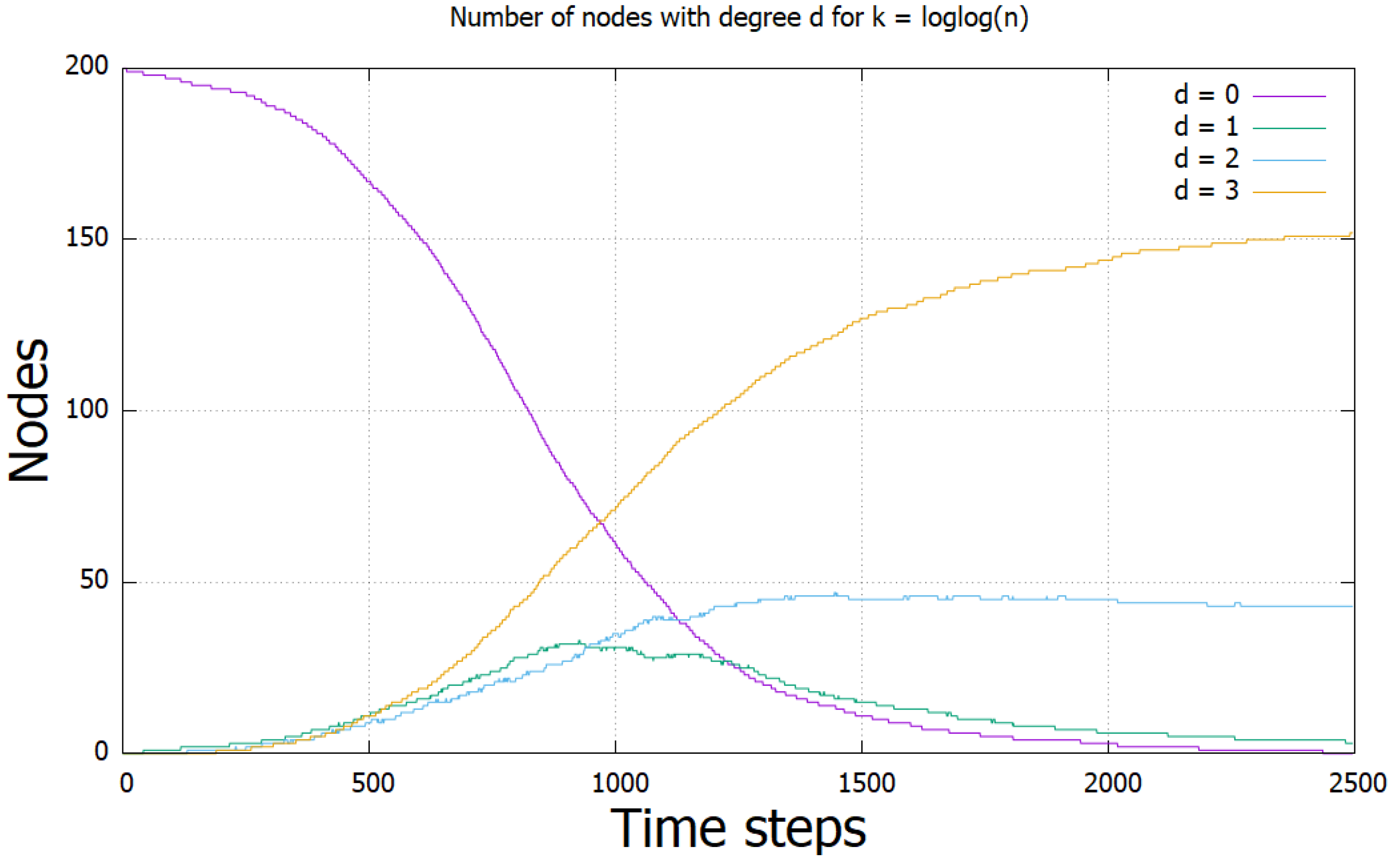
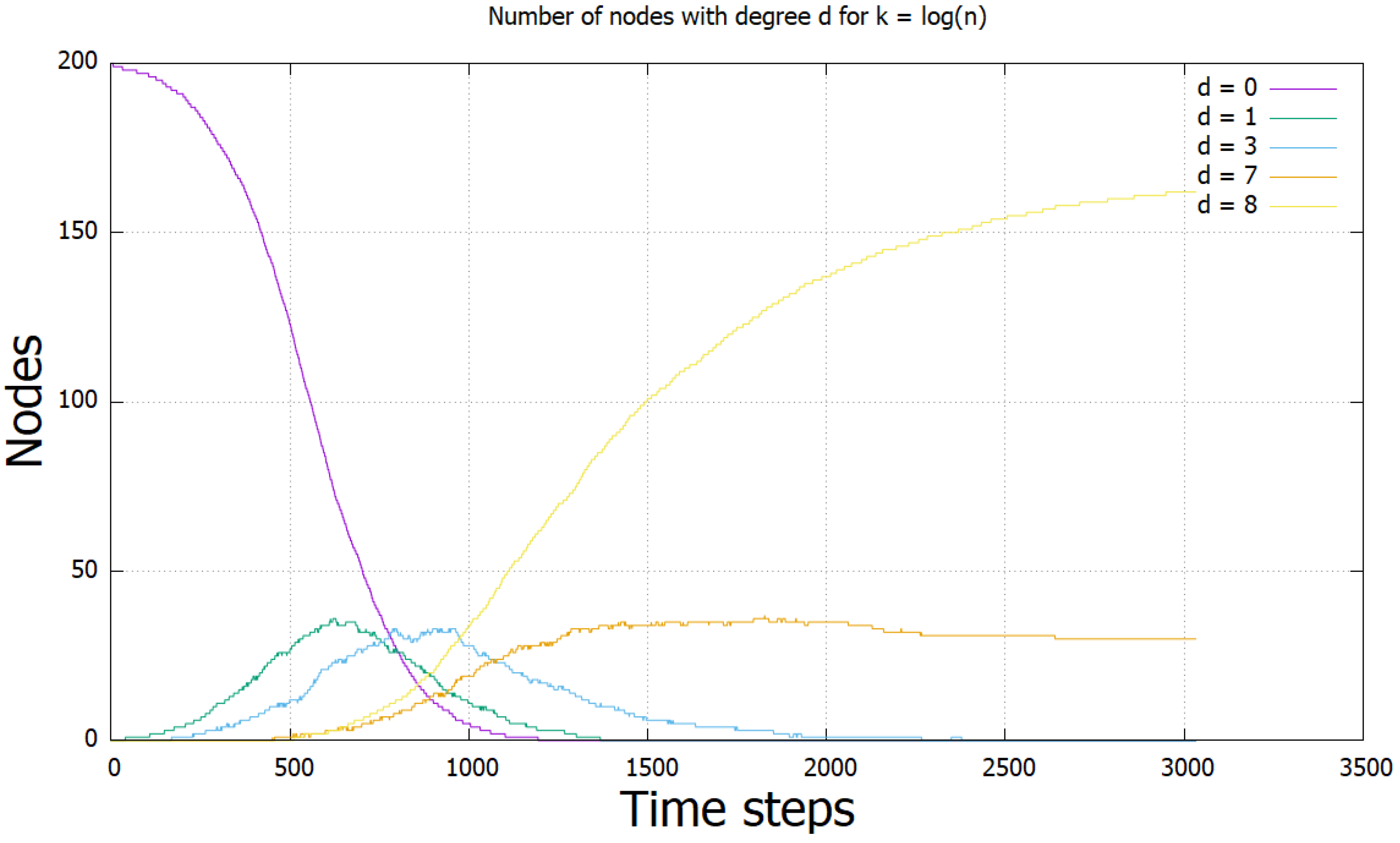
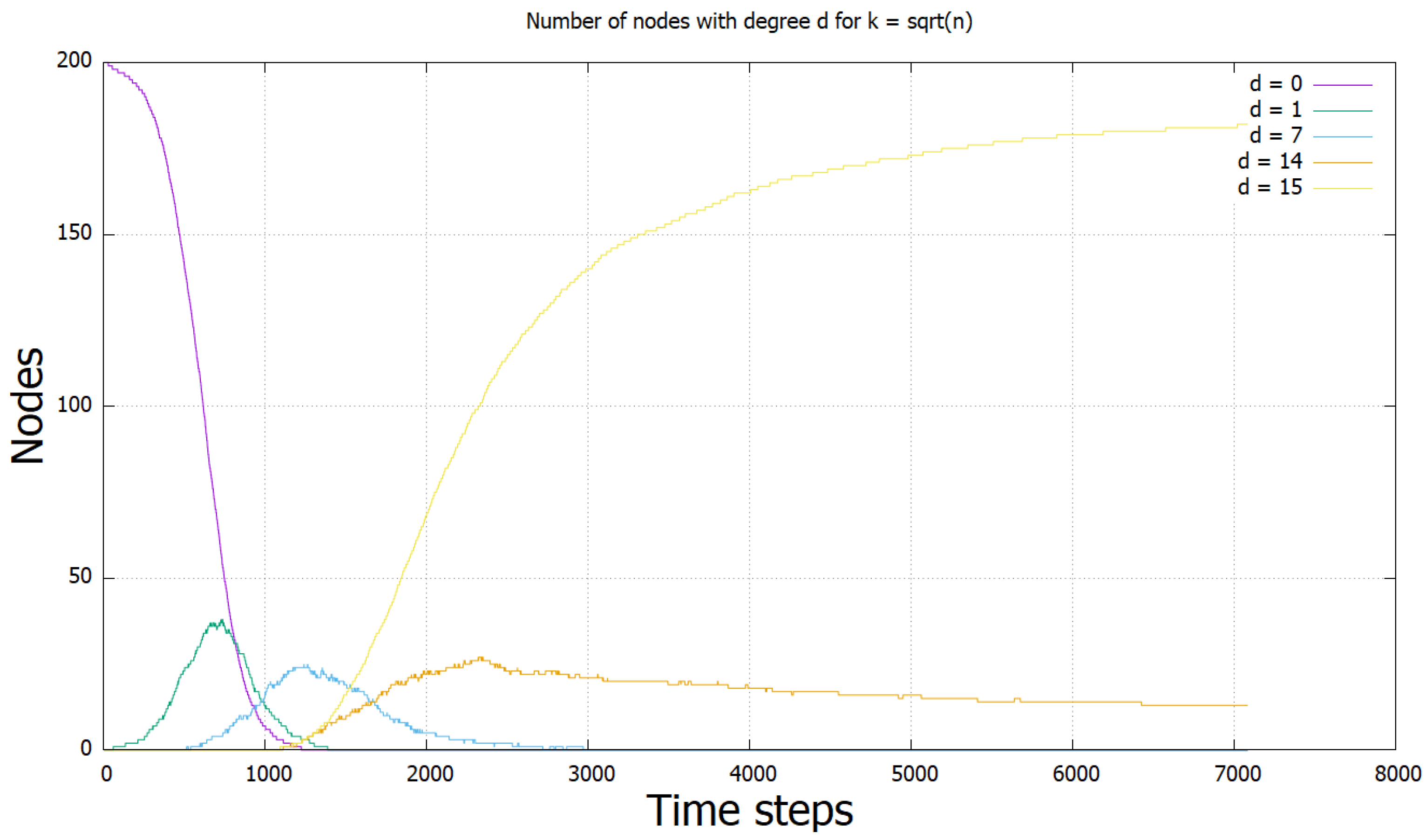
3.2. Time Thresholds for -Regular Networks
| Algorithm 2Cross-edges Tree |
| :
|
Stabilisation Conditions of the -Regular Network
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angluin, D.; Aspnes, J.; Diamadi, Z.; Fischer, M.J.; Peralta, R. Computation in networks of passively mobile finite-state sensors. Distrib. Comput. 2006, 18, 235–253. [Google Scholar] [CrossRef]
- Dan Alistarh, R.G. Polylogarithmic-time leader election in population protocols. In Proceedings of the 42nd International Colloquium on Automata, Languages, and Programming (ICALP), Kyoto, Japan, 6–10 July 2015; pp. 479–491. [Google Scholar]
- Gasieniec, L.; Stachowiak, G. Fast Space Optimal Leader Election in Population Protocols. In Proceedings of the 2018 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA18), New Orleans, LA, USA, 7–10 January 2018; pp. 2653–2667. [Google Scholar]
- Alistarh, D.; Aspnes, J.; Eisenstat, D.; Gelashvili, R.; Rivest, R.L. Time-space trade-offs in population protocols. In Proceedings of the 2017 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA17), Barcelona, Spain, 16–19 January 2017; pp. 2560–2579. [Google Scholar]
- Doty, D.; Eftekhari, M.; Michail, O.; Spirakis, P.G.; Theofilatos, M. Brief Announcement: Exact Size Counting in Uniform Population Protocols in Nearly Logarithmic Time. In Proceedings of the 32nd International Symposium on Distributed Computing (DISC), Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, New Orleans, LA, USA, 15–19 October 2018; pp. 46:1–46:3. [Google Scholar] [CrossRef]
- O’Dell, R.; Wattenhofer, R. Information dissemination in highly dynamic graphs. In Proceedings of the 2005 Joint Workshop on Foundations of Mobile Computing (DIALM-POMC), Cologne, Germany, 2 September 2005; pp. 104–110. [Google Scholar] [CrossRef]
- Kuhn, F.; Lynch, N.; Oshman, R. Distributed computation in dynamic networks. In Proceedings of the Forty-Second ACM Symposium on Theory of Computing (STOC), Cambridge, MA, USA, 5–8 June 2010; pp. 513–522. [Google Scholar]
- Michail, O.; Chatzigiannakis, I.; Spirakis, P.G. Causality, Influence, and Computation in Possibly Disconnected Synchronous Dynamic Networks. In Proceedings of the 16th International Conference on Principles of Distributed Systems (OPODIS), Rome, Italy, 18–20 December 2012; pp. 269–283. [Google Scholar]
- Angluin, D.; Aspnes, J.; Chen, J.; Wu, Y.; Yin, Y. Fast Construction of Overlay Networks. In Proceedings of the 17th ACM symposium on Parallelism in Algorithms and Architectures (SPAA), Las Vegas, NV, USA, 18–20 July 2005; pp. 145–154. [Google Scholar]
- Aspnes, J.; Shah, G. Skip Graphs. ACM Trans. Algorithms (TALG) 2007, 3, 37. [Google Scholar] [CrossRef]
- Aspnes, J.; Wu, Y. O(log n)-Time Overlay Network Construction from Graphs with Out-Degree 1. In Proceedings of the 11th International Conference on Principles of Distributed Systems (OPODIS), Guadeloupe, France, 17–20 December 2007; pp. 286–300. [Google Scholar]
- Götte, T.; Hinnenthal, K.; Scheideler, C. Faster Construction of Overlay Networks. In Proceedings of the 26th International Colloquium on Structural Information and Communication Complexity (SIROCCO), L’Aquila, Italy, 1–4 July 2019; pp. 262–276. [Google Scholar]
- Michail, O.; Skretas, G.; Spirakis, P.G. Distributed Computation and Reconfiguration in Actively Dynamic Networks. In Proceedings of the 39th ACM Symposium on Principles of Distributed Computing (PODC), Virtual Event, Italy, 3–7 August 2020; pp. 448–457. [Google Scholar]
- Michail, O.; Spirakis, P.G. Simple and efficient local codes for distributed stable network construction. Distrib. Comput. 2016, 29, 207–237. [Google Scholar] [CrossRef]
- Michail, O. Terminating distributed construction of shapes and patterns in a fair solution of automata. Distrib. Comput. 2018, 31, 343–365. [Google Scholar] [CrossRef]
- Gmyr, R.; Hinnenthal, K.; Scheideler, C.; Sohler, C. Distributed Monitoring of Network Properties: The Power of Hybrid Networks. In Proceedings of the 44th International Colloquium on Automata, Languages, and Programming (ICALP), Warsaw, Poland, 10–14 July 2017; pp. 137:1–137:15. [Google Scholar]
- Becchetti, L.; Bergamini, L.; Ficarola, F.; Salvatore, F.; Vitaletti, A. First Experiences with the Implementation and Evaluation of Population Protocols on Physical Devices. In Proceedings of the 2012 IEEE International Conference on Green Computing and Communications, Besancon, France, 20–23 November 2012; pp. 335–342. [Google Scholar] [CrossRef]
- Atzori, L.; Lera, A.; Morabito, G. The Internet of Things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Holub, S.; Khymytsia, N.; Holub, M.; Fedushko, S. The Intelligent Monitoring of Messages on Social Networks. CEUR Workshop Proc. 2020, 2616, 308–317. [Google Scholar]
- Àlvarez, C.; Chatzigiannakis, I.; Duch, A.; Gabarró, J.; Michail, O.; Serna, M.; Spirakis, P.G. Computational models for networks of tiny artifacts: A survey. Comput. Sci. Rev. 2011, 5, 7–25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Connor, M.; Michail, O.; Spirakis, P. On the Distributed Construction of Stable Networks in Polylogarithmic Parallel Time. Information 2021, 12, 254. https://doi.org/10.3390/info12060254
Connor M, Michail O, Spirakis P. On the Distributed Construction of Stable Networks in Polylogarithmic Parallel Time. Information. 2021; 12(6):254. https://doi.org/10.3390/info12060254
Chicago/Turabian StyleConnor, Matthew, Othon Michail, and Paul Spirakis. 2021. "On the Distributed Construction of Stable Networks in Polylogarithmic Parallel Time" Information 12, no. 6: 254. https://doi.org/10.3390/info12060254
APA StyleConnor, M., Michail, O., & Spirakis, P. (2021). On the Distributed Construction of Stable Networks in Polylogarithmic Parallel Time. Information, 12(6), 254. https://doi.org/10.3390/info12060254




