A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher
Abstract
1. Introduction
2. Preliminaries
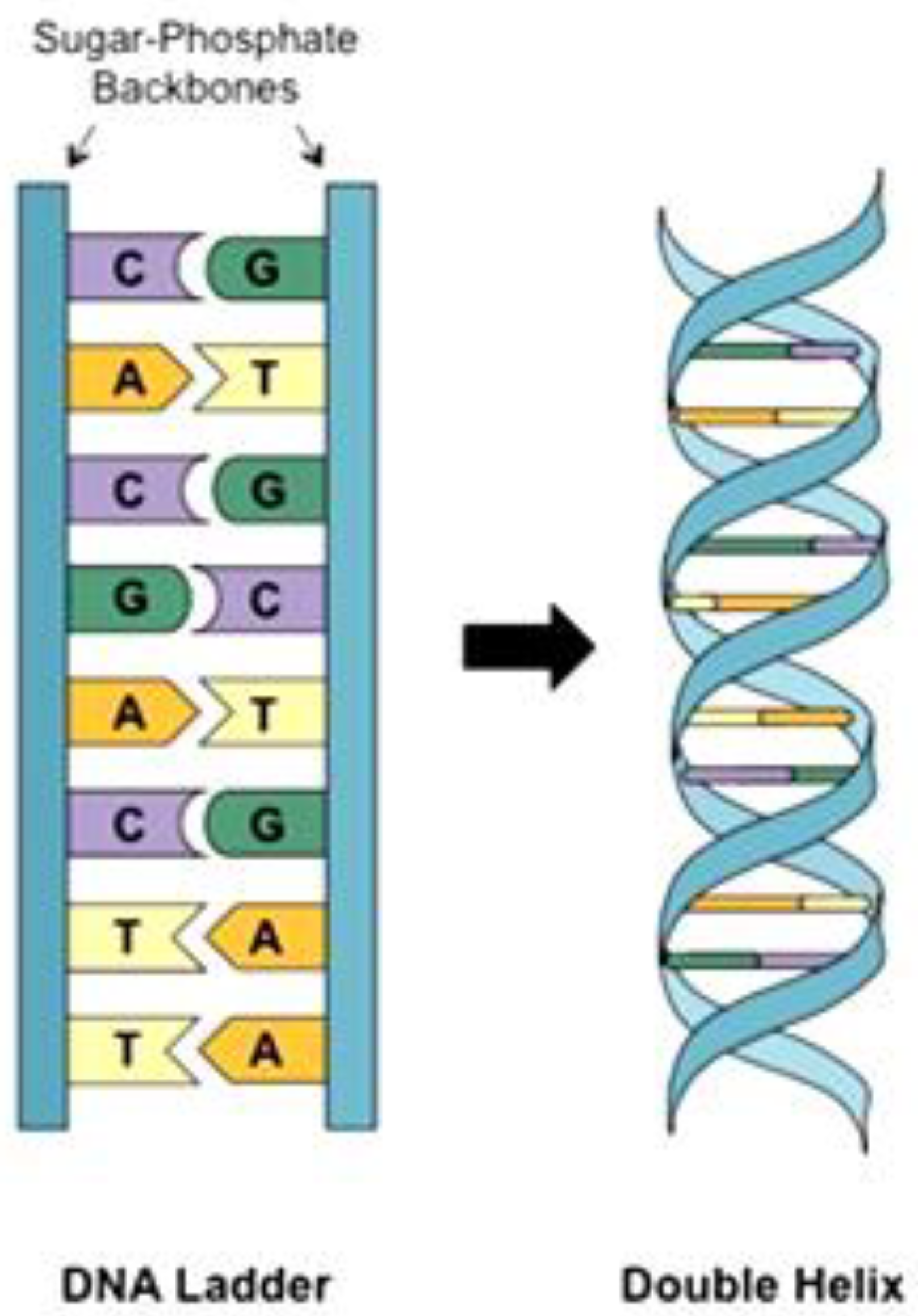
2.1. DNA
2.2. The Multinomial Model
| Algorithm 1. Generate Sequence |
| Input:Seq: A pattern DNA sequence Seed: The seed value for the random number generator Output: randSeq: A random DNA sequence 1. Compute the multinomial parameters 1.1 let L be the length of Seq 1.2 Count the bases in Seq as countA, countC, countG, countT 1.3 Compute the probabilities as: pA = countA/L pC = countC/L pG = countG/L pT = countT/L 2. Generate the sequence 2.1 Compute the cumulative probabilities as: cpA = pA cpC = cpA + pC cpG = cpC + pG cpT = cpG + pT 2.2 Initialize the random number generator with Seed. 2.3 for i = 1 to L Generate a random number (b) between 0 and 1 if b < cpA then randSeqi = A else if b < cpC then randSeqi = C else if b < cpG then randSeqi = G else randSeqi = T end 3. return randSeq |
2.3. The XOR Cipher
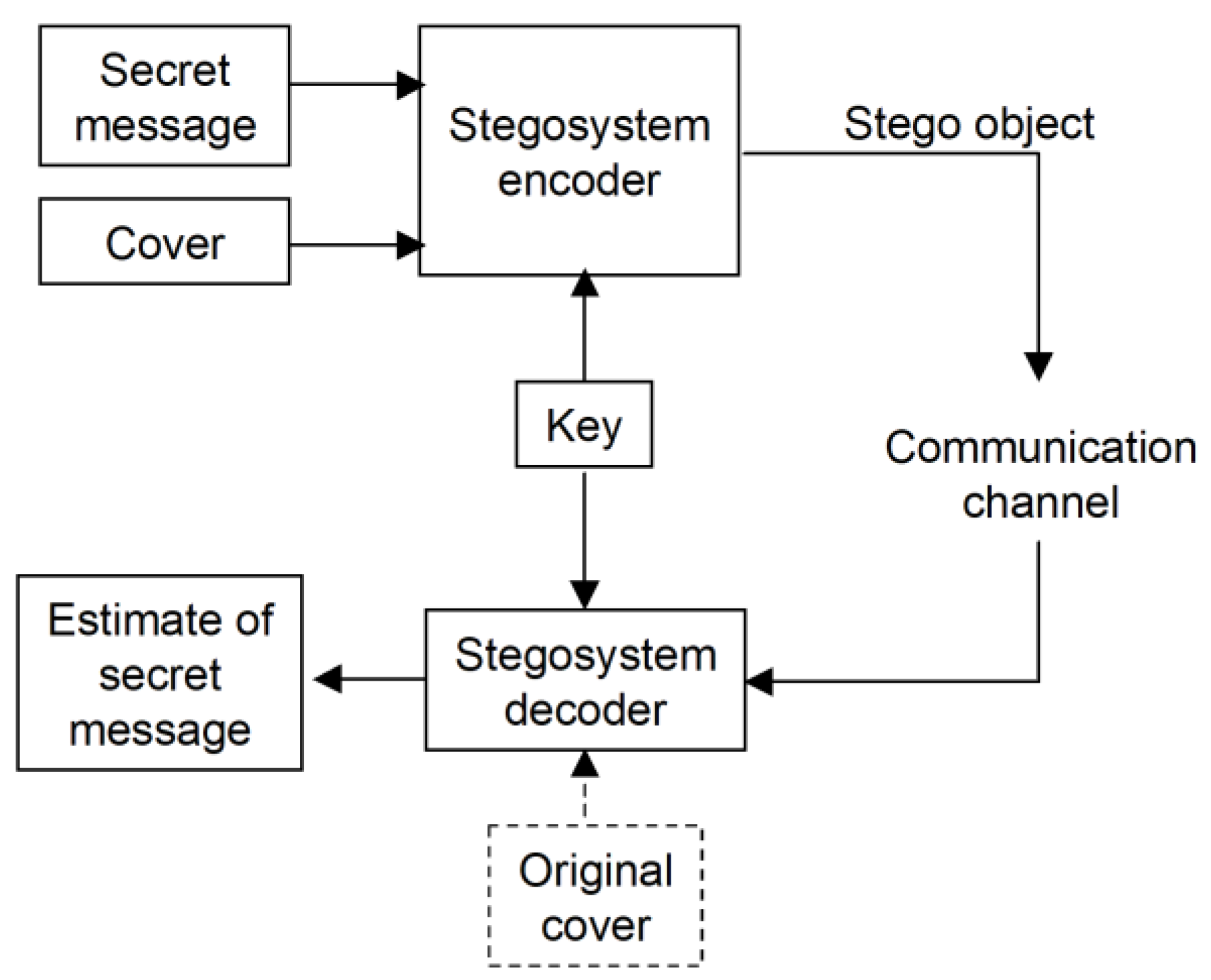
3. The Steganographic Approach
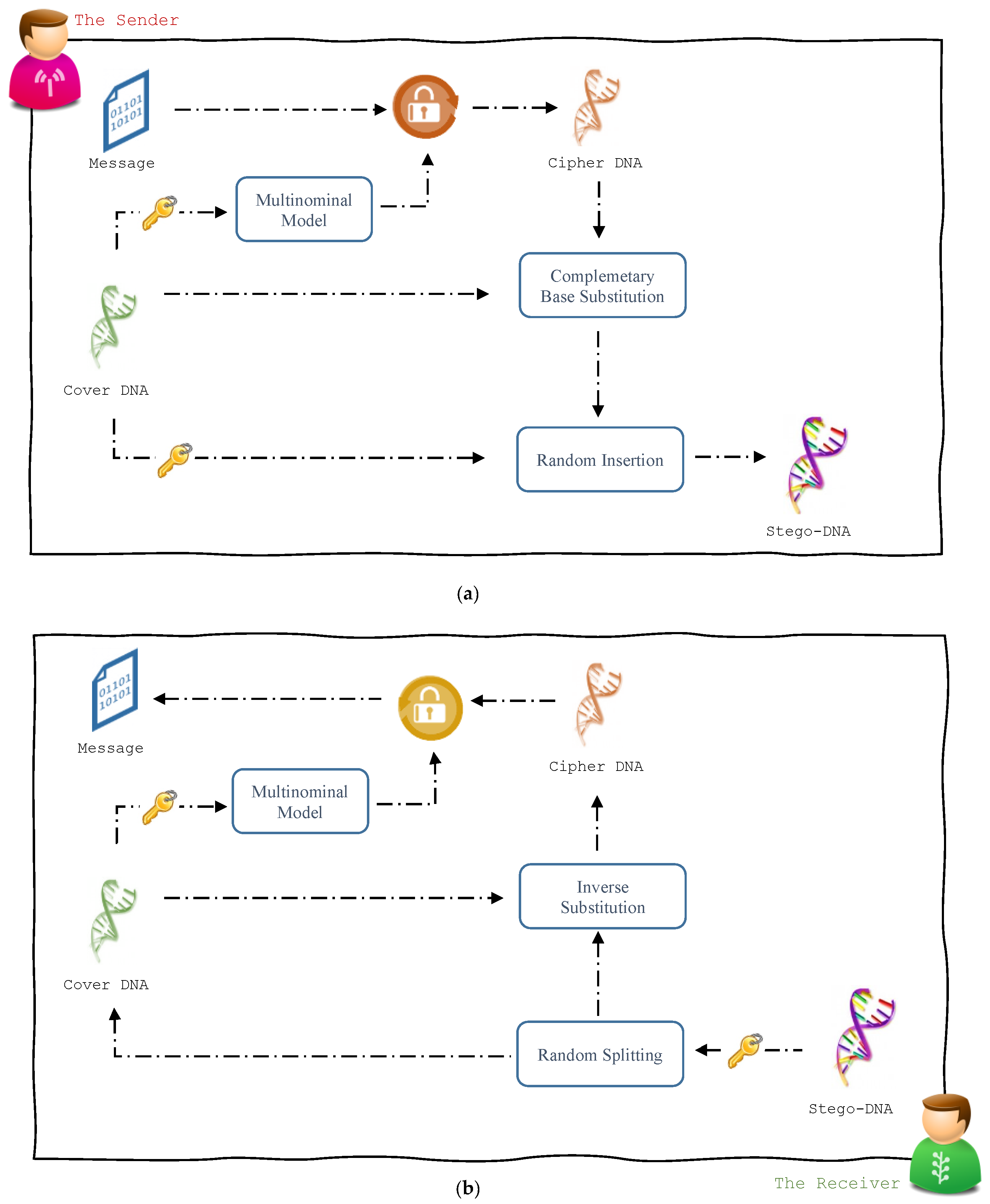
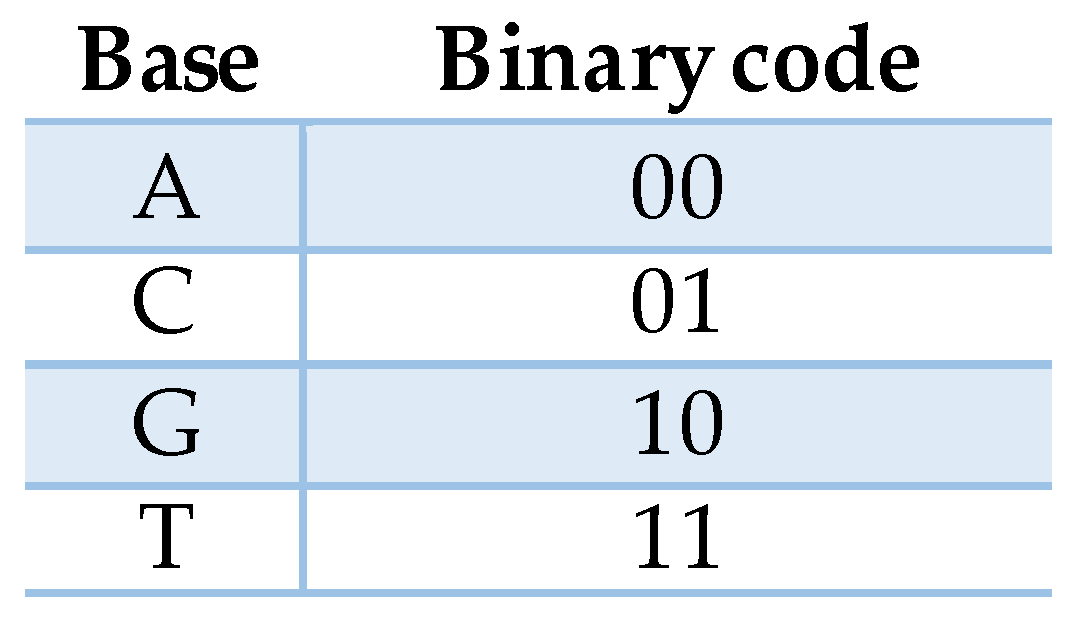
3.1. Message Hiding Module
| Algorithm 2. Message Hiding |
| Input:Cover: reference DNA sequence, used as a cover media Msg: secret message Key: secret key-word Output: Stego: Stego-DNA sequence 1. Message Encryption 1.1 Encode Msg into a DNA sequence MsgDNA using a coding rule. 1.2 Let seed be a value derived from Key. 1.3 Generate Keyxor using multinominal model where Cover is the pattern sequence and seed as the seed value. 1.4 Let m = |MsgDNA| 1.5 for i = 1 to m Msgcph[i] = MsgDNA[i] XOR Keyxor[i] end 2. Header Preparation 2.1 Let m = |Msgcph| 2.2 Let Head be the DNA representation of the binary value of m. 2.3 Concatenate Head with Msgcph. 3. The Substitution Phase: 3.1 Let n = |Cover| and Let m = |Msgcph| 3.2 Generate a set (p1, p2, p3, …., pn) as the random permutation of n using seed 3.3 Initialize Coversub to be a copy of Cover 3.4 Initialize i to 1 3.5 for j = 1 to m if Msgcph [j] is equal to A then Coversub [pi] = Cover [pi] else if Msgcph [j] is equal to C then Coversub [pi] = C(Cover[pi]) else if Msgcph [j] is equal to G then Coversub [pi] = C(C(Cover[pi])) else Coversub [pi] = C(C(C(Cover[pi]))) end Increment i end 4. The Insertion Phase: 4.1 Let i and j be two different values derived from Key 4.2 Generate a sequence of random numbers (i1, i2, i3, ….) using i as the seed value 4.3 Generate a sequence of random numbers (j1, j2, j3, ….) using j as the seed value 4.4 Find the smallest integer tc such that Find the smallest integer tm such that 4.5 if tc < tm then return else Let t = tm end 4.6 Divide Cover into t − 1 segments (C1, C2, C3, ….) with lengths (i1, i2, i3, ….) respectively and keep the residual part in Ct 4.7 Divide Coversub into t − 1 segments (M1, M2, M3, ….) with lengths (j1, j2, j3, ….) respectively and keep the residual part in Mt 4.8 Initialize Stego as an empty sequence. 4.9 for k = 1 to t Append Ck to Stego Append Mk to Stego end 5. return Stego |
3.2. Message Recovery Module
| Algorithm 3. Message Retrieval |
| Input:Stego: Stego-DNA sequence Key: secret key-word Output: Msg: secret message 1. Sequence Splitting 1.1 Let i and j be two different values derived from Key 1.2 Generate a sequence of random numbers (i1, i2, i3, ….) using i as the seed value 1.3 Generate a sequence of random numbers (j1, j2, j3, …. using j as the seed value 1.4 Let n = |Stego|/2 1.5 Find the smallest integer t such that 1.6 Divide S into t − 1 segments (S1, S2, S3, …. St−1) with lengths (i1 + j1, i2 + j2, i3 + j3…., it−1 + jt−1) respectively and keep the residual in St 1.7 Initialize Cover as an empty sequence 1.8 Initialize Coversub as an empty sequence 1.9 for k = 1 to t − 1 Append the ik bases of Sk to Cover Append the jk bases of Sk to Coversub end 1.10 Append the it bases of St to Cover 1.11 Append the jt bases of St to Coversub 2. Header Retrieval 2.1 Let seed be a value derived from Key. 2.2 Generate a set (p1, p2, p3, …., pn) as the random permutation of n using seed 2.3 Initialize Head as fixed length sequence 2.4 Initialize i to 1 2.5 for j = 1 to |Head| if Coversub [j] == Cover [pi] then Head[j] = A else if Coversub [j] == C(Cover [pi]) then Head[j] = C else if Coversub [j] == C(C(Cover [pi])) then Head[j] = G else Head[j] = T end Increment i end 2.6 Convert Head into an integer m 3. Inverse Substitution: 3.1 Initialize Msgcpr as an empty sequence 3.2 for j = |Head|+1 to m + |Head| if Coversub [j] == Cover [pi] then Msgcpr [j] = A else if Coversub [j] == C(Cover [pi]) then Msgcpr [j] = C else if Coversub [j] == C(C(Cover [pi])) then Msgcpr [j] = G else Msgcpr [j] = T end Increment i end 4. Message Decryption 4.1 Generate Keyxor using multinominal model where Cover is the pattern sequence and seed as the seed value. 4.2 Initialize MsgDNA as an empty sequence 4.3 for i = 1 to m MsgDNA [i] = Msgcpr[i] XOR Keyxor[i] end 4.4 Decode MsgDNA into Msg using the coding rule 5. return Msg |
4. Experimental Results
5. Performance Evaluation
5.1. Hiding Capacity
5.2. Security
5.3. Comparisons
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Simmons, G. The Prisoner’s Problem and the Subliminal Channel. In Advances in Cryptology; Springer: Boston, MA, USA, 1984; pp. 51–67. [Google Scholar]
- Herodotus. Herodotus: The History; University of Chicago Press: Chicago, IL, USA, 1987. [Google Scholar]
- Xiang, L.; Yang, S.; Liu, Y.; Li, Q.; Zhu, C. Novel Linguistic Steganography Based on Character-Level Text Generation. Mathemathics 2020, 8, 1558. [Google Scholar] [CrossRef]
- Järpe, E.; Weckstén, M. Velody 2—Resilient High-Capacity MIDI Steganography for Organ and Harpsichord Music. Appl. Sci. 2021, 11, 39. [Google Scholar] [CrossRef]
- Aziz, F.; Ahmad, T.; Malik, A.H.; Uddin, M.I.; Ahmad, S.; Sharaf, M. Reversible data hiding techniques with high message embedding capacity in images. PLoS ONE 2020, 15, e0231602. [Google Scholar] [CrossRef]
- Kwak, M.; Cho, Y. A Novel Video Steganography-Based Botnet Communication Model in Telegram SNS Messenger. Symmetry 2021, 13, 84. [Google Scholar] [CrossRef]
- Borah, S.; Borah, B. Watermarking Techniques for Three Dimensional (3D) Mesh Authentication in Spatial Domain. 3D Res. 2018, 9, 43. [Google Scholar] [CrossRef]
- Bedi, P.; Dua, A. Network Steganography Using Extension Headers in IPv6. In Communications in Computer and Information Science; Springer Science and Business Media LLC: New York, NY, USA, 2020; pp. 98–110. [Google Scholar]
- Risca, V.I. DNA-based steganography. Cryptologia 2001, 25, 37–49. [Google Scholar] [CrossRef]
- Khalifa, A.; Khalifa, A. LSBase: A key encapsulation scheme to improve hybrid crypto-systems using DNA steganography. In Proceedings of the 2013 8th International Conference on Computer Engineering & Systems (ICCES) 2013, Cairo, Egypt, 26–28 November 2013; pp. 105–110. [Google Scholar]
- Jiao, S.-H.; Goutte, R. Hiding data in DNA of living organisms. Nat. Sci. 2009, 1, 181–184. [Google Scholar] [CrossRef]
- Arita, M.; Ohashi, Y. Secret Signatures Inside Genomic DNA. Biotechnol. Prog. 2004, 20, 1605–1607. [Google Scholar] [CrossRef] [PubMed]
- Heider, D.; Barnekow, A. DNA-based watermarks using the DNA-Crypt algorithm. BMC Bioinform. 2007, 8, 176. [Google Scholar] [CrossRef] [PubMed]
- Heider, D.; Pyka, M.; Barnekow, A. DNA watermarks in non-coding regulatory sequences. BMC Res. Notes 2009, 2, 125. [Google Scholar] [CrossRef] [PubMed]
- Na, D. DNA steganography: Hiding undetectable secret messages within the single nucleotide polymorphisms of a genome and detecting mutation-induced errors. Microb. Cell Factories 2020, 19, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Shiu, H.; Ng, K.; Fang, J.; Lee, R.; Huang, C. Data hiding methods based upon DNA sequences. Inf. Sci. 2010, 180, 2196–2208. [Google Scholar] [CrossRef]
- Khalifa, A.; Hamad, S. Hiding Secret Information in DNA Sequences Using Silent Mutations. Br. J. Math. Comput. Sci. 2015, 11, 1–11. [Google Scholar] [CrossRef]
- Khalifa, A.; Elhadad, A.; Hamad, S. Secure Blind Data Hiding into Pseudo DNA Sequences Using Playfair Ciphering and Generic Complementary Substitution. Appl. Math. Inf. Sci. 2016, 10, 1483–1492. [Google Scholar] [CrossRef]
- Malathi, P.; Manoaj, M.; Manoj, R.; Raghavan, V.; Vinodhini, R.E. Highly Improved DNA Based Steganography. Procedia Comput. Sci. 2017, 115, 651–659. [Google Scholar]
- Lee, S.-H. Reversible Data Hiding for DNA Sequence Using Multilevel Histogram Shifting. Secur. Commun. Netw. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, Y. Advancing DNA Steganography with Incorporation of Randomness. ChemBioChem 2020, 21, 2503–2511. [Google Scholar] [CrossRef]
- Ghosh, A.; Bansal, M. A glossary of DNA structures from A to Z. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, 59, 620–626. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, A.; Atito, A. High-Capacity DNA-based Steganography. In Proceedings of the 8th International Conference on INFOrmatics and Systems (INFOS2012), Cairo, Egypt, 14–16 May 2012. [Google Scholar]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions, 3rd ed.; Wiley: New York, NY, USA, 2010; pp. 134–136. [Google Scholar]
- Hoare, G.; Churchhouse, R. Codes and Ciphers: Julius Caesar, the Enigma, and the Internet; Cambridge University Press: Cambridge, UK, 2002; pp. 13–27. [Google Scholar]
- Giel-Pietraszuk, M.; Hoffmann, M.; Dolecka, S.; Rychlewski, J.; Barciszewski, J. Palindromes in Proteins. Protein J. 2003, 22, 109–113. [Google Scholar] [CrossRef]
| a | b | a XOR b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| a | b | a XOR b |
|---|---|---|
| A | A | A |
| A | C | C |
| A | T | T |
| A | G | G |
| C | A | C |
| C | C | A |
| C | T | G |
| C | G | T |
| T | A | T |
| T | C | G |
| T | T | A |
| T | G | C |
| G | A | G |
| G | C | T |
| G | T | C |
| G | G | A |
| Accession Number | Length (bp) | Base Composition (pA, pC, pG, pT) | Payload (bpn) | Longest Palindrome Word Length (bp) | Shortest Palindrome Word and Repeat | |
|---|---|---|---|---|---|---|
| AL645637 | 207,629 | (0.27, 0.21, 0.21, 0.32) | 1.205 | 52 | GAATTC | 57 |
| AAEX03000080 | 305,811 | (0.33, 0.18, 0.17, 0.32) | 0.818 | 44 | TATATA | 284 |
| AAEX03000038 | 133,800 | (0.29, 0.21, 0.20, 0.29) | 1.870 | 39 | AAGCTT | 26 |
| AAEX03000069 | 474,719 | (0.31, 0.19, 0.19, 0.31) | 0.527 | 48 | TGATCA | 147 |
| AL772265 | 212,009 | (0.31, 0.18, 0.17, 0.33) | 1.18 | 40 | GAATTC | 75 |
| AL645625 | 226,754 | (0.24, 0.26, 0.26, 0.23) | 1.103 | 42 | GAATTC | 47 |
| AC153526 | 200,117 | (0.28, 0.21, 0.20, 0.31) | 1.250 | 66 | TATATA | 96 |
| ADDN03000005 | 7,768,011 | (0.26, 0.24, 0.24, 0.26) | 0.032 | 106 | AAATTT | 6033 |
| ADDN03000030 | 633,545 | (0.26, 0.24, 0.25, 0.25) | 0.395 | 32 | CCGCGG | 158 |
| ADDN03000022 | 380,649 | (0.25, 0.25, 0.24, 0.26) | 0.657 | 27 | ATGCAT | 188 |
| AAEX03000999 | 22,099 | (0.23, 0.27, 0.26, 0.23) | -- | 25 | AGGCCT | -- |
| SOZC01000013 | 50,017 | (0.30, 0.21, 0.19, 0.30) | -- | 20 | ATATAT | -- |
| Author | Method | Capacity (bpn) | Security | Extraction |
|---|---|---|---|---|
| Shiu [16], 2010 | Insertion | 0.58 | Non-blind | |
| Complementary | 0.07 | Non-blind | ||
| Substitution | 0.82 | Non-blind | ||
| Khalifa [18], 2016 | Generic Complementary Base Substitution (GCBS) | 1.5 | Blind | |
| Malathi [19], 2017 | Improved Insertion | 1.52 | Non-blind | |
| Lee [20], 2018 | Noncircular type (NHS) | 1.243 | NA | Blind |
| Circular type (CHS) | 1.865 | NA | Blind | |
| Proposed | Enhanced GCBS | 2 | Blind |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalifa, A. A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher. Information 2021, 12, 253. https://doi.org/10.3390/info12060253
Khalifa A. A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher. Information. 2021; 12(6):253. https://doi.org/10.3390/info12060253
Chicago/Turabian StyleKhalifa, Amal. 2021. "A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher" Information 12, no. 6: 253. https://doi.org/10.3390/info12060253
APA StyleKhalifa, A. (2021). A Secure Steganographic Channel Using DNA Sequence Data and a Bio-Inspired XOR Cipher. Information, 12(6), 253. https://doi.org/10.3390/info12060253






