Sub-Tree-Based Approach for Reconfiguration of Light-Tree Pair without Flow Interruption in Sparse Wavelength Converter Network
Abstract
1. Introduction
1.1. Context
1.2. Problem Overview
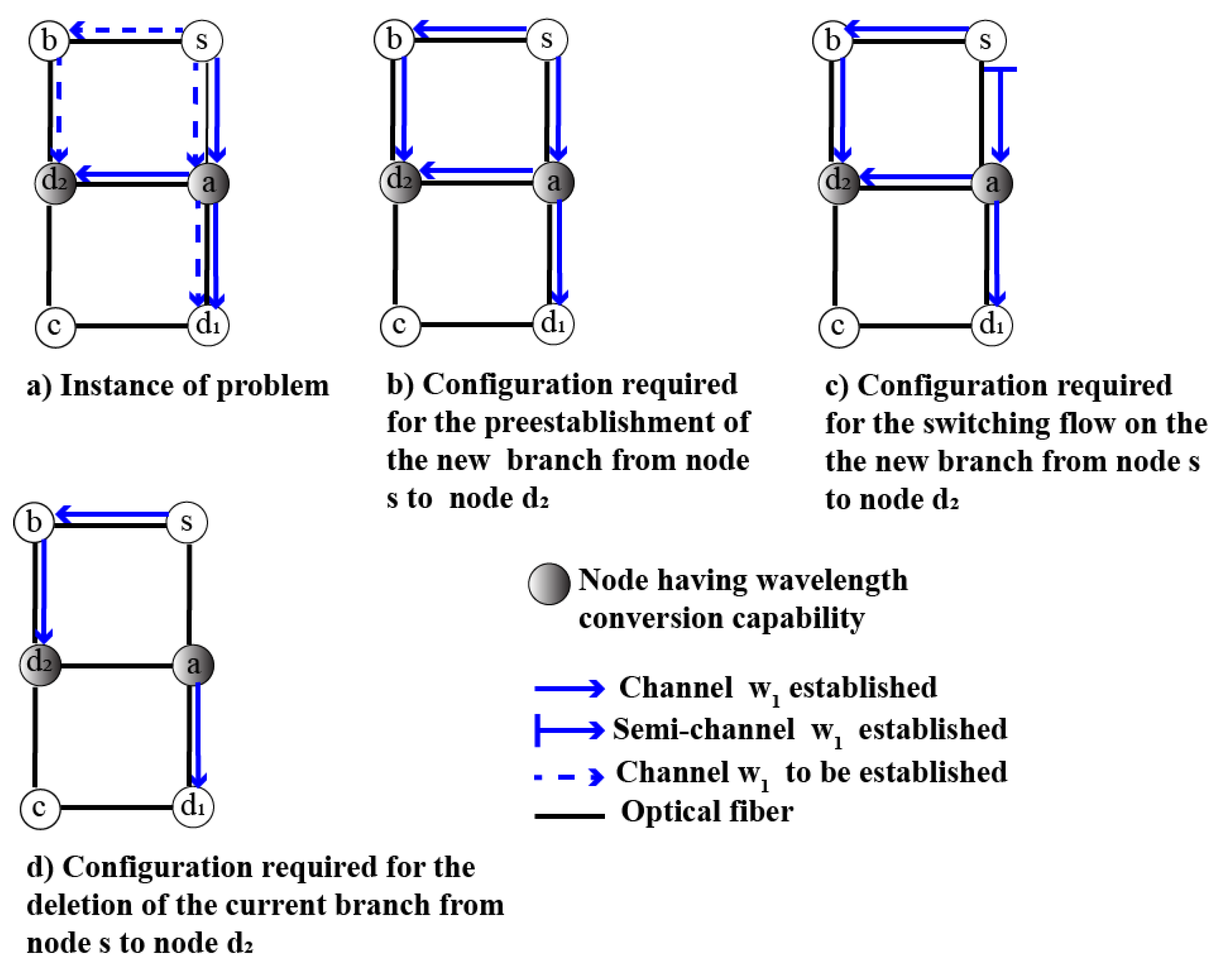
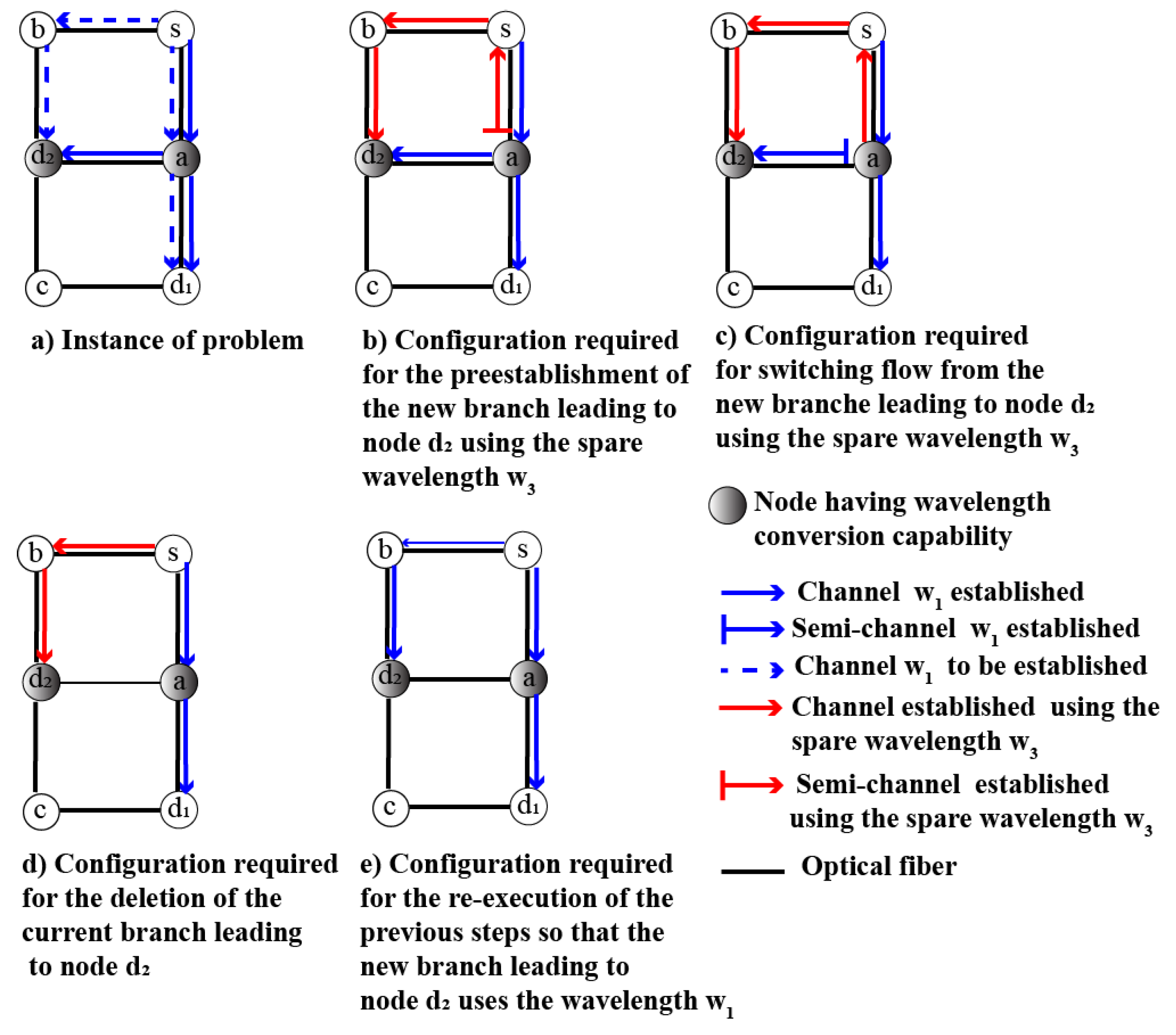
- New sub-paths pre-establishment denoted by PREESTAB_SPs(New_SUBPATHS, ): based on node configuration operation, such as the addition of wavelength switching [21], PREESTAB_SPs returns the set of established wavelength channels (using wavelength ) required for the simultaneous pre-establishment of the sub-paths belonging to New_SUBPATHS. This set of established wavelength channels is added to the current configuration to obtain a new configuration.
- Optical flow switching denoted by SWITCH(CUR_SUBPATHS,NEW_SUBPATHS, ): based on a node configuration operation called changeover, which combines other operations such as the addition, the deletion of wavelength switching and the wavelength conversion [21]. SWITCH returns the set of established wavelength channels (using wavelength ) required to simultaneously switch an optical flow from the current sub-paths (belonging to CUR_SUBPATHS) to the new sub-paths belonging to NEW_SUBPATHS. This set of established wavelength channels is added from the current configuration to obtain a new configuration. Note that SWITCH uses a set of switching nodes such that each switching node belongs to a sub-path pair (i.e., a current sub-path belonging to CUR_SUBPATHS, a new sub-path belonging to NEW_SUBPATHS). In addition, the default value of the switching node of a sub-path pair is the common root node of this sub-path pair.
- Current sub-paths deletion by DELETE_SPs(CUR_SUBPATHS, : based on node configuration operations such as the deletion of wavelength switching, DELETE_SPs returns the set of established wavelength channels (using wavelength ) required for the simultaneous deletion of the sub-paths belonging to CUR_SUBPATHS. This set of established wavelength channels is deleted from the current configuration to obtain a new configuration.
1.3. Contribution and Outline of Paper
- Characterization of sub-tree pairs to know how to select sub-tree pairs from a light-tree pair to be reconfigured.
- Proof of simultaneous reconfigurability of a set of sub-tree pairs.
- A method denoted by LRASRS to solve the reconfiguration problem. This method is based on the two aforementioned contributions.
2. Related Works
3. Problem Formulation
- Input: The initial light-tree , which is used to transfer an optical flow before the reconfiguration process, and the final light-tree .
- Output: The sequence of configurations SC to migrate an optical flow from to .
- Objective: Avoidance of flow interruptions (which corresponds to an average rate of flow interruptions equal to zero) while minimizing the cost of spare wavelengths.
4. Our Methodology
- : Current tree-shaped path
- : Final light-tree
- : Current sub-tree of
- : New sub-tree of
- : Subset of the destination nodes of a light-tree T such that each element of this subset is reachable from a sub-tree .
- : Subset of destination nodes of a light-tree T such that each element of this subset has an ancestor on T that is on the segment (or path) from node x to node y. Note that node v is an ancestor of node w on the tree T, which means that there is a path from v to w on T.
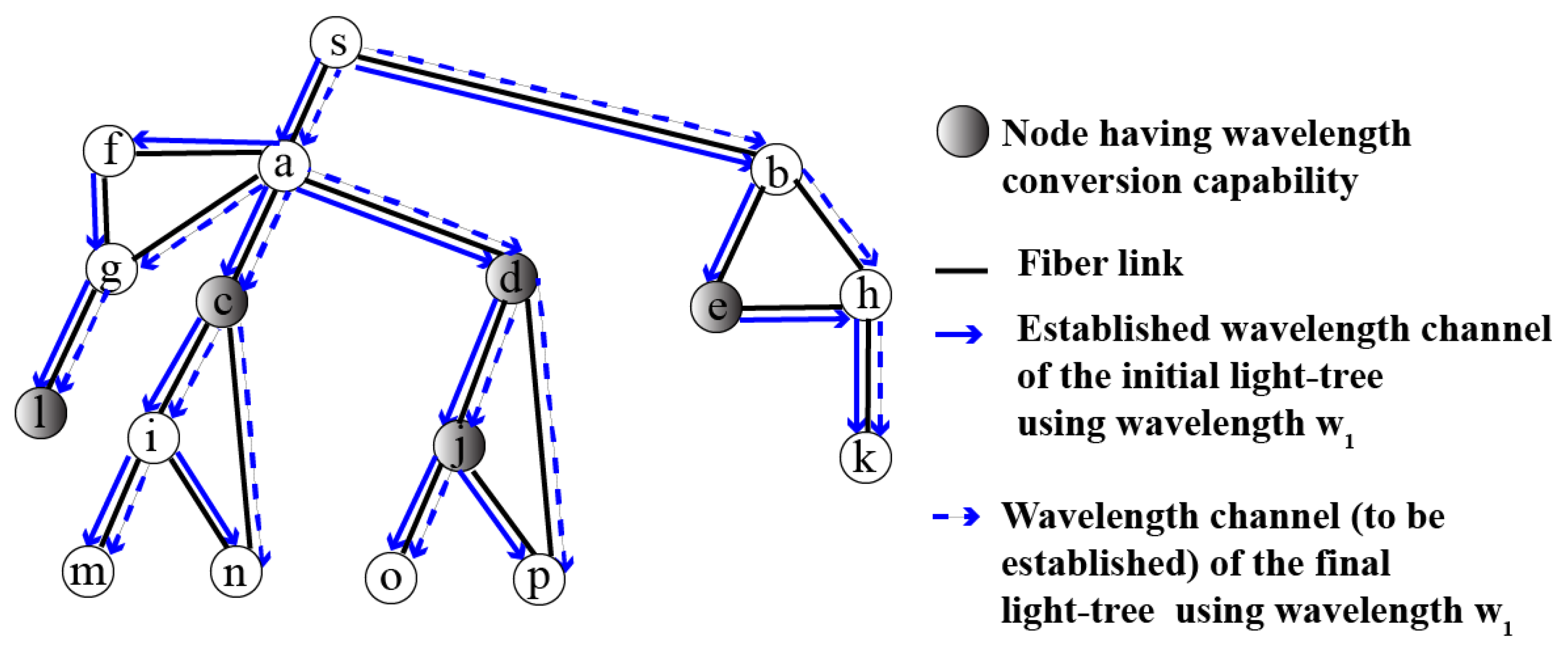
4.1. Characterization of Sub-Tree Pairs
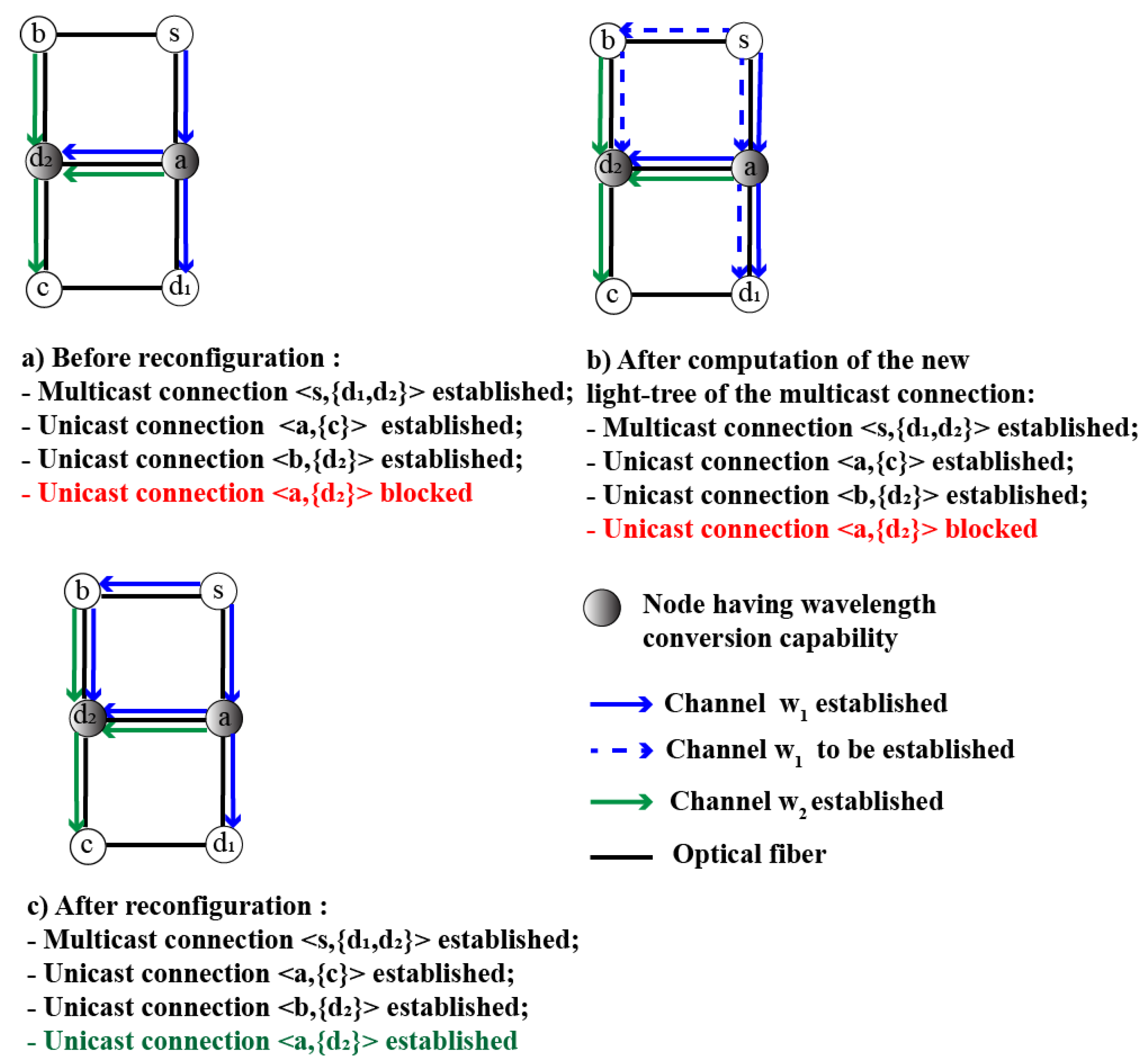
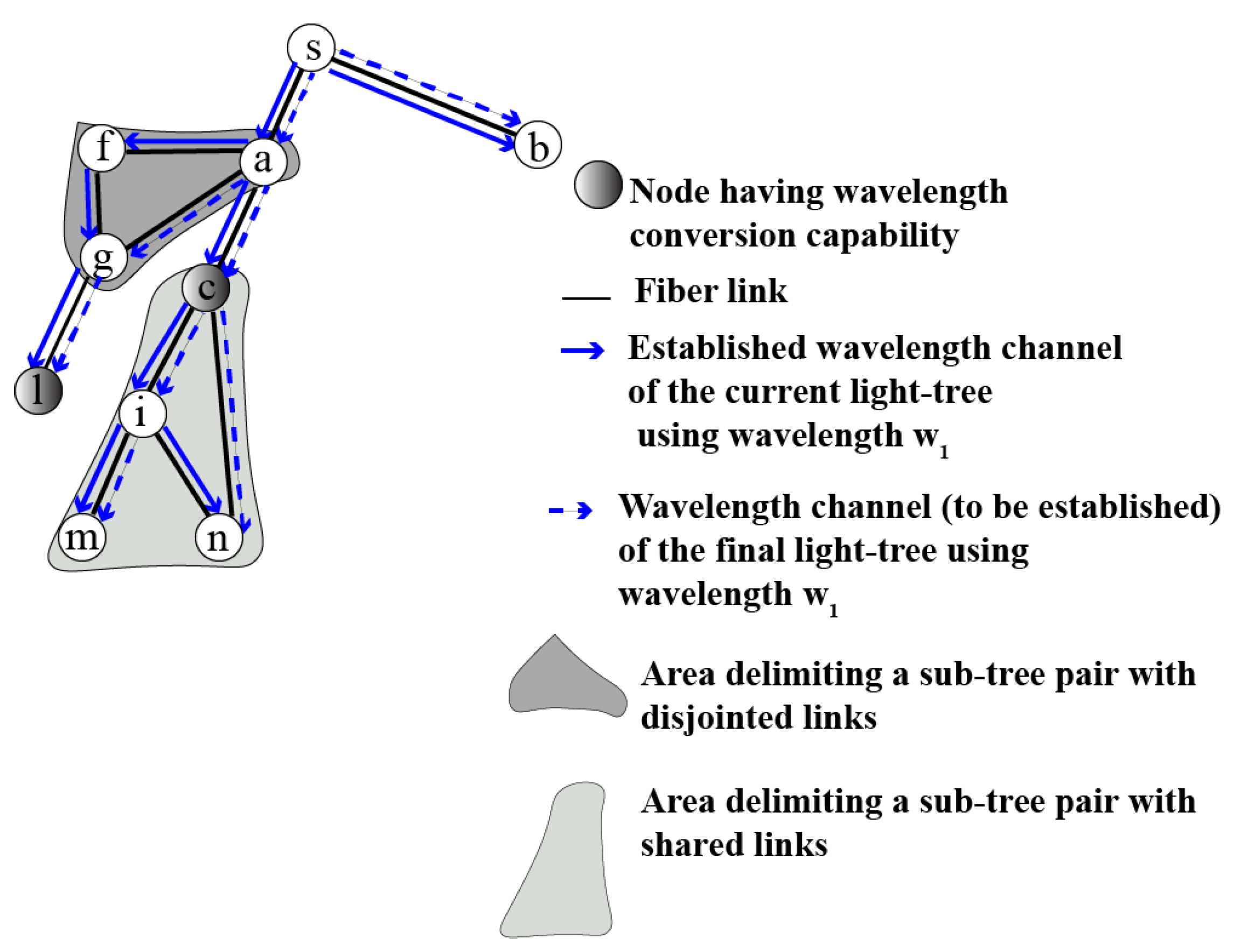
4.1.1. Sub-Tree Pair with Disjointed Links
4.1.2. Sub-Tree Pair with Shared Links
4.2. Proof of Simultaneous Reconfigurability of Sub-Tree Pairs
- Let us show that the sub-tree does not share any links with the sub-tree : The sub-tree pair is a sub-tree pair with disjointed links. This means that the sub-tree does not share any links with . Moreover, is a sub-tree of . Therefore, the sub-tree does not share any links with the sub-tree .
- Let us show that the sub-tree does not share any links with the sub-tree : The sub-tree pair is a sub-tree pair with disjointed links. This means that the sub-tree does not share any links with . Moreover, is a sub-tree of . Therefore, the sub-tree does not share any links with the sub-tree .
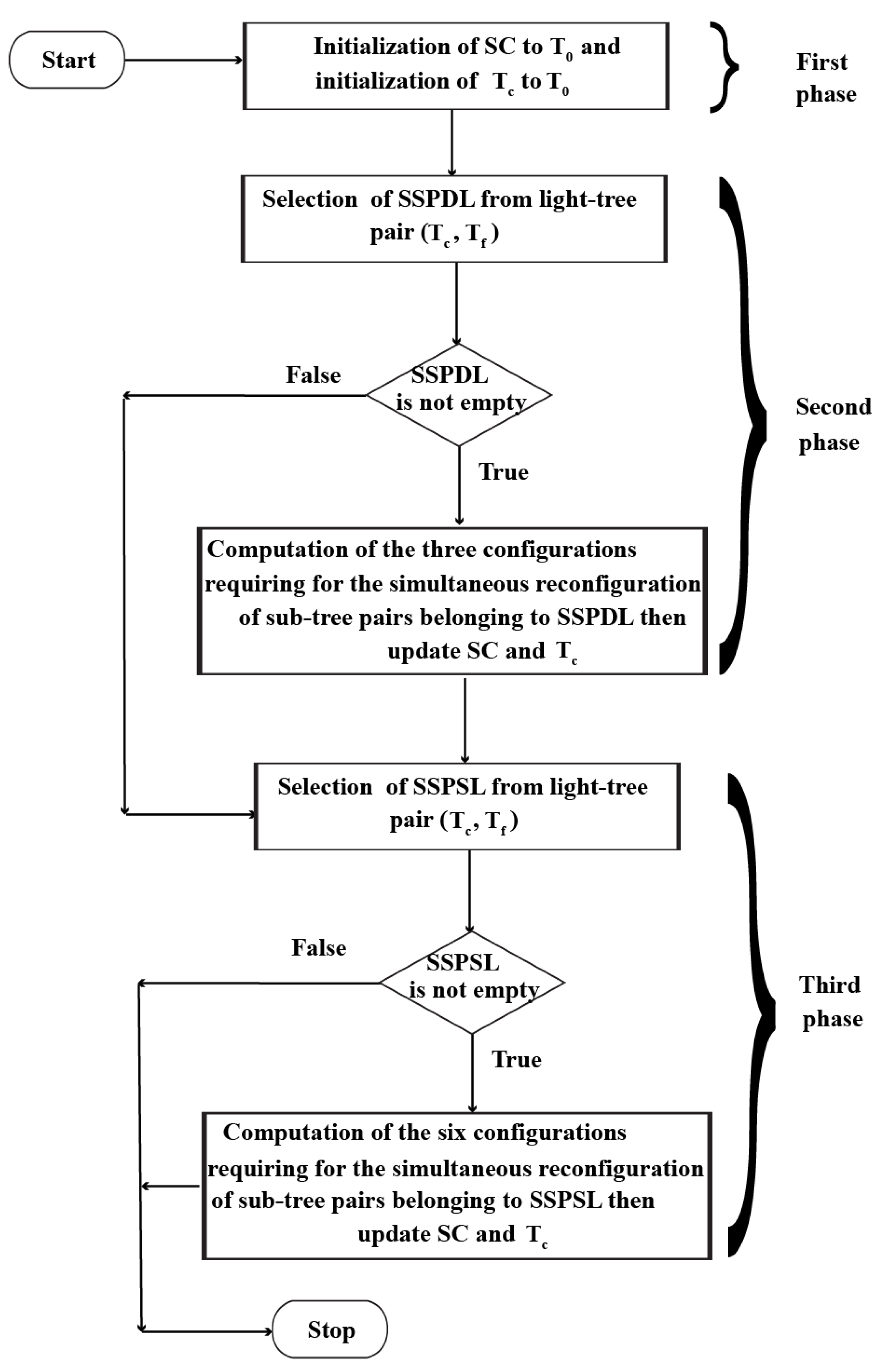
4.3. Proposed Method
| Algorithm 1 Light-tree pair reconfiguration algorithm by simultaneous reconfiguration of sub-tree pairs (LRASRS). |
| Input:T0, Tf // T0: The initial light-tree; Tf: The final light-tree Onput:SC // Sequence (or list) of configurations 1: ; ; // F irst phase 2: // Start of second phase 3: set of sub-tree pairs with disjointed links from // 4: if is not null then 5: list of new sub-trees from // 6: list of current sub-trees from // 7: ∪ PREESTAB_SPs; 8: ∪ ; 9: \ DELETE_SPs; 10: 11: end if // End of second phase 12: set of sub-tree pairs with shared links from // Start of third phase 13: if is not null then 14: 15: Run instructions from line 5 to line 10 by replacing with at lines 7 and 8 16: list of new sub-trees from 17: Run instructions from line 7 to line 10 by replacing with only at line 9 18: end of // End of third phase 19: Return |
5. Simulations
5.1. Performance Criteria
5.2. Simulation Setup
- Randomly select a node, which is taken as the source node of a multicast connection.
- Randomly select some nodes, which are used as the destination nodes of the multicast connection.
- The initial tree of the multicast connection is built by generating the tree of the shortest paths that spans the source node and the destination nodes using the Dijkstra algorithm [28].
- The final tree is built by generating the spanning tree of minimum weight that spans the source and destination nodes using the Prim algorithm [29].
- Both trees are assigned the same randomly selected wavelength (uniform law) in the set of available wavelengths to obtain the initial light-tree and the final light-tree.
- The light-tree pair (initial light-tree, final light-tree) is used as an input by three methods: MBB_1, RCBRwPR, and our method (i.e., LRASRS).
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Puche, W.S.; Vesga, J.C.; Sierra, J. Routing and Allocation of Wavelengths in Elastic Optical Networks: A Survey. Indian J. Sci. Technol. 2018, 11, 1–8. [Google Scholar] [CrossRef]
- Wu, Q.; Zhou, X.; Wang, J.; Yin, Z.; Lin, L. Multicast routing and wavelength assignment with delay constraint in WDM networks with sparse wavelength conversions. Photonic Netw. Commun. 2009, 19, 144–154. [Google Scholar] [CrossRef]
- Iness, J.; Mukherjee, B. Sparse Wavelength Conversion in Wavelength-Routed WDM Optical Networks. Photonic Netw. Commun. 1999, 1, 183–205. [Google Scholar] [CrossRef]
- Petale, S.; Jaisingh, T. Optimal of wavelength converter deployment in WDM optical networks. In Proceedings of the 3rd International Conference on Microwave and Photonics (ICMAP), Dhanbad, India, 9–11 February 2018; pp. 1–2. [Google Scholar]
- Wu, Y.; Xu, S. An Algorithm for Dynamic Routing and Wavelength Assignment in WDM Network. In Proceedings of the 2016 Joint International Information Technology, Mechanical and Electronic Engineering, Xi’an, China, 4–5 October 2016; pp. 293–299. [Google Scholar]
- Zakouni, A.; Toumi, H.; Saidi, A.; Mabrouk, A. Wavelength Assignment Vs. Wavelength Converter Placement in Wavelength-Routed Optical WDM Networks. Procedia Comput. Sci. 2019, 160, 766–771. [Google Scholar] [CrossRef]
- Pinto-Roa, D.P.; Brizuela, C.A.; Barán, B. Multi-objective routing and wavelength converter allocation under uncertain traffic. Opt. Switch. Netw. 2015, 16, 1–20. [Google Scholar] [CrossRef]
- Cisco Annual Internet Report (2018–2023). Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 28 April 2020).
- Zhou, F.; Molnar, M.; Cousin, B. Light-hierarchy: The optimal structure for multicast routing in WDM mesh networks. In Proceedings of the 15th IEEE Symposium on Computers and Communications, Riccione, Italia, 22–25 June 2010; pp. 611–616. [Google Scholar]
- Le, D.D.; Zhou, F.; Molnár, M. Minimizing Blocking Probability for the Multicast Routing and Wavelength Assignment Problem in WDM Networks: Exact Solutions and Heuristic Algorithms. J. Opt. Commun. Netw. 2015, 7, 36–48. [Google Scholar] [CrossRef]
- Zhou, F.; Ait-ouahmed, A.; Cheref, A. QoT-aware multicast provisioning using column generation in mixed-line-rate optical networks. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar]
- Zhou, F.; Ju, M.; Ait-ouahmed, A. Joint Optimization for Multicast Provisioning in Mixed-Line-Rate Optical Networks With a Column Generation Approach. J. Lightwave Technol. 2018, 36, 637–649. [Google Scholar] [CrossRef]
- Barat, S.; Keshri, B.N.; De, T. A Cost Function Based Multi-objective Multicast Communication over WDM Optical Fiber Mesh Network. In Advances in Computer, Communication and Control; Springer: Singapore, 2019; pp. 75–85. [Google Scholar]
- Lin, H.C.; Wang, S.W. Splitter placement in all-optical WDM networks. In Proceedings of the IEEE Global Telecommunications Conference, St. Louis, MO, USA, 28 November–2 December 2005. [Google Scholar]
- Li, H.; Wu, J. Survey of WDM network reconfiguration: Topology migrations and their impact on service disruptions. Telecommun. Syst. 2015, 60, 349–366. [Google Scholar] [CrossRef]
- Chlamtac, I.; Ganz, A.; Karmi, G. Lightpath communications: An approach to high bandwidth optical WAN’s. IEEE Trans. Commun. 1992, 40, 1171–1182. [Google Scholar] [CrossRef]
- Wu, J. A survey of WDM network reconfiguration: Strategies and triggering methods. Comput. Netw. 2011, 55, 2622–2645. [Google Scholar] [CrossRef]
- Solano, F.; Pióro, M. WDM network re-optimization avoiding costly traffic disruptions. Telecommun. Syst. 2011, 52, 907–918. [Google Scholar] [CrossRef][Green Version]
- Cousin, B.; Adépo, J.C.; Babri, M.; Oumtanaga, S. Tree Reconfiguration without Lightpath Interruption in Wavelength Division Multiplexing Optical Networks with Limited Resources. Int. J. Comput. Sci. Issues 2014, 11, 7–17. [Google Scholar]
- Solano, F. Slick Lightpath Reconfiguration Using Spare Resources. J. Opt. Commun. Netw. 2013, 5, 1021–1031. [Google Scholar] [CrossRef]
- Cousin, B.; Adépo, J.C.; Oumtanaga, S.; Babri, M. Tree reconfiguration without lightpath interruption in WDM optical networks. Int. J. Internet Protoc. Technol. 2012, 7, 85–95. [Google Scholar] [CrossRef]
- Solano, F. Analyzing Two Conflicting Objectives of the WDM Lightpath Reconfiguration Problem. In Proceedings of the IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–7. [Google Scholar]
- Jaumard, B.; Duong, H.Q.; Armolavicius, R.; Morris, T.; Djukic, P. Efficient Real-Time Scalable Make-Before-Break Network Re-Routing. J. Opt. Commun. Netw. 2019, 11, 52–66. [Google Scholar] [CrossRef]
- Adépo, J.C.; Aka, B.; Babri, M. Tree Reconfiguration with Network Resources Constraint. Int. J. Comput. Sci. Telecommun. 2016, 7, 1–4. [Google Scholar]
- Pavan, C.; Morais, R.M.; da Rocha, J.R.F.; Pinto, A.N. Generating Realistic Optical Transport Network Topologies. J. Opt. Commun. Netw. 2010, 2, 80–90. [Google Scholar] [CrossRef]
- The Internet Topology Zoo. Available online: http://www.topology-zoo.org/dataset.html (accessed on 18 December 2020).
- Hagberg, A.; Swart, P.; Chult, D.S. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conferences, Pasadena, CA, USA, 21 August 2008; pp. 11–15. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Prim, R.C. Shortest Connection Networks And Some Generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Shuai, T.; Ai, W. New algorithms for multicast routing and wavelength assignment in multi-hop optical WDM networks. Photonic Netw. Commun. 2011, 23, 53–59. [Google Scholar] [CrossRef]

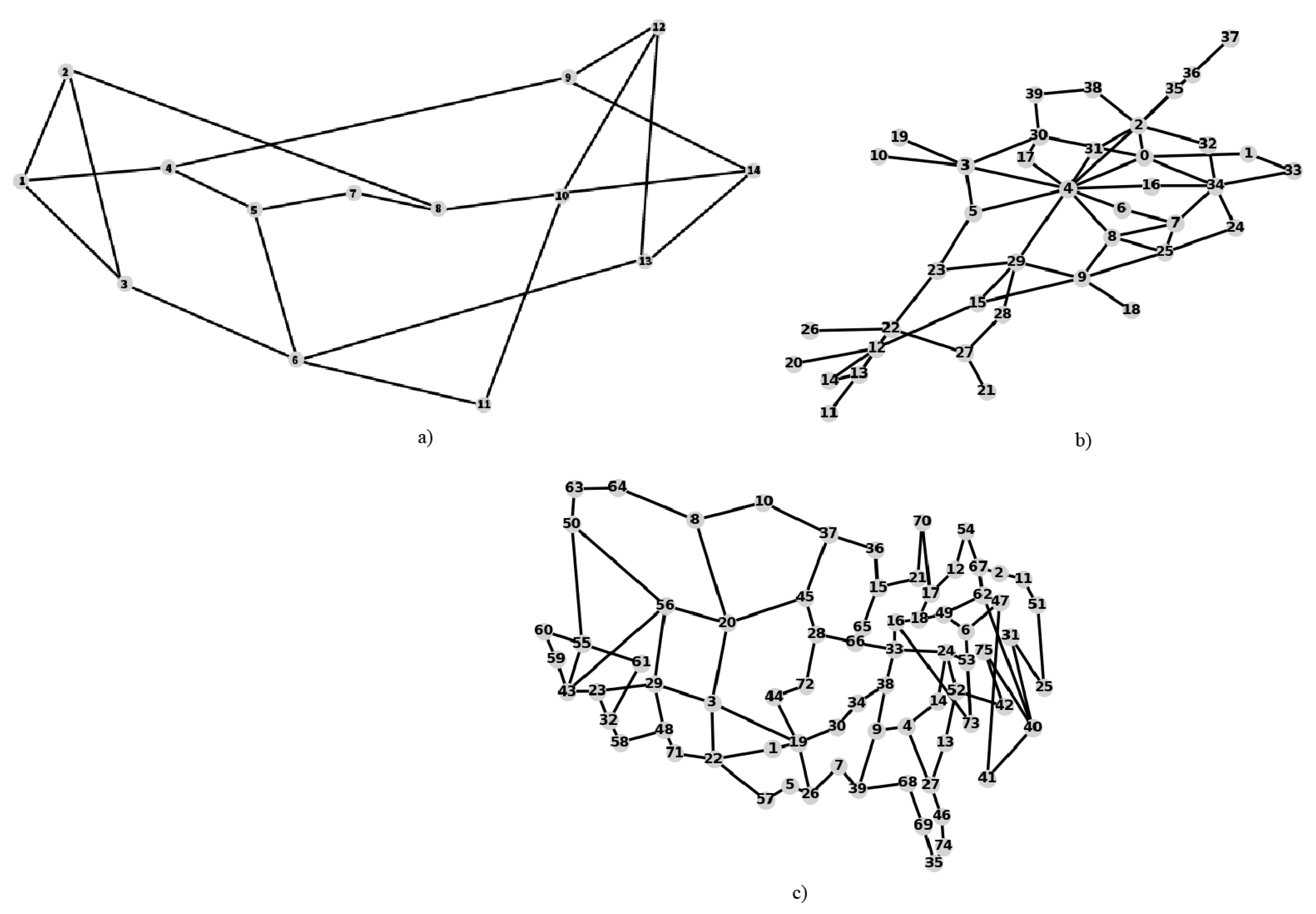
| Network | Num. of Nodes | Num. of Links |
|---|---|---|
| NSFNET | 14 | 21 |
| GEANT | 40 | 75 |
| CORONET | 75 | 99 |
| Methods | NSFNET | GEANT | CORONET | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AVG | SD | m/M | AVG | SD | m/M | AVG | SD | m/M | |
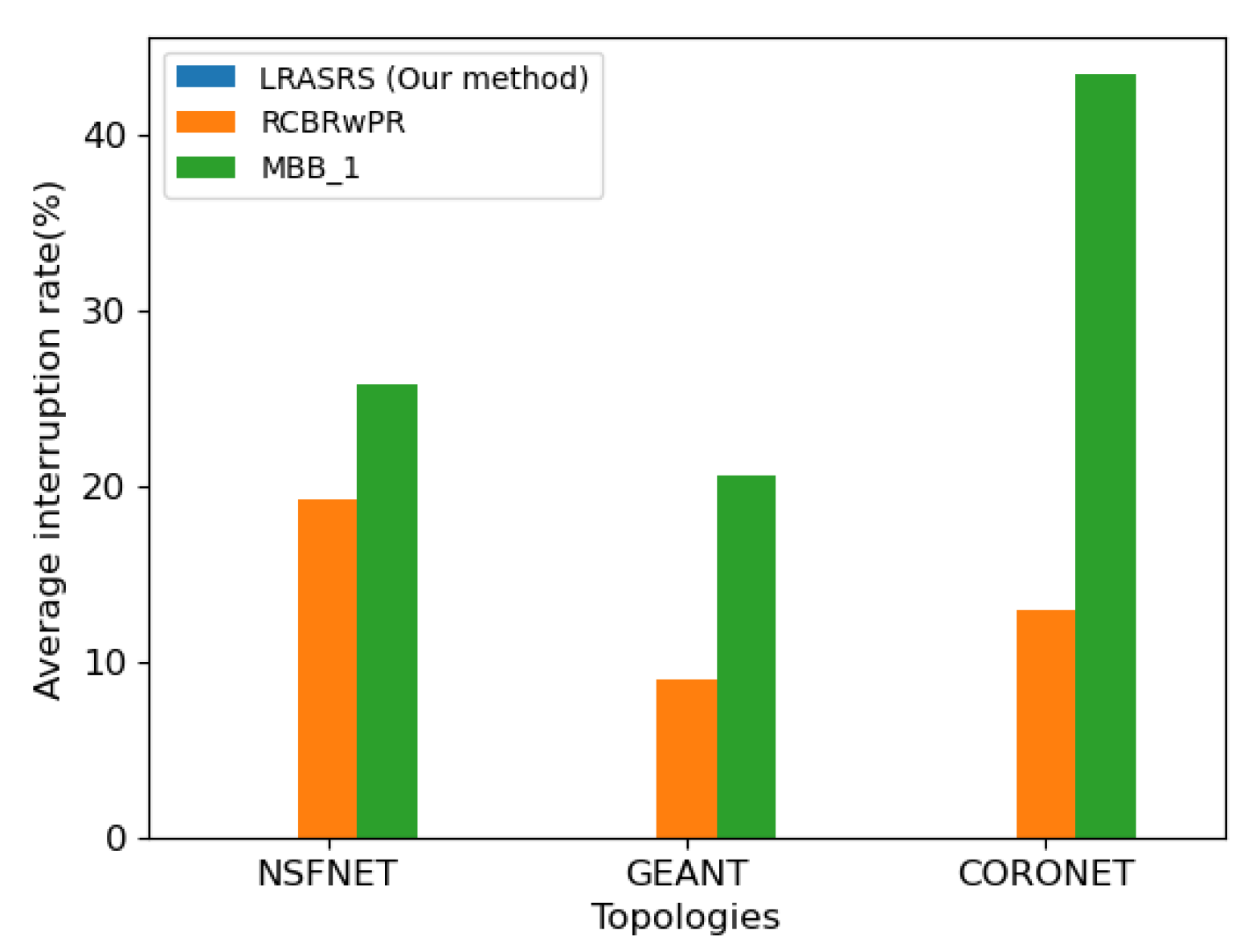
| LRASRS | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 0 | 0 | 0/0 |
| RCBRwPR | 19.25 | 22.54 | 0/66 | 9.09 | 9.38 | 0/77 | 12.98 | 12.95 | 0/78 |
| MBB_1 | 25.90 | 16.28 | 2/83 | 20.69 | 13.95 | 0/94 | 43.48 | 21.47 | 1/96 |
| Methods | NSFNET | GEANT | CORONET | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AVG | SD | m/M | AVG | SD | m/M | AVG | SD | m/M | |
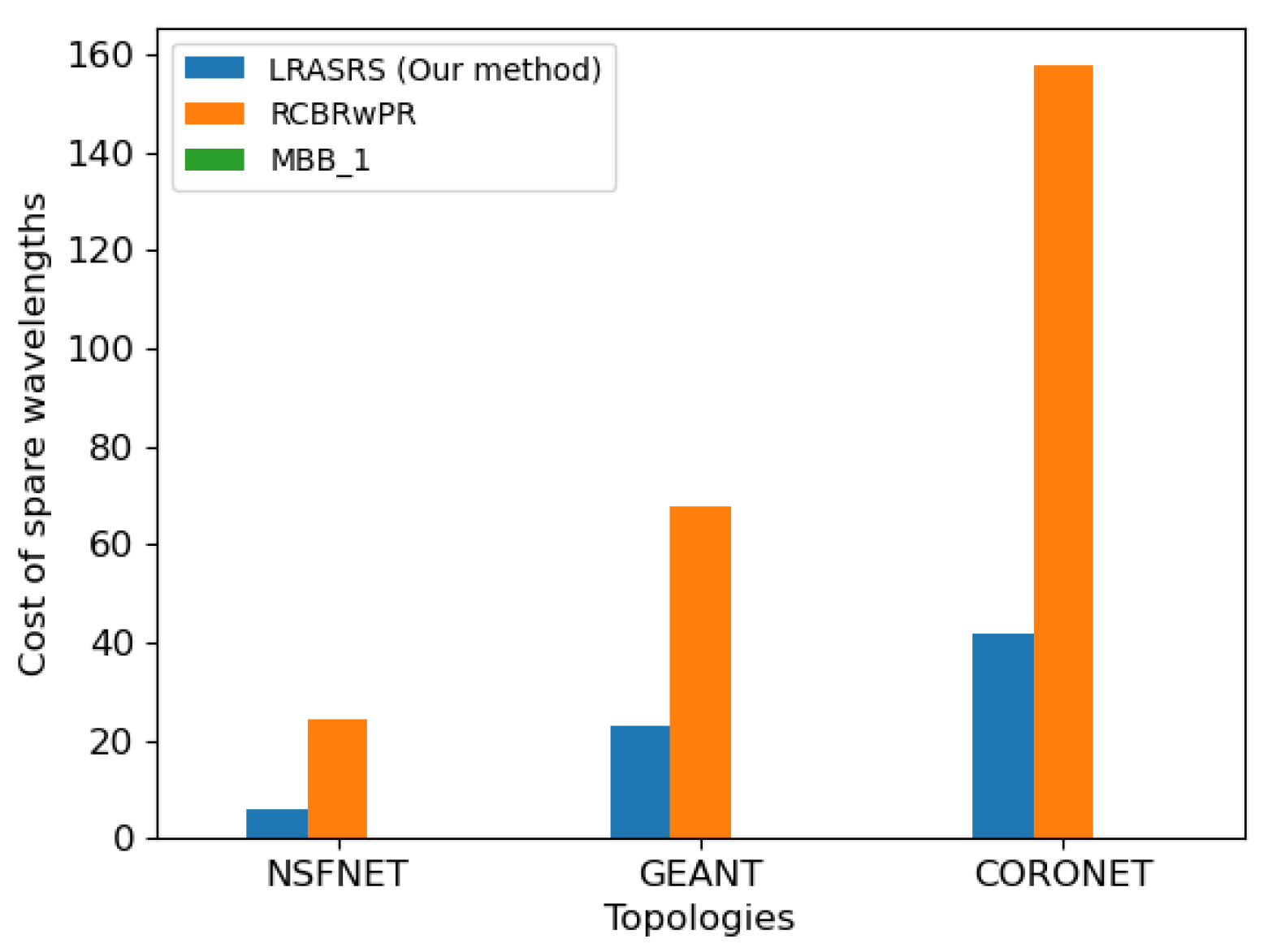
| LRASRS | 6.06 | 4.46 | 0/20 | 22.87 | 13.48 | 0/73 | 41.92 | 19.86 | 0/93 |
| RCBRwPR | 24.19 | 10.49 | 6/48 | 67.64 | 55.07 | 4/264 | 157.76 | 94.41 | 8/434 |
| MBB_1 | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 0 | 0 | 0/0 |
| Methods | NSFNET | GEANT | CORONET | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AVG | SD | m/M | AVG | SD | m/M | AVG | SD | m/M | |
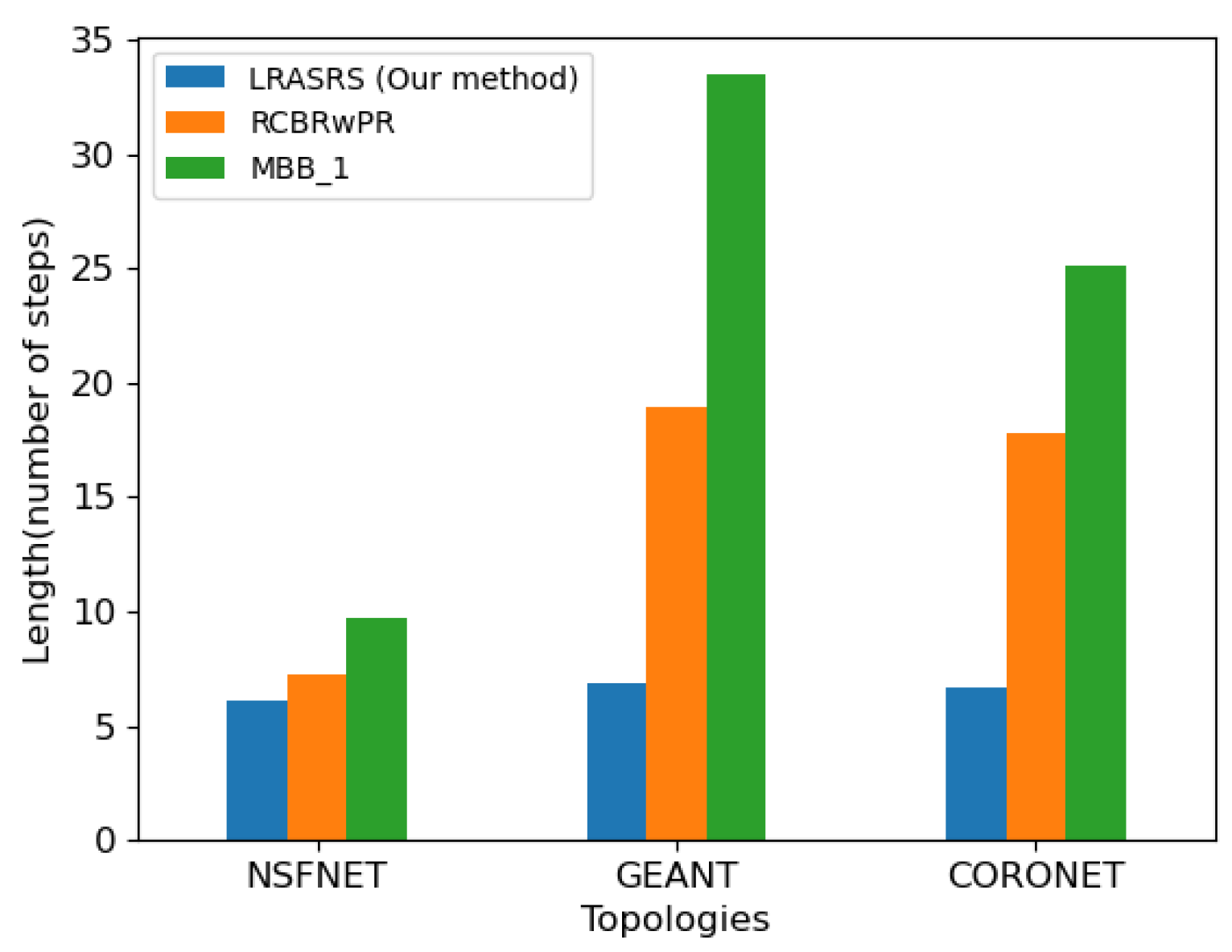
| LRASRS | 6.11 | 2.21 | 3/9 | 6.87 | 1.91 | 3/9 | 6.68 | 1.41 | 3/9 |
| RCBRwPR | 7.25 | 3.06 | 3/14 | 18.98 | 13.15 | 3/59 | 17.79 | 8.91 | 3/35 |
| MBB_1 | 9.75 | 3.58 | 6/21 | 33.48 | 15.13 | 6/63 | 25.11 | 12.72 | 6/60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atta, A.F.; Adépo, J.C.; Cousin, B.; Oumtanaga, S. Sub-Tree-Based Approach for Reconfiguration of Light-Tree Pair without Flow Interruption in Sparse Wavelength Converter Network. Information 2021, 12, 211. https://doi.org/10.3390/info12050211
Atta AF, Adépo JC, Cousin B, Oumtanaga S. Sub-Tree-Based Approach for Reconfiguration of Light-Tree Pair without Flow Interruption in Sparse Wavelength Converter Network. Information. 2021; 12(5):211. https://doi.org/10.3390/info12050211
Chicago/Turabian StyleAtta, Amanvon Ferdinand, Joël Christian Adépo, Bernard Cousin, and Souleymane Oumtanaga. 2021. "Sub-Tree-Based Approach for Reconfiguration of Light-Tree Pair without Flow Interruption in Sparse Wavelength Converter Network" Information 12, no. 5: 211. https://doi.org/10.3390/info12050211
APA StyleAtta, A. F., Adépo, J. C., Cousin, B., & Oumtanaga, S. (2021). Sub-Tree-Based Approach for Reconfiguration of Light-Tree Pair without Flow Interruption in Sparse Wavelength Converter Network. Information, 12(5), 211. https://doi.org/10.3390/info12050211








