Author Contributions
Conceptualization, S.L., F.P.-C. and A.A.; methodology, M.Z., F.P.-C. and A.A.; software, M.Z. and S.L.; validation, J.S., J.C.d.P. and A.A.; formal analysis, M.Z. and S.L.; investigation, J.S., J.C.d.P. and D.R.; resources, J.S. and D.R.; data curation, J.S., J.C.d.P. and D.R.; writing—original draft preparation, S.L. and M.Z.; writing—review and editing, J.S., J.C.d.P., F.P.-C., D.R. and A.A.; visualization, S.L. and M.Z.; funding acquisition, J.S. and A.A. All authors have read and agreed to the published version of the manuscript.
Figure 1.
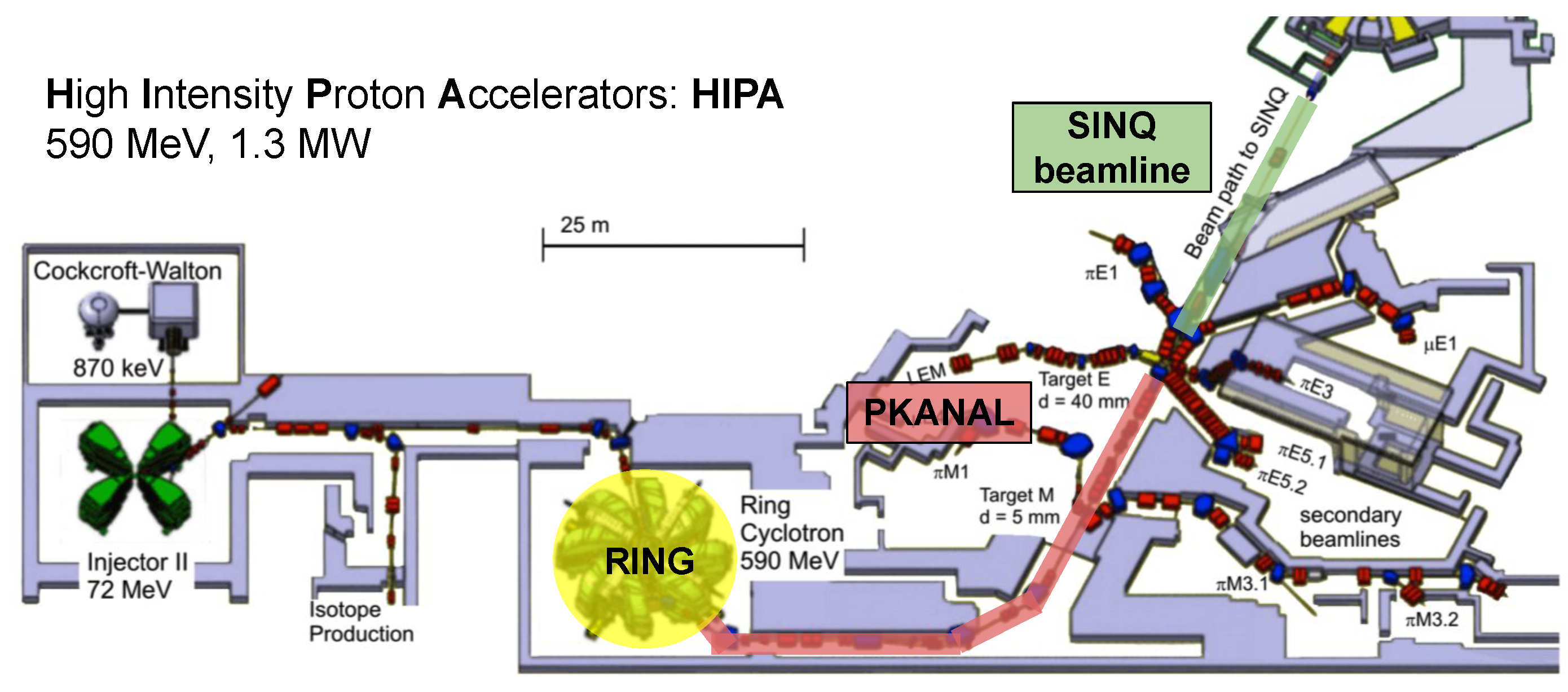
Different HIPA sections of the channels.
Figure 2.
Example interlock record messages.
Figure 3.
Distribution of the interlock events by type. “Other Types” denotes all interlock causes that are not prevalent enough to have a separate category. Please note that an interlock may be labeled as more than one type.
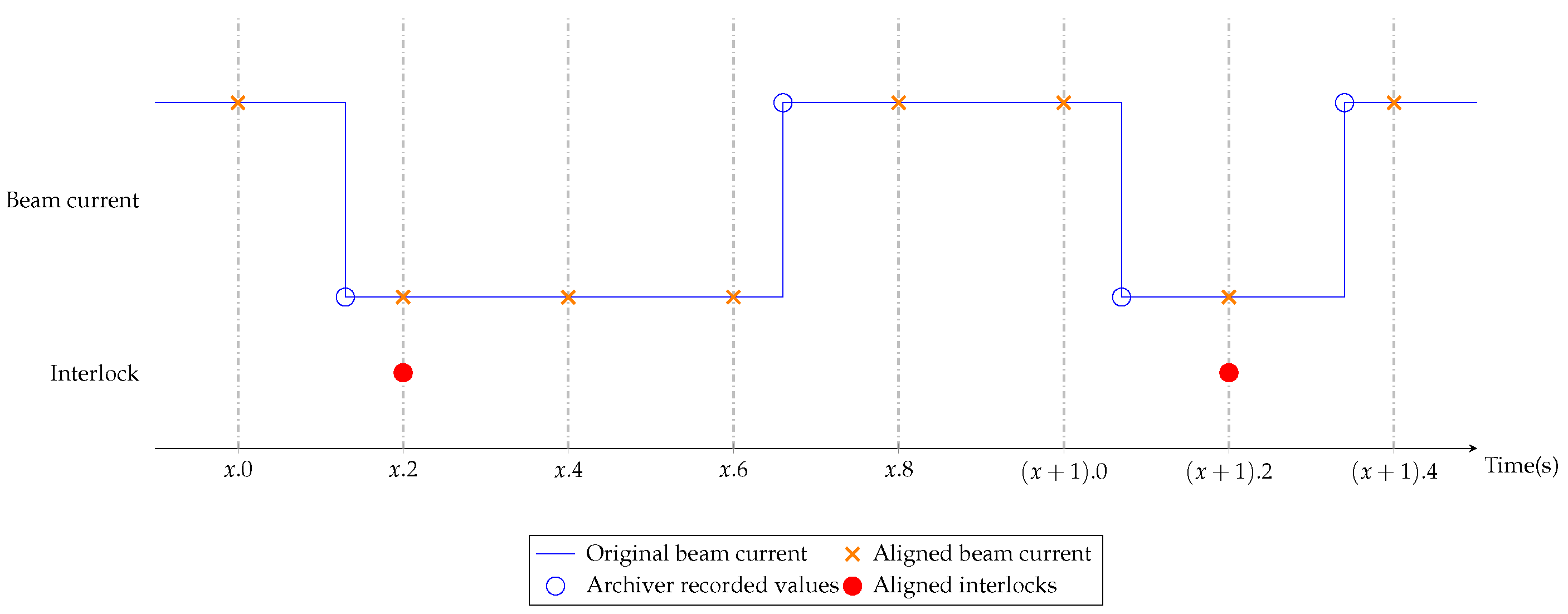
Figure 4.
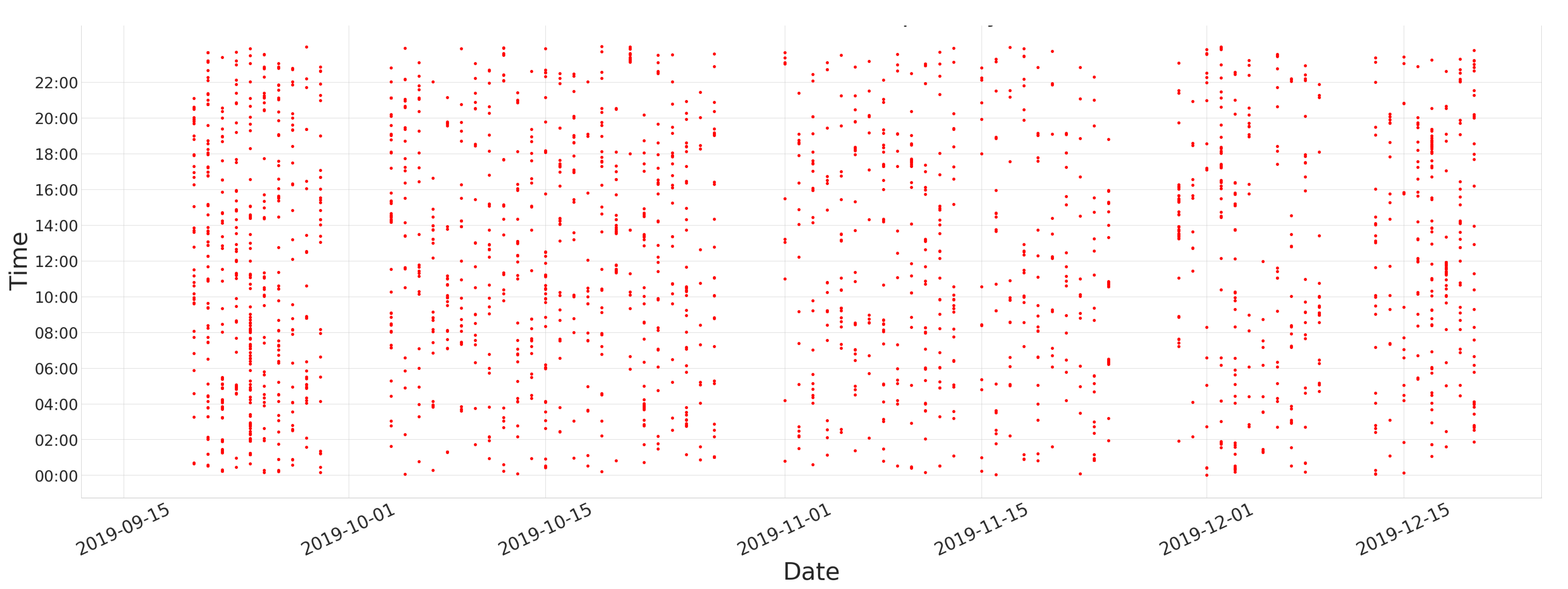
Synchronization of the beam current as an example channel and the interlocks.
Figure 5.
Definition of interlock windows (orange) and stable windows (green). 5 overlapping interlock windows are cut at 1 s before the interlocks, and non-overlapping stable windows are cut in between two interlocks with a 10-min buffer region. Each window has a length of 12.8 s (64 timesteps).
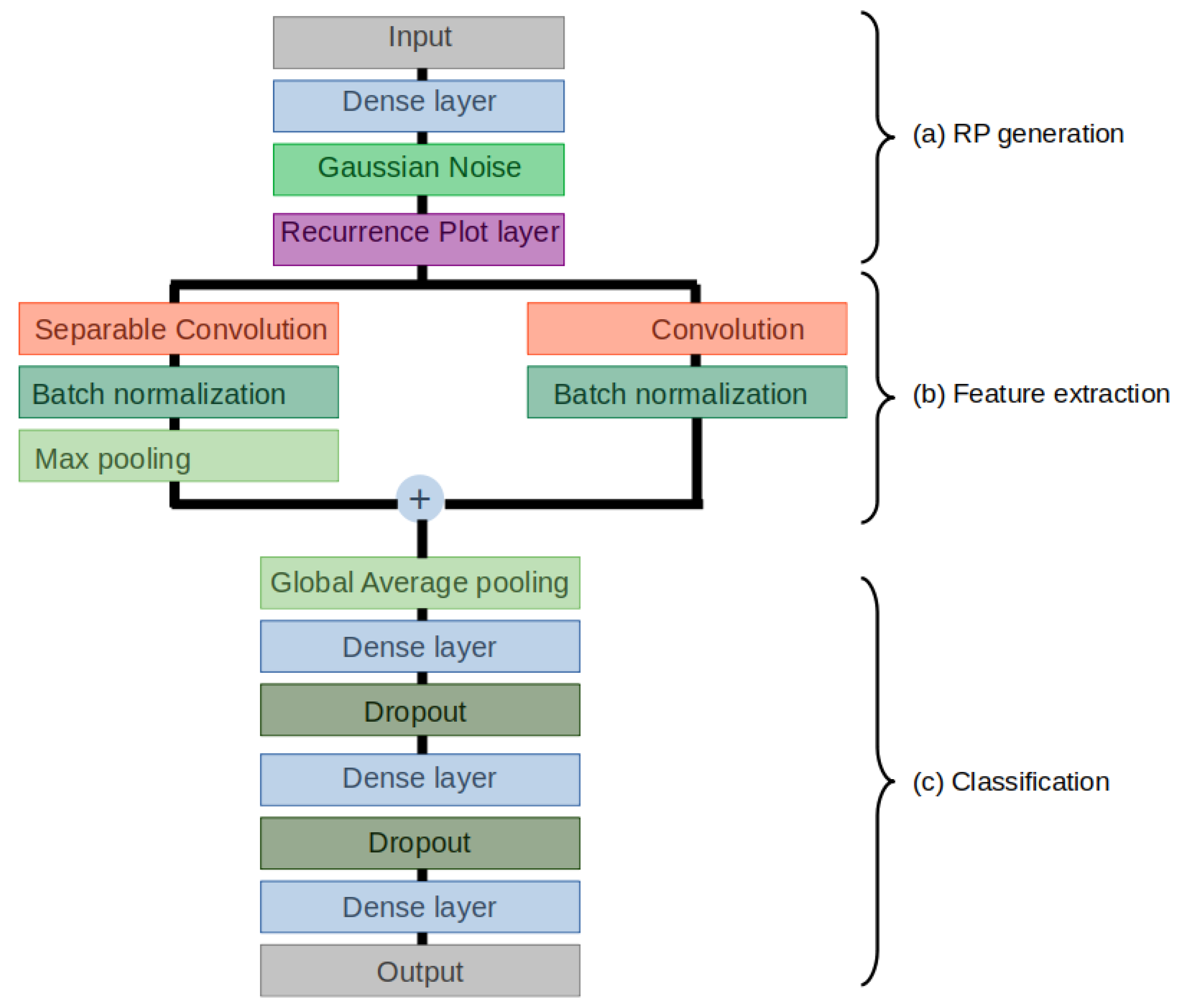
Figure 6.
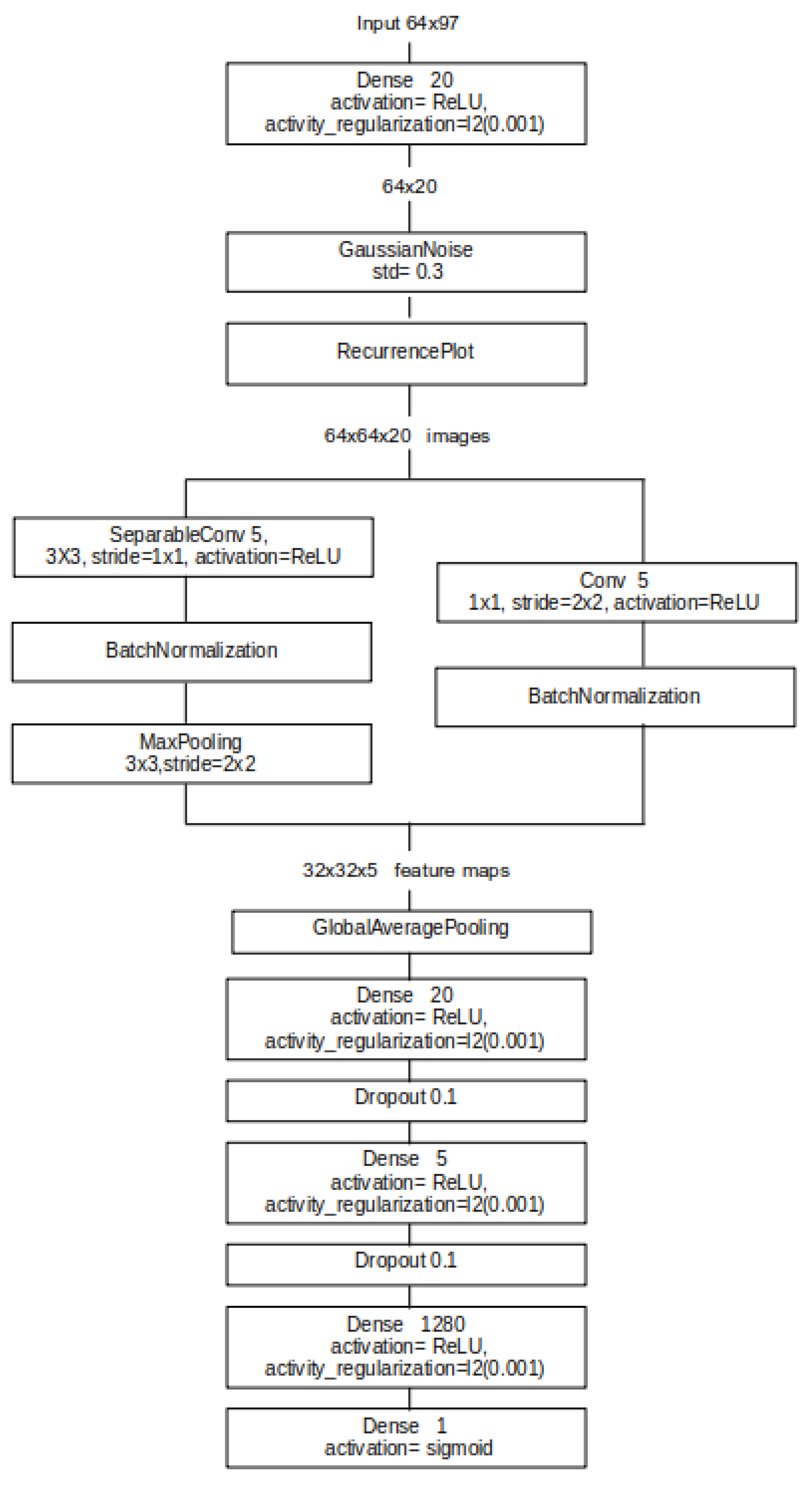
Schematic representation of the RPCNN model architecture.
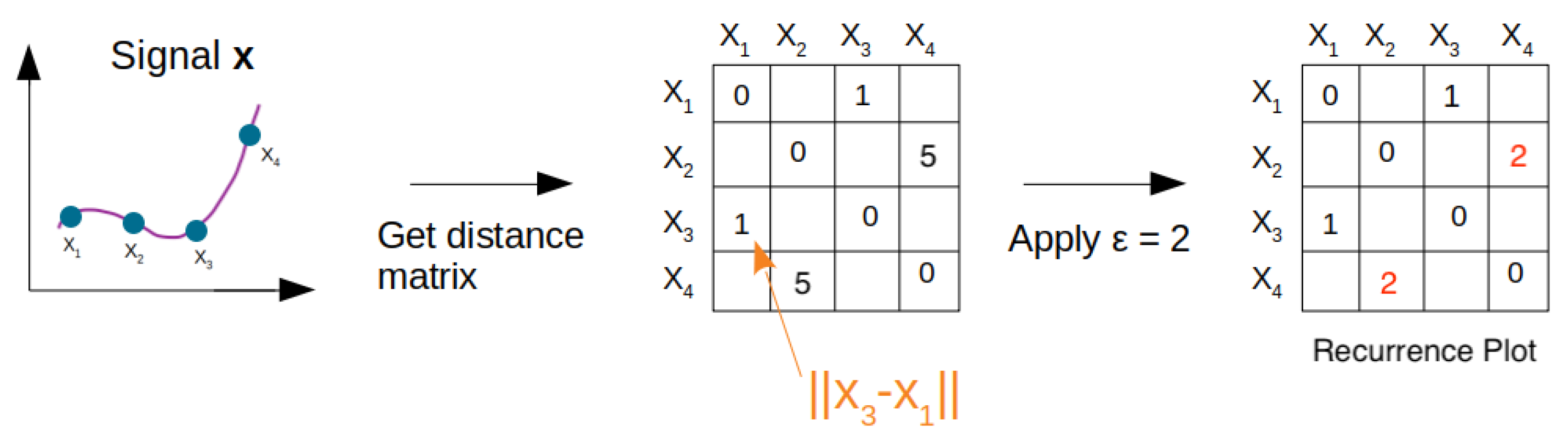
Figure 7.
Generation of recurrence plot from a signal with fixed .
Figure 8.
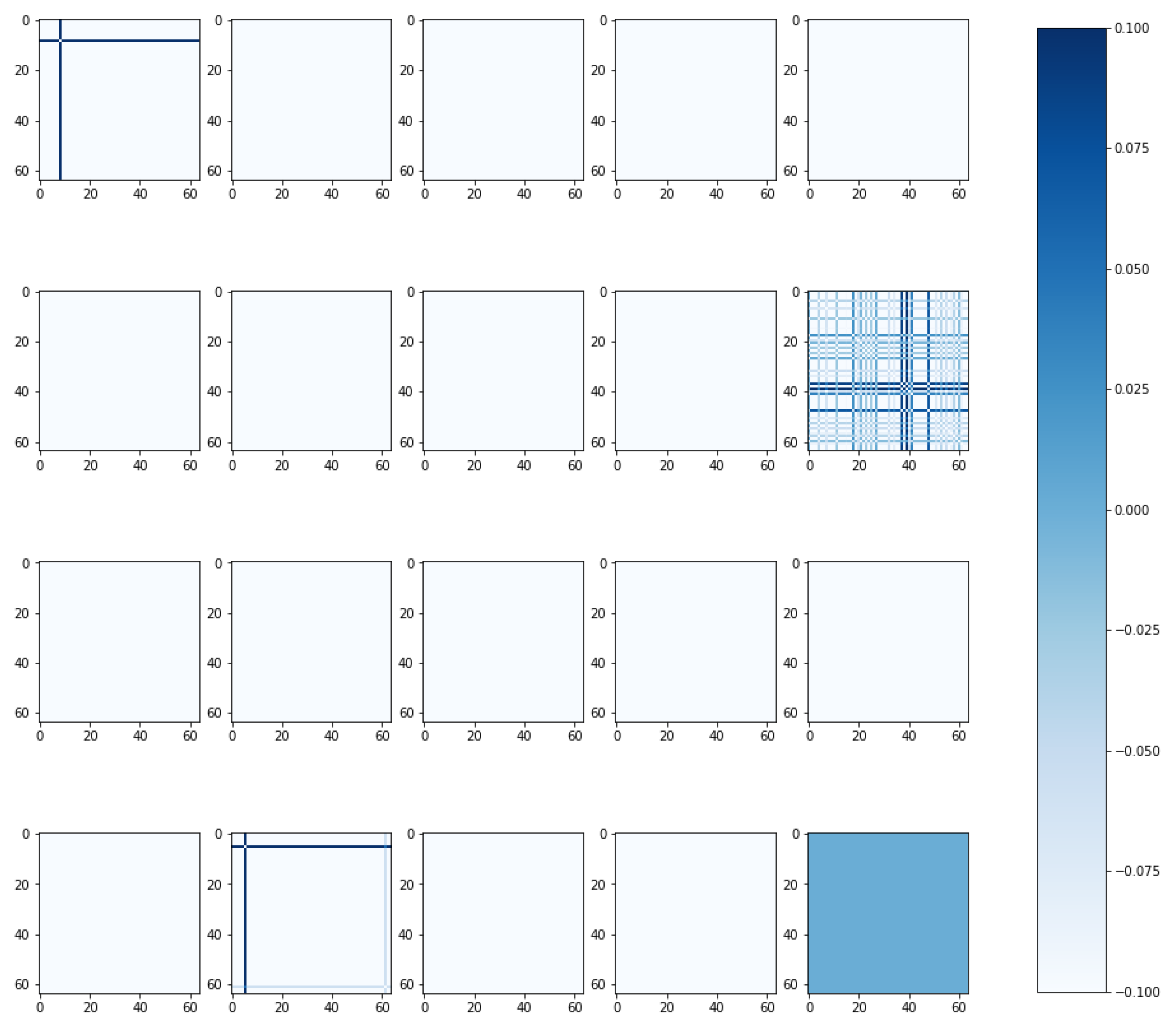
Examples of recurrence plots generated from the RPCNN model. From left to right: uncorrelated stochastic data, data starting to grow, and stochastic data with a linear trend. The top row shows the signals before the recurrence plot generation, and the bottom row shows the corresponding recurrence plots.
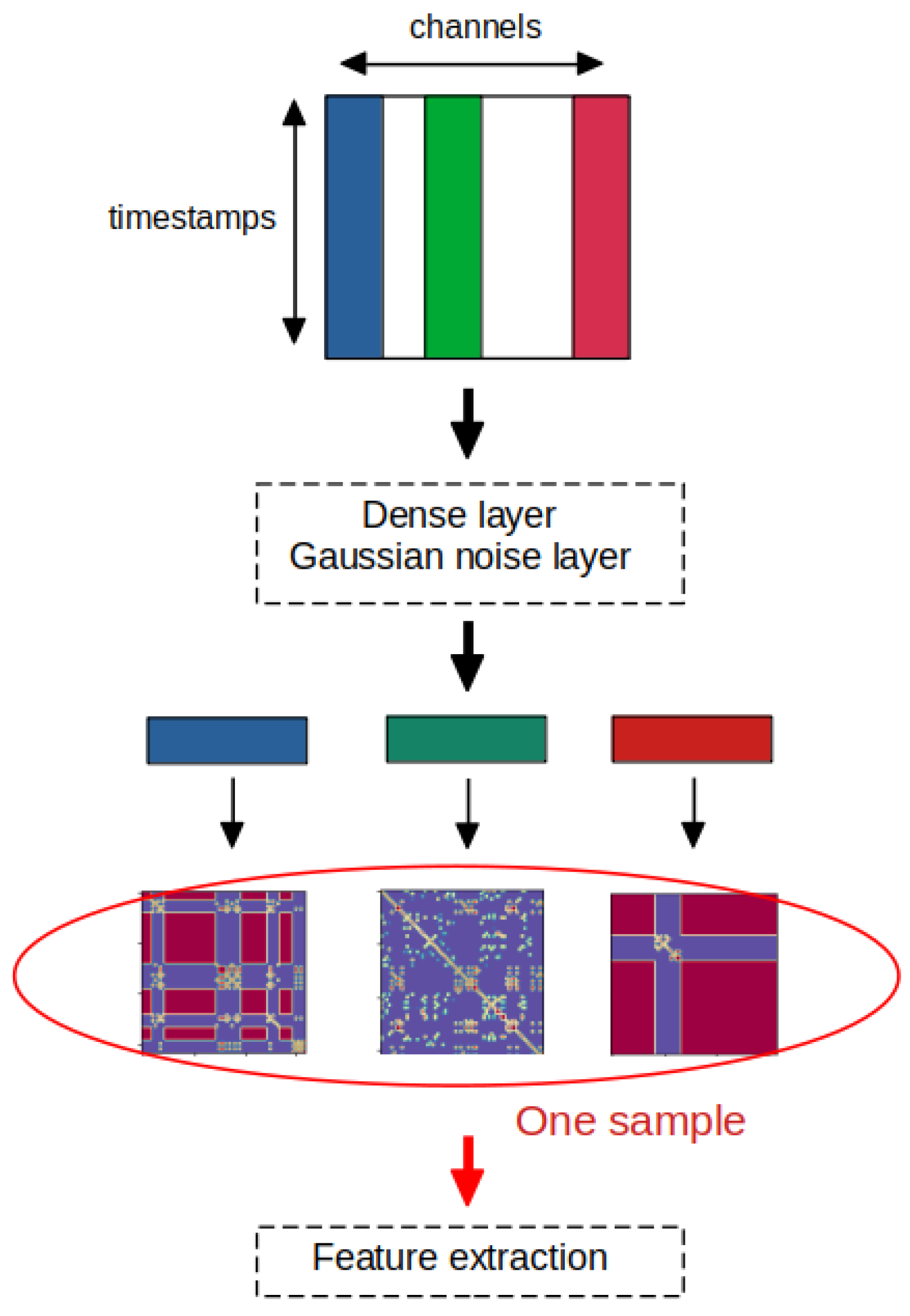
Figure 9.
Illustration of section (a) RP generation of the RPCNN model (c.f.
Figure 6).
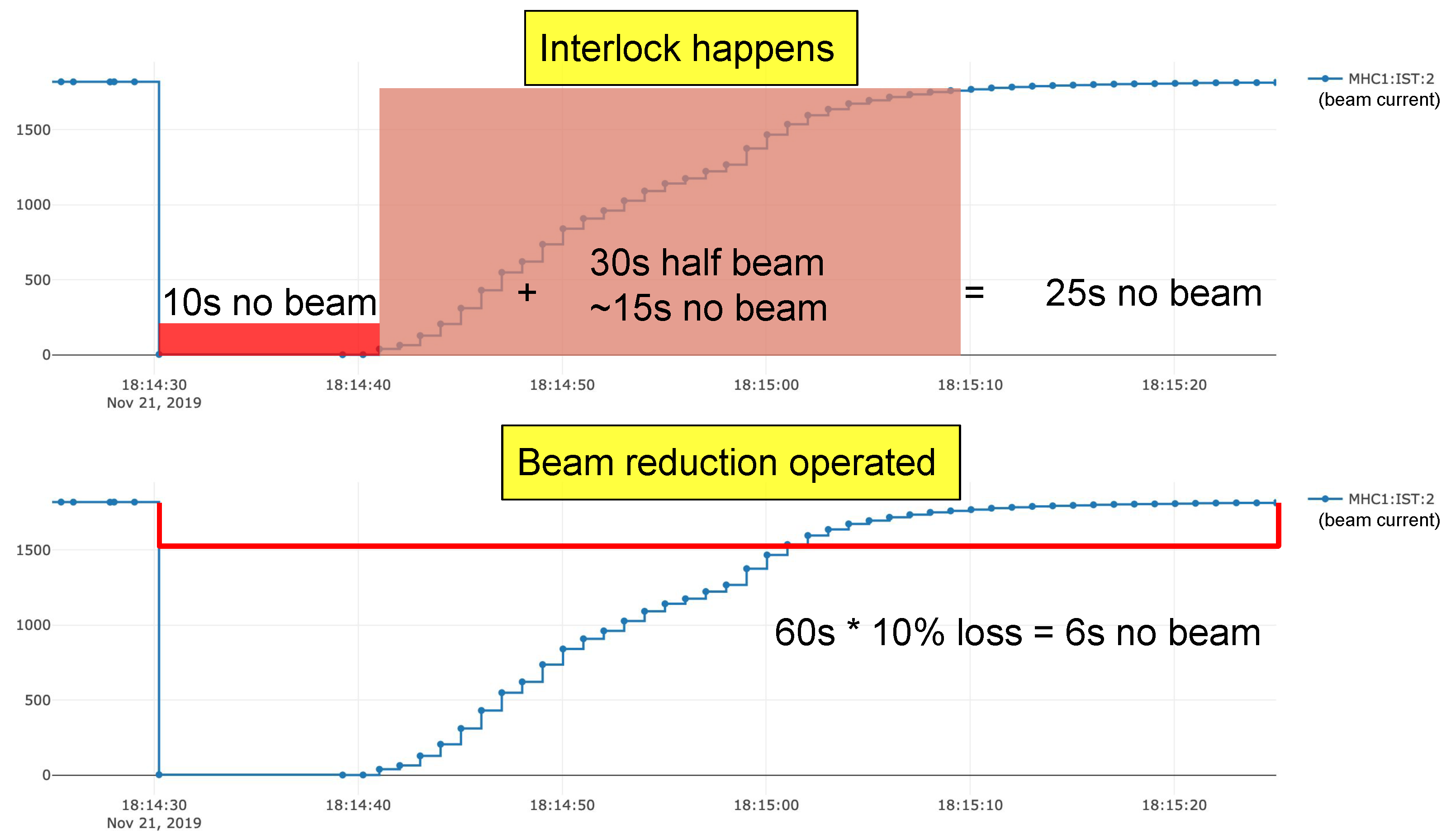
Figure 10.
Expected lost beam time without (top) and with (bottom) the proposed 10% current reduction. An interlock equivalently leads to 25 s of lost beam time, i.e., s of beam time saved. With the current reduction, the interlock is expected to be avoided with a cost of six s of lost beam time, i.e., s of beam time saved.
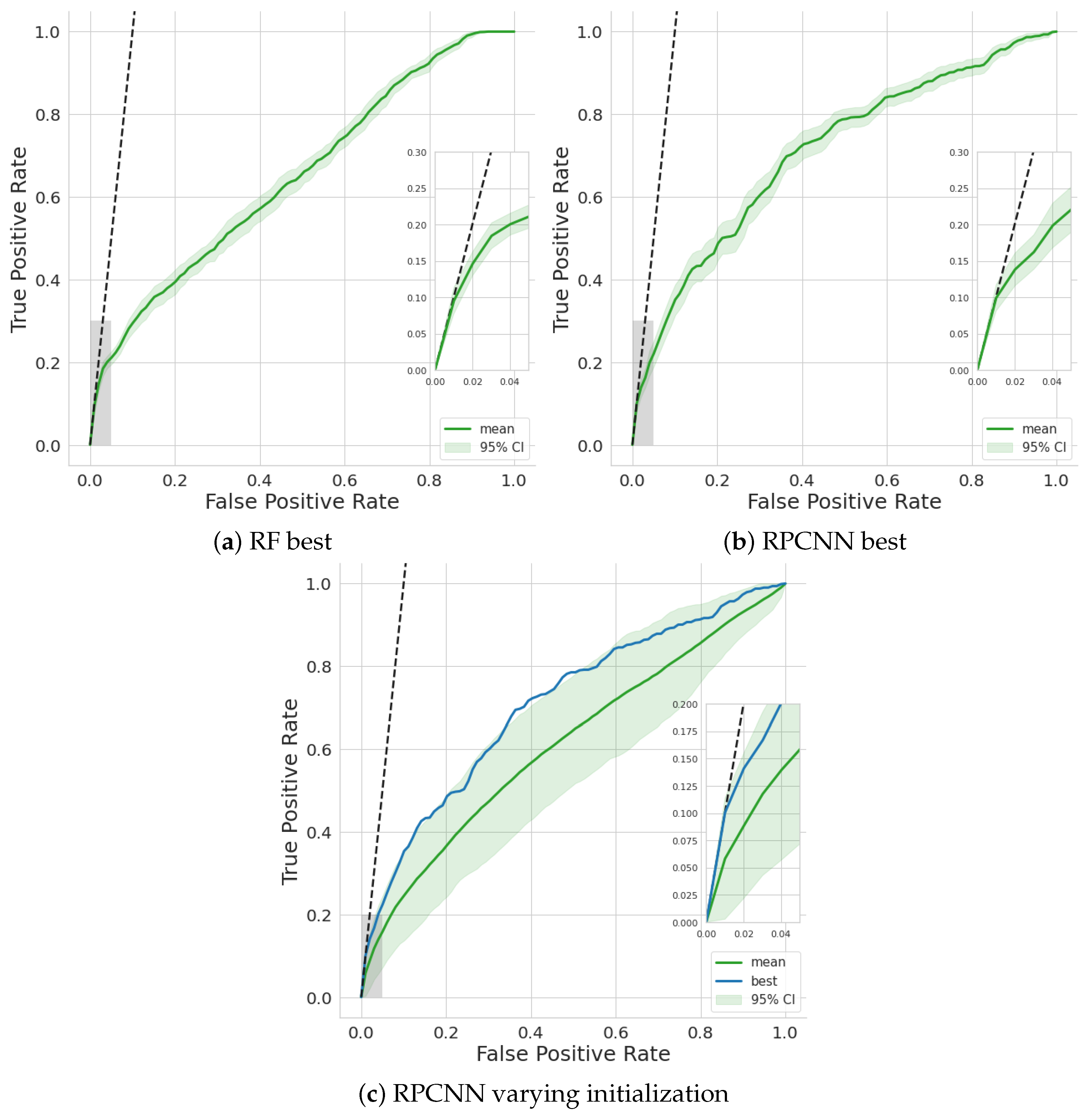
Figure 11.
ROC curves of the best-performing models in terms of Beam time saved and AUC: (a) RF; (b) RPCNN. The mean and 95% confidence interval is calculated from re-sampling of the validation sets. (c) Varying initialization of the same RPCNN model as in (b). The mean and 95% confidence interval are calculated from the validation results of 25 model instances.
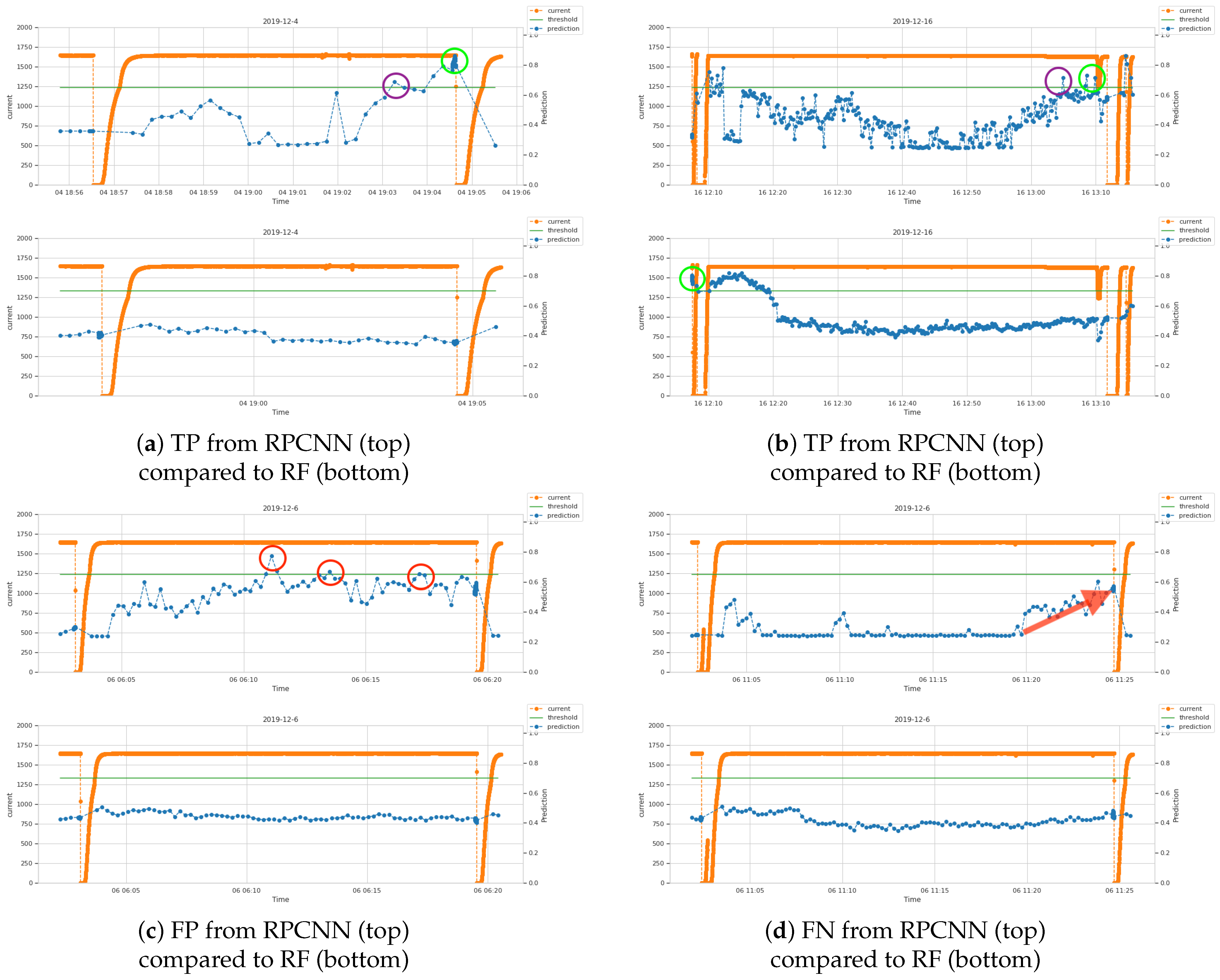
Figure 12.
Screenshots from simulated live predictions over the validation data. The blue line is the prediction value from the model, with higher values indicating higher probability that interlocks are approaching. The orange line is the readout of the beam current channel “MHC1:IST:2” where a drop to zero indicates an interlock. The green line is the binary classification threshold, here taking for the RPCNN and for the RF. (a,b) show two examples of successful prediction of interlocks by RPCNN compared to the result of RF on the same time periods. The positive predictions closer to interlocks are regarded as TP marked by green circles, and the earliest times that the model output cross the threshold are enclosed in purple circles. (c) shows the FPs from the RPCNN in red circles, compared to the result of RF. (d) shows an example of FN from the RPCNN compared to the result of RF. A clear trend increasing with time is present in the output of RPCNN, shown by the red arrow.
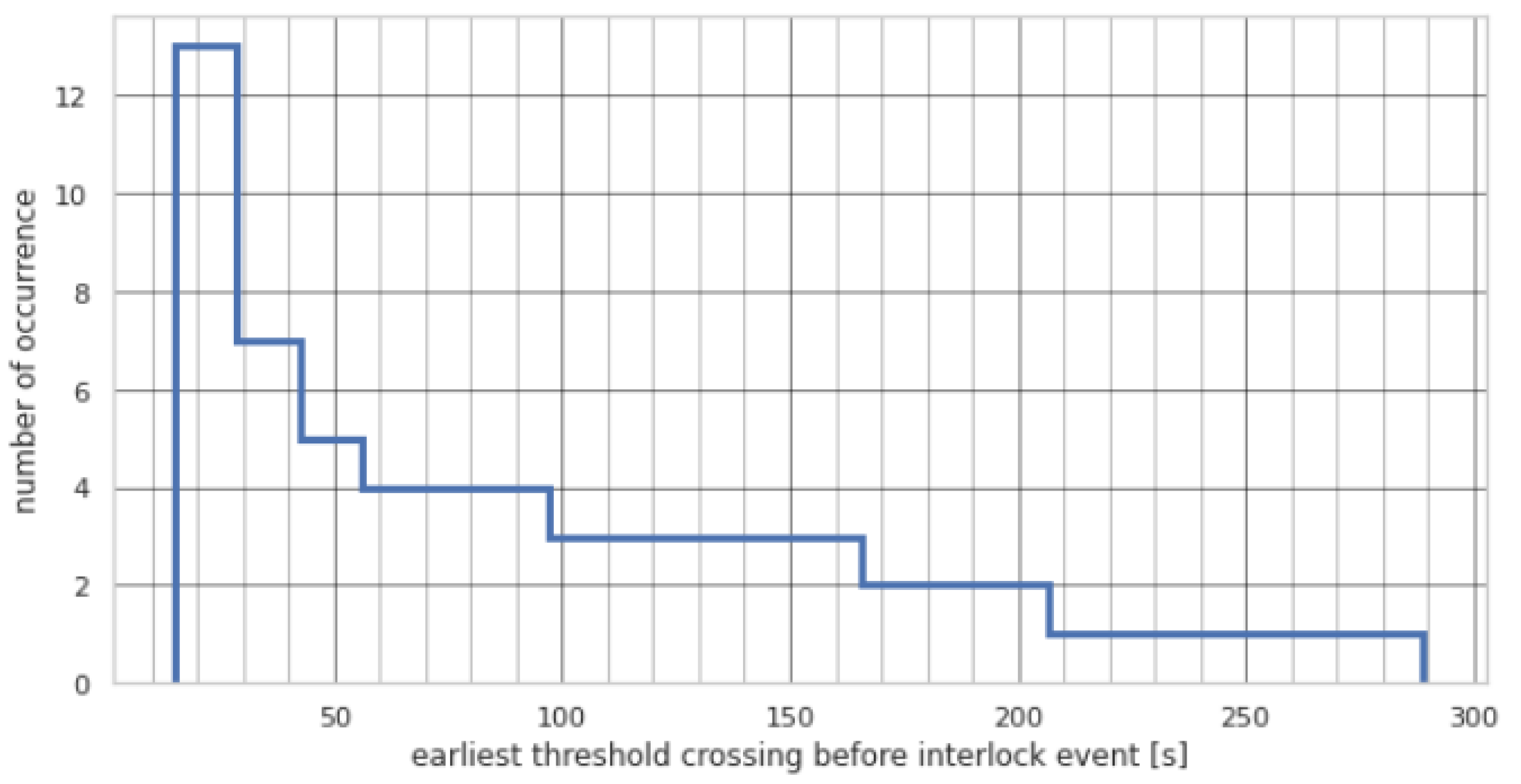
Figure 13.
Reverse cumulative histogram of the first instance the alarm threshold was crossed before an interlock event and the model prediction values remained above the threshold. From evaluation of the ROC curve, a threshold value of is chosen. Displayed are the results for the best-performing RPCNN model. Please note that the interlock event is at 0 s, i.e., time runs from right to left.
Table 1.
List of some example channels.
| Channel | Section | Description (Unit) |
|---|
| AHA:IST:2 | PKANAL | Bending magnet () |
| CR1IN:IST:2 | RING | Voltage of Ring RF Cavity 1 () |
| MHC1:IST:2 | PKANAL | Beam current measurement at the ring exit () |
Table 2.
The different types of interlocks in the dataset.
| Type | Description |
|---|
| Electrostatic | Interlock related to electrostatic elements |
| Transmission | Interlock related to transmission through target |
| Losses | Interlock related to beam losses |
| Other type | Interlock related to another type or unknown |
Table 3.
Numbers of samples in the training and validation sets, before and after bootstrapping, where interlock samples are randomly drawn to have the same number as stable samples.
| | # Interlock Events | # Interlock Samples | # Stable Samples | # Interlock Samples after Bootstrapping |
|---|
| Training set | 731 | 3655 | 176,046 | 176,046 |
| Validation set | 163 | 815 | 44,110 | not applied |
Table 4.
Overview of the RPCNN model training parameters.
| Parameter | Value |
|---|
| Learning rate | 0.001 |
| Batch size | 512 |
| Optimizer | Adam |
| Window size | 12.8 s |
| Number of channels | 97 |
| Std of the Gaussian noise | |
| Dropout ratio | |
Table 5.
Overview of the RF model training parameters.
| Parameter | Value |
|---|
| Number of estimators | 90 |
| Maximum depth | 9 |
| Number of channels | 376 |
| Maximum leaf nodes | 70 |
| Criterion | Gini |
Table 6.
Detail of beam time saved according to different classification result and action for one sample.
| | per TP(s) | per FN (s) | per FP(s) | per TN(s) |
|---|
| Without current reduction | −25 | −25 | 0 | 0 |
| With current reduction | −6 | −25 | −6 | 0 |
| Incentive | 19 | 0 | −6 | 0 |
Table 7.
Beam time saved () and AUC results of the best-performing RF and RPCNN models over re-sampling of the validation sets.
| Model | [s/interlock] | AUC |
|---|
| RF best | | |
| RPCNN best | | |
| RPCNN mean over initialization | | |
Table 8.
Classification results in terms of True Positive (TP), False Positive (FP), True Negative (FN), False Negative (FN), True Positive Rate (TPR) and True Negative Rate (TNR) of the best-performing RF and RPCNN models. The thresholds for both models were obtained from the ROC curves so that the beam time saved is maximized, with for the RF and for the RPCNN.
| Model | TP | FP | TN | FN | TPR or Recall | TNR or Specificity |
|---|
| RF best | 25 | 28 | | 790 | | |
| RPCNN best | 40 | 75 | | 775 | | |