Analysis of Gradient Vanishing of RNNs and Performance Comparison
Abstract
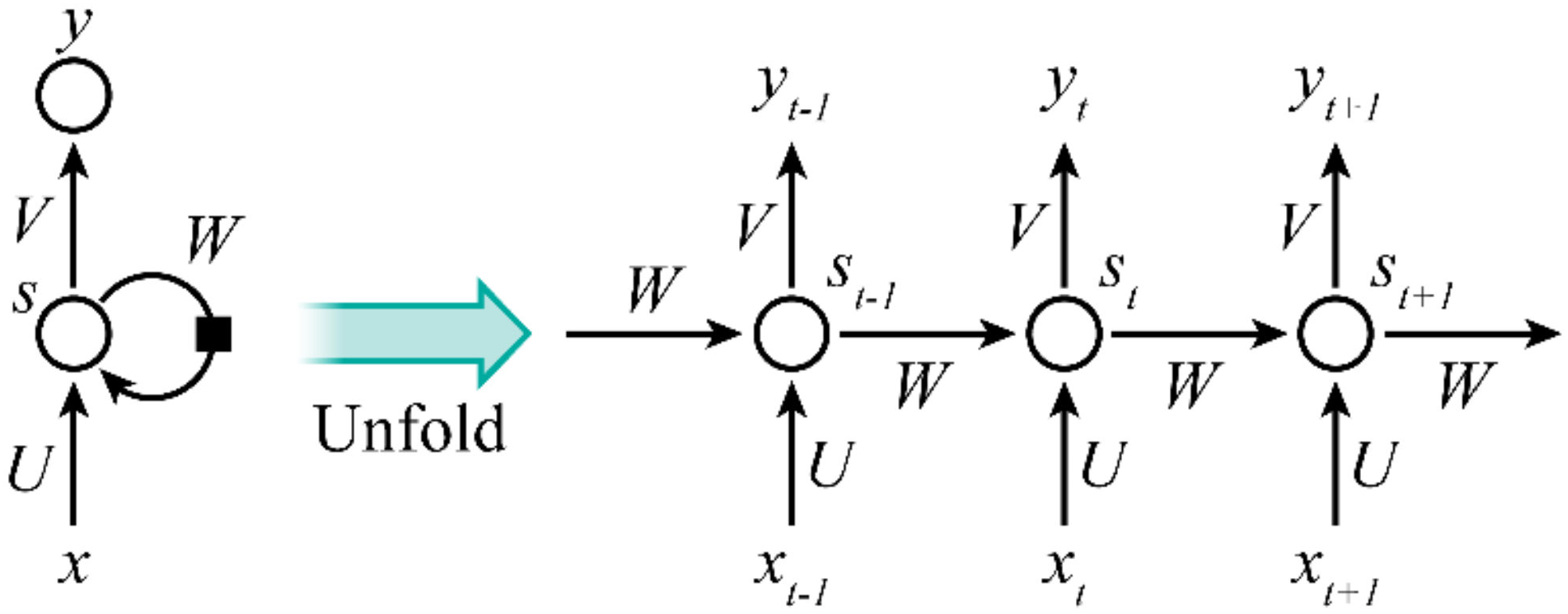
:1. Introduction
2. Previous Works
3. Research Results
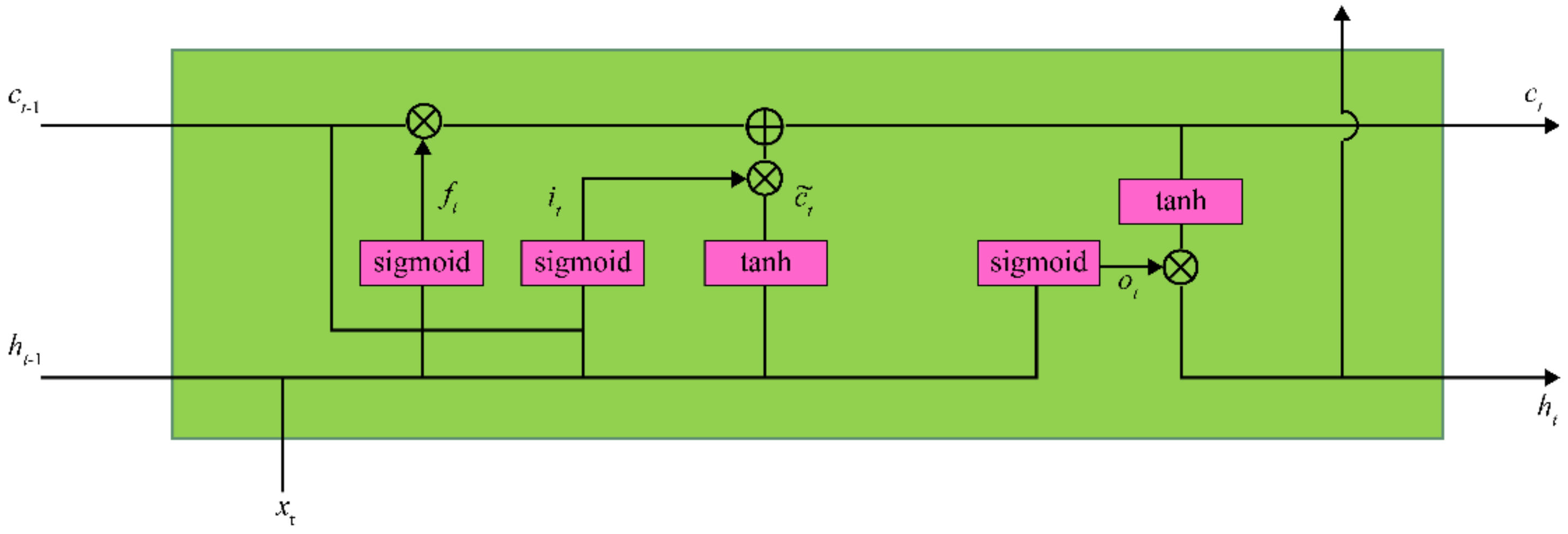
3.1. Analysis of Gradient Vanishing
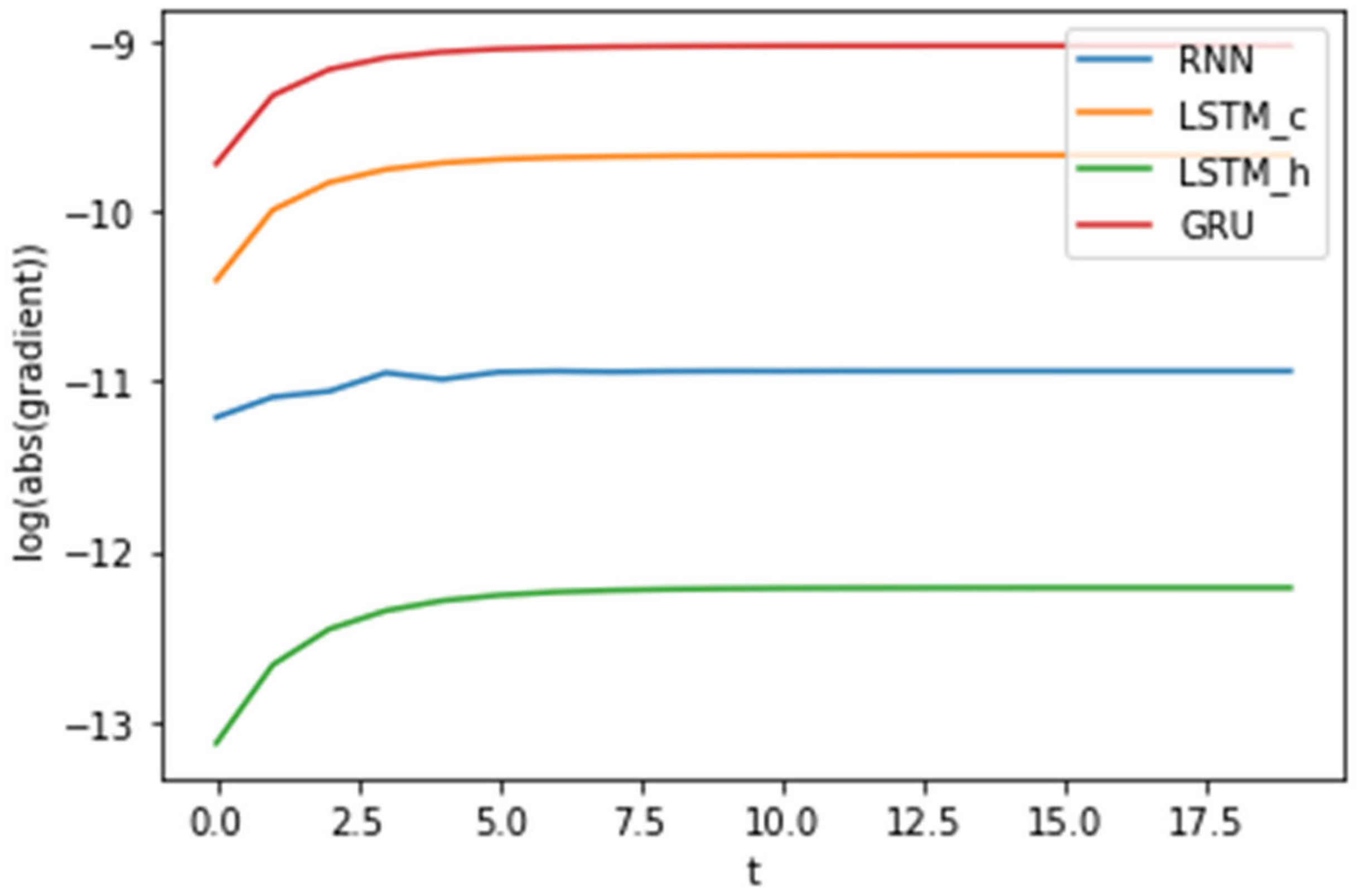
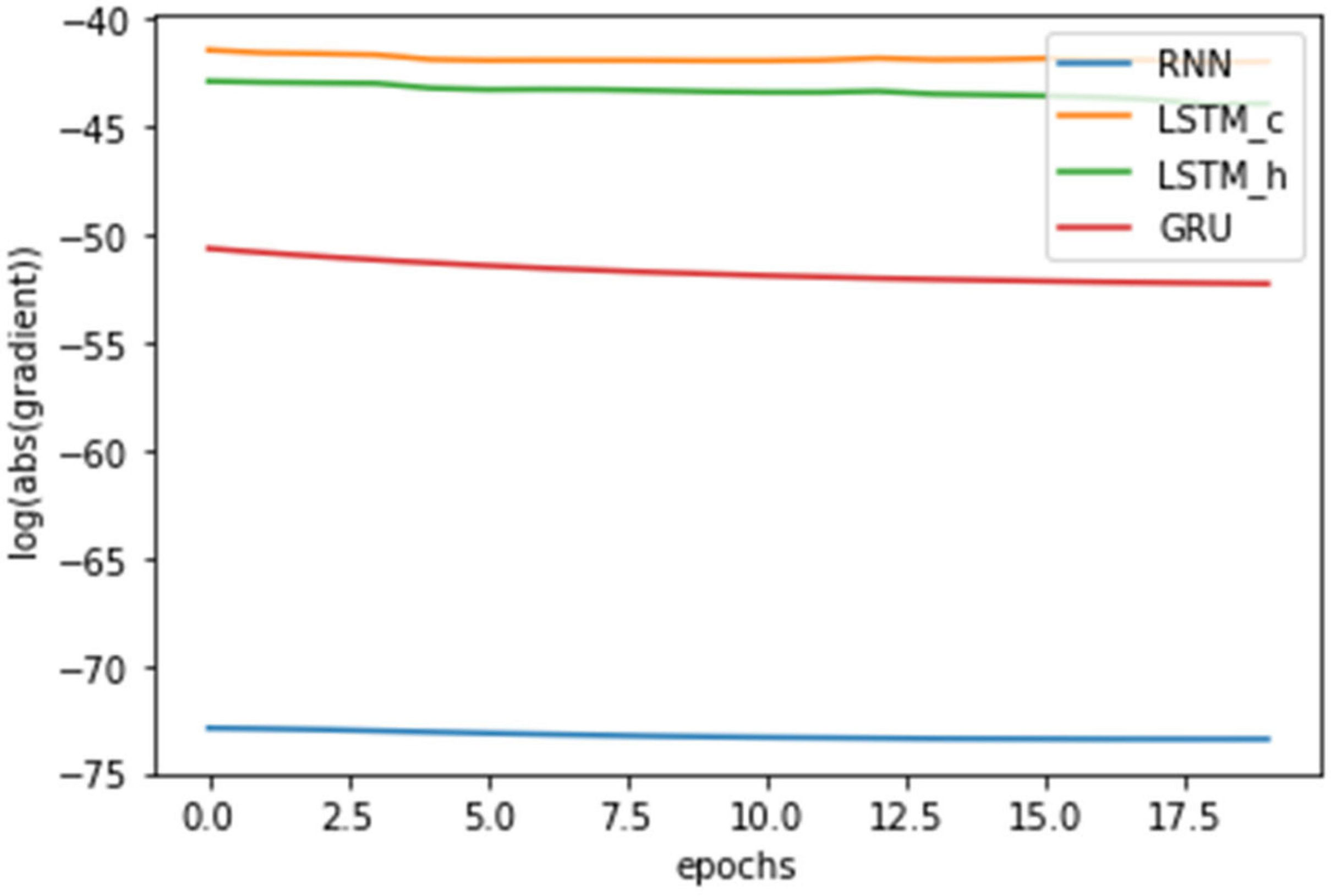
3.2. Numerical Example
4. Discussion of Other Works
5. Conclusions
Funding
Conflicts of Interest
References
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Elman, J. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Tran, Q.K.; Song, S. Water level forecasting based on deep learning: A use case of Trinity River-Texas-The United States. J. KIISE 2020, 44, 607–612. [Google Scholar] [CrossRef]
- Cho, W.; Kang, D. Estimation method of river water level using LSTM. In Proceedings of the Korea Conference on Software Engineering, Busan, Korea, 20–22 December 2017; pp. 439–441. [Google Scholar]
- Kim, H.; Tak, H.; Cho, H. Design of photovoltaic power generation prediction model with recurrent neural network. J. KIISE 2019, 46, 506–514. [Google Scholar] [CrossRef]
- Son, H.; Kim, S.; Jang, Y. LSTM-based 24-h solar power forecasting model using weather forecast data. KIISE Trans. Comput. Pract. 2020, 26, 435–441. [Google Scholar] [CrossRef]
- Yi, H.; Bui, K.N.; Seon, C.N. A deep learning LSTM framework for urban traffic flow and fine dust prediction. J. KIISE 2020, 47, 292–297. [Google Scholar] [CrossRef]
- Jo, S.; Jeong, M.; Lee, J.; Oh, I.; Han, Y. Analysis of correlation of wind direction/speed and particulate matter (PM10) and prediction of particulate matter using LSTM. In Proceedings of the Korea Computer Congress, Busan, Korea, 2–4 July 2020; pp. 1649–1651. [Google Scholar]
- Munir, M.S.; Abedin, S.F.; Alam, G.R.; Kim, D.H.; Hong, C.S. RNN based energy demand prediction for smart-home in smart-grid framework. In Proceedings of the Korea Conference on Software Engineering, Busan, Korea, 20–22 December 2017; pp. 437–439. [Google Scholar]
- Hidasi, B.; Karatzoglou, A.; Baltrumas, L.; Tikk, D. Session-based recommendations with recurrent neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Wu, S.; Ren, W.; Yu, C.; Chen, G.; Zhang, D.; Zhu, J. Personal recommendation using deep recurrent neural networks in NetEase. In Proceedings of the IEEE International Conference on Data Engineering (ICDE), Helsinki, Finland, 16–20 May 2016. [Google Scholar]
- Kwon, D.; Kwon, S.; Byun, J.; Kim, M. Forecasting KOSPI Index with LSTM deep learning model using COVID-19 data. In Proceedings of the Korea Conference on Software Engineering, Seoul, Korea, 5–11 October 2020; Volume 270, pp. 1367–1369. [Google Scholar]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning (PMLR), Atlanta, GA, USA, 17–19 June 2013. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Hwang, M.-Y.; Yao, K.; Larson, M. Speed up of recurrent neural network language models with sentence independent subsampling stochastic gradient descent. In Proceedings of the INTERSPEECH, Lyon, France, 25–29 August 2013; pp. 1203–1207. [Google Scholar]
- Khomenko, V.; Shyshkov, O.; Radyvonenko, O.; Bokhan, K. Accelerating recurrent neural network training using sequence bucketing and multi-GPU data parallelization. In Proceedings of the IEEE Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 23–27 August 2016; pp. 100–103. [Google Scholar]


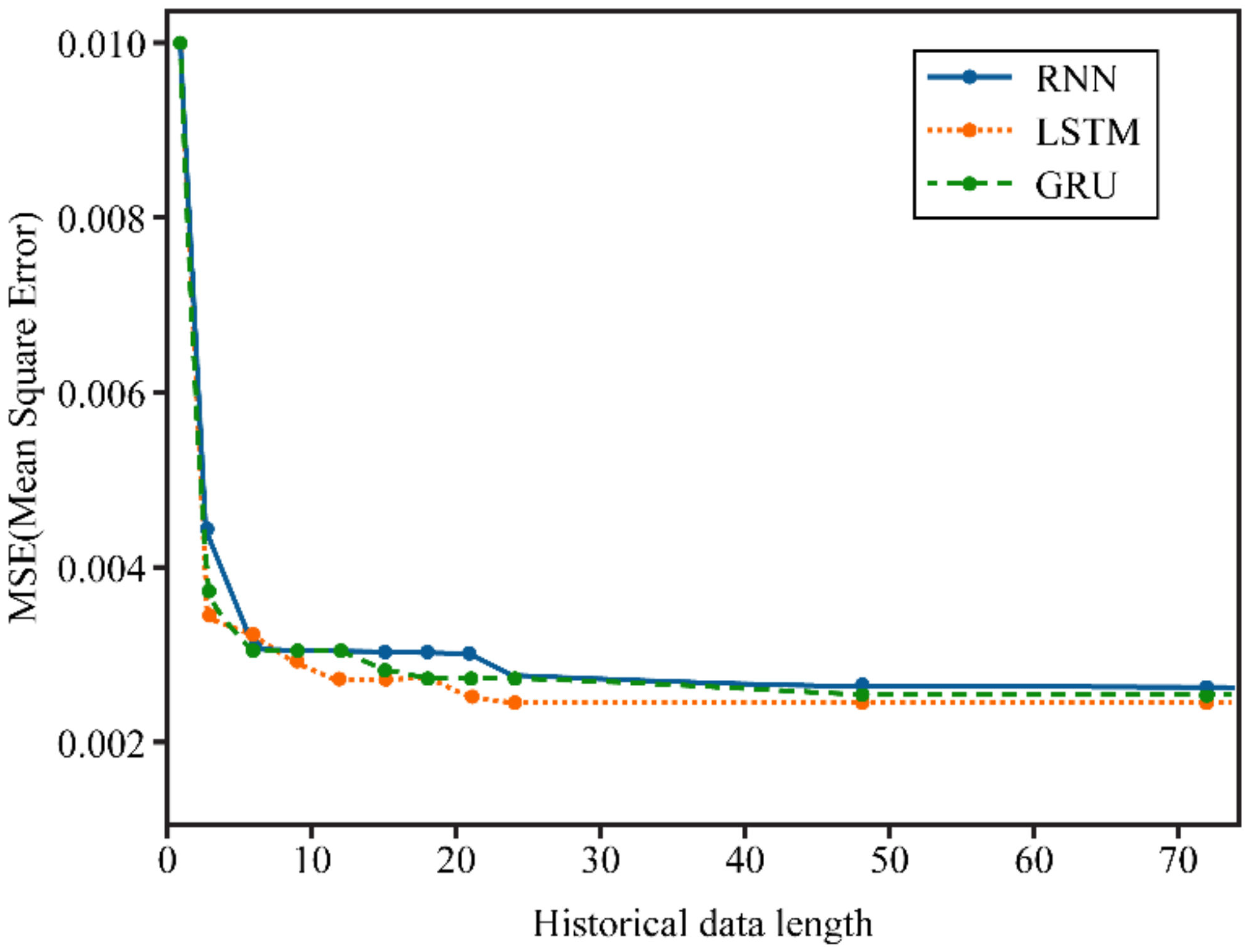
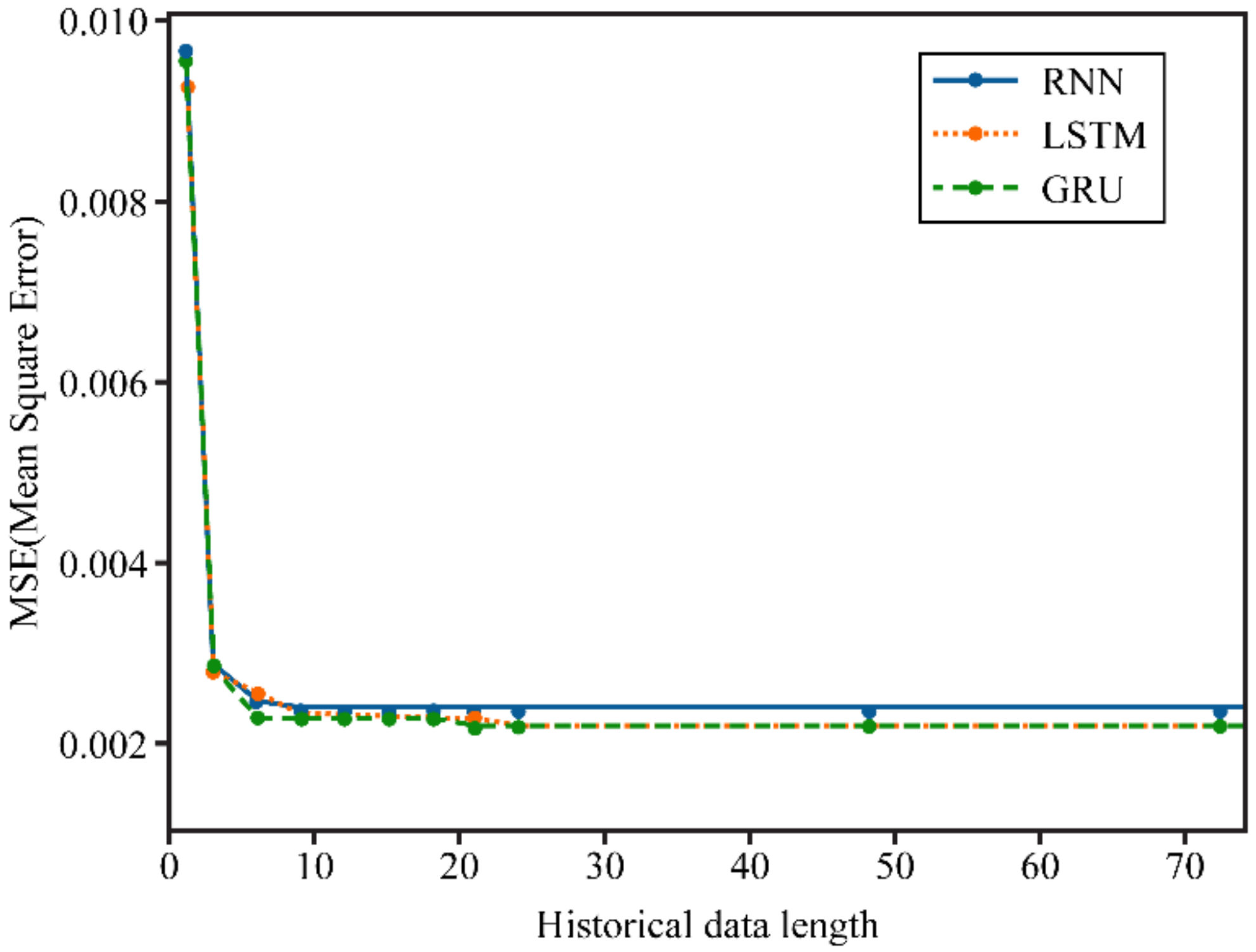
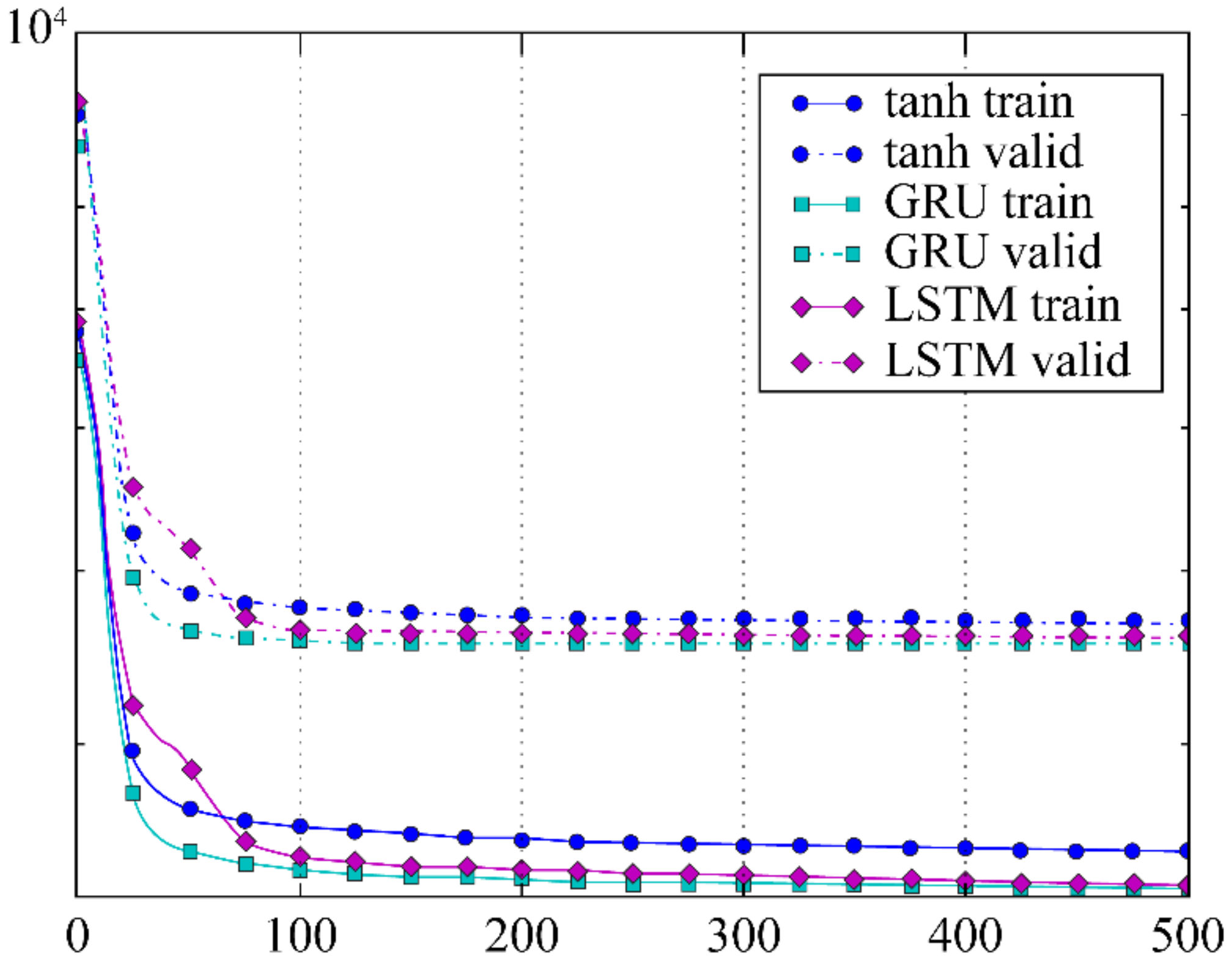

| Standard RNN | RNN-BPTT | LSTM | ||
|---|---|---|---|---|
| Training | Training time (hours) | ~14 | ~22 | ~67 |
| Validation (RMSE) | 0.0076 | 0.0064 | 0.0045 | |
| Testing | One prediction (milliseconds) | ~1.6 | ~1.6 | ~2.8 |
| RMSE (30 min) | 0.0102 | 0.0091 | 0.0077 | |
| RMSE (60 min) | 0.0105 | 0.0092 | 0.0079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, S.-H. Analysis of Gradient Vanishing of RNNs and Performance Comparison. Information 2021, 12, 442. https://doi.org/10.3390/info12110442
Noh S-H. Analysis of Gradient Vanishing of RNNs and Performance Comparison. Information. 2021; 12(11):442. https://doi.org/10.3390/info12110442
Chicago/Turabian StyleNoh, Seol-Hyun. 2021. "Analysis of Gradient Vanishing of RNNs and Performance Comparison" Information 12, no. 11: 442. https://doi.org/10.3390/info12110442
APA StyleNoh, S.-H. (2021). Analysis of Gradient Vanishing of RNNs and Performance Comparison. Information, 12(11), 442. https://doi.org/10.3390/info12110442






