Predicting the Generalization Ability of a Few-Shot Classifier
Abstract
1. Introduction
- To the best of our knowledge, we propose the first benchmark of generalization measures in the context of transfer-based few-shot learning.
- We conduct experiments to stress the ability of the measures to correctly predict generalization using different settings related to few-shot: (i) supervised, where we only have access to a few labeled samples, (ii) semi-supervised, where we have access to both a few labeled samples and a set of unlabeled samples and (iii) unsupervised, where no label is provided.
2. Related Work
2.1. Few-Shot Learning
2.1.1. With Meta-Learning
2.1.2. Without Meta-Learning
2.2. Better Backbone Training
2.2.1. Learning Diverse Visual Features
2.2.2. Using Additional Unlabeled Data Samples
2.2.3. Learning Good Representations
2.3. Evaluating the Generalization Ability
3. Background
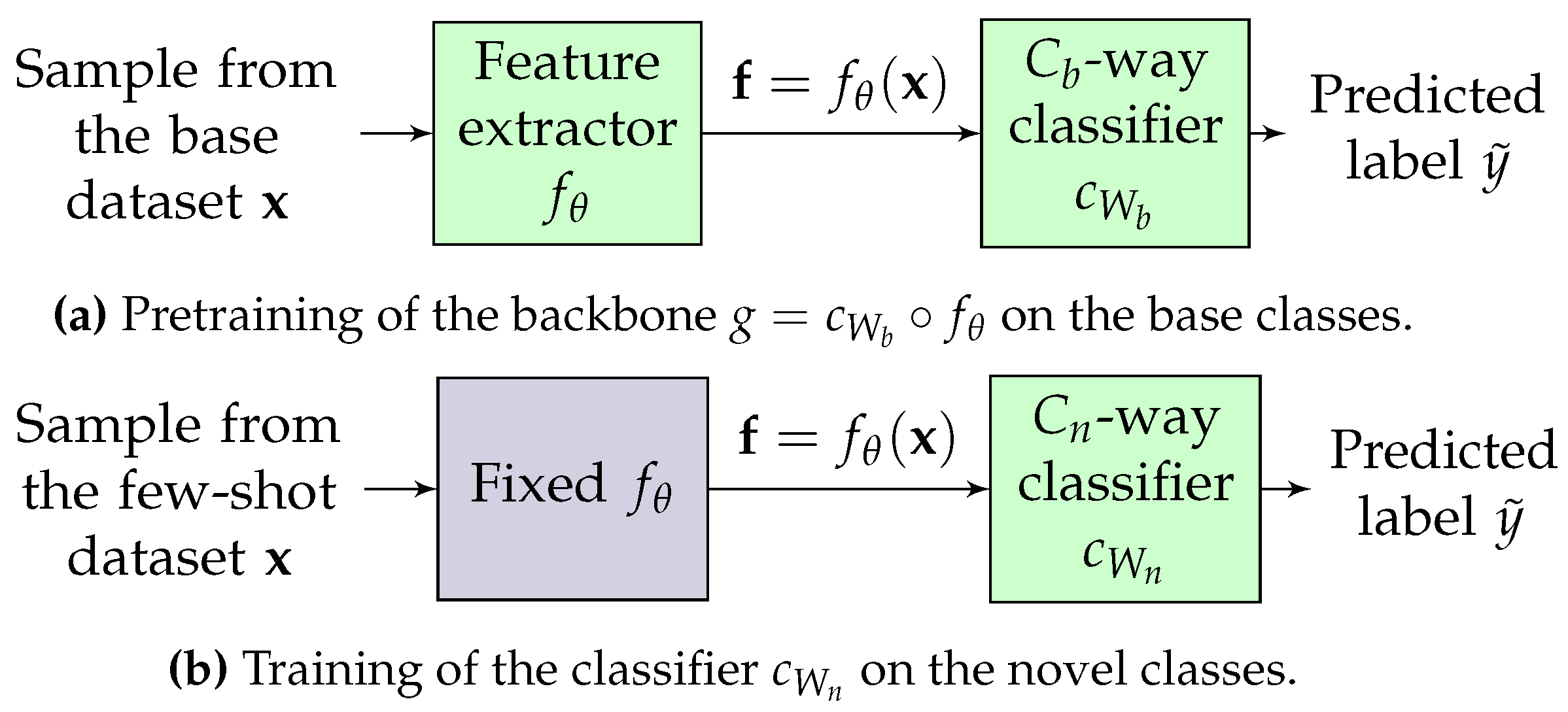
3.1. Few-Shot Classification: A Transfer-Based Approach
3.2. Studied Settings
3.3. Studied Classifiers
3.3.1. Supervised Setting
3.3.2. Semi-Supervised Setting
3.3.3. Unsupervised Setting
4. Predictive Measures
4.1. Supervised Setting
4.1.1. LR Training Loss
4.1.2. Similarity
4.2. Unsupervised Setting
4.2.1. Davies-Bouldin Score after a N-means Algorithm
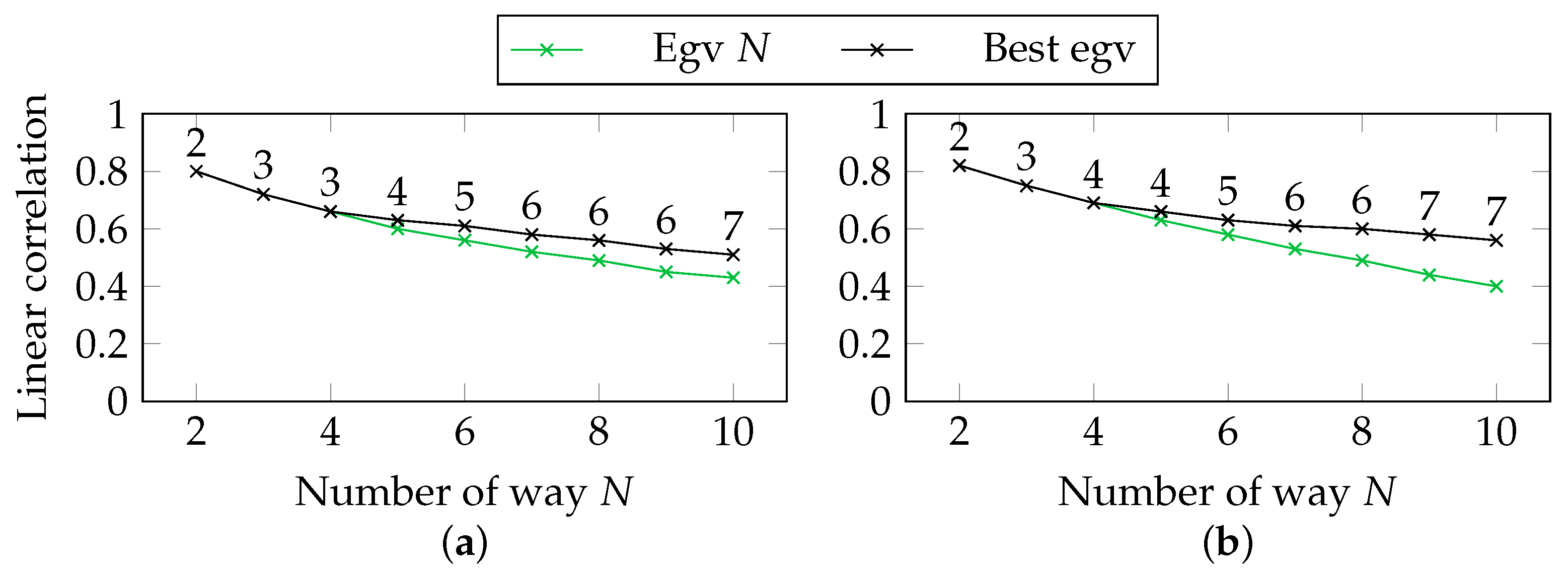
4.2.2. Laplacian Eigenvalues
4.3. Semi-Supervised Setting
5. Experiments
5.1. Datasets
5.2. Backbones
5.3. Evaluation Metrics
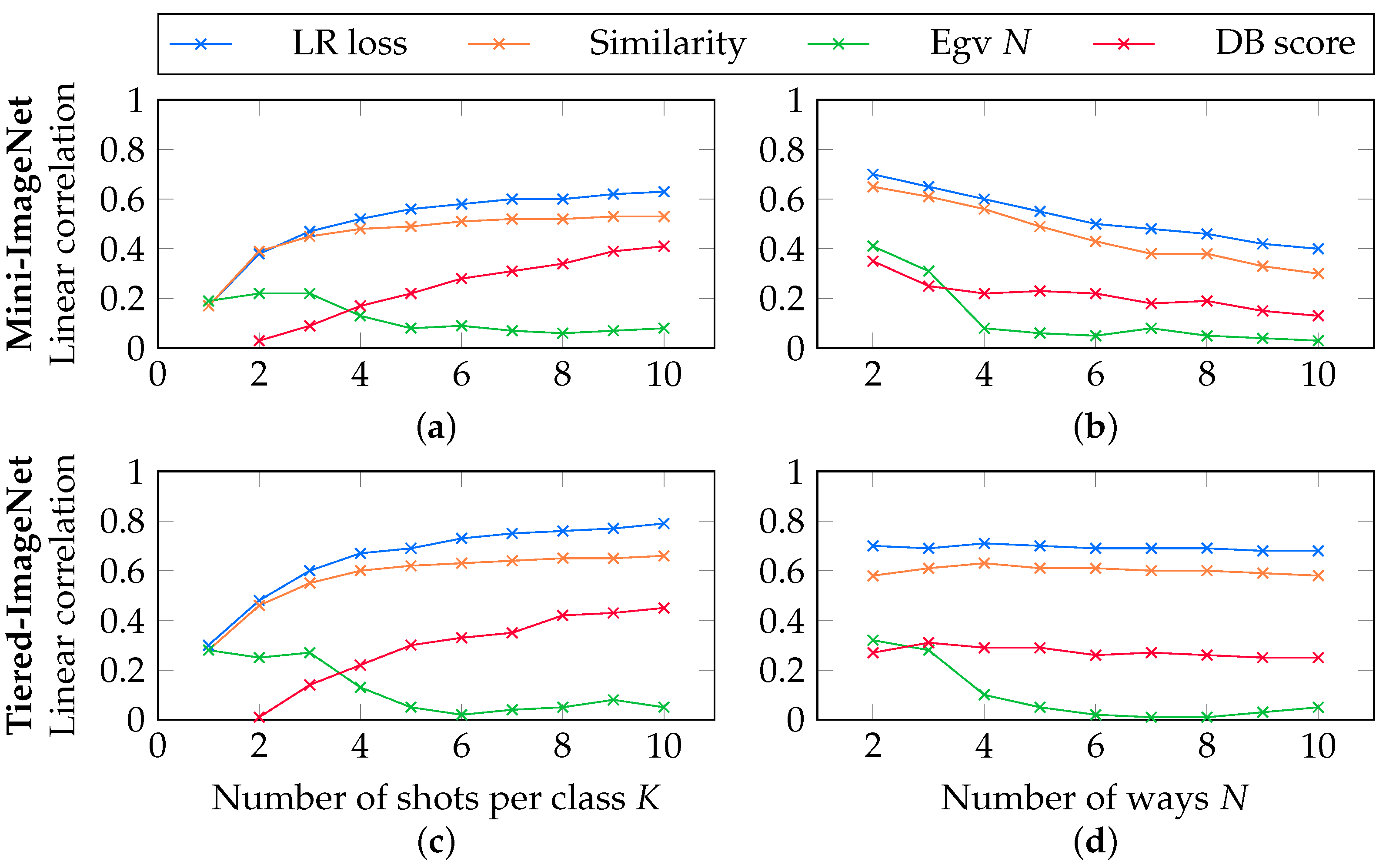
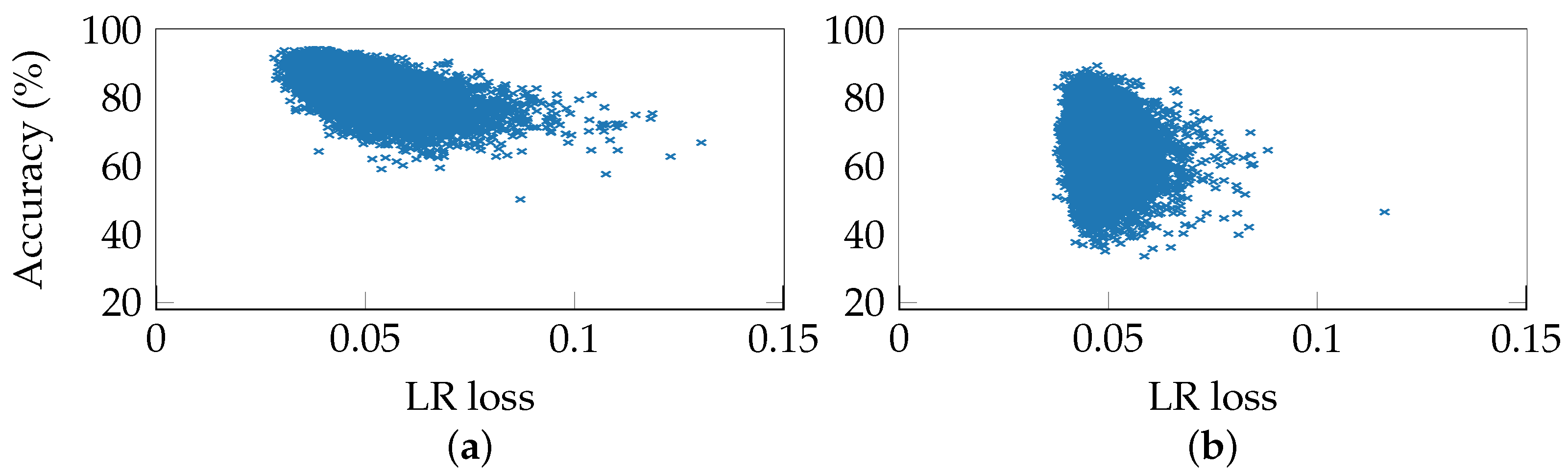
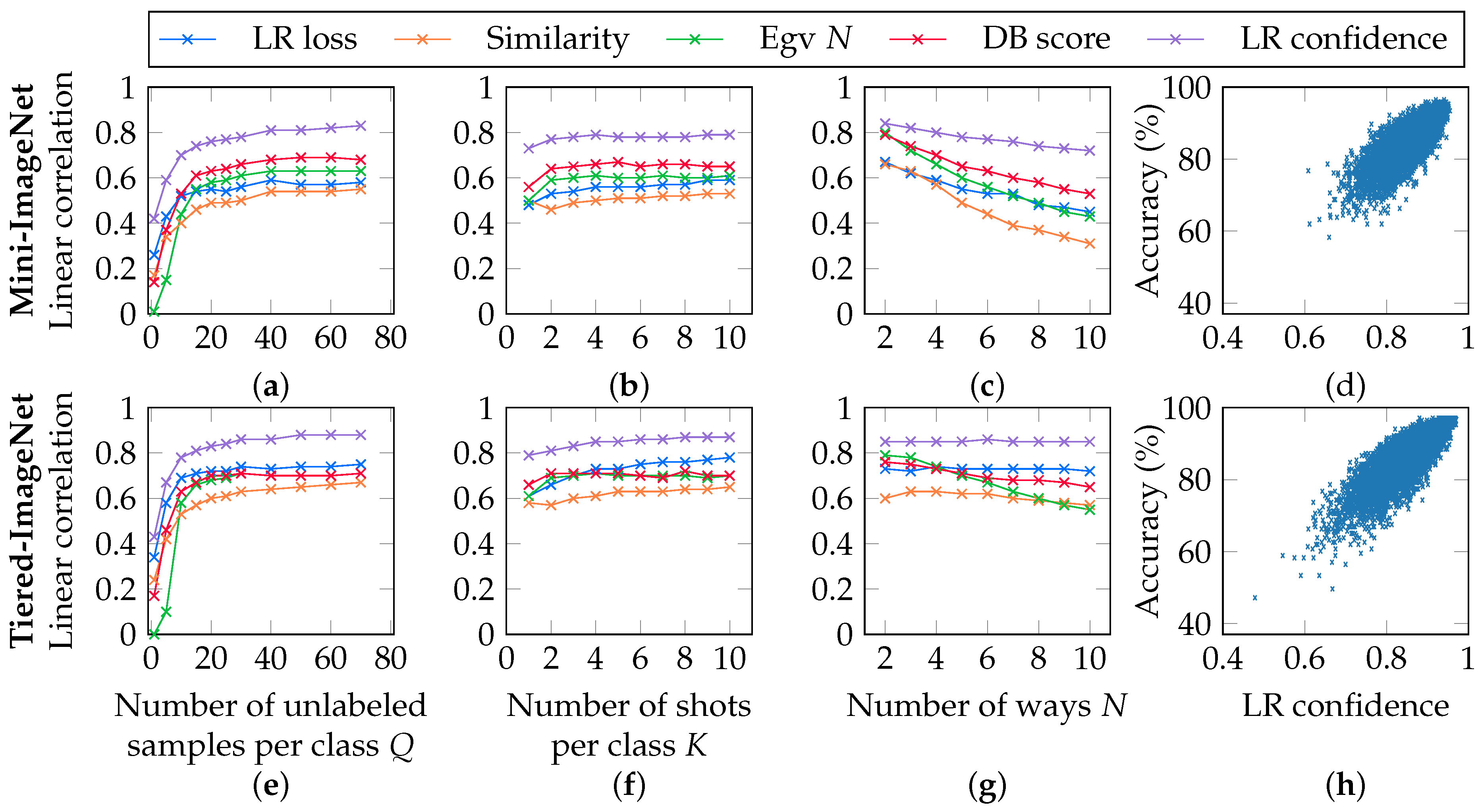
5.4. Correlations in the Supervised Setting
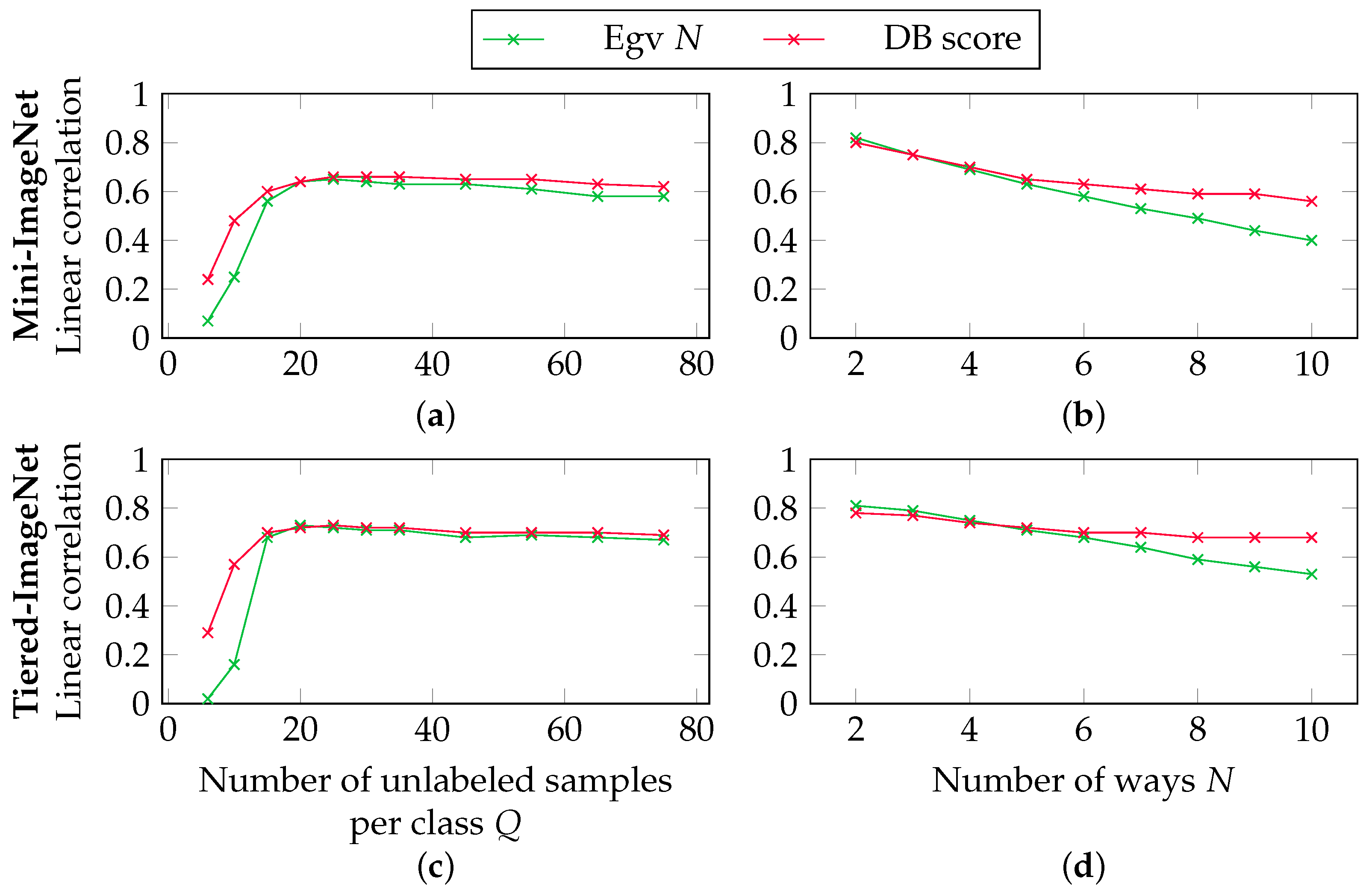
5.5. Correlations in the Unsupervised Setting
5.6. Correlations in the Semi-Supervised Setting
5.7. Predicting Task Accuracy
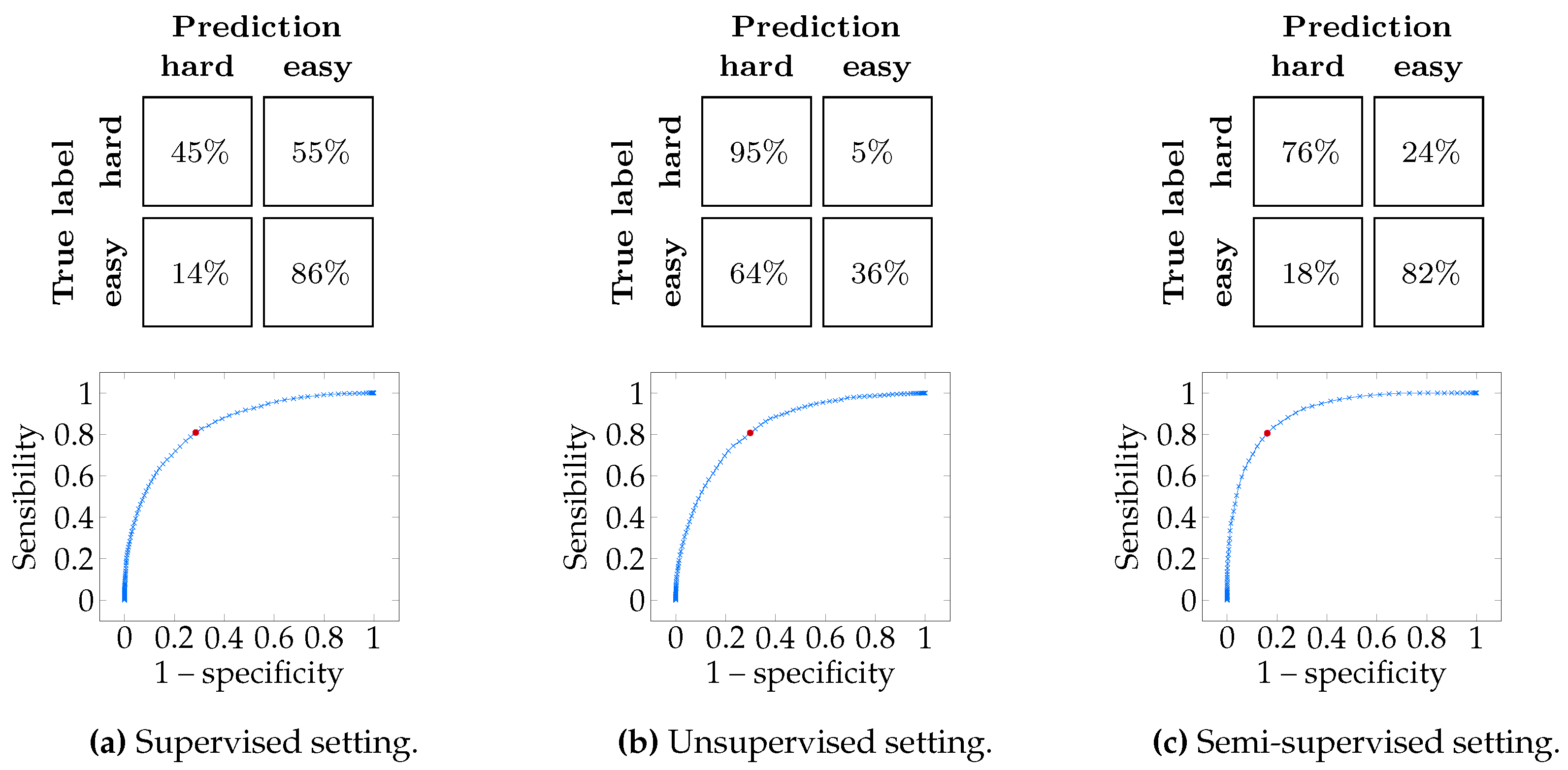
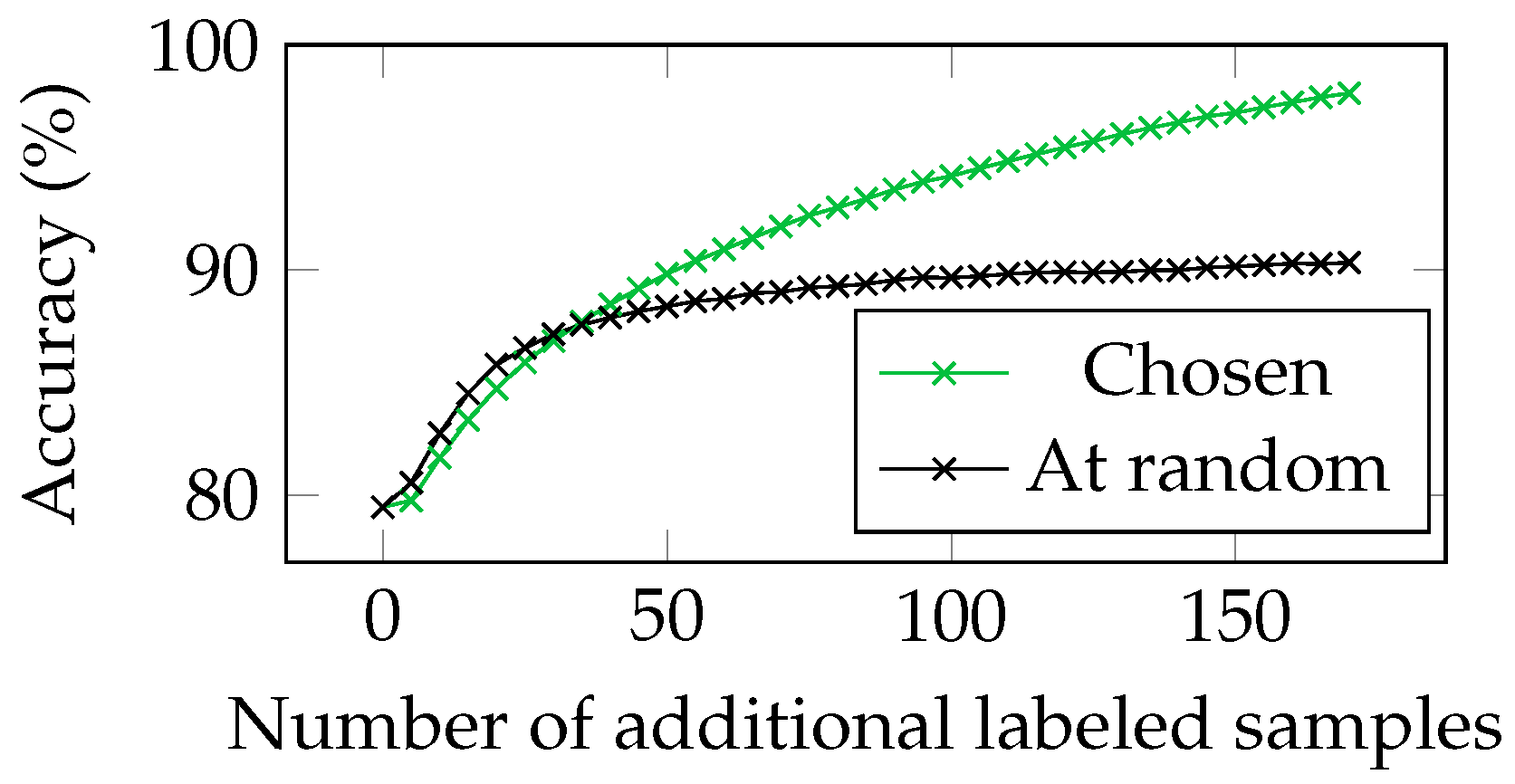
5.8. Using Per-Sample Confidence to Annotate the Hardest Samples
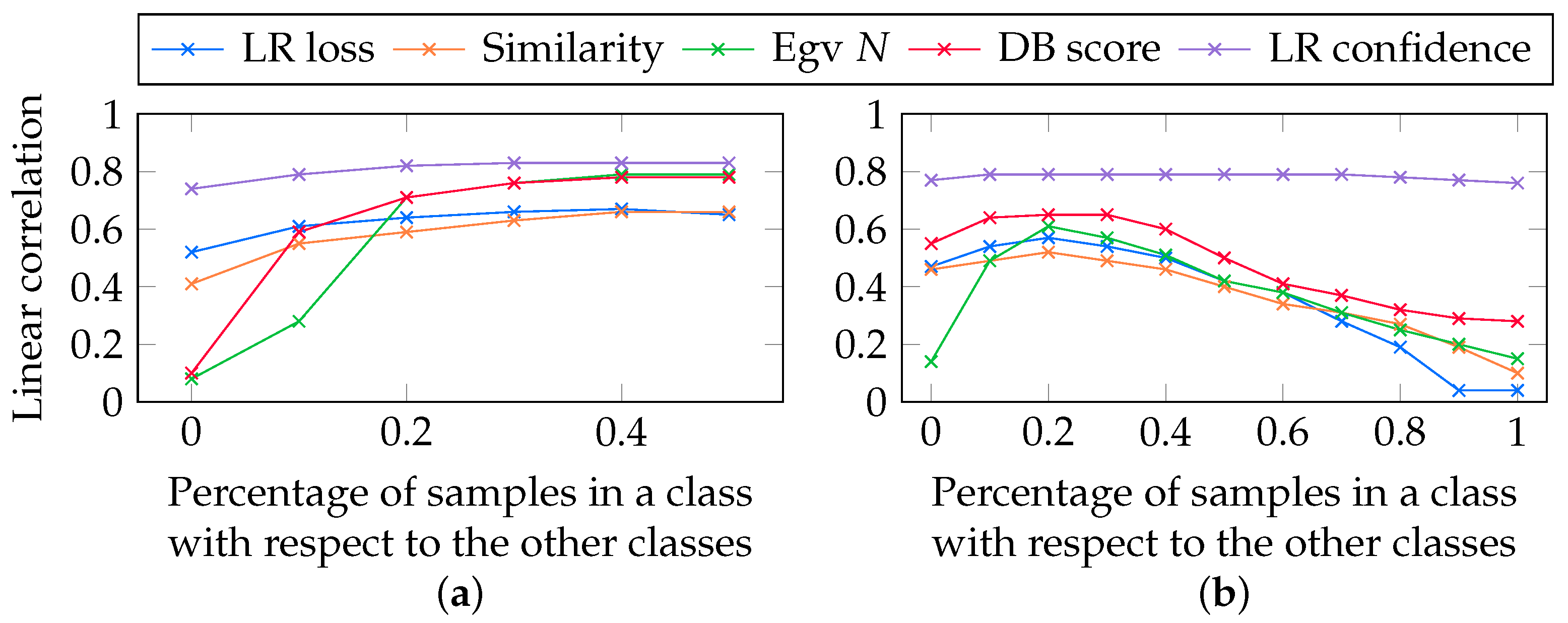
5.9. Additional Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Details about the Training of the Classifiers
Appendix B. Models Performance on Various Tasks

Appendix C. Influence of the Number of Nearest Neighbors

References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Aytar, Y.; Vondrick, C.; Torralba, A. Soundnet: Learning sound representations from unlabeled video. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 892–900. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354. [Google Scholar] [CrossRef] [PubMed]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Burt, J.R.; Torosdagli, N.; Khosravan, N.; RaviPrakash, H.; Mortazi, A.; Tissavirasingham, F.; Hussein, S.; Bagci, U. Deep learning beyond cats and dogs: Recent advances in diagnosing breast cancer with deep neural networks. Br. J. Radiol. 2018, 91, 20170545. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, C.; Cui, P.; Yang, H.; Zhu, W. Learning disentangled representations for recommendation. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 5711–5722. [Google Scholar]
- Gupta, V.; Sambyal, N.; Sharma, A.; Kumar, P. Restoration of artwork using deep neural networks. Evol. Syst. 2019. [Google Scholar] [CrossRef]
- Caruana, R.; Lawrence, S.; Giles, C.L. Overfitting in neural nets: Backpropagation, conjugate gradient, and early stopping. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 402–408. [Google Scholar]
- Guyon, I. A Scaling Law for the Validation-Set Training-Set Size Ratio. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.1337&rep=rep1&type=pdf (accessed on 9 January 2021).
- Mangla, P.; Kumari, N.; Sinha, A.; Singh, M.; Krishnamurthy, B.; Balasubramanian, V.N. Charting the right manifold: Manifold mixup for few-shot learning. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 2218–2227. [Google Scholar]
- Wang, Y.; Chao, W.L.; Weinberger, K.Q.; van der Maaten, L. SimpleShot: Revisiting Nearest-Neighbor Classification for Few-Shot Learning. arXiv 2019, arXiv:1911.04623. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Rusu, A.A.; Rao, D.; Sygnowski, J.; Vinyals, O.; Pascanu, R.; Osindero, S.; Hadsell, R. Meta-Learning with Latent Embedding Optimization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 4077–4087. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3630–3638. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Oreshkin, B.; López, P.R.; Lacoste, A. Tadam: Task dependent adaptive metric for improved few-shot learning. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 721–731. [Google Scholar]
- Ye, H.J.; Hu, H.; Zhan, D.C.; Sha, F. Learning embedding adaptation for few-shot learning. arXiv 2018, arXiv:1812.03664. [Google Scholar]
- Chen, W.Y.; Liu, Y.C.; Kira, Z.; Wang, Y.C.F.; Huang, J.B. A Closer Look at Few-shot Classification. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Tian, Y.; Wang, Y.; Krishnan, D.; Tenenbaum, J.B.; Isola, P. Rethinking Few-Shot Image Classification: A Good Embedding Is All You Need? arXiv 2020, arXiv:2003.11539. [Google Scholar]
- Milbich, T.; Roth, K.; Bharadhwaj, H.; Sinha, S.; Bengio, Y.; Ommer, B.; Cohen, J.P. DiVA: Diverse Visual Feature Aggregation forDeep Metric Learning. arXiv 2020, arXiv:2004.13458. [Google Scholar]
- Lichtenstein, M.; Sattigeri, P.; Feris, R.; Giryes, R.; Karlinsky, L. TAFSSL: Task-Adaptive Feature Sub-Space Learning for few-shot classification. arXiv 2020, arXiv:2003.06670. [Google Scholar]
- Hu, Y.; Gripon, V.; Pateux, S. Exploiting Unsupervised Inputs for Accurate Few-Shot Classification. arXiv 2020, arXiv:2001.09849. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893. [Google Scholar]
- Xu, Y.; Zhao, S.; Song, J.; Stewart, R.; Ermon, S. A Theory of Usable Information under Computational Constraints. arXiv 2020, arXiv:2002.10689. [Google Scholar]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Wang, Z.; Du, B.; Guo, Y. Domain adaptation with neural embedding matching. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2387–2397. [Google Scholar] [CrossRef]
- Lu, J.; Jin, S.; Liang, J.; Zhang, C. Robust Few-Shot Learning for User-Provided Data. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef]
- Jiang, Y.; Neyshabur, B.; Mobahi, H.; Krishnan, D.; Bengio, S. Fantastic Generalization Measures and Where to Find Them. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Jiang, Y.; Krishnan, D.; Mobahi, H.; Bengio, S. Predicting the Generalization Gap in Deep Networks with Margin Distributions. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J.B.; Larochelle, H.; Zemel, R.S. Meta-learning for semi-supervised few-shot classification. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Miller, G.A. WordNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016; pp. 87.1–87.12. [Google Scholar] [CrossRef]
- Verma, V.; Lamb, A.; Beckham, C.; Najafi, A.; Mitliagkas, I.; Lopez-Paz, D.; Bengio, Y. Manifold Mixup: Better Representations by Interpolating Hidden States. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| SETTINGS | ||||
|---|---|---|---|---|
| Supervised | Semi-Supervised | Unsupervised | ||
| N-Way K-Shot | N-Way K-Shot | N-Way Q-Query * | ||
| Q-Query * | ||||
| SOLUTIONS | Using available labels and features of data samples | |||
| Training loss of the logistic regression | √ | √ | × | |
| Similarities between labeled samples | √ | √ | × | |
| Confidence in the output of the logistic regression | × | √ | × | |
| Using only data relationships | ||||
| Eigenvalues of a graph Laplacian | √ | √ | √ | |
| Davies-Bouldin score after a N-means algorithm | √ | √ | √ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bontonou, M.; Béthune, L.; Gripon, V. Predicting the Generalization Ability of a Few-Shot Classifier. Information 2021, 12, 29. https://doi.org/10.3390/info12010029
Bontonou M, Béthune L, Gripon V. Predicting the Generalization Ability of a Few-Shot Classifier. Information. 2021; 12(1):29. https://doi.org/10.3390/info12010029
Chicago/Turabian StyleBontonou, Myriam, Louis Béthune, and Vincent Gripon. 2021. "Predicting the Generalization Ability of a Few-Shot Classifier" Information 12, no. 1: 29. https://doi.org/10.3390/info12010029
APA StyleBontonou, M., Béthune, L., & Gripon, V. (2021). Predicting the Generalization Ability of a Few-Shot Classifier. Information, 12(1), 29. https://doi.org/10.3390/info12010029





