Robot Evacuation on a Line Assisted by a Bike

Abstract

Two robots and a bike are initially placed at the origin of an infinite line. The robots are modelled as autonomous mobile agents whose communication capabilities are either in the wireless or face-to-face model, while the bike neither can move nor communicate on its own. Thus, the bike is not autonomous but rather requires one of the robots to ride it. An exit is placed on the line at distance d from the origin; the distance and direction of the exit from the origin is unknown to the robots. Only one robot may ride the bike at a time and the goal is to evacuate from the exit in the minimum time possible as measured by the time it takes the last robot to exit. The robots can maintain a constant walking speed of 1, but when riding the bike they can maintain a constant speed $v>1$ (same for both robots). We develop algorithms for the evacuation of the two robots from the unknown exit and analyze the evacuation time defined as the time it takes the second robot to evacuate. In the wireless model we present three algorithms: in the first the robots move in opposite direction with max speed, in the second with a specially selected “optimal” speed, and in the third the robot imitates the biker (i.e., robot riding the bike). We also give three algorithms in the Face-to-Face model: in the first algorithm the robot pursues the biker, in the second the robot and the biker use zig-zag algorithms with specially chosen expansion factors, and the third algorithm establishes a sequence of specially constructed meeting points near the exit. In either case, the optimality of these algorithms depends on $v>1$. We also discuss lower bounds.

1. Introduction

Recent years have witnessed an explosive growth of research studies on search from the perspective of mobile agent computing. One of the reasons is because one finds countless natural applications of search and exploration in distributed systems in order to facilitate information exchange between communicating entities. Moreover, there are also applications in numerous other computing areas such as data mining, web crawlers, monitoring and surveillance, just to mention a few.

Evacuation, which is the main theme of our present investigation, is related to search in that one is also interested in searching and exploring a domain in order to find a target. However evacuation usually involves many cooperating entities forming an ensemble or group all of whose members are searching simultaneously by exchanging information (according to a predefined communication model); and unlike search which typically involves only one agent, it is aiming to optimize the arrival time of the last entity in the ensemble. There are many factors that affect how linear search and evacuation problems are solved. Let us assume that the exit is located on a line at a distance d from the origin where the robot starts. The orientation represents the direction that the robot must proceed to reach the exit. The simplest case would be if a robot moving with unit speed knows the distance and the orientation and can thus reach the exit in time d. In this case, the competitive ratio will be the time needed by the robot to reach the exit, which is d, divided by the time needed by the adversary to head to the exit directly, which is d as well. Thus the competitive ratio will be 1. A more complicated case would be if the distance is known and the orientation is not known. As a worst case scenario, it may take the robot $3d$ to find the exit since the robot may move d in the wrong direction and thus it will need to switch the direction and move back $2d$ to reach the exit. The competitive ratio in this case is 3. The problem is even more complicated if both the distance and the orientation are not known. The robot starts at the origin and can move with speed 1. The robot needs to explore both directions in order to find the exit. The best way to achieve this goal is to select a direction and move distance 1. If the exit is not found, the robot will reverse direction and move double the previous distance up until the exit is found. The movement, which is repeated periodically, and which uses a sequence of positive distances that specifies the turning points, is called the Zig-Zag search algorithm. The competitive ratio for the Zig-Zag search algorithm is known to be 9 [1]. Most of the linear search and evacuation problems in the literature were studied using single or multiple robots. Introducing a tool such as a bike to aid the robots was not considered before in any previous work. The study of this paper is based on a new paradigm concerning two robots (also called hikers) aided by a bike and searching for an unknown exit placed somewhere on an infinite line. More specifically, in the “bike assisted evacuation” problem, the hikers and the bike all start at the origin and want to evacuate from an exit placed at an unknown distance and direction (either left or right from the origin) on the infinite line. Evacuation means that eventually both robots must find the exit by reaching its exact location (not necessarily at the same time) on the infinite line. The quality of an evacuation algorithm is measured by the time it takes the second hiker to find the exit, which is also referred to as evacuation time of the ensemble.

1.1. Model and Notation

To analyze the problem proposed, first we describe details concerning mobility and communication of the hikers and describe the role that the bike will play in improving the overall evacuation time.

Mobility and Trajectories.The infinite line is the search domain. It is bidirectional in that the hikers can move in either direction without this affecting their speeds. The hikers can stop at any time and wait as long as they wish, can walk with maximum speed 1 or may ride the bike with speed $v>1$. An evacuation algorithm is a complete description of the trajectories traced by the two hikers either waiting, walking or riding the bike until they both find the exit. Throughout this paper we are interested in evacuation algorithms.

Sharing the bike. An interesting feature of our problem is the distinction between the hikers and the bike. On the one hand, the hikers are autonomous mobile agents that can move around on their own with speed 1 and communicate with each other. On the other hand, the bike is not autonomous and cannot move and/or communicate on its own and thus plays only the role of assistant in the search. The hiker using the bike has an advantage in that it can move with speed $v>1$ which is of course faster than its walking speed 1. However, in our model the bike is also a limited resource in that it can be used by only one hiker at a time. This creates an interesting trade off for the evacuation time. The hikers would want to ride the bike to find the exit earlier. However, if the bike is not shared the evacuation time may get worse as the hiker not using the bike may worsen the overall evacuation time. This also implies that the hiker riding the bike has an advantage in sharing the bike with the other hiker as this will ultimately improve the overall evacuation time.

Bike Switching. An important aspect in our algorithms will be “bike switching”, by which we mean changing the rider of the bike. We will assume throughout the paper that bike switching between hikers is instantaneous and at no time cost. Note that the hikers may recognize the presence of the bike when they are at the same location as the bike. From now on, to facilitate our discussions we will refer to the hiker riding the bike as the biker, which may be either of the two hikers.

Communication. A designated point on the infinite line is the exit and can be recognized as such by any of the hikers when they are at the same location as the exit. The hikers may communicate throughout the execution of the algorithms. Two types of communication will be studied, namely wireless (also known as wifi) and face-to-face. In the former, the hikers can communicate instantaneously and at any distance, while in the latter only when they are at the same location and at the same time. The fact that a hiker is riding the bike does not diminish its ability to communicate. A typical communication exchange may involve, e.g., “exit is found”, “bike released”, “switch bike”, etc. Note that the hikers are endowed with pedometers and have computing abilities so that they can deduce the location of the other hiker and/or the bike from relevant communications exchanged and/or the protocols they execute.

Notation. Throughout the paper we will be using $R_1$ and $R_2$ to denote the two hikers and B to denote the bike. The hikers are equipped with pedometers and are identical in all their capabilities (locomotion and communication) and the subscripts $i=1,2$ in $R_i$ do not imply that the hikers have identifiers. The origin of the real line will be at the point $x=0$ on the x-axis and this will also be the starting location of the hikers and the bike. The adversary may place the exit at either of the points ±d, where $d>0$ will denote the unknown distance of the exit from the origin. In addition, $v>1$ will denote the speed that a biker can attain when riding the bike.

1.2. Related Work

The continuous infinite line is a widely-used search domain. It is in this particular domain that the first search problems in the literature were proposed in the seminal papers [2,3] with a focus on stochastic search models and their analysis. Influential research for deterministic search by a single robot in the infinite line was developed in the work of [1] by proving that searching for a target has competitive ratio equal to 9, and for randomized search on the star graph by [4].

Evacuation is a form of group search in which the robots need to cooperate so that they all find the exit. It arises as a natural problem on the infinite line for the case of robots with faults (crash and/or Byzantine). The two important papers are [5] for robots with crash faults and [6] for robots with Byzantine faults. The study of evacuation in distributed computing for a unit disk is also related and was initiated in the paper [7] for both the wireless and face-to-face models. The reader can find additional related work on the continuous search domain in the survey paper [8].

The addition of an immobile token to aid in the exploration has been considered in the context of the rendezvous problem on a ring [9]. An extension of this work to mobile tokens can be found in [10]. In both of these papers the token is passive and is merely being used as a marker for the presence of the most recent “visit” of another agent. Similarly, in [11] the authors consider searching for a non-adversarial, uncooperative agent, called bus, which is moving with constant speed along the perimeter of a cycle. A different related model was investigated in [12] in which during search a robot can encounter a point or a sequence of points enabling faster and faster movement and the main goal is to adopt the route which allows a robot to reach the destination as quickly as possible.

Two related papers are [13] and its followup journal version [14]. In the former paper the authors introduce evacuation on an infinite line in the F2F model for two robots having max speed 1 and prove that 9 is a tight bound for evacuation. In the followup paper [14] tight bounds are shown for two robots with different speeds in the F2F model. In their model the robots can vary their speed between the min and max value. However, unlike our model, the slower robot is never able to move at the speed of the faster robot. As a consequence in our model a “shared” bike has the effect of averaging the speeds and improving the overall evacuation time of the ensemble. The main idea considered in the present paper of bike assisted evacuation modelled as a passive agent that can enhance the robots’ evacuation time has not been considered in the relevant literature on search and evacuation before. (The present study is revised and updated from the first author’s MCS Thesis [15]. A preliminary study without proofs in [16]).

It is also worth mentioning a different line of research that has evolved in recent years, concerning bike sharing systems in complementing traditional public transportation to reduce traffic congestion and mitigate atmospheric pollution. As a consequence bike-sharing has grown explosively everywhere [17]. This has led to extensive technical literature on different aspects of the performance of bike based transportation systems. For example, Ref. [18] addresses uncertainty in resource availability, Ref. [19] considers bike utilization conflict, Ref. [20] studies system balance maintainance, Ref. [21] investigates the efficient operation of shared mobility systems, Ref. [22] studies balancing, and [23] proposes a spatio-temporal bicycle mobility model. Finally we mention the recent paper [24] which gives a polynomial time algorithm for the Bike Sharing problem that produces an arrival-time optimal schedule for bikers to travel across the interval.

1.3. Outline and Results of the Paper

Our main results in the Wireless model are presented in Section 3. We give three algorithms: in the first the robots move in opposite direction with max speed, in the second with a specially selected “optimal” speed, and in the third the hiker imitates the biker. Results on the Face-to-Face model are presented in Section 4. We give three algorithms: in the first algorithm the hiker pursues the biker, in the second the hiker and the biker use zig-zag algorithms with specially chosen expansion factors, and in the third the algorithm establishes a sequence of specially constructed meeting points near the exit. In either communication model we conclude that the optimal algorithm depends on the speed v of the bike which we also determine. Details of the results are in

Table 1. Main algorithms presented in the paper in the WiFi (top three) and Face-to-Face (F2F) (bottom three) models, the theorem where the analysis, and their corresponding evacuation time as a function of the bike’s speed v, where $v>1$.

Algorithm	Theorem	Evacuation Time
Algorithm 2 (WiFi)	Theorem 1	$max\left\{2d+\frac{d}{v},\frac{2d}{v}+\frac{d}{2}+\frac{d}{2v^2}\right\}$
Algorithm 3 (WiFi)	Theorem 2	$\frac{3d+3vd+d\sqrt{v^2+26v+9}}{4v}$
Algorithm 4 (WiFi)	Theorem 3	$\frac{9d}{v}+\frac{d}{2}-\frac{d}{2v^2}$
Algorithm 5 (F2F)	Theorem 4	$\frac{9d}{v}+d-\frac{5d}{8v^2}$
Algorithm 6 (F2F)	Theorem 5	$\frac{3d{v}^3+63d{v}^2+15dv-9d}{2v^2(3v+1)}$
Algorithm 7 (F2F)	Theorem 6	$3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{5v^2-12v-1}{v(v-1)(3v-1)}d$    if $1<v\le \frac{6+\sqrt{41}}{5}$
		$3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{4(5v^2-12v-1)}{v(v-1)(3v-1)}d$    if $\frac{6+\sqrt{41}}{5}\le v$

.

We also establish lower bounds in Section 5. The competitive ratio of the algorithms can be given by dividing by $\frac{v+1}{2v}d$, where d is the distance of the exit from the origin (see Theorem 7). The main motivation of our current study on robot evacuation from an unknown target is to better understand the effect that communication models (F2F and Wireless) have on search and evacuation time for an autonomous mobile agent which is aided by another mobile agent (bike) which has limited mobility capabilities.

2. Preliminaries

In this section we remind the reader that the competitive ratio for the Zig-Zag search algorithm is known to be at most 9. A canonical Zig-Zag search algorithm is defined as follows (Algorithm 1):

Algorithm 1: Zig-Zag Algorithm

The competitive ratio for Algorithm 1 is calculated as follows:

Every time the robot changes direction and moves twice the previous distance. Thus, if the exit is at distance d, then $2^k<d\le 2^{k+2}$ for some k. Hence the search time T will be calculated as follows:

$$\begin{array}{ccc}\hfill T& =2·1+2·2+\cdots +2·2^{k+1}+d\hfill & \\ \hfill & =2·(2^{k+2}-1)+d=2^3·2^k-2+d\le 8d+d=9d\hfill \end{array}$$

Thus, the competitive ratio of this algorithm is $\frac{9d}{d}=9$. The lower bound proof can be found in [1].

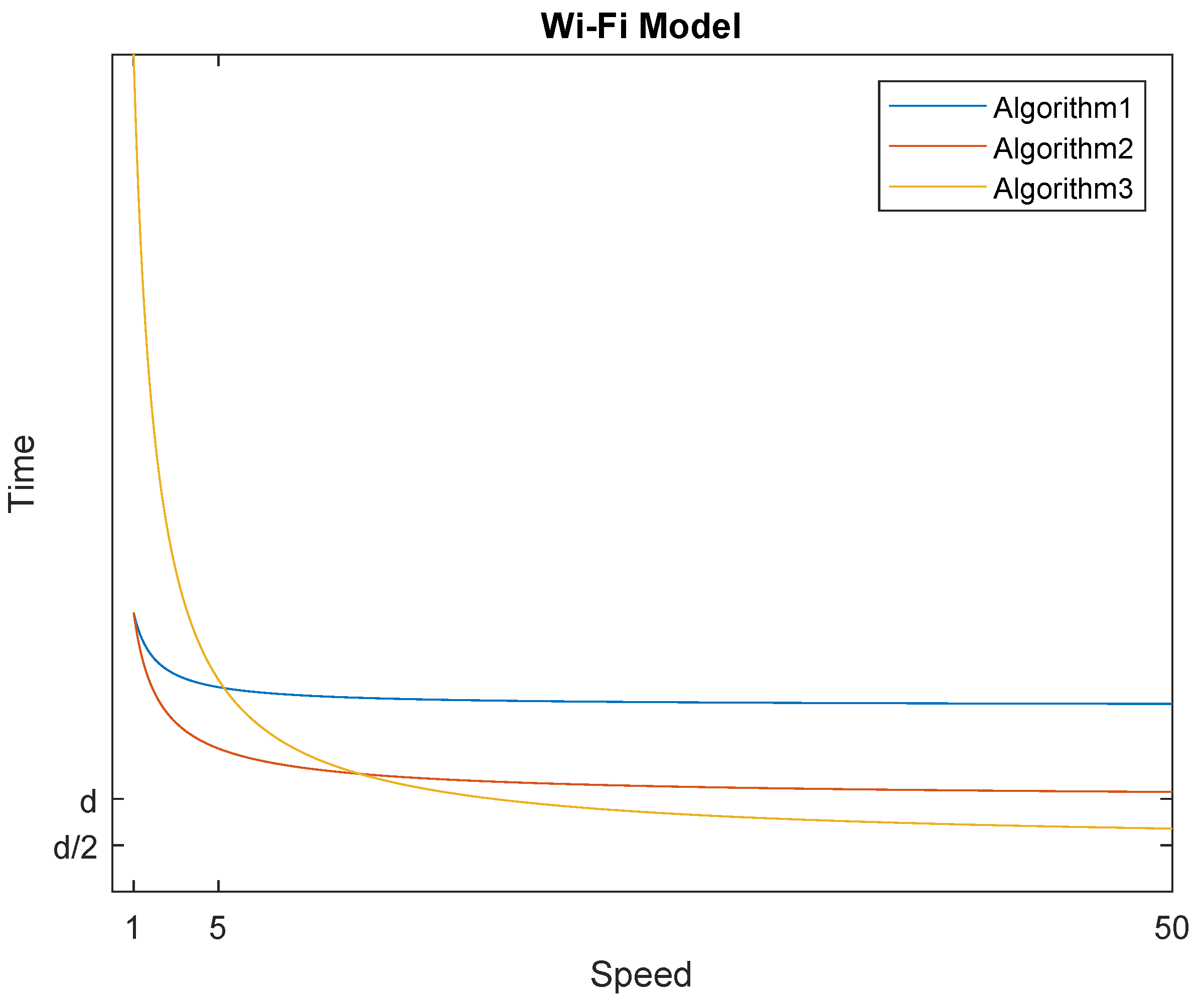
3. Evacuation in the Wireless (WiFi) Model

In this section we provide our main algorithms in the wireless communication model. In this model the two hikers can communicate instantaneously at any distance. Three algorithms will be considered and analyzed their evacuation time depends on the maximum speed v of the biker.

3.1. Opposite Direction with Max Speed

In Algorithm 2, the hiker and the biker move in opposite directions with their maximum speed, assuming that the biker moves with speed v. The one which finds the exit first will communicate with the other to proceed to the exit. Moreover, if it is the biker that found the exit first it returns the bike to a suitable position and shares it with the hiker. Details of the algorithm are as follows.

Algorithm 2: (OppDirectionWithMaxSpeedWiFi)

Theorem 1.

The evacuation time for Algorithm 2 in the WiFi model is at most$2d+\frac{d}{v}.$

Proof of Theorem 1.

Without loss of generality assume the hiker moves in the leftward and the biker in the rightward direction both starting from the origin. There are two cases to consider depending on whether the hiker or the biker finds the exit first.

Case 1: The exit is found by the biker.

When the biker finds the exit, which is at distance d from the origin, it has spent time $\frac{d}{v}$. The biker will communicate with the hiker, to come to the exit. Since the exit is found by the biker first, the biker can help the hiker by returning and dropping off the bike at some distance x away from the exit such that the hiker can pick it up and arrive to the exit at the same time as the other robot. It is easy to see that to find the distance x where the bike is dropped off, we need to solve the equation $\frac{x}{v}+x=d+\frac{d}{v}-x+\frac{x}{v}$. This leads to the solution $x=\frac{d}{2}+\frac{d}{2v}$. Hence the hiker which is at distance $\frac{d}{v}$ when the biker reaches the exit, will need $\frac{d}{v}$ to reach the origin, in addition to $d-x+\frac{x}{v}=\frac{d}{2}+\frac{d}{2v^2}$ to reach the exit. Therefore, the evacuation time will be $\frac{2d}{v}+\frac{d}{2}+\frac{d}{2v^2}$.

Case 2: The exit is found by the hiker.

When the hiker finds the exit which is at distance d to the left of the origin, the biker will be at distance $dv$ to the right of the origin. The hiker will communicate with the biker to come to the exit. The biker turns back and goes to the exit which takes additional time $d+\frac{d}{v}$. It follows that the evacuation time in this case will be $d+d+\frac{d}{v}=2d+\frac{d}{v}$.

Therefore, by combining the two cases above, we conclude that the evacuation time for this algorithm will be $max\left\{2d+\frac{d}{v},\frac{2d}{v}+\frac{d}{2}+\frac{d}{2v^2}\right\}$. This completes the proof of Theorem 1. □

3.2. Opposite Direction with Optimal Speed

Unlike Algorithm 2 in which the hiker and biker use their maximum speed, in the next Algorithm 3 the biker will not use its maximum speed v. Instead it will move with a specially chosen speed u which is less than v. The hiker or the biker which finds the exit first will communicate with the other which will then move towards the exit with its maximum speed. It turns out that the modified algorithm performs better than the previous one and it is optimal up to a certain maximum speed v. Assuming that $R_1$ is the hiker and $R_2$ is the biker, the algorithm will be as follows.

Algorithm 3: (OppDirectionWithOptimalSpeedWiFi)

Theorem 2.

The evacuation time for Algorithm 3 using the WiFi model is at most$\frac{3d+3vd+d\sqrt{v^2+26v+9}}{4v}$.

Proof of Theorem 2.

Assume that $R_1$ which is the hiker moves in the leftward direction and $R_2$, which is the biker, moves in the rightward direction. There are two cases to consider depending on who reaches the exit first.

Case 1: Hiker reaches the exit first.

The time needed by $R_1$ to reach the exit is d. At this point $R_2$ will be at distance $du$ away from the origin since it is moving with speed u. As mentioned in the algorithm, $R_2$ will use its maximum speed v on the way back. Thus, it needs $\frac{du}{v}$ to reach the origin and it will need additional time $\frac{d}{v}$ to join $R_1$ and reach the exit. Therefore, the evacuation time in this case will be

$$\begin{array}{c}\hfill T_1=d+\frac{du}{v}+\frac{d}{v}=\frac{dv+du+d}{v}\end{array}$$

Case 2: Biker reaches the exit first.

The time needed by $R_2$ to reach the exit is $\frac{d}{u}$. As soon as $R_2$ reaches the exit, it will inform $R_1$ immediately. At this point in time, $R_1$ will be at distance $\frac{d}{u}$ on the other side of the origin since it is moving with unit speed. $R_2$ will go back distance x to drop off the bike for $R_1$. The key point to find x is to have $R_2$ drop off the bike in a way that $R_1$ can pick it up and arrive at the same time as $R_2$. We know from Algorithm 2 that $R_2$ will not use its maximum speed and will move with speed u only until it reaches the exit. The only reason for not using its maximum speed before reaching the exit is to avoid having $R_1$ and $R_2$ farther apart from each other since this will increase the overall evacuation time. Thus when $R_2$ goes back to drop off the bike, it will use its maximum speed v. Based on that we have the following equation.

$$\begin{array}{cc}\hfill & x+\frac{x}{v}=d+\frac{d}{u}-x+\frac{x}{v}\hfill \end{array}$$

whose solution is $x=\frac{d}{2}+\frac{d}{2u}$. Substituting x in order to calculate the evacuation time $T_2$ yields:

$$\begin{array}{cc}\hfill T_2& =\frac{d}{u}+x+\frac{x}{v}\hfill \\ \hfill & =\frac{d}{u}+\frac{d}{2}+\frac{d}{2u}+\frac{d}{2v}+\frac{d}{2uv}\hfill \\ \hfill & =\frac{2dv+duv+dv+du+d}{2uv}\hfill \\ \hfill & =\frac{3dv+du+duv+d}{2uv}\hfill \end{array}$$

In order to find the best evacuation time, we need to find the best value of u which makes the maximum of $T_1$ and $T_2$ minimized given that $1\le u\le v$. This means that the objective is to minimize the following quantity

$$max\{T_2,T_2\}=max\left\{\frac{dv+du+d}{v},\frac{3dv+du+duv+d}{2uv}\right\}$$

(1)

In order to find the solution for (1), we determine the point of intersection of the evacuation time plots for $T_1$ and $T_2$. This will give the following:

$$\begin{array}{cc}\hfill \frac{u+v+1}{v}=\frac{3v+u+uv+1}{2uv}& \Rightarrow 2u^{2}v+2u{v}^2+2uv=3v^2+uv+u{v}^2+v\hfill \\ \hfill & \Rightarrow 2u^{2}v+(v^2+v)u-3v^2-v=0\hfill \end{array}$$

The last equation will have two roots, and choosing the positive one gives the following solution for u:

$$\begin{array}{cc}\hfill u& =\frac{1}{4v}(-v^2-v+\sqrt{v^4+2v^3+v^2-8v(-3v^2-v)}))\hfill \\ & =\frac{1}{4v}(-v^2-v+\sqrt{v^4+2v^3+v^2+24v^3+8v^2})\hfill \\ & =\frac{1}{4v}(-v^2-v+\sqrt{v^4+26v^3+9v^2})\hfill \\ \hfill & =\frac{1}{4}(-v-1+\sqrt{v^2+26v+9})\hfill \end{array}$$

In order to get the evacuation time T, we can substitute u in $T_1$ or $T_2$, we get the following:

$$\begin{array}{cc}\hfill T& =\frac{dv+du+d}{v}\hfill \\ \hfill & =\frac{1}{v}(dv+\frac{-dv-d+d\sqrt{v^2+26v+9}}{4}+d)\hfill \\ \hfill & =\frac{4dv-dv-d+d\sqrt{v^2+26v+9}+4d}{4v}\hfill \\ \hfill & =\frac{3d+3dv+d\sqrt{v^2+26v+9}}{4v}.\hfill \end{array}$$

This completes the proof of Theorem 2. □

3.3. Slower Imitates Faster

In the next Algorithm 4 the robots perform a “doubling zig-zag” strategy with different parameters. The biker is using a doubling strategy to search for the exit and moves a distance $2^k$ during the k-th iteration. The hiker is also using a doubling strategy but since it is moving with unit speed it will try to stay as close as possible to the biker. This can be achieved by having the hiker move a distance $\frac{2^k}{v}$ during the k-th iteration, since moving any further will cause the hiker to be farther away from the biker during the $(k+1)$-st iteration. Assuming that robot $R_1$ is the biker and robot $R_2$ is the hiker, the algorithm will be as follows.

Algorithm 4: (SlowerImitateFasterWiFi)

Theorem 3.

The evacuation time for Algorithm 4 using the WiFi model is at most$\frac{9d}{v}+\frac{d}{2}-\frac{d}{2v^2}.$

Proof of Theorem 3.

In this algorithm the biker uses a doubling strategy with maximum speed v. The hiker will follow the biker but will move $\frac{2^k}{v}$ in each iteration instead of $2^k$. The biker will reach the exit first then will communicate with the hiker to proceed to the exit. The biker will go back distance $\frac{d}{2}-\frac{d}{2v}$ to drop off the bike so that the hiker can pick it up on its way to the exit. We will justify why biker $R_1$ needs to move $\frac{d}{2}-\frac{d}{2v}$ after reaching the exit to leave the bike for hiker $R_2$.

After biker $R_1$ reaches the exit, there is no benefit to stay at the exit with the bike since hiker $R_2$ which is moving with unit speed can benefit from the bike to reach the exit faster. The key to find the distance x which is the distance between the exit and the point where the bike is dropped off is to have biker $R_1$, drop it off at a point such that when it goes back to the exit it will reach the exit at the same time as hiker $R_2$. If we consider that d is the distance from the origin to the exit and x is the distance from the exit to the point where biker $R_1$ drops off the bike, then we have $d-x+\frac{x}{v}=\frac{d}{v}+\frac{x}{v}+x$ which leads to $x=\frac{d}{2}-\frac{d}{2v}$. This will guarantee that when the biker drops off the bike at distance x, it will reach the exit at the same time as the hiker. Hence we guarantee that the bike is not kept unnecessarily with the robot which reaches the exit first.

Assume that the exit is found during the kth iteration, then $2^{k-2}<d\le 2^k$. We can calculate the evacuation time as follows:

$$\begin{array}{cc}\hfill T& =\frac{2·2^0}{v}+\frac{2·2^1}{v}+\cdots +\frac{2·2^{k-1}}{v}+d-x+\frac{x}{v}\hfill \\ \hfill & =\frac{2(2^k-1)}{v}+d-x+\frac{x}{v}\hfill \\ \hfill & =\frac{2^{k+1}}{v}-\frac{2}{v}+d-\frac{d}{2}+\frac{d}{2v}+\frac{d}{2v}-\frac{d}{2v^2}\hfill \\ \hfill & =\frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{2}+\frac{d}{v}-\frac{d}{2v^2}\hfill \\ \hfill & \le 2^3.\frac{2^{k-2}}{v}-\frac{2}{v}+\frac{d}{2}+\frac{d}{v}-\frac{d}{2v^2}\hfill \\ \hfill & \le \frac{8d}{v}-\frac{2}{v}+\frac{d}{2}+\frac{d}{v}-\frac{d}{2v^2}\hfill \\ \hfill & \le \frac{9d}{v}+\frac{d}{2}-\frac{d}{2v^2}-\frac{2}{v}\hfill \\ \hfill & \le \frac{9d}{v}+\frac{d}{2}-\frac{d}{2v^2}\hfill \end{array}$$

This completes the proof of Theorem 3. □

Figure 1 depicts and compares the performance of the three algorithms presented for the WiFi model.

4. Evacuation in the Face-to-Face (F2F) Model

In this section we provide our main algorithms in the face-to-face communication model. Recall that in this model the hikers can exchange messages only if they occupy the same location at the same time.

4.1. Slower Pursues Faster

In the first Algorithm 5, we assume that the hiker will follow the biker. Since the biker is using a “doubling zig-zag” strategy, during any iteration, let us say the k-th one, the biker will reverse the direction after reaching $2^k$ and will meet the hiker at some point $X_k$. At the meeting point the hiker will reverse its direction. We notice from this that the hiker is following a deterministic strategy specified through a sequence of points $X_1,X_2,\dots ,X_k,\dots$ (to be defined later), where each $X_k$ represents the meeting point for the hiker and the biker during the k-th iteration. In other words, the biker will follow a doubling strategy with factor $2^k$ while the hiker will follow the sequence $X_1,X_2,\dots ,X_k,\dots$ above. When the biker reaches the exit, it will go back a certain distance x, which will be determined later, to drop off the bike and then will return back walking toward the exit.

In the algorithm below we use the parameters $a:=\frac{1-v}{1+v}$, $b:=\frac{1}{1+v}$. Further, we assume that $R_1$ is the biker and $R_2$ is the hiker.

Algorithm 5: (SlowerPursueFasterF2F)

Theorem 4.

The evacuation time for Algorithm 5 using the F2F model is at most$\frac{9d}{v}+d-\frac{5d}{8v^2}.$

Proof of Theorem 4.

In order to find the sequence $\{X_1,X_2\cdots X_k\}$, we argue as follows. During the 1st iteration, in order to calculate $X_1$, we know that the biker will move $2^0$ to reach the peak point and then will come back $2^0-X_1$ with speed v to reach point $X_1$ while the hiker will move $X_1$ with unit speed during the same time. Given that $a=\frac{1-v}{1+v}$ and $b=\frac{1}{1+v}$, we have the following:

$$\begin{array}{c}\hfill X_1=\frac{2^0}{v}+\frac{2^0}{v}-\frac{X_1}{v}\Rightarrow X_1=\frac{2}{1+v}=2·b\end{array}$$

During the 2nd iteration we have the following:

$$\begin{array}{cc}\hfill & X_1+X_2=\frac{1}{v}(X_1+2+2-X_2)\hfill \\ \hfill & \Rightarrow X_2=\frac{4}{1+v}+\frac{1-v}{1+v}·X_1=a·X_1+2^2·b\hfill \end{array}$$

Since $X_2=a·X_1+2^2·b$, then for the kth iteration we have:

$$\begin{array}{c}\hfill X_k=a·X_{k-1}+2^k·b\end{array}$$

Replacing $X_{k-1}=a·X_{k-2}+b·2^{k-1}$ in the above equation gives

$$\begin{array}{c}\hfill X_k=a(a·X_{k-2}+b·2^{k-1})+2^k·b\end{array}$$

Similarly replacing $X_{k-2}=a·X_{k-3}+b·2^{k-2}$ gives

$$\begin{array}{c}\hfill X_k=a^3·X_{k-3}+a^2·2^{k-2}·b+a·b·2^{k-1}+2^k·b\end{array}$$

Recursing down to $X_1$ leads to the following calculation:

$$\begin{array}{cc}\hfill X_k& =b·2^k\left({\left(\frac{a}{2}\right)}^0+\cdots +{\left(\frac{a}{2}\right)}^{k-1}\right)\hfill \\ \hfill & =\frac{b·2^k(1-{(\frac{a}{2})}^k)}{1-\frac{a}{2}}\hfill \\ \hfill & =\frac{2·b(2^k-a^k)}{2^k(2-a)}·2^k·b\hfill \\ \hfill & =\frac{2·b(2^k-a^k)}{2-a}\hfill \end{array}$$

Assume that the exit is found during the kth iteration of the algorithm. Before writing down the evacuation time, let us find the distance x away from the exit, where the bike will be dropped off by the biker. We know that the biker and the hiker will meet at each entry of the sequence and eventually they will meet at $X_{k-1}$.

• Define $T_1$ to be the time needed by the biker to go to the exit from the point of intersection between the the biker and the hiker at $X_{k-1}$ then to return distance x to drop off the bike and subsequently go back to the exit. Thus $T_1$ can be defined as follows:

  $$T_1=\frac{1}{v}(X_{k-1}+x+d)+x.$$
• Define $T_2$ to be the time needed by the hiker to go from the point of intersection between the hiker and the biker at $X_{k-1}$ to the exit while picking up the bike on its way. Thus $T_2$ can be defined as follows:

  $$T_2=X_{k-1}+d-x+\frac{x}{v}.$$

The best thing that the biker can do is to drop off the bike and arrive at the same time to the exit with the hiker who will pick up the bike on its way. This can be achieved by having $T_1=T_2$. In turn, this yields

$$\begin{array}{cc}\hfill & \frac{1}{v}(X_{k-1}+x+d)+x=X_{k-1}+d-x+\frac{x}{v}\hfill \\ \hfill & \Rightarrow x=\frac{1}{2}(X_{k-1}+d)-\frac{1}{2v}(d+X_{k-1})\hfill \end{array}$$

Thus, the evacuation time T can be written as follows:

$$\begin{array}{c}\hfill T=\frac{1}{v}(2·2^0+2·2^1+\cdots +2·2^{k-1})+\frac{d}{v}+\frac{x}{v}+x\end{array}$$

Replacing the value of x which was calculated above gives:

$$\begin{array}{cc}\hfill T& =\frac{2}{v}(2^k-1)+\hfill \\ \hfill & \frac{d}{v}+\frac{d}{2v}-\frac{d}{2v^2}+\frac{d}{2}-\frac{d}{2v}+\frac{1}{2v}{X}_{k-1}-\frac{1}{2v}{X}_{k-1}+\frac{1}{2}{X}_{k-1}-\frac{1}{2v^2}{X}_{k-1}\hfill \\ & =\frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2}-\frac{d}{2v^2}+\left(\frac{1}{2}-\frac{1}{2v^2}\right)X_{k-1}\hfill \end{array}$$

Now recall that $X_{k-1}=\frac{2b(2^{k-1}-a^{k-1})}{2-a}$, where $a=\frac{1-v}{1+v}$ and $b=\frac{1}{1+v}$. Since $-1<a<0$ and $0<b\le \frac{1}{2}$ it is obvious that $X_{k-1}\le \frac{1}{2}(2^{k-1}+1)=2^{k-2}+\frac{1}{2}$. Moreover, knowing that $2^{k-2}<d\le 2^k$, the evacuation time T can be simplified as follows:

$$\begin{array}{cc}\hfill T& \le \frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2}-\frac{d}{2v^2}+(\frac{1}{2}-\frac{1}{2v^2})(2^{k-2}+\frac{1}{2})\hfill \\ \hfill & \le \frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2}-\frac{d}{2v^2}+2^{k-3}+\frac{1}{4}-\frac{2^{k-2}}{2v^2}-\frac{1}{4v^2}\hfill \\ \hfill & \le \frac{8d}{v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2}-\frac{d}{2v^2}+\frac{d}{2}+\frac{1}{4}-\frac{d}{8v^2}-\frac{1}{4v^2}\hfill \\ \hfill & \le \frac{9d}{v}+d-\frac{5d}{8v^2}-\frac{1}{4v^2}+\frac{1}{4}-\frac{2}{v}\hfill \\ \hfill & \le \frac{9d}{v}+d-\frac{5d}{8v^2}\hfill \end{array}$$

This completes the proof of Theorem 4. □

4.2. Slower Evacuation Close to Exit without Aid

In the second Algorithm 6, the biker uses a “doubling zig-zag” strategy with its maximum speed v, while the hiker will try to be as close as possible to the biker. In order to achieve that, the hiker will use a doubling strategy as well but will use its own “expansion” factor. The factor will be determined based on the fact that both the hiker and the biker should meet at a specific point during each iteration. These meeting points will form a sequence whose k-th element during iteration k is taken to be equal to $\frac{2^{k+2}}{3v+1}$. During the last iteration, when the biker finds the exit, the hiker will eventually reach the meeting point and will not find the biker there. This will let it know that it should keep going toward the exit. Assuming that initially $R_1$ is the biker and $R_2$ is the hiker, the algorithm will be as follows:

Algorithm 6: (SlowerEvacuationCloseToExitWithoutAidF2F)

Theorem 5.

The evacuation time for Algorithm 6 using the F2F model is at most$\frac{3d{v}^3+63d{v}^2+15dv-9d}{2v^2(3v+1)}$.

Proof of Theorem 5.

The biker is using a doubling strategy and is moving $2^k$ during each iteration k. The hiker will use a doubling strategy as well and it will follow the biker. In order to keep the hiker as close as possible to the biker, we must find the sequence that the hiker should follow. We assume that both the hiker and the biker meet at a certain point $X_k$ and that they are willing to meet at point $X_{k+1}$ at the same time without waiting for one another, taking into consideration that $X_{k+1}=2X_k$. The sequence can be calculated as follows:

$$\begin{array}{cc}\hfill & X_k+X_{k+1}=\frac{1}{v}(X_k+2^{k+1}+2^{k+1}-X_{k+1})\hfill \\ \hfill & \Rightarrow X_k+2X_k=\frac{1}{v}(X_k+2^{k+1}+2^{k+1}-2X_k)\hfill \\ \hfill & \Rightarrow \frac{3v+1}{v}{X}_k=\frac{2^{k+2}}{v}\hfill \\ \hfill & \Rightarrow X_k=\frac{2^{k+2}}{3v+1}\hfill \end{array}$$

We have the sequence $\{X_0,X_1,\dots ,X_k\}$ given that $X_k=\frac{2^{k+2}}{3v+1}$ where $k\ge 1$. Each of the hiker and the biker will use its own doubling strategy. During each iteration, they will meet on both sides at specific points which are elements of the above sequence. During the kth iteration, when the biker reaches the exit, it will move back distance x to drop off the bike such that the hiker can pick it up and reach the exit at the same time as itself. The distance x can be calculated as follows: $\frac{d}{v}+\frac{1}{v}·X_{k-1}+\frac{x}{v}+x=d+X_{k-1}-x+\frac{x}{v}.$ Substituting $X_{k-1}$ this becomes $\frac{d}{v}+\frac{2^{k+1}}{v(3v+1)}+\frac{x}{v}+x=d+\frac{2^{k+1}}{3v+1}-x+\frac{x}{v}$ Solving for x, the last equation yields $x=\frac{d}{2}-\frac{d}{2v}+\frac{2^k(v-1)}{v(3v+1)}$. Assuming that $2^{k-2}<d\le 2^k$ and replacing x which was calculated above, the evacuation time T can be computed as follows:

$$\begin{array}{cc}\hfill T& =\frac{1}{v}(2·2^0+2·2^1+\cdots +2·2^{k-1})+\frac{d}{v}+\frac{x}{v}+x\hfill \\ \hfill & =\frac{2}{v}(2^k-1)+\frac{d}{v}+\frac{x}{v}+x\hfill \\ \hfill & =\frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{x}{v}+x\hfill \\ \hfill & =\frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2v}-\frac{d}{2v^2}+\frac{2^k(v-1)}{v^2(3v+1)}+\frac{d}{2}-\frac{d}{2v}+\frac{2^k(v-1)}{v(3v+1)}\hfill \\ \hfill & \le \frac{16d}{2v}-\frac{2}{v}+\frac{d}{v}+\frac{d}{2}-\frac{d}{2v^2}+\frac{4d(v-1)}{v^2(3v+1)}+\frac{4d(v-1)}{v(3v+1)}\hfill \\ \hfill & \le \frac{18d}{2v}+\frac{d}{2}-\frac{d}{2v^2}+\frac{4d(v-1)}{v^2(3v+1)}+\frac{4d(v-1)}{v(3v+1)}-\frac{2}{v}\hfill \\ \hfill & \le \frac{54d{v}^2+18dv+3d{v}^3+d{v}^2-3dv-d+8vd-8d+8d{v}^2-8dv}{2v^2(3v+1)}-\frac{2}{v}\hfill \\ \hfill & \le \frac{3d{v}^3+63d{v}^2+15dv-9d}{2v^2(3v+1)}-\frac{2}{v}\hfill \\ \hfill & \le \frac{3d{v}^3+63d{v}^2+15dv-9d}{2v^2(3v+1)}\hfill \end{array}$$

This completes the proof of Theorem 5. □

4.3. Nearest Meeting to Exit

In order to reduce the evacuation time, it is more suitable for the biker to search for the exit while the hiker follows a “doubling zig-zag” strategy that will keep it as close as possible to the biker and will expedite its travel time to the exit during the last iteration of the evacuation algorithm. In order to achieve that, the purpose of the next algorithm will be to find this deterministic doubling strategy that the hiker should follow. Assuming that $R_1$ is the biker and $R_2$ is the hiker, Algorithm 7 will be as follows.

Algorithm 7: (EvacuatingWithBikeF2F)

Theorem 6.

The evacuation time for Algorithm 7 using the F2F model is upper bounded by

$$\begin{array}{cc}\hfill & 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{5v^2-12v-1}{v(v-1)(3v-1)}dif1<v\le \frac{6+\sqrt{41}}{5}\hfill \\ \hfill & 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{4(5v^2-12v-1)}{v(v-1)(3v-1)}dif\frac{6+\sqrt{41}}{5}\le v\hfill \end{array}$$

Proof of Theorem 6.

Let us consider the sequence: $X=\{X_1,X_2,X_3,\cdots ,X_k\}$, where $X_k=r·X_{k-1}$. The purpose is to find the best value of r which is the factor related to the doubling strategy that the hiker follows. Definitely the best meeting point would be the peak point reached by the hiker during each iteration, since it will be the closest to the exit. Assume that both the hiker and the biker meet at some point $X_{k-1}$ during the $k-1$ iteration and they are willing to meet during the k-th iteration without waiting for one another, then we have:

$$\begin{array}{cc}\hfill & X_{k-1}+X_k=\frac{1}{v}·(2^{k-1}-X_{k-1})+\frac{2^{k-1}}{v}+\frac{X_k}{v}\hfill \end{array}$$

and after substituting $X_k$

$$\begin{array}{cc}\hfill & X_{k-1}+r·X_{k-1}=\frac{1}{v}·(2^{k-1}-X_{k-1})+\frac{2^{k-1}}{v}+\frac{r}{v}·X_{k-1}.\hfill \end{array}$$

In turn, this implies

$$\begin{array}{cc}\hfill & (r+1)·X_{k-1}=\frac{2^k}{v}+\frac{r-1}{v}·X_{k-1}\hfill \\ \hfill & \Rightarrow r·v·X_{k-1}+v·X_{k-1}-r·X_{k-1}+X_{k-1}=2^k\hfill \\ \hfill & \Rightarrow X_{k-1}=\frac{2^k}{r·v+v-r+1}\hfill \end{array}$$

Similarly we have $X_k=\frac{2^{k+1}}{r·v+v-r+1}$. Consider $X_k=r·X_{k-1}$, then we can deduce that $r=2$. Substituting $r=2$ gives $X_k=\frac{2^{k+1}}{3v-1}$. So we conclude that the hiker will use doubling strategy and will follow the sequence $X=\{\frac{4}{3v-1},\frac{8}{3v-1},\cdots ,\frac{2^{k+1}}{3v-1}\}$. Assume that $R_1$ is the biker which moves with speed v and $R_2$ is the hiker which moves with unit speed. Consider $d=\frac{2^{k+1}}{3v-1}+e$ where $e\ge 0$. Definitely $R_1$ will reach the exit before $R_2$. Since the exit is at distance e from the meeting point, then from that point on, $R_1$ needs time $\frac{e}{v}$ to reach the exit. During this time, $R_2$ will be at distance e on the other side of the meeting point. Therefore, when $R_1$ reaches the exit, $R_2$ will be at distance $e+\frac{e}{v}=e\frac{v+1}{v}$ away from the exit. The distance z that hiker $R_2$ moves from the point where $R_1$ reaches the exit till the point it meets $R_1$ will be as follows:

$$\begin{array}{cc}\hfill & z=\frac{e(v+1)}{v^2}+\frac{z}{v}\hfill \\ \hfill & \Rightarrow \frac{z(v-1)}{v}=\frac{e(v+1)}{v^2}\hfill \\ \hfill & \Rightarrow z=\frac{v+1}{v-1}·\frac{e}{v}\hfill \end{array}$$

Therefore, when biker $R_1$ reaches hiker $R_2$ to inform it about the exit, $R_2$ will be far from the exit by a distance $x=\frac{v+1}{v-1}·\frac{e}{v}+e\frac{v+1}{v}$. Now it is required to find at what distance y away from the exit should biker $R_1$ drop off the bike so that hiker $R_2$ can pick it up and proceed to the exit and reach it at the same time as $R_1$. After we find out the distance y, we will go back to create the algorithm for the two hikers with a bike model. In order to find out the distance y we have the following:

$$\begin{array}{cc}\hfill & \frac{x}{v}-\frac{y}{v}+y=x-y+\frac{y}{v}\hfill \\ \hfill & \Rightarrow \frac{x}{v}-\frac{y}{v}+2y=x+\frac{y}{v}\hfill \\ \hfill & \Rightarrow y(2v-2)=x(v-1)\hfill \\ \hfill & \Rightarrow y=\frac{x(v-1)}{2(v-1)}=\frac{x}{2}\hfill \end{array}$$

The evacuation time T can be calculated as follows:

$$\begin{array}{cc}\hfill T& =\frac{2·2^0+2·2^1+\cdots +2·2^{k-1}}{v}+\frac{d}{v}+\frac{x}{v}+\frac{y}{v}+y\hfill \\ \hfill & =\frac{2(2^k-1)}{v}+\frac{d}{v}+\frac{x}{v}+\frac{x}{2v}+\frac{x}{2}\hfill \\ \hfill & =\frac{2^{k+1}}{v}-\frac{2}{v}+\frac{d}{v}+\frac{3}{2v}(e+\frac{e}{v}+\frac{v+1}{v-1}·\frac{e}{v})+\frac{1}{2}(e+\frac{e}{v}+\frac{v+1}{v-1}·\frac{e}{v})\hfill \end{array}$$

Since $d=e+\frac{2^{k+1}}{3v-1}$, replacing $\frac{2^{k+1}}{v}=3d-3e-\frac{d}{v}+\frac{e}{v}$ in the above equation gives the following:

$$\begin{array}{cc}\hfill T& =3d-\frac{d}{v}-3e+\frac{e}{v}-\frac{2}{v}+\frac{d}{v}+\frac{3e}{2v}+\frac{3e}{2v^2}+\frac{3e(v+1)}{2v^2(v-1)}+\frac{e}{2}+\frac{e}{2v}+\frac{e(v+1)}{2v(v-1)}\hfill \\ \hfill & =3d-\frac{2}{v}+\frac{3e}{v}-\frac{5e}{2}+\frac{3e}{2v^2}+\frac{3ev+3e+e{v}^2+ev}{2v^2(v-1)}\hfill \\ \hfill & =3d-\frac{2}{v}+\frac{3e}{v}-\frac{5e}{2}+\frac{3e}{2v^2}+\frac{e{v}^2+4ev+3e}{2v^2(v-1)}\hfill \\ \hfill & =3d-\frac{2}{v}+e·\frac{6v^2-6v-5v^3+5v^2+3v-3+v^2+4v+3}{2(v-1)v^2}=\hfill \\ \hfill & =3d-\frac{2}{v}-e·\frac{5v^2-12v-1}{2v(v-1)}\hfill \\ \hfill & =3d-\frac{2}{v}-\frac{5v^2-12v-1}{2v(v-1)}(d-\frac{2^{k+1}}{3v-1})\hfill \\ \hfill & =3d-d·\frac{5v^2-12v-1}{2v(v-1)}+2^k\frac{5v^2-12v-1}{v(v-1)(3v-1)}-\frac{2}{v}\hfill \end{array}$$

There are two cases to consider here:

Case 1: $1<v\le \frac{6+\sqrt{41}}{5}$.

Since $5v^2-12v-1\le 0$ and $d\le 2^k$ we have that

$$\begin{array}{cc}\hfill T& \le 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{5v^2-12v-1}{v(v-1)(3v-1)}d-\frac{2}{v}\hfill \\ \hfill & \le 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{5v^2-12v-1}{v(v-1)(3v-1)}d\hfill \end{array}$$

Case 2: $\frac{6+\sqrt{41}}{5}\le v$.

Since $0\le 5v^2-12v-1$ and $2^{k-2}\le d$ we conclude that

$$\begin{array}{cc}\hfill T& \le 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{5v^2-12v-1}{v(v-1)(3v-1)}·2^2·2^{k-2}-\frac{2}{v}\hfill \\ \hfill & \le 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{4(5v^2-12v-1)}{v(v-1)(3v-1)}d-\frac{2}{v}\hfill \\ \hfill & \le 3d-\frac{5v^2-12v-1}{2v(v-1)}d+\frac{4(5v^2-12v-1)}{v(v-1)(3v-1)}d\hfill \end{array}$$

This completes the proof of Theorem 6. □

Figure 2 depicts and compares the performance of the three algorithms presented for the face-to-face model.

5. Lower Bounds

In this section we establish lower bounds on the competitive ratio in the WiFi and F2F models. Using bike sharing, first we prove a tight bound on the evacuation time when the robots know in which direction from the origin the exit is. Note that Theorem 7 can readily be used to compute the competitive ratio of the algorithms presented in Section 3 and Section 4.

Theorem 7.

If the direction of the exit is known to the robots then evacuation time is$\frac{v+1}{2v}·d$and this is optimal.

Proof of Theorem 7.

Consider the algorithm whereby robot $R_1$ rides the bike for a distance x, releases the bike at x and continues by walking the remaining distance $d-x$, while robot $R_2$ walks for a distance x, picks up the bike at x and rides it for the remaining distance $d-x$. Note that robot $R_1$ reaches the exit at time $\frac{x}{v}+d-x$, while robot $R_2$ reaches the exit at time $x+\frac{d-x}{v}$. For the two robots to arrive at the same time it is required that $\frac{x}{v}+d-x=x+\frac{d-x}{v}$, which solves for $x=\frac{d}{2}$. Hence, the algorithm ensures that the two robots evacuate in time $\frac{1}{2}+\frac{1}{2v}=\frac{v+1}{2v}$.

Next we prove that the evacuation time above is optimal. If the robots never share the bike then the evacuation time will be d, which is also the arrival time of the slowest robot. So we may assume the robots share the bike. Let $t_i$ be the termination time for robot $R_i$ in an optimal algorithm. Let $x_i$ be the distance that robot $R_i$ rides the bike. Without loss of generality let $R_1$ be the robot that fetches the bike from the origin. Clearly, this takes time $\frac{x_1}{v}+d-x_1$. Therefore $t_1\ge \frac{x_1}{v}+d-x_1$. Similarly, for robot $R_2$ we have that $t_2\ge \frac{x_2}{v}+d-x_2$. It follows that

$$\begin{array}{cc}\hfill max\{t_1,t_2\}& \ge \frac{1}{2}\left(\frac{x_1}{v}+d-x_1+\frac{x_2}{v}+d-x_2\right)\hfill \\ \hfill & =d-\frac{x_1}{2}-\frac{x_2}{2}+\frac{x_1}{2v}+\frac{x_1}{2v}\hfill \\ \hfill & =d-(x_1+x_2)\frac{v-1}{2v}\hfill \\ \hfill & \ge d-\frac{v-1}{2v}·d=\frac{v+1}{2v}·d,\hfill \end{array}$$

where in the last inequality we used the fact that $x_1+x_2\le d$, since by assumption only one robot can ride the bike at a time. This completes the proof of Theorem 7. □

Using Theorem 7 we can prove the following result.

Theorem 8.

The evacuation time of any algorithm in either the WiFi or F2F model is bounded from below by$min\left\{\frac{d}{v}+\frac{v+1}{2v}·d,d+\frac{v+1}{v}·d\right\}.$

Proof of Theorem 8.

Assume the two robots are starting at the origin and that the exit is placed at one of the two locations $\pm d$ which are unknown to the robots. Lets call the points $\pm d$ endpoints of the interval $[-d,+d]$. Without loss of generality assume that $-d$ is the first endpoint visited by a robot.There are two cases to consider depending on who is visiting this endpoint first.

Case 1: The biker visits $-d$ first.

To arrive at the endpoint $-d$ the biker has already spent time at least $\frac{d}{v}$ since he travels with speed v. At the time the biker arrives at $-d$ the hiker may be located either in the subinterval $[-d,0]$ or in the subinterval $[0,+d]$. There are two subcases to consider depending on which of the two subintervals the hiker is located

• If the hiker is located in the interval $[-d,0]$ then the adversary places the exit at $+d$ in which case by Theorem 7 the evacuation time will be at least $\frac{d}{v}+\frac{v+1}{2v}·d$.
• If the hiker is located in the interval $[0,+d]$ then the adversary places the exit at $-d$ in which case again by Theorem 7 the evacuation time will be at least $\frac{d}{v}+\frac{v+1}{2v}·d$.

Therefore regardless of the position of the hiker the evacuation time in this case is at least $\frac{d}{v}+\frac{v+1}{2v}·d$.

Case 2: The hiker visits $-d$ first.

To arrive at the endpoint $-d$ the hiker has already spent time d since he travels with speed v. As before, the adversary will place the exit at the other endpoint $+d$. Unaided from the bike the hiker will take additional time $2d$ to arrive at the exit which is located at $+d$. However, in the wireless model the hiker can announce the exit has been found and therefore the two robots can share the bike to arrive at the exit $+d$. In view of Theorem 7 this takes additional time at least $\frac{v+1}{2v}·2d=\frac{v+1}{v}·d$. Hence, in this case a lower bound on the evacuation time is $d+\frac{v+1}{v}·d$.

Combining the two cases completes the proof of Theorem 8. □

6. Conclusions

We proposed several evacuation algorithms in the wireless and face-to-face models. For each communication model we presented three algorithms which take advantage of the existence of the bike, a limited resource which can increase the search speed of the system of two robots. The resulting trajectories of the robots are specially designed so as to share the bike and ultimately reduce the overall evacuation time. We also discussed lower bounds.

The problem investigated is of theoretical nature and helps illuminate the trade offs between communication, and search time in search with mobile agents. Our study gives rise to several challenging open problems. For two robots, one could consider the problem when the speed of the bike depends on the hiker riding it. The case of multiple hikers and multiple bikes (not necessarily the same number) has never been investigated before. Additionally, one could also consider the case of faulty robots (crash or Byzantine). It would also be interesting to investigate other search domains such as stars and cycles or robots with reduced and/or enhanced capabilities.