Abstract
End-user devices and applications (data locations) are becoming more capable and user friendly and are used in various Health Information Systems (HIS) by employees of many health organizations to perform their day to day tasks. Data locations are connected via the internet. The locations have relatively good information security mechanisms to minimize attacks on and through them in terms of technology. However, human factors are often ignored in their security echo system. In this paper, we propose a human factor framework merged with an existing technological framework. We also explore how human factors affect data locations via linear regression computations and rank data location vulnerability using collaborative filtering. Our results show that human factors play a major role in data location breaches. Laptops are ranked as the most susceptible location and electronic medical records as the least. We validate the ranking by root mean square error.
1. Introduction
There is an ever-increasing use of diverse computing devices in the generation and use of health data in digital and non-digital forms. The result of this is a huge amount of personal health data stored in different digital and non-digital formats with different Health information systems (HIS). Health data containing protected health information (PHI) have now become a gold mine for cybercriminals [1]. The security of a HIS must deal with the protection of personal and medical data from cyber attacks. In doing so, it must ensure that it provides some basic security characteristics such as confidentiality, integrity, availability and non repudiation of health data. It is common to find the use of security and privacy as synonyms. Even though there is an intersection between the two, they are technically different.
- Security, according to Conger and Landry [2], is a condition of safeguarding data against danger or loss and is typically associated with confidentiality, integrity, availability and non-repudiation. Confidentiality is the assurance that data or information is not disclosed to unauthorized individuals. It is essential to clarify that confidentiality is different from privacy. Access to data or information is granted or denied based upon authorization. Hence, data or information may be confidential but not private [2]. The accuracy of data or information is what will constitute integrity, including technological controls put in place to protect against unauthorized modification or destruction. Therefore, data or information may be private but may not have integrity because it may be modified or deleted [3]. The timely and reliable access to data or information services under restrictions for authorized users only is referred to as availability [2,3]. Availability may probably be considered as the most antithetical to privacy. Making data or information available makes it public, not private [2]. The assurance that the sender of data or information is provided with proof of delivery, and the recipient is also being provided with proof of the sender’s identity, is known as non-repudiation. It is a condition where neither can later deny having processed the data [2].
- To manage risk effectively, systems must be designed to depend on confidential and preferably anonymous incident monitoring processes that record the individual, task, situational, and organizational factors connected with incidents and near misses.
- Privacy has many faces and can be defined in many ways. It is the safeguarding of a user’s identity and personal data. Privacy generally applies to keeping secret anything an individual does not want to be known, such as a person’s location and personal data. The rationale is to allow individuals, groups, or institutions to determine for themselves when, how, and what data or information about them may be communicated to others [2].
There are a lot of privacy concerns surrounding personally identifiable information, which has become a major challenge for medical practitioners. There have been numerous technologies in the areas of encryption, data masking, and authentications to preserve data privacy while making it available only to the authorized persons [4,5]. However, information security is not about technology alone, but also about people. Advances made in technological armory have become very impressive on one hand, and on the other hand, human factors have been the staging area for information security attacks. For any security system to be designed and deployed successfully, it must also rely on people. Human factors have played a critical role in the majority of the information security incidents in organizations and yet research into human factors with regard to information security remains neglected [6]. Various human factors have the ability to deeply shape the management of information security in an organization, irrespective of any sophisticated technology at play [7]. Human factors are suspected to be at play in most information security incidents in organizations [8]. In examining human factors in information security, it is imperative not to overlook end-user devices or media with the capability of storing health data in one form or the other. In this paper, we refer to user-devices or applications as data locations. Our use of data locations is not limited to only the aforementioned, but also to papers or films.
This paper seeks to contribute to the following:
- To propose a human factor framework that merges existing information security technological framework with human factors.
- To explore the extent to which human factors aid data breaches in various data locations.
- To investigate the most vulnerable data locations as a result of human factors by ranking them using collaborative filtering.
The rest of the paper covers the literature review in Section 2, the proposed human factor framework in Section 3, data classification in Section 4, characterization of breached data locations in Section 5, and the results of the experiment in Section 6. Thenm the discussion and conclusion are Section 7 and Section 8, respectively.
2. Literature Review
2.1. Human Loopholes
Over the years, there have been different models or frameworks aimed at solving some of the issues related to human loopholes concerning information security. One such framework or model is a conceptual goal-modeling framework by Alavi et al. [9], that provides an understanding of the things or forces that may promote information security posture and satisfaction of information Security Management System (ISMS) goals in the context of an organization. This goal model contributes to the risk of migration and the effectiveness of the Information Security Management System (ISMS) in an organization. Even though this work underlines the importance of understanding some of the main human factors for effective ISMS, it does not provide the generalized framework across organizational context in real-world cases. The framework does not also provide any expansion in information security assurance and the return on investment and their concepts. Alhogail et al. [10] conceptualized an information security culture framework, which seeks to provide a base for organizations to make an effective information security culture. The framework is designed to protect information assets and its application improves employee behavior and their interactions with information assets. This in turn leads to a positive impact and protects against information security threats posed by insider. This framework serves as a guide to the many issues that can be considered as cultural and improves employee values, assumptions, and knowledge, to help the organization achieve its objectives while reducing economic loss as a result of internal information security threats. The framework can also be used to identify vulnerabilities and weaknesses and corrective actions can be taken. The frameworkm however, needs application with several case studies to provide solid evidence of the theoretical framework.
Liginlal et al. [11] analyzed the significance of human error as a cause of privacy breaches. Their work being an empirical study, a framework for error management, showed that privacy breach incidents were as a result of two things, slips and mistakes. There has been a steady increase in slips and mistakes which has led to a steady increase in malicious attacks, mostly in public firms. Their work provides evidence of human mistakes in information processing constituting the highest percentage of errors. There needs to be an urgent enforcement of very effective organizational policies geared towards reducing human mistakes during the information processing stage. Their results were based on secondary data and so there exists the possibility that not all privacy breach incidents were reported publicly.
Evans et al. [12] also evaluated human factor issues and proposed a novel technique for evaluating human error-related information security incidents. From their results and discussions, they believed that organizations could benefit from the concept of embedding the description of a human error-related information security incident, defined as human factors, because the majority of reported information security incidents pertain to human error. Thus, they proposed the Human Error Assessment and Reduction Technique (HEART) which can be used to analyze human error related incidents in information security. The study showed that the information security community needed to address the numerous incidents and breaches occurring regularly and the human-related incidents to it must be understood. A reduction in human error is significant in reducing the amount of information security incidents being witnessed on a regular basis.
2.2. Collaborative Filtering
Collaborative filtering is one of the most prevent techniques in Recommender Systems [13,14,15]. This typically makes a collection of past user behavior and makes a rating prediction based on the similarity between behavioral patterns of users [13]. Collaborative filtering follows two approaches:
- Neighborhood Model is a predictive model that uses the similarity of users or items [13,16]. This is utilizes a user-based algorithm [16] and item-based algorithm [13].
- Latent Factor is a learning model on hidden patterns from ratings observed using matrix factorization techniques [17,18]. Such a well established technique is the Single Value Decomposition (SVD) [13,19,20,21,22].
The benefit of using collaborative filtering emanates from the concepts that people often get the best recommendations from someone with a similar taste to theirs. The recommendation system can also be based on the similarity between items determined by using the rating given to items by users. This approach helps solve issues associated with user-based collaborative filtering, when the system has many items with fewer items rated [15]. In this paper, data breach incidents underpinned by human factors are computed as recommendations and data locations where these breaches took place as items, resulting in the TOP-N vulnerable data locations.
2.3. Ranking-Oriented Collaborative Filtering
Lately, a great deal of attention has been given to developing effective techniques for retrieval in scientific information systems, relational databases and ad-hoc searches, document and multimedia databases, and so on. One such paradigm for tackling this problem is TOP-N querying. The ranking of the results and returning the N results with the highest scores. There are numerous reasons for computing TOP-N objects. For example, in the case of search engines and recommender systems, the user will consider only the first N items. Therefore, the results must be the first elements of the search result that are the N most relevant items [13]. A significant portion of this study is focused on the application of a TOP-N algorithm to the most susceptible data locations breached as a result of human factors.
To compute the TOP-N objects, consideration is given to the ranking of items. Algorithms such as EigenRank were developed to rank items using the neighborhood method [13,23]. Cofi-Rank uses the maximum margin factorization to optimize the ranking of items [24]. Another model is preference-relation-based similarity which measures multi-criteria dimensions [25]. A Bayesian personalized ranking model was proposed by Rendel et al. [26] as a better alternative. It works by maximizing the likelihood of pair-wise preferences between observed and unobserved items. They then modified it with a new objective function that aims to achieve higher accuracy for TOP-N recommendation [26]. A method that makes use of a combined collaborative filtering with learning to rank, is one that optimizes the ranking of items [13,27]. To further optimize it, Shi et al. [28] proposed an approach of combined rating and ranking oriented algorithms. The combination was proposed with a linear combination function. An extended probabilistic model with matrix factorization with list-wise preferences was proposed by Liu et al. [29]. A sparse linear model that can learn from a coefficient matrix of item similarity for TOP-N ratings was proposed by Ning and Karypis [30] and a hybrid approach to combine the content-based and the collaborative filtering method was proposed by Tejeda et al. [31]. The proposal allows user participation in the feedback process and ranks interest in user profiles.
3. Proposed Information Security Framework for Human Factors Merged with Existing Technology
In this section, we purpose a framework for human factors and the technology that helps toward information security breach prevention and mitigation in organizations. We concentrate on the human factor aspect more than the technological. The proposed framework is based on the literature associated with the subject. It is a hybrid framework adopted from the human factor framework by Alhogail et al. [10] and the technical framework by Ren et al. [32] as illustrated in Figure 1.
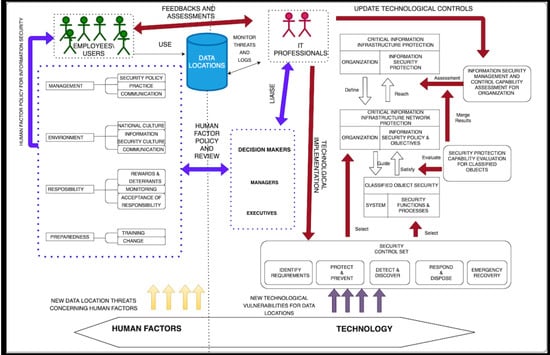
Figure 1.
Human factors and technological framework for information security.
Our proposed framework can help prevent or reduce data breach incidents in organizations. It is an integration of human factors and technology. These two domains are essential issues in information security in organizations with the latter being given much more attention by practitioners. The human factor domain is composed of four subdomains as suggested by Alhogail et al. [10]@ Management, Environment, Responsibility, and preparedness. Furthermore, the technological subdomain which is more of a technical framework by Ren et al. [32] is made up of several components. The framework is aimed at providing a better understanding of human factors that top-level management can consider when it desires to implement an information security policy and solution for an organization. Many organizations do not address human factor issues as being a part of the whole information security assurance process. Human factors are only addressed when they arise. Top-level management needs a proactive information security policy and not just reactive. The novelty of the proposed framework is that it provides an understanding of how human factors can be integrated into a good technological solution for information security to make it robust. It is a solution that takes into account the critical role played by employers or users in information security through management, organizational environment, responsibility, and preparedness. By incorporating such concepts into an organization’s security strategy, the organization becomes better positioned in designing, developing, and deploying a security solution that guards against threats emanating from human factors. The addition of human factors can not be a one-phase process or a one-time event but a continuous one. Employees can not be assumed to comply every time concerning information security [1]. As illustrated in Figure 1, there must be an interconnection between human factors and technology. IT professionals can interact with employees or users to collect feedback from users, data locations, and situations (such as threats, risks, and IT events) frequently and liaise with top-level management to design or update the human factor policy for a better information security. This is important to mapping information security needs, risks or threats and will pave the way for the initiation of the appropriate process, which will make it more secure.
3.1. Human Factors
The security of information assets usually relies on the success of a ’good’ information security policy and various security controls that are implemented as part of such a policy. Aside from the usual technological controls, there must also be considerable dependence on human involvement and this human factor in information security is directly related to human management, control of work environment, a clear understanding of employee responsibility and training. In this subsection, critical human factors that can help reduce human factor problems are discussed.
Management: In an Information Security Survey 2013 by Caldwell et al. [33], setting up security policies is one of the most critical aspects of achieving information security in an organization and this must be considered as one the human factors component. When a security policy is lacking in an organization it affects the effectiveness of information security. As a matter of fact, studies show that an inhibitor to effective information security in an organization can be attributed to a lack of security policy initiated and implemented by management and 93% of organizations that experienced employee-related breaches were as a result of poor understanding of existing security policies and only 47% had policies understood. Furthermore, poor implementation security policies are as bad as their lack of making the organization vulnerable to security breaches. It is also important to note that the existence of an information security policy does not directly impact the number of breach incidents or their seriousness when they do occur [10,34].
Practice subdomain is a matter of the posture of the senior management toward information security. This tends to greatly affect the way employees of the organization perceive the importance of information security, which also leads to an unfavorable behavior towards the same. Therefore, management must have a good attitude or behavior towards information security, and to achieve better employee security behavior, senior management support and prioritization of information security should be visibly demonstrated [10,35].
The next important component of the management subdomain is communication. A very essential issue. Perhaps, the aforementioned two will be greatly affected without the existence of good commination from management. Hence, effective interactions and communications are essential in attaining mutual understandings about security risks among different players in an organization [35]. According to Koskosas et al. [36] in their study of the subject, communication has a significant role in security management, to the extent that it has an effect on the setting of organizations’ security goals. Therefore, effective communication has proven to have a great effect on security behavior and the overall information security of the organization.
Environment: The organizational environment subdomain is also a critical component when developing a human factor domain of information security. Alhogail et al. [10] divides this subdomain into three important parts being National culture, information security culture, and standards and regulations. There is a tendency for employees to adopt a behavior that is more in line with what they see rather than what they are instructed. This is because informal norms like culture tend to be more important than formalized organizational policies. Again, organizational information security culture has a bearing on the information security behavior of employees. Da Veiga et al. [37] argue that this informal culture can be used by management as a critical lever to direct or influence the actions of employees. This will go a long way in reducing data breach threats as a result of human factors. It is vital for management to understand that national or regional culture influences the values and beliefs as it has the capacity to influence how employees view their duties and interact with others and define what constitutes acceptable and unacceptable behavior [7,38]. The development of information security must be compatible with the essential norms, ethics, and values of that society [39]. Standards and regulations are also important components and to some extent, national and regional culture must be considered with designing security policies and rules for a set of standards and regulations for information security. This will have a great impact on influencing user behavior with respect to information security [40].
Responsibility: Employee responsibility is a human factor subdomain with three divisions, rewards and deterrence, monitoring and control, and acceptance of responsibility. When management wants to promote good information security behavior, one effective tool is reward and deterrence. Formal procedures for penalties have been found to be an effective method for influencing user information security behavior. This is a useful method that can be used to minimize employee information security carelessness, error, and possibly negligence. Another way of doing this is through encouragement as studies have shown that it improves the security behavior of employees and allows greater participation in reaching organizational information security goals [10]. According to Colwill [41] monitoring and control are essential and must be in place to ensure that the risk to security risks. He argues that passwords, account management systems, and policies must be monitored and controlled and monitored to ensure the separation of different user access privileges to data and information. Even though continuous monitoring would prevent costly threats to the organization’s information assets, it could contradict with employees’ privacy, liberty, and responsibility. So there must be a balance between security and usability [10]. A human factor affected by norms, values, and belief systems is the accepting of responsibility or the employee acceptance responsibility. This can be said to be employees’ disposition to act in accordance with the interest of the information security requirements of an organization. Van Niekerk et al. [42] noted that if employees have the required knowledge and yet have a view of information security as an obstacle in doing their work, it leads to an insecure behavior. Therefore, employee acceptance is a vital human factor for information security in an organization.
Preparedness: Alhogail et al. [10] partitions the human factor of preparedness into two folds; training (which includes awareness) and change. They make conclusions based on the study by Stanton et al. [43], where a study was conducted on 1167 users. The study showed that training and awareness led to good password practices and when there are naive mistakes, it led to avoidable security incidents. Therefore, there must be a continuous training which provides continues awareness for employees or end-users, to help provide an up to date information on security requirements, new threats and security topics for good information security practices so as to reduce or prevent avoidable security risks and incidents.
3.2. Technological Factors
Human factors are important, but they only form one side of the equation. To balance this equation, technological factors in the organization can not be ignored. In this subsection, the paper dives into a technological framework that can be merged with the human factors discussed in Section 3.1 to provide a holistic information security framework. As illustrated in Figure 1, once the requisite human factor framework is established, there must now be a technological framework. Note that technology at this stage cannot exist on its own, but also requires senior management involvement to provide a technical hinge between human factors and technological factors. From the organizational managerial perspective, Ren et al. [32] indicate that functions must follow the general approach of security incident management, which helps demonstrate the effectiveness of information security, and must also be a reflection of the risk management decision-making process. Security controls on the role of security protection and risk control are different because every security control category and subcategory are of diverging functions. The Functions shape information security at the highest level in the organization. These functions as proposed by Ren et al. [32] are made up of five characteristics: Identify requirements, Protect and Prevent, Detect and Discover, Respond and Dispose, Emergency Recover. Furthermore, suggestions that critical infrastructure can have their own choice to strengthen the security control capability of certain functions based on ensuring the basic security protection capabilities, according to their own security strategy and the requirement to confront the threats. Security control Categories are the subdivisions of a Function into groups of cybersecurity controls closely tied to effects and particular activities. Security control Subcategories further divide a Category into specific outcomes of technical and/or management activities. Subcategories are intended to cover all known activities to achieve the effects of the Category from different aspects. Now the corresponding Level provides a correspondence between security control Subcategories and “GB/T 22239 Baseline for classified protection of information system”. The set of security control centralizes security controls from GB/T 22239, ISO/IEC 27001 and NIST SP800-53 and others [32,44,45].
The consideration of human factors in an information security framework must be dedicated to improving the quality of security and privacy protection. Technology alone can not guarantee the security and privacy of a HIS or any other information system. Human factors must be equally considered. The practice of designing, developing, deploying, or buying technology to provide an information security solution must go hand in hand with consideration of human factors right from the very beginning [6]. It is evident from the framework, that ’good’ management, a conducive organizational environment, preparedness(education and training), and employee responsibility are determinants to reducing human factors that may compromise security and privacy. Managing human factors in an organization is essential to prevent major information security incidents on data locations, which can cost the organization money, reputation, and potentially their continued existence. When good technology is combined with the ’best’ human factors will provide a secure system. The framework can be used to introduce and promote good human factors or behavior concerning HIS to healthcare employees, professionals, and educators. Knowledge of human factors as a part of information security is essential to provide security and privacy of health data. Reason’s [46], concept of human factors in systems and its importance was extended to the proposed framework for organizations and can be summarized as follows:
- There needs to be an effective information security risk management. It must be a simultaneous and targeted deployment of security and privacy solutions at different levels of the system. It must not only focus on the technology but also the individual or team, the task, the situation, and the organization as a whole.
- People rather than technical lapses represent the greatest threat to the security and privacy of the data on information systems. This includes HIS.
- Managing threats associated with employees will never be a 100% effective. Human imperfection can be controlled, but it cannot be eliminated
- To control human error, measures that involve deterrents and rewards could prove to be effective, especially when one is not dealing with highly trained information technology professionals
- Security and privacy significant errors will occur at all levels of an organizational information system, not just at the sharp end. Therefore, decisions made by the top echelons of the organization should create conditions in the workplace that do not subsequently promote individual errors and violations.
- Different human error types have different underlying security and privacy implications, and can occur in different parts of the organization, and may require different methods of mitigation.
- Human factors problems are as a result of a chain of causes in which the unique psychological factors are the ultimate and least manageable links. Preoccupation or distraction is a necessary condition for the commission of slips and lapses in security and privacy protection. However, its occurrence is almost impossible to predict or control effectively. Similar to factors associated with forgetting. The states of mind of an employee will contribute to error, hence extremely challenging to manage; they can happen to the best of people at any time.
- Management of organizations should note that people do not act in isolation. Human behavior is shaped by circumstances, and the same is true for errors and violations. The likelihood of a risky act being committed is greatly influenced by the nature of the job and by the local workplace conditions.
- Automation and increasingly advanced technology will not cure human factors problems. It will merely relocate them. Thus training people to work effectively will costs little but will achieve significant enhancements of human performance in security and privacy of health data.
4. Data Classification
We used dataset collected by or through Health Insurance Portability and Accountability Act, a USA law designed to afford privacy standards to guard patients’ medical records and other health information given to health plans, doctors, hospitals, and other health care providers [47]. The dataset consists of over 1600 recorded cases of data breaches, specifying the location of the breach, name of the covered entity (CE), the State the entity is located in, the number of individual affected, date of submission of the breach, type of the breach, business associate present and the description of the breach from October 2009 to November 2017. To stay within the objective of predicting how human factors can lead to data breach incidents on data locations for an organizations, only a selected number of parameters are considered; date of submission of the breach, the data location breached, and the description. The descriptive parameter narrates what led to the breach. Some of the records had missing values in all the columns except for the year (date of submission of breach). Such records were removed and not considered in this study. To clean data in a way that will be supported by quantitative analysis, the descriptive column, which is a string format was examined, record by record, case by case and where it was indicative of human factors such that the underlying cause of the breach was directly due to human error or behavior, a score of 1 was assigned otherwise 0. For example, a breach on a desktop in 2009 has the description:
“The covered entity (CE) changed the business associate (BA) it used as its information technology vendor. During the transition, a workforce member of the outgoing BA entered the CE’s computer system, changed the passwords, disabled all accounts, and removed drive mappings on the computer server for all of the workstations. The BA also removed the CE’s backup program and deactivated all of its antivirus software. The breach affected approximately 2,000 individuals. The protected health information (PHI) involved in the breach included patients’ names, addresses, dates of birth, social security numbers, appointments, insurance information, and dental records. The CE provided breach notification to affected individuals, HHS, and the media. Following the breach, the CE implemented security measures in its computer system to ensure that its information technology associates do not have access to the CE’s master system and enabled direct controls for the CE. A new server was installed with no ties to the previous BA. The new BA corrected the CE’s passwords and settings, mitigating the issues caused by the previous vendor. The CE provided OCR with copies of its HIPAA security and privacy policies and procedures, and its signed BA agreements that included the appropriate HIPAA assurances required by the Security Rule. As a result of OCR’s investigation, the CE improved its physical safeguards and retrained employees.”
The events that preceded the breach and the Office for Civil Rights (OCR) investigation indicates that the breach was aided by the human factor problem, so a score of 1 will be assigned to a desktop computer for the year 2009. This process is performed for each recorded breach. The data were then extracted according to the data breach location, the year the breach happened, and the number of human factors associated with it for that particular year. We assume that even though undetected and unreported data breach incidences may be significant to the findings of this study, we are confident that the reported data breach cases typify data breach incidences in general.
The experiment of this study is in two major parts.
First, an analysis of variance (ANOVA) for linear regression is used for the analysis of the study and we implored Pearson’s r, which measures the linear relationship between two continuous variables. The regression line used is, , that is:
where the first term is the total variation in the dependent variable(s) y from the dataset, the second term is the variation in the mean observation, while the third term is the residual value. We now square each of the given terms in Equation (1) and add them over all the observations n, which gives the equation
Equation (2) can be rewritten as , where SST is the notation for the total sums of square, SSE error sums of square and SSM is the model sums of squares. The sum of the samples is equal to the ratio of the model’s sums of square, . With this, there is a formalization that the interpretation which explains the fraction of the variability in the data that is explained by the regression model. The variance is given by:
where DFT is the total degree of freedom.
where DFM is a model degree of freedom. In Equation (4) the mean square model (MSM) applies because the regression model has one explanatory variable x. The corresponding mean square error (MSE) is the estimate of the variance of the population of the regression line
The ANOVA calculations for the regression are shown in Table 1.

Table 1.
Anova for regression of human factors and breached locations.
Equation (6) is used to compute the correlation matrix of all the dependent variables. It is a Pearson correlation matrix between the variables and .
Next, We ranked the most to the least susceptible data locations in the event of a breach due to human factors. We used collaborative filtering for performing the data location ranking. We first determined the number of data locations similar to a data location (), then a calculation of the number of breaches(B) that for a certain year Y. The Ranking R for data location is close to the average of the rankings given to . The mathematical formula for the average ranking given by n data locations looks like this:
The formula shows that the average ranking given by n data locations is equal to the sum of the ranking given by them, divided by the number of data locations, which is n.
The next step is to find the similarity of the data locations using angles, we use a computation that returns a higher similarity or smaller distance for a lower angle and a lower similarity or larger distance for a higher angle as illustrated in Equation (8). The cosine of an angle is given by a function that decreases from 1 to −1 as the angle increases from 0 to 180. The cosine of the angle is used to find the similarity between two data locations. The higher the angle, the lower will be the cosine and hence, the lower will be the similarity of the data locations. It is also accurate to compute the inverse of the value of the cosine angle to get the cosine distance between the data locations by subtracting it from 1.
To obtain the final ranking, the weighted average approach is used, multiplying each ranking by a similarity factor. By doing this, weights are added to the rankings. The heavier the weight, the more the ranking would matter. The similarity factor, which would serve as weights, should be the inverse of the distance explained above because less distance implies higher similarity. For example, a deduction of the cosine distance can be made from 1 to get a cosine similarity. Using the similarity factor S for each data location similar to the target data location , we calculate the weighted average using this formula:
In Equation (9), every ranking is multiplied by the similarity factor of the data location that was breached. The final predicted ranking by data location will be equal to the sum of the weighted rankings divided by the sum of the weights.
We then evaluated the accuracy of the predicted rankings, using the root square mean error (RMSE). This was done by computing the mean value of all the differences squared between the true and the predicted values.
where is the rank in the ith year and is the predicted rank.
RMSE values that are greater or equal to 0.5 are a reflection of a poor ability of a model to accurately predict the data [48].
5. Characterization of Breached Data Locations
We characterizes the different types of data location breached using the location type as described in the reported datase. All the data locations described in the subsections of this section have protected health information (ePHI), store ePHI, or are used to access ePHI and are all electronic except for paper and films:
- Network Server:Data locations characterized as network servers (NS) are computer systems, which are used as a central repository of data and various applications that are shared by users via an organization’s network.
- Desktop Computer:Data locations are designated as desktop computers (DC) if they are personal computers that fit on or under a desk, having displays (i.e monitors), keyboards, mice, and form factors that can either be horizontal or vertical and are meant to stay at a particular location.
- Laptops:Laptop computers (LAP) are data locations that are portable personal computers that one can carry and use in different environments on which data were breached. They are sometimes referred to as notebooks in the dataset. LAPs must also include screens, keyboards, and trackpads or trackballs, that serve as mice. In other words, they must be personal computers meant to be used on the go, they have a battery which allows them to operate without being plugged into a power outlet.
- Other Portable Devices:Other Portable devices (OPD) are designations given to data locations that are not laptops yet electronic, portable and/or mobile. They included personal media players, flash memory drives, external or portable hard drives, smartphones, tablets. Furthermore, any other handheld computer devices with Liquid Crystal Display (LCD) or an organic light-emitting diode (OLED) flatscreen interface, providing touchscreen interfaces with digital buttons and keyboards or physical buttons along with physical keyboards.
- Electronic Medical Records:Unlike the data locations that are devices, Electronic medical records (EMR), digital versions of the paper charts in clinician offices, clinics, and hospitals, are also designated as data locations. These applications were breached on various devices in different organizations. EMRs contain notes and information collected by and for the clinicians in the office, clinic, or hospital and are mostly used by providers for diagnosis and treatment.
- Electronic Mail:Electronic Mails (Email) like EMR are applications that were breached on various devices and so email becomes a data location of interest.
- Paper or Films:These are breaches which occurred on paper or films (PF). Even though they are not electronic, we still identified them as a data location to gain a better insight. However, paper or film data locations are not used in the data location rankings.
- Others:Data locations that we designated as ’Others’, are those that have breaches that took place on backup tapes or the breach was as a result as an authorized user sending protected data to the wrong address, receiver or an unauthorized user accidentally.
6. Results
The results in Table 1 are linear regression computations in which the following observations are seen between HF (the predictor) and the different dependent variables. The dependent variable NS can be statistically and significantly predicted by HF, with an F statistics of 42.492 and a distribution of [1,7) and the probability of observing the value is greater than or equal to 42.492 is less than 0.01. The computation on HF and DC also proved that DC can be statistically and significantly predicted by HF, giving an F statistic of 6.059 and the probability of observing greater or equal to the F statistic is less than 0.05 with a distribution of [1,7). Next, we see the dependent variable LAP can be statistically and significantly predicted by HF, with an F statistic of 6.145 and a distribution of [1,7). The probability of observing the value greater than or equal to its F statistic is less than 0.05. With an F statistic of 5.757 and a distribution of [1,7), OPD’s probability of observing the value greater than or equal to its F statistic is as LAP which is less than 0.05. HF can statistically and significantly predict OPD. EMR and EMAIL both being non-hardware locations, have the probability of observing their values greater than or equal to their F statistic 13.705, and 15.474 respectively to be less than 0.01. They are both statistically and significantly predicted by HF, with a distribution of [1,7). Last but not least, the dependent variable OTHERS can be statistically and significantly be predicted by HF, with an F statistic of 8.079 and a distribution of [1,7). The probability of observing the value greater than or equal to its F statistic is less than 0.05.
The proportion of the variation of the dependent variables explained by the independent variables is shown in Table 2. HF accounts for , , , , , , and of the explained variability in NS, DC, LAP, OPD, EMR, EMAIL, PF and OTHERS respectively. While these results suggest that non-human factors also account for , , , , , , and of the explained variability in NS, DC, LAP, OPD, EMR, EMAIL, PF and OTHERS respectively, an empirical study to better understand how they affect breached locations will be required. The results from Table 2 establishes that breached locations are hugely influenced by human factors.

Table 2.
Model summary of human factors and breached locations.
Table 3 provides the analysis for the linear regression between each of the dependent variables and HF. The predictions show that (). An increase or change in human factors, projects a mean of 0.286 in a network server breach. The regressional equation of () predicts a mean of 0.139 each in desktop computers, for an increase or change in human factors. For laptops, there is a mean 0.275 increase or change in human factors, with the regressional equal of (). The prediction also shows (), () and (, where there are mean changes of 0.129, 0.111 and 0.187 in other portable devices, electronic medical records and emails, respectively, for increases in human factors. Lastly, () and () are the predictions for paper-films and other locations respectively. An increase or change in human factors, project means of 0.385 and 0.283 in paper-films and others respectively.

Table 3.
Coefficients of human factors and breached locations.
Computation of the Pearson correlation coefficient in Table 4 is indicative of the strength of the relationship between HF and the dependent variables when a location is breached. There exists a very strong positive correlation of and between HF and NS, and HFand PF respectively. p is significant at 0.000 for both. HF also has a strong positive correlation of and , with EMR and EMAIL sequentially and p is significant at 0.008 and 0.006, respectively. A moderate positive correlation of , , and exists between HF, and DC, LAP, OPD and OTHERS accordingly with each having p significant at 0.043, 0.042, 0.048 and 0.025 in that order.

Table 4.
Correlations matrix of data locations concerning human factors.
The correlation matrix in Table 4 also epitomizes how close some of the data locations are. For example, the network server is a good correlation with all the electronic data locations. This can especially be seen with the two non-hardware electronic data locations (EMR and EMAIL), which have high degrees of correlations with network servers (NS). Network servers provide multiple resources to workstations and other servers on the network. The shared resources can be hardware such as disk space or hardware access and application access (i.e., email services).
Table 5 shows the ranking results of the most susceptible data locations in a data breach incident as a result of human factors using a collaborative filtering algorithm. The dataset extracted only included breaches on data locations that had human factor problems. The result may be different it non-human factor breaches were to be added or analyzed separately. The ranking shows Laptops to be the most susceptible data location and electronic medical records the least. The ranking of Network servers is quite intriguing. Mostly, network servers are manned by IT professions, who we assume are well positioned in terms of knowledge not to compromise the security of the system, especially as a result of human factors. However, network servers rank number two. Even though an empirical study may be needed to ascertain why network servers rank high. We believe it will not be academically strange to conclude per these results, that the other data locations have an indirect effect on a network server being breached due to human factors. The result also shows that human factors make affect data locations different when if come to data breach incidents.

Table 5.
Ranking of most susceptible electronic data locations.
The root mean square error (RMSE) was used to evaluate the accuracy of the ranking results as illustrated in Figure 2. The evaluation of the differences between the true ranking and the predicted ranking ranges of 0.22 to 0.39. This is an indication that the ranking obtained from the collaborative filtering has a high degree of accuracy and therefore our ranking is reliable.
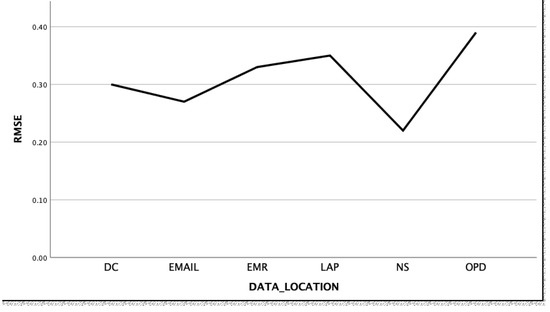
Figure 2.
Ranking evaluation.
7. Discussion
7.1. Human Factors Are a Real Risk
The above findings show data locations to be a critical factor when it comes to the role of human factors in Information Security breach incidents. The results are statistically significant at 0.01 and 0.05, depicted in Table 6. Organizations need to come up with policies that seek to halt or minimize information security incidents stemming from data locations as a result of human factors. With the proliferation of different types of user devices and applications, their advanced capabilities and user friendliness, more and more organizations including those in the health sectors are going to require employees to perform their daily tasks on these devices and applications via a network or the internet. Due to novel coronavirus, most employees may do their work from the comfort of their home through the internet. Furthermore, so if there was ever a time that organizations face information security risk concerning human factors, that time is now. Therefore, human factors need to be addressed comprehensively, to minimize the threats or risk data locations may pose to the overall information security.

Table 6.
Significance level of breached locations.
In Table 4, we see a strong positive correlation between network servers and electronic medical records and emails as compared with the other electronic data locations. This is perhaps the reason why our ranking of the most susceptible data location concerning human factors has a network server at position two(see Table 5). As we have already explained in the previous section, network servers are usually operated by IT professionals, and one would not expect that position. So there may be a possibility that the other electronic devices and application breaches also affect or causes a breach on the network server. Again this will have to be investigated in the future as this study did not cover that.
7.2. Data Location Vulnerability
The many technological advances in information technology, such as data locations, do not always make them more secure. Underlying human factor problems can also make them vulnerable. Thus, information security cannot be understood or described as solely a technical problem. Data locations are operated by people and this means that information security is also a human factors issue [1,12]. Human factors affect how individuals interact with information security technology. An interaction that is often detrimental to security and privacy. It is evident that solely technical solutions are unlikely to prevent security breaches on data locations. It is, therefore, imperative for organizations to input and maintain a culture where positive information security behaviors are appreciated. Usability hurdles connected with information security requirements must be understood and mitigated to better protect data locations. By this, security functions require meaningful, easy to locate, visible, and convenient use. Organizations need to facilitate training about the importance of security and privacy awareness, and this should incorporate education on information security behavior in data locations. The type of interaction between individuals and data locations and the decisions that are made in regard to information security is a dynamic and complex issue. Indeed many factors must be considered. There are also preferences and heuristics that influence how people perceive risk on data locations and can help clarify why individuals make certain decisions and why specific behaviors may be observed [9]. Culture, climate, and religion can unquestionably have a significant influence on values, behaviors, and attitudes. Therefore, understanding an organization’s culture and security climate can give great acumens into certain behaviors concerning the use of data locations in the organization. Cybercriminals understand this as a major weakness within information security and will use social engineering as a tool to launch their attacks. These types of attacks are carried out in an effort to gain sensitive information, which is then used maliciously to the disadvantage of individuals and organizations. Undoubtedly, social engineering poses a great threat to all organizations and to reduce this threat, employees need to not only be aware of potential attacks, but also taught the relevant tools to reduce their risks of becoming a target and a victim [7].
8. Conclusions
In this work, we have proposed a human factor framework merged with existing technological framework. Our results have added to the body of knowledge that technology is not the sole panacea to information security threats and risks and that human factors are also important. The security of data locations, which in turn affects the overall information security, is not only assured in their technical designs and deployments, but also human factors. Data locations do not have the same vulnerability concerning human factors. Some are more vulnerable than others, and so the organization must consider which ones they may want to allow to minimize their vulnerability concerning human factors. Future studies, will have to investigate what specific human factors make what data location more vulnerable and also explore the most critical human factor(s) that make(s) an organization’s information security most vulnerable. The limitations of this paper are that, the dataset does not include ’all’ data locations that may be vulnerable in an organization, also the analysis does not take into account data breach incidents that had no underlying human factor problems.
Author Contributions
Conceptualization, K.H.-L.; methodology, K.H.-L.; validation, Z.Q.; formal analysis, Z.Q.; investigation, F.E.B.; resources, K.H.-L.; data curation, S.D.-N.; writing—original draft preparation, K.H.-L.; writing—review and editing, K.H.-L., F.E.B. and S.D.-N.; supervision, Z.Q.; project administration, Z.Q.; funding acquisition, Z.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (No.61672135), the Frontier Science and Technology Innovation Projects of National Key R&D Program (No.2019QY1405), the Sichuan Science and Technology Innovation Platform and Talent Plan (No.20JCQN0256), and the Fundamental Research Funds for the Central Universities (No.2672018ZYGX2018J057).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HF | Human Factors |
| NS | Network Server |
| DC | Desktop Computer |
| LAP | Laptop |
| Electronic Mail | |
| EMR | Electronic Medical Record |
| PF | Paper or Films |
| HIS | Health Information System |
| PHI | Protected Health Information |
| ePHI | Electronic Protected Health Information |
| CE | Covered Entity |
| ISMS | Information Security Management System |
References
- Khan, S.; Hoque, A. Digital health data: A comprehensive review of privacy and security risks and some recommendations. Comput. Sci. J. Moldova 2016, 71, 273–292. [Google Scholar]
- Conger, S.; Landry, B.J. The Intersection of Privacy and Security. 2008. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.550.5689&rep=rep1&type=pdf (accessed on 22 June 2020).
- Merkow, M.; Breithaupt, J. Securing information assets. In Information Security Principles and Practices; Prentice Hall: Upper Saddle River, NJ, USA, 2005; p. 27. [Google Scholar]
- Robichau, B.P. Healthcare Information Privacy and Security: Regulatory Compliance and Data Security in the Age of Electronic Health Records; Apress: New York, NY, USA, 2014. [Google Scholar]
- Tipton, H.F.; Krause, M. Information Security Management Handbook; CRC Press: Boca Raton, FL, USA, 2006; Volume 3. [Google Scholar]
- Gonzalez, J.J.; Sawicka, A. A framework for human factors in information security. In Proceedings of the Wseas International Conference on Information Security, Rio de Janeiro, Brazil, 15–17 October 2002; p. 448-187. [Google Scholar]
- Al-umaran, S. Culture Dimensions of Information Systems Security in Saudi Arabia National Health Services; De Montfort University: Leicester, UK, 2015. [Google Scholar]
- Schneier, B. Schneier on Security; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Alavi, R.; Islam, S.; Mouratidis, H. A conceptual framework to analyze human factors of information security management system (ISMS) in organizations. In Proceedings of the International Conference on Human Aspects of Information Security, Privacy, and Trust; Springer: Berlin/Heidelberg, Germany, 2014; pp. 297–305. [Google Scholar]
- Alhogail, A.; Mirza, A.; Bakry, S.H. A comprehensive human factor framework for information security in organizations. J. Theor. Appl. Inf. Technol. 2015, 78, 201–211. [Google Scholar]
- Liginlal, D.; Sim, I.; Khansa, L. How significant is human error as a cause of privacy breaches? An empirical study and a framework for error management. Comput. Secur. 2009, 28, 215–228. [Google Scholar] [CrossRef]
- Evans, M.; He, Y.; Maglaras, L.; Janicke, H. Heart-is: A novel technique for evaluating human error-related information security incidents. Comput. Secur. 2019, 80, 74–89. [Google Scholar] [CrossRef]
- Lee, J.; Lee, D.; Lee, Y.C.; Hwang, W.S.; Kim, S.W. Improving the accuracy of top-n recommendation using a preference model. Inf. Sci. 2016, 348, 290–304. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Ricci, F.; Rokach, L.; Shapira, B. Introduction to recommender systems handbook. In Recommender Systems Handbook; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–35. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Borchers, A.; Riedl, J. An algorithmic framework for performing collaborative filtering. In ACM SIGIR Forum; ACM: New York, NY, USA, 2017; Volume 51, pp. 227–234. [Google Scholar]
- Hofmann, T. Latent semantic models for collaborative filtering. ACM Trans. Inf. Syst. (TOIS) 2004, 22, 89–115. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Koren, Y. Collaborative filtering with temporal dynamics. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 447–456. [Google Scholar]
- Koren, Y. Factor in the neighbors: Scalable and accurate collaborative filtering. ACM Trans. Knowl. Discov. Data (TKDD) 2010, 4, 1–24. [Google Scholar] [CrossRef]
- Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. In Advances in Neural Information Processing Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1257–1264. [Google Scholar]
- Liu, N.N.; Yang, Q. Eigenrank: A ranking-oriented approach to collaborative filtering. In Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Singapore, 20–24 July 2008; pp. 83–90. [Google Scholar]
- Weimer, M.; Karatzoglou, A.; Le, Q.V.; Smola, A.J. Cofi rank-maximum margin matrix factorization for collaborative ranking. In Advances in Neural Information Processing Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1593–1600. [Google Scholar]
- Hu, Y.C. Recommendation using neighborhood methods with preference-relation-based similarity. Inf. Sci. 2014, 284, 18–30. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Balakrishnan, S.; Chopra, S. Collaborative ranking. In Proceedings of the Fifth ACM International Conference on Web Search and Data Mining, Seattle, WA, USA, 8–12 February 2012; pp. 143–152. [Google Scholar]
- Shi, Y.; Larson, M.; Hanjalic, A. Unifying rating-oriented and ranking-oriented collaborative filtering for improved recommendation. Inf. Sci. 2013, 229, 29–39. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Xiong, Y.; Liu, W. List-wise probabilistic matrix factorization for recommendation. Inf. Sci. 2014, 278, 434–447. [Google Scholar] [CrossRef]
- Ning, X.; Karypis, G. Slim: Sparse linear methods for top-n recommender systems. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11 December 2011; pp. 497–506. [Google Scholar]
- Tejeda-Lorente, Á.; Porcel, C.; Peis, E.; Sanz, R.; Herrera-Viedma, E. A quality based recommender system to disseminate information in a university digital library. Inf. Sci. 2014, 261, 52–69. [Google Scholar] [CrossRef]
- Ren, W.; Yuan, J.; Jiang, L.; Zhao, T. Technical Framework Research on Critical Information Infrastructure Cybersecurity Classified Protection. In Proceedings of the 2016 4th International Conference on Machinery, Materials and Information Technology Applications, Xi’an, China, 10–11 December 2016; Atlantis Press: Paris, France, 2017. [Google Scholar]
- Caldwell, T. Plugging the cyber-security skills gap. Comput. Fraud Secur. 2013, 2013, 5–10. [Google Scholar] [CrossRef]
- Wiant, T.L. Information security policy’s impact on reporting security incidents. Comput. Secur. 2005, 24, 448–459. [Google Scholar] [CrossRef]
- Hu, Q.; Dinev, T.; Hart, P.; Cooke, D. Managing employee compliance with information security policies: The critical role of top management and organizational culture. Decis. Sci. 2012, 43, 615–660. [Google Scholar] [CrossRef]
- Koskosas, I.; Kakoulidis, K.; Siomos, C. Information security: Corporate culture and organizational commitment. Int. J. Humanit. Soc. Sci. 2011, 1, 192–195. [Google Scholar]
- Da Veiga, A.; Eloff, J.H. A framework and assessment instrument for information security culture. Comput. Secur. 2010, 29, 196–207. [Google Scholar] [CrossRef]
- Selamat, M.H.; Babatunde, D.A. Mediating effect of information security culture on the relationship between information security activities and organizational performance in the Nigerian banking setting. Int. J. Bus. Manag. 2014, 9, 33. [Google Scholar] [CrossRef][Green Version]
- Alnatheer, M.; Nelson, K. Proposed Framework for Understanding Information Security Culture and Practices in the Saudi Context; Security Research Centre, School of Computer and Security Science, Edith Cowan University: Perth, Western Australia, 2009. [Google Scholar]
- Alfawaz, S.; Nelson, K.; Mohannak, K. Information security culture: A behaviour compliance conceptual framework. In Proceedings of the Eighth Australasian Conference on Information Security-Volume 105; Australian Computer Society, Inc.: Darlinghurst, Australia, 2010; pp. 47–55. [Google Scholar]
- Colwill, C. Human factors in information security: The insider threat—Who can you trust these days? Inf. Secur. Tech. Rep. 2009, 14, 186–196. [Google Scholar] [CrossRef]
- Van Niekerk, J.; Von Solms, R. Information security culture: A management perspective. Comput. Secur. 2010, 29, 476–486. [Google Scholar] [CrossRef]
- Stanton, J.M.; Stam, K.R.; Mastrangelo, P.; Jolton, J. Analysis of end user security behaviors. Comput. Secur. 2005, 24, 124–133. [Google Scholar] [CrossRef]
- Force, J.T.; Initiative, T. Security and privacy controls for federal information systems and organizations. NIST Spec. Publ. 2013, 800, 8–13. [Google Scholar]
- Zong, J.; Chen, L.; Li, Q.; Liu, Z. The construction and management of industrial park digitalization and its application services. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 153, p. 032019. [Google Scholar]
- Reason, J. Understanding adverse events: Human factors. BMJ Qual. Saf. 1995, 4, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Molloy, M. Dataset—Kaggle. 2020. Available online: https://www.kaggle.com/forgotyourpassword/hipaa-data-breaches (accessed on 22 June 2020).
- Hanan Hamid. RSME— Researchgate, Question. 2017. Available online: https://www.researchgate.net/post/Whats_the_acceptable_value_of_Root_Mean_Square_Error_RMSE_Sum_of_Squares_due_to_error_SSE_and_Adjusted_R-square (accessed on 22 June 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).