Abstract
Intervertebral disc (IVD) localization and segmentation have triggered intensive research efforts in the medical image analysis community, since IVD abnormalities are strong indicators of various spinal cord-related pathologies. Despite the intensive research efforts to address IVD boundary extraction based on MR images, the potential of bimodal approaches, which benefit from complementary information derived from both magnetic resonance imaging (MRI) and computed tomography (CT), has not yet been fully realized. Furthermore, most existing approaches rely on manual intervention or on learning, although sufficiently large and labelled 3D datasets are not always available. In this light, this work introduces a bimodal segmentation method for vertebrae and IVD boundary extraction, which requires a limited amount of intervention and is not based on learning. The proposed method comprises various image processing and analysis stages, including CT/MRI registration, Otsu-based thresholding and Chan–Vese-based segmentation. The method was applied on 98 expert-annotated pairs of CT and MR spinal cord images with varying slice thicknesses and pixel sizes, which were obtained from 7 patients using different scanners. The experimental results had a Dice similarity coefficient equal to 94.77(%) for CT and 86.26(%) for MRI and a Hausdorff distance equal to 4.4 pixels for CT and 4.5 pixels for MRI. Experimental comparisons with state-of-the-art CT and MRI segmentation methods lead to the conclusion that the proposed method provides a reliable alternative for vertebrae and IVD boundary extraction. Moreover, the segmentation results are utilized to perform a bimodal visualization of the spine, which could potentially aid differential diagnosis with respect to several spine-related pathologies.
1. Introduction
Intervertebral disc (IVD) localization and segmentation has triggered activity in the medical image analysis community, since IVD abnormalities are strongly associated with various chronic diseases, including disk herniation and slipped vertebrae [1]. Most works utilize magnetic resonance imaging (MRI) due to its superior soft-tissue contrast and non-invasive nature [2]. On the other hand, computed tomography (CT) often provides essential cues aiding diagnosis, leading to a minority of CT-based methods [3,4,5]. Still, there is a lack of bimodal approaches, based on complementary information derived from both MRI and CT imaging.
Several works are devoted to IVD localization, either in semi-automatic or fully automatic fashion. Zheng et al. employed the Hough transform (HT) to localize discs in videofluoroscopic CT images, only to refine the manually determined IVD location [6]. Peng et al. employed MRI-derived intensity profiles to localize the articulated vertebrae based on a manual selection of the ‘best’ MRI sagittal slice [7]. Schmidt et al. proposed a part-based, probabilistic inference method for spine detection and labelling [8]. Their method uses a tree classifier and relies on a set of manually marked lumbar region disc from MRI images. The inference algorithm uses a heuristic-based A* search to prune the exponential search space for efficiency. Similar models have been proposed by [9,10]. Stern et al. proposed an automatic method for IVD localization, which starts by extracting spinal centerlines and then detects the centers of vertebral bodies and IVDs by analyzing the image intensity and gradient magnitude profiles extracted along the spinal centerline [11]. There are also localization methods using Markov Random Field (MRF)-based inference. Donner et al. used MRF to encode the relation between an IVD model and the entire search image [12]. Later, Oktay and Akgul described a supervised method to simultaneously localize lumbar vertebrae and IVDs from 2D sagittal MR images using support vector machine (SVM)-based MRF [1]. As a first step, their method uses the local image gradient information of each vertebra and disc and locally searches for the candidate structure positions. As a second step, the method takes advantage of the Markov-chain-like structure of the spine by assuming latent variables for the disc and vertebrae positions. Kelm et al. introduced another machine learning-based method employing marginal space learning for spine detection in CT and MR images [13]. Instead of simultaneously estimating object position, orientation, and scale, they applied a classifier trained to estimate object position, then a second classifier trained to estimate both position and orientation, and a third classifier dealing with all parameters. They used this strategy for efficient IVD localization and performed segmentation by means of a case-adaptive graph cut.
IVD segmentation was addressed by manual as well as by semi-automatic and fully-automatic methods. Chevrefils et al. used texture analysis to extract IVD boundaries by automatically segmenting 2D MR images of scoliotic spines [14,15]. Their watershed-based method exploited statistical and spectral texture features to identify closed regions representing IVDs. Michopoulou et al. proposed a semi-automatic method, which requires an interactive selection of leftmost and rightmost disk points [16]. This information guides their probabilistic atlas-based segmentation algorithm. A semi-automatic statistical method based on shape models was proposed by Neubert et al. [17]. Their method required an interactive placement of a set of initial rectangles along the spine curve. Later, Neubert et al. proposed a segmentation method based on the analysis of the image intensity profile. As a first step, they identify the 3D spine curve and localize IVDs using a Canny edge detector and intensity symmetry [18]. As a second step, the 3D mean shape model is placed on the locations and iterative refinement is conducted by matching the image intensity profile of each mesh vertex. Different types of graph-based methods are also popular [19,20,21,22]. Law used the anisotropic oriented flux detection scheme to extract IVDs, requiring minimal user interaction [23]. The segmentation step of this method is performed using a level set-based active contour. Zhan used Haar filters, an Adaboost classifier and a local articulated model for calculating the spatial relations between vertebrae and discs [24]. A combination of the wavelet-based classification approach, which employs Adaboost, and iterative normalized cuts was proposed by Huang for detection and segmentation [3]. Glocker et al. used random forest (RF) regression and hidden Markov models (HMMs) for localization and identification of vertebrae in arbitrary field-of-view CT scans [25,26]. Later, Lopez Andrade and Glocker used two complementary RFs for IVD localization, followed by a graph-cut-based segmentation stage [27]. The RF-based component of their method is based on [28] and requires training. Wang and Forsberg used integral channel features, a graphical parts model, and a set of registered IVD atlases to obtain combined localization and segmentation [29]. Korez et al. proposed a supervised framework for fully automated IVD localization and segmentation by integrating RF-based anatomical landmark detection, surface enhancement, Haar-like features, a self-similarity context descriptor, and shape-constrained deformable models [30]. Chen et al. proposed a unified data-driven regression and classification framework to tackle the problem of localization and segmentation of IVDs from T2-weighted MR data [31].
More recently, deep learning provided another course of effective methods for spinal image analysis. Cai et al. proposed to use a hierarchical 3D deformable model for multi-modality vertebra recognition, where multi-modal features extracted from deep networks were used for vertebra landmark detection [32]. The recognition result guides a watershed-based segmentation algorithm. However, their deep network is trained in a set of only 1200 pairs of CT/MRI patches, whereas there is no convincing check for overfitting in the evaluation of the recognition part. Moreover, no actual details are provided with respect to the segmentation algorithm, as well as no study on the dependency between the segmentation quality and the recognition accuracy. Despite these shortcomings, the method of Cai et al. is interesting in the sense that it combines information from CT and MRI data [32]. Similar criticism with respect to the size of the training dataset and overfitting applies on other deep learning applications, such as those of [33], who used feed-forward neural networks on CT data and Chen et al., who used 3D fully convolutional networks (FCNs) with flexible 3D convolutional kernels on MRI data [34]. Overall, the main problem arising when considering deep learning is the availability of sufficiently large 3D datasets. More so in the case of a potential bimodal approach which requires pairs of CT/MRI data.
A recent comparative study of several state-of-the-art methods, focusing on MRI, both for localization and segmentation, can be found in [5]. Most of these works, require human intervention, whereas they operate on 2D sagittal images instead of 3D volumes. Most importantly, apart from the work [32], all works operate on a single modality, either CT or MRI. Table 1 summarizes the advantages and limitations of several state-of-the-art methods, including information originally presented in [5] (in the case of MR methods). These methods are included in the experimental comparisons presented in this work.

Table 1.
Summary of limitations of state-of-the-art methods [5].
This work introduces a bimodal method for vertebrae and IVD boundary extraction. Although it assumes the availability of both CT and MR images for each case, the proposed method derives complementary information from both modalities and does not depend on learning or on the availability of large datasets, whereas it requires a limited degree of human intervention. Moreover, it is capable to obtain segmentation results of at least comparable quality to the ones obtained by state-of-the-art methods, although it is not learning-based. Beyond segmentation, it offers a bimodal visualization of the spine, which could potentially aid differential diagnosis with respect to several spine-related pathologies. It is based on the observation that vertebrae are much more prominent in CTs. In this light, each MRI image is geometrically transformed to be aligned with its CT counterpart. As a next stage, vertebral regions are extracted from sagittal CT and projected on the corresponding sagittal MRI. The projected vertebra regions naturally define the boundaries of IVD regions and thus can be used to guide localization. In the final stage, segmentation is performed using a region-based active contour, initialized and guided by the localization result.
The rest of this paper is organized as follows: Section 2 presents the various stages of the proposed method, whereas Section 3 provides an experimental evaluation on actual CT/MRI pairs, as well as comparisons with the state of the art. Finally, Section 4 discusses the main results and summarizes the conclusions of this work.
2. Materials and Methods
The proposed method aims to extract IVD boundaries and provide a bimodal visualization of the spine, using imaging data from both CT and MR images. It consists of six main stages, as illustrated in Figure 1: (1) geometric transformation in order to derive the rules for the projection of structures identified in CT in the context of MR, (2) CT segmentation for vertebral boundary extraction, taking into account that vertebra are prominent and thus easier to identify in the context of this modality. Linear gray level normalization and Otsu thresholding with 3 gray levels are applied at this stage, (3) vertebral region projection on MRI, using the rules derived in stage 1, (4) IVD localization by means of a simple heuristic, (5) CT/MRI-based segmentation for IVD boundary extraction, using the boundaries defined by the vertebra projected in stage 3, the coarse IVD regions obtained in stage 4, and the Chan–Vese active contour, (6) CT/MRI image fusion, offering a bimodal visualization of the spine. The proposed method is based on 3D images (CT and MR), although some of its components are applied on 2D slices of each 3D image.
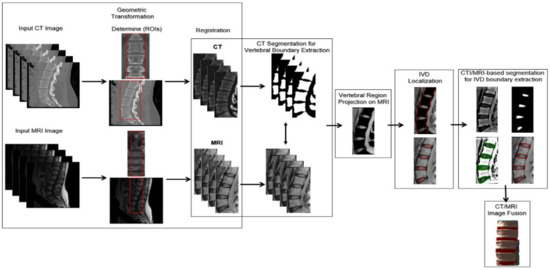
Figure 1.
Summary of the main stages of the proposed method.
2.1. Geometric Transformation
A pair of CT and MRI 3D images is used as the input and the user is asked to manually determine a pair of 3D regions of interest (ROIs). Although these ROIs are selected to approximately match each other, they have a different number of slices, as well as different pixel sizes. It should be remarked that determining ROIs is the only human intervention required by the proposed method. The MRI 3D ROI is geometrically transformed to match the CT 3D ROI, by means of one-to-one evolutionary optimization [36] and the geometric transformation method of Wells et al. [37], which is based on mutual information (Figure 2). This method considers that both MR and CT are informative of the same underlying anatomy and share mutual information. In this light, a transformation function T is found by maximizing this mutual information, as quantified by means of entropy I:
in which:
where x are voxel coordinates, u(x) is a voxel of the reference volume (e.g., CT), υ(x) is a voxel of the target volume (e.g., MR), h(u) and h(υ) are the entropies of random variables u and υ, respectively, and is the joint entropy of random variables u, υ. The calculation of entropies is based on estimating the underlying probability density function by means of Parzen window density. Further details can be found in [36].
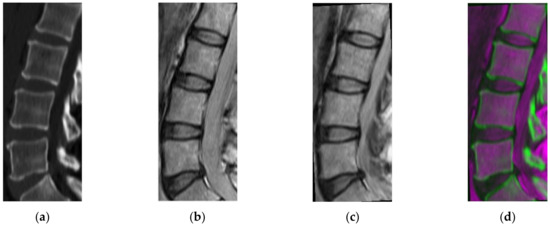
Figure 2.
(a) Initial computed tomography (CT) image, (b) initial magnetic resonance imaging (MRI) image, (c) register MRI, (d) fusion CT and MRI.s.
2.2. CT Segmentation for Vertebral Boundary Extraction
Taking into account that vertebral regions are much more prominent in CT, we focused on this modality for vertebral boundary extraction. Still, there are several challenges for accurate vertebral boundary extraction in CT, including the intensity inhomogeneity within each structure, which may result in the identification of false ‘gaps’ as well as the presence of noise, which along with intensity inhomogeneity may lead to segmentation artifacts. Linear gray-level normalization is applied on the CT (Figure 3) as a pre-processing stage, aiming to further enhance the intensity distribution. In the resulting pre-processed CT image, vertebral regions are even more distinguishable. In the following step, the well-known Otsu’s thresholding with three classes is applied to extract vertebral boundaries. Otsu’s thresholding is ‘a non-parametric, unsupervised method for automatic threshold selection’ [38]. The algorithm exhaustively searches k−1 thresholds for k classes, maximizing inter-class variance. Its main stages are: (1) intensity distributions and probabilities of each class are initialized; (2) iteratively, all possible threshold combinations are examined, class probabilities and mean intensity values for each class are updated, and inter-class variance is calculated; (3) threshold values, corresponding to maximum inter-class variance, are selected. Figure 3 illustrates a flowchart for Otsu’s thresholding. The three classes considered are associated with background, vertebral bodies, and vertebral contours (Figure 4b). In this subfigure, the presence of ‘gaps’ as a result of intensity inhomogeneity is evident. The regions marked with the latter two classes are maintained (Figure 4c).
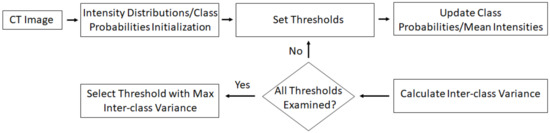
Figure 3.
Flowchart for Otsu thresholding.

Figure 4.
(a) Initial CT image, (b) Otsu thresholding with three labels, where label ‘1′ is assigned to background (black) and labels ‘2,3′ are assigned to vertebrae (gray and white pixels), (c) binary image, (d) resulting image after applying dilation and the inter-slice-based correction, (e) boundaries of extracted vertebrae, marked as red.
Aiming to cope with the effects of intensity inhomogeneity in the results of Otsu thresholding, we compactify the resulting regions by means of morphological closing operations, with a size of 10 × 10 and a disk-shaped structuring element with a radius equal to 2. At this stage, some segmentation artifacts are generated in the form of ‘islands’ of background pixels, implausibly isolated on the z-axis. Aiming to cope with this, we utilize the extra information of the third dimension and consider an inter-slice window in the z-axis. The labels are corrected by means of a voting scheme, taking into account all corresponding labels in the neighboring slices (Figure 4d,e). As a result, the ‘islands’ of background pixels are re-labelled as parts of vertebral bodies. Note that only the central regions will eventually be maintained, whereas the rest of the extracted regions (e.g., at the right of Figure 4d,e) will be discarded in the following stage.
2.3. Vertebral Region Projection on MRI
The sagittal MRI images are linearly normalized with respect to gray-levels. The vertebral regions identified in CT, as described in stage 2, are projected on the pre-processed MRIs by means of the geometrical transformation derived in stage 1, and the gray-levels associated with the projected regions are set to zero (Figure 5). The accuracy of the subsequent IVD localization stage is inherently determined by this stage.
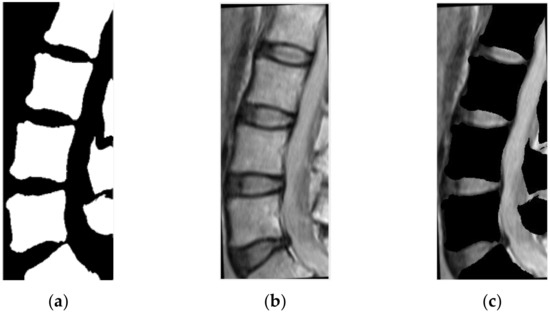
Figure 5.
(a) The result of CT segmentation, (b) registered MRI image, (c) the result of masking between the two previous images.
2.4. IVD Localization
IVD regions are localized by means of a simple heuristic applied on the result of stage 3: non-zero regions (Figure 5c) within an empirically defined stripe approximating the spine are determined as IVD regions. The stripe is defined by scanning the registered image from left to the right and marking the first vertebra pixel. The same process is also performed reversely, from right to left. Eventually, for each row, two pixels are marked defining the stripe (illustrated as red in Figure 6a). Although this empirically determined stripe provides a rough approximation of the spinal regions, when combined with the result of stage 3, the derived localizations are robust (Figure 6b,c). It should be stressed that the localization result of this stage is a rough approximation used to initialize the Chan–Vese active contour model described in the next sub-section.
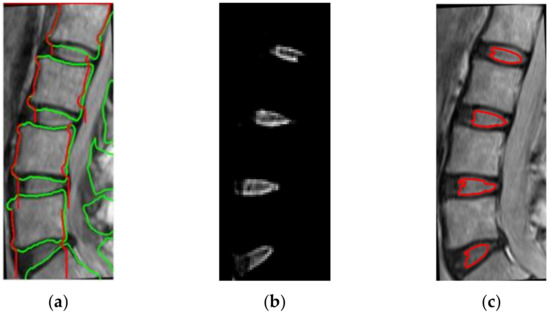
Figure 6.
(a) The boundary of vertebral stripe, which is marked as red, is derived by the boundaries of the vertebrae, marked as green, (b) localization of intervertebral disk (IVD) positions, (c) the IVD boundaries extracted after localization.
2.5. CT/MRI-Based Segmentation for IVD Boundary Extraction
Starting from the rough approximation of the spinal regions, which is obtained at stage 4, this stage aims at accurately extracting IVD boundaries. For this task, the Chan-Vese active contour model [39] is the segmentation approach of choice, since it is relatively insensitive to initialization and robust against weak edges and noise. The steps followed at this stage are: (1) MR image enhancement by means of the sharpening technique of Saleh and Nordin [40] (Figure 7a), (2) initialization of the Chan–Vese model by the rough approximations of the spinal region derived at stage 4 (Figure 7b), (3) contour evolution on contrast enhanced images (Figure 7c), (4) IVD boundary extraction after active contour convergence (Figure 7d).

Figure 7.
(a) Unsharp mask applied to registered MR image, (b) binary image derived from stage 4, used for active contour initialization, (c) active contour applied on contrast-enhanced images with 40 iterations, (d) IVD boundary extraction.
2.6. CT/MRI Image Fusion
Apart from the segmentation result, the proposed method provides a hybrid, CT/MRI-based, visualization of the spine. Vertebral regions identified on CT (stage 2) are super-imposed on spinal regions identified on MR (stage 5). Figure 8 illustrates an example of different views of such a visualization, in which both vertebral (marked with gray) and IVD (marked with red) regions are identified. This bimodal-based illustration of both regions provides a valuable tool, potentially aiding differential diagnosis with respect to various spine-related pathologies.
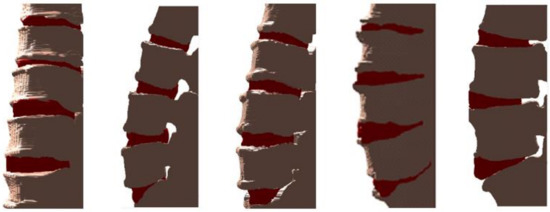
Figure 8.
Examples of 3D visualizations of vertebrae (marked with gray) and IVD (marked with red).
3. Experimental Evaluation
The proposed method was applied on 7 pairs of CT and MR images with 98 images using different scanners. The pixel size and slice thickness differed within the ranges of 0.33–0.37 mm and 1.5–3 mm for CT and 0.47–0.55 mm and 3–4 mm for MRI, respectively. This dataset is publicly available (http://spineweb.digitalimaginggroup.ca).
3.1. Evaluation Metrics
The method was quantitatively evaluated, using CT and MRI ground truth segmentations obtained by a medical expert. The Dice similarity coefficient (DSC) [41] and Hausdorff distance (HD) [42] were adopted to evaluate the segmentation accuracy. DSC depends on the number of common pixels between the images compared, whereas HD is derived from distances of all pairs of pixels.
Let and be the binary images that are obtained from the manual and the proposed segmentation, respectively. In both images, the pixels of the structures are set to 1 and the rest are set to 0. Let also and be the boundaries of structures in and , respectively. DSC and HD are defined in Equations (3) and (4):
where the metric d employed is the Euclidean distance.
3.2. Results and Discussion
The CT segmentation of the proposed method was quantitatively compared with the methods of Huang and Isaac [3,4] (Table 2). The IVD segmentations obtained by the proposed method were quantitatively compared with four state-of-the-art methods [5] (Table 3). Figure 9 and Figure 10 illustrate the results of Table 2 and Table 3, respectively. Figure 11 illustrates the segmentation quality obtained by all methods compared in both modalities. It can be noted that when considering both quality measures, the proposed method is at least comparable to state-of-the-art learning-based methods in both modalities. Apart from the dependency on training, the state-of-the-art methods compared have also numerous limitations, which include difficulties in the presence of severe pathologies or when certain structures are absent, memory requirements, dependency on atlases etc. These limitations are summarized in Table 1. Figure 11 and Figure 12 illustrate example CT and MRI segmentations obtained by the proposed method. In Figure 11, it can be observed that the vertebra boundaries extracted are plausible. This is also confirmed by a medical expert who was asked to qualitatively evaluate the segmentation result. Similarly, in Figure 12, it can be observed that the IVD boundaries extracted are plausible, whereas this is confirmed by the medical expert. Figure 13 presents example visualizations obtained by the proposed method, marking vertebrae and IVDs with different colors.

Table 2.
CT image segmentation quality of the proposed method and state-of-the-art.

Table 3.
MR image segmentation quality of the proposed method and state of the art.
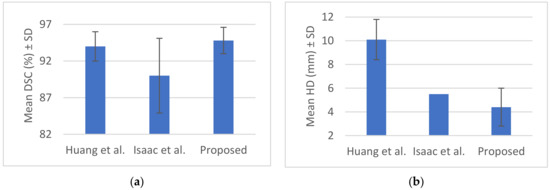
Figure 9.
(a) Mean Dice similarity coefficient (DSC) (%) ± SD, (b) mean Hausdorff distance HD (mm) ± SD from Table 2.
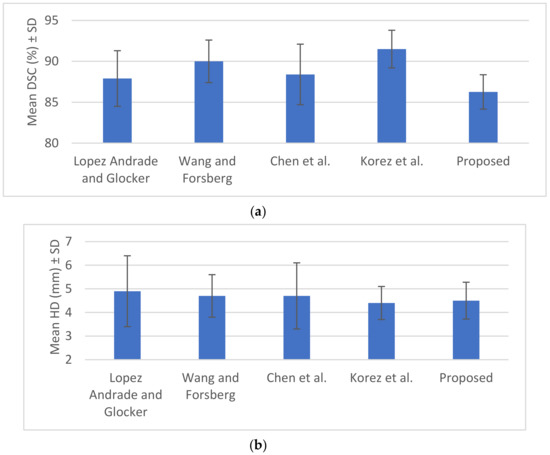
Figure 10.
(a) Mean DSC (%) ± SD, (b) mean HD (mm) ± SD from Table 3.
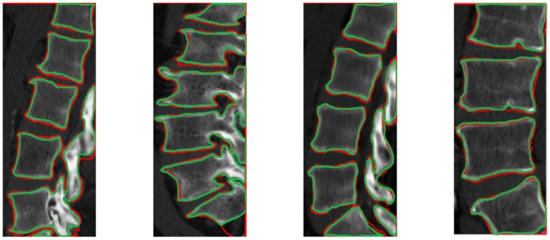
Figure 11.
Segmentation results from our automatic method, illustration CT images from different data with red color. The ground truth contours are described with green color.
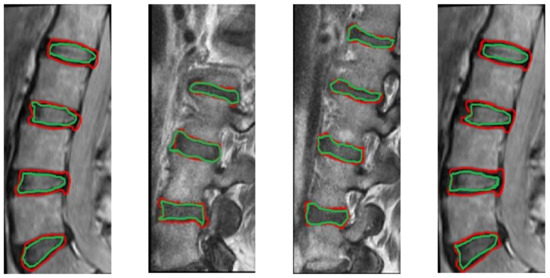
Figure 12.
Segmentation results from our method, illustration MRI images from different data sets with red color. The ground truth contours are described with green color.

Figure 13.
Example visualizations obtained by the proposed method, marking vertebrae and IVDs with gray and red, respectively.
Another set of experiments involved the evaluation of the robustness of the proposed method against various parameters. Two different transformation types where tested: affine and similarity-based. In addition, three different interpolation methods where tested: linear, nearest neighbor, and cubic. Similarity-based transformation and linear interpolation led to the highest segmentation quality with 100 iterations, a radius growth factor equal to 1.05, and an initial search radius equal to 0.004. The DSC and HD of the segmentation result obtained for various settings of the mask size for morphological filtering on CT (blue line) and MRI (red line) are illustrated in Figure 14a,b. It can be observed that the differences in the accuracy obtained are less than 5% with respect to DSC and less than 0.2 pixels with respect to HD, as this parameter ranges from 8 to 12. In the previously presented experimental comparisons, this value was set to 10. In addition, the variances in DSC and HD as the number of active contour iterations ranges from 20 to 65 are illustrated in Figure 14c,d. It can be observed that the differences in the accuracy obtained are less than 6% with respect to DSC and less than 1.5 pixels with respect to HD. In the previously presented experimental comparisons, this value was set to 30. It should be remarked that, unlike these parameters, the thresholds involved in CT segmentation (Section 2.2) are automatically selected.
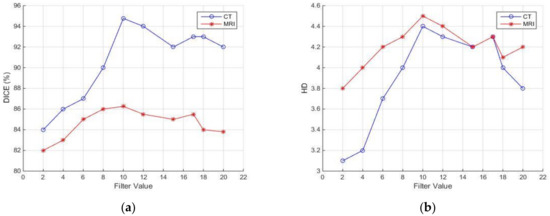
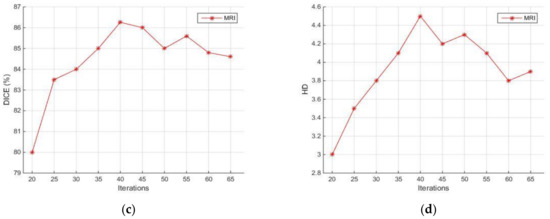
Figure 14.
Sensitivity of segmentation quality with respect to DSC and HD against filter mask size (a,b) and active contour iterations (c,d). MR with red lines and CT with blue lines. The second parameter applies only to MR.
As a final remark, for our suboptimal Matlab (Mathworks, MA, USA) implementation, the CT-based and MR-based stages are currently applied sequentially, with an effect on overall time cost, which is approximately 3 min. Parallelization of these stages is expected to drastically reduce time cost.
4. Conclusions
This work introduces a computational approach for vertebrae and IVD boundary extraction, based on CT and MRI data. The proposed method (1) derives complementary information from both modalities; (2) is not learning-based and is not dependent on the availability of large, labelled datasets, unlike the vast majority of state-of-the-art methods; (3) is capable of obtaining segmentation results of at least comparable quality to the ones obtained by state-of-the-art methods, although it is not learning-based; (4) provides a bimodal visualization of the spine, which could potentially aid differential diagnosis with respect to several spine-related pathologies. In addition, the proposed method requires a limited amount of intervention. It starts from aligning corresponding CT and MR images, whereas the CT images are segmented to extract vertebrae boundaries. The result of CT segmentation is fused with MR images to guide the subsequent localization and segmentation stages. The result of CT segmentation guides IVD localization and the exact IVD boundaries are extracted by applying the Chan–Vese active contour model on a contrast-enhanced version of the MR image. Finally, the extracted vertebrae and IVD boundaries can be used to provide a hybrid 3D visualization of the spine. The proposed method was compared with state-of-the-art methods, with respect to: (1) CT image segmentation for vertebrae boundary extraction, (2) MR image segmentation for IVD boundary extraction. In both cases, the obtained segmentation quality, as quantified by means of the DICE and HD measures, was at least comparable to the one obtained from state-of-the-art learning-based methods. In addition, unlike competing methods, the proposed method requires no prior knowledge in the form of an atlas or learning from annotated samples. On the other hand, the proposed method depends on the availability of CT/MR image pairs, which could limit its applicability, taking into account that several currently adopted clinical practices are single-modal. Moreover, our suboptimal Matlab implementation is relatively slower than some of the state-of-the-art methods.
A research challenge for future work is the design of hybrid approaches that incorporate learning-based components, which can take advantage of the potential availability of small-sized, labelled CT/MR image pairs. Moreover, the development of an optimized implementation, as well as additional experiments on clinically important cases, such as those involving the presence of dehydrated discs, are the subject of our ongoing research.
Author Contributions
Conceptualization, M.L., M.A.S., P.A.A., M.G.L. and G.K.M.; methodology, M.L., M.A.S., P.A.A. and G.K.M.; software, M.L.; validation, M.G.L.; writing—original draft preparation, M.L., M.A.S.; writing—review and editing, M.A.S., P.A.A., M.G.L., G.K.M.; supervision, G.K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oktay, A.; Akgul, A. Simultaneous localization of lumbar vertebrae and intervertebral discs with SVM-based MRF. IEEE Trans. Biomed. Eng. 2013, 60, 2375–2383. [Google Scholar] [CrossRef] [PubMed]
- Emch, T.; Modic, M. Imaging of lumbar degenerative disk disease: History and current state. Skelet. Radiol. 2011, 40, 1175–1189. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Jian, F.; Wu, H.; Li, H. An improved level set method for vertebra CT image segmentation. Biomed. Eng. Online 2013, 12, 48. [Google Scholar] [CrossRef] [PubMed]
- Castro-M, I.; Pozo, J.M.; Pereañez, M.; Lekadir, K.; Lazary, A.; Frangi, A.F. Statistical interspace models (SIMs): Application to robust 3D spine segmentation. Trans. Med. Imaging 2015, 34, 1663–1675. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Chu, C.; Belavý, D.L.; Ibragimov, B.; Korez, R.; Vrtovec, T.; Hutt, H.; Everson, R.; Meakin, J.; Andrade, I.L.; et al. Evaluation and comparison of 3D intervertebral disc localization and segmentation methods for 3D T2 MR data: A grand challenge. Med. Image Anal. 2017, 35, 327–344. [Google Scholar] [CrossRef]
- Zheng, Y.; Nixon, M.S.; Allen, R. Automated segmentation of lumbar vertebrae in digital videofluoroscopic images. IEEE Trans. Med. Imag. 2004, 23, 45–52. [Google Scholar] [CrossRef]
- Peng, Z.; Zhong, J.; Wee, W.; Lee, J.H. Automated vertebra detection and segmentation from the whole spine MR images. In Proceedings of the IEEE-EMBC, Shanghai, China, 1–4 September 2005; pp. 2527–2530. [Google Scholar]
- Schmidt, S.; Kappes, J.; Bergtholdt, M.; Pekar, V.; Dries, S.; Bystrov, D.; Schnörr, C. Spine detection and labeling using a parts-based graphical model. In Proceedings of the IPMI, Kerkrade, The Netherlands, 2–6 July 2007; Volume 20, pp. 122–133. [Google Scholar]
- Corso, J.J.; Alomari, R.S.; Chaudhary, V. Lumbar disc localization and labeling with a probabilistic model on both pixel and object features. In Proceedings of the MICCAI, New York, NY, USA, 6–10 September 2008; Volume 11, pp. 202–210. [Google Scholar]
- Alomari, R.S.; Corso, J.; Chaudhary, V. Labeling of lumbar discs using both pixel and object-level features with a two-level probabilistic model. IEEE Trans. Med. Imaging 2011, 30, 1–10. [Google Scholar] [CrossRef]
- Stern, D.; Likar, B.; Pernus, F.; Vrtovec, T. Automated detection of spinal centrelines, vertebral bodies and intervertebral discs in CT and MR images of lumbar spine. Phys Med. Biol. 2010, 55, 247–264. [Google Scholar] [CrossRef]
- Donner, R.; Langs, G.; Micusik, B.; Bischof, H. Generalized sparse MRF appearance models. Image Vis. Comput. 2010, 28, 1031–1038. [Google Scholar] [CrossRef]
- Kelm, M.B.; Wels, M.; Zhou, K.S.; Seifert, S.; Suehling, M.; Zheng, Y.; Comaniciu, D. Spine detection in CT and MR using iterated marginal space learning. Med. Image Anal. 2013, 17, 1283–1292. [Google Scholar] [CrossRef]
- Chevrefils, C.; Cheriet, F.; Grimard, G.; Aubin, C.E. Watershed segmentation of intervertebral disk and spinal canal from MRI images. In Proceedings of the ICIAR LNCS, Montreal, QC, Canada, 22–24 August 2007; pp. 1017–1027. [Google Scholar]
- Chevrefils, C.; Farida, C.; Aubin, C.E.; Grimad, G. Texture analysis for automatic segmentation of intervertebral disks of scoliotic spines from MR images. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 608–620. [Google Scholar] [CrossRef] [PubMed]
- Michopoulou, S.; Costaridou, L.; Panagiotopoulos, E. Atlas-based segmentation of degenerated lumbar intervertebral discs from MR images of the spine. IEEE Trans. Biomed. Eng. 2009, 56, 2225–2231. [Google Scholar] [CrossRef] [PubMed]
- Neubert, A.; Fripp, J.; Engstrom, C.; Schwarz, R.; Lauer, L.; Salvado, O.; Crozier, S. Automated detection, 3D segmentation and analysis of high resolution spine MR images using statistical shape models. Phys. Med. Biol. 2012, 57, 8357–8376. [Google Scholar] [CrossRef]
- Neubert, A.; Fripp, J.; Chandra, S.S.; Engstrom, C.; Crozier, S. Automated intervertebral disc segmentation using probabilistic shape estimation and active shape models. In Proceedings of the MICCAI Workshop & Challenge on Computational Methods and Clinical Applications for Spine Imaging, Munich, Germany, 5–9 October 2015; pp. 144–151. [Google Scholar]
- Carballido, G.J.; Belongie, S.J.; Majumdar, S. Normalized cuts in 3D for spinal MRI segmentation. IEEE Trans. Med. Imaging 2004, 23, 36–44. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Chu, S.; Lai, S.H.; Novak, C.L. Learning-based vertebra detection and iterative normalized cut segmentation for spinal MRI. IEEE Trans. Med. Imaging 2009, 28, 1595–1605. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.M.; Aslan, A.S.; Farag, A.A. Vertebral body segmentation with prior shape constraints for accurate BMD measurements. Comput. Med. Imaging Graph. 2014, 38, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Ayed, I.B.; Punithakumar, K.; Garvin, G.J.; Romano, W.M.; Li, S. Graph cuts with invariant object-interaction priors: Application to intervertebral disc segmentation. In Proceedings of the IPMI, Kloster Irsee, Germany, 3–8 July 2011; pp. 221–232. [Google Scholar]
- Law, M.; Tay, K.; Leung, A.; Garvin, G.; Li, S. Intervertebral disc segmentation in MR images using anisotropic oriented flux. Med. Image Anal. 2013, 17, 43–61. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Maneesh, D.; Harder, M.; Zhou, X. Robust MR spine detection using hierarchical learning and local articulated model. In Proceedings of the MICCAI, Nice, France, 1–5 October 2012; Volume 1, pp. 141–148. [Google Scholar]
- Glocker, B.; Feulner, J. Automatic localization and identication of vertebrae in arbitrary field-of-view CT scans. In Proceedings of the MICCAI, Nice, France, 1–5 October 2012; pp. 590–598. [Google Scholar]
- Glocker, B.; Zikic, D.; Konukoglu, E. Vertebrae localization in pathological spine CT via dense classification from sparse annotations. In Proceedings of the MICCAI, Nagoya, Japan, 22–26 September 2013; pp. 262–270. [Google Scholar]
- Andrade, I.L.; Glocker, B. Complementary classification forests with graph-cut refinement for IVD localization and segmentation. In Proceedings of the MICCAI Workshop & Challenge on Computational Methods and Clinical Applications for Spine Imaging, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Glocker, B.; Konukoglu, E.; Haynor, D. Random forests for localization of spinal anatomy. In Medical Image Recognition, Segmentation and Parsing: Methods, Theories and Applications; Academic Press: Orlando, FL, USA, 2016; pp. 94–110. [Google Scholar]
- Wang, C.; Forsberg, D. Segmentation of intervertebral discs in 3D MRI data using multi-atlas based registration. In Proceedings of the MICCAI Workshop & Challenge on Computational Methods and Clinical Applications for Spine Imaging, Munich, Germany, 5–9 October 2015; pp. 101–110. [Google Scholar]
- Korez, R.; Ibragimov, B.; Likar, B.; Pernus, F.; Vrtovec, T. Deformable model-based segmentation of intervertebral discs from MR spine images by using the SSC descriptor. In Proceedings of the MICCAI Workshop & Challenge on Computational Methods and Clinical Applications for Spine Imaging, Munich, Germany, 5–9 October 2015; pp. 111–118. [Google Scholar]
- Chen, C.; Belavy, D.; Yu, W.; Chu, C.; Armbrecht, G.; Bansmann, M.; Felsenberg, D.; Zheng, G. Localization and segmentation of 3D intervertebral discs in MR images by data driven estimation. IEEE Trans. Med. Imaging 2015, 34, 1719–1729. [Google Scholar] [CrossRef]
- Cai, Y.; Osman, S.; Sharma, M.; Landis, M.; Li, S. Multi-modality vertebra recognition in artbitrary view using 3D deformable hierarchical model. IEEE Trans. Med. Imaging 2015, 34, 1676–1693. [Google Scholar] [CrossRef]
- Suzani, A.; Seitel, A.; Liu, Y.; Fels, S.; Rohling, N.R.; Abolmaesumi, P. Fast automatic vertebrae detection and localization in pathological CT scans—A deep learning approach. In Proceedings of the MICCAI, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Chen, H.; Shen, C.; Qin, J. Automatic localization and identification of vertebrae in spine CT via a joint learning model with deep neural network. In Proceedings of the MICCAI, Munich, Germany, 5–9 October 2015; Volume 1, pp. 515–522. [Google Scholar]
- Chen, H.; Dou, Q.; Wang, X.; Heng, P.A. Deepseg: Deep segmentation network for intervertebral disc localization and segmentation. In Proceedings of the MICCAI Workshop & Challenge on Computational Methods and Clinical Applications for Spine Imaging, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Styner, M.; Brechbühler, C.; Székely, G.; Gerig, G. Parametric estimate of intensity inhomogeneities applied to MRI. IEEE Trans. Med. Imaging 2000, 19, 153–165. [Google Scholar] [CrossRef]
- Wells, W.M.; Viola, P.; Atsumi, H.; Nakajima, S.; Kikinis, R. Multi-modal volume registration by maximization of mutual information. Med. Image Anal. 1996, 1, 35–51. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cyber. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active Contours Without Edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef]
- Saleh, H.; Nordin, M.J. Improving diagnostic viewing of medical images using enhancement algorithms. J. Comput. Sci. 2011, 7, 1831–1838. [Google Scholar]
- Taha, A.A.; Hanbury, A. Metrics for evaluation 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef]
- Huttenlocher, D.; Klanderma, G.; Rucklidge, W. Comparing Images Using the Hausdorff Distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).