Exploiting the User Social Context to Address Neighborhood Bias in Collaborative Filtering Music Recommender Systems

Abstract

Recent research in the field of recommender systems focuses on the incorporation of social information into collaborative filtering methods to improve the reliability of recommendations. Social networks enclose valuable data regarding user behavior and connections that can be exploited in this area to infer knowledge about user preferences and social influence. The fact that streaming music platforms have some social functionalities also allows this type of information to be used for music recommendation. In this work, we take advantage of the friendship structure to address a type of recommendation bias derived from the way collaborative filtering methods compute the neighborhood. These methods restrict the rating predictions for a user to the items that have been rated by their nearest neighbors while leaving out other items that might be of his/her interest. This problem is different from the popularity bias caused by the power-law distribution of the item rating frequency (long-tail), well-known in the music domain, although both shortcomings can be related. Our proposal is based on extending and diversifying the neighborhood by capturing trust and homophily effects between users through social structure metrics. The results show an increase in potentially recommendable items while reducing recommendation error rates.

1. Introduction

Social networks are currently the focus of intensive research, as they are a great source of information that can be used in multiple domains for multiple purposes. Recommender systems are one of the areas in which social data can be exploited to improve the reliability of recommendations. The adoption of streaming music services as a common way of listening to music has allowed its use in this domain since most of these platforms are, in turn, equipped with some kind of social functionality, such as establishing friendship connections. In addition, streaming systems collect user interactions, which allows implicit feedback from users to be used instead of explicit ratings as an expression of user preferences. This has promoted the development of recommender systems for these platforms. Nevertheless, the implementation of methods that take advantage of social information is scarce in the music streaming services environment, because the mechanisms of social interaction are much more limited than in social networks such as Facebook, Twitter, etc.

Currently, the methods most extensively used in recommender systems are based on Collaborative Filtering (CF). This approach requires either explicit or implicit user ratings or preferences for some products that users have already consumed. The larger is the number of ratings, the higher is the reliability of the recommendations provided by these methods. Many proposals that make use of social data are precisely aimed at minimizing the drawback of insufficient ratings, while others are just focused on improving rating prediction without dealing with problems concerning recommendation bias.

In this work, we introduce the concept of neighborhood bias that takes place in the context of collaborative filtering methods and causes a limitation in the number of potentially recommendable items. In these approaches, the recommendations made to a given user are restricted to items rated by other users with similar tastes, who are called his/her nearest neighbors. This fact prevents the user from discovering other items that he/she might like. The neighborhood bias is caused by the way neighbors are found since this process is based on the similarity of users’ ratings about the same products. For example, two users may have the same musical tastes, but those users cannot be neighbors if they have rated different artists or songs. This problem is related to popularity bias because it is more likely that the most popular items are the most rated and, therefore, the most recommended. However, the bias that we try to address in this work is not the same since the objective is to extend the range of potentially recommended items but not necessarily with the less popular items. To achieve this, we propose to extend the neighborhood by considering social factors that may have some impact on user preferences. Thus, the neighborhood of a given user is calculated not only on the basis of affinity in preferences with other users, but also on the influence received from other users in the social network. When extending the neighborhood using social factors, the number of potentially recommendable items is also extended, since the greater is the number of neighbors, the greater is the number of items with which they interact. Trust and homophily are two factors that influence users when choosing products or services, and, therefore, must be considered when predicting their interests and preferences. Trust refers to individuals who are more likely to adopt recommendations not only from opinion leaders but from their closest social context, while homophily refers to the similarity of connected users in social networks since they usually share tastes and interests. The graph of social connections between users can be the subject of structural measures that capture these two factors and allow their influence on recommendations to be considered. Many methods have been proposed in the literature for such purpose, although it has been shown that their performance depends largely on the application domain [1] and most of them have been validated in specific domains other than music [2,3]. In the music area, they have not been sufficiently tested, mainly due to the difficulty of obtaining the necessary social information from streaming platforms. For instance, friendship connections are only bidirectional, and there is only one between each pair of users. This makes it impossible to apply well known graph-based metrics, such as centrality, page-rank, etc., which work with unidirectional connections, to establish two connections between each pair of users, one in each direction. In addition, that information has usually been used to improve the reliability of recommendations. It has not been exploited to deal with neighborhood bias, which is the main purpose of our work. It is therefore necessary to develop effective techniques to obtain these factors in this environment to integrate them into traditional recommendation methods and benefit from them.

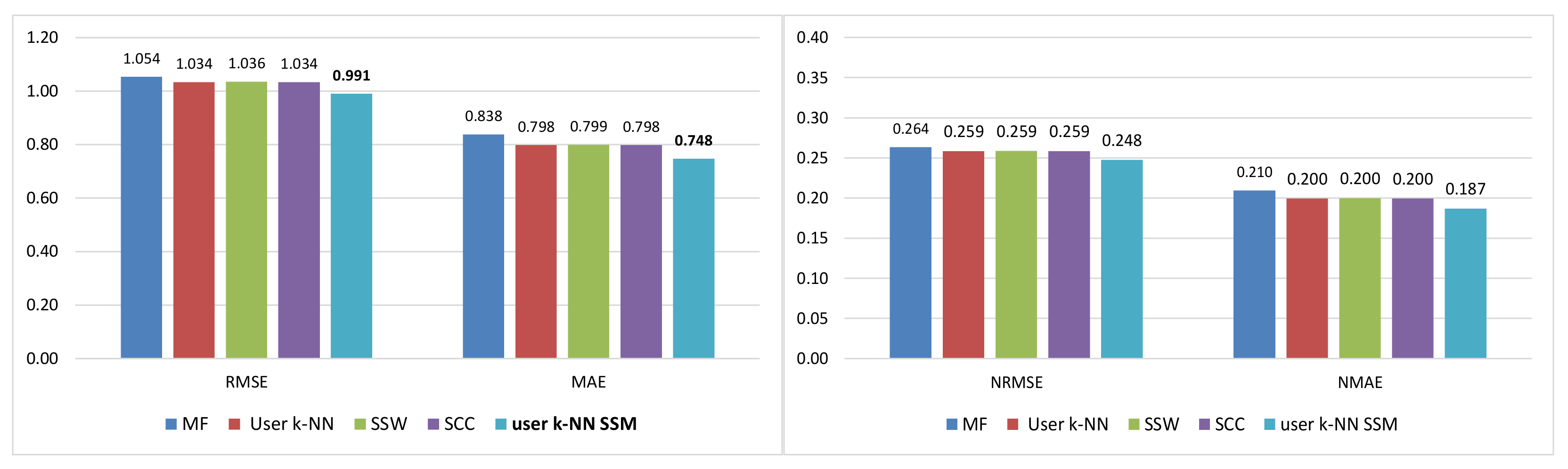
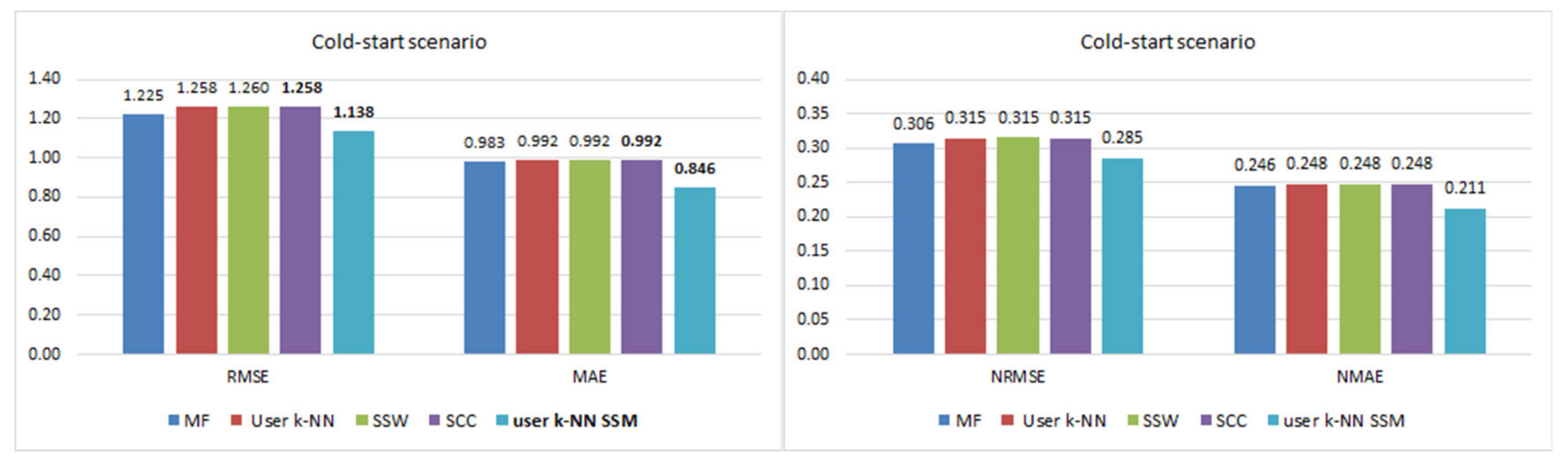
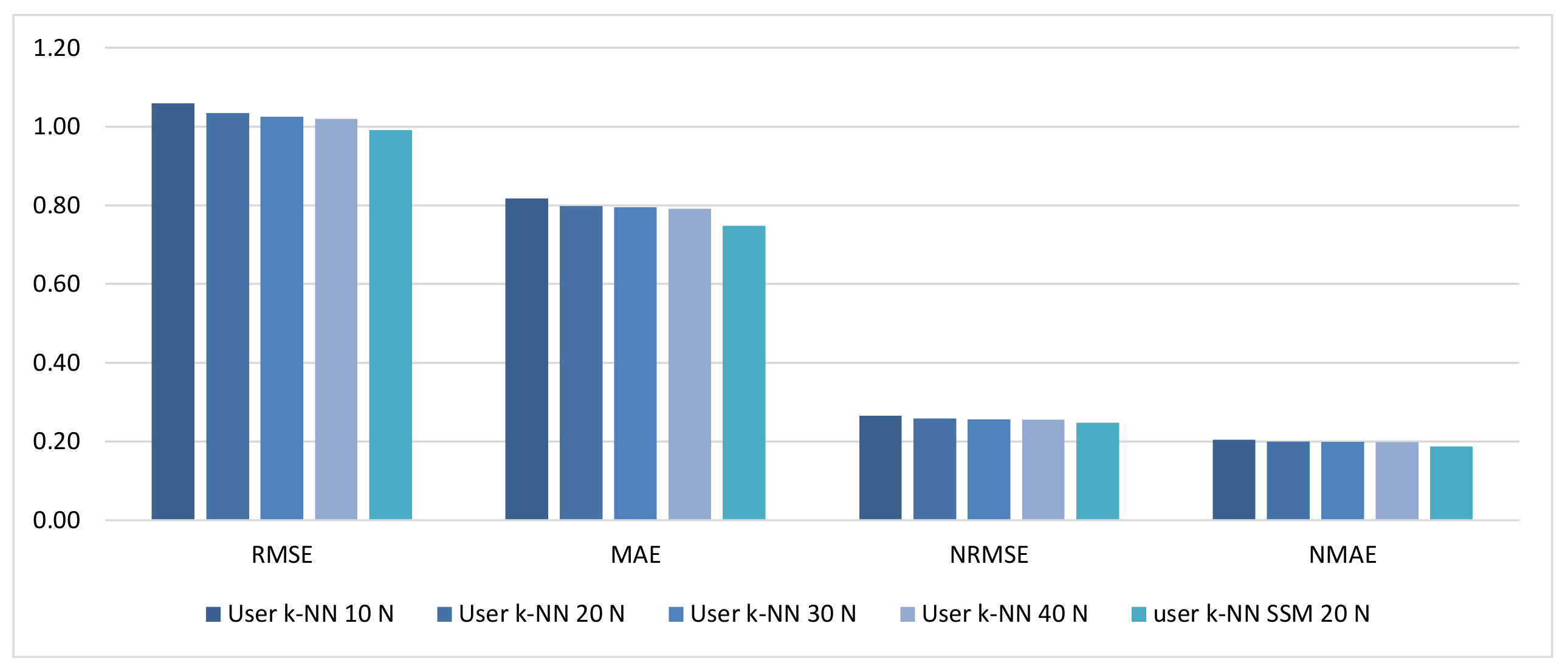
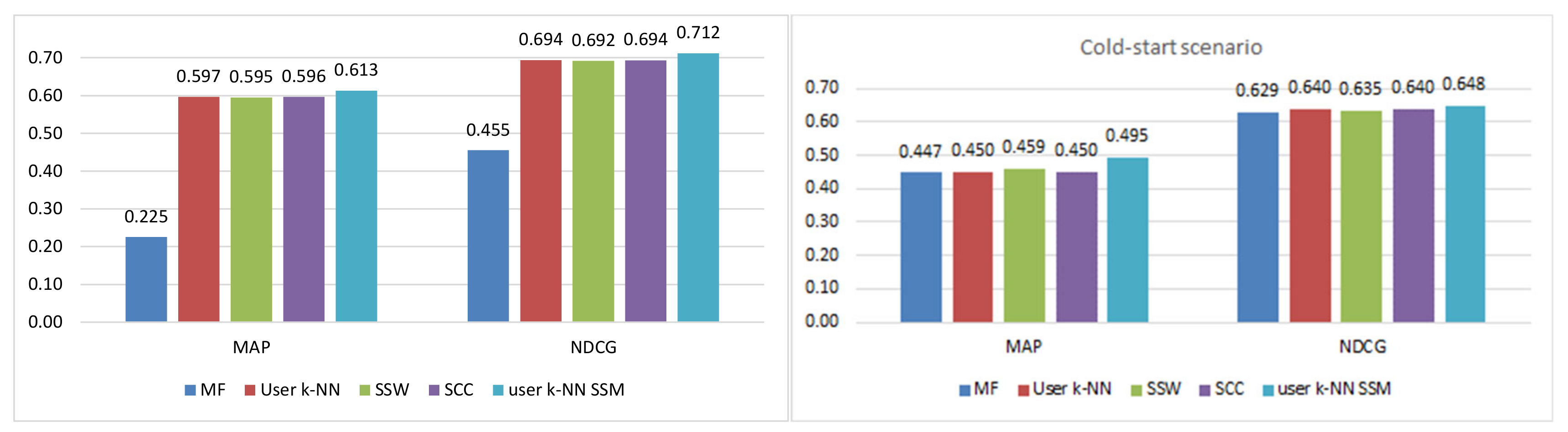
This work addresses the problem of incorporating social information obtained from music streaming systems into CF methods to improve the recommendations provided to users. Although their reliability is taken into account, the improvement is mainly focused on widening their variety by dealing with the problem of the neighborhood bias, which has great importance in this type of systems. To achieve this objective, social structure metrics that capture the concepts of trust and homophily are incorporated into the recommendation process. Our approach differs from existing ones in that social information is not used to modify the value of rating predictions but to complement them. In addition, this proposal significantly improves predictions, while most proposals focus on extending the variety of recommendations at the cost of losing accuracy or maintaining it at best. This improvement is also achieved by using only the limited social data available on streaming platforms.

Another aspect addressed in this paper is the lack of explicit ratings on music items. This inconvenience is overcome by calculating implicit ratings from the frequency of plays, recorded by streaming systems.

The rest of the paper is organized as follows. Section 2 presents a summary of the related work. The approach to incorporate structural metrics into CF methods is described in Section 3. The experimental study conducted to validate the proposal and the discussion of results are included in Section 4. Finally, the conclusions are presented in Section 5.

2. Related Work

Both the use of social information and dealing with bias is the focus of much recent research in recommender systems, but there is little work in the literature in which both topics are addressed together. The objective generally pursued in studies that exploit social information is to improve recommendations by including social data processing into the rating prediction method so that the predicted value is closer to the actual value. This is mostly done by modifying either neighborhood-based CF techniques [4,5] or matrix factorization methods [6]. Regarding the work facing recommendation bias, the main proposals involve data preprocessing as resampling or clustering or postprocessing procedures as reranking, as set out below.

Bias in machine learning models is a widely studied and discussed problem that can be seen from different perspectives. Several types of bias have been studied in the recommender systems area, although most are related to unfair recommendations, from race or gender discrimination [7] to popularity bias [8]. In the former, the problem is usually addressed through recommendation algorithms that are sensitive to this bias and focus on the protection of discriminated groups. Burke et al. [9] introduced the concept of a balanced neighborhood with respect to the protected and unprotected classes to enhance the fairness of recommendations without compromising personalization. In our work context, some artists in the music domain may be harmed by biased recommendations, while user satisfaction may be affected by the limited choice of items that can be recommended to them, especially to the so-called grey sheep users whose tastes are unusual. However, these unfair recommendations are not associated with any specific attribute, such as gender or race.

Popularity bias is mainly associated with neighborhood-based methods, the most frequently used, and is one of the major concerns of recent research in this field. There are proposals for facing this problem that focus on improving recommendations for grey sheep users [10,11], while others are focused on increasing the recommendations of the less frequently rated items and improving item diversity. This can be achieved through probabilistic models [12], data preprocessing [13] or postprocessing [14,15]. There are studies that address aggregate diversity that refers not only to diversity of individual recommendations but also across recommendations of all users [16,17]. The aim of these studies is to improve diversity while maintaining accuracy or with a minimum loss of it. Our proposal is different since it is a user-centered approach, which aims to expand the possibilities of the items to be recommended, but, in this case, by diversifying the user neighborhood. This is done by drawing on factors, such as trust and homophily, derived from the social network structure.

The concept of social trust is the most studied in the literature about recommender systems. It is usually used to give more relevance to the ratings of trusted users against others [18] since it can be considered as a form of social influence that is often obtained from friendship connections, comments, messages, etc. Some systems allow users to explicitly express their trust on opinions, reviews and comments given by other users, but, in most cases, this is not possible, and it is necessary to infer it implicitly [1].

Social trust can be used locally when only opinions of connected friends are taken into account and globally when reputed individuals in the entire network are considered [19]. On the other hand, some approaches use social trust without considering similarity between users, while, in others, it is used jointly with similarity values [20,21] or even with additional factors, such as different types of interactions in social networks [19]. There are many works in the literature where diverse factors affecting social influence are addressed, but most of them are focused on social networks such as Facebook or Twitter, from which a great variety of social information can be extracted.

Homophily and trust are two related concepts [22]. The effect of homophily can even be used for trust prediction [23], although homophily effects have been less studied and are often included in the general study of social influence without explicitly differentiating. Some recent work analyzes the influence of homophily on consumers’ purchasing decisions in the context of YouTube and Instagram influencers’ popularity [24,25]. However, in these works, homophily is treated as a complex factor that encompasses aspects such as attitude, background, morality and appearance. Therefore, it cannot only be inferred from the structure of social relations. In the area of recommender systems, the study of homophily is much scarcer. In [3], recommendations of tourist attractions are generated by classifying users into several types, depending on factors such as homophily. This factor is determined by the membership of users in social communities.

Although trust and homophily principles have been much less studied in the field of music recommendation, we can highlight the work of Fields et al. [26], where music recommendations are based on the social relevance of musical data obtained through complex network technologies. A different objective is pursued in [23], in which the factors influencing the music listening homophily are analyzed. The analysis includes social information and user demographic attributes. None of these studies have addressed the problem of bias in the recommendations.

This section describes relevant work that is closely related to the proposal presented here. However, current approaches to improving recommender systems are many and varied. Among them is the promising field of cognitive computing that would allow an interaction between users and recommender systems similar to human interaction [27]. Emotion and sentiment analysis is also being widely used in the recommendation area, especially in context-aware systems where recommendations depend on the emotional state of the user [28]. Although social information can be used to infer emotions, it is usually textual information from comments or reviews that is not always available [29]. Another trend in this field, although more distant from our proposal, is the research on binary codes that is focused on efficiency and storage optimization in large-scale recommender systems [30].

3. Incorporating Social Structure Metrics into User-Based Collaborative Filtering

Collaborative filtering methods is to predict how much a user would like an item from the ratings that other users have given to that item. User-based or user-user collaborative filtering methods base the recommendations on the similarity between users, considering that two users are similar if they have similarly rated the same items.

Given a set of m users U = {u₁, u₂, …, u_m} and a set of n items I = {i₁, i₂, …, i_n}, each user u_i has a list of ratings that he/she has given to a set of items I_ui, where I_ui ⊆ I. In this context, a recommendation for the active user u_a ∈ U involves a set of items I_ui, where I_ui ⊆ I. In this context, a recommendation for the active user u_a ∈ U involves a set of items I_ra ⊂ I that fulfill the condition I_ra ∩ I_ua = ∅, since only items not rated by u_a can be recommended. The similarity between users is computed from ratings by means of different distance-based measures such as cosine, Chebyshev and Jaccard or correlations coefficients such as Pearson, Kendall and Spearman. Among them, the most extensively used in the field of recommender systems are the Pearson coefficient and cosine similarity. The similarity between the active user $u_a$ and another user $u_i$ is denoted as $sim\left(u_a, u_i\right)$.

$$sim{\left(u_a, u_i\right)}_{Pearson}=\frac{{\sum }_j\left(r_{aj} - {\overline{r}}_a\right)\left(r_{ij} - {\overline{r}}_i\right)}{\sqrt{{\sum }_j{\left(r_{aj} - {\overline{r}}_a\right)}^2{\left(r_{ij} - {\overline{r}}_i\right)}^2}}$$

(1)

where r_aj and r_ij are the ratings of user u_a and user u_i for item i_j, respectively, and ${\overline{r}}_a$ and ${\overline{r}}_i$ are the average ratings of user u_a and user u_i, respectively. The Pearson coefficient can represent inverse and direct correlation with its values in the interval [−1, 1], where the value 0 corresponds to the absence of correlation.

The well-known cosine similarity metric for two given users, u_a and u_i, is computed according to Equation (2), where $V_{u_a}$ ${\mathrm{R}}_{{\mathrm{u}}_{\mathrm{a}}}$ and $V_{u_i}$ are the vectors containing the ratings given to items by users u_a and u_i, respectively.

$$sim\left(u_a, u_i\right)= cos \left(V_{u_a},V_{u_i} \right) =\frac{V_{u_a}, V_{u_i}}{||V_{u_a}|| ||V_{u_i}||}$$

(2)

The items recommended to the active user are the best evaluated by the users most similar to him/her.

CF methods can be improved by introducing social information. Trust and homophily are two factors influencing the recommendations that can be inferred from the structure of relationships between users and other social network resources. However, in most music streaming services, those resources are much more limited, and the structure is restricted to bidirectional friendship relations, which does not allow centrality, page-rank and other graph-based metrics to be applied. In this work, we use the friendship structure to derive trust and homophily factors to include them in the recommendation process.

3.1. Structural Equivalence for Homophily Inference

Structural equivalence is a property applicable to social communities in social networks, often used to identify implicit communities by computing the equivalence similarity between pairs of nodes in the network. Equivalence similarity is based on the overlap between the neighborhood of those nodes. In the context of this work, this metric can be applied to friendship structure whose nodes represent the users. Nodes with high similarity are considered to be part of the same implicit community. This is a way to capture the homophily concept since users belonging to the same community usually share interests and preferences. Therefore, their ratings can be used by the recommendation methods.

Let us consider two nodes representing two users $u_i$ and $u_j$ of the social network, and $\mathrm{N}\left(u_i\right)$ and $\mathrm{N}\left(u_j\right)$ their respective neighborhoods. In this context, two users are only considered neighbors if there is a direct link between them in the friendship structure. A measure of the similarity between a pair of nodes can be defined in terms of the neighbors common to both, as follow:

$$socialSi{m}_{abs}\left(u_i,u_j\right)= \left|N\left(u_i\right)\cap N\left(u_j\right)\right|$$

(3)

To get a similarity value in the range [0, 1], some metrics, such as Jaccard or cosine, can be used for normalization (Equations (4) and (5)). These similarities are used together with the similarities derived from the ratings in the framework proposed in this work.

$$socialSi{m}_{Jaccard}\left(u_i,u_j\right)=\frac{\left|\mathrm{N}\left(u_i\right)\cap \mathrm{N}\left(u_j\right)\right|}{\left|\mathrm{N}\left(u_i\right)\cup \mathrm{N}\left(u_j\right)\right|}$$

(4)

$$socialSi{m}_{Cosine}\left(u_i,u_j\right)=\frac{\left|\mathrm{N}\left(u_i\right)\cap \mathrm{N}\left(u_j\right)\right|}{\sqrt{\left|\mathrm{N}\left(u_i\right)\right|\left|\mathrm{N}\left(u_j\right)\right|}}$$

(5)

A possible problem with the structural equivalency measure lies in the fact that nodes $u_i$ and $u_j$ are excluded from both neighborhoods. Therefore, if those nodes are directly connected and their similarity is very low or even zero, those nodes would not belong to the same community. This is not a drawback in our study since direct friend relationships are also treated in the proposed recommendation approach. The way to approach these types of connections is explained below.

3.2. Friendship Connections for Trust Inference

There are some systems in which users are allowed to make revisions about products and other users can explicitly express their confidence in them by rating such revisions. However, these mechanisms are not available in most systems, so trust has to be inferred from comments, relationships and other types of interaction between users.

On streaming music platforms, bidirectional friendship relationships can be used to infer trust. In the same way that people ask their friends for opinions in the real-world and are influenced by them, users are influenced locally by other users through the friendship connections they establish in social networks. It can be said that users have more trust in those users directly linked to them than the rest. Social trust can be used to improve recommender systems. However, due to the trust that friends exert, the influence is not the same in all circumstances but depends on many factors. If we only focus on the social structure, we can infer trust from the friendship connections.

Any user of the streaming platform can be connected directly with other users of the platform who we call friends. The set of friends of a user $u_i\in U$ is denoted as $F_i\subseteq U$.

We are assuming that the trust of one user in another depends on the influence that the latter has on the former. On the one hand, it seems reasonable that the influence of friends on a given user is greater the fewer friends he has. On the other hand, those users who are more influential are those who have more friends. Taking these premises into account, we can obtain a function that represents the degree of trust that a user has in another user belonging to his group of friends. To establish the relationship between influence and number of friends, we define for each user $u_i$ a logarithmic function of the number of friends:

$$logF\left(u_i\right)=\log \left(\left|F_i\right|\right)$$

(6)

where $F_i$ is the set of friends of the user $u_i$.

From the above equation, we can define the trust of the active user $u_a$ in any of the users $u_f\in F_a$ connected to him directly, that is, his friends in the social network.

$$t \left(u_a,u_f\right)=\frac{1}{1+logF\left(u_a\right)}logF\left(u_f\right)$$

(7)

These values are also used in the proposed recommendation process, which is presented in Section 3.3.

3.3. Recommendation Method Based on Social Structure Metrics

In most recommendation methods that exploit the user’s social context, social information is used to modify the value of the predictions for a given item: it can be used by modifying the similarity between users based on ratings, as a function that combines predictions based on ratings and those based on social information is applied, as social regularization term added to the rating-based function used to make predictions, etc.

The approach proposed in this paper is very different, since our purpose is to use social structure metrics that capture trust and homophily to complement predictions based on ratings, in order to increase the number and variety of recommended items while also increasing the reliability of the recommendations.

The proposed algorithm combines three types of recommendations: based on rating similarity, based on social equivalence similarity and based on friend influence.

3.3.1. Recommendations Based on Rating Similarity

These types of recommendations are those made in traditional CF systems. The procedure for obtaining them is detailed below.

Let us consider the set $U$ of $m$ users and the set $I$, of $n$ items. Each user $u_i\in U$ has rated or interacted with a subset of items I_ui ⊆ I. Ratings are stored in an $m\times n$ matrix $R$ called the rating matrix, where each element is the rating that a user $u_i$ gives to an item $j$.

$$R := r_{i,j}, R ϵ M_{m\times n}\left(\mathbb{N}\right)$$

(8)

When explicit ratings are not available or they are scarce, some strategies to compute implicit ratings can be used. In the field of music, where the items to be recommended are artists or songs, a common way is to calculate them from the frequency of plays. In our case, instead of using binary or simple frequency functions, we apply a linear function of the frequency percentile [31]. In this method, the play frequency for a given user $u_i$ and an item (artist/song) $i_j$ is computed from an $m\times n$ matrix of plays $:= p_{i,j}$, which is analogous to the rating matrix, but contains the number of plays of each user for each artist/song. The play frequency is defined as follows:

$$pFre{q}_{i,j}= \frac{p_{i,j}}{{\sum }_{j’}{p}_{i,j’}}$$

(9)

where p_i,j is the number of times that a user $u_i$ plays an artist/song $i_j$ and j’ represents each of the items (artists/songs) played by user $u_i$.

These items are ordered by their frequency values for the user $u_i$. $Fre{q}_{k’}\left(i\right)$ denotes the frequency $Fre{q}_{i,j}$ of an item $i_j$ with rank $k´$, being k’ = 1 for the artist/song having the highest frequency. A rating for an item with rank k is computed as a linear function of the frequency percentile:

$$r_{i,j}=4 \left(1-{\sum }_{k´=1}^{k-1} \mathrm{p}Fre{q}_{k´}\left(i\right)\right)$$

(10)

The factor with value 4 in the equation is used to obtain rating values in the interval (0, 4].

These implicit ratings are used in the same way as the explicit ones in the CF methods. When using this approach, the recommendations for the active user u_a are calculated from the ratings of other users by means of techniques such as k Nearest Neighbors (k-NN). They require computing the similarity between users by using some of the available metrics. The most used, Pearson correlation coefficient and cosine similarity can be computed by means of Equations (1) and (2), respectively.

The similarity between the active users and the rest of the users, $sim\left(u_a,u_i\right)$, calculated by any of the metrics, is used to predict the rating that the active user would give to an item i_j that he/she has not played yet, by means of Equation (11). Only the set $k\_N{N}_a\subseteq U$ of k nearest neighbors, that is, those with the highest similarity values, will be taken to make the predictions $p{r}_{aj}$.

$$p{r}_{aj}= {\overline{r}}_a+\frac{{\sum }_{i=1}^{k}sim\left(u_a,u_i\right)\left(r_{ij} -{ \mathrm{r} ¯}_i\right)}{{\sum }_{i=1}^k\left|sim\left(u_a,u_i\right)\right|}$$

(11)

where ${\overline{r}}_a$ and ${\overline{r}}_i$ are average values for user $u_a$ and user $u_i$, respectively:

$${\overline{r}}_i= \frac{1}{\left|I_i\right|} {\sum }_{j\in I_i{r}_{ij}}$$

(12)

The recommendations obtained by this method are those used as a starting point in the approach proposed in this paper.

3.3.2. Recommendations Based on Structural Equivalence

A problem that occurs when making the rating prediction for a certain item $j$ by applying the previous procedure derives from the fact that some items whose ratings for the active we want to predict, have not been evaluated by the nearest neighbors. This introduces the neighborhood bias that greatly limits the number of potentially recommendable items for a given user. To address this drawback, we make use of the measures related to structural equivalence that can be obtained from the friendship network.

We introduce the concept of social similarity, $si{m}_{social}\left(u_i,u_j\right),$ as the similarity obtained with any of the equivalence metrics defined in Section 3.1 (Equations (4) and (5)). Social similarity is used jointly with similarity based on ratings $si{m}_{rat}\left(u_i,u_j\right),$ using some combination function. The combined similarity $si{m}_c\left(u_i,u_j\right)$ is used to find a different set $k\_N{N}_{social}{}_a$ of $k$ nearest neighbors for the active user $u_a$, which is defined as follows:

$$k\_N{N}_{social}{}_a\subseteq U$$

(13)

$$k\_N{N}_{social}{}_a= \left\{u_1, u_2, . . ., u_k\right\}$$

(14)

where $si{m}_c\left(u_a,u_1\right)>si{m}_c\left(u_a,u_2\right)>\dots > si{m}_c\left(u_a,u_k\right).$ We use Equation (15) to calculate the combined similarity. In this way, we use the homophily concept to find new users in the social environment of the active user with potentially similar preferences, and whose ratings can be used in the recommendation process.

$$si{m}_c\left(u_i,u_j\right)=\sqrt{\alpha si{m}_{rat}{\left(u_i,u_j\right)}^2+\left(1-\alpha \right) si{m}_{social}{\left(u_i,u_j\right)}^2}$$

(15)

To make the predictions $p{r}_{aj}$ in this case, Equation (11) is also used, but utilizing the combined similarity and with a different set of neighbors. The set $k\_N{N}_{social}{}_a$ obtained from social similarities is used instead of the set based on rating similarity.

3.3.3. Recommendations Based on Friendship Connections

Analogous to the process described in the previous subsection, we can exploit the concept of trust derived from the friendship connections to find users who are likely to influence the preferences of the active user. Then, a new subset of k nearest neighbors, $k\_N{N}_{friends}$, is formed with the most influential friends of the active user.

To determine the degree of influence or trust, $t\left(u_a,u_f\right)$, of a friend $u_f\in F_a$ on the active user $u_a$, we make use of the Equations (6) and (7). This value is used in Equation (18) to predict the ratings for the active user. Within the set of friends of $u_a$, the subset of the k nearest neighbors used to compute the predictions for $u_a$ is defined as follows:

$$k\_N{N}_{friends}{}_a\subseteq U$$

(16)

$$k\_N{N}_{friends}{}_a= \left\{u_1, u_2, . . ., u_k\right\} \left| t\left(u_a,u_1\right)\right.〉 t\left(u_a,u_2\right)>\dots >t\left(u_a,u_k\right)$$

(17)

This type of recommendations, based on trust between friends, are obtained by using the set of nearest neighbors $k\_N{N}_{friends}{}_a$ and Equation (18), in which the rating-based similarity is multiplied by a weight given by that trust.

$$p{r}_{aj}= {\overline{r}}_a+\frac{{\sum }_{i=1}^{k}t \left(u_a,u_f\right) sim\left(u_a,u_i\right)\left(r_{ij} -{ \overline{\mathrm{r}}}_i\right)}{{\sum }_{i=1}^k\left|t \left(u_a,u_f\right)sim\left(u_a,u_i\right)\right|}$$

(18)

3.3.4. Recommendation Algorithm

The idea of the approach proposed in this paper is to complement the recommendations generated by traditional collaborative filtering methods with recommendations based on the structure of the users’ social network. Thus, all types of recommendations described in the previous subsections are involved in the recommendation algorithm. The goal is to increase the number of predictions in order to expand the set of potentially recommendable items and reduce the neighborhood bias, while improving the reliability of the recommendations. The algorithm is shown in Figure 1.

The only input data required by the algorithm is the matrix of plays $P := p_{i,j}$, defined in Section 3.3.1, and the matrix of friends $F$, defined as follows:

$$F := f_{i,j},F ϵ M_{m\times m}\left(\mathbb{N}\right) | f_{i,j}=\left\{\begin{array}{c}1, u_i is friend of u_j\\ 0, otherwise \end{array}\right.$$

(19)

Prior to the recommendation process, it is necessary to calculate the implicit ratings from the play matrix according to the procedure described in Section 3.3.1. Steps 3–13 of the algorithm are those corresponding to this calculation from which the matrix of ratings $R$ is obtained.

Similarities based on ratings, social and combined similarities and trust $t\left(u_i,u_j\right)$ between users are calculated in Steps 14–17. Steps 17–23 are devoted to obtaining the different sets of k nearest neighbors. First, the value of $k$ is set, and then the sets $k\_N{N}_i$,$k\_N{N}_{social}{}_i$ and $k\_N{N}_{friends}{}_i$ for each user $u_i$ are created.

Subsequent steps contain the complete recommendation process for a given active user $u_a$. The basic CF method is first applied using the set of the nearest neighbors $k\_N{N}_a$ obtained from the rating-based similarities, according to the procedure described in Section 3.3.1. The number of predictions $p{r}_{aj}$ obtained in this way is lower than all the possible ones since many items have not been rated by the users who are in the set $k\_N{N}_a$. To achieve a greater number of predictions, the procedures defined for making both predictions based on structural equivalence (Section 3.3.2) and predictions based on friendship connections (Section 3.3.3) are applied. This last one is applied first to the items without predicted ratings by the basic CF method, and the ratings for the remainder items are tried to be predicted from the set of k nearest neighbor $k\_N{N}_{social}{}_a$.

4. Validation of the Proposed Approach

4.1. Dataset

Since our proposal is specifically designed for the field of music recommendation, its validation was carried out with a dataset obtained from Hetrec2011-lastfm [32]. The only information needed to apply the recommendation method is the data about the playing songs by users, in particular the number of plays, as well as the friendship connections between users in the social network of the streaming system.

The play frequency is used to compute implicit ratings according to the procedure described in Section 3.3.1. The availability of implicit or explicit ratings is a prerequisite for applying CF techniques since user similarities are based on these ratings. Friendship connections are required to compute social structure metrics, used in this work to extend the basic CF methods in the previously explained manner.

4.2. Baseline Methods

To validate the proposed method, its results were compared with those of other proposals in the literature. For this purpose, two methods that do not use social information and two other methods that make use of information inferred from the friendship structure of the social network were tested with the same dataset. Among the former, the most representative ones were chosen, user-based k-NN and matrix factorization. Among those that exploit social information, the baseline methods were an approach in which CF is constrained to the user social context (SCC) and another that combines social similarities and rating-based similarities (SSW).

The tested user-based k-NN method is the same one described in Section 3.3.1, while matrix factorization is a well-known technique in the area of recommender systems.

The methods that constrain CF to the social context are those in which the set of nearest neighbors is formed only with users connected directly to the active user $u_a$, i.e., their friends ($k\_NN\subseteq F_a$) [22]. Similarity metrics used to find the neighbors are based on ratings, no social similarity metrics are applied. The procedure for making predictions can be the same as in user-based k-NN (Equation (11)).

Regarding the last type of methods, these make use of some function to combine social similarities,$si{m}_{social}\left(u_i,u_j\right), and$ rating-based similarities, $si{m}_{rat}\left(u_i,u_j\right)$. Then, the final similarity is used in the prediction of ratings. In this case, user-based k-NN and Equation (11) can also be utilized. The set $k\_NN$ is created by using the combined similarity $si{m}_c\left(u_i,u_j\right)$ defined by Equation (15).

The specific social similarity used in our study is based on structural equivalence and α was set to 0.7.

There are other methods that extend matrix factorization approaches to incorporate social data, but we only tested k-NN-based approaches because these give better results than matrix factorization, as can be seen in the following section.

4.3. Empirical Study

This study was conducted to compare the proposed approach against the baseline methods. The metrics used to evaluate rating prediction reliability were Root-Mean-Square Error (RMSE), Mean Absolute Error (MAE), Normalized RMSE (NRMSE) and Normalized MAE (NMAE). Mean Average Precision (MAP) and Normalized Discounted Cumulative Gain (NDCG) were used for the evaluation of top-N recommendations. In all the experiments, five-fold cross validation was applied.

The first step of the study was to determine the number of nearest neighbors to use in k-NN-based methods. Thus, the results of the application of the user-based k-NN method were compared with a variable number of neighbors, from 10 to 40. Figure 2 shows the error rates produced. Since the increase of k value from 20 produces a very small decrease in errors, we decided to conduct the tests with k = 20.

The comparative study of different methods was then carried out to validate our proposal. The value k = 20 was used in all methods, except for Matrix Factorization (MF) since it is not a k-NN-based technique. In addition, the rating-based similarities of all k-NN-based methods were calculated using the cosine metric. Social similarities were obtained with the Jaccard equivalence similarity metric.

In addition to the study carried out with all the users in the dataset, we also studied the behavior of our proposal for the cold-start scenario. As mentioned above, this is a problem of CF methods that occurs mainly with new users because they have a few ratings/interactions with the items. In that case, the recommendations they receive are not very reliable.

To determine the performance on the cold-start scenario, the users with a low number of plays in relation to the other users were selected. Only the records of these users were kept in the test sets of all the folds, the rest was eliminated. In this case three-cross-validation was applied since the number of users was much lower. Taking into account that the average number of plays per user in the dataset is 37,275, the users with fewer than 2000 plays were selected.

Figure 3 shows the error rates of the methods. When comparing the two basic methods MF and user k-NN, a better behavior of the latter is observed. Regarding the methods that exploit social information, we see that no improvements are obtained with respect to k-NN but the results are even worse, both with CF restricted to the user social context (SCC) and with the method using weighted social and rating-based similarities (SSW). However, our proposal to combine user k-NN with Social Structure Metrics (user k-NN SSM) provides a clear improvement over all baseline methods.

Table 1. Improvement of user k-NN SSM over the baseline methods for all users (left) and for users with the cold-start problem (right).

	All Users		Cold-Start
Baseline Method	RMSE	MAE	RMSE	MAE
MF	6.00%	10.79%	7.06%	13.96%
User k-NN	4.18%	6.32%	9.51%	14.76%
SSW	4.34%	6.46%	9.66%	14.77%
SCC	4.18%	6.32%	9.51%	14.76%

shows this percentage improvement for RMSE and MAE.

Figure 4 presents the results obtained in the cold-start scenario. As expected, the errors are higher than those obtained with all users, although user k-NN SSM is again the method with the lowest error rates. We can see in Table 1 that the percentages of improvement are even better for this scenario than for the previous one. The figure also shows that, in this case, MF provides better results than the other KNN-based methods. This can be explained by the fact that matrix factorization approaches behave better against sparsity.

However, the goal of our work is not only to improve the reliability of the rating predictions, but also to increase their number in order to have more potentially recommendable items. This way we would be able to increase the variety of recommendations and minimize the bias toward the most popular items.

A way to increase the number of predictions while decreasing their errors is to work with larger sets of nearest neighbors, although we previously showed that the improvement in predictions is very small above 20 neighbors. Figure 5 shows this decrease in error rates for user k-NN from 10 to 40 neighbors, as well as for the proposed method, user k-NN SSM, with 20 neighbors. We can see that the lowest error rates are given by our proposal even compared to user k-NN errors with a larger number of neighbors.

Since the main objective of the work is to increase the number of potentially recommendable items, we must demonstrate that our approach covers more rating predictions on the items in the test set. Figure 6 shows the coverage for both methods in each cross-validation fold. The graph on the left shows the results obtained for all users and the graph on the right those for users with few plays (cold-start). This graph clearly shows the significant increase in coverage over the k-NN method. Most methods that focus on expanding coverage result in increased error rates and their goal is usually to keep this increase to a minimum. In the case of our proposal, however, the errors actually decrease.

Finally, to confirm the validity of the approach presented in this paper, the evaluation was also performed for top-N recommendations. In the rating prediction validation, errors were calculated for all predicted ratings. However, it is also necessary to make the validation for the lists of items with the highest ratings values because those items are the ones that are recommended to the user. Thus, we ensure that the higher reliability of the proposal is not only due to the predictions of low values but also to the predictions of the high values that are the most interesting for recommendation. We used the rank-based metrics MAP and NDCG for top-N lists where N was set to 5. Figure 7 shows these results, which prove that the best performance of the proposed method is also achieved for top-N recommendations. The behavior is similar in both scenarios, although, as in the case of rating prediction, in the cold-start scenario lower values of these metrics are obtained.

4.4. Discussion

The above results prove that the proposed method increases the coverage of the recommendations in relation to the potentially recommendable items. Furthermore, this increase does not come at the expense of the recommendation reliability but, on the contrary, results in an error decrease in predicting the ratings of these items as well as in an increase in the values of the rank-based metrics used to evaluate the quality of the recommended top-N lists. In the different proposals in the literature related to our work, as far as we know, both improvements are not obtained together. In addition, most of these works address the popularity bias while our aim is to increase the spectrum of potentially recommendable items regardless of whether these items are popular or not. We also did not find any work that uses social connections to expand the neighborhood in CF methods. Below, we discuss the differences between our proposal and some relevant work aimed at improving the diversity of the recommendations.

The re-ranking approach [14], which involves changing the ranking of items, addresses the popularity bias and improves recommendation diversity, but at the expense of recommendation accuracy. The local scoring model presented in [33] aiming at dealing with scalability and sparsity problems, provides a more efficient way to select the best neighbors and improves the recommendation diversity without compromising accuracy. In [16], a graph-based method that maximizes diversity for a given level of accuracy is presented. In the trade-off between diversity and accuracy shown in the work, it can be seen that as the diversity increases, the accuracy decreases, although more slowly than using the re-ranking-based methods. A more recent graph-based approach also focused on increase the recommendations of unpopular items is proposed in [17]. Although this proposal also does not improve accuracy when increasing diversity, it manages to maintain it, which is an important advantage over other methods. The calibration, a problem related to diversity is studied in [13]. The purpose is dealing with the problem that recommendations are biased to the main areas of interest of a user instead of proportionally reflecting the different interests of the user. This work shows that as the degree of calibration increases, the accuracy decreases.

Since the objective of the previous work is not exactly the same as ours, we cannot make comparisons with the coverage results obtained with our proposal. However, none of these methods improve accuracy and ours does. Another difference that could be considered a disadvantage of our method with respect to others is the need for social information, in addition to ratings. Although this information is restricted to friendship connections and is easily obtainable from streaming platforms.

5. Conclusions

The growing use of music streaming services and the interest in their personalization is unquestionable nowadays. Thus, this is one of the main motives why the surge in intensive research in many areas on the exploitation of information from social networks has been extended to music recommender systems.

In this work, an approach focused on exploiting social information available on streaming music platforms is proposed. It is a collaborative filtering scheme that extends classical methods based on nearest neighbors by using structural metrics obtained from the network of user friendships. The goal is to minimize the neighborhood bias as well as to increase the reliability of recommendations. The proposal differs from others in the literature in the fact that it is a user-centered approach instead of being centered on items. In addition, it is not specifically addressed to increase the diversity or reduce popularity bias but to extend and diversify the user neighborhood by exploiting user social context. The results show that the proposed approach outperforms other methods in both reducing prediction error rates and increasing the number of potentially recommendable items.