2. Related Work
Artificial Neural Networks (ANNs) are structures composed of groups of simple and complex cells. Simple cells are responsible for extracting basic features, while complex ones combine local features producing abstract representations [
8]. This structure hierarchically manipulates data through layers (complex cells), each using a set of processing units or neurons (simple cells) to extract local features. In classification tasks, each neuron divides input data space using a linear function (i.e., hyperplane), which is positioned to obtain the best separation as possible between labels of different classes. Thus, the connections among processing units are responsible for combining the half-spaces built up by those linear functions to produce nonlinear separability of data spaces [
1]. Deep Neural Networks (DNNs) are artificial neural network models that contain a large number of layers between input and output, generating more complex representations. Such networks are called convolutional neural networks (CNNs) when convolutional filters are employed.
In the past few years, the use of visualization tools and techniques to support the understanding of neural network models has become more prolific, with many different approaches focusing on exploring and explaining different aspects of DNN training, topology, and parametrization [
9]. As deep models grow more complex and sophisticated, understanding what happens to data inside these systems is quickly becoming key to improving their efficiency and designing new solutions.
When exploring layers of a DNN, a common source of data are the hidden layer
activations: the output value of each neuron of a given layer when subjected to a data instance (input). Many DNN visualization approaches are focused on understanding the high-level abstract representations that are formed in hidden layers. This is often attained by transferring the activations of hidden layer neurons back to the feature space, as defined by the Deconvnet [
10] and exemplified by applications such as the Deep Dream [
11]. Commonly associated with CNNs, techniques based on this approach often try to explain and represent which feature values in a data object generate activations in certain parts of hidden layers. The Deconvnet is capable of reconstructing input data (images) at each CNN layer to show the features extracted by filters, supporting the detection of incidental problems based on user inspections.
Other techniques focus on identifying content that activates filters and hidden layers. Simonyan et al. [
12] developed two visualization tools based on Deconvnet to support image segmentation, allowing feature inspection and summarization of produced features. Zintgraf et al. [
13] introduced a feature-based visualization tool to assist in determining the impact of filter size on classification tasks and identifying how the decision process is conducted. Erhan et al. [
14] proposed a strategy to identify features detected by filters after their activation functions, allowing the visual inspection of the impact of network initialization as well as if features are humanly understandable. Similarly, Mahendran et al. [
15] presented a triple visualization analysis method to inspect images. Babiker et al. [
16] also proposed a visual tool to support the identification of unnecessary features filtered in the layers. Liu et al. [
17] present a system capable of showing a CNN as an acyclic graph with images describing each filter.
Other methods aim to explore the effects of different parameter configurations in training, such as regularization terms or optimization constraints [
5]. These can also be connected to different results in layer activations or classification outcomes. Some techniques are designed to help evaluate the effectiveness of specific network architectures, estimating what kind of abstraction can be learned in each section, such as the approach described by Yosinki et al. [
18].
The research previously described is focused on identifying and explaining
what representations are generated. However, it is also important to understand
how those representations are formed, regarding both the training process and the flow of information inside a network. Comprehending these aspects can lead to improvements in network architecture and the training process itself. The DeepEyes framework, developed by Pezzotti et al. [
19], provides an overview of DNNs identifying when a network architecture requires more or fewer filters or layers. It employs scatterplots and heatmaps to show filter activations and allows the visual analysis of the feature space. Kahng et al. [
20] introduce a method to explore the features produced by CNN’s projecting activation distances and presenting a neuron activation heatmap for specific data instances. However, these techniques are not designed for projecting multiple transition states, and their projection methods require complex parametrization to show the desired information.
Multidimensional projections (or dimensionality reduction techniques) [
2] are popular tools to aid the study of how abstract representations are generated inside ANNs. Specific projection techniques, such as the UMAP [
21], were developed particularly with machine learning applications in mind. While dimensionality reduction techniques are generally used in ANN studies to illustrate model efficacy [
4,
5,
22,
23,
24], Rauber et al. [
3] showed their potential on providing valuable visual information on DNNs to improve models and observe the evolution of learned representations. Projections were used to reveal hidden layer activations for test data before and after training, highlighting the effects of training, the formation of clusters, confusion zones, and the neurons themselves, using individual activations as attributes. Despite offering insights on how the network behaves before and after training, the visual representation presented by the authors for the evolution of representations inside the network or the effects of training between epochs displays a great deal of clutter; when analyzing a large number of transition states, information such as the relationships between classes or variations that occur only during intermediate states may become difficult to infer. Additionally, the method used to ensure that all projections share a similar 2D space is prone to problems in alignment. In this paper, we propose a visualization scheme that employs a flow-based approach to offer a representation better suited to show transition stated and evolving data in DNNs. We also briefly address certain pitfalls encountered when visualizing neuron activation data using standard projection techniques, such as t-SNE [
25], and discuss why these pitfalls are relevant to our application.
3. Visualizing the Activity Space
Our visual representation is based on gathering hidden layer activation data from a sequence of ANN outputs (steps), then projecting them onto a 2D space while sharing information to ensure semantically similar data remain in similar positions between projections. The movement of the same data instance throughout each projected step generate trajectories, which are then condensed into vector fields that reflect how data flows throughout the sequence. There are two main sequential aspects to be visualized with ANN outputs: how abstract data representations inside the network change and evolve with training and how representations are built and connected as one layer forwards information to the next. For each aspect, a different sequence of hidden layer outputs is needed: outputs from the same given layer during different epochs of training are used to visualize how training changes data representations in that layer, while outputs from different layers from the same network are used to visualize how data representations evolve as layers propagate information.
To build this representation, we first extract activation sets representing network outputs from T sequential steps of the process we want to explore. In this paper, we either (a) save a network model at different epochs of training, choose a slicing layer, feed the same set of input data to the saved models, and then save the outputs from the slicing layer, or (b) pick a given network model, slice it at different layers, feed the input data set, and save the outputs from these layers as activation sets.
Once the activation data are extracted, it is projected onto a 2D space using a multidimensional projection technique, obtaining
. To produce coherent projections, an alignment method is applied, ensuring that projections stay similar to each other while preserving original multidimensional distances. Then, positions of the same points in two subsequent projections form movement vectors
that describe how data instances in one output changed to the next. This movement data are joined for all output transitions, generating trajectories (or
trails) for each data instance across all
T steps, which are then used to compute vector fields. Finally, projections, trajectories, and vector fields are combined to create visualizations. The 2D space shared by all projections is our
visual activity space, and trajectories and vector fields describe how network outputs flow through it.
Figure 1 summarizes this process.
The following sections detail how data are projected, and how vector fields are generated and visualized in our model.
Author Contributions
Conceptualization, G.D.C. and F.V.P.; data curation, G.D.C.; investigation, G.D.C.; methodology, G.D.C.; supervision, F.V.P.; validation, E.E.; visualization, G.D.C.; writing—original draft, G.D.C.; writing—review & editing, E.E. and F.V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank CAPES and FAPESP (2017/08817-7, 2015/08118-6) for the financial support. We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC).
Conflicts of Interest
The authors declare no conflict of interest.
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Nonato, L.G.; Aupetit, M. Multidimensional Projection for Visual Analytics: Linking Techniques with Distortions, Tasks, and Layout Enrichment. IEEE Trans. Vis. Comput. Graphics 2018, 25, 2650–2673. [Google Scholar] [CrossRef]
- Rauber, P.E.; Fadel, S.G.; Falcao, A.X.; Telea, A.C. Visualizing the hidden activity of artificial neural networks. IEEE Trans. Vis. Comput. Graphics 2017, 23, 101–110. [Google Scholar] [CrossRef]
- Mahendran, A.; Vedaldi, A. Understanding deep image representations by inverting them. In Proceedings of the IEEE IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5188–5196. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Cantareira, G.D.; Paulovich, F.V.; Etemad, E. Visualizing Learning Space in Neural Network Hidden Layers. In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Valetta, Malta, 27–29 February 2020; pp. 110–121. [Google Scholar] [CrossRef]
- Cantareira, G.D.; Paulovich, F.V. A Generic Model for Projection Alignment Applied to Neural Network Visualization. EuroVis Workshop on Visual Analytics (EuroVA); Turkay, C., Vrotsou, K., Eds.; The Eurographics Association: Aire-la-Ville, Switzerland, 2020. [Google Scholar] [CrossRef]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2010; pp. 92–101. [Google Scholar]
- Hohman, F.M.; Kahng, M.; Pienta, R.; Chau, D.H. Visual Analytics in Deep Learning: An Interrogative Survey for the Next Frontiers. IEEE Trans. Vis. Comput. Graphics 2018, 25, 2674–2693. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Zintgraf, L.M.; Cohen, T.S.; Adel, T.; Welling, M. Visualizing deep neural network decisions: Prediction difference analysis. arXiv 2017, arXiv:1702.04595. [Google Scholar]
- Erhan, D.; Bengio, Y.; Courville, A.; Vincent, P. Visualizing higher-layer features of a deep network. Univ. Montr. 2009, 1341, 1. [Google Scholar]
- Mahendran, A.; Vedaldi, A. Visualizing deep convolutional neural networks using natural pre-images. Int. J. Comput. Vis. 2016, 120, 233–255. [Google Scholar]
- Babiker, H.K.B.; Goebel, R. An Introduction to Deep Visual Explanation. arXiv 2017, arXiv:1711.09482. [Google Scholar]
- Liu, M.; Shi, J.; Li, Z.; Li, C.; Zhu, J.; Liu, S. Towards better analysis of deep convolutional neural networks. IEEE Trans. Vis. Comput. Graphics 2017, 23, 91–100. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Nguyen, A.; Fuchs, T.; Lipson, H. Understanding neural networks through deep visualization. arXiv 2015, arXiv:1506.06579. [Google Scholar]
- Pezzotti, N.; Höllt, T.; Van Gemert, J.; Lelieveldt, B.P.; Eisemann, E.; Vilanova, A. Deepeyes: Progressive visual analytics for designing deep neural networks. IEEE Trans. Vis. Comput. Graphics 2018, 24, 98–108. [Google Scholar] [CrossRef]
- Kahng, M.; Andrews, P.Y.; Kalro, A.; Chau, D.H.P. A cti V is: Visual Exploration of Industry-Scale Deep Neural Network Models. IEEE Trans. Vis. Comput. Graphics 2018, 24, 88–97. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Donahue, J.; Jia, Y.; Vinyals, O.; Hoffman, J.; Zhang, N.; Tzeng, E.; Darrell, T. Decaf: A deep convolutional activation feature for generic visual recognition. In Proceedings of the International conference on machine learning, Beijing, China, 21–26 June 2014; pp. 647–655. [Google Scholar]
- Hamel, P.; Eck, D. Learning features from music audio with deep belief networks. ISMIR 2010, 10, 339–344. [Google Scholar]
- Mohamed, A.r.; Hinton, G.; Penn, G. Understanding how deep belief networks perform acoustic modelling. Neural Netw. 2012, 6–9. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Hinton, G. Visualizing high-dimensional data using t-sne. journal of machine learning research. J. Mach. Learn. Res. 2008, 9, 26. [Google Scholar]
- Joia, P.; Coimbra, D.; Cuminato, J.A.; Paulovich, F.V.; Nonato, L.G. Local affine multidimensional projection. IEEE Trans. Vis. Comput. Graphics 2011, 17, 2563–2571. [Google Scholar] [CrossRef]
- Rauber, P.E.; Falcão, A.X.; Telea, A.C. Visualizing time-dependent data using dynamic t-SNE. In Eurographics/IEEE VGTC Conference on Visualization; Eurographics Association: Goslar, Germany, 2016; pp. 73–77. [Google Scholar]
- Hilasaca, G.; Paulovich, F. Visual Feature Fusion and its Application to Support Unsupervised Clustering Tasks. arXiv 2019, arXiv:1901.05556. [Google Scholar] [CrossRef]
- Wattenberg, M.; Viégas, F.; Johnson, I. How to use t-sne effectively. Distill 2016, 1, e2. [Google Scholar] [CrossRef]
- Ferreira, N.; Klosowski, J.T.; Scheidegger, C.E.; Silva, C.T. Vector Field k-Means: Clustering Trajectories by Fitting Multiple Vector Fields. Comput. Graph. Forum. 2013, 32, 201–210. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W.; Li, S. From numerics to combinatorics: A survey of topological methods for vector field visualization. J. Vis. 2016, 19, 727–752. [Google Scholar] [CrossRef]
- Sanna, A.; Montuschi, P.; Montuschi, P. A Survey on Visualization of Vector Fields By Texture-Based Methods. Devel. Pattern Rec. 2000, 1, 2000. [Google Scholar]
- Peng, Z.; Laramee, R.S. Higher Dimensional Vector Field Visualization: A Survey. TPCG 2009, 149–163. [Google Scholar] [CrossRef]
- Bian, J.; Tian, D.; Tang, Y.; Tao, D. A survey on trajectory clustering analysis. arXiv 2018, arXiv:1802.06971. [Google Scholar]
- Kong, X.; Li, M.; Ma, K.; Tian, K.; Wang, M.; Ning, Z.; Xia, F. Big Trajectory Data: A Survey of Applications and Services. IEEE Access 2018, 6, 58295–58306. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hurter, C.; Ersoy, O.; Fabrikant, S.I.; Klein, T.R.; Telea, A.C. Bundled visualization of dynamicgraph and trail data. IEEE Trans. Vis. Comput. Graphics 2013, 20, 1141–1157. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
Figure 1.
Overview of the learning space vector field generation. From a DNN model, we obtain sequential data in the form of hidden layer activations. We compute projections from this highly multivariate data, aligning them to ensure that obtained projections are synchronized. Differences between each pair of projections in the sequence (transition steps) are turned into trajectories and then processed to obtain vector fields representing changes in data. Finally, everything is combined to compose distinct visual representations of the neural network.
Figure 2.
Example of visual representations for projection, trajectory, and vector field components stacked together. The vector field representation overviews the whole flow of the data inside a network, supporting the analysis of instance grouping over time. The scatterplot metaphor, used to represent a projection, enables the analysis of specific instances at a particular moment in time, and trajectory bundling can be used to derive insights about instances’ behavior over time. Together, these representations define a powerful visual metaphor, providing abstract and detailed views of the dynamics of neural networks.
Figure 3.
Outputs from the last hidden layer of a 4-layer MLP were gathered during training, after 0, 1, 3, and 20 epochs. Projected data refer to a sample of MNIST test set, with 2000 instances. Instance projected position at each epoch define trajectories that were used to approximate vector fields, as shown on the right side of the figure. A clear expansion pattern can be observed, as instances move outwards to form groups as the network is trained.
Figure 4.
Outputs from the last hidden layer of a 4-layer MLP after 20 training epochs, using MNIST test data input, projected over streamlines. Streamlines are calculated based on three other outputs from the same layer during training, at epochs 0, 1, and 3. Activity between projections is turned into a vector field, which is then used to generate streamlines that offer additional insight into data flow during training without displaying points from other projections. For streamlines, color intensity represents flow speed (L2 norm of vectors) and arrows indicate direction.
Figure 5.
Trajectory data from the same outputs as the
Figure 4 (last hidden layer of MLP after 20 epochs using MNIST test data as input). Lines start from instance positions at epoch 0 and end in instance positions at epoch 20. Control points were set along the streamlines defined previously, attracting lines near them into bundles.
Figure 6.
When visualizing trajectories, it is possible to highlight the ones that attained high error values when approximating the vector field, in search of outliers. (a) shows trajectories with the error above a certain threshold (0.1) highlighted in red, while all others are shown in black; (b) filters the projection to only instances corresponding to label “7”, which seem to contain a few outliers. Data points were plotted again and colored according to which feature set they were taken from, so trajectory direction can be better understood. In this case, the highlighted trajectories move through long distances, at times in the exact opposite way of the vector field.
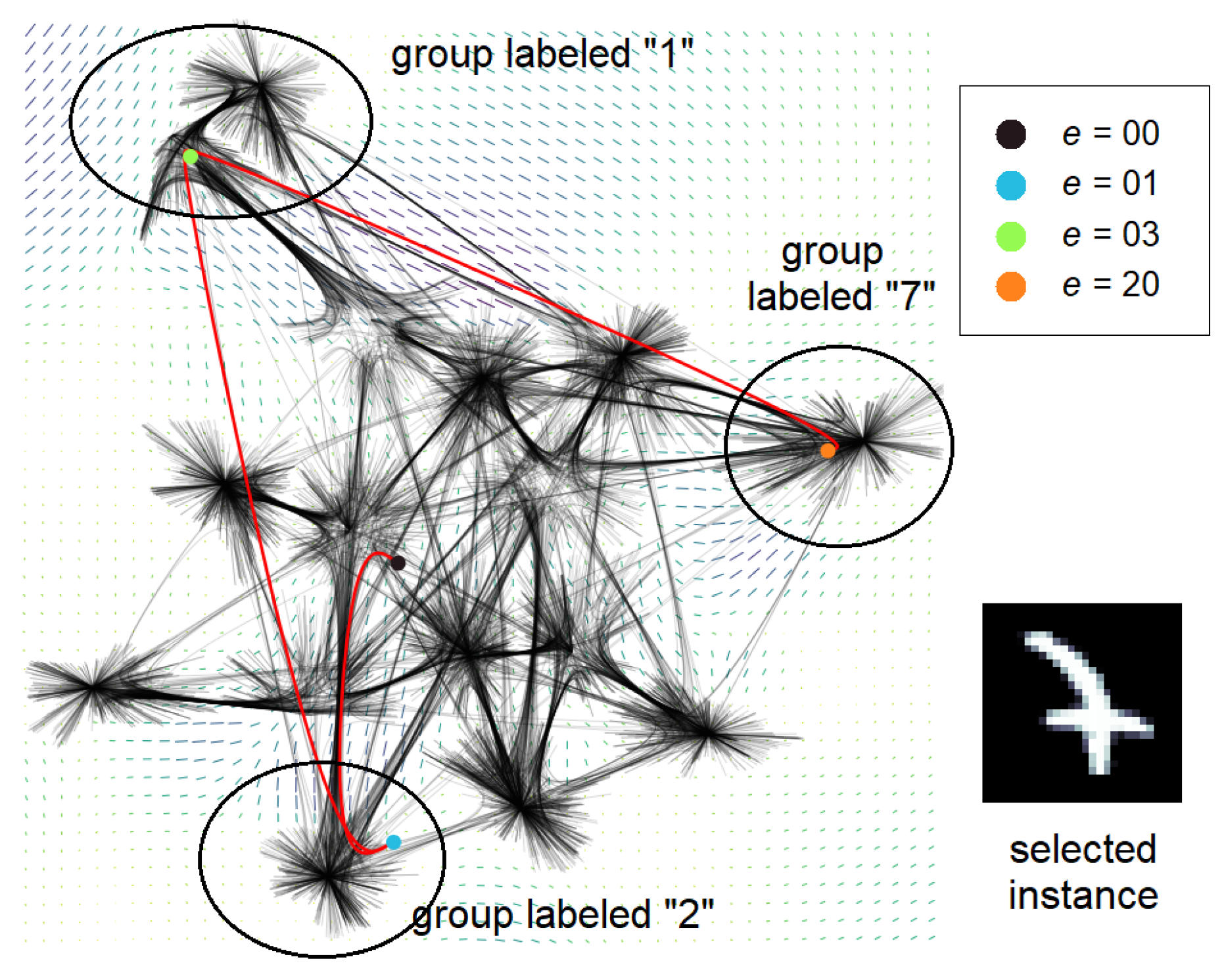
Figure 7.
A single outlier trajectory is selected for examination. This data point was at the middle area at epoch 0, moved to an area containing many examples labeled as “2” at epoch 1, moved again to an area containing examples labeled “1” at epoch 3, and finally moved to another area, which contains a group of examples labeled “7”, at epoch 20. We can then examine the instance to search for reasons behind this atypical behavior.
Figure 8.
Projected sequential output data from six hidden layers of pre-trained MobileNetV2 using 1000 ImageNet inputs. Projections are shown in left-to-right, upper-to-lower order. It is possible to notice that, while still concentrated in the middle area in the first upper projections, points are slowly separated into classes before finally expanding in the last two projections. On the right side is the generated vector field. A high concentration of movement in all directions in the middle area makes the resulting field rather muted, but its intensity increases in outer areas of the image.
Figure 9.
(a) projection from the last hidden layer of MobileNetV2 (global average pooling layer) over streamlines from movement trajectories of previous layers. It is possible to see paths that led from a central position to the positions occupied at the current projection, for all points; (b) trajectories of points over six layer outputs in the same network model. There is a high amount of clutter in the central section due to the resulting projections of the first layers, but certain movement patterns can be identified. Projected data are obtained using 1000 ImageNet data samples.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).