A Note on Ultrametric Spaces, Minimum Spanning Trees and the Topological Distance Algorithm
Abstract
:1. Introduction
2. Greedy Algorithms and Optimality Results
2.1. Introduction and Notation
- M1
- (trivial axiom).
- M2
- implies (hereditary axiom).
- M3
- If and , then there exists such that (exchange axiom).
- 1.
- Set .
- 2.
- For to n, repeat step (3):
- 3.
- Find the nearest neighbor with respect to d of in T and add together with the connecting edge to T.
2.2. Optimality Results
- 1.
- Case : By symmetry of d for any two vertices we have .
- 2.
- Case : Denote by the tree obtained by joining x and y in this order to a given tree Z applying the join algorithm.
- (a)
- We consider three cases 2(a)i–2(a)iii:
- i.
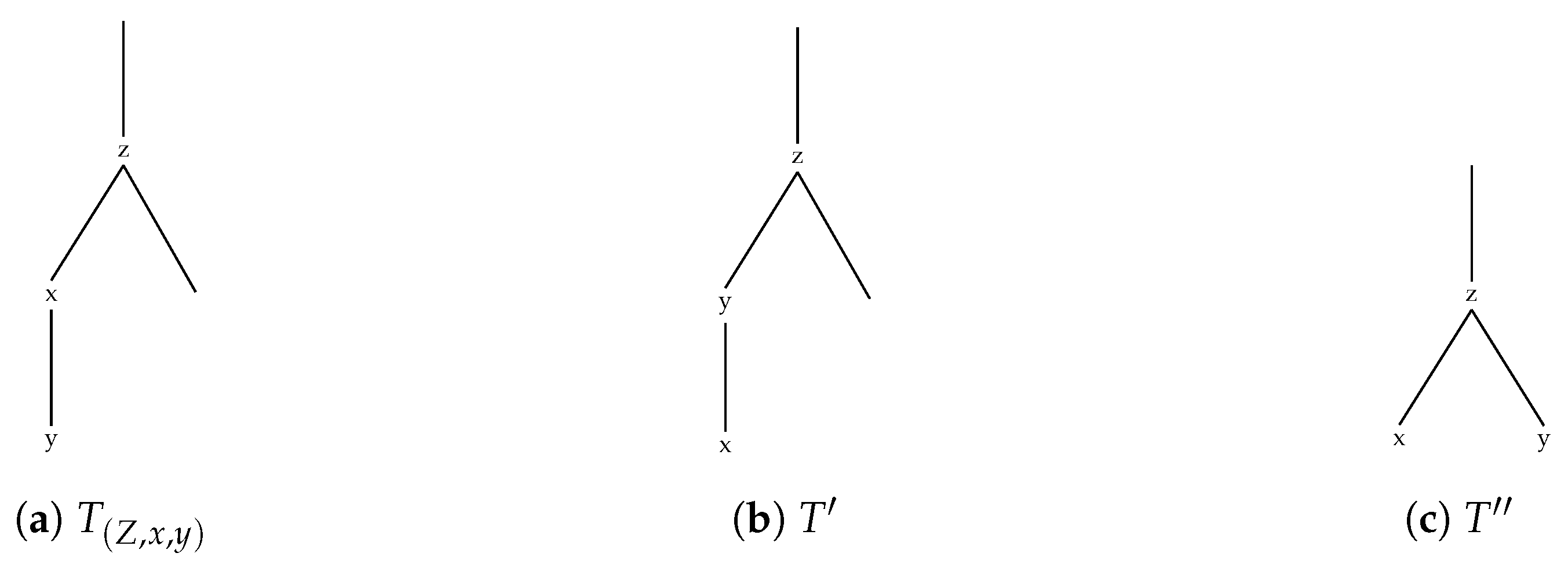
- Let ; then by Corollary 1 we conclude that = , and henceforth if we define as in Figure 1b, we conclude that . Thus is equivalent to with regard to its total distance. However, as can be greedily constructed by first joining y and then x, we conclude
- ii.
- Let ; then by Corollary 1 we conclude that = , and henceforth if we define as in Figure 1c, we get . Again as can be greedily constructed by first (Note, that the tree is symmetric with respect to the order x and y that are added) joining y and then x, we conclude
- iii.
- Finally, let ; then . Henceforth for defined as in Figure 1c we infer . However, as is obtained by greedily minimizing the distance of y, only equality can hold and we get
- (b)
- On the other hand, assume that is such that x and y are not directly linked; then by the greedy choice of the join algorithm we conclude that
Therefore putting (2a) and (2b) together we conclude that in all cases we have . By exchanging the roles of x and y, i.e., a symmetrization argument, we conclude that only equality can hold. □
- 1.
- Consider x as the root of the subtree denoted by and find all children of x in .
- 2.
- For each child find the nearest neighbor with respect to d of in and add together with the connecting edge to .
3. Applications
3.1. Topological Distance
- 1.
- d is a metric.
- 2.
- d satisfies the strong triangle axiom; i.e., X is an ultrametric space if endowed with d.
3.2. Latency
3.3. Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- Alekseev, S.; Schäfer, J. A New Algorithm for Construction of a P2P Multicast Hybrid Overlay Tree Based on Topological Distances. In Proceedings of the Seventh International Conference on Networks & Communications, Zürich, Switzerland, 2–3 January 2016; pp. 307–321. [Google Scholar] [CrossRef]
- Alekseev, S.; Schäfer, J. Evaluation of a Topological Distance Algorithm for Construction of a P2P Multicast Hybrid Overlay Tree. Int. J. Comput. Netw. Commun. 2016, 8, 1–20. [Google Scholar] [CrossRef]
- Krasner, M. Nombres semi-réels et espaces ultramétriques. C. R. Acad. Sci. 1944, 219, 433–435. [Google Scholar]
- Korte, B.; Lovasz, L.; Schrader, R. Greedoids; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Korte, B.; Lovász, L. Structural properties of greedoids. Combinatorica 1983, 3, 359–374. [Google Scholar] [CrossRef]
- Korte, B.; Lovász, L. Greedoids—A Structural Framework for the Greedy Algorithm. In Progress in Combinatorial Optimization; Pulleyblank, W.R., Ed.; Academic Press: Cambridge, MA, USA, 1984; pp. 221–243. [Google Scholar] [CrossRef]
- Silva, M.A.; Bertone, R.; Schäfer, J. Topology Distribution for Video-Conferencing Applications. In Proceedings of the 2019 10th International Conference on Networks of the Future (NoF), Rome, Italy, 1–3 October 2019; Volume 10. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Szeszlér, D. Optimality of the Greedy Algorithm in Greedoids. In Proceedings of the 11th Hungarian-Japanese Symposium on Discrete Mathematics and Its Applications, Tokyo, Japan, 27–30 May 2019; Volume 11, pp. 438–445. [Google Scholar]
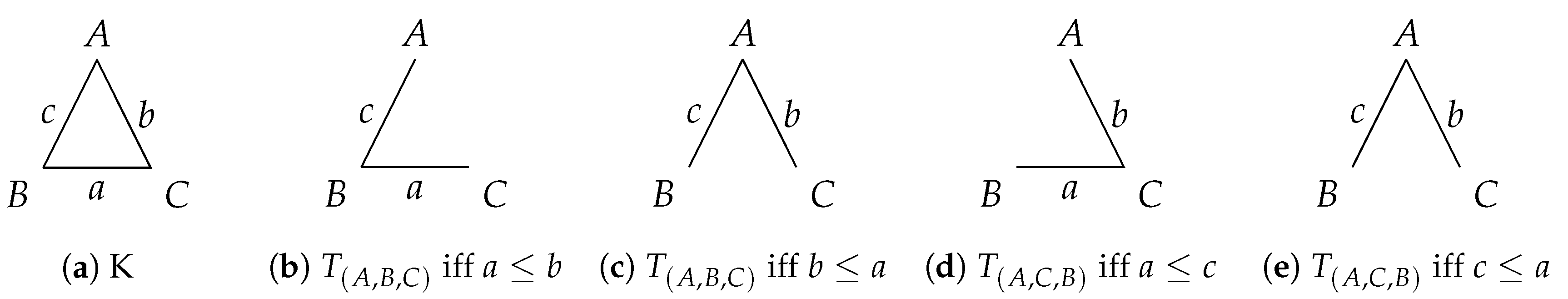
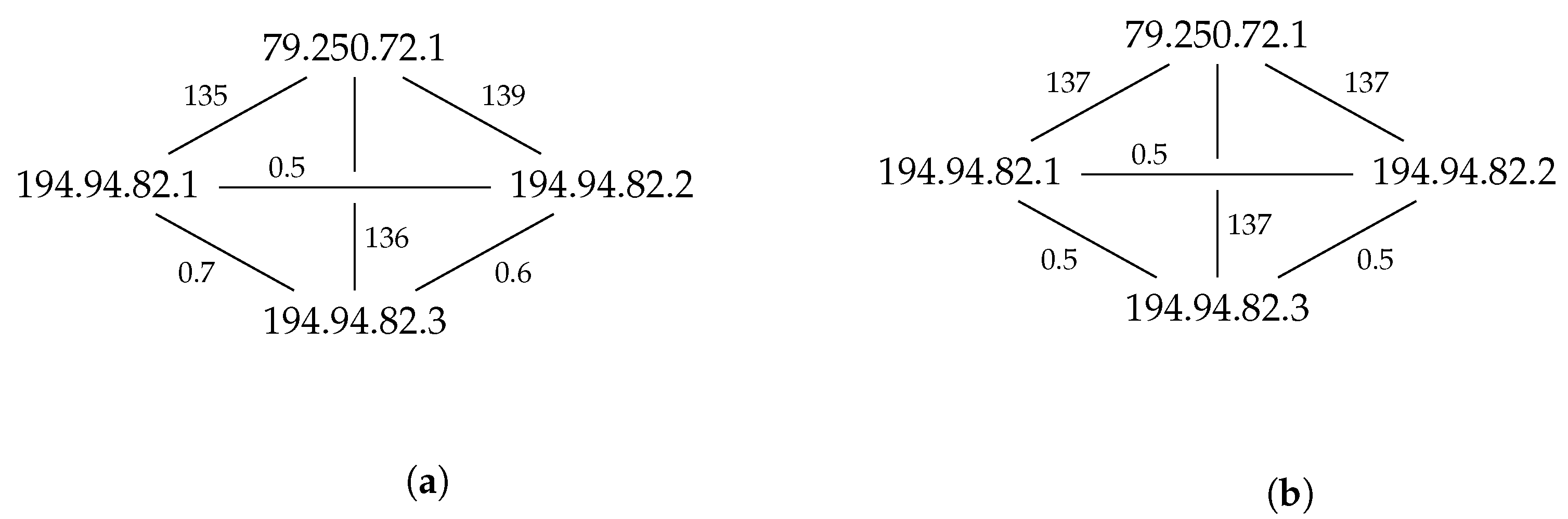
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schäfer, J. A Note on Ultrametric Spaces, Minimum Spanning Trees and the Topological Distance Algorithm. Information 2020, 11, 418. https://doi.org/10.3390/info11090418
Schäfer J. A Note on Ultrametric Spaces, Minimum Spanning Trees and the Topological Distance Algorithm. Information. 2020; 11(9):418. https://doi.org/10.3390/info11090418
Chicago/Turabian StyleSchäfer, Jörg. 2020. "A Note on Ultrametric Spaces, Minimum Spanning Trees and the Topological Distance Algorithm" Information 11, no. 9: 418. https://doi.org/10.3390/info11090418
APA StyleSchäfer, J. (2020). A Note on Ultrametric Spaces, Minimum Spanning Trees and the Topological Distance Algorithm. Information, 11(9), 418. https://doi.org/10.3390/info11090418




