Public Data Integrity Verification Scheme for Secure Cloud Storage

Abstract

Although cloud storage provides convenient data outsourcing services, an untrusted cloud server frequently threatens the integrity and security of the outsourced data. Therefore, it is extremely urgent to design security schemes allowing the users to check the integrity of data with acceptable computational and communication overheads. In this paper, we first propose a public data integrity verification scheme based on the algebraic signature and elliptic curve cryptography. This scheme not only allows the third party authority deputize for users to verify the outsourced data integrity, but also resists malicious attacks such as replay attacks, replacing attack and forgery attacks. Data privacy is guaranteed by symmetric encryption. Furthermore, we construct a novel data structure named divide and conquer hash list, which can efficiently perform data updating operations, such as deletion, insertion, and modification. Compared with the relevant schemes in the literature, security analysis and performance evaluations show that the proposed scheme gains some advantages in integrity verification and dynamic updating.

1. Introduction

As a new computing paradigm, cloud storage has been popular for providing great data storage and management services. More and more organizations and individuals outsource their data in the cloud via a pay-as-you-go approach. Nevertheless, cloud outsourcing storage service heavily relieves the local storage burden for the cloud clients. The data integrity verification becomes a critical security challenge for cloud technology to be adopted [1,2]. On the one hand, downloading the complete data frequently for integrity verification will dramatically increase communication and computation overhead. On the other hand, when the cloud storage devices are damaged or hackers steal the outsourced data, the cloud service provider (CSP) might choose to conceal the data corruption or loss for maintaining the user’s trust. Furthermore, the CSP might save storage space by intentionally deleting the less frequently accessed data [3] or leak users’ privacy information for interest. Hence, cloud users must find an efficient way to verify the integrity of the outsourced data.

The schemes presented in the literature provide models supporting private verification and public verification to solve the above problem. Private verification only allows users to check the outsourced data’s integrity by themselves that brings great computing burden to resource constraint users. On the contrary, public verification reduces the user’s computational cost by introducing a third-party authority (TPA) to verify integrity. Due to the potential of practical use, public verification has received more attention [4,5,6,7,8,9,10,11]. Ateniese et al. [4] proposed the first publicly verifiable cloud data integrity scheme, which utilizes the RSA-based homomorphic linear authenticator to check the integrity of outsourced data. Shacham et al. [12] presented a public data integrity verification scheme with the Boneh–Lynn–Shacham (BLS) signature [13]. In this scheme, multiple tags are aggregated into a single tag and verified the tag with bilinear maps. However, these schemes incur heavy communication and computational costs for expensive exponentiation operations. Chen [14] presented an algebraic signatures-based public verification scheme, which used a short bit string compressed by a data block to achieve efficient integrity verification without the comparison with original data. Unfortunately, it is insecure against the replay attack. Furthermore, it fails to support dynamic data updating.

To support dynamic updating, researchers have presented many schemes to update data without downloading the whole data. Erway et al. [5] proposed the first verification scheme, which supports dynamic data updating with a rank-based authenticated skip list. However, the list requires massive auxiliary information to achieve integrity verification. It leads to high communication and computational costs. Subsequently, a number of improved schemes are proposed, such as [3,10,15,16,17,18]. Note that a Divide and Conquer Table (DCT) data structure was introduced by [17,18] to support dynamic data updating. According to the table’s division into separate sections, DCT performs better than the Index-Hash-Table (IHT) [10] in data block insertion and deletion. However, some drawbacks are still found. First, many continuous storage spaces are essential for the outsourced data blocks that are not practical for some distributed storage. Second, operations such as insertion and deletion result in additional computational costs because data block movement can not be generally avoided. Third, due to the lack of links among the DCTs, it is hard to locate the required data blocks for use quickly. Furthermore, the scheme is fragile to resist the forgery attack, replay attack, and replacing attack.

Considering the above problems, in this paper, we propose a public verification scheme based on the algebraic signature and elliptic curve cryptography. The scheme supports efficient public verification while resisting the possible attacks such as the forgery attack, the replacing attack, and the replay attack. Furthermore, a novel data structure called Divide and Conquer Hash List (DCHL) is introduced to achieve dynamic data updating. DCHL takes advantage of the hash table and linked list to reduce the computational costs. In addition, either in the cloud or during the verification process, data encryption ensures data privacy. Main contributions of the proposed scheme are listed as follows:

• Based on algebraic signature and elliptic curve cryptography, we propose a public verification scheme that supports efficient data integrity verification with low communication and computational overheads. Furthermore, symmetric encryption in the scheme guarantees the privacy of data blocks.
• To support dynamic updating, a novel data structure named DCHL is designed and stored in the TPA to make operations such as data insertion, modification and deletion more flexible and efficient.
• Using the proposed scheme in cloud storage, security analysis suggests that even a malicious CSP cannot launch a forgery attack, replacing attack and replay attack to pass integrity verification. Meanwhile, the proposed scheme frequently outperforms the relevant data verification schemes in terms of efficiency that is confirmed by numerical analysis and real experiments.

The remainder of the paper is organized as follows. Section 2 briefly reviews the related works. The system model and the design goals are described in Section 3. In Section 4, some necessary preliminaries are presented for a better understanding of the proposed scheme. Section 5 presents the details of the scheme and the corresponding dynamic updating operations. Section 6 gives the security analysis of our scheme, while its comparisons with the state-of-the-art schemes are shown in Section 7. Finally, conclusions are drawn in Section 8.

2. Related Work

Recently, growing attention has been paid to data integrity verification in the cloud storage. In 2007, Juels et al. [19] proposed the concept of “proof of retrievability (PoRs)”. This scheme not only verifies the integrity of data stored in the cloud, but also ensures data retrievability with error-correcting code. Nevertheless, it only can audit privately [15]. In 2008, Ateniese et al. [20] first proposed a scheme that could verify the integrity of data publicly in the cloud storage. Their scheme combines the block tags into a single one with the RSA-based Homomorphic Verifiable Tag (HVT) without downloading all the data. However, researches [17,18,21,22] indicated that this technique uses lots of communication and computational resources since it utilized the RSA numbers. Shacham et al. [12] presented a public data integrity verification scheme with the BLS signature. Since the model operation is not required to be carried out, the BLS [13] consumes less communication and computation resources. However, a malicious attacker could access the outsourced data in interactive proof systems that threaten data privacy.

In 2013, Wang et al. [6] presented a privacy-preserving auditing scheme. It combines random mask with the homomorphic to prevent the TPA from getting any information about the outsourced data in the cloud. Later, Worku et al. [23] proposed a privacy-preserving public auditing scheme of which performance is considered better than [6]. It verifies data integrity with a ring signature and protects the identity information of users. Recently, Yu et al. [24] proposed an identity-based verification scheme to protect data privacy, which uses the identity information of the user as a key to verify the data integrity. However, these privacy protection schemes are extremely unsafe for the outsourced data. Furthermore, the above schemes incur high communication and computational costs.

Based on an algebraic signature, Chen et al. [14] proposed an efficient integrity verification scheme. It improves the verification efficiency without using the public key technique. However, this scheme achieves an unlimited number of verifications by frequently updating the challenge process, which causes extra communication and computational costs. Furthermore, this scheme is vulnerable to a replay attack. Recently, Sookhak et al. [17,18] presented a scheme supporting unlimited verification. However, some security vulnerabilities are also found. The CSP is likely to compute the secret key of the signature with the remaining data blocks and tags when some data blocks and tags are corrupted. In addition, this scheme cannot resist replay attack and replacing attack.

Generally, we cannot guarantee that the outsourced data is kept unchanged during the whole period of the cloud [25,26,27,28,29]. Users might update their data and require the integrity of updated data to be verified. More and more researches have put forward many schemes to update data without downloading the whole data efficiently. For instance, Erway et al. [5] utilized a rank-based authenticated skip list to construct a dynamic provable data possession scheme. The scheme supports dynamic updating by adding the rank information at an RSA tree. Wang et al. [3] proposed a typical public auditing scheme with a Merkle Hash Tree to achieve dynamic updating. When we want to update data, the CSP updates the leaf node of the MHT and re-calculates the root of the new MHT. However, these schemes are frequently inapplicable due to pricey computation and communication resources required by their updating procedures.

Zhu et al. [10] designed the IHT to support dynamic updating, for example, fast data modification. However, additional computational costs for data insertion and data deletion are essential. Schemes in [15,16] utilized a Dynamic Hash Table (DHT) and a Doubly Linked Info Table (DLIT) to achieve dynamic updating operations. They take advantage of the linked list to reduce the cost of data insertion and deletion. However, along with the stored list increases, the query time would increase dramatically in the verification and update. Then an emerging increase in the computational cost cannot be avoided.

Later, Sookhak et al. [17,18] utilized the DCT to achieve dynamic updating. They split a large table into several separate parts. Although it seems that the costs of data insertion and deletion are reduced, new problems occur. For instance, multiple contiguous blocks of memory are required, and the connection between data is also interrupted by the fragmentation of the table that undoubtedly increases data access time.

3. System Model and Design Goals

Initially, we illustrate the system model and the design goal of the proposed scheme.

3.1. System Model

As shown in Figure 1, the proposed public verification scheme adopts a three-party model. Roles in this model are as follows: (1) Users, who draw support from a cloud to store their data. (2) Cloud Server Provider (CSP), which sells abundant storage and computational resources to users. (3) Third-Party Authority (TPA), who verifies the integrity of data in response to user requests.

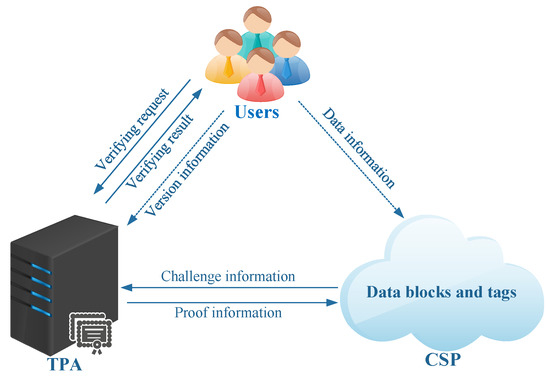
Figure 1. The system model for the proposed scheme.

Following [12], we present the ability of each party for the proposed model. First, the TPA is considered to be honest-but-curious. In other words, the TPA is honest in verifying data integrity, but it might be curious about the data. Furthermore, the CSP is untrusted because it can choose to conceal the data corruption or loss for maintaining the user’s trust. Therefore, the CSP can launch the following attacks.

• Forgery attack: The CSP might forgery-proof information to pass verification during which the outsourced data is deleted or corrupted.
• Replacing attack: The CSP might replace the corrupted data blocks and tags with other valid uncorrupted data blocks and tags if the challenged data blocks are corrupted.
• Replay attack: To pass verification, the CSP might send the former valid proof information or other information to the TPA.

3.2. Design Goals

To guarantee security and efficiency, the design goals should achieve the following requirements:

• Public verification: The scheme allows the TPA to verify the outsourced data’s integrity as an agent.
• Correctness: If the CSP correctly stores the user’s data, it could successfully pass integrity verification.
• Privacy preserving: The scheme can be securely stored in the cloud and prevent privacy from leaking during the verification process.
• Unforgeability: If the outsourced data is corrupted, the CSP cannot forge the proof information to deceive the TPA.
• Dynamic data updating: Users could perform the modification, insertion, and deletion operation on the data stored in the cloud.
• Lightweight: The scheme requires low communication and computational costs in verification and dynamic updating.

4. Preliminaries

4.1. Elliptic Curve Discrete Logarithm Problem

Let $E\left(F_q\right)$ be an elliptic curve over a large prime q order finite field $F_q$, where q is a large prime. The Elliptic Curve Discrete Logarithm Problem (ECDLP) is a well-known hard problem, which can be described as follows: Given an equation $A=xB$, where $A,B\in E\left(F_q\right)$ and $x<q$. It is easy to compute A with x and B. However, it is hard to compute x with A and B. Here, we omit the detailed proof, which can be found in [30].

4.2. Algebraic Signatures

According to Litwin et al.’s definition [31], the algebraic signature defined in the Galois field is a type of hash function and supports the homomorphic addition. It is utilized to calculate data tags and verify the integrity of the outsourced data f including n data blocks $\left\{m_1,\cdots ,m_i,\cdots ,m_n\right\}$. Therefore, the algebraic signature of data f can be computed by

$$Si{g}_{\alpha }\left(f\right)=\sum _{i=1}^n{m}_i{\alpha }^i.$$

(1)

Here $\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)$ is a vector of different non-zero elements ${\alpha }_i(i\in [1,n])$ of the Galois field.

An algebraic signature could ensure that the signature for the sum of some random blocks is equal to the sum of the signatures for these blocks [17,18,31]. The property can be described by

$$Si{g}_{\alpha }\left(m_1+\cdots +m_n\right)=Si{g}_{\alpha }\left(m_1\right)+\cdots Si{g}_{\alpha }\left(m_n\right),$$

(2)

where $\left(m_1,\cdots ,m_n\right)$ are n data blocks.

When all the data blocks are identical, a property of the algebraic signature can be obtained through

$$Si{g}_{\alpha }\left(nm\right)=nSi{g}_{\alpha }\left(m\right).$$

(3)

5. The Proposed Scheme

5.1. Divide and Conquer Hash List

To support dynamic data updating, in this section, a novel data structure DCHL is designed. It combines the advantages of the hash table and linked list stored in the TPA. Differing from the DCT, the DCHL is composed of a hash table and many linked lists. The user divides the data blocks into k groups and each group’s length is $L_i$ ($i=1,\cdots ,k$). The index and length of each group are stored in the hash table. The data version information (VI) in the same group is linked with pointers. Here, VI is a number indicating the version of the data block. For each VI, the storage location is unique in the DCHL. When we query the VI of a data block, the TPA quickly locates the group location of VI in the hash table and then traverses the linked list to get the precise location based on the length of the linked list. Figure 2 details a sample structure of the DCHL. Based on Figure 2, for instance, when the TPA queries the ith data block, the TPA first locates the group index of the ith data block and gets the determined group’s length. Then, the TPA finds the corresponding position on the determined linked list. Finally, the queried VI will be found.

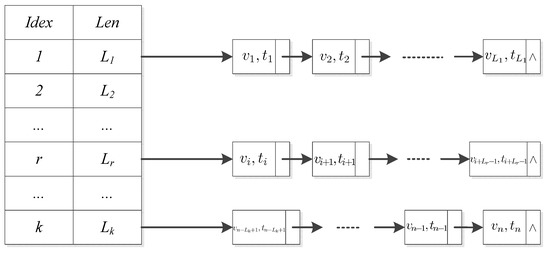
Figure 2. Divide and conquer hash list.

This data structure has advantages over the DCT in schemes [17,18]. Firstly, the TPA only needs to modify the list pointer for insertion and deletion operations. Secondly, only a continuous space is required to store and manage the group index, which is very acceptable in practice. Thirdly, the TPA can flexibly adjust the DCHL if the insertion or deletion operations are frequent. Thus, the data structure can significantly reduce the computational and communication costs of updating processes. A simulated experiment in the following text will demonstrate the conclusion.

5.2. Verification Scheme Against Malicious Attacks

Let $F_q$ be a large prime q order finite field, and $E\left(F_q\right)$ be an elliptic curve defined in the $F_q$. Set the point G as the base point of $E\left(F_q\right)$. H is a collusion-resistance hash function $H:{\left\{0,1\right\}}^{*}\to {\left\{0,1\right\}}^l$. Assume that the outsourced data is divided into n data blocks, i.e., $f=\left\{m_1,\cdots ,m_i,\cdots ,m_n\right\}$ and the length of each data block is l. The proposed verification scheme against malicious attacks involves the following steps:

(1)

Key initiation: The user first generates a symmetric key $dk$ for encrypting data blocks. Then, he randomly selects $x\in {\mathbb{Z}}_q$, and calculates $G_A=xG$, where G is known by the user and the TPA. Meanwhile, the user chooses a secure element $\alpha$ for an algebraic signature. Here, we set $\left(dk,x\right)$ as the secret key and $G_A$ as the public key.

(2)

Data blocks encryption: The user uses a symmetric encryption algorithm $Enc(·)$ with key $dk$ to encrypt each data block $m_i$ and get the encrypted $M_i$ = $En{c}_{dk}\left(m_i\right)$ where $1\le i\le n$.

(3)

Tag initiation: The user computes the data block tag ${\sigma }_i$ for each encrypted data block $M_i$

$${\sigma }_i=Si{g}_{\alpha }\left(x\left(M_i+H\left(v_i∥t_i\right)\right)\right),$$

(4)

where $v_i$ is the version of the data block $M_i$, $t_i$ is the timestamp, and $\left|\right|$ denotes concatenation. Then, the user uploads $\left\{f,\left\{{\sigma }_i,1\le i\le n\right\}\right\}$ to the CSP, and routes $\left\{v_i,t_i,1\le i\le n\right\}$ as the VI to the TPA. After that, the user removes the locally stored information. The TPA is delegated to launch a verification challenge to verify the integrity of the outsourced data. Notice that the proposed scheme respectively uses $dk$ to protect data block and x in tag initiation for public verification. By exploiting the property of ECDLP, it is hard for attackers to extract x with $x\left(M_i+H\left(v_i∥t_i\right)\right)$ and the public key $G_A$.

(4)

Challenge: First, the user transmits a verification request to the TPA. Then, the TPA randomly chooses c data blocks from n data blocks. Finally, the TPA launches a challenge by sending the challenge information $chal=\left\{s_1,\cdots ,s_c\right\}$ to the CSP where $s_i(1\le i\le c)$ is the index of the selected data block.

(5)

Proof generation: After receiving the challenge information, the CSP first calculates $M^{\prime }={\sum }_{i\in chal}{M}_i$ and $\sigma ={\sum }_{i\in chal}{\sigma }_i$, where $M^{\prime }$ is the data proof and $\sigma$ is the tag proof. Then, the CSP returns $\left(M^{\prime },\sigma \right)$ to TPA as the proof.

(6)

Proof verification: The TPA calculates the sum of hash values by

$$H^{\prime }=\sum _{i\in chal}H\left(v_i∥t_i\right).$$

(5)

Then, the TPA checks the following equation to verify the proof:

$$G_A·\left(Si{g}_{\alpha }\left(M^{\prime }+H^{\prime }\right)\right)\begin{array}{c}\underline{\underline{?}}\\ \end{array}G·\sigma$$

(6)

Equation (6) outputs ‘TRUE’ if the equation holds. Finally, the TPA sends the result to the user. Figure 3 illustrates the challenge-verification procedure.

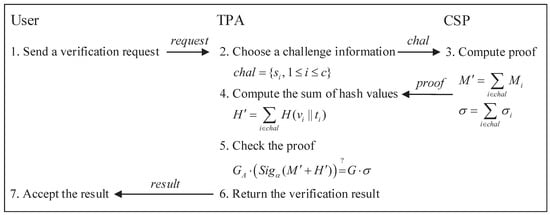
Figure 3. The challenge-verification procedure.

5.3. Dynamic Data Updating

Dynamic data updating operations mean that the users could update their outsourced data without downloading the whole data. These operations include data modification $\left(U_M\right)$, data insertion $\left(U_I\right)$ and data deletion $\left(U_D\right)$. In practice, it is unreasonable for the user to download the entire data before he can update some data blocks. So, we utilize the DCHL to support efficient data updating operations.

5.3.1. Data Modification

Data modification operation replaces a number of blocks with new blocks. Given a new block $M_i^{\prime }$, the modification algorithm is performed by the following six steps:

(1)

With the help of TPA, the user finds the specific DCHL that has the required block and gets the version number $v_i$. Then, the user generates the new version and timestamp $\left(v_i^{\prime }\leftarrow v_i+1,t_i^{\prime }\right)$ for $M_i^{\prime }$, and then calculates the tag of the data block $M_i^{\prime }$ by

$${\sigma }_i^{\prime }=Si{g}_{\alpha }\left(x\left(M_i^{\prime }+H\left(v_i^{\prime }∥t_i^{\prime }\right)\right)\right).$$

(7)

(2)

The user sends the data updating request $U_{M_{CSP}}=\left\{i,M_i^{\prime },{\sigma }_i^{\prime }\right\}$ and the VI updating request $U_{M_{TPA}}=\left\{i,v_i^{\prime },t_i^{\prime }\right\}$ to the CSP and the TPA, respectively.

(3)

After receiving $U_{M_{CSP}}=\left\{i,M_i^{\prime },{\sigma }_i^{\prime }\right\}$, the CSP replaces the block with $M_i^{\prime }$ and changes tag ${\sigma }_i$ to ${\sigma }_i^{\prime }$.

(4)

After receiving $U_{M_{TPA}}=\left\{i,v_i^{\prime },t_i^{\prime }\right\}$, the TPA first finds the group index of the i-th data block from the DCHL;

(5)

Then, the TPA determines the location of the data block, which needs to be modified in the linked list.

(6)

Finally, the TPA modifies $\left\{v_i,t_i\right\}$ to $\left\{v_i^{\prime },t_i^{\prime }\right\}$.

Figure 4 describes the modification operation on DCHL.

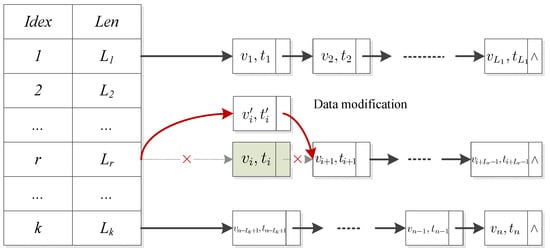
Figure 4. Data block modification operation.

5.3.2. Data Insertion

If the entire file is not required to be downloaded, the user can insert a new data block after some particular positions. Suppose the user wants to insert a new block after $M_i$, he has to perform as follows:

(1)

The user first generates the version and timestamp $\left(v_i^{*},t_i^{*}\right)$ for $M_i^{*}$, and then he computes the tag by

$${\sigma }_i^{*}=Si{g}_{\alpha }\left(x\left(M_i^{*}+H\left(v_i^{*}∥t_i^{*}\right)\right)\right).$$

(8)

(2)

The user respectively sends the data updating request $U_{I_{CSP}}=\left\{i,M_i^{*},{\sigma }_i^{*}\right\}$ and the VI updating request $U_{I_{TPA}}=\left\{i,v_i^{*},t_i^{*}\right\}$ to the CSP and the TPA.

(3)

The CSP inserts data block ${M_i}^{*}$ after $M_i$ and stores the corresponding tag ${\sigma }_i^{*}$ upon receiving $U_{I_{CSP}}=\left\{i,M_i^{*},{\sigma }_i^{*}\right\}$.

(4)

After receiving $U_{I_{TPA}}=\left\{i,v_i^{*},t_i^{*}\right\}$, the TPA finds the position of i-th data block in the DCHL and inserts $\left\{i,v_i^{*},t_i^{*}\right\}$ after it. Finally, the TPA sets the length of the group in which the i-th data block is located $L_r=L_r+1$.

Figure 5 depicts the insertion operation in the DCHL.

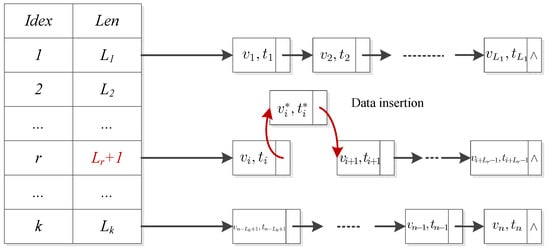
Figure 5. Data block insertion operation.

5.3.3. Data Deletion

Data deletion operation deletes a specific data block. If a user wants to delete the data block $M_i$, he achieves this objective according to the following steps.

(1)

The user sends the data updating request $U_{D_{CSP}}=\left\{i\right\}$ and the VI updating request $U_{D_{TPA}}=\left\{i\right\}$ to the CSP and the TPA, respectively;

(2)

After receiving $U_{D_{CSP}}=\left\{i\right\}$, the CSP deletes the block $M_i$ and tag ${\sigma }_i$, respectively;

(3)

Similar to the insertion operation, the TPA deletes $\left(v_i,t_i\right)$ and sets the length of the group in which the i-th data block is located $L_r=L_r-1$ in DCHL.

Figure 6 illustrates this deletion operation.

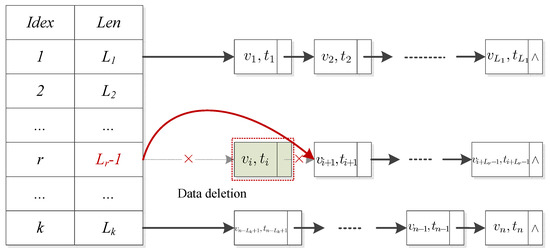
Figure 6. Data block deletion operation.

6. Security Analysis

To conduct security analysis, in this section, the completeness of the proposed scheme is first elaborated. Then, we prove that the scheme resists some attacks well.

Theorem 1

(Completeness). The CSP pass the verification if it correctly stores the outsourced data according to the TPA’s challenge.

Proof. 

Given a response information $\left(M^{\prime },\sigma \right)$ from the CSP, where $M^{\prime }={\sum }_{i\in chal}{M}_i$, the TPA computes $H^{\prime }={\sum }_{i\in chal}H\left(v_i∥t_i\right)$. Then, the TPA gets

$$G_A·\left(Si{g}_{\alpha }\left(M^{\prime }+H^{\prime }\right)\right)=G·x·\left(Si{g}_{\alpha }\left(M^{\prime }+H^{\prime }\right)\right)$$

(9)

According to Equation (3), the TPA computes

$$\begin{array}{cc}\hfill G·x·\left(Si{g}_{\alpha }\left(M^{\prime }+H^{\prime }\right)\right)& =G·Si{g}_{\alpha }\left(x·\left(M^{\prime }+H^{\prime }\right)\right)\hfill \\ \hfill & =G·\sum _{i\in chal}Si{g}_{\alpha }\left(x·\left(M_i+H_i\right)\right)\hfill \\ \hfill & =G·\sigma \hfill \end{array}$$

(10)

Thus, the equation holds if and only if the CSP correctly stores the outsourced data according to the TPA’s challenge. This completes the proof of the theorem. □

Lemma 1

(Unforgeability of the proof). The CSP cannot pass the verification by forging a proof.

Proof. 

If a data block or tag is corrupted, the CSP might falsify a tag proof and a data proof to pass the verification. Following [12], we define the security game as follows.

According to the challenge information $chal=\left\{s_i,1\le i\le c\right\}$, the CSP generates a forgeable proof $\left(M^{″},{\sigma }^{\prime }\right)$. If it cannot pass the verification, the CSP loses the game; otherwise, the TPA has

$$G_A·\left[Si{g}_{\alpha }(M^{″}+H^{\prime })\right]=G·{\sigma }^{\prime }.$$

(11)

Then, from Equation (2), the TPA can learn that

$$G_A·Si{g}_{\alpha }\left(M^{″}\right)+G_A·Si{g}_{\alpha }\left(H^{\prime }\right)=G·{\sigma }^{\prime }.$$

(12)

According to Equation (3), Equation (12) can be reformulated by

$$G·{\sigma }^{\prime }-G_A·Si{g}_{\alpha }\left(M^{″}\right)=G_A·Si{g}_{\alpha }\left(H^{\prime }\right).$$

(13)

Then, the TPA gets

$$G·\left({\sigma }^{\prime }-x·Si{g}_{\alpha }\left(M^{″}\right)\right)=G·\left(x·Si{g}_{\alpha }\left(H^{\prime }\right)\right).$$

(14)

Let P be $G·\left(x·Si{g}_{\alpha }\left(H^{\prime }\right)\right)$ and k denote ${\sigma }^{\prime }-x·Si{g}_{\alpha }\left(M^{″}\right)$, Equation (14) can be rewritten by

$$G·k=P.$$

(15)

Apparently, the CSP can pass the verification if and only if there is an efficient algorithm to solve the ECDLP. Unfortunately, this is in contradiction with the assumption. Thus, we can conclude that the CSP cannot forge the proof to pass the integrity verification successfully. □

Based on the aforementioned analysis, we can further prove that the proposed scheme is immunity from replacing attack and replay attack.

Lemma 2

(Immunity from replacing attack). For verification, it is unavailing for the CSP to replace a specified block and the corresponding tag with others.

Proof. 

Similarly, the replacing attack game can be described as follows. The TPA sets $chal=\left\{s_i,1\le i\le c\right\}$ as the challenge information and transmits it to the CSP. After receiving $chal$, the CSP returns a checking proof $\left(M^{″},{\sigma }^{\prime }\right)$. When the proof is generated, the information of the j-th block is replaced with the k-th block’s $\left(k\ne j\right)$. The CSP will win the game if the proof is verified.

If the CSP wins the game, the TPA thus gets

$$G_A·Si{g}_{\alpha }(M^{″}+H^{\prime })=G·{\sigma }^{\prime }.$$

(16)

It can deduce that

$$G_A·Si{g}_{\alpha }(M^{″}+H^{\prime })=G_A·(\sum _{\begin{array}{c}i\in chal\\ \&i\ne j\hfill \end{array}}{M}_i+M_k+\sum _{\begin{array}{c}i\in chal\\ \&i\ne j\hfill \end{array}}H\left(v_i\parallel t_i\right)+H\left(v_j\parallel t_j\right)).$$

(17)

The right half of Equation (17) can be computed by

$$G·{\sigma }^{\prime }=G·(\sum _{\begin{array}{c}i\in chal\\ \&i\ne j\hfill \end{array}}{\sigma }_i+{\sigma }_k).$$

(18)

The TPA thus get

$$G_A·\left[Si{g}_{\alpha }(M_k+H\left(v_j∥t_j\right))\right]=G·{\sigma }_k.$$

(19)

On the basis of the properties of the algebraic signature, Equation (19) can be expressed as

$$\begin{array}{cc}\hfill G_A·Si{g}_{\alpha }(M_k+H(v_j\parallel t_j))& =G·Si{g}_{\alpha }\left(x(M_k+H(v_k\parallel t_k)\right)\hfill \\ \hfill & =G_A·Si{g}_{\alpha }(M_k+H(v_k\parallel t_k)).\hfill \end{array}$$

(20)

Thus, the TPA obtains

$$Si{g}_{\alpha }(M_k+H(v_j\parallel t_j))=Si{g}_{\alpha }(M_k+H(v_k\parallel t_k)).$$

(21)

If Equation (21) holds, the equation $H\left(v_j∥t_j\right)=H\left(v_k∥t_k\right)$ holds either. It means that $v_j=v_k$ and $t_j=t_k$. However, we have $t_j\ne t_k$ since $j\ne k$. In addition, the hash function is collision resistant. Hence, $H\left(v_j∥t_j\right)$ is not the same as $H\left(v_k∥t_k\right)$. Consequently, the CSP loses the game, and the proposed is immune from the replacing attack. □

Lemma 3

(Immunity from replay attack). For the proposed scheme, the CSP is incapable of passing the verification with the former challenge information.

Proof. 

First, the TPA transmits the challenge information to the CSP. After receiving the challenge information, the CSP returns the checking proof $\left(M^{″},{\sigma }^{\prime }\right)$. Similarly, the information of the j-th block is replaced by its previous information while the proof is generated. The CSP will win the game if and only if it can pass the verification. Unfortunately, the CSP cannot pass the verification since the current timestamp is different from the old one. The details are omitted here. □

Theorem 2

(Security). The proposed scheme is secure against the threat model.

Proof. 

As discussed in Section 3.1, the threat model of the proposed scheme consists of forgery attack, replacing attack, and replay attack. From Lemmas 1, 2, and 3, the CSP cannot win in the three attacks. Thus, we can conclude that the proposed scheme is secure against the threat model. □

7. Performance Analysis

7.1. Misbehavior Detection

Towards an affordable and practical verification with high-accuracy for both the TPA and the CSP, sampling verification is preferred by our following scheme [15,17,18]. If the outsourced data is divided into n blocks, and m out of n are corrupted (or modified by the CSP), we can check random sampled c blocks to detect the misbehavior. Generally, the fractions of the corrupted data is $\frac{m}{n}$. Therefore, the detection probability of verification is $P=1-{(1-m/n)}^c$. Particularly, when $m/n=0.02$, the probability of detection is greater than 0.9976 if the TPA verifies 300 randomly chosen blocks.

7.2. Communication Costs

In this section, we discuss the communication costs compared with the state-of-the-art schemes. The challenge-verification process mainly causes communication costs. First, the user consigns the TPA to verify the integrity of the outsourced data with $O\left(1\right)$ communication costs. The TPA launches a challenge with $O\left(c\right)$ communication costs, where c is the number of challenging blocks. Then the CSP sends the proof to the TPA, and this step brings $O\left(1\right)$ communication costs. Finally, the TPA transmits the verifying result to the user, bringing $O\left(1\right)$ communication costs. Hence, the communication costs of the whole process are $O\left(c\right)$. Table 1 shows the communication costs compared with several popular auditing schemes, such as Erway et al.’s scheme [5], Chen et al.’s scheme [14], Tian et al.’s scheme [15], Shen et al.’s scheme [16] and Sookhak et al.’s [17,18]. We can find that the communication costs are the same as the latter two schemes but more effective than the former.

Table 1. Comparison of communication costs.

Schemes	Communication Costs
Erway [5]	$O(clogn)$
Chen [14]	$O\left(c\right)$
Tian [15]	$O\left(c\right)$
Shen [16]	$O\left(c\right)$
Sookhak [17,18]	$O\left(c\right)$
Our scheme	$O\left(c\right)$

7.3. Computational Costs

In terms of computation complexity, we compare our scheme with the state-of-the-art schemes, i.e., Chen et al.’s scheme [14], Tian et al.’s scheme [15], Shen et al.’s scheme [16] and Sookhak et al.’s scheme [17,18]. To achieve clear comparisons, let P be the point multiplication in ECC, M be the point multiplication in the multiplicative cyclic group, G be the modular exponentiation in the multiplicative cyclic group, B be the bilinear pairing operation, S be the algebraic signature, E be the symmetric encryption, D be the symmetric decryption, c is the number of challenging blocks in each auditing query, and k be the number of DCTs. Table 2 details the comparisons among these schemes.

Table 2. Comparisons of computational complexity.

Schemes	Computational Costs
	Tag Generation	Proof Verification	Modification	Insertion	Deletion
Chen [14]	$nS+nE$	$c(D+S)$	—	—	—
Tian [15]	$nM+nG$	$(c+1)M+1G+1B$	$O\left(c\right)$	$O\left(c\right)$	$O\left(c\right)$
Shen [16]	$2nM+nG$	$(c+1)G+3B$	$O\left(c\right)$	$O\left(c\right)$	$O\left(c\right)$
Sookhak [17,18]	$2nS$	$1S$	$O\left(c\right)$	$O(n/k+c)$	$O(n/k+c)$
Our scheme	$nS$	$1S+2P$	$O\left(c\right)$	$O\left(c\right)$	$O\left(c\right)$

Note: “—” means not available.

In the tag generation phase, scheme [14] spends $(nS+nE)$ for the tags generation and tag encryption. Scheme [15] and scheme [16] cost $(nM+nG)$ and $(2nM+nG)$ to calculate the data tags, respectively. Scheme [17,18] costs $2nS$ to generate data block tags and auxiliary tags. The auxiliary tags are used to resist replay attack, but it does not work from the verification process. For the proposed scheme, the costs of tags generation are $nS$, which are acceptable for the users. We neglect the computational costs of hash operation and addition operation. In the challenge-verification phase of the scheme, verifying proof is $(1S+2P)$. The speed of point multiplication in the ECC is relatively fast. So, it is acceptable for the TPA (the illustration given by the experiment later). Furthermore, as shown in Table 2, schemes of [15,16,17,18] support modification, insertion and deletion while the main objective of [14] is remote data possession checking based on the algebraic signature. Although Sookhak et al.’s scheme [17,18] outperforms [15,16] in tag generation and proof verification, it consumes more when performs insertion and deletion. To insert a new block or delete an existing block, it must move forward or backward the remaining $(n/k-i)$ blocks of the DCT, which contains $(n/k)$ blocks. Obviously, in terms of computational complexity, the proposed scheme performs better than Sookhak et al.’s scheme [17,18] if we want to update data blocks.

Table 2 details the comparisons.

To demonstrate the efficiency, we further conducted simulations in MATLAB 2014 and Eclipse 2012 on a machine with Dual Core 2.60 GHz. As shown in Table 1, schemes [15,16] perform multiple modular multiplication operations to generation tags from Table 2, which has more computation costs than our scheme. Meanwhile, since the number of verification for scheme [14] is finite, we prefer simulating the comparison of our scheme with scheme [17,18]. For consistency, the 160-bit order elliptic curve is applied for both schemes, and the experiment results are the average of the running time.

Figure 7 shows the computational costs of tag generation, where the size of the block is 8KB, and the number is from 100 to 1000. The experimental results of Figure 7 are in agreement with the numerical analysis.

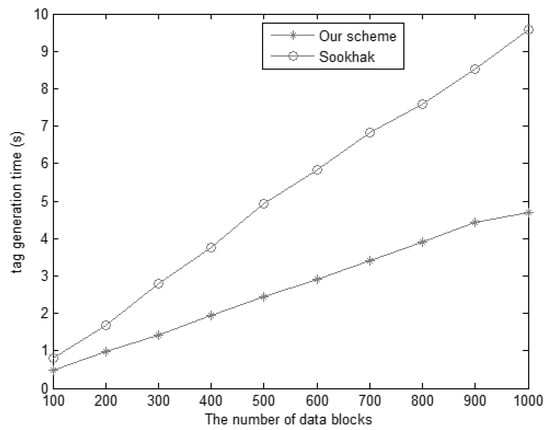
Figure 7. The computational time of generating data block tags.

The computational overheads of proof verification with the number of the challenged blocks from 50 to 500 are shown in Figure 8. We add two-point multiplication operations in the verification process. However, the time difference is less than $1ms$ compared with the scheme [17,18], which is negligible in actual verification. Therefore, the proposed scheme has an acceptable computational cost while achieving higher security, which is very practical for the actual situation.

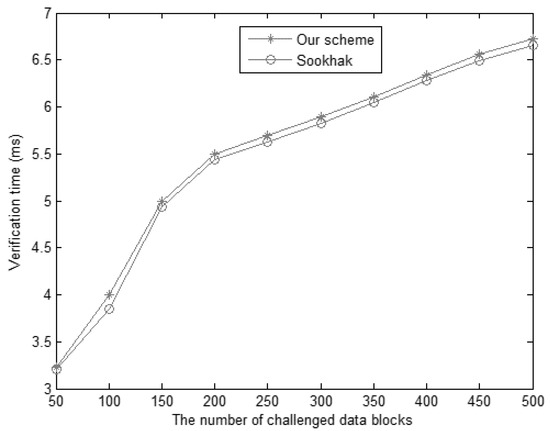
Figure 8. The verification time for different challenged data blocks.

For dynamic updating, the computational costs are smaller than the scheme [17,18] in Figure 9. When the number of updated data blocks is 500, the time of scheme [17,18] is nearly 300 ms, which is almost three times that of the proposed scheme. Hence, we suggest that the proposed data structure is more effective.

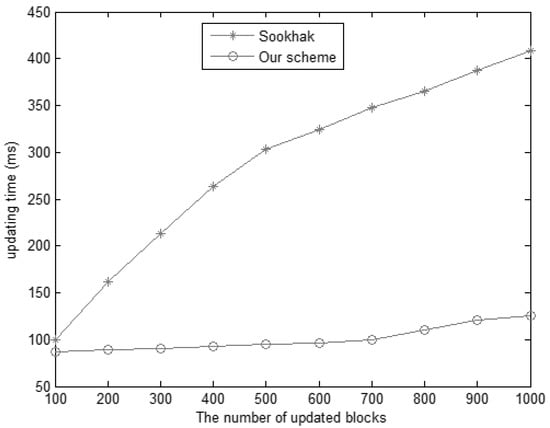
Figure 9. The updating time for different updated data blocks.

8. Conclusions

Towards making several attacks never hurt the cloud storage, in this paper, we propose a public data verification scheme that ensures efficient verification and resists the malicious attacks. Unlike traditional solutions, the proposed scheme introduces symmetric encryptions to protect data privacy that is critical and suitable for practical use. Meanwhile, a novel data structure named DCHL is designed to support dynamic updating with low communication and computational costs. Theoretical analysis shows that the TPA can detect the corrupted data blocks with a high probability, even though the CSP conducts the misbehavior. Furthermore, real experimental results make the proposed scheme substantially more convincing.

Moreover, no single method can achieve perfect data integrity verification for various scenarios. Due to the query, the complexities of the operations on a linked list are not constant in different scenarios. Frequent data changes on a massive number of data blocks put forward higher requirements for the query performance. Therefore, how to improve the efficiency with specially designed data structures is expected to be tackled in the future.