Multi-Fault Diagnosis Approach Based on Updated Interacting Multiple Model for Aviation Hydraulic Actuator

Abstract

The aviation hydraulic actuator (HA) is a key component of the flight control system in an aircraft. It is necessary to consider the occurrence of multiple faults under harsh conditions during a flight. This study designs a multi-fault diagnosis method based on the updated interacting multiple model (UIMM). The correspondence between the failure modes and the key physical parameters of HA is found by analyzing the fault mode and mechanism. The key physical parameters of HA can be estimated by employing a series of extended Kalman filters (EKF) related to the different modes of HA. The models in UIMM are updated once the fault is determined. UIMM can reduce the number of fault models and avoid combinatorial explosion in the case of multiple faults. Simulation results indicate that the multi-fault diagnosis method based on UIMM is effective for multi-fault diagnosis of electro-hydraulic servo actuation system.

1. Introduction

The aviation hydraulic actuator (HA) is a key component of aircraft flight control system [1,2,3,4]. It receives the command of the flight control system to drive the control surfaces to control the flight attitude and trajectory. With the increasing requirements for reliability and safety of the flight control system, the requirements for HA as a key part of this system are also increasing [5,6]. Therefore, there is a growing requirement for advance fault diagnosis methods to enhance the reliability of the HA.

HA is a complex mechanical-electrical system that consists of mechanical, electrical, and hydraulic. Due to the harsh working environment and heavy working loads, the performance of HA would degrade gradually until the system has a fault. A typical fault of HA is oil contamination, which is caused by solid particles in the oil or the mixing of oil with the air [7,8]. These solid particles or oil mixed with air will seriously affect the operation of the components. Leakage is another problem for hydraulic system [9,10]. Leakage not only wastes energy, but can also cause serious failures. Overall, it is clearly necessary to study the failure modes and failure mechanism of HA caused by oil pollution and leakage. Real-time condition monitoring of the aviation actuation system would allow identification of faults in time to make an appropriate diagnosis.

Many researchers have done significant studies of fault diagnosis of the hydraulic actuation system. R. Isermann described existing fault diagnosis techniques in detail [11]. The fault diagnosis method based on state observer is the most effective current method [12,13]. H. Wang et al. used an adaptive observer to diagnose the key parameters of the actuator and mainly considered the mutation parameter of the system [14]. D. Yu et al. proposed a bilinear fault detection observer for a hydraulic system, which was constructed as a discrete-time model of a bilinear model. This observer can detect actuator faults, component faults, and sensor faults through residual vectors [15]. L. An et al. presented an application of an extended Kalman filter (EKF) to identify leakage fault in hydraulically powered actuators [16]. However, all these methods assume the occurrence of only a single fault at one time.

The complexity of the HA and the harsh working conditions increase the possibility of simultaneous occurrence of multiple failure modes. J. Du et al. proposed a cluster analysis method for multi-fault diagnosis of the axial piston pump with a three-layered diagnosis reasoning engine for five possible failures [17]. P. Garimella et al. presented the application of a nonlinear model based on the adaptive robust observer for multi-fault detection and the isolation of some common hydraulic system faults [18]. This approach consists of three adaptive robust observers and a parameter estimator to monitor parameters of interest like the coefficient of bulk modulus and the coefficient of internal leakage, but is computationally costly.

Multi-fault diagnosis of the HA is more complex than single-fault diagnosis, requiring the detection of multiple faults at the same time and the extraction of fault characteristics for each of the potentially multiple faults. The interacting multiple model (IMM) was first proposed for multi-fault diagnosis of complex system by H. A. Blom [19]. Y. Zhang proposed a multi-fault diagnosis approach based on IMM for a dynamic system, and its superiority is illustrated by two aircraft examples for single and double faults of both sensors and actuators [20]. N. Tudoroiu developed IMM for partial or total failures of the spacecraft attitude control system [21]. He developed healthy models under various operating conditions and constructed faulty modes for various changes. S. A. Gadsden et al. applied both the Kalman filter (KF) and IMM to detect and identify leakage and friction faults on electro-hydrostatic actuator prototype [22]. However, the number of mathematical models in these above methods will radically increase with the number of fault modes to be diagnosed, which would significantly increase the computational complexity.

In this study, a multi-fault diagnosis method based on the updated interacting multiple model (UIMM) is designed for effective diagnosis of HA without increasing additional computational complexity. The relationships between the key parameters of the HA system and the faults are obtained after fault mode and mechanism analysis. These key physical parameters are used to establish a set of models that represent the system status under normal or faulty modes. Then, a series of extended Kalman filters, each designed based on a particular mode (i.e., normal mode or faulty one), are executed in a parallel manner, and their interaction and the likelihood function can track the system status based on mode probability. Considering that the fault in the physical system is irreversible, once a fault occurs, all fault models can be updated according to the occurred fault. The proposed UIMM approach can significantly decrease the number of fault models and economize the calculation resources, which is essential for efficient online computation of an aircraft. Finally, the simulation results validate the effectiveness of the proposed multi-fault diagnosis method.

This paper is organized as follows. Section 2 investigates the multiple fault modes and mechanisms of the HA to obtain the key physical parameters related to the system status. Section 3 presents the UIMM-based multi-fault diagnosis algorithm. In Section 4, applications of the proposed algorithm on the HA are demonstrated. Finally, conclusions are drawn in Section 5.

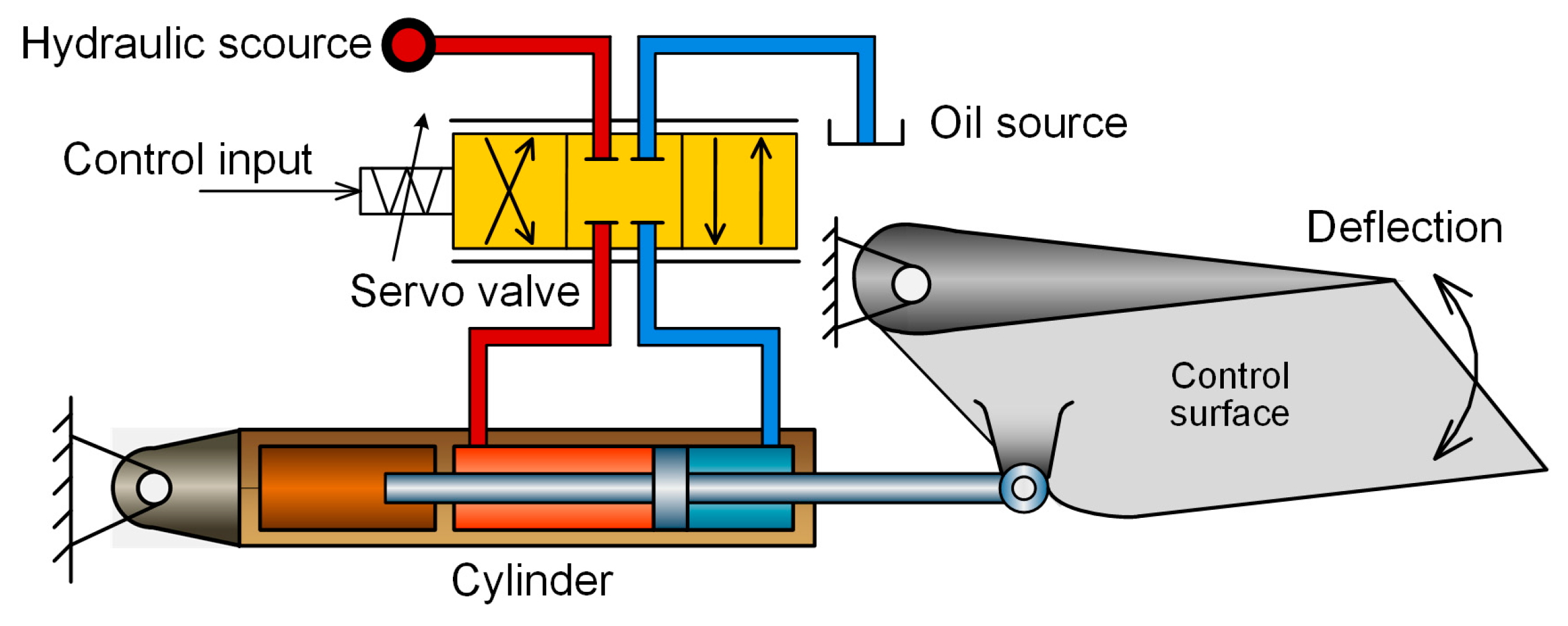
2. Failure Mode and Mechanical Analysis

Typically, HA consists of an electro-hydraulic servo valve and a double-rod hydraulic cylinder, as shown in Figure 1. The servo valve controls the displacement of the piston rod of the hydraulic cylinder to meet the desired angular displacement of the control surface from the flight control system. The hydraulic cylinder transfers the hydraulic power to mechanical power and drives the control surface to achieve the aircraft attitude control.

Since most of the faults are caused by solid particle contamination and leakage, we should determine how solid particles and leakage cause undesired performance degradation of the HA system and then establish a corresponding failure model. This is helpful for multi-fault diagnosis of the HA system.

2.1. Mathematical Model of HA under Fault-Free State

The fault-free models of the electro-hydraulic servo valve and hydraulic cylinder have been widely studied [1,3,4] and can be described as follows.

For the servo valve, the relationship between the input current $i_v$ and the spool displacement $x_v$ can be described as:

$$x_v=K_v{i}_v$$

(1)

where $K_v$ is proportional gain of servo valve.

The dynamic model of the cylinder has been described in [5,23]. Select the displacement of the hydraulic cylinder piston rod $x_p$, the piston rod speed $v_p$ and load pressure $p_h$ as three state variables, i.e., $x_1=x_p$, $x_2=v_p$, $x_3=p_h$, then the state space model of the HA can be given as:

$$\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\\ -\frac{K_h}{m_h}& -\frac{B_h}{m_h}& \frac{A_h}{m_h}\\ 0& -\frac{4E_h{A}_h}{V_h}& -\frac{4E_h(K_c+C_{ip})}{V_h}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ \frac{4E_h{K}_v{K}_q}{V_h}\end{array}\right)x_v$$

(2)

where $K_h$ is the elastic load stiffness, $B_h$ is piston’s viscous damping coefficient, $A_h$ is the effective area of the piston, $m_h$ is the total mass of the hydraulic cylinder piston rod, $E_h$ is the effective bulk modulus of the hydraulic fluid in the container, $V_h$ is the total volume of the cylinder, $C_{ip}$ is the total leakage coefficient, $K_q$ is the flow/opening gain and $K_c$ is the flow/pressure gain.

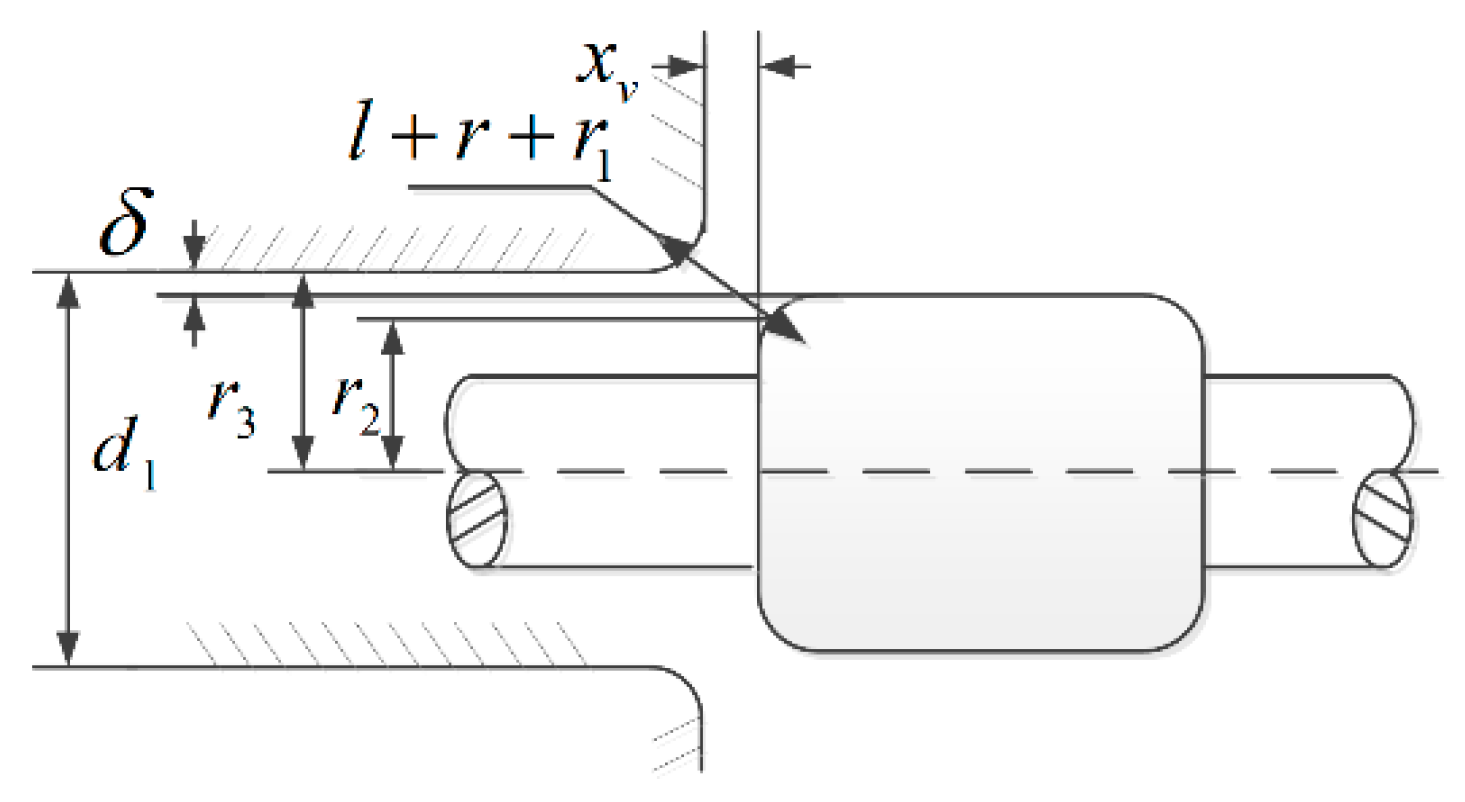
2.2. Mathematical Model of HA under Fault State

If the oil contains contamination particles, the spool valve is impacted constantly, so that there will be a gradual increase in the amount of particle debris in the oil, which can reduce the flow gain of the valve. With the movement of the spool, these contaminating particles can cause the material wear of the motion pair and increase the radial clearance. The working edges of the electro-hydraulic servo valve will suffer wear and the radial clearance of the spool will become larger as it is affected by contamination wear [24,25].

For nozzle flapper valve, according to the simulation results in [24] and the symmetrical structure, the key performance is affected by the wear of nozzle–flapper gap. The slight change of the gap does not affect the flow under the same pressures. Therefore, the impact of the baffle wear on the nozzle baffle valve flow can be neglected.

If the oil is mixed with solid particles, the sharp edges of the spool and the sleeve will have rounded corners after an extensive period of impact wear, as shown in Figure 2. The radii of the round corners of the valve core and the valve sleeve are $r$ and $r_1$, respectively. The spool opening size is $x_v$. The radial clearance after wear is $\delta$. The inner diameter of the sleeve before wear is $d_1$. The solid particles in the oil cause wear between the spool and the sleeve due to the frequent relative movement, resulting in an increase in the radial clearance.

Considering the rounded corners and the radial clearance between the spool and the sleeve, the flow area $l$ is:

$$l=\sqrt{{(r+r_1+\delta )}^2+{(x_v+r+r_1)}^2}-(r+r_1)$$

(3)

The radius of the spool $r_2$ is:

$$r_2=\frac{d_1}{2}-\frac{l\delta +rl+r_1\delta }{l+r+r_1}$$

(4)

The inner radius of the sleeve after wear $r_3$ is:

$$r_3=\frac{d_1}{2}+\frac{r_{1}l-r_1\delta }{l+r+r_1}$$

(5)

Their relationship is shown in Figure 2. So:

$$A=\pi (r_2+r_3)l$$

(6)

The linearized flow equation of spool valve is:

$$Q_h=K_q{x}_v-K_c{P}_h$$

(7)

Here the flow/opening gain $K_q$ and the flow/pressure gain $K_c$ have to be rewritten as:

$$K_q=\frac{\partial Q_h}{\partial x_v}=C_{\mathrm{d}}\pi (r_2+r_3)\sqrt{\frac{1}{\rho }\left(p_s-p_h\right)}$$

(8)

$$K_c=-\frac{\partial Q_h}{\partial P_h}=\frac{C_{\mathrm{d}}A\sqrt{\left(p_s-p_h\right)/\rho }}{2\left(p_s-p_h\right)}$$

(9)

The orifice flow area $A$ contains parameters $r$, $r_1$, and $\delta$ that reflect the wear of the spool. The spool is constantly wearing, so these parameters will gradually increase to be greater than the normal value, as well $K_q$ and $K_c$ will become larger with constant wear. We then define these two abnormal parameters as $K_{fq}$ and $K_{fc}$, and these parameters can reflect the wear of the electro-hydraulic servo valve.

The amount of leakage is caused by the pressure difference and can reflect the internal leakage. Additionally, the effective bulk modulus of the hydraulic fluid $E_h$ can reflect the degree of oil affected by the air. So, the leakage coefficient $C_l$ and the effective bulk modulus $E_h$ are the key parameters for fault diagnosis of the HA.

During operation of the system and with the aging of components, the model parameters will change. Through tracking changes of the system parameters, the system health status can be obtained.

The root-cause of the faults considered in this study may be:

The wear of the spool and the sleeve to increase $K_q$ and $K_c$;

Unexpectedly increased leakage coefficient $C_{ip}$ due to fast wear of the dynamic seal;

Unexpectedly decreased effective bulk modulus $E_h$ due to oil contamination or oil mixed with air.

The key parameters of HA are the flow gain $K_q$ and the flow-pressure coefficient $K_c$, the internal leakage coefficient $C_{ip}$, and the effective bulk modulus $E_h$. These parameters can reflect the potential causes except for artificial or processing errors and electrical failures.

3. UIMM Algorithm

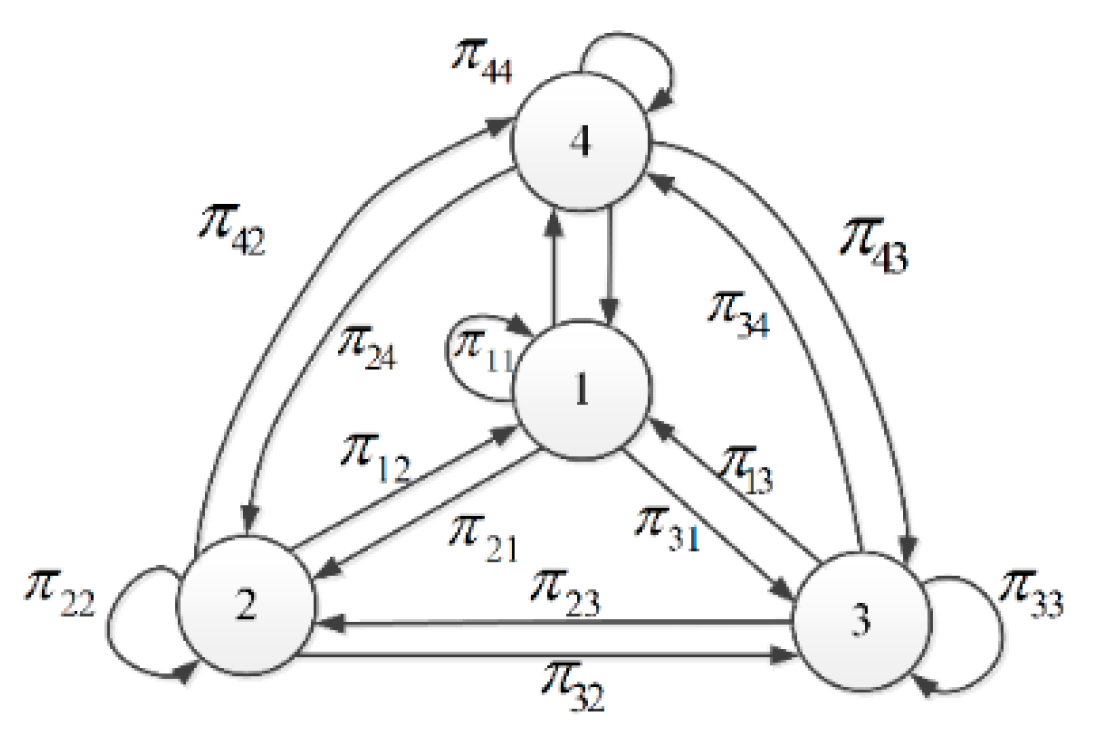
3.1. Model Set Design

After obtaining the system key parameters, the system model set should be designed based on the system fault threshold. Based on the analysis in the last section, the key parameters can be defined with major fault magnitude, which can monitor the system status. For the single fault situation of the servo valve, two models can be designed with a major magnitude of the $K_{fq}$ and $K_{fc}$. A similar model design strategy can be used for the other key parameters.

To use UIMM, the state space model of HA must first be discretized. The discretized system is:

$$x_{k+1}=G{x}_k+Hu$$

(10)

where $u=x_v$ is system input, $G$ and $H$ are system matrix and input matrix of the discretized system, respectively. We then define the fault-free system model with the normal values as:

$$x_{k+1}=G_1{x}_k+H_{1}u$$

(11)

where $G_1$ and $H_1$ are system matrix and input matrix of the fault-free system model. Then, change the key parameters in $G$ and $H$ to define the fault models. For example, use the major fault magnitude of $K_{fq}$ and $K_{fc}$ to define a model of minor wear fault of the servo valve. The corresponding discretized system is defined as:

$$x_{k+1}=G_2{x}_k+H_{2}u$$

(12)

where $G_2$ and $H_2$ represent the new system matrix and new input matrix of the system with fault.

This can then be done with the other fault models. For $M$ faults, $M$ fault models can be obtained. The mode (normal or faulty mode) of the system at time $k$ can be selected by a discrete process; $m_j(\mathrm{k})$, $m_j(\mathrm{k})$ is the discrete-valued modal state, which denotes the mode in effect at the end of the sampling period. The system mode sequence is assumed to be a first-order Markov chain with transition probabilities:

$$p_{ij}(\mathrm{k})=P\left\{m_j(\mathrm{k}+1)|m_i(\mathrm{k})\right\},\forall m_i,m_j\in S$$

(13)

$${\displaystyle \sum _j^{}{p}_{ij}}(\mathrm{k})=1,i=1,2,\cdots ,M$$

(14)

where $P$ denotes probability; $S=\left\{m_1,m_2,\cdots ,m_M\right\}$ represents the set of all possible system modes. The system (9) and (10) may randomly jump from one mode to another due to the occurrence of faults. The system mode sequence is an indirectly observed Markov chain, from which the transition probability matrix $p=\left\{p_{ij}\right\}$ is a design parameter. The model probabilities provide an indication of the mode in effect at any given time. Since each system mode is equivalent to a specific fault scenario, model probabilities describe the probability of the occurrence of the corresponding fault scenario.

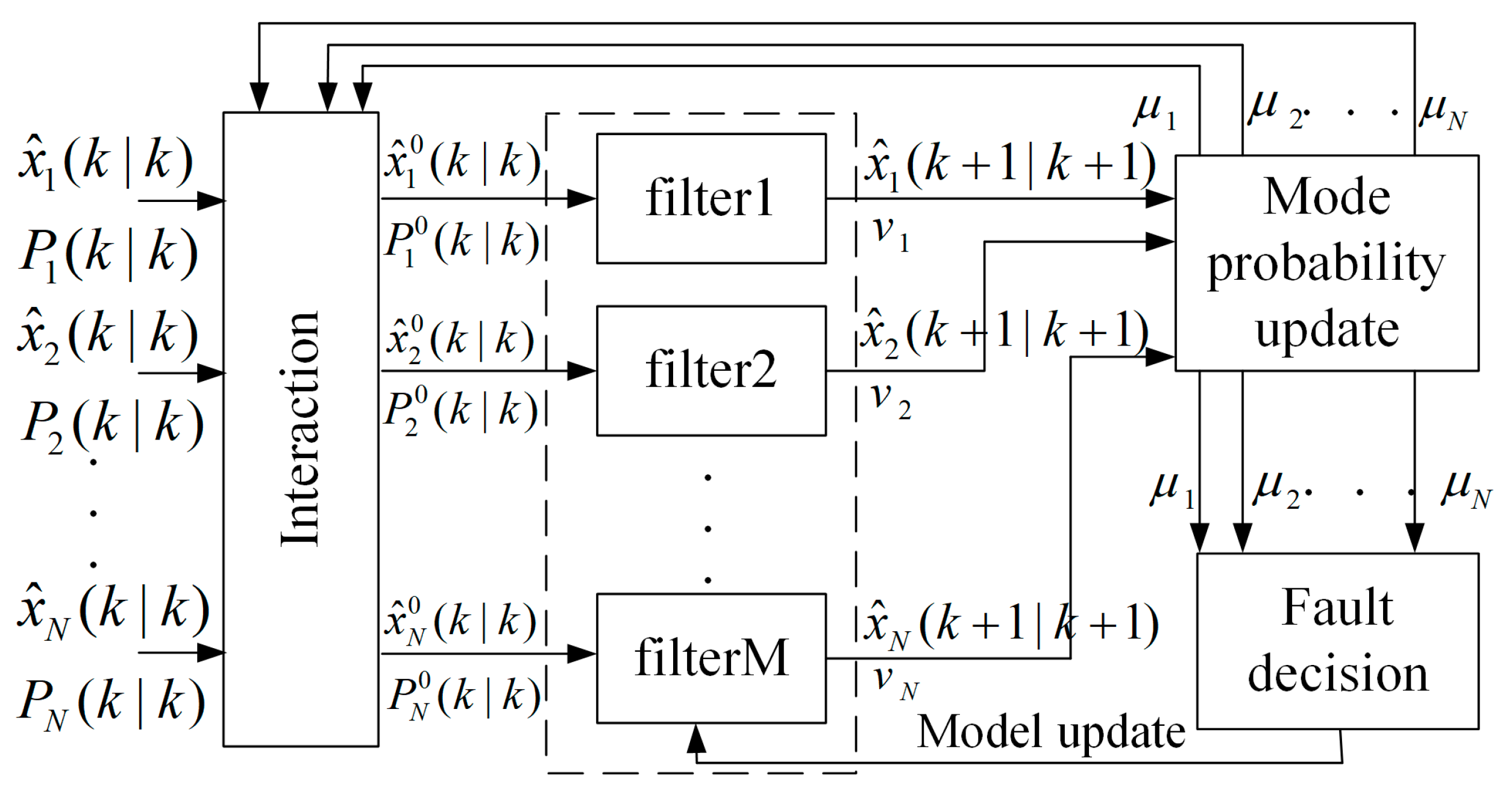
3.2. The Updated Interacting Multiple Model

The UIMM is composed of a series of EKF operating in parallel. Each filter is associated with a system behavior pattern. The mode probability is assigned to each filter based on its measurement residual to indicate the correspondence between the filter and the system status. Changes in system parameters are characterized by switching between models. When the failure mode changes, the fault pattern corresponding to the system can be found by model switching using the predefined mode transition probability. The updating and switching of the fault models can reflect the process of the system from single fault to multiple faults. The block diagram of the UIMM is shown in Figure 3.

One of the characteristics of the UIMM algorithm is the interaction of knowledge. The current pattern is calculated by merging the knowledge of the previous moment to improve the accuracy of the estimate. This process is done at the beginning of each iteration, and the last estimated information (mode probability ${\mu }_{i,k|k}$, state estimation ${\widehat{x}}_{i,k|k}$ and error covariance $P_{i,k|k}$) is used to calculate the initial value (${\widehat{x}}_{0j,k|k},P_{0j,k|k}$) of each filter. IMM based on EKF can be used for real-time fault diagnosis [26,27,28]. The IMM algorithm has equivalent performance and complexity compared with other single-model algorithm [29]. The specific calculation process is described by the following equations.

Step 1. Assuming that the system has $M$ models, the mixing probability ${\mu }_{i|j,k|k}$ can be calculated at the beginning of each cycle as:

$${\mu }_{i|j,k|k}=\frac{p_{ij}{\mu }_{i,k|k}}{{\displaystyle \sum _{i=1}^M{p}_{ij}{\mu }_{i,k|k}}}$$

(15)

Step 2. After obtaining the mixing probability, the initial value of each filter can be calculated using the previous estimate and the error variance:

$${\widehat{x}}_{0j,k|k}={\displaystyle \sum _{i=1}^M{\widehat{x}}_{i,k|k}{\mu }_{i|j,k|k}}$$

(16)

$$P_{oj,k|k}={\displaystyle \sum _{i=1}^M{\mu }_{i|j,k|k}\left\{P_{i,k|k}+\left({\widehat{x}}_{i,k|k}-{\widehat{x}}_{0j,k|k}\right){\left({\widehat{x}}_{i,k|k}-{\widehat{x}}_{0j,k|k}\right)}^T\right\}}$$

(17)

Step 3. Next, the filters representing the different models are used to estimate the state in parallel. Execute EKF based on the system model and the initial value to predict the state and output:

$$\{\begin{array}{c}{\widehat{x}}_{j,k+1|k}=f_j({\widehat{x}}_{0j,k|k},u_k)\hfill \\ {\widehat{z}}_{j,k+1|k}=h_j({\widehat{x}}_{j,k|k})\hfill \end{array}$$

(18)

For non-linear system models, the system needs to be linearized. The Jacobian matrix $F_{sys}$ and $H_{sys}$ are:

$$F_{j,sys}=\frac{\partial f_j(x)}{\partial x}{|}_{x={\widehat{x}}_{0j,k|k,u_k}}$$

(19)

$$H_{j,sys}=\frac{\partial h_j(x)}{\partial x}{|}_{x={\widehat{x}}_{0j,k+1|k}}$$

(20)

Then the measurement error $e_{j,k+1|k}$, the covariance of the priori state $P_{j,k+1|k}$ and the a priori error covariance $S_{j,k+1}$ are:

$$e_{j,k+1|k}=z_{k+1}-{\widehat{z}}_{j,k+1|k}$$

(21)

$$P_{j,k+1|k}=F_{j,sys}{P}_{0j,k|k}{F}_{j,sys}^T+Q$$

(22)

$$S_{j,k+1}=H_{j,sys}{P}_{j,k+1|k}{H}_{j,sys}^T+R$$

(23)

The filter gain $K_{j,k+1}$ is defined as:

$$K_{j,k+1}=P_{j,k+1|k}{H}_{j,sys}^T{(H_{j,sys}^{}{P}_{j,k+1|k}{H}_{j,sys}^T+R)}^{-1}$$

(24)

and its function is used to correct the priori estimate and to obtain the posteriori estimate as:

$${\widehat{x}}_{j,k+1|k+1}={\widehat{x}}_{j,k+1|k}+K_{j,k+1}(z_{k+1}-{\widehat{z}}_{j,k+1|k})$$

(25)

$$P_{j,k+1|k+1}=(I-K_{j,k+1}{H}_{j,sys})P_{j,k+1|k}$$

(26)

Step 4. Assume that the measurement error is a normal distribution with mean 0 and variance $S_{j,k+1}$. Then the likelihood function:

$$L_{j,k+1}=\frac{1}{\sqrt{\left|2\pi S_{j,k+1}\right|}}\exp \left(\frac{-\frac{1}{2}{e}_{j,z,k+1}^T{e}_{j,z,k+1}^{}}{S_{j,k+1}}\right)$$

(27)

Step 5. According to the update of the likelihood function $L_{j,k+1}$, the probability of the pattern gives the degree of matching for each pattern:

$${\mu }_{j,k+1}=L_{j,k+1}{\displaystyle \sum _{i=1}^M{p}_{ij}{\mu }_{i,k}}/{\displaystyle \sum _{i=1}^M{L}_{j,k+1}{\displaystyle \sum _{i=1}^M{p}_{ij}{\mu }_{i,k}}}$$

(28)

Step 6. Then the fault decision can be made by:

$${\mu }_j(k+1)=\underset{i}{\max }{\mu }_i(k+1)=\{\begin{array}{l}\ge {\mu }_f,\mathrm{fault}\mathrm{j}\mathrm{occurred}\hfill \\ <{\mu }_f,\mathrm{no}\mathrm{fault}\hfill \end{array}$$

(29)

where ${\mu }_f$ is a decision threshold selected based on historical experience. If a fault occurs, the corresponding parameters in all models should be alternative with the corresponding fault value.

Step 7. The combination of estimation is:

$${\widehat{x}}_{k+1,k+1}={\displaystyle \sum _{i=1}^M{\widehat{x}}_{i,k+1|k+1}{\mu }_{i,k+1}}$$

(30)

$$P_{k+1|k+1}={\displaystyle \sum _{i=1}^M{\mu }_{j,k+1}\left\{P_{i,k+1|k+1}+\left({\widehat{x}}_{i,k+1|k+1}-{\widehat{x}}_{j,k+1|k+1}\right){\left({\widehat{x}}_{i,k+1|k+1}-{\widehat{x}}_{j,k+1|k+1}\right)}^T\right\}}$$

(31)

The main result of UIMM algorithm is that the current state of the system can be estimated and the fault decision can be made after the calculation of UIMM from Step 1 to Step 7. At Step 5, the maximum value in the pattern probability ${\mu }_{j,k+1}$ means the corresponding model is the closest to the current state of the system, and the corresponding model can represent the current state of the system.

The main difference between UIMM and IMM is that, in UIMM, once the system state is detected to be closest to a fault model, then parameters representing such a fault in all fault models will be updated to the fault value to indicate that such a fault has occurred. But in IMM, no parameter in fault models will be updated.

3.3. Comparison of IMM and UIMM

To describe the problem more easily, let $f_1,f_2,\cdots ,f_M$ denote a series of single faults, and define ${\theta }_1,{\theta }_2,\cdots ,{\theta }_M$ as the corresponding parameters in the matrix $A_1,A_2,\cdots ,A_M$. These key physical parameters are located in different positions in matrix $A$ and represent unrelated faults of bigger or smaller magnitude compared with the normal values. When a single fault occurs, matrixes $A_1,A_2,\cdots ,A_M$ will form $M$ models. Considering the probability of multiple faults, these key parameters will combine with each other to represent multiple faults. For example, change ${\theta }_1$ and ${\theta }_2$ to form a new matrix $A_{12}$, which represents the faults of $f_1$ and $f_2$. Change ${\theta }_1$ and ${\theta }_3$ to form a new matrix $A_{13}$, which represents the faults of $f_1$ and $f_3$. According to the same law, there will be an increase of $C_M^2$ matrixes to represent the modes of two-fault. In consideration of the occurrence of three or more faults that occur simultaneously, the $C_M^2+C_M^3+\cdots +C_M^{M-1}+C_M^M$ matrixes will increase to represent more multi-fault situations compared with the single fault situation, causing a combinatorial explosion.

For more faults, the comparison of the two methods for the number of models is shown in Figure 4. As the number of failures increases, the number of required failure models in IMM increases dramatically. The number of failure models required by UIMM is much smaller than the number required for IMM, as the number of failure models required for UIMM is equal to the number of system modes of interest.

The computational complexity will reduce significantly by using UIMM. The key improvement is the increase of the update step. If a fault $f_i,i=1,2,\cdots ,M$ occurs, the model with matrix $A_i$ will match the system status. Then all $M$ models should be updated, that is, ${\theta }_i$ in all models should be replaced with the fault value. If one more fault $f_j,j=1,2,\cdots ,M$ occurs, then an update step should be executed. So, use fault values of ${\theta }_j$ to replace the normal value of ${\theta }_j$ in every model to form a series of new matrixes. Then, the matrix $A_{ij}$, which represents two faults of $f_i$ and $f_j$, will match the system status. According to this rule, if a new fault $f_m$ occurs, use the fault value of ${\theta }_m$ to replace every normal value of ${\theta }_m$ in all models. The system always has $m$ models and updates all the models if a fault occurs. Less computation is required compared with an increased number of models to represent multi-fault situations.

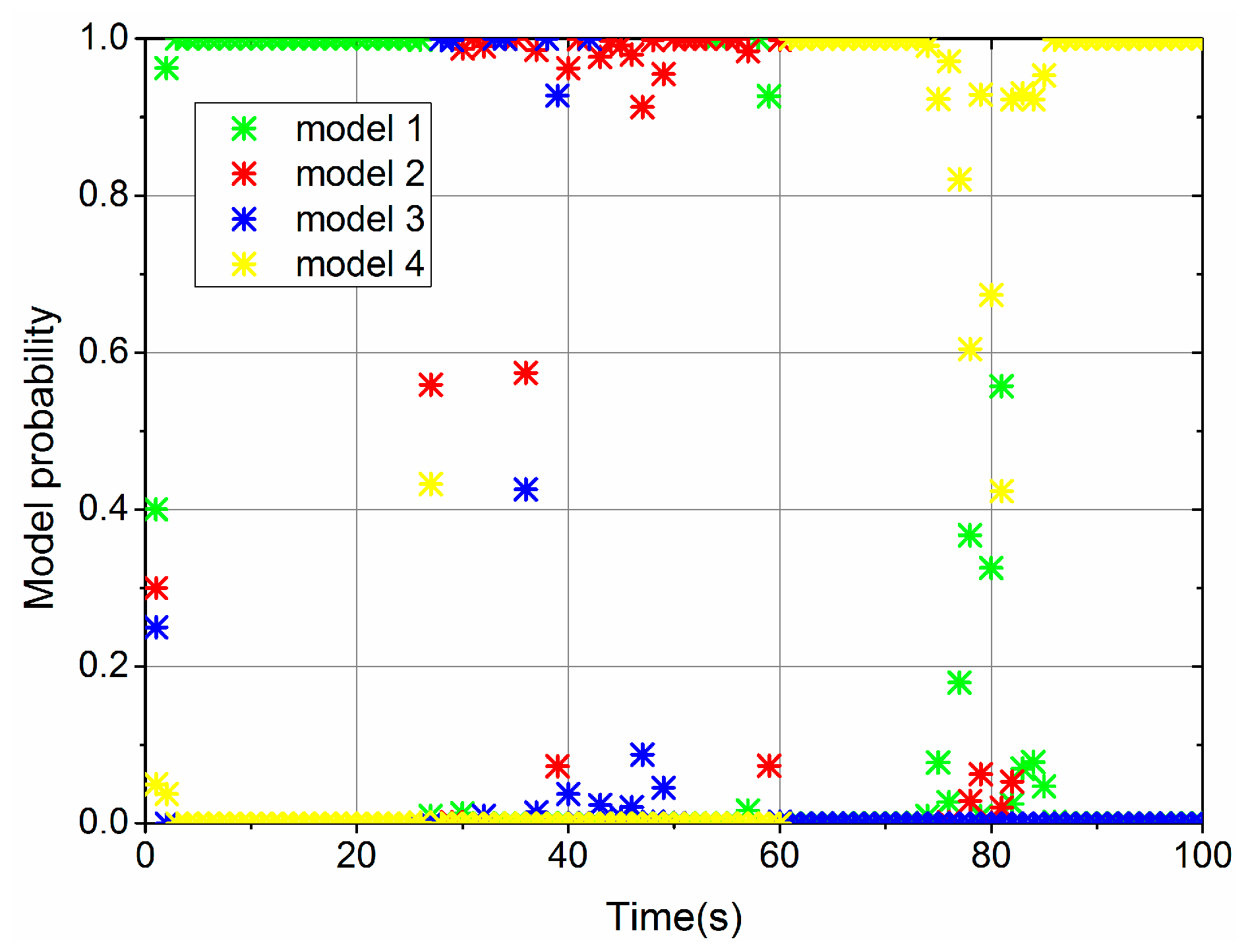
4. Simulation Results and Discussion

4.1. Simulation Environment Settings

To assess the validity of the proposed method, simulation programs were developed in MATLAB environment. The parameters of HA in normal and fault modes are shown in

Table 1. Parameters of HA in normal and fault modes.

Parameter (Unit)	Normal Value	Faulty Value
$K_v (\mathrm{m}/\mathrm{A})$	$3.04\times {10}^{-3}$
$K_c (\mathrm{N}/\mathrm{m})$	$1.75\times {10}^{-10}$	$5.175\times {10}^{-9}$
$B_h (\mathrm{kg}/\mathrm{s})$	$1\times {10}^4$
$A_h ({\mathrm{m}}^2)$	$1.4726\times {10}^{-2}$
$m_h (\mathrm{kg})$	$55$
$E_h (\mathrm{Pa})$	$6\times {10}^6$	$6\times {10}^5$
$K_h (\mathrm{kg}/{\mathrm{s}}^2)$	$1\times {10}^5$
$V_h ({\mathrm{m}}^3)$	$1.4726\times {10}^{-1}$
$K_q \left({\mathrm{m}}^2/\mathrm{s}\right)$	$2.7$	$2.95$
$C_l \left(\left({\mathrm{m}}^3/\mathrm{s}\right)/\mathrm{Pa}\right)$	$1.0\times {10}^{-10}$	$5.0\times {10}^{-9}$

.

A set of system models representing the different states of the system can be defined according to Table 1. These modes are labelled by the indexes $1,2,3\cdots$, respectively for convenience. The sampling time $T=0.0001$. The modes of the system are assigned as follows.

The discretized normal model (defined as model 1) is:

$$x_{k+1}=G_1{x}_k+H_{1}u$$

(32)

If the spool tip has a rounded corner and the spool edge is worn due to pollution wear, the discretized model (defined as model 2) is:

$$x_{k+1}=G_2{x}_k+H_{2}u$$

(33)

When the actuator leaks, the discretized system model (defined as model 3) is:

$$x_{k+1}=G_3{x}_k+H_{3}u$$

(34)

In the HA, when oil is mixed with the air, the discretized system model (defined as model 4) is:

$$x_{k+1}=G_4{x}_k+H_{4}u$$

(35)

The observation matrix $C$ is given as a unit array $I$ of three orders. The simulated piston velocity and displacement are used as measurements. The initialization settings of every scenario are given as: ${\widehat{x}}_{0|0}={\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^T$, $P_{0|0}=0.1I$, $Q=\left[\begin{array}{ccc}1\times {10}^{-12}& 0& 0\\ 0& 1\times {10}^{-12}& 0\\ 0& 0& 1\times {10}^{-4}\end{array}\right]$ and $R=\left[\begin{array}{ccc}1\times {10}^{-12}& 0& 0\\ 0& 1\times {10}^{-12}& 0\\ 0& 0& 1\end{array}\right]$.

4.2. Simulation 1—Wear of the Servo Valve and Leakage of the Hydraulic Cylinder

The results of applying the proposed method to HA are explained in this section and the wear of the servo valve and leakage of the cylinder are considered. So, models 1, 2 and 3 are needed in this section. Initially, the system has a high probability of normal operation, and then the initial mode probability is defined as:

$${\mu }_{i,0}=\left[\begin{array}{cccc}0.4& 0.3& 0.25& 0.25\end{array}\right]$$

(36)

The state transition among modes in this scenario is shown in Figure 5. After the system starts running, the given mode transition probability $p_{ij}$ matrix is given:

$$p_{ij}=\left[\begin{array}{cccc}0.9& 0.05& 0.025& 0.025\\ 0.1& 0.85& 0.025& 0.025\\ 0.05& 0.05& 0.85& 0.05\\ 0.05& 0.05& 0.05& 0.85\end{array}\right]$$

(37)

The element in $p_{ij}$ is the probability that one mode switches to another mode, and the value on the diagonal means that it will maintain the same pattern with the probability of 0.9 or 0.85, and the non-diagonal elements represent a probability of 0.1, 0.05 or 0.025 to switch to different patterns. Total simulation time $t=100\mathrm{s}$. The fault modes of the system are listed in

Table 2. The operating modes of HA in simulation 1.

$\mathbf{Time}(\mathbf{s})$	Operating Mode
$1~30\mathrm{s}$	fault-free (model 1)
$30~60\mathrm{s}$	wear of the servo valve (model 2)
$60~100\mathrm{s}$	wear of the servo valve and leakage of the hydraulic cylinder (model 3)

.

The results of multi-fault diagnosis using UIMM are shown in Figure 6. The mode recognition results in Figure 7 are highly consistent with the settings in Table 2, and only few dots identify incorrect modes. The results show that the system is model 1 when $t<30\mathrm{s}$, the system is model 2 when $30\le t\le 60\mathrm{s}$, and the system is model 4 when $60\le t\le 100\mathrm{s}$. So, the system is normal when $t<30\mathrm{s}$, the system has the fault of servo valve wear when $30\le t\le 60\mathrm{s}$, and the system has faults of servo valve wear and leakage of the hydraulic cylinder when $60\le t\le 100\mathrm{s}$.

4.3. Simulation 2—Wear of the Servo Valve and Oil Mixed with the Air

Other faults are considered in this section. The leakage of the cylinder and the oil mixed with the air are considered, so, models 1, 2 and 4 are needed in this section. Initially, the system has a high probability of normal, and then the initial mode probability is defined as in Equation (36). After the system starts running, the given mode transition probability $p_{ij}$ matrix is given in Equation (37).

The state transition between modes in this scenario is shown in Figure 5. As above, the mode transition matrix $p_{ij}$ is shown in Equation (37). Total simulation time $t=100\mathrm{s}$. The potential fault modes of the system are listed in

Table 3. The operating modes of HA in simulation 2.

$\mathbf{Time}(\mathbf{s})$	Operating Mode
$1~30\mathrm{s}$	fault-free (model 1)
$30~60\mathrm{s}$	wear of the servo valve (model 2)
$60~100\mathrm{s}$	wear of the servo valve and oil mixed with the air (model 4)

.

The mode probability distribution and mode recognition using the UIMM algorithm are shown in Figure 8 and Figure 9. The UIMM algorithm recognition results in Figure 9 are highly consistent with the settings in Table 3, and only a few data points identify the wrong modes. The results show that the system is model 1 when $t<30\mathrm{s}$, the system is model 2 when $30\le t\le 60\mathrm{s}$, and the system is model 4 when $60\le t\le 100\mathrm{s}$. Thus, the system is normal when $t<30\mathrm{s}$, the system has a servo valve wear fault when $30\le t\le 60\mathrm{s}$, and the system has faults of servo valve wear and oil mixed with the air when $60\le t\le 100\mathrm{s}$.

5. Conclusions

To address the issue of multiple faults occurring in HA of a flight control system, this study designed a multi-fault diagnosis method for the HA based on UIMM. In this strategy, after analyzing the typical failure modes and failure mechanisms of HA, the key physical parameters of the system are obtained and models that can reflect different typical single fault of the system are established. This allows tracking of the real state of the system in real time by matching the model with the system state. System failure is not reversible without troubleshooting. If a new fault occurs, all corresponding parameters in the fault models are replaced by fault values. In the case of multiple faults, this approach can greatly reduce the number of system fault models. Compared with traditional IMM, UIMM can diagnosis multiple faults with fewer models to avoid combination explosions. The simulation results indicate the effectiveness of the novel method. Nevertheless, coupling faults are not considered here, which should be addressed in the future.