Optimization of Demand-Response-Based Intelligent Home Energy Management System with Binary Backtracking Search Algorithm
Abstract
1. Introduction
- The development and creation of an intelligent HEM system with DR-enabled considering the cost of electricity, home occupancy, and achieving the best energy savings, costs, and the optimal schedule for home appliances.
- Considering user comfort as the main energy management process priority to promote the integration of the program into the consumer’s everyday routine without impacting their lifestyle.
- Inverter appliances are used for the first time because most studies focused on older appliances as the use of inverter appliances is more suitable and better than traditional devices in loads management in terms of energy and cost savings.
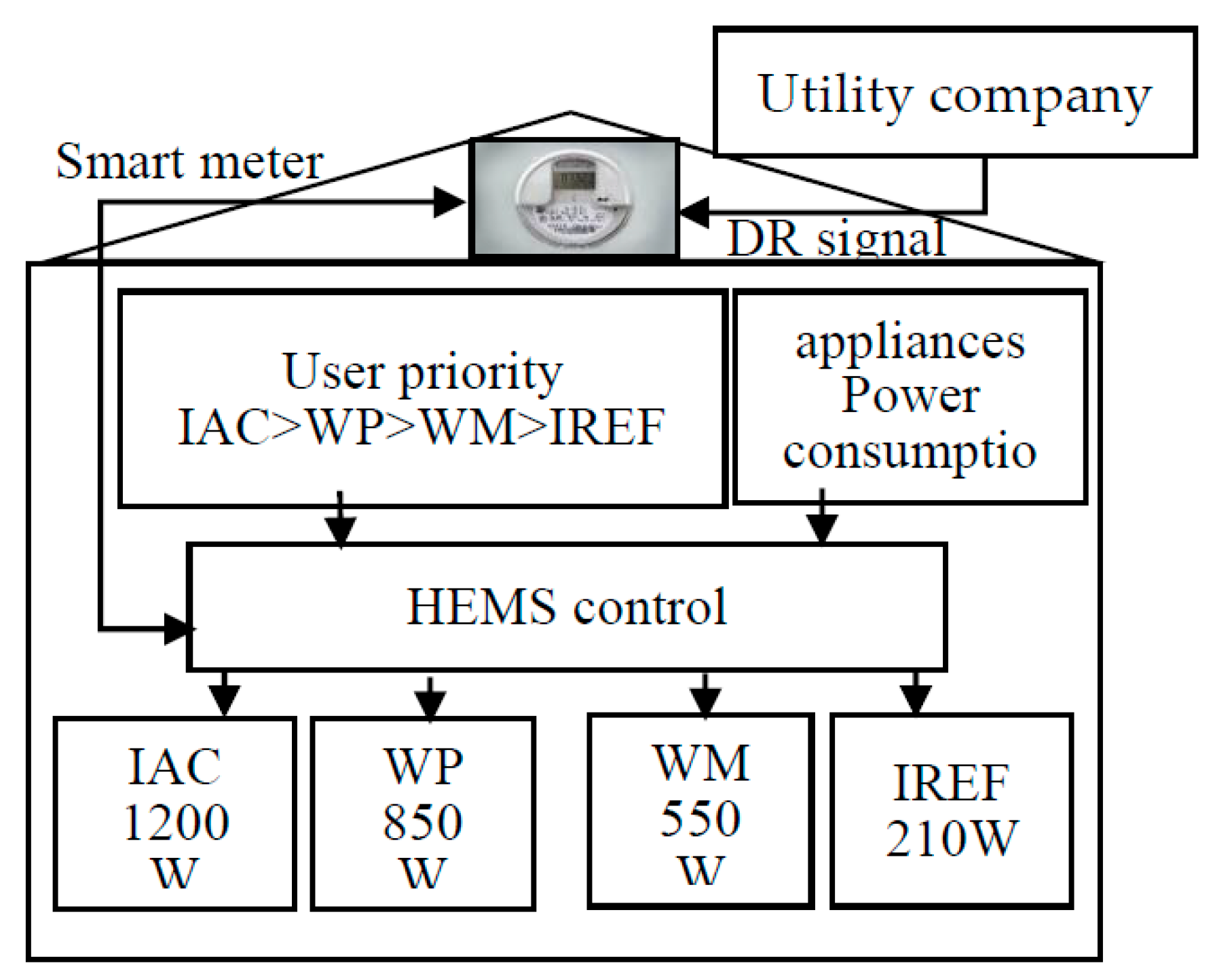
2. Novel Home Energy Management System Software Implementation
3. Home Energy Management System Strategy by Electrical Device Type
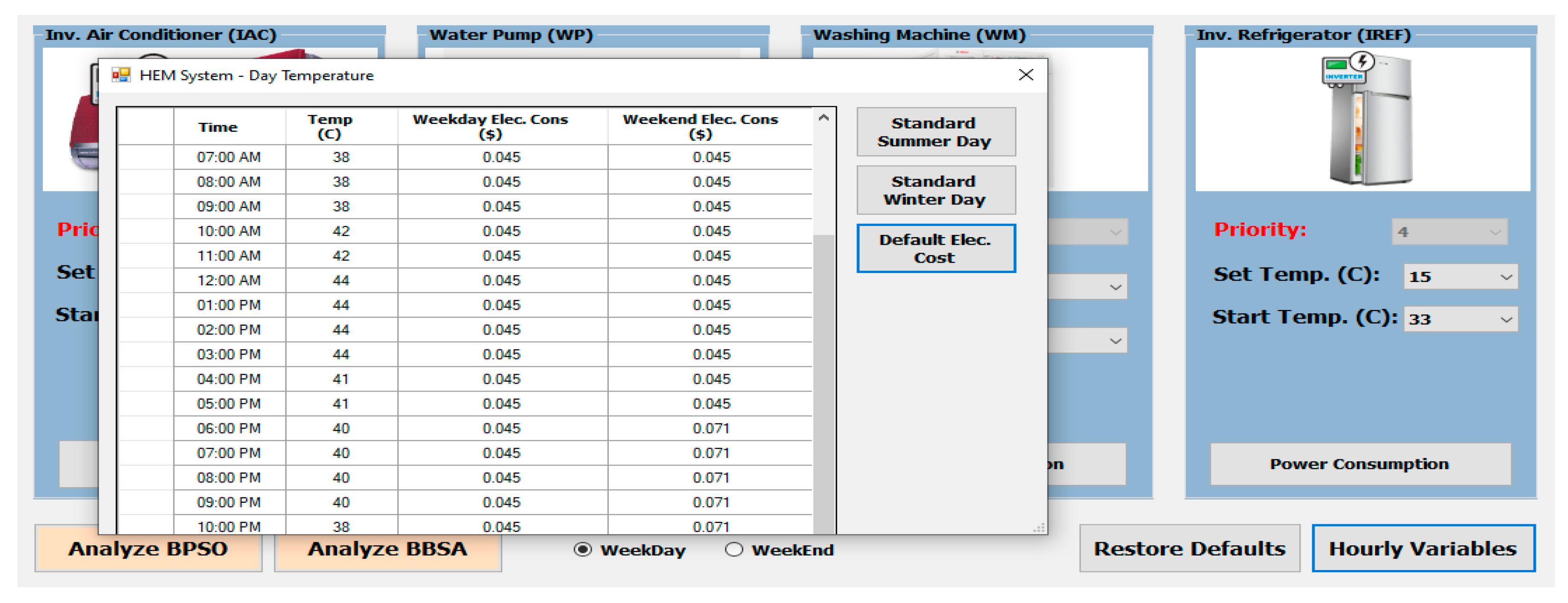
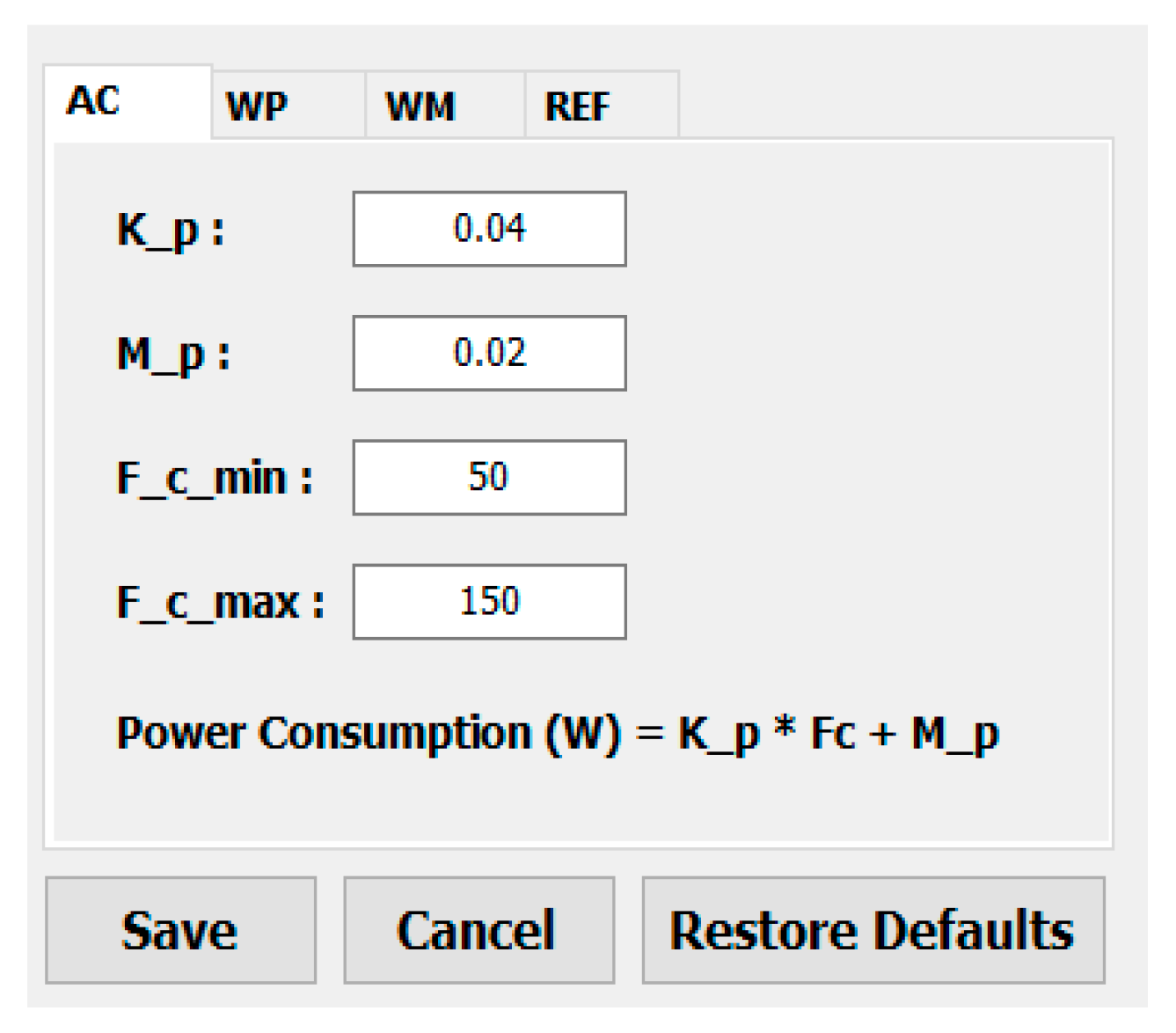
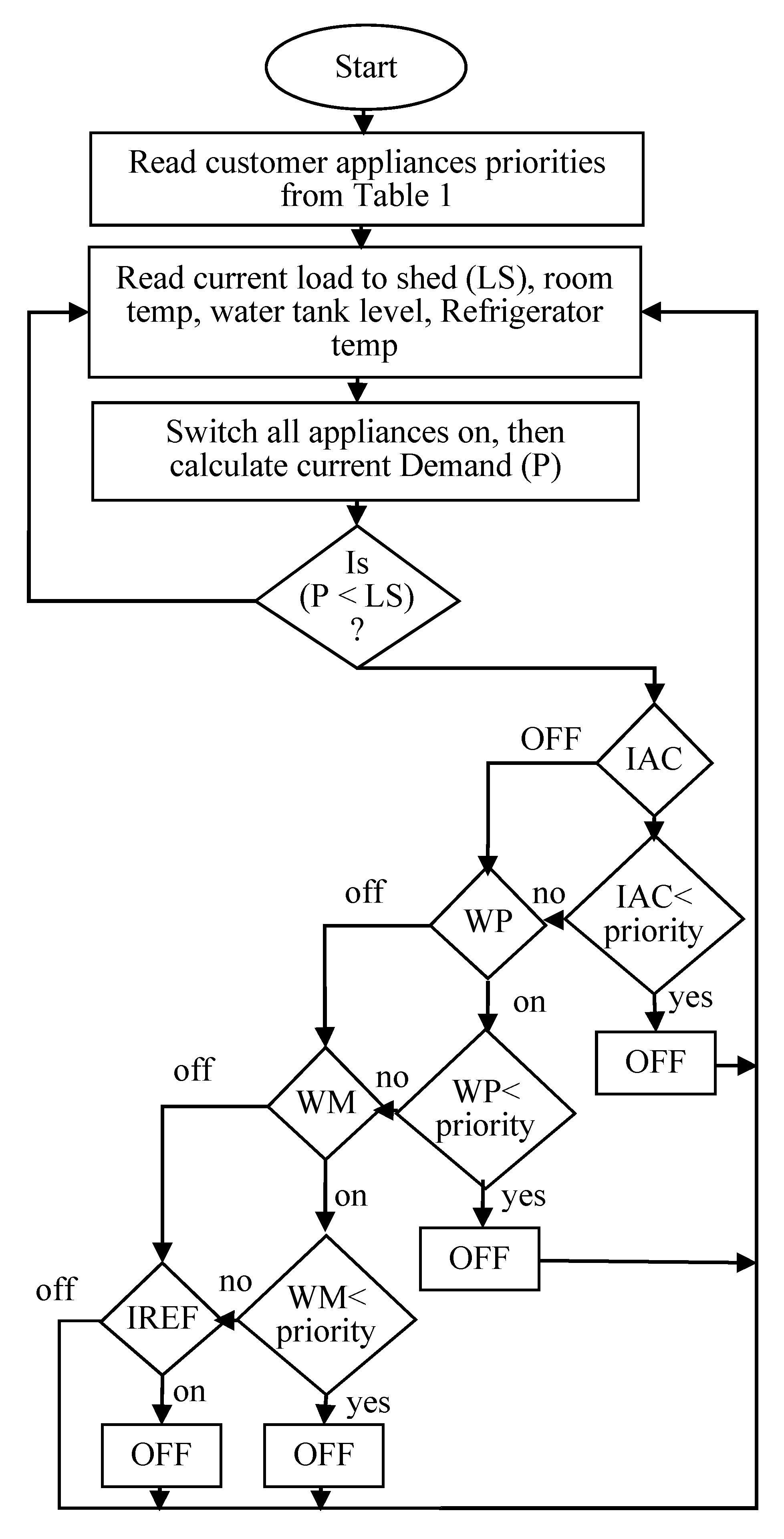
3.1. Inverter Air Conditioner (IAC)
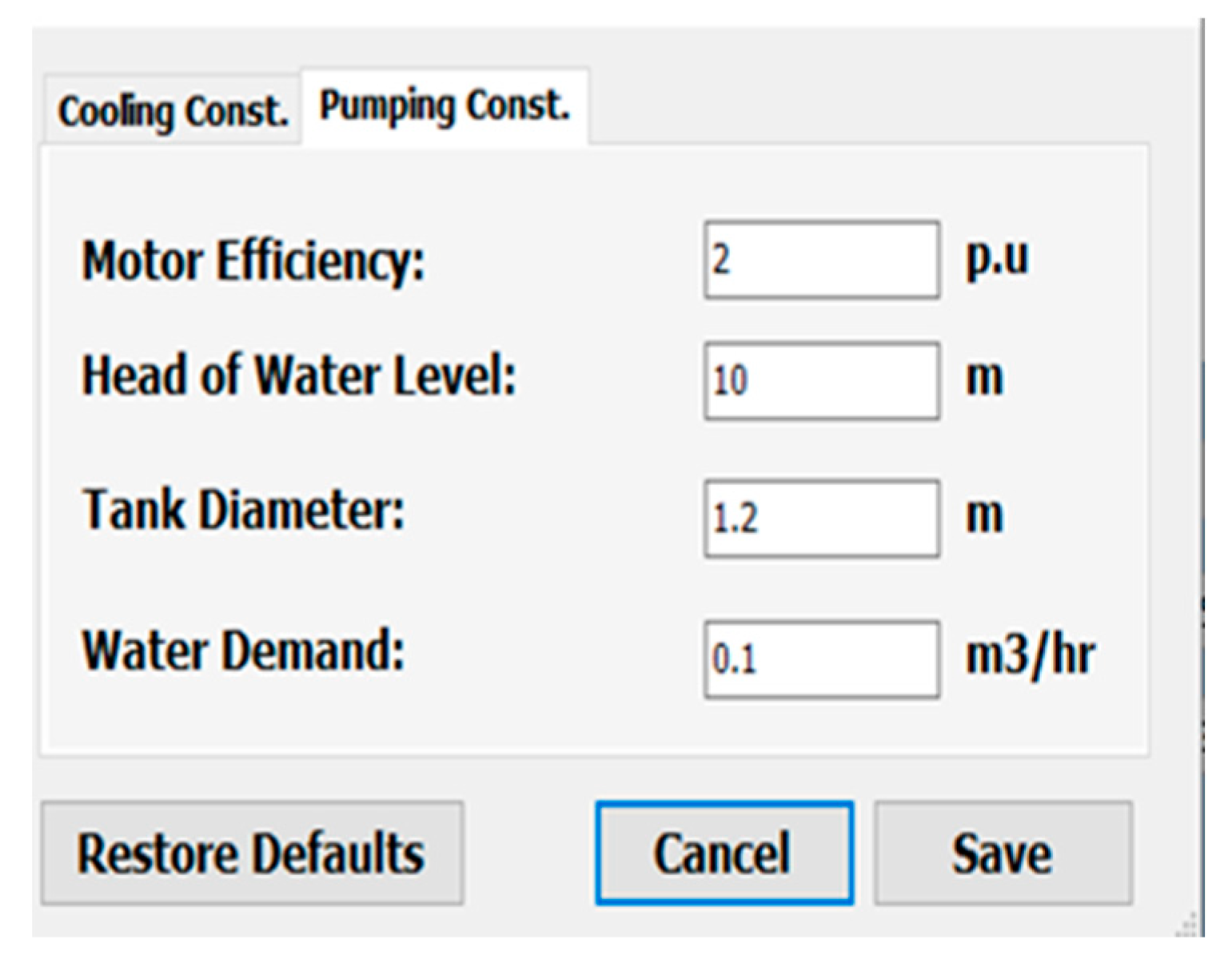
3.2. Water Pump (WP)
3.3. Washing Machine (WM)
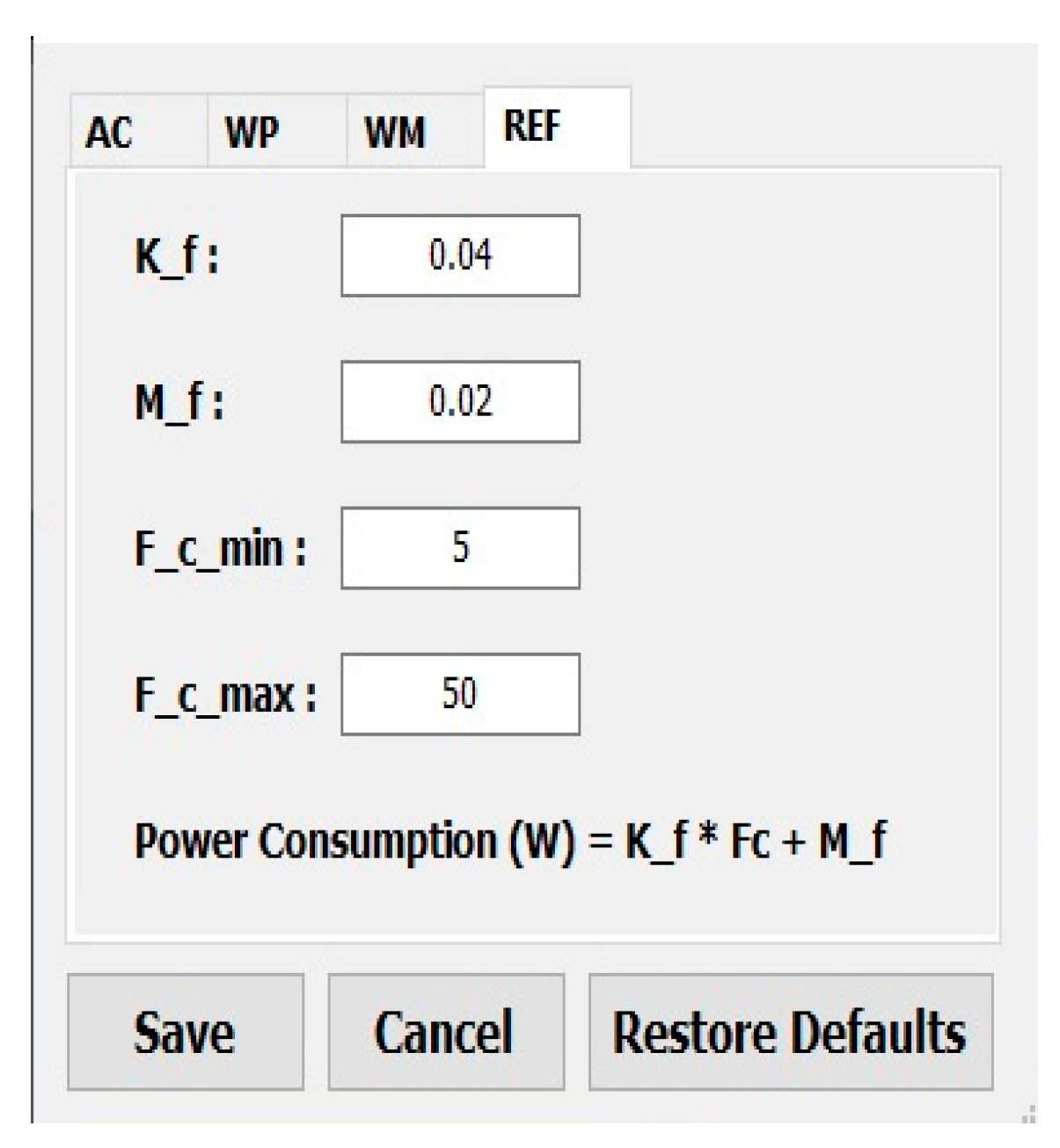
3.4. Inverter Refrigerator (IREF)
4. Proposed HEMS
5. Objective Function and Constraint
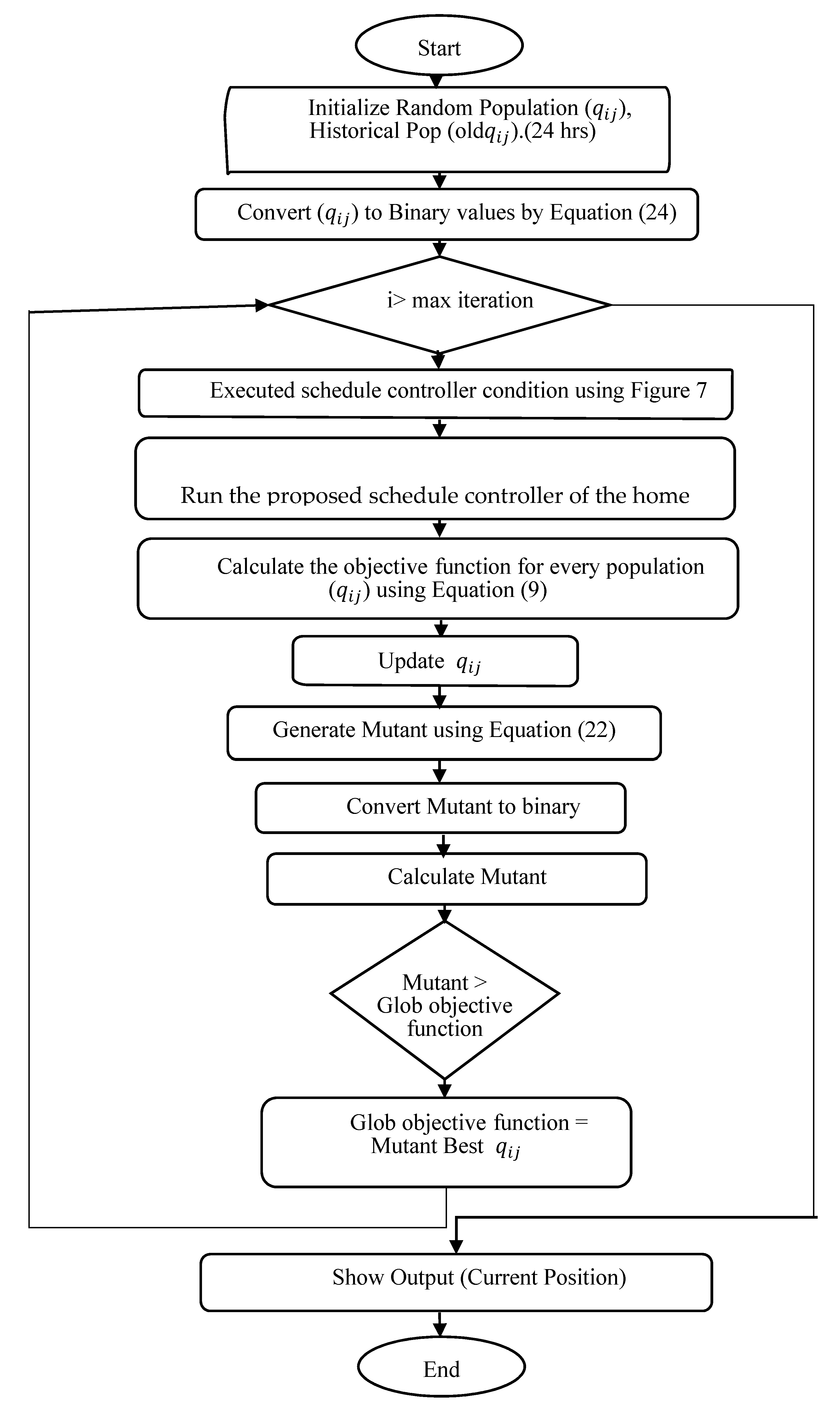
6. Binary Back Tracking Search Algorithm (BBSA) Optimization
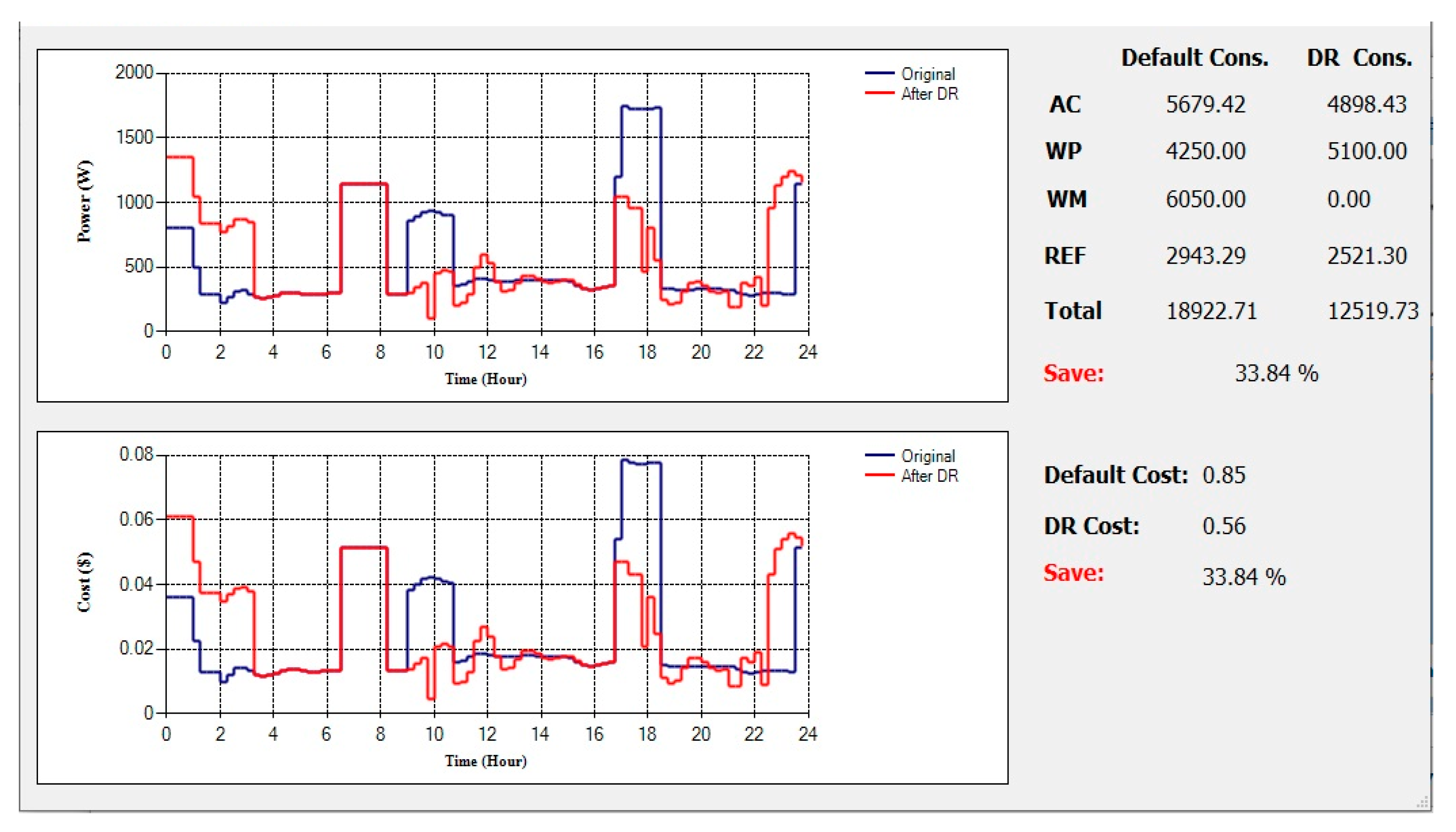
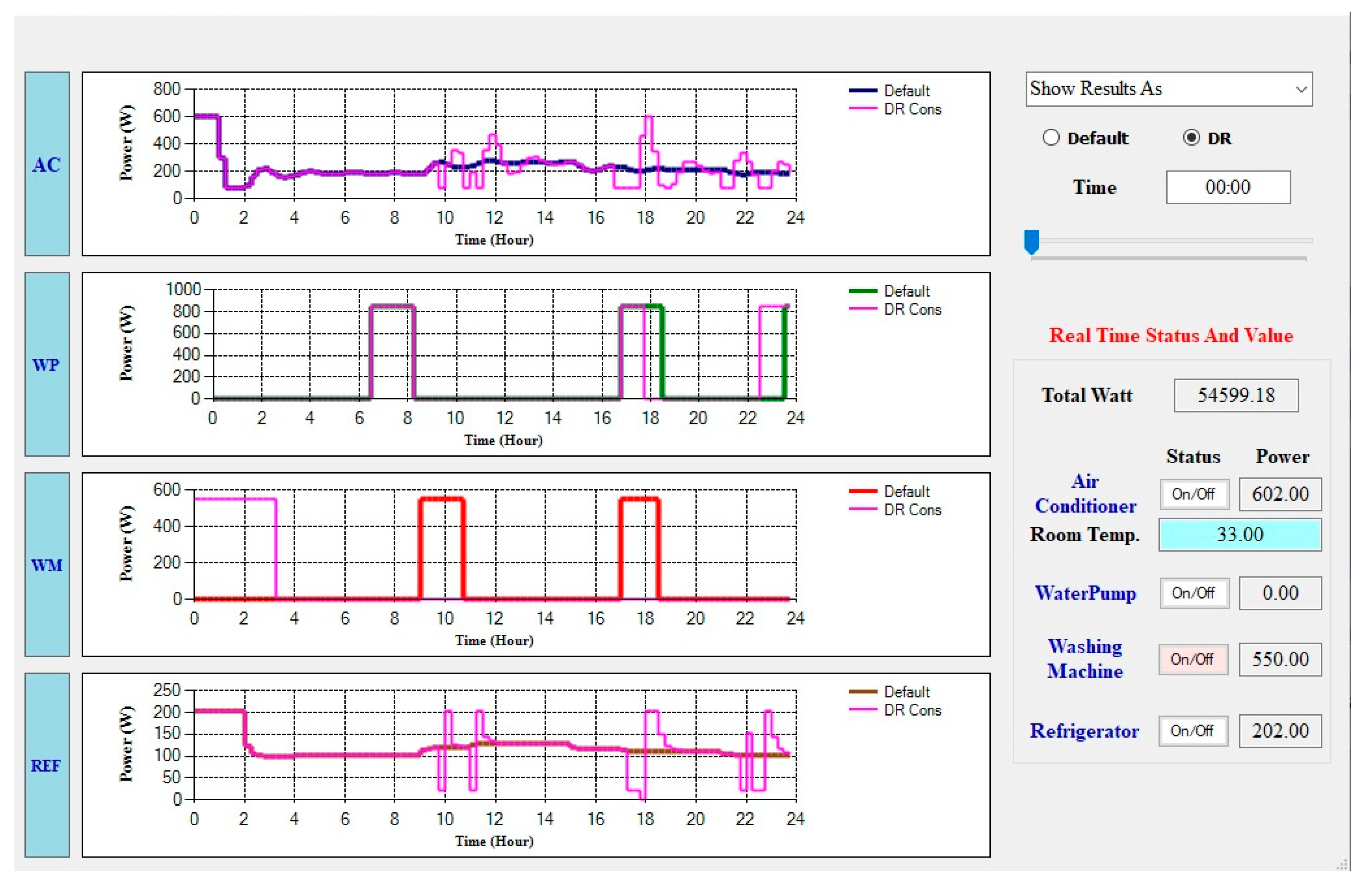
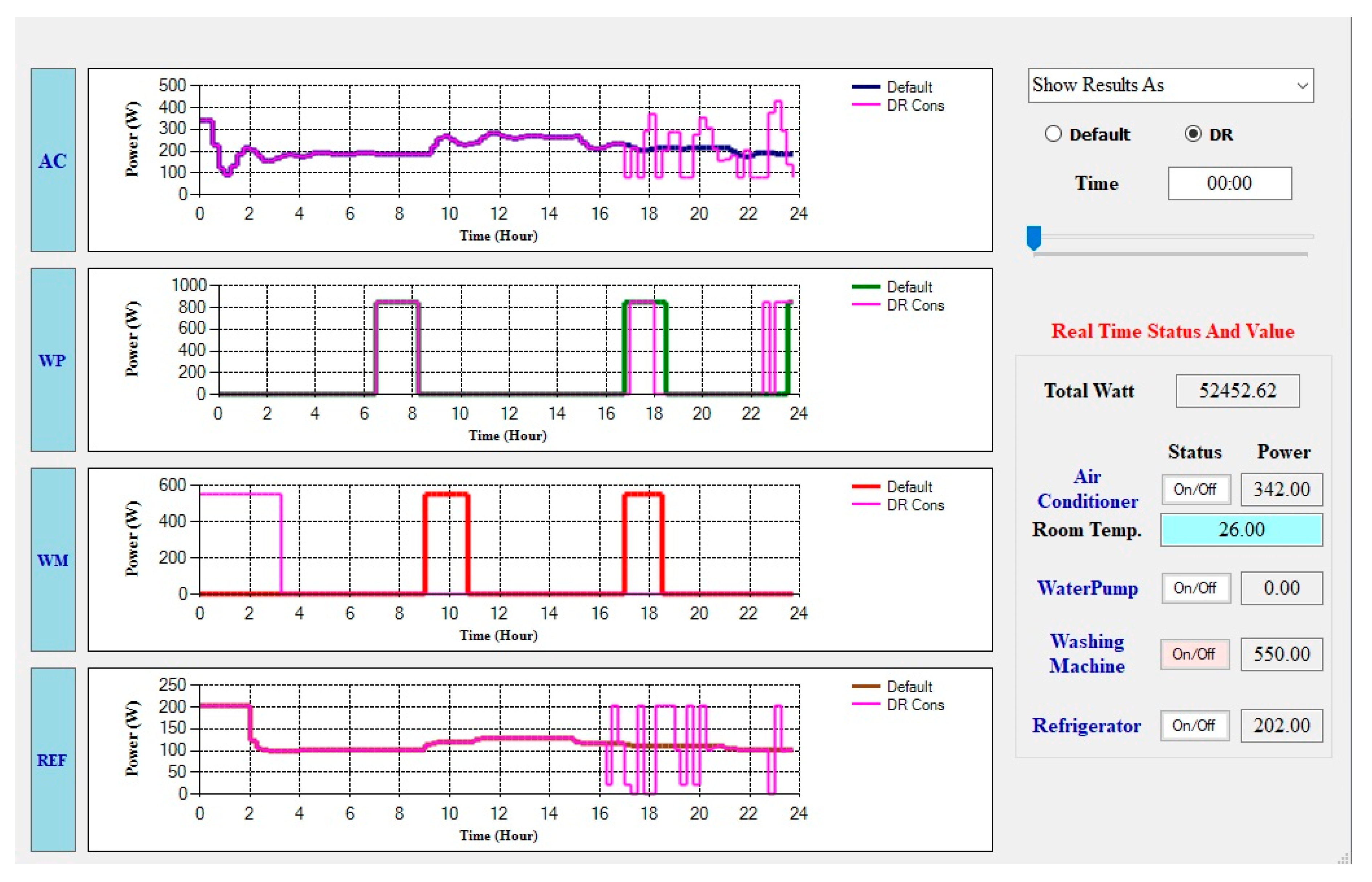
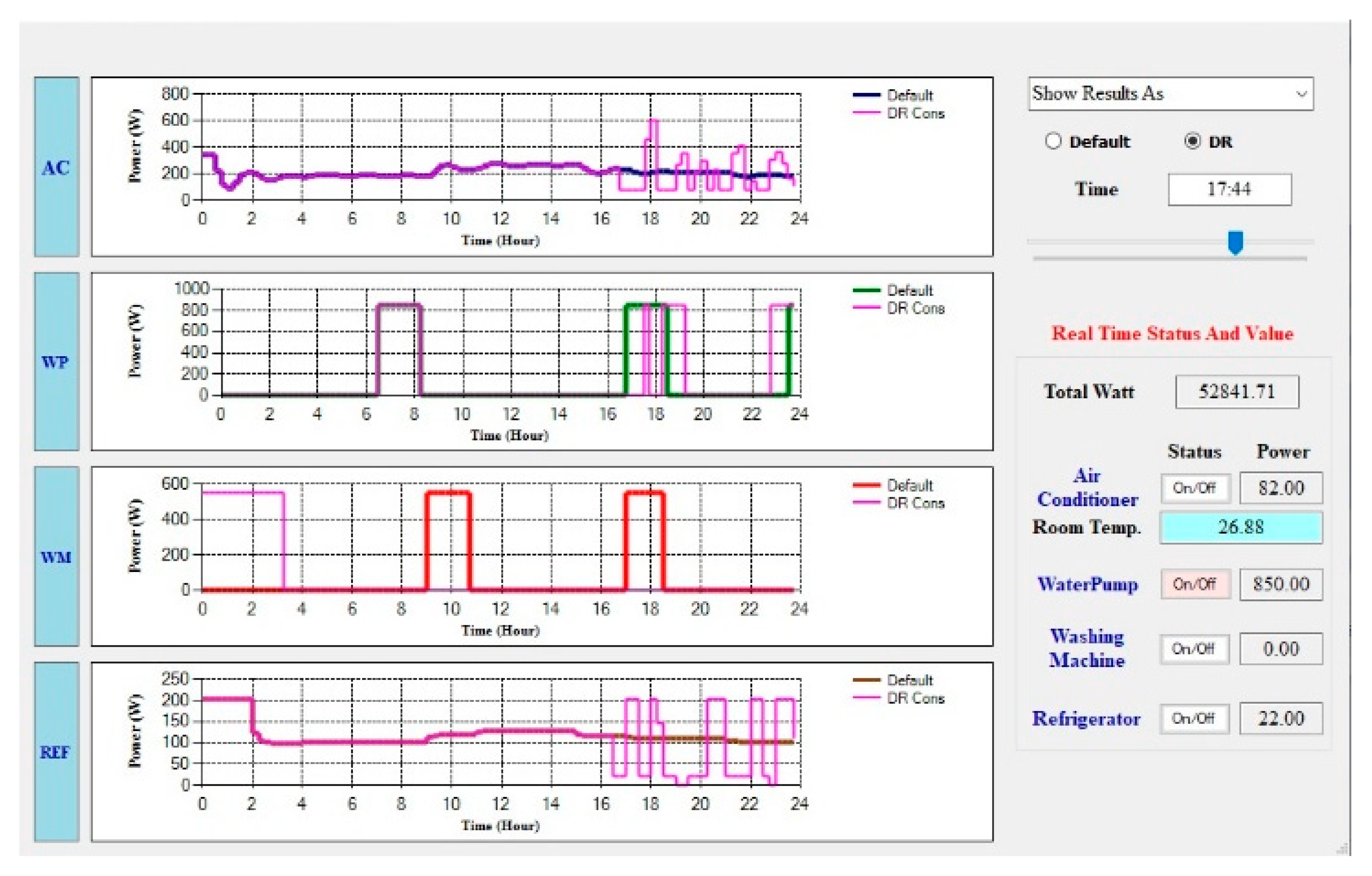
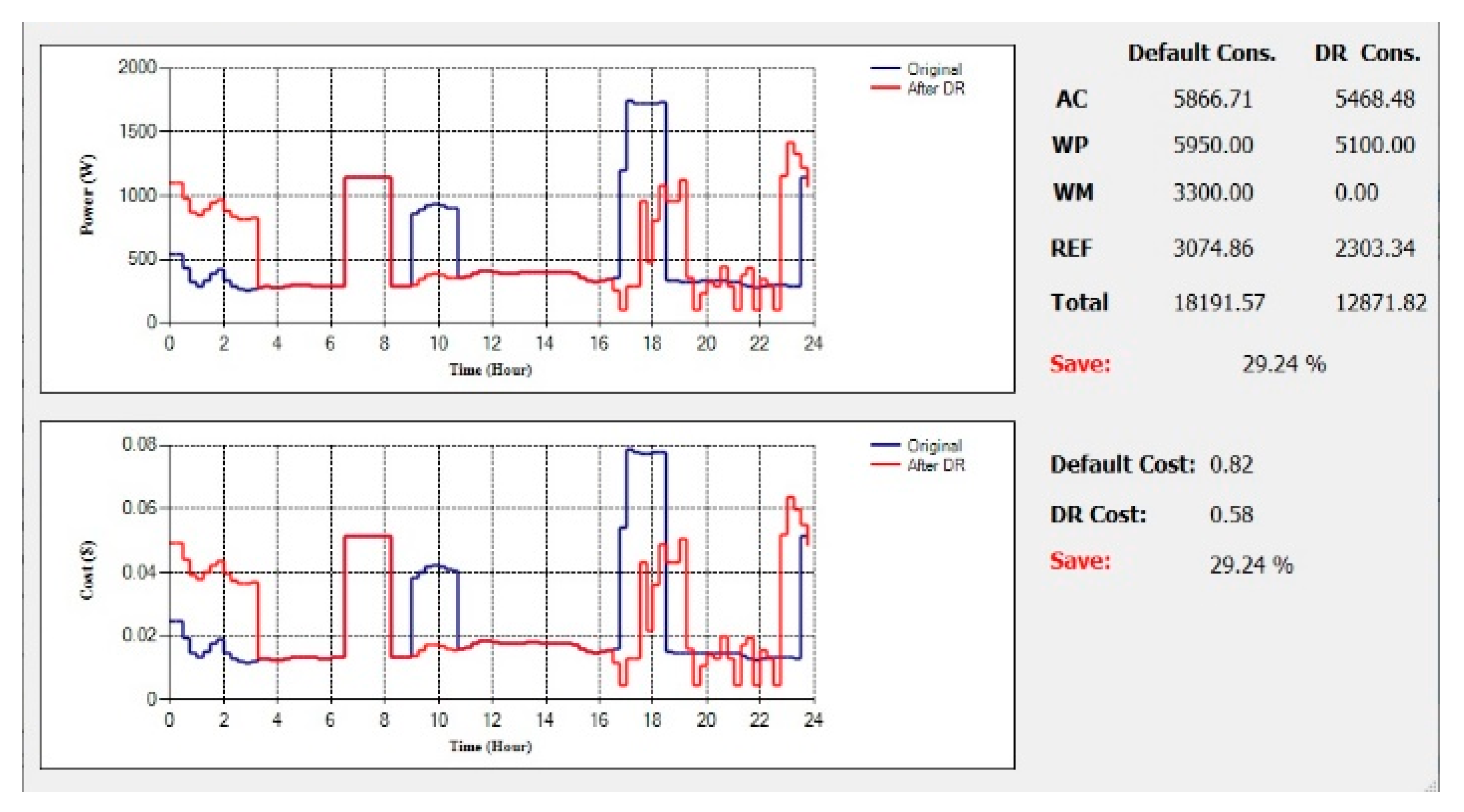
7. Results
7.1. Optimal Weekend Controller Schedule
7.2. Optimal Weekday Controller Schedule
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, G.; Yang, Y.; Pan, F.; Zhang, S.; Wang, F.; Fan, S. An optimal energy-saving strategy for home energy management systems with bounded customer rationality. Future Internet 2019, 11, 88. [Google Scholar] [CrossRef]
- Shareef, H.; Ahmed, M.S.; Mohamed, A.; Al Hassan, E. Review on home energy management system considering demand responses, smart technologies, and intelligent controllers. IEEE Access 2018, 6, 24498–24509. [Google Scholar] [CrossRef]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. In Energy Solutions to Combat Global Warming; Springer: New York, NY, USA, 2017; pp. 753–793. [Google Scholar]
- Ahmed, M.; Mohamed, A.; Homod, R.; Shareef, H. Hybrid LSA-ANN based home energy management scheduling controller for residential demand response strategy. Energies 2016, 9, 716. [Google Scholar] [CrossRef]
- Leitão, J.; Gil, P.; Ribeiro, B.; Cardoso, A. A survey on home energy management. IEEE Access 2020, 8, 5699–5722. [Google Scholar] [CrossRef]
- Shakeri, M.; Shayestegan, M.; Abunima, H.; Reza, S.S.; Akhtaruzzaman, M.; Alamoud, A.; Sopian, K.; Amin, N. An intelligent system architecture in home energy management systems (HEMS) for efficient demand response in smart grid. Energy Build. 2017, 138, 154–164. [Google Scholar] [CrossRef]
- Ghadimi, N.; Nojavan, S.; Abedinia, O.; Dehkordi, A.B. Deterministic-based energy management of DC microgrids. In Risk-Based Energy Management; Academic Press: Cambridge, MA, USA, 2020; pp. 11–30. [Google Scholar]
- Sisodiya, S.; Kumbhar, G.; Alam, M. A home energy management incorporating energy storage systems with utility under demand response using PSO. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–6. [Google Scholar]
- Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
- Ko, W.; Vettikalladi, H.; Song, S.-H.; Choi, H.-J. Implementation of a demand-side management solution for South Korea’s demand response program. Appl. Sci. 2020, 10, 1751. [Google Scholar] [CrossRef]
- Gupta, A.; Singh, B.P.; Kumar, R. Optimal provision for enhanced consumer satisfaction and energy savings by an intelligent household energy management system. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Perez, K.X.; Baldea, M.; Edgar, T.F. Integrated HVAC management and optimal scheduling of smart appliances for community peak load reduction. Energy Build. 2016, 123, 34–40. [Google Scholar] [CrossRef]
- Silva, B.N.; Han, K. Mutation operator integrated ant colony optimization based domestic appliance scheduling for lucrative demand side management. Future Gener. Comput. Syst. 2019, 100, 557–568. [Google Scholar] [CrossRef]
- Jamil, A.; Alghamdi, T.A.; Khan, Z.A.; Javaid, S.; Haseeb, A.; Wadud, Z.; Javaid, N. an innovative home energy management model with coordination among appliances using game theory. Sustainability 2019, 11, 6287. [Google Scholar] [CrossRef]
- Thaeer Hammid, A.; Awad, O.I.; Sulaiman, M.H.; Gunasekaran, S.S.; Mostafa, S.A.; Manoj Kumar, N.; Khalaf, B.A.; Al-Jawhar, Y.A.; Abdulhasan, R.A. A review of optimization algorithms in solving hydro generation scheduling problems. Energies 2020, 13, 2787. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Optimal scheduling of household appliances with a battery storage system and coordination. Energy Build. 2015, 94, 61–70. [Google Scholar] [CrossRef]
- Purcaru, C.; Precup, R.-E.; Iercan, D.; Fedorovici, L.-O.; David, R.-C.; Dragan, F. Optimal robot path planning using gravitational search algorithm. Int. J. Artif. Intell. 2013, 10, 1–20. [Google Scholar]
- Precup, R.-E.; David, R.-C.; Petriu, E.M.; Szedlak-Stinean, A.-I.; Bojan-Dragos, C.-A. Grey wolf optimizer-based approach to the tuning of pi-fuzzy controllers with a reduced process parametric sensitivity. IFAC-PapersOnLine 2016, 49, 55–60. [Google Scholar] [CrossRef]
- Goli, A.; Aazami, A.; Jabbarzadeh, A. Accelerated cuckoo optimization algorithm for capacitated vehicle routing problem in competitive conditions. Int. J. Artif. Intell. 2018, 16, 88–112. [Google Scholar]
- Zeng, G.-Q.; Xie, X.-Q.; Chen, M.-R.; Weng, J. Adaptive population extremal optimization-based PID neural network for multivariable nonlinear control systems. Swarm Evol. Comput. 2019, 44, 320–334. [Google Scholar] [CrossRef]
- Nunna, H.V.K.; Aziz, N.A.B.; Srinivasan, D. A smart energy management framework for distribution systems with perceptive residential consumers. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Malaysia, 7–10 October 2018; pp. 434–438. [Google Scholar]
- Carli, R.; Dotoli, M.; Palmisano, V. A distributed control approach based on game theory for the optimal energy scheduling of a residential microgrid with shared generation and storage. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 960–965. [Google Scholar]
- Fan, W.; Liu, N.; Zhang, J. An event-triggered online energy management algorithm of smart home: Lyapunov optimization approach. Energies 2016, 9, 381. [Google Scholar] [CrossRef]
- Faria, P.; Soares, J.; Vale, Z.; Morais, H.; Sousa, T. Modified particle swarm optimization applied to integrated demand response and DG resources scheduling. IEEE Trans. Smart Grid 2013, 4, 606–616. [Google Scholar] [CrossRef]
- Tsui, K.M.; Chan, S.-C. Demand response optimization for smart home scheduling under real-time pricing. IEEE Trans. Smart Grid 2012, 3, 1812–1821. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Monsef, H.; Rahimi-Kian, A. Optimal smart home energy management considering energy saving and a comfortable lifestyle. IEEE Trans. Smart Grid 2014, 6, 324–332. [Google Scholar] [CrossRef]
- Mirabbasi, D.; Beydaghi, S. Optimal scheduling of smart home appliances considering PHEV and energy storage system. In Proceedings of the 2015 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, UAE, 24–26 November 2015; pp. 1–6. [Google Scholar]
- Wang, Z.; Yang, R.; Wang, L. Multi-agent control system with intelligent optimization for smart and energy-efficient buildings. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1144–1149. [Google Scholar]
- Pedrasa, M.; Spooner, E.; MacGill, I. Robust scheduling of residential distributed energy resources using a novel energy service decision-support tool. In Proceedings of the ISGT, Anaheim, CA, USA, 17–19 January 2011; pp. 1–8. [Google Scholar]
- Fernandes, F.; Sousa, T.; Silva, M.; Morais, H.; Vale, Z.; Faria, P. Genetic algorithm methodology applied to intelligent house control. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence Applications In Smart Grid (CIASG), Paris, France, 11–15 April 2011; pp. 1–8. [Google Scholar]
- Ogwumike, C.; Short, M.; Denai, M. Near-optimal scheduling of residential smart home appliances using heuristic approach. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 3128–3133. [Google Scholar]
- Zhang, Y.; Zeng, P.; Zang, C. Optimization algorithm for home energy management system based on artificial bee colony in smart grid. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 734–740. [Google Scholar]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An efficient power scheduling scheme for residential load management in smart homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic scheduling mechanism for smart homes. Energies 2016, 9, 202. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. Dynamic residential load scheduling based on adaptive consumption level pricing scheme. Electr. Power Syst. Res. 2016, 133, 27–35. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, W.; Zeng, G.; Zheng, Y. Constrained population extremal optimization-based robust load frequency control of multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2019, 105, 249–271. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Ali, J.A. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Che, Y.; Yang, J.; Zhao, Y.; Xue, S. Control strategy for inverter air conditioners under demand response. Processes 2019, 7, 407. [Google Scholar] [CrossRef]
- Sun, L.; Jin, Y.; Pan, L.; Shen, J.; Lee, K.Y. Efficiency analysis and control of a grid-connected PEM fuel cell in distributed generation. Energy Convers. Manag. 2019, 195, 587–596. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Huang, L. Extraction of high frequency operating parameters of a compressor motor for a variable frequency air conditioner. J. Tsinghua Univ. (Sci. Technol.) 2011, 1, 8. [Google Scholar]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S. An algorithm for intelligent home energy management and demand response analysis. IEEE Trans. Smart Grid 2012, 3, 2166–2173. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Homod, R.Z.; Shareef, H. A home energy management algorithm in demand response events for household peak load reduction. PrzeglAd Elektrotechniczny 2017, 93, 2017. [Google Scholar] [CrossRef][Green Version]
- Bertoldi, P.; Hirl, B.; Labanca, N. Energy Efficiency Status Report 2012–Electricity Consumption and Efficiency Trends in the EU-27; European Commission Joint Research Centre Institute for Energy and Transport: Ispra, Italy, 2012. [Google Scholar]
- Hui, H.; Ding, Y.; Lin, Z.; Siano, P.; Song, Y. Capacity allocation and optimal control of inverter air conditioners considering area control error in multi-area power systems. IEEE Trans. Power Syst. 2019, 35, 332–345. [Google Scholar] [CrossRef]
- Chen, D.; Zou, F.; Lu, R.; Li, S. Backtracking search optimization algorithm based on knowledge learning. Inf. Sci. 2019, 473, 202–226. [Google Scholar] [CrossRef]
- Lin, Q.; Gao, L.; Li, X.; Zhang, C. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]


| Appliance | Priority | Comfortable Level |
|---|---|---|
| Inverter AC (IAC) | 1 | Room temperature 20–26 °C |
| Water pump (WP) | 2 | Water level 20–80% |
| Washing machine (WM) | 3 | Different intervals |
| IREF | 4 | 24 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latif, S.N.A.; Shi, J.; Salman, H.A.; Tang, Y. Optimization of Demand-Response-Based Intelligent Home Energy Management System with Binary Backtracking Search Algorithm. Information 2020, 11, 395. https://doi.org/10.3390/info11080395
Latif SNA, Shi J, Salman HA, Tang Y. Optimization of Demand-Response-Based Intelligent Home Energy Management System with Binary Backtracking Search Algorithm. Information. 2020; 11(8):395. https://doi.org/10.3390/info11080395
Chicago/Turabian StyleLatif, Suhaib N. Abdul, Jinjing Shi, Hasnain Ali Salman, and Yongze Tang. 2020. "Optimization of Demand-Response-Based Intelligent Home Energy Management System with Binary Backtracking Search Algorithm" Information 11, no. 8: 395. https://doi.org/10.3390/info11080395
APA StyleLatif, S. N. A., Shi, J., Salman, H. A., & Tang, Y. (2020). Optimization of Demand-Response-Based Intelligent Home Energy Management System with Binary Backtracking Search Algorithm. Information, 11(8), 395. https://doi.org/10.3390/info11080395





