Abstract
With the rapid development of cloud computing, massive data are transferred to cloud servers for storage and management savings. For privacy concerns, data should be encrypted before being uploaded. In the encrypted-domain (ED), however, many data computing methods working in the plain-domain are no longer applicable. Data retrieval has become a significant obstacle to cloud storage services. To break through this limitation, we propose a multi-keyword searchable encryption scheme by introducing probability trapdoors. Firstly, a keywords probability trapdoor is established to ensure that the scheme can resist indistinguishable attacks. Based on the keywords trapdoor, we present the keywords vector to make the scheme realize multi-keyword search in the process of data retrieval in the ED. Both security and performance analysis confirm the advantages of the proposed scheme in terms of search functionality and complexity.
1. Introduction
Presently, with the rapid development of Internet technology, data undergo explosive growth. It leads to an increasing burden of data management and computations until the cloud computing appears. As a new data processing mode, the cloud computing began to be popular worldwide and favored by users or organizations with the strong promotion of IBM, Google, Yahoo, and other companies.
Cloud storage, an extension of the cloud computing application field, provides users with data storage and access. Besides, due to its convenience, low cost, and flexible access, it is becoming more and more popular with outsourcing local data to cloud servers. However, due to the cloud server’s vulnerability and the uncertainty of the external environment, data stored in the cloud suffers from the problem of privacy leakage [1,2,3,4,5]. Therefore, users prefer making the private data encrypted and then uploading data in the encrypted-domain (ED) to the cloud server. Traditionally, the ciphertext retrieval method downloads the entire set of documents in ED to the local first and decrypts all the ciphertext to get the required data and documents. However, it is inefficient to outsource data to the cloud that is not meant for the traditional ciphertext retrieval methods [6,7]. Intuitively, users expect an efficient ciphertext retrieval method that gets the required data in cloud storage without downloading and decrypting the entire ciphertext. Thus, the practical ability of cloud storage can be unleashed.
Towards this requirement, searchable encryption technology [8] is created. It completes data retrieval in ED that prevents data privacy from being disclosed. Due to ciphertext retrieval, the cloud server only needs to complete a ciphertext search according to the keyword trapdoor provided by the users without downloading the entire ciphertext documents. Thus, the ciphertext queries are accelerated while the bandwidth consumption can be saved. Unfortunately, most of the existing searchable encryption schemes are based on the deterministic trapdoor scheme to complete ciphertext retrieval, making the scheme unable to resist the indistinguishable attacks. Some searchable encryption schemes based on probabilistic trapdoor can resist indistinguishable attacks at the cost of the schemes’ functionality. In other words, these schemes can only complete a single keyword search but cannot accomplish a multi-keyword search. Consequently, in this paper, we propose a searchable encryption scheme which supports multi-keyword searches. The main contributions are as follows.
(1) A multi-keyword searchable encryption scheme is presented. By introducing the keyword vector when constructing the trapdoor, the scheme can realize multi-keyword searches in the ciphertext search process, thus enhancing the scheme’s functionality.
(2) In this scheme, the probability trapdoor construction makes the scheme resistant to indistinguishable attacks and ensures the scheme’s security.
(3) The comparison results between this scheme and other searchable encryption schemes prove that this scheme has distinct advantages over other schemes in terms of the search function and storage complexity.
The remainder of this paper is organized as follows. Section 2 gives a brief review of related works in literature. Section 3 presents the system model, threat model, and design goal, as well as introduces the definitions and preliminaries. Section 4 gives the whole process of multi-keyword search based on probability trapdoor. Security analysis of the mechanism, storage complexity, and performance analysis are presented in Section 5. The conclusions are drawn in the Section 6.
2. Related Works
Generally, the searchable encryption scheme has begun to take shape and can be roughly divided into three categories: single-keyword search, multi-keyword search, and fuzzy keyword search. The specific research work is shown as follows.
2.1. Single Keyword Search
The concept of searchable encryption was proposed by Song et al. [7], who also presented the first symmetric searchable encryption scheme for ciphertext data retrieval. However, the search complexity of the scheme increases linearly with the size of the document collection. It can only do a simple keyword search with a high cost yet low efficiency. Later, Boneh et al. [9] proposed the first public key-based searchable encryption scheme (PKES), which was based on bilinear mapping operation, resulting in rising computation and low search efficiency. By considering the privacy of trapdoor, Curtmola et al. [10] adopted inverted index technology to improve search efficiency. The inverted index’s adoption makes the complexity of scheme search only relates to the number of keywords and has nothing to do with the size of the document collection. Notice that this scheme defines the security target of a symmetric searchable encryption scheme for the first time.
2.2. Multi-Keyword Search
Undoubtedly, the single-keyword searchable scheme can not meet the user’s requirement of retrieving data with multiple keywords. In 2004, Golle et al. [11] proposed the first multi-keyword searchable encryption scheme supporting simple query. A more practical query scheme was immediately given by Boneh et al. [12], which supports any joint query, such as comparative query, and subset query. Actually, Cao et al. [13] introduced the first searchable encryption scheme, which truly supports multiple keywords search. It gives a sorted output according to the relative weight of documents, which saves network bandwidth. Later, in 2014, Cao et al. [14] put forward a multi-keyword searchable encryption scheme that supports privacy protection. It is the first scheme that introduced the coordinate system matching search into the multi-keyword sorting search, even though its accuracy is insufficient due to the lack of consideration of the weights’ differences among keywords. In 2015, the inverted index was first employed to realize a multi-keyword search by Wang et al. [15]. Towards efficiency improvement for the multi-keyword scheme, Xia et al. [16] designed the index based on tree structure according to the vector model, word frequency and inverse document frequency model in the scheme, and introduced the index into the search process. Recently, Ding et al. [17] constructed the index based on tree structure in the scheme and proposed the random traversal algorithm, which enables the scheme to complete ciphertext search more quickly.
2.3. Fuzzy Keyword Search
Fuzzy keyword search allows users to input content with subtle errors or format inconsistency. It greatly improves the practicality of the scheme and user experience. In 2010, the fuzzy keyword search scheme was firstly proposed by Li et al. [18]. The similarities of keywords were measured by editing distance. For massive data collection, this approach is not feasible because the size of the fuzzy keyword set might grow exponentially, leading to pricey memory consumption and resource waste. To overcome this problem, the Locality Sensitive Hashing (LSH) was introduced to improve the fuzzy search by Wang et al. [19]. Thus, the fuzzy keyword set with massive memory consumption can be abandoned. Unfortunately, due to the predefined bloom filter or vector requirement, pricey storage overhead cannot be well avoided. Therefore, it cannot work well when the objective data set is too large. In [20], Fu et al. employs a gram-based fuzzy set to implement a fuzzy keyword search that reaches a better efficiency. However, the scheme cannot withstand the indistinguishable attacks because of the deterministic keyword trapdoor generated in the scheme. Tahir et al. [21] proposed a keyword search scheme based on a probability trapdoor, which can resist indistinguishable attacks. This scheme supports deterministic single-keyword search, but could not complete multi-keyword search. To support logic queries over encrypted data, ref. [8] presented a fuzzy search scheme which is expected to be combined with exact search.
3. Constructions and Definitions
3.1. System Model
As illustrated in Figure 1, the system model includes two main entities: the Cloud Servers (CS) and the Client User (CU). With sufficient computation and storage resources, CS provides users or organizations with management and maintenance of massive data, storage services, quick access, and complex computing services to obtain commercial benefits. CU uses these services provided by CS. Generally, for data privacy and security, CU prefers data being outsourced to CS in ED, i.e., data should be encrypted first. To search the interested data, CU submits the corresponding keyword trapdoor to CS. Then CS returns the corresponding document data.
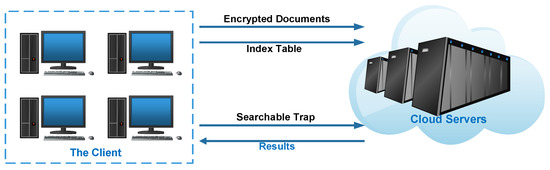
Figure 1.
The system model of our scheme.
3.2. Threat Model
In this scheme, we consider that CS as “semi-honest” since it can be any third party providing cloud service. In other words, the cloud server must satisfy the following descriptions.
(1) CS should ensure data security and integrity, and it will not remove or tamper the outsourced data by CU.
(2) CS should execute CU’s query request honestly according to the preset protocol and return the complete query result.
(3) CS is curious and wants to infer and analyze additional privacy based on the retrieved data.
Throughout the scenario, CU is an honest entity who honestly encrypts the outsourced document, builds the searchable index table, and uploads it to CS without colluding with CS.
3.3. Design Goal
To complete a multi-keyword search on ciphertext in the above model, the proposed scheme’s objectives are as follows.
- Data privacy: It ensures data security and prevents CS from getting any additional private information during the whole interactive processes, including document collection, index table, queries, and so on.
- Trapdoor unlinkability: CU generates two keyword trapdoors. Even if the two trapdoors are generated by the same keywords, CS cannot distinguish whether the same keyword generates the two trapdoors in polynomial time.
- Multi-keyword search: When CU submits multiple trapdoors of keywords, our scheme must guarantee that each document returned by CS contains the set of keywords.
3.4. Notations
Before presenting algorithms in the proposed scheme, we list the used notations in Table 1.

Table 1.
Notaions.
3.5. Definitions
3.5.1. Multi-Keyword Searchable Encryption Scheme
The proposed multi-keyword searchable encryption (MSE) scheme is composed of five polynomial time algorithms ∏ = (KeyGen, Build_Index, Build_Trap, Search_Output, Dec_Documents) as follows.
- : a probabilistic algorithm run by CU, which takes a security parameters as input, and outputs the master key K, a session key and a prime number p.
- : a deterministic algorithm run by CU, which takes the master key K and a documents collection D as input, and then outputs the secure index table I.
- : a probabilistic algorithm run by CU. It inputs the master key K, a session key and a set of keywords to be searched , and then outputs a set of trapdoors of keywords .
- : a deterministic algorithm run by CU. It inputs the session key , the secure index table I, and a set of trapdoors of keywords , and then outputs a collection of ciphertext documents containing the set of the keywords to be searched F.
- : a deterministic algorithm run by CU, which takes the master key K and the collection of ciphertext documents F as input, and then outputs a collection of plaintext documents f.
3.5.2. Correctness
Generally, a MSE Scheme ∏ is correct, if for any outputs by , any I outputs by , any outputs by , any F outputs by , any f outputs by .
(1) For , if , ;
(2) , but , .
Here, is the set of the keywords to be searched, and is the set of keywords extracted from the plaintext documents.
3.5.3. Threshold
In the considered scenario, CU sets the threshold which is critical for controlling the extraction of keywords. When the threshold is met, it indicates that the word can be used as a keyword. In this paper, is set according to CUs’ requirements.
3.6. Preliminaries
For a searchable encryption scheme, keyword extraction is crucial for subsequent ciphertext search. In this paper, we use the TF*IDF technique to extract keywords from plaintext documents. The specific progress is described as follows.
(1) For each word w in the plaintext documents , CU calculates its frequency by
were represents the term frequency of w in the documents.
(2) CU calculates the inverse document frequency of the document following
Here, , represents the total number of document , and represents the total number of documents which contain w.
(3) CU computes , and takes the word w as the keyword of the plaintext document when the value is larger than or equal to the preset threshold .
4. System Design
4.1. KeyGen Phase
CU inputs a security parameter , and gets the master key K and a session key . In addition, a prime number p is generated randomly using the Cryptographically Secure Pseudo-Random Number Generator (CSPRN). In this phase, , , .
4.2. Build_Index Phase
According to the keyword collection W extracted from the plaintext documents collection D, CU builds the index table I. Steps in this build_index phase are as follows.
(1) Extract the keyword set of each plaintext document in the plaintext document set , and put it into the keyword set .
(2) Select a hash function H following Ref. [11], and use the master key K to calculate the keyword hash value, where the expression of H is described by
(3) Initialize a two-dimensional array , where n represents the number of plaintext documents and m represents the total number of keywords. The first column of the array A contains the encrypted document identifiers of the document in the documents collection . The first row of the array A contains the hash value inverse of all keywords in the keyword set W. The values of other position elements in array A represent the relative frequency of keywords relative to the document, where , .
(4) Set the two-dimensional array , where represents the identifier of the document , and represents the result after encrypting the identifier .
(5) Calculate the hash value of the keyword through the master key K and hash function H, and the inverse of the hash value under the module p condition. Finally, set the array , where , .
(6) Set the element of the array if the keyword exists in the document; otherwise, , where r represents a random number, and is the correlation frequency of the keyword with the document . The random number r multiplied is used to cover up the relative frequency of the keywords relative to the document, which helps prevent frequency analysis attacks and the leakage of document size.
(7) Take the array A as an index table I and send it to CS.
4.3. Build_Trap Phase
In the build_trap phase, CU constructs keyword trapdoors set . The implemented steps are as follows.
(1) Calculate the hash value of the keyword according to the hash function H and the master key K, and set , where , , of which l represents the number of keywords in the keyword set .
(2) Use the master key K to encrypt the keyword , and get the ciphertext of the keyword , and then set .
(3) Calculate , and the hash value of the keyword ciphertext according to the hash function H and the session key . Finally, set .
(4) Calculate the vector . If the keyword appears in the corresponding position of m keywords, the value of the corresponding position of the vector is r; otherwise, the value of the corresponding position of the vector is 0.
(5) Get the trapdoor .
(6) Get the trapdoors collection and sends it to CS.
4.4. Search_Output Phase
In the phase of search_output, CS performs keywords search on the ciphertext document according to the received index table I and trapdoors set . The specific steps are as follows.
(1) Create three collections of ciphertext documents , , .
(2) Search the first row elements in the index table I, whose elements makes the identity hold. Then, locate the ciphertext document corresponding to the document identifier when r is not zero in the column , and add to the collection of ciphertext documents , where , .
(3) Extract the first tuple element of in each row of the index table I to form a vector , and calculate , making the calculation result satisfy . If , then return the document , which is related with the document identifier , and add it to , where , .
(4) Intersect the ciphertext document set and , and get the final result .
(5) Send a collection of ciphertext documents to CU, where .
4.5. Dec_Documents Phase
To obtain the required data, in this dec_document phase, CU decrypts the ciphertext document set through the master key K and gets the plaintext document set , which contains the multi-keyword set .
5. Performance Analysis
5.1. Security Analysis
5.1.1. Privacy Leakage
This section consists of the examination of any information that might be compromised by the scheme, as well as components of the polynomial-time algorithm that might reveal private information: index table I, trapdoors sets , and search output . Under the standard model, the privacy leakage of the scheme in this paper is defined as follows.
- Leakage :This leak function is related to the index table I. It is assumed that the index table I generated by the client user is leaked to the cloud server and the attacker . The leakage function is formulated by
- Leakage :This leak function is related to the trapdoor of the keyword . It is presumed that the trapdoor generated by the client user is released to the cloud server and the attacker . The leakage function is formulated by
- Leakage :This leak function is related to the result generated by the trapdoor . It is supposed that the result is revealed to the client user and the attacker . The leakage function is formulated by
5.1.2. Privacy Leakage
Since the trapdoor is generated based on probabilistic encryption algorithms and hash functions, the leak information associated with the trapdoor is meaningless and will not be discussed in this subsection. In the proposed MSE scheme, random numbers are deployed to obscure the related frequency, which will also expose the information whether the keyword is in the document or not. However, the leaked information will not affect the nature of trapdoor untraceability and indistinguishability, which is the private information about the leakage of related frequency. Therefore, we focus on the security and privacy issues caused by the leak function and the leak function .
Now, the scheme is still secure even though the privacy of functions is disclosed. It can be seen that the leaked information of the functions could be encrypted information, the hash value, or hidden by random numbers. It is presumed that the adversary will not acquire the master key K and hash function H. Therefore, it is believed that the leaked information of the functions has no influence on our scheme. More precisely, no one can guess the hash message in polynomial time with a given the hash value because the hash function is not invertible. Besides, we use a probabilistic encryption algorithm to encrypt the message. Therefore, the attacker is not possible to obtain meaningful information in polynomial time.
5.2. Storage Overhead
To evaluate our scheme’s storage overhead, we consider it for the CU and the CS separately. In our scheme, the CU stores a master key K, a session key , and a prime number p. Given the security parameter , the size of p is bits. If we use 128 bit AES-CBC to achieve confidentiality and SHA-256 for the keyed cryptographic hash function, the keys and K require 256 bits. Obtained from the output of SHA-256, we have 256 bits for and 257 bits for p. Totally, the CU will consume bytes in terms of storage overhead.
Referring to the CS, it should keep the encrypted documents and the secure index table. Following Ref. [21], we use to represent the average storage consumption of an encrypted document. Thus, the document set with n documents require . For the secure index, the storage overhead is bytes where represent the total number of documents, the total number of keywords and the number of bytes required by each item of A in Section 4.2. For instance, ℓ can be 32 if we use SHA-256 in the scheme. Hence the total storage overhead at the CS would be .
5.3. Performance Analysis
In this section, we conduct performance analysis by comparing our scheme with the state-of-the-art schemes [21,22,23,24,25] in terms of functionalities and computational complexities. Let n denote the total number of the plaintext document, m be the number of distinct keywords extracted from the entire plaintext document set, h represent the computational complexity of the hash function (e.g., SHA-256), and e is the complexity of the encryption algorithm (e.g., AES-CBC). Similar to our scheme discussed in Section 3.5, these schemes comprise of five phases, i.e., KeyGen, Build_Index phase, Build_Trap phase, Search_Output phases, and Dec_Documents phase. Generally, the KeyGen and Dec_Documents phases of them are fairly the same with each other. Therefore, we focus on the remaining three phases, which are detailed in Table 2. Notice that Ref. [21] provides schemes considering ranking and no-ranking. We can find the corresponding computational complexities for the Build_Index phases are or , respectively. In our scheme, the Build_Index phase requires since we prefer no-ranking strategy for multi-keyword search. Unlike the single keyword search, it is inevitable to find the intersection of sets extracted by different keywords in our scheme. So the Build_Trap phase is bound by for multi-keyword search support, where is the number of words used for search. In contrast, Ref. [21] only consumes for single keyword search. As discussed in Section 4.4, in theoretical, traversing the two-dimensional array A, calculating and getting the final results want , and , respectively. However, on the one hand, calculating consumes less than for sparsity. On the other hand, getting the final results is done between and , which are subsets of the ciphertext documents F. The computational complexity can be where . In practical, we can have . Consequently, the Search_Output phase is bound by .

Table 2.
Comparisons of function and computational complexity.
Based on the scheme of Tahir et al. [21], which only support single keyword search, we give an improved scheme to support multi-keyword searchable encryption. As discussed previously, three out of five phases in our scheme are the same as [21]. Besides, our scheme consumes more in the Build_Trap phase and Search_Output phase because the second retrieval cannot be avoided despite searching in plaintext. For the Build_Trap phase, the complexity of our scheme is linear to [21]. If , the complexity of the Search_Output phase will be times of [21] where . In practice, the improved functionality will take more time than that of [21]. In this study, therefore, we omit the simulation details for the computation overhead.
6. Conclusions
In this paper, a searchable encryption scheme based on probabilistic trapdoors is proposed, which cannot only support multi-keyword search but also resist indistinguishable attacks. The construction of probability trapdoors makes our scheme resistant to indistinguishable attacks. Besides, by introducing the keyword vector when constructing the trapdoor, the scheme can realize the multi-keyword search in the ciphertext search process. Finally, comparison results between this scheme and other searchable encryption schemes prove that our scheme has distinct advantages over other schemes in terms of search functionality and storage complexity.
Author Contributions
Conceptualization, Y.P. and B.W.; formal analysis, Y.P. and Z.Z.; funding acquisition, B.W.;investigation, Y.P. and W.S.; methodology, Y.P., W.S. and W.W.; project administration, B.W.; resources, W.W.; supervision, Z.Z. and B.W.; validation, Y.P., W.S., Z.Z. and B.W.; writing—original draft, Y.P.; writing—review & editing, W.S. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key R&D Program of China under Grant No. 2017YFB0802000, the National Natural Science Foundation of China under Grant Nos. 61572390, U1736111, 81961138010, the National Cryptography Development Fund under Grant No. MMJJ20180111, the Plan For Scientific Innovation Talent of Henan Province under Grand No. 184100510012, the Program for Science & Technology Innovation Talents in Universities of Henan Province under Grant No. 18HASTIT022, the University of Science and Technology Beijing under Grant FRF-TP-19-005A3, the Innovation Scientists and Technicians Troop Construction Projects of Henan Province.
Acknowledgments
The authors would like to thank the Associate Editor and the anonymous reviewers for their constructive comments that greatly improved the quality of this manuscript.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript or in the decision to publish the results.
References
- Dixit, P.; Gupta, A.K.; Trivedi, M.C.; Yadav, V.K. Traditional and Hybrid Encryption Techniques: A survey. In Networking Communication and Data Knowledge Engineering; Springer: Singapore, 2018; pp. 239–248. [Google Scholar]
- Alabdulatif, A.; Khalil, I.; Yi, X. Towards Secure Big Data Analytic for Cloud-enabled Applications with Fully Homomorphic Encryption. J. Parallel Distrib. Comput. 2020, 137, 192–204. [Google Scholar] [CrossRef]
- Qian, J.; Hua, C.; Guan, X.; Xin, T.; Zhang, L. A Trusted-ID Referenced Key Scheme for Securing SCADA Communication in Iron and Steel Plants. IEEE Access 2019, 7, 46947–46958. [Google Scholar] [CrossRef]
- Grammatikis, P.I.R.; Sarigiannidis, P.G.; Moscholios, I.D. Securing the Internet of Things: Challenges, threats and solutions. Internet Things 2019, 5, 41–70. [Google Scholar] [CrossRef]
- Moysiadis, V.; Sarigiannidis, P.; Moscholios, I. Towards Distributed Data Management in Fog Computing. Wirel. Commun. Mob. Comput. 2018, 2018, 7597686. [Google Scholar] [CrossRef]
- Mustafa, M.A.; Cleemput, S.; Aly, A.; Abidin, A. A Secure and Privacy-Preserving Protocol for Smart Metering Operational Data Collection. IEEE Trans. Smart Grid 2019, 10, 6481–6490. [Google Scholar] [CrossRef]
- Song, D. Practical Techniques for Searches on Encrypted Data. In Proceedings of the 2000 IEEE Security and Privacy Symposium (SP), San Jose, CA, USA, 22–26 May 2017; pp. 44–55. [Google Scholar]
- Fu, S.; Zhang, Q.; Jia, N.; Xu, M. A Privacy-preserving Fuzzy Search Scheme Supporting Logic Query over Encrypted Cloud Data. Mob. Netw. Appl. 2020, 1–12. [Google Scholar] [CrossRef]
- Boneh, D. Publickey Encryption with Keyword Search. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—Eurocrypt 2004, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3027, pp. 506–522. [Google Scholar]
- Curtmola, R. Searchable Symmetric Encryption: Improved Definitions and Efficient Constructions. In Proceedings of the 2006 ACM Conference on Computer and Communications Security (CCS), Alexandria, VA, USA, 30 October–3 November 2006; pp. 79–88. [Google Scholar]
- Golle, P. Secure Conjunctive Keyword Search Over Encrypted Data. In Proceedings of the 2004 Applied Cryptography and Network Security Conference (ACNS), Yellow Mountain, China, 8–11 June 2004; pp. 31–45. [Google Scholar]
- Boneh, D.; Waters, B. Conjunctive, Subset, and Range Queries on Encrypted Data. In Proceedings of the International Conference on Theory of Cryptography (TCC), Amsterdam, The Netherlands, 21–24 February 2007; pp. 535–554. [Google Scholar]
- Cao, N.; Wang, C.; Li, M.; Ren, K.; Lou, W. Privacy-preserving Multi-keyword Ranked Search over Encrypted Cloud Data. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011; pp. 829–837. [Google Scholar]
- Cao, N.; Wang, C.; Li, M.; Ren, K.; Lou, W. Privacy-preserving Multi-keyword Ranked Search over Encrypted Cloud Data. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 222–333. [Google Scholar] [CrossRef]
- Wang, B.; Song, W.; Lou, W.; Thomas, Y.H. Inverted Index based Multi-keyword Public-key Searchable Encryption with Strong Privacy Guarantee. In Proceedings of the 2015 IEEE INFOCOM—IEEE Conference on Computer Communications, Hong Kong, China, 26 April–1 May 2015; pp. 2092–2100. [Google Scholar]
- Xia, Z.; Wang, X.; Sun, X.; Wang, Q. A Secure and Dynamic Multi-keyword Ranked Search Scheme over Encrypted Cloud Data. IEEE Trans. Parallel Distrib. Syst. 2015, 27, 340–352. [Google Scholar] [CrossRef]
- Ding, X.; Liu, P.; Jin, H. Privacy-Preserving Multi-keyword Top-k Similarity Search Over Encrypted Data. IEEE Trans. Dependable Secur. Comput. 2017, 16, 344–357. [Google Scholar] [CrossRef]
- Li, J.; Wang, Q.; Wang, C.; Cao, N.; Ren, K.; Lou, W. Fuzzy Keyword Search over Encrypted Data in Cloud Computing. In Proceedings of the 2010 INFOCOM, San Diego, CA, USA, 15–19 March 2010; pp. 441–445. [Google Scholar]
- Wang, B.; Yu, S.; Lou, W.; Thomas, Y.H. Privacy-Preserving Multi-Keyword Fuzzy Search over Encrypted Data in the Cloud. In Proceedings of the 2014 IEEE INFOCOM—IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 2112–2120. [Google Scholar]
- Fu, Z.; Wu, X.; Guan, C.; Sun, X.; Ren, K. Toward Efficient Multi-Keyword Fuzzy Search Over Encrypted Outsourced Data With Accuracy Improvement. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2706–2716. [Google Scholar] [CrossRef]
- Tahir, S.; Ruj, S.; Rahulamathavan, Y.; Rajarajan, M. A New Secure and Lightweight Searchable Encryption Scheme over Encrypted Cloud Data. IEEE Trans. Emerg. Top. Comput. 2017, 7, 530–544. [Google Scholar] [CrossRef]
- Kamara, S.; Papamanthou, C.; Roeder, T. Dynamic Searchable Symmetric Encryption. In Proceedings of the 2012 ACM Conference on Computer and Communications Security (CCS), Raleigh, NC, USA, 16–18 October 2012; pp. 965–976. [Google Scholar]
- Wang, C.; Cao, N.; Ren, K.; Lou, W. Enabling Secure and Efficient Ranked Keyword Search over Outsourced Cloud Data. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1467–1479. [Google Scholar] [CrossRef]
- Wang, B.; Li, M.; Wang, H. Geometric Range Search on Encrypted Spatial Data. IEEE Trans. Inf. Forensics Secur. 2016, 11, 704–719. [Google Scholar] [CrossRef]
- Tang, Q. Nothing is for Free: Security in Searching Shared and Encrypted Data. IEEE Trans. Inf. Forensics Secur. 2014, 11, 1943–1952. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).