Quantitative Cluster Headache Analysis for Neurological Diagnosis Support Using Statistical Classification
Abstract
1. Introduction
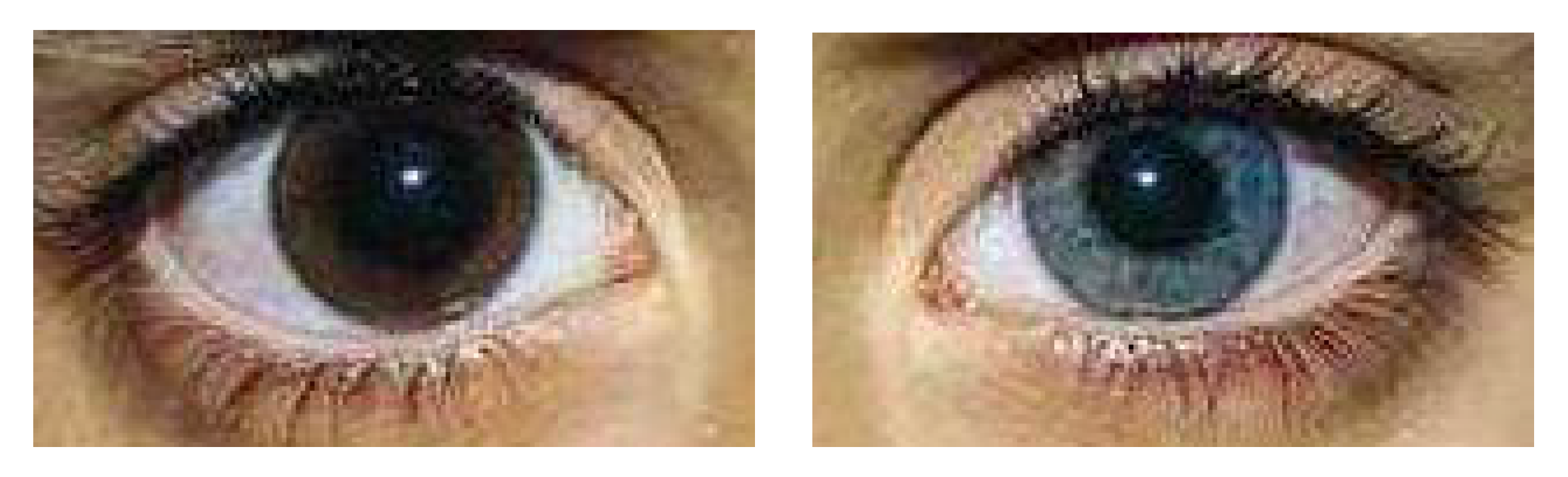
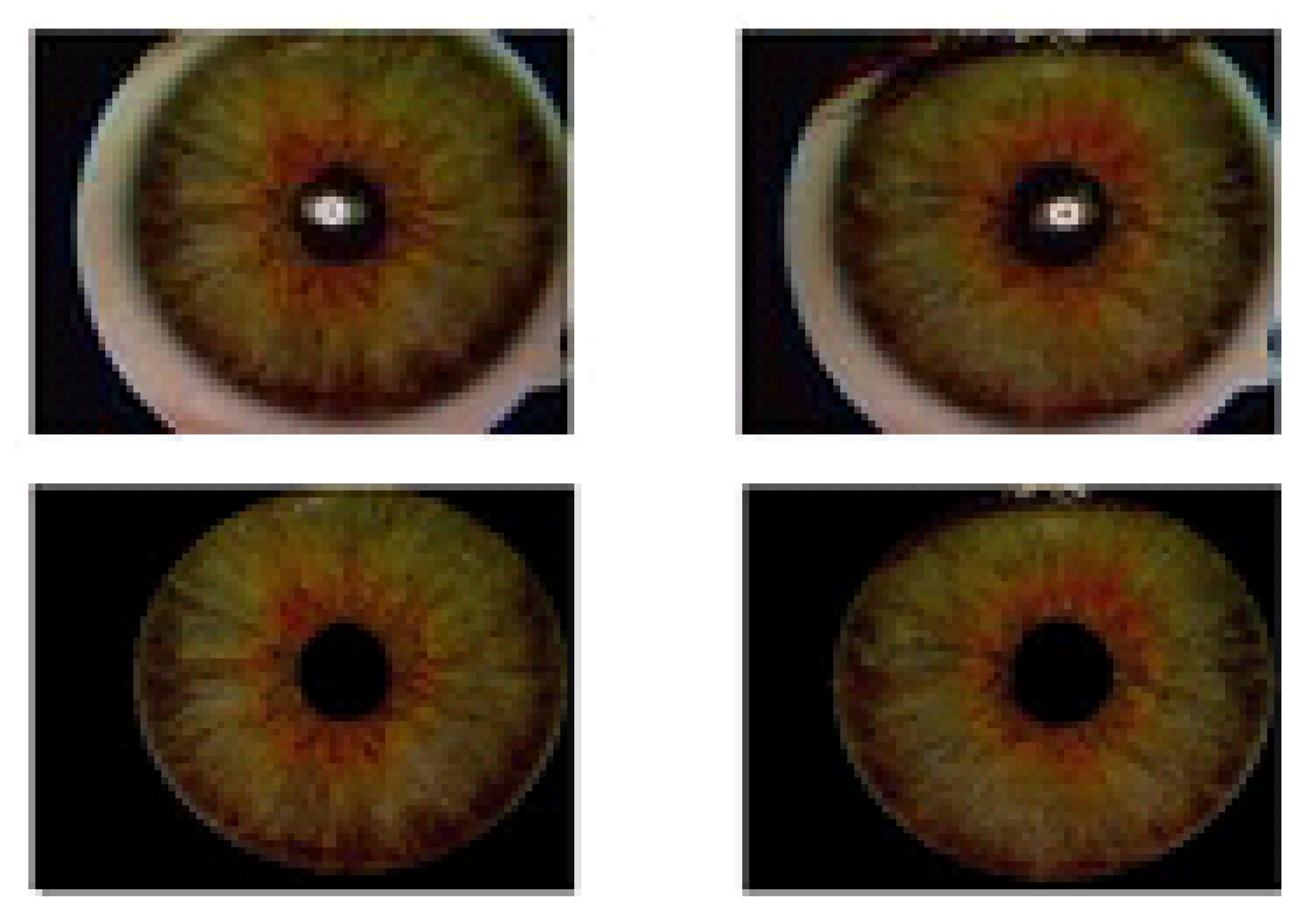
2. Image Database
3. Support Vector Classifier Approach
4. Experiments and Results
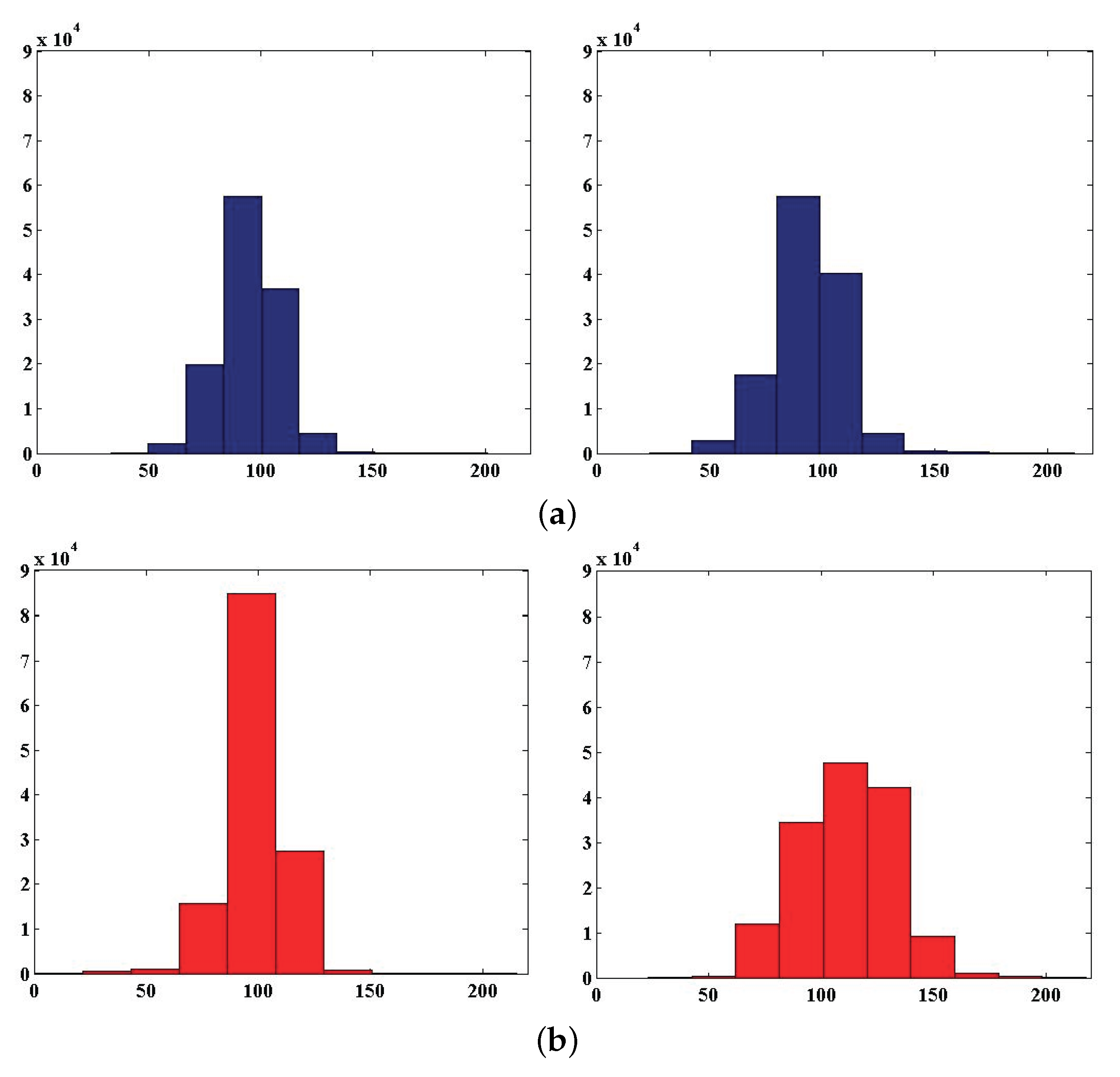
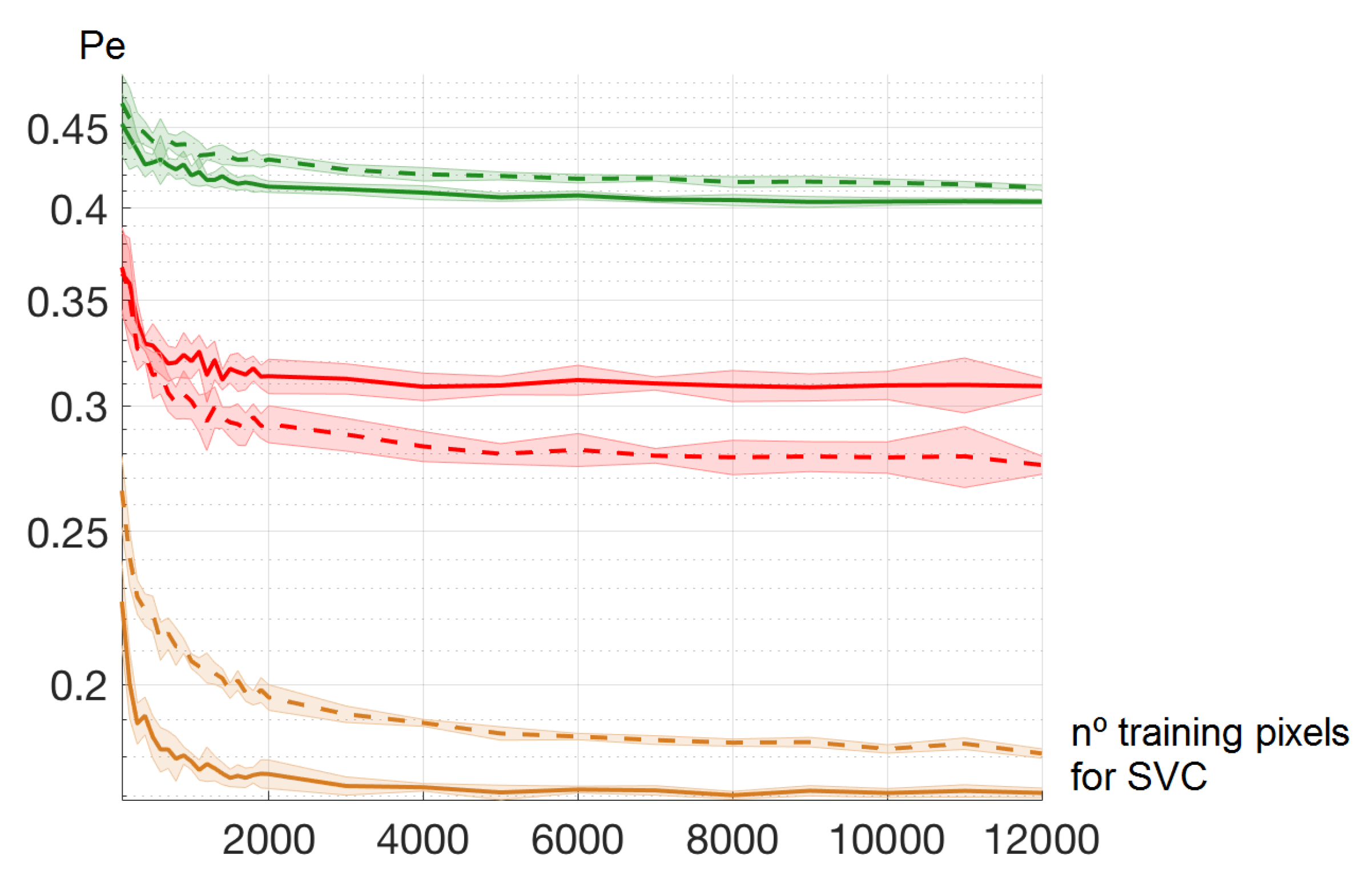
4.1. Number of Training Pixels for SVC Learning
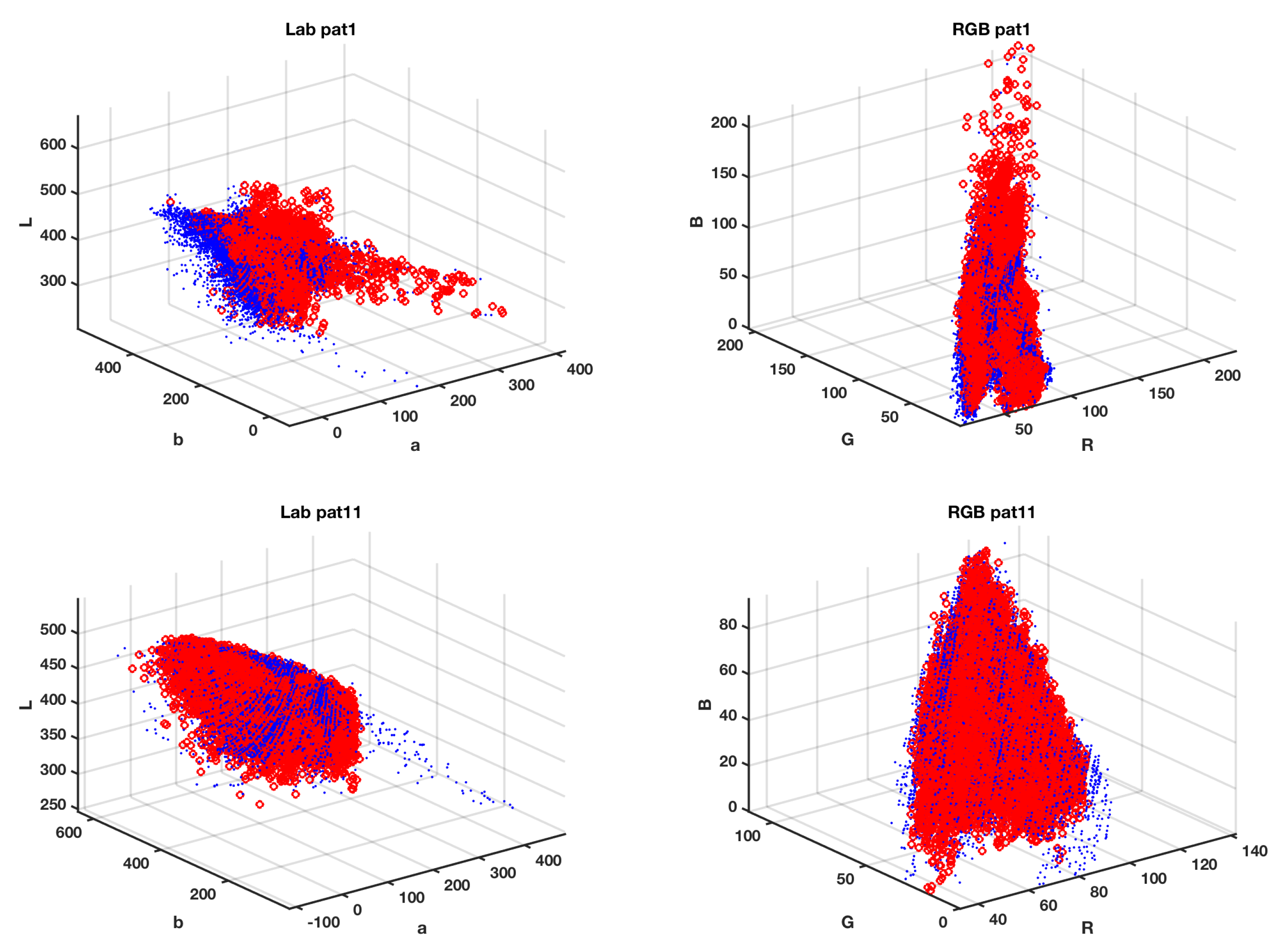
4.2. Color Spaces
4.3. Effect of Neighbor Pixels and Textures
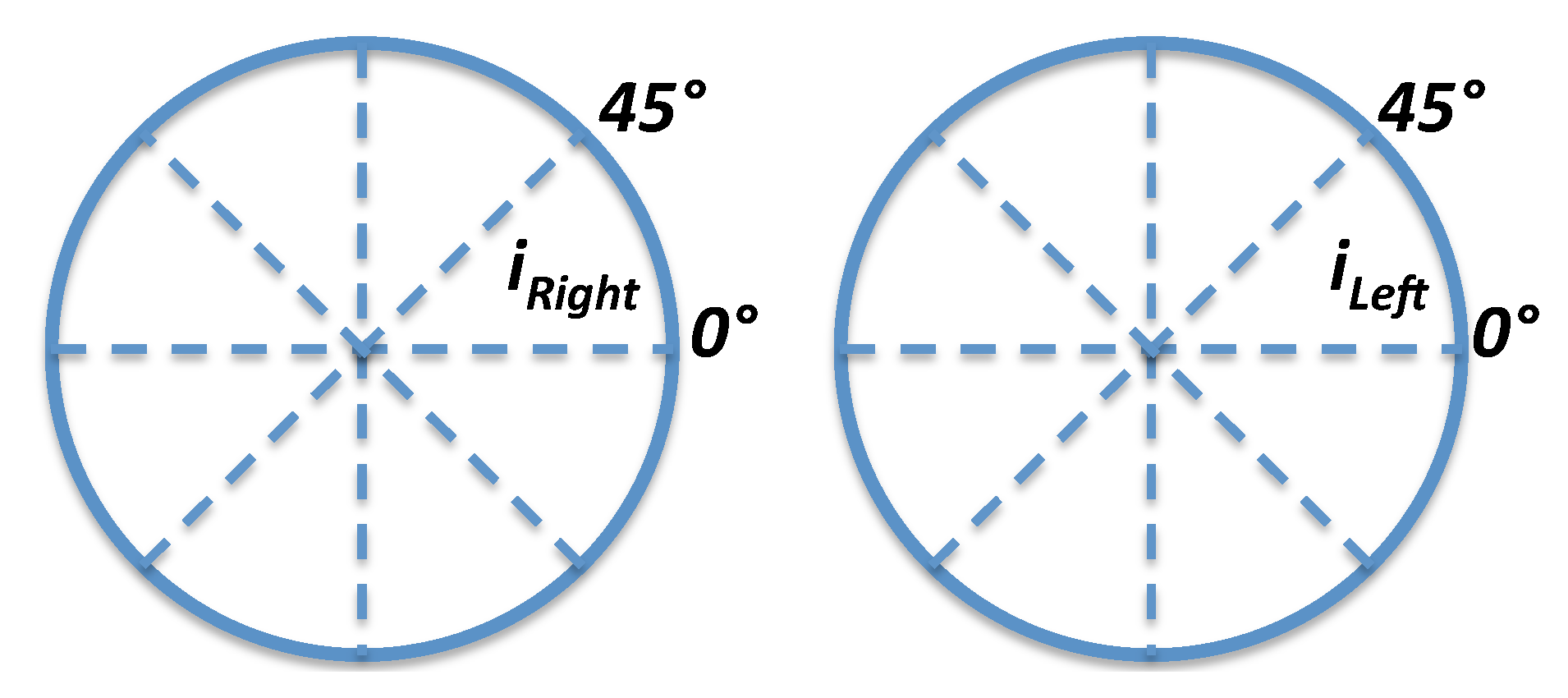
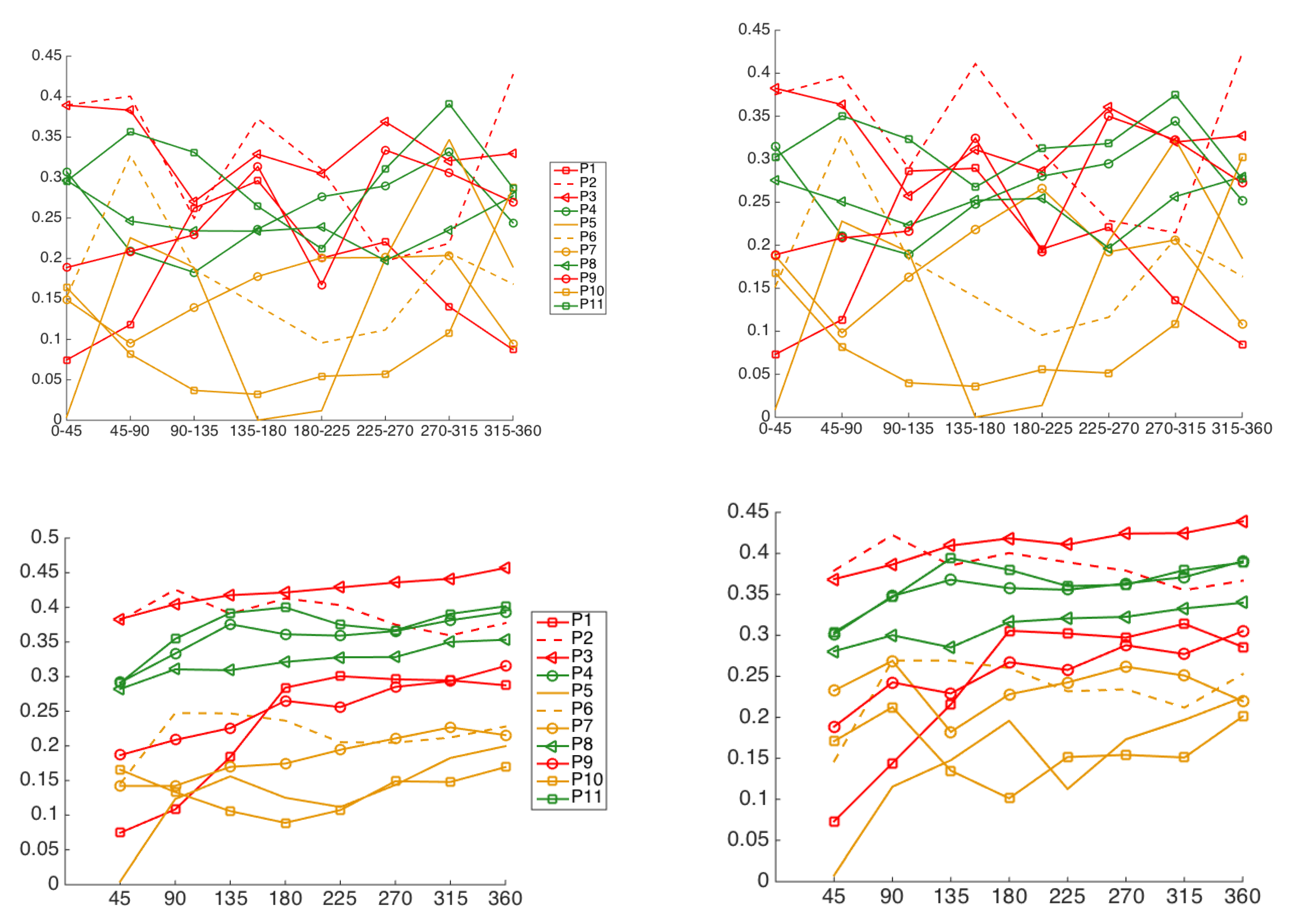
4.4. Iris Image-Region Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wielgus, A.; Sarna, T. Melanin in human irides of different color and age of donors. Pigment Cell Res. 2005, 18, 454–464. [Google Scholar] [CrossRef]
- McGowan, A.; Silvestri, G.; Moore, E.; Silvestri, V.; Patterson, C.C.; Maxwell, A.P.; McKay, G.J. Retinal Vascular Caliber, Iris Color, and Age-Related Macular Degeneration in the Irish Nun Eye Study. Investig. Ophthalmol. Vis. Sci. 2015, 56, 382–387. [Google Scholar] [CrossRef][Green Version]
- Zebenholzer, K.; Wöber, C.; Vigl, M.; Wessely, P.; Wöber-Bingöl, C. Facial pain in a neurological tertiary care centre–evaluation of the International Classification of Headache Disorders. Cephalalgia 2005, 25, 689–699. [Google Scholar] [CrossRef]
- Gladstone, R.M. Development and significance of heterochromia iridis. Arch. Neurol. 1969, 21, 184–192. [Google Scholar] [CrossRef]
- Pareja, J.A.; Espejo, M.; Trigo, M.; Sjaastad, O. Congenital Horners Syndrome and Ipsilateral Headache. Funct. Neurol. 1997, 12, 123–131. [Google Scholar] [PubMed]
- Messina, R.; Leech, R.; Zelaya, F.; Dipasquale, O.; Wei, D.; Filippi, M.; Goadsby, P. Migraine and Cluster Headache Classification Using a Supervised Machine Learning Approach: A Multimodal MRI Study (P4.10-016). Neurology 2019, 92, 4–10. [Google Scholar]
- Vandewiele, G.; De Backere, F.; Lannoye, K.; Vanden Berghe, M.; Janssens, O.; Van Hoecke, S.; Keereman, V.; Paemeleire, K.; Ongenae, F.; De Turck, F. A decision support system to follow up and diagnose primary headache patients using semantically enriched data. BMC Med. Inform. Decis. Mak. 2018, 18, 98. [Google Scholar] [CrossRef] [PubMed]
- Keight, R.; Aljaaf, A.J.; Al-Jumeily, D.; Hussain, A.J.; Özge, A.; Mallucci, C. An Intelligent Systems Approach to Primary Headache Diagnosis. In Lecture Notes in Computer Science, Proceedings of the ICIC 2017, Intelligent Computing Theories and Application, Liverpool, UK, 7–10 August 2017; Huang, D.S., Jo, K.H., Figueroa-García, J., Eds.; Springer: Cham, Swizterland, 2017; Volume 10362. [Google Scholar]
- Krawczyk, B.; Simic, D.; Simic, S.; Woźniak, M. Automatic diagnosis of primary headaches by machine learning methods. Cent. Eur. J. Med. 2012, 8, 157–165. [Google Scholar] [CrossRef]
- El-Yaagoubi, M.; Mora-Jiménez, I.; Rojo-Álvarez, J.L.; Jabrane, Y.; Pareja-Grande, J.A. Extended Iris Color Features Analysis and Cluster Headache Diagnosis Based On Support Vector Classifier. In Proceedings of the IEEE International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 17–19 April 2017. [Google Scholar]
- International Headache Society. The international classification of headache disorders. 2nd ed. Cephalalgia 2004, 24, 1–160. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Boser, E.; Guyon, I.; Vapnik, V. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: Harlow, UK, 2018. [Google Scholar]
- Daugman, J. The importance of being random: Statistical principles of iris recognition. Patt. Recog. 2003, 36, 279–291. [Google Scholar] [CrossRef]
- Manzo, M.; Pellino, S. FastGCN+ARSRGemb: A novel framework for object recognition. arXiv 2020, arXiv:2002.08629. [Google Scholar]
- Ghosh, A.K. On optimum choice of k in nearest neighbor classification. Comput. Stat. 2006, 50, 3113–3123. [Google Scholar] [CrossRef]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inform. Theory. 1968, 13, 21–27. [Google Scholar] [CrossRef]
- Trippa, L.; Waldron, L.; Huttenhower, C.; Parmigiani, G. Bayesian nonparametric cross-study validation of prediction methods. Ann. Appl. Stat. 2015, 9, 402–428. [Google Scholar] [CrossRef]
- Plataniotis, K.N.; Venetsanopoulos, A.N. Color Image Processing and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Vezhnevets, V.; Sazonov, V.; Andreeva, A. A Survey on Pixel-Based Skin Color Detection Techniques. Proc. Graphicon. 2003, 3, 85–92. [Google Scholar]
- Palus, H. Representations of colour images in different colour spaces. In The Colour Image Processing Handbook; Sangwine, S.J., Horne, R.E.N., Eds.; Springer: Boston, MA, USA, 1998; pp. 67–90. [Google Scholar]
- Ohta, Y.I.; Kanade, T.; Sakai, T. Color information for region segmentation. Comput. Graph. Image Process. 1980, 13, 222–241. [Google Scholar] [CrossRef]
- Krasnianski, M.; Georgiadis, D.; Grehl, H.; Lindner, A. Correlation of clinical and magnetic resonance imaging findings in patients with brainstem infarction. Fortschr. Neurol. Psychiatr. 2001, 69, 236–241. [Google Scholar] [CrossRef] [PubMed]

| Group | Pat. no. | RGB | Lab | La | Lb | ab | HSI | IH | IS | |
|---|---|---|---|---|---|---|---|---|---|---|
| HSV | VH | VS | Fleck | Ohta | RGBLab | |||||
| 1 | 0.34 | 0.32 | 0.34 | 0.35 | 0.32 | 0.35 | 0.34 | 0.33 | 0.35 | |
| 0.31 | 0.38 | 0.34 | 0.39 | 0.34 | 0.54 | 0.30 | 0.31 | |||
| 2 | 0.37 | 0.39 | 0.40 | 0.41 | 0.42 | 0.40 | 0.41 | 0.41 | 0.42 | |
| 1 | 0.39 | 0.39 | 0.42 | 0.43 | 0.42 | 0.50 | 0.39 | 0.41 | ||
| 3 | 0.43 | 0.45 | 0.49 | 0.48 | 0.48 | 0.47 | 0.48 | 0.45 | 0.45 | |
| 0.46 | 0.45 | 0.48 | 0.47 | 0.47 | 0.51 | 0.46 | 0.47 | |||
| 9 | 0.39 | 0.38 | 0.41 | 0.40 | 0.44 | 0.41 | 0.41 | 0.40 | 0.44 | |
| 0.38 | 0.41 | 0.44 | 0.43 | 0.45 | 0.42 | 0.38 | 0.41 | |||
| 4 | 0.44 | 0.40 | 0.45 | 0.44 | 0.41 | 0.43 | 0.45 | 0.42 | 0.43 | |
| 0.39 | 0.46 | 0.44 | 0.43 | 0.44 | 0.47 | 0.42 | 0.41 | |||
| 8 | 0.37 | 0.38 | 0.40 | 0.43 | 0.46 | 0.37 | 0.39 | 0.42 | 0.41 | |
| 2 | 0.35 | 0.42 | 0.42 | 0.43 | 0.40 | 0.49 | 0.36 | 0.38 | ||
| 11 | 0.43 | 0.43 | 0.46 | 0.46 | 0.46 | 0.44 | 0.46 | 0.47 | 0.44 | |
| 0.45 | 0.47 | 0.47 | 0.46 | 0.45 | 0.50 | 0.44 | 0.45 | |||
| 5 | 0.19 | 0.18 | 0.21 | 0.24 | 0.22 | 0.21 | 0.20 | 0.27 | 0.24 | |
| 0.22 | 0.19 | 0.29 | 0.25 | 0.24 | 0.53 | 0.21 | 0.21 | |||
| 6 | 0.22 | 0.20 | 0.41 | 0.27 | 0.24 | 0.20 | 0.35 | 0.24 | 0.26 | |
| 0.23 | 0.41 | 0.23 | 0.23 | 0.23 | 0.49 | 0.20 | 0.21 | |||
| 3 | 7 | 0.28 | 0.31 | 0.30 | 0.38 | 0.31 | 0.29 | 0.34 | 0.39 | 0.44 |
| 0.29 | 0.31 | 0.35 | 0.44 | 0.44 | 0.50 | 0.29 | 0.33 | |||
| 10 | 0.17 | 0.20 | 0.22 | 0.22 | 0.22 | 0.18 | 0.23 | 0.22 | 0.24 | |
| 0.18 | 0.25 | 0.26 | 0.24 | 0.23 | 0.52 | 0.17 | 0.17 |
| Group | Pat. no. | RGB | Lab | La | Lb | ab | HSI | IH | IS | |
|---|---|---|---|---|---|---|---|---|---|---|
| HSV | VH | VS | Fleck | Ohta | RGBLab | |||||
| 1 | 0.32 | 0.29 | 0.34 | 0.32 | 0.37 | 0.33 | 0.33 | 0.36 | 0.38 | |
| 0.30 | 0.36 | 0.32 | 0.34 | 0.35 | 0.47 | 0.29 | 0.28 | |||
| 2 | 0.38 | 0.40 | 0.41 | 0.42 | 0.40 | 0.40 | 0.41 | 0.42 | 0.41 | |
| 1 | 0.38 | 0.39 | 0.41 | 0.41 | 0.41 | 0.49 | 0.38 | 0.38 | ||
| 3 | 0.44 | 0.46 | 0.47 | 0.48 | 0.46 | 0.46 | 0.47 | 0.46 | 0.46 | |
| 0.45 | 0.47 | 0.47 | 0.47 | 0.47 | 0.49 | 0.44 | 0.45 | |||
| 9 | 0.37 | 0.36 | 0.38 | 0.38 | 0.42 | 0.36 | 0.40 | 0.39 | 0.42 | |
| 0.34 | 0.40 | 0.39 | 0.43 | 0.43 | 0.51 | 0.34 | 0.37 | |||
| 4 | 0.42 | 0.39 | 0.43 | 0.42 | 0.44 | 0.40 | 0.45 | 0.42 | 0.42 | |
| 0.39 | 0.44 | 0.43 | 0.40 | 0.40 | 0.45 | 0.41 | 0.37 | |||
| 8 | 0.36 | 0.37 | 0.35 | 0.42 | 0.43 | 0.38 | 0.37 | 0.41 | 0.42 | |
| 2 | 0.38 | 0.42 | 0.42 | 0.41 | 0.43 | 0.50 | 0.35 | 0.32 | ||
| 11 | 0.43 | 0.43 | 0.44 | 0.43 | 0.40 | 0.45 | 0.45 | 0.43 | 0.42 | |
| 0.48 | 0.43 | 0.45 | 0.44 | 0.43 | 0.50 | 0.43 | 0.41 | |||
| 5 | 0.19 | 0.18 | 0.20 | 0.24 | 0.22 | 0.20 | 0.19 | 0.26 | 0.25 | |
| 0.19 | 0.18 | 0.25 | 0.27 | 0.21 | 0.52 | 0.20 | 0.17 | |||
| 6 | 0.22 | 0.21 | 0.39 | 0.25 | 0.21 | 0.19 | 0.34 | 0.24 | 0.24 | |
| 0.22 | 0.38 | 0.20 | 0.23 | 0.23 | 0.48 | 0.19 | 0.18 | |||
| 3 | 7 | 0.28 | 0.27 | 0.27 | 0.45 | 0.39 | 0.29 | 0.30 | 0.39 | 0.46 |
| 0.27 | 0.29 | 0.34 | 0.45 | 0.43 | 0.49 | 0.28 | 0.27 | |||
| 10 | 0.17 | 0.16 | 0.19 | 0.19 | 0.22 | 0.17 | 0.20 | 0.19 | 0.23 | |
| 0.17 | 0.19 | 0.23 | 0.23 | 0.23 | 0.48 | 0.16 | 0.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Yaagoubi, M.; Mora-Jiménez, I.; Jabrane, Y.; Muñoz-Romero, S.; Rojo-Álvarez, J.L.; Pareja-Grande, J.A. Quantitative Cluster Headache Analysis for Neurological Diagnosis Support Using Statistical Classification. Information 2020, 11, 393. https://doi.org/10.3390/info11080393
El-Yaagoubi M, Mora-Jiménez I, Jabrane Y, Muñoz-Romero S, Rojo-Álvarez JL, Pareja-Grande JA. Quantitative Cluster Headache Analysis for Neurological Diagnosis Support Using Statistical Classification. Information. 2020; 11(8):393. https://doi.org/10.3390/info11080393
Chicago/Turabian StyleEl-Yaagoubi, Mohammed, Inmaculada Mora-Jiménez, Younes Jabrane, Sergio Muñoz-Romero, José Luis Rojo-Álvarez, and Juan Antonio Pareja-Grande. 2020. "Quantitative Cluster Headache Analysis for Neurological Diagnosis Support Using Statistical Classification" Information 11, no. 8: 393. https://doi.org/10.3390/info11080393
APA StyleEl-Yaagoubi, M., Mora-Jiménez, I., Jabrane, Y., Muñoz-Romero, S., Rojo-Álvarez, J. L., & Pareja-Grande, J. A. (2020). Quantitative Cluster Headache Analysis for Neurological Diagnosis Support Using Statistical Classification. Information, 11(8), 393. https://doi.org/10.3390/info11080393








