Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders
Abstract
1. Introduction
2. Basic Decoding Algorithm of LDPC Codes
2.1. BP Algorithm
2.2. MS Algorithm
3. Proposed DT-SCMS Algorithm
3.1. SCMS Algorithm
3.2. DT-SCMS Algorithm
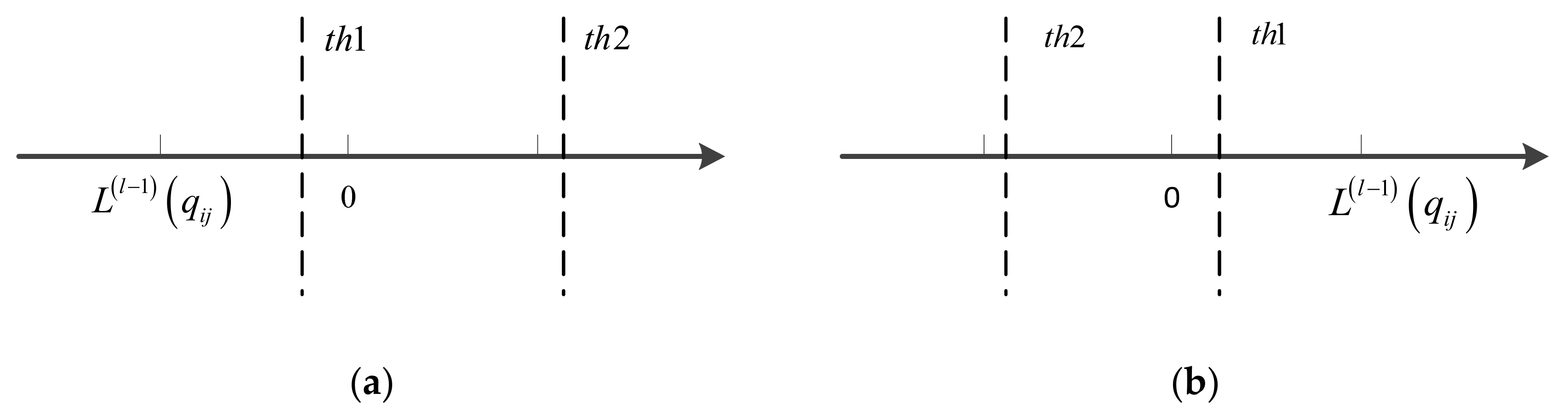
3.3. Thresholds Setting
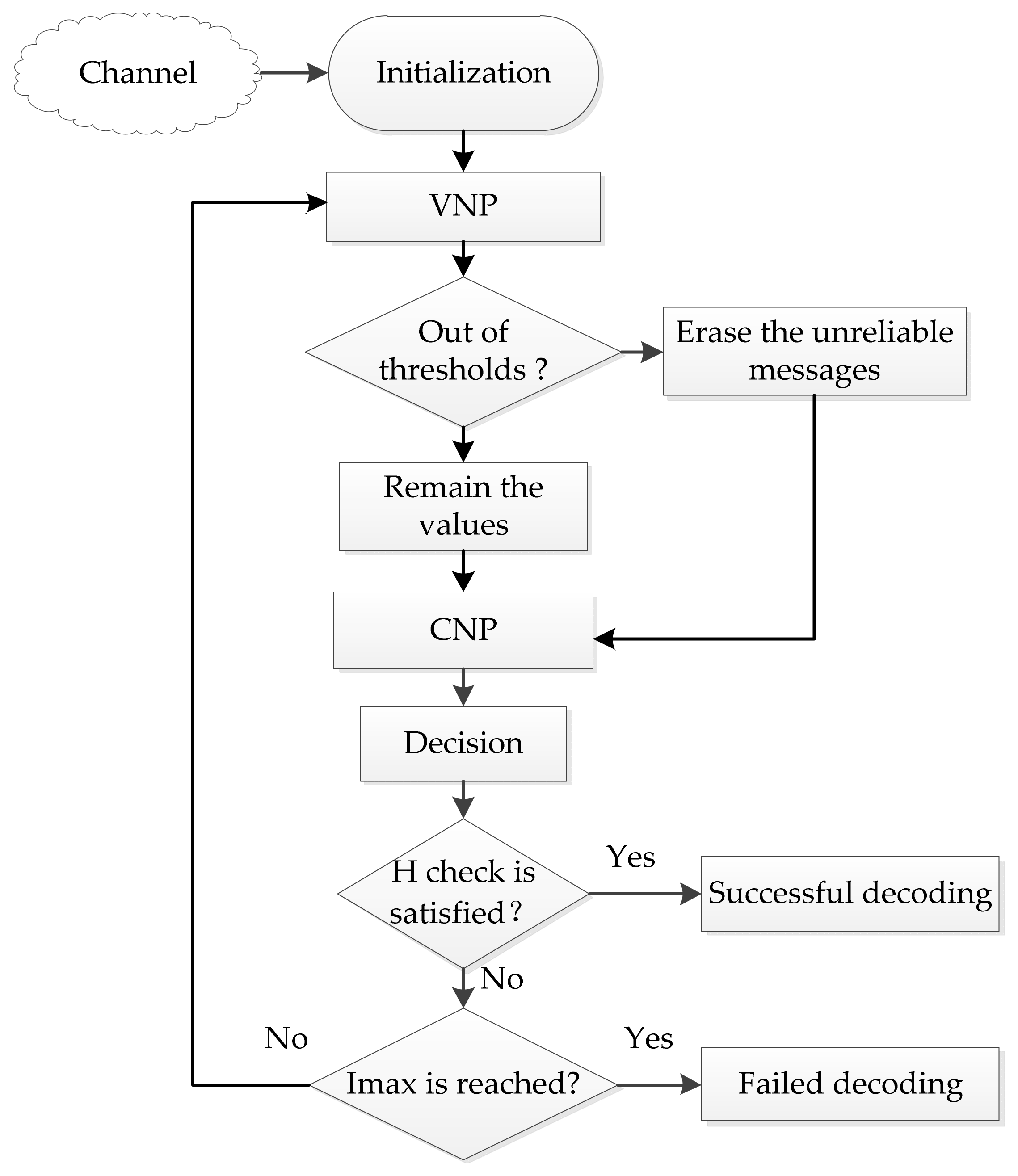
3.4. Iterative Process
4. Performance Analysis and Comparisons
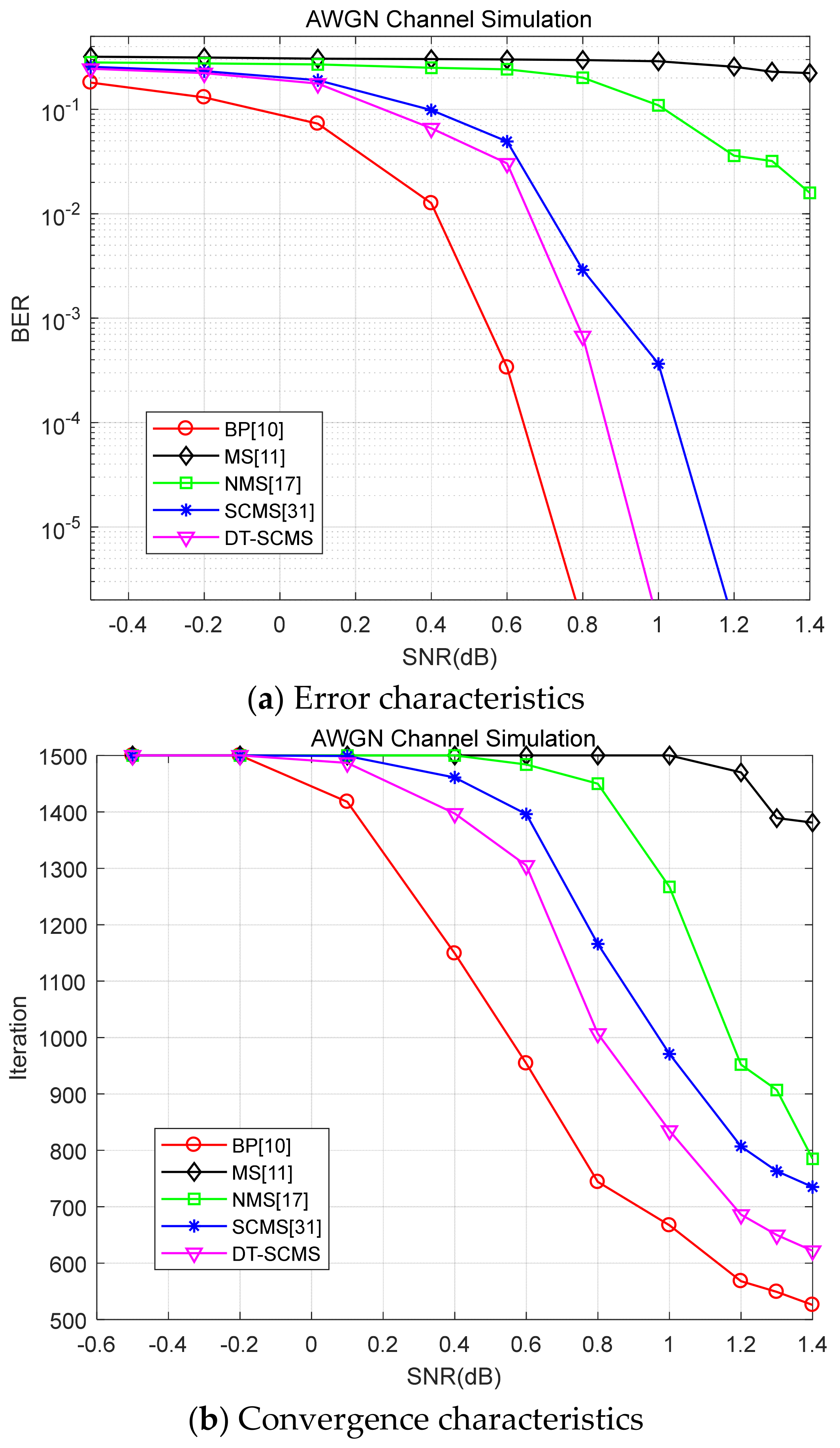
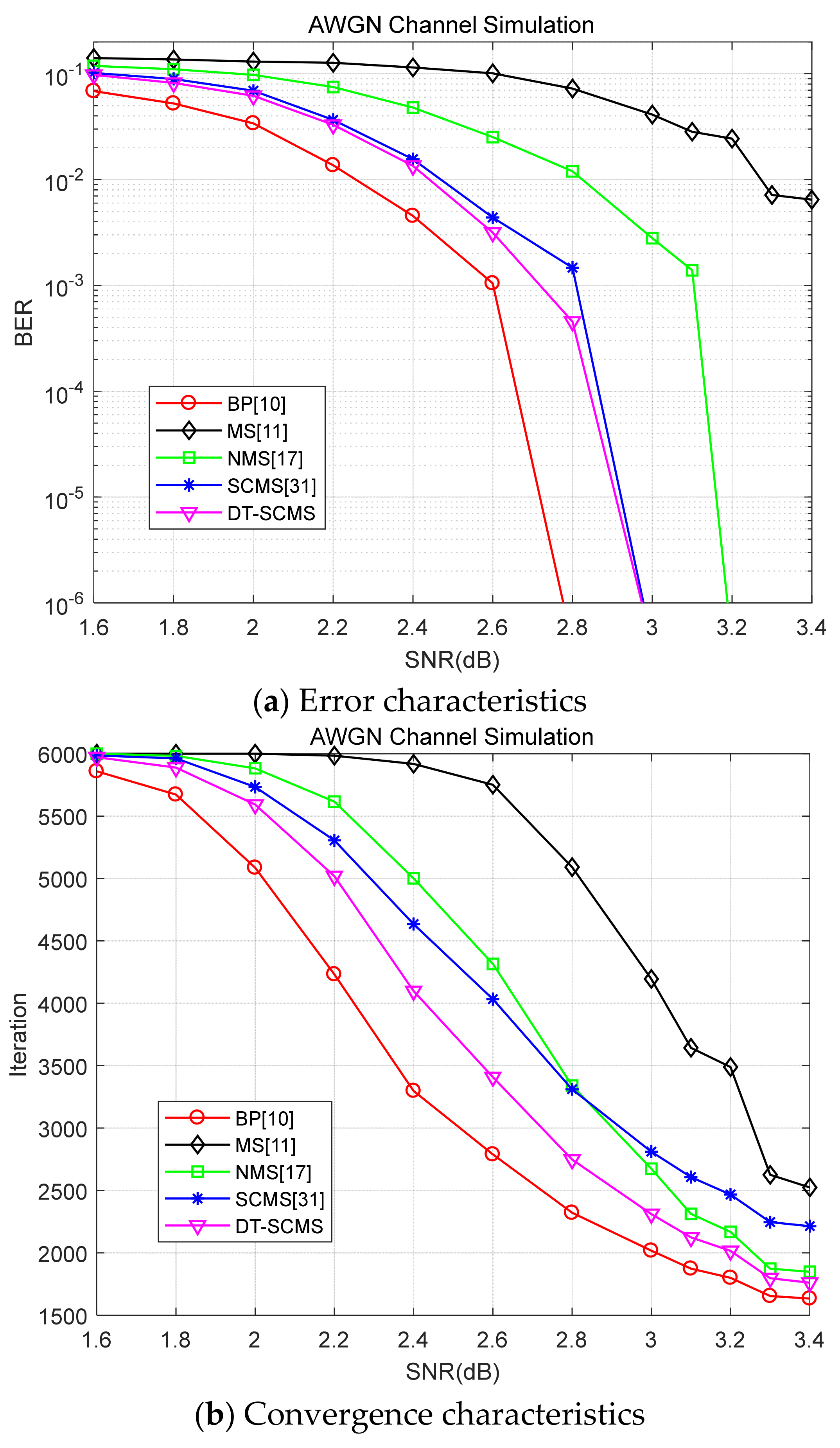
4.1. Experiments and Simulations
4.2. Complexity Analyses
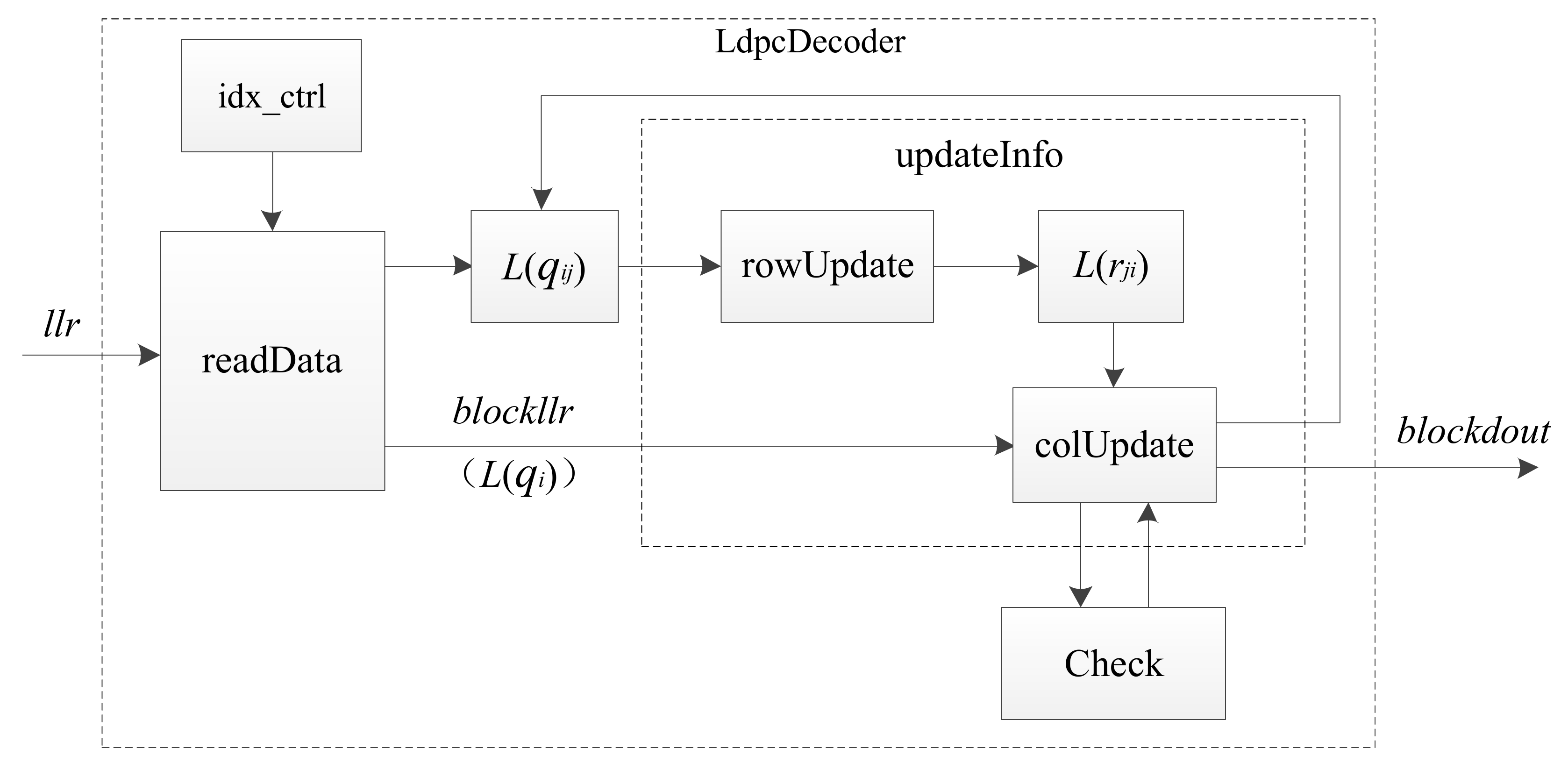
5. Design Architecture and Implementation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huo, Y.; Dong, X.; Xu, W.; Yuen, M. Enabling Multi-Functional 5G and Beyond User Equipment: A Survey and Tutorial. IEEE Access 2019, 7, 116975–117008. [Google Scholar] [CrossRef]
- 3GPP. NR; Multiplexing and Channel Coding (TS 38.212 Release 15). 3GPP TS 38.212 V15.0.0. Available online: https://www.3gpp.org/specifications (accessed on 2 November 2019).
- Richardson, T.; Kudekar, S. Design of Low-Density Parity Check Codes for 5G New Radio. IEEE Commun. Mag. 2018, 56, 28–34. [Google Scholar] [CrossRef]
- Nguyen, T.T.B.; Nguyen Tan, T.; Lee, H. Efficient QC-LDPC Encoder for 5G New Radio. Electronics 2019, 8, 668. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check code. Ire Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Jung, Y.M.; Jung, Y.H.; Lee, S.J.; Kim, J. Low-complexity multi-way and reconfigurable cyclic shift network of QC-LDPC decoder for Wi-Fi/WIMAX applications. IEEE Trans. Consum. Electron. 2013, 59, 467–475. [Google Scholar] [CrossRef]
- Liu, Y.F.; Olmos, P.M.; Mitchell, G.M. Generalized LDPC codes for ultra reliable low latency communication in 5G and beyond. IEEE Access 2018, 6, 72002–72014. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Zhang, C.; Yan, Z.Y.; Chen, S.; Jiang, H.J. A high-throughput multi-rate LDPC decoder for error correction of solid-state drives. In Proceedings of the 2015 IEEE Workshop on Signal Processing Systems (SiPS), Hangzhou, China, 14–16 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, Z.J.; Jin, S.; Zhang, C.; Yan, F. A low complexity LDPC-BCH concatenated decoder for NAND flash memory. IEICE Electron. Express 2018, 15, 20180103. [Google Scholar] [CrossRef]
- MacKay, D.J.C.; Neal, R.M. Near Shannon limit performance of low density parity check codes. Electron. Lett. 1996, 32, 1645–1646. [Google Scholar] [CrossRef]
- Fossorier, M.P.C.; Mihaljevic, M.; Imai, H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation. IEEE Trans. Commun. 1999, 47, 673–680. [Google Scholar] [CrossRef]
- Jiang, M.; Zhao, C.M.; Shi, Z.H.; Chen, Y. An Improvement on the Modified Weighted Bit Flipping Decoding Algorithm for LDPC Codes. IEEE Commun. Lett. 2005, 9, 814–816. [Google Scholar] [CrossRef]
- Lee, C.H.; Wolf, W. Implementation-efficient reliability ratio based weighted bit-flipping decoding for LDPC codes. Electron. Lett. 2005, 41, 755–757. [Google Scholar] [CrossRef]
- Balasuriya, N.; Wavegedara, C.B. Improved symbol value selection for symbol flipping-based non-binary LDPC decoding. Eurasip J. Wirel. Commun. Netw. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Ren, D.; Sha, J. Improved gradient descent bit flipping decoder for LDPC codes on BSC channel. IEICE Electron. Express 2018, 15, 20180195. [Google Scholar] [CrossRef]
- Cho, K.; Chung, K.S. Conditional termination check min-sum algorithm for efficient LDPC decoders. IEICE Electron. Express 2015, 12, 20150738. [Google Scholar] [CrossRef][Green Version]
- Chen, J.; Fossorier, M.P.C. Density evolution for two improved BP-based decoding algorithms of LDPC codes. IEEE Commun. Lett. 2002, 6, 208–210. [Google Scholar] [CrossRef]
- Chen, J.; Fossorier, M.P.C. Near optimum universal belief propagation based decoding of low-density parity check codes. IEEE Trans. Commun. 2002, 50, 406–414. [Google Scholar] [CrossRef]
- Wu, X.F.; Song, Y.; Jiang, M.; Zhao, C.M. Adaptive-normalized/offset min-sum algorithm. IEEE Commun. Lett. 2010, 14, 667–669. [Google Scholar] [CrossRef]
- Myung, S.; Park, S.I.; Kim, K.J.; Lee, J.Y.; Kwon, S.; Kim, J. Offset and normalized min-sum algorithms for ATSC 3.0 LDPC decoder. IEEE Trans. Broadcasting 2017, 63, 734–739. [Google Scholar] [CrossRef]
- Hu, X.Y.; Eleftheriou, E.; Arnold, D.M.; Dholakia, A. Efficient implementations of the sum-product algorithm for decoding LDPC codes. In Proceedings of the GLOBECOM’01. IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001. [Google Scholar] [CrossRef]
- Chen, J.; Dholakia, A.; Eleftheriou, E.; Fossorier, M.P.C.; Hu, X.Y. Reduced-complexity decoding of LDPC codes. IEEE Trans. Commun. 2005, 53, 1288–1299. [Google Scholar] [CrossRef]
- Papaharalabos, S.; Mathiopoulos, P.T. Simplified sum-product algorithm for decoding LDPC codes with optimal performance. Electron. Lett. 2009, 45, 116–117. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Ye, T.C. An improved implementation of sum-product algorithm for LDPC decoder. IEICE Electron. Express 2019, 16, 20180828. [Google Scholar] [CrossRef]
- Fan, J.; Yang, H. A new forced convergence decoding scheme for LDPC codes. In Proceedings of the 2009 IEEE International Conference on Communications Technology and Applications, Beijing, China, 16–18 October 2009; pp. 576–580. [Google Scholar] [CrossRef]
- Dai, L.Y.; Yang, H.W.; Fan, J.X.; Rao, W.Y. Forced-convergence decoding for LDPC-coded modulation. Sci. China Inf. Sci. 2013, 56, 1–11. [Google Scholar] [CrossRef][Green Version]
- Shin, D.; Heo, K.; Oh, S.; Ha, J. A Stopping Criterion for Low-Density Parity-Check Codes. In Proceedings of the IEEE 65th Vehicular Technology Conference, VTC Spring 2007, Dublin, Ireland, 22–25 April 2007; pp. 1529–1533. [Google Scholar] [CrossRef]
- Marchand, C.; Boutillon, E. Before convergence early stopping criterion for inner LDPC code in DVB standards. Electron. Lett. 2014, 51, 114–116. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, X.L.; Zhao, L.; Chen, L. Design of a high-throughput QC-LDPC decoder with TDMP scheduling. IEEE Trans. Circuits Syst. II Express Briefs 2014, 62, 56–60. [Google Scholar] [CrossRef]
- Declercq, D.; Savin, V.; Boncalo, O.; Ghaffari, F. An imprecise stopping criterion based on in-between layers partial syndromes. IEEE Commun. Lett. 2018, 22, 13–16. [Google Scholar] [CrossRef]
- Savin, V. Self-corrected min-sum decoding of ldpc codes. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 146–150. [Google Scholar] [CrossRef]
- Boncalo, O.; Alexandria, A.; Savin, V. Memory efficient implementation of self-corrected min-sum LDPC decoder. In Proceedings of the 21st IEEE International Conference on Electronics, Circuits and Systems (ICECS), Marseille, France, 7–10 December 2014; pp. 295–298. [Google Scholar] [CrossRef]
- Boncalo, O.; Amaricai, A.; Mihancea, P.F.; Savin, V. Memory trade-offs in layered self-corrected min-sum LDPC decoders. Analog Integr. Circuits Signal Process. 2016, 87, 169–180. [Google Scholar] [CrossRef]
- Diamantopoulos, D.; Xydis, S.; Siozios, K.; Soudris, D. Dynamic memory management in vivado-hls for scalable many-accelerator architectures. In Proceedings of the 11th International Symposium on Applied Reconfigurable Computing, Bochum, Germany, 14–17 April 2015; pp. 117–128. [Google Scholar] [CrossRef]
- Salaskar, A.; Chandrachoodan, N. FFT/IFFT implementation using Vivado™ HLS. In Proceedings of the 20th IEEE International Symposium on VLSI Design and Test (VDAT), Guwahati, India, 24–27 May 2016; pp. 1–2. [Google Scholar] [CrossRef]

| Symbol | Definition |
|---|---|
| H | The parity check matrix |
| i | A variable node in H, |
| j | A check node in H, |
| C(i) | A collection of check nodes connected to variable node i |
| R(j) | A collection of variable nodes connected to check node j |
| C(i)\ j | A set of check nodes connected to variable node i except j |
| R(j)\ i | A set of variable nodes connected to check node j except i |
| L(Pi) | Channel initial probability likelihood ratio message |
| L(rji) | The check node message (extrinsic probability likelihood ratio message from variable node i to check node j) |
| L(qij) | The variable node message (extrinsic probability likelihood ratio message from check node j to variable node i) |
| L(qi) | All messages collected by variable node i |
| The correction factor in the NMS algorithm | |
| Decoding sequence obtained by decoding decision |
| Parameters | R = 1/3 | R = 2/3 |
|---|---|---|
| Code length (bits) | 4224 | 1584 |
| SNR (dB) | [−0.5:1.4] | [1.6:3.4] |
| Maximum number of iterations | 30 | 30 |
| Correction factor α | 1.2 | 1.2 |
| Adjustment factor | 0.1 | 0.125 |
| Adjustment factor | −1.2 | −1.125 |
| SNR (dB) | 2.8 | 3 | 3.1 | 3.2 | 3.3 | 3.4 |
|---|---|---|---|---|---|---|
| SCMS [31] | 3311 | 2811 | 2607 | 2467 | 2246 | 2214 |
| DT-SCMS | 2748 | 2311 | 2124 | 2016 | 1797 | 1761 |
| −1.1247 | 5.2952 | −3.9980 | 8.1010 | 3.2369 | |
|---|---|---|---|---|---|
| −0.1406 | 0.6619 | −0.4998 | 1.0126 | 0.4046 | |
| 1.2653 | −5.9571 | 4.4977 | −9.1136 | −3.6415 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Chen, L. Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders. Information 2020, 11, 355. https://doi.org/10.3390/info11070355
Chen R, Chen L. Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders. Information. 2020; 11(7):355. https://doi.org/10.3390/info11070355
Chicago/Turabian StyleChen, Rong, and Lan Chen. 2020. "Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders" Information 11, no. 7: 355. https://doi.org/10.3390/info11070355
APA StyleChen, R., & Chen, L. (2020). Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders. Information, 11(7), 355. https://doi.org/10.3390/info11070355





