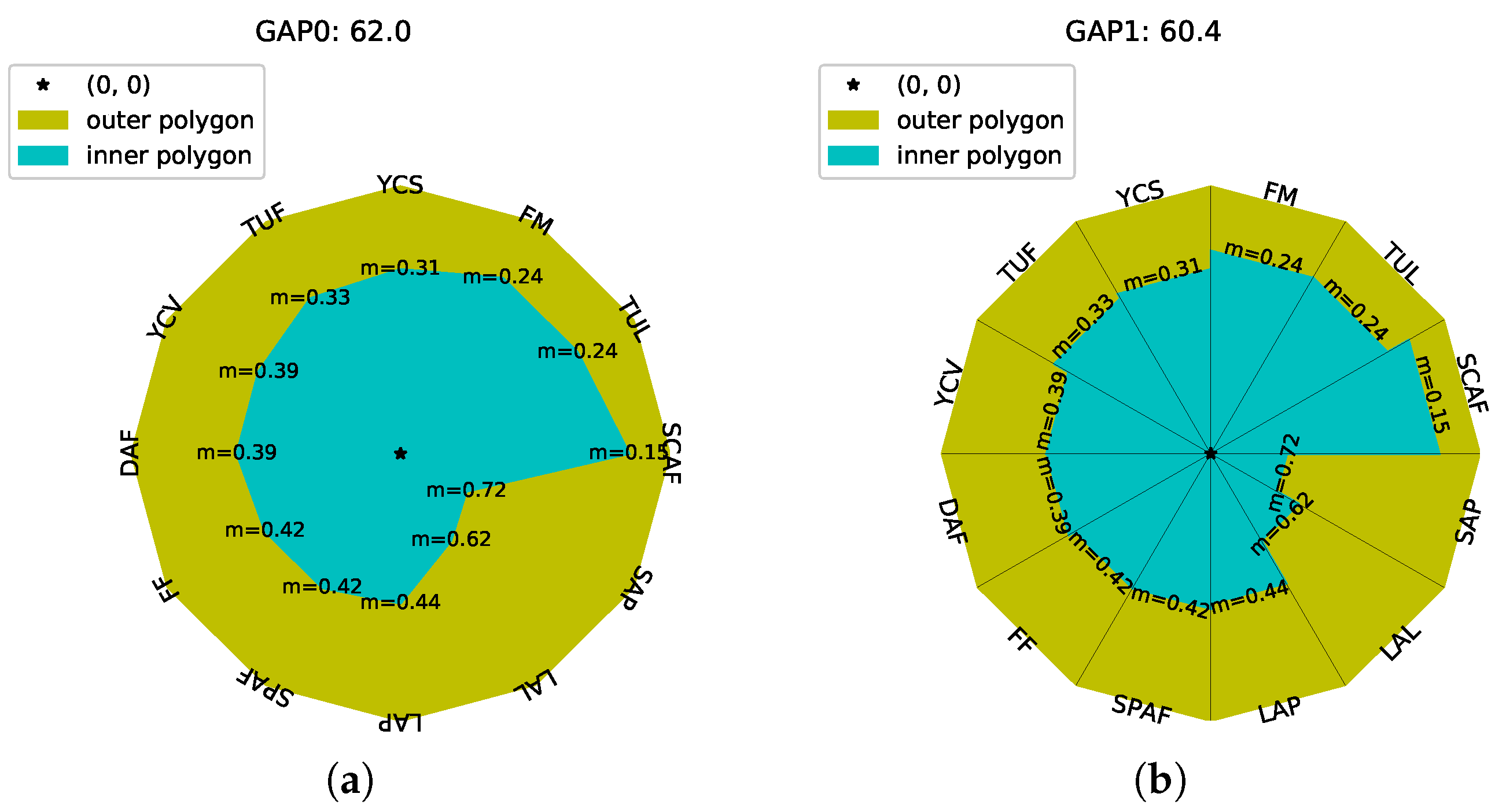
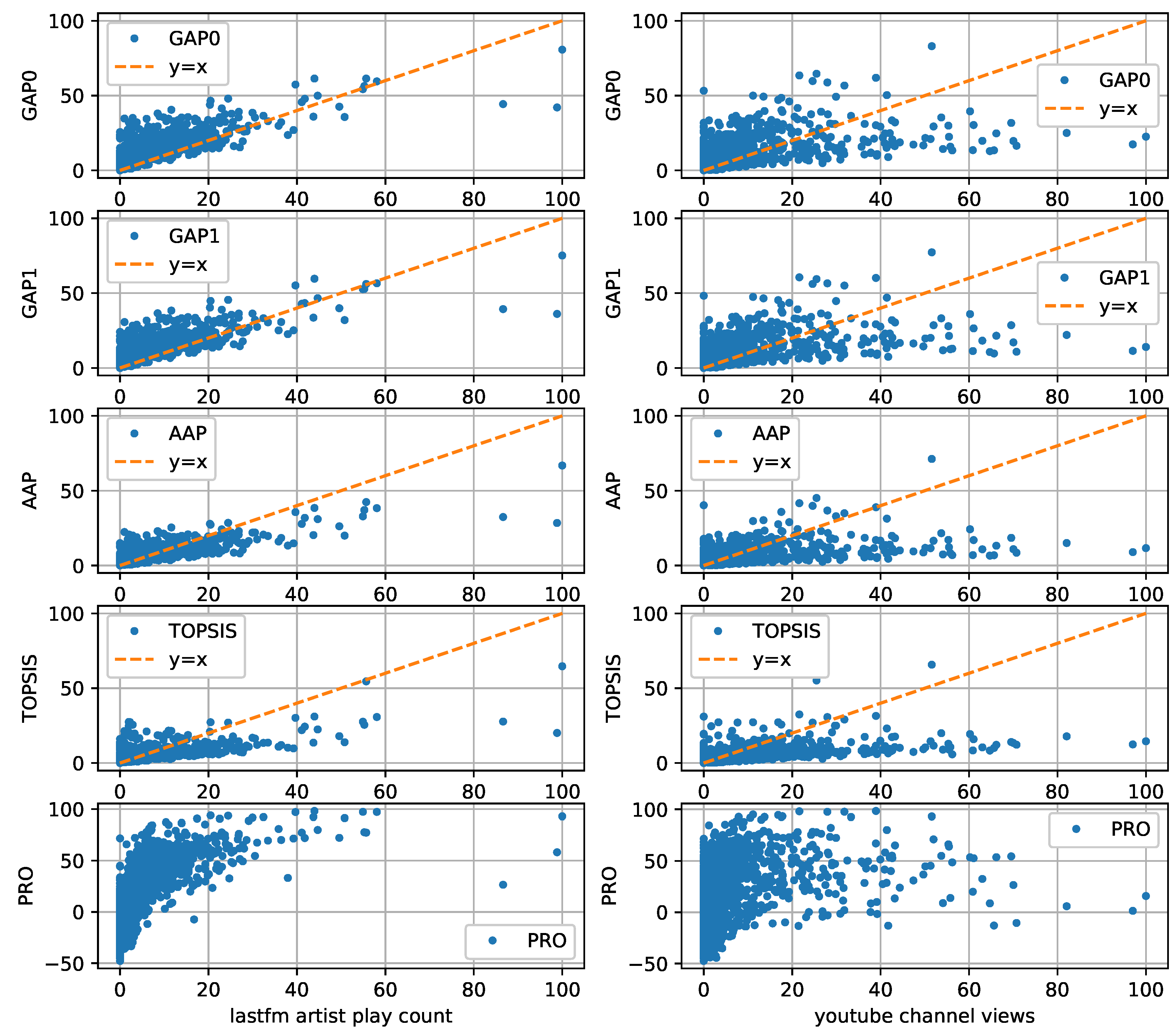
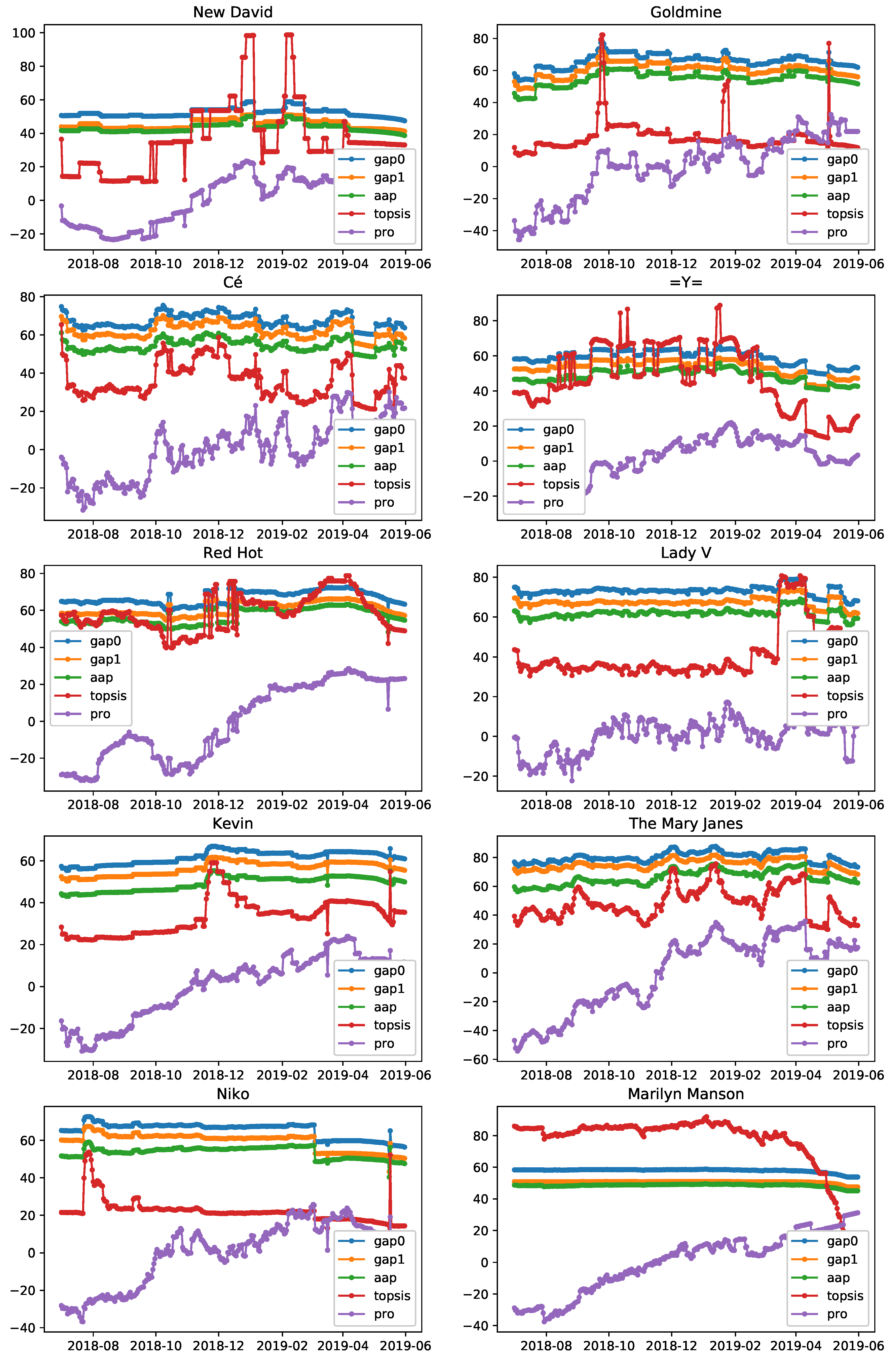
3.4. Results
In the Introduction, we cited many studies that considered already existing popularity metrics as the ground truth in order to evaluate other popularity scores. We accordingly opted for Last.fm play counts and YouTube channel views (summed streams over the last 30 days) as the ground truth for evaluation purposes. We chose these metrics because we believed that streaming activity reflected artist popularity more accurately than fan count (followers are not always committed to the artist), social media mentions (which are not always related to music), or proprietary “black-box” popularity scores (e.g., Spotify popularity). Furthermore, streaming activity is considered by music business stakeholders as more closely related to artist profits than all other metrics. The five aforementioned aggregation methods, GAP0, GAP1, AAP, TOPSIS, and PRO, were compared and the results are presented here.
In
Figure 2, we compare the values of all aggregation methods with the normalized Last.fm artist plays and YouTube channel views with regard to a certain date, being 2 April 2019, using scatter plots. Furthermore, in
Table 3, we present the corresponding similarity measures: Pearson correlation (
) and Mutual Information (MI) for the linear and non-linear interrelationship between the aggregation methods and the target variables. We also investigated if the best aggregation method differed significantly from the other methods, in terms of similarity to the target. The statistical significance of the differences was estimated as proposed in [
21] (dependent overlapping variables) for Pearson correlation and using a randomization test (We denote by
the target variable, by
and
the under comparison aggregation methods, and by
the test statistic, where
is the mutual information. Considering an approach similar to the permutation test proposed in [
22], the test statistic value
of the
Monte-Carlo simulation was computed by the permuted data, which were obtained by pooling
and
and assigning
N of them randomly sampled without replacement to the
group. The rest were assigned to the
group. We considered
R = 1000 Monte-Carlo simulations for the computation of the
p-values, which were then determined by Equation (
3):
where
denotes the cardinality of a set.) for mutual information. To the best of our knowledge, there are many parametric statistical tests for differences in Pearson correlation [
23], yet none for differences in mutual information; thus, we opted for the randomization test. It was apparent, from the scatter plots of
Figure 2 where the dots are more concentrated and from the correlation analysis of
Table 3 where higher similarity scores are illustrated, that all aggregation methods were correlated with Last.fm artist plays to a much higher degree than with YouTube channel views. Thus, we finally chose Last.fm artist plays as the ground truth for our experiments. In
Table 4, the similarity of the aggregation methods with Last.fm artist plays on 2 April 2019 is illustrated using all measures of similarity. The statistical significance of the corresponding differences was estimated by Zoo’s method [
21] for Pearson correlation and also using the previously described randomization test for all measures of similarity.
In
Table 5, the average similarity between Last.fm artist plays and the aggregation methods across time (from 1 July 2018 until 31 May 2019) is exemplified in terms of linear/non-linear correlation and rank correlation/distance. The results showed that GAP1 exhibited the best performance in three out of seven measures of similarity, while AAP in two, GAP0 and PRO in one each, and TOPSIS in zero. Furthermore, the statistical significance of the differences in average similarity was investigated for all similarity measures, using Student’s
t-test and by correcting the
p-values using the Bonferroni correction for multiple comparisons (
). (For each similarity measure, we conducted four comparisons (the best aggregation method vs. each of the rest), so
comparisons were considered, and the 28 corresponding
p-values were modified through the Bonferroni correction).
Although the aggregation methods produced similar artist popularities and rankings (not many statistical significant differences were observed), the correlation analysis showed that GAP produced popularity values that were closer to the target than the other aggregation methods when considering the non-linear similarity measure of mutual information and not when considering the linear correlation. This indicated the advantage of GAP to capture more complex popularity patterns than the simple average, which produced higher values only in linear correlation. In terms of ranking, GAP exhibited less distance from the target’s ranking with regard to Spearman’s footrule and Kendall’s tau distance measures and more proximity to the target’s ranking with regard to Kendall’s tau. PRO approximated best the target’s artist ranking with regard to the Spearman correlation coefficient, and both GAP and AAP showed almost identical rankings with regard to overall rank overlap.
In
Figure 3, we present the aggregation methods’ timelines for 10 popular artists with the highest discrepancy among the monitored popularity metrics. We focused on artists that exhibited differences in their popularity among different popularity metrics, because otherwise, the aggregation methods would provide the same information as the individual metrics and the comparison among them would not yield noteworthy conclusions. In order to select them, we first uncovered the set
A of the 100 most popular artists on a certain date, being 1 April 2019, by sorting the sums of differences between each artist’s metric values and the maximum metric values in our dataset, as shown in Equation (
4):
where
n is the number of metrics,
= 1 April 2019,
is the vector of normalized metric values for metric
i, time
, and all artists, and
is the maximum value in vector
v. Consequently, we employed Shannon entropy [
24] as a measure of discrepancy on the distribution of normalized metric values per artist and selected the 10 artists of set
A that exhibited the highest discrepancy, namely lowest entropy, as shown in Equation (
5):
where
is the vector of normalized metric values regarding artist
a at time
and
is the Shannon entropy computed on vector
v. The vector
was divided by the sum of its elements in order to sum to one, prior to entropy calculation.
It was observed that these 10 artists retained high aggregated popularity values, in terms of GAP, despite the low level of popularity in some individual metrics, while AAP produced lower popularity values as a result of low popularity in some individual metrics. Furthermore, a more stable trajectory was exhibited by GAP0, GAP1, and AAP compared with TOPSIS and PRO, which were more volatile, which partly explained their inferior performance. The fact that GAP produced higher popularity values when the artist was popular in one or some metrics while not popular in the others was considered as a major advantage comparing to AAP. The reason for that was twofold: (a) first, because it was not common for artists to be popular in all platforms; they tended to be active mainly in one or some of them; and (b) second, because being popular in one or some platforms was sufficient for an artist to be characterized as popular in general.
In
Table 6, we present a simulated example in order to showcase this advantage. It was observed that although in most metrics, a low popularity level was exhibited, being popular in Metric 4 enabled GAP to also exhibit a relatively high popularity estimate. On the contrary, AAP assigned a relatively low popularity estimate to the same entity. Finally, in
Table 7, three cases of the artists of our dataset with metric values distributed as in the simulated case are exemplified, and the same conclusion was drawn again from these example cases.