1. Introduction
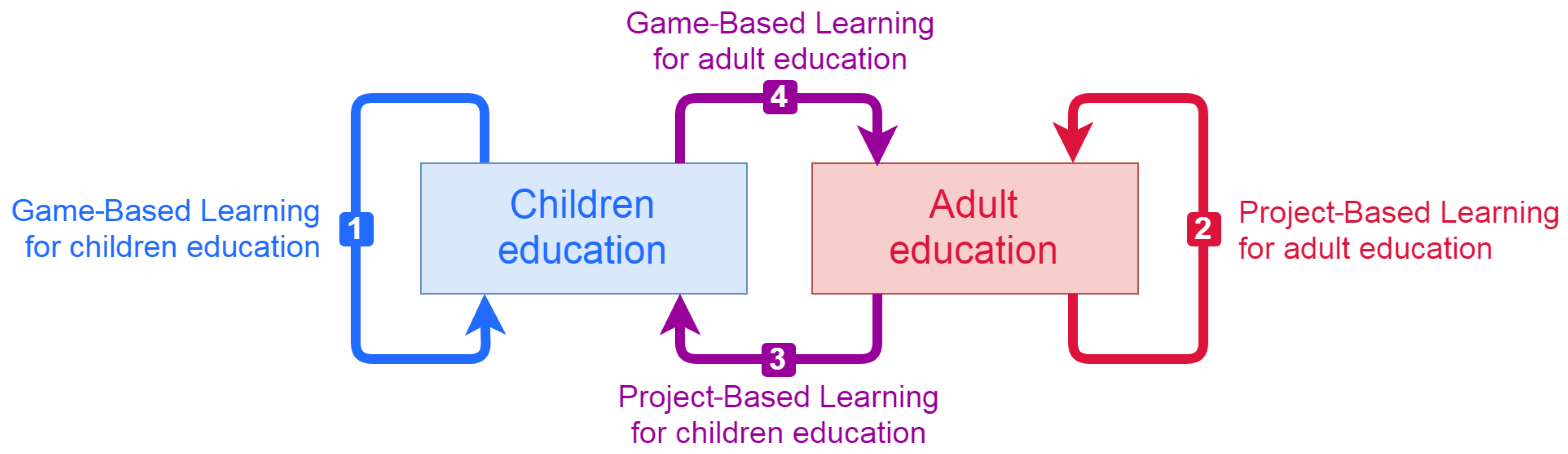
As a technological society we strive to introduce technology in all aspects of our life. This includes education. However, just using technology does not lead to better teaching or better learning. Traditionally, children’s education relies on Game-Based Learning (GBL), shown as arrow (1) in
Figure 1. On the other hand, university and adult education is more focused on specific problems, thus allowing easier implementation of Project-Based Learning (PBL)—this is arrow (2). The introduction of PBL to the education of pupils and young students is a way to provide a fruitful context for learning. This approach is represented by arrow (3). PBL for children requires significant modification of the educational content in order to simplify the management of a project and make it comprehensible by young students. Educators and researchers also explore ways of applying GBL to university-level and adult education, as indicated by arrow (4). This application of GBL is the main focus of our article.
Some non-gaming elements can be successfully implemented in an educational context and used as game mechanics, such as badges, reward systems and points. They are often used in the corporate sector to increase the loyalty of employees. Many game elements are also presented in the traditional educational environment, such as (i) different levels of difficulties; (ii) sandbox mode, where users freely explore task without penalties; and (iii) time restrictions for completion of tasks. Despite the many interrelationships between traditional learning and games, the main content of the lessons is still in non-game form. This requires gamification—a conversion of non-gaming entities into gaming entities.
Gamification is one of the emerging learning paradigms that is gaining popularity. It has been successfully applied at different levels and subjects in education equally or in combination with traditional teaching methods. A systematic review of gamification is presented in Reference [
1], while a systematic mapping study can be found in Reference [
2]. A comprehensive study for gamification in Science, Technology, Engineering, and Mathematics (STEM) learning is presented by Kim et al. [
3]. Although the application of gamification in STEM courses seems straight forward, there are several examples of how technology dominates and lacks important pedagogical aspects. Researchers and educators provide examples of successful application of gamification in STEM university courses covering a wide range of topics, such as fundamental computer programming courses with gamification [
4] or online frameworks [
5], C–programming [
6], Software Engineering [
7], Computer Organization [
8], and some more specialized advanced courses in the computer science curricula like Computer Graphics with WebGL [
9], Game Development [
10], Emerging Technology of Cloud Computing [
8]. In this article we present software, developed by us, which is used by Computer Sciences (CS) students learning Computer Graphics. Apart from programming and mathematics, such learning requires many artistic activities, like working with colours, managing proportions, building virtual scenes, defining natural-looking motion and so on. Thus we consider our software and our approach not just STEM-oriented, but also Science, Technology, Engineering, the Arts and Mathematics (STEAM)-oriented.
Learning outcomes and student needs are the key in effective learning through gamification. It is also important to take into account the specific aspects of the subject being taught. The authors of Reference [
11] explore different types of issues encountered while applying gamification. Based on their analyses, they propose various heuristics regarding the characteristics of the target audience, the contextual requirements, the design and the properties of the system.
Student engagement, motivation and active participation play a central role in such courses. The study in Reference [
12] shows the gamification impact can vary depending on the types of student motivation. One of the most effective ways of learning is through the engagement and active participation of students in the perception and understanding of the nature of the learning material. A comparative analysis of traditional and active learning confirms this hypothesis [
13], the results of which are based on a meta-analysis of a large body of research on student learning in STEM courses. Alongside with gamification, some other commonly used methods for active learning are Instruction-Based Learning (IBL), PBL and learning by doing.
Based on a literature review and our yearslong experience in teaching we formulated a working hypothesis that gamification evaluation can be improved by dynamic evaluation of all steps during the whole timespan of the gameplay. The formal description of this type of gamification evaluation inspired us to develop a new student evaluation methodology. It is used as a basis for designing and implementing software and evaluation tools. End-user tests are conducted with different cohorts of students. The quantitative methods (e.g., surveys) for assessment are used for measuring the efficiency and feasibility of the proposed gamified evaluation.
Although Game-Based Learning could be implemented in university-level education by mere technologisation of the educational content, this article focuses on using technology for student evaluation in a gamified educational environment and proposes a new evaluation method. We want to capture and automatically evaluate streaming scores generated by students as they explore educational content. This provides new challenges, which do not appear in the traditional evaluation.
Our gaming environment consists of several interactive 3D models that evaluate a set of 17 competences related to Computer Graphics—this is our initial test-bed environment. If the proposed gaming evaluation provides acceptable results, then it will be linked to the existing Learning Management System (LMS) and it will be applied to several disciplines, taught at Sofia University.
This article is structured as follows—
Section 2 describes the main characteristics of the evaluation in gamification;
Section 3 outlines the methodology, describes the implementation of the gamified evaluation system, defines the student competences profiles and the formal model for aggregation of streaming scores;
Section 4 presents the design concept of the 3D models and details about some of them;
Section 5 discusses some of the preliminary results of the end-user tests conducted with students;
Section 6 summarizes the presented evaluation method and the virtual models and briefly sketches plans for further work.
4. Virtual Models
This section presents the overall design concepts of the models with respect to their visual appearance, interaction with the user and the major pedagogical properties. Five of the models are described, including primary information about what they do and how they support the gameplay.
4.4. The Cohen-Sutherland’s Thimble
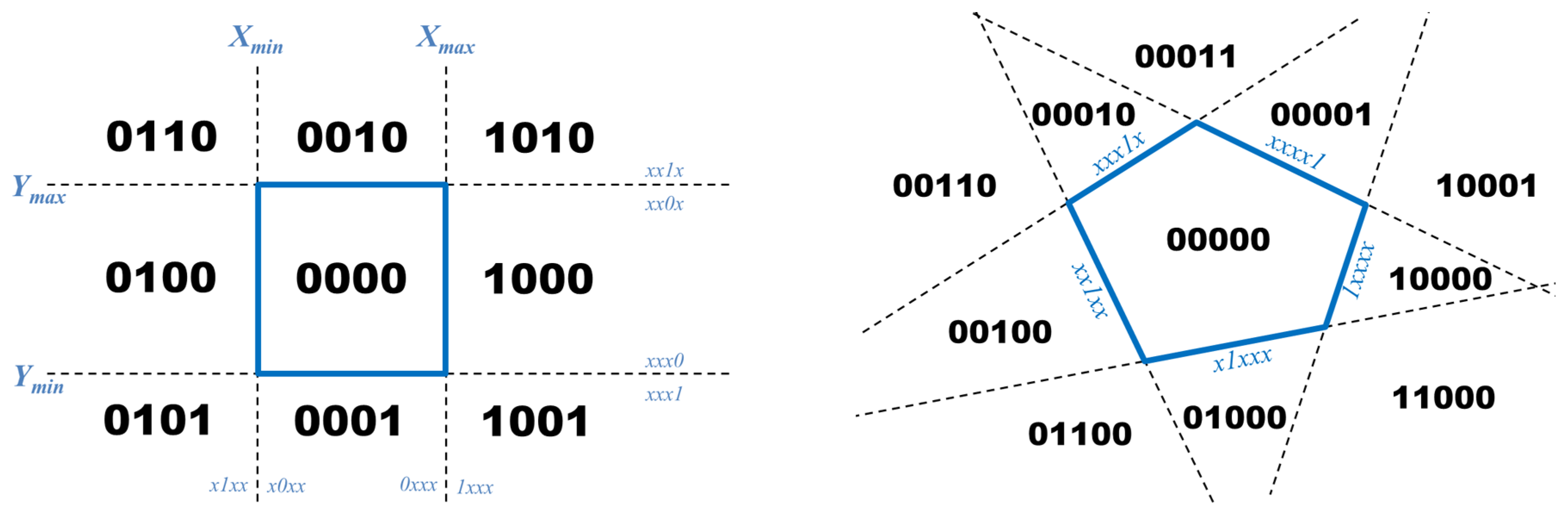
One of the fundamental operations in computer graphics is line clipping. This operation removes the portions of a segment, which are outside a rectangular viewport or window. In 1967 Danny Cohen and Ivan Sutherland developed an algorithm that splits the plane into nine areas by the lines that frame the viewport. Each area gets a bitmask code depending on its position in respect to the framing lines. The central area corresponds to the viewport, where lines are visible, and its bitmask code is always 0000, while the bitmasks of the other areas depend on the mapping between the framing lines and the bit positions in the bitmask.
The left image in
Figure 11 represents one possible assignment of bitmasks. The framing lines are labeled
,
,
and
. The left-most bit of the bitmask is associated with the
line. As a result, all areas to the left of this line (i.e.,
) get bitmasks 0xxx, and areas to the right—1xxx.
The Cohen-Sutherland algorithm uses these bitmask codes to quickly identify cases when a line is completely visible or completely invisible. In such cases the intersection with the framing lines is not performed. In all other cases, the algorithm uses the codes to identify how to clip a line, so that one of the branches can be eliminated right away.
The original Cohen-Sutherland algorithm for line clipping uses rectangular clipping areas. The algorithm could be extended for convex non-rectangular viewports by using bitmasks with length equal to the number of sides of the viewport polygon. The right illustration in
Figure 11 is an example of a pentagonal viewport and some of its 5-bit bitmasks.
This extended case is transformed into a more complex visual representation in the 3D model named Cohen-Sutherland’s thimble. The lines are represented as arcs, and the plane is shrunk into a circle.
Figure 12 shows a snapshot of the thimble from the outside. For some of the areas there are bitmasks attached to the external surface of the thimble. The problem is to calculate the bitmask represented as empty panels.
The first issue, which students face when they try to solve the model, is the layout of areas. A top view of the model reveals the interior with the arcs, splitting the circle into areas.
Figure 13 shows several configurations—the left-most one has two arcs forming 4 areas; while the right-most one has 5 arcs forming 13 areas. The curved areas and the lack of central area force the students to invent their own extension of the algorithm.
Several clues support the solving process, some of them could be observed visually, while others can be deduced by reasoning. For example, a visual clue is the mapping between arcs and bit positions. Bumps correspond to vertical positions, which are bound to bit positions in the masks. A non-visual clue is a property, which can be extracted from the bitmask code assignment in the original Cohen-Sutherland algorithm. Namely, the bitmask codes of two neighbouring areas differ by the value of exactly one bit and the position of this bit corresponds to the arc, separating the two areas.
Like all other models, the Cohen-Sutherland’s thimble is related to some practical knowledge of the original algorithm, it requires research and investigation efforts of extending ideas into non-traditional layouts. It utilizes some graphical skills like mapping perspective view of arcs in the interior onto the linear relative positions of bit labels on the outside of the thimble. The right-most snapshot in
Figure 13 is an illustration that challenges this particular graphical skill—finding the correct order of arcs requires a good depth perception.
4.5. The Matrix Carousel
There are three approaches to expressing animation in Computer Graphics. The descriptive approach defines explicitly the values of properties. For example, an object motion along a path is defined by a sequence of coordinates. In some cases it is easier to use the differential approach in which motion is expressed as differences between a frame and its previous frame. Internally, both of these approaches are implemented as the transformational approach that transforms coordinates and other values by matrix multiplication. Matrices can be used to implement translation, scaling, rotation, mirroring, and projection. They are widely used in Computer Graphics, because they:
provide a unified way to represent various transformations—they are all expressed as matrices;
allow packing several transformations into a single matrix by multiplying matrices in advance;
control working in local or global coordinate systems by premultiplication or postmultiplication;
support nested transformations by using a matrix stack;
are fast to compute as there is hardware support for matrix operations in GPUs and shader languages.
Although the matrix content easily becomes very complex, transformations are usually expressed in terms of basic transformations for which the matrices are simple—they are slight modifications of the identity matrix.
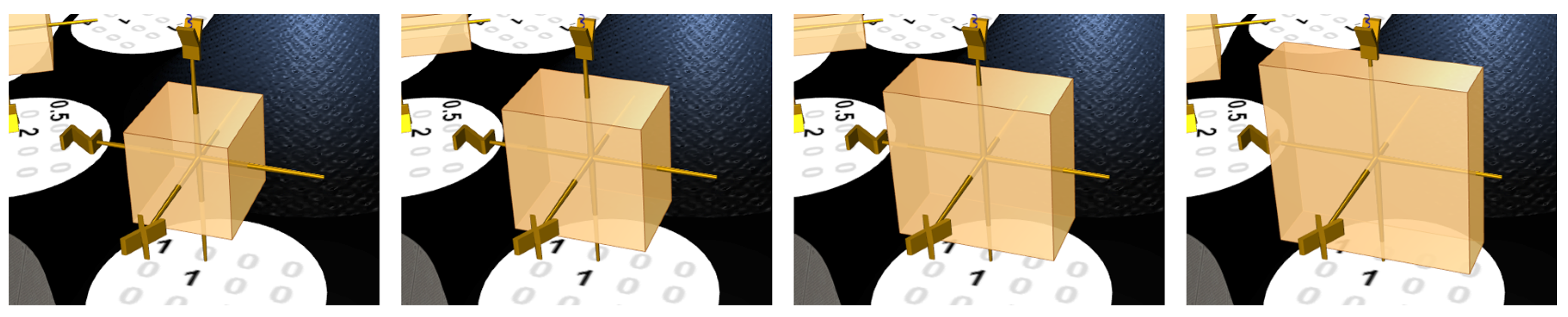
We developed the Matrix carousel model as a tool for the students to explore the basic matrices and to map them to various graphical transformations. The model shows several coordinate systems riding a carousel—
Figure 14. Each coordinate system represents a specific matrix transformation. There are matrices painted on the floor of the carousel. The student plays the model by spinning the carousel and stopping it so that each coordinate system is above the matrix, corresponding to the transformation.
A design challenge in this model is the graphical representation of matrix transformations. We solve the challenge by placing unit cubes in each coordinate system. These cubes are continuously transformed via the transformation of the coordinate system—
Figure 15.
This representation of transformations is intuitive, but it forces some discrepancy between animations and painted matrices. The animation shows small steps, which accumulated produce the same result as the matrix. For example, the rotation matrix defines a rotation around one of the axes, while its animation shows the initial cube for 1 s, then for 4 s smoothly rotates it to and finally waits for another second before starting over. The gradual transformation of the cube is done by applying a matrix that is generated by linear interpolation of the identity matrix and the desired matrix.
Depending on the selected level of difficulty, the model is generated with a set of randomly selected types of matrices. These are a few of the 70 matrix transformations, used in the model: a translation matrix
T, a scaling matrix
S, a rotation matrix
R and a perspective projection matrix
P:
Another option to fine-tune the difficulty is the orientation of the coordinate system. Students are accustomed to specific orientations of coordinate systems. For example, in a 2D Cartesian coordinate system the axis points to the right and the axis points upwards. When the model is generated, each coordinate system is randomly rotated in one of the 24 possible orientations— could point up, down, left, right, front, back and for each of these orientations, there are 4 possibilities for and .
5. Preliminary Results
This section presents the preliminary results from testing the models with our FMI students. Further analyses are needed to extract all information from the tests.
The 3D models described in the previous section will be used as 3D models in Meiro for students’ evaluation and assessment. The target course is Fundamentals of Computer Graphics, which is compulsory for second-year Computer Sciences students at the Faculty of Mathematics and Informatics, Sofia University. The number of enrolled students varies between 130 and 180 each year.
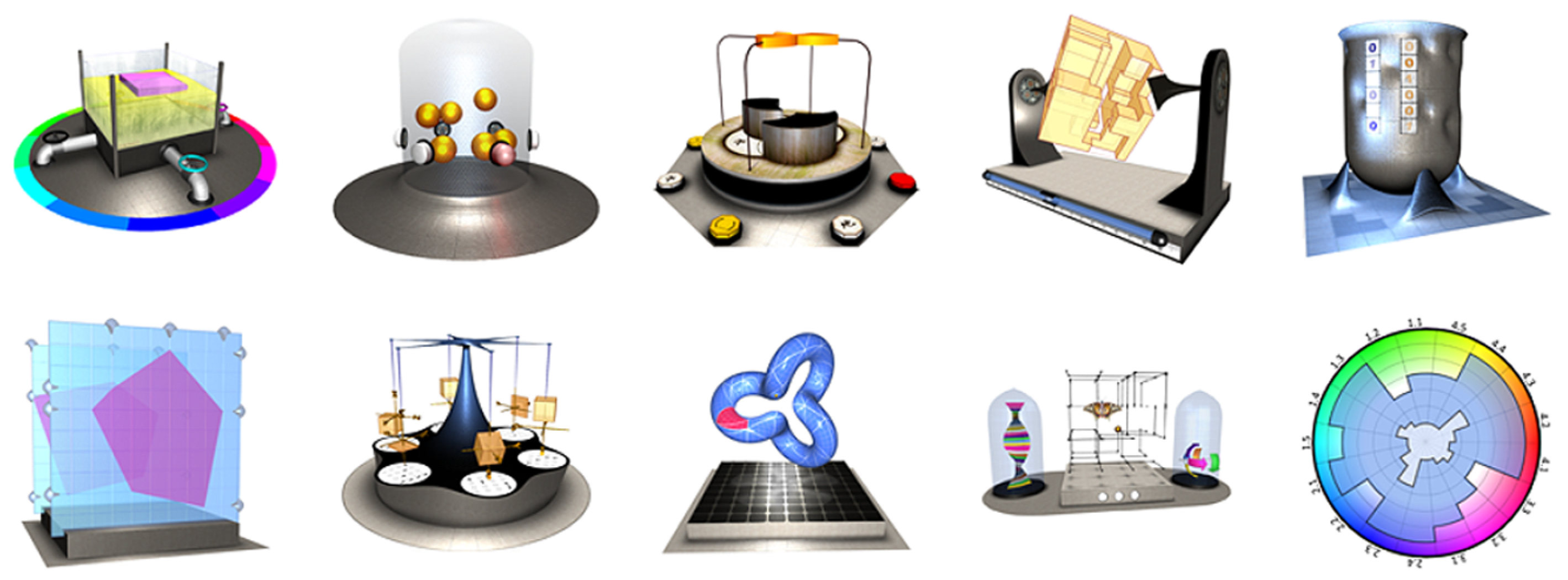
The ten developed models, shown in
Figure 7, have been packed in a test suite open to 151 students from December 2019 until mid-January 2020. The students had to play with the models and report any positive and negative observations. This end-user testing was completely voluntary, but students get a bonus for their participation. The achieved scores by playing with the models did not affect the bonus, thus students were free from test fright.
Two types of data were collected during these tests—automatically collected data, containing general statistics of each student’s gameplay, and a survey where students describe their observations and comments.
5.1. Automatically Collected Data
The gameplay of each model sends data back to the server where it is processed and stored in log files. In order to minimize the volume of these data, game data are sent only at the start and at the end of playing a model.
Table 2 lists the log data when a model is closed. The parameter SCORE is the score, achieved by the student. This value is multiplied by the competence scores of the model and the result is stored in COMPETENCES, which a vectored score containing a score for each of the 17 competences in
Table 1.
There is a separate log file for each student. The data from these logs files are used to identify the engagement of each student. A part of the bonus for the students is calculated on the aggregated data from the logs. In real tests, the log files may indicate the skill of students. For example, if a model is solved by using too many clicks, most likely it is solved by trial and error. It is yet to be analyzed whether there is a need to capture more log data or to distinguish navigational clicks (i.e., when the students rotate the model or zoom in or out) from operational clicks (i.e., when the students turn on or off parts of the model).
The other important purpose of the log files is to capture possible cheats and hack attempts. Because students have access to the source code, they might find a way to calculate the correct answer (by a script) instead of solving the problem. Such attempts could be captured if the score, the time and the clicks do not match. For example, solving the model with 0 clicks is an indication of such cheating.
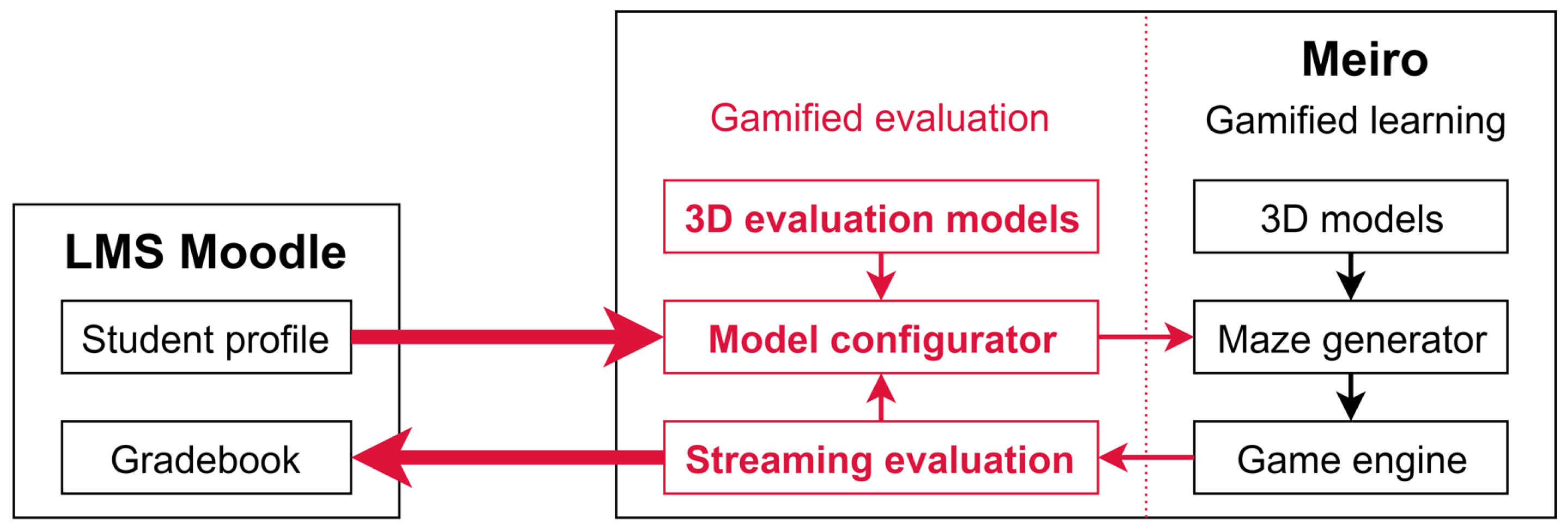
The models are accessed through the Moodle LMS. Students log-in into Moodle and then Moodle sends data to the Extended Meiro—
Figure 3. Thus, Meiro “knows” who is playing with the 3D models. However, some students accessed Meiro directly in an attempt to bypass Moodle and logging. Meiro captures these attempts and creates the log files as if it were anonymous users. Such hacking during the tests reduces the bonus of the students, as their gameplay activity is left anonymous. Using the same technique during the actual evaluation tests has no benefit, because students will have access to the test for the whole semester, so they can experiment as long as they want. The temporal average score will reduce the impact of their initial attempts to almost 0, thus the self-testing will not affect the actual testing.
During the end-user tests we observed some attempts of hard hacking—bypassing not only Moodle, but also Meiro and sending directly data packages to the evaluation generator. All such attempts were successfully captured, because the log data were malformated or incomplete—they lack the session identification data, exchanged between Moodle and Meiro.
Totally, the log files recorded 186 users playing with the 3D models, 121 of them were via Moodle and the rest 65 were anonymous.
Table 3 presents general statistical information. On average a logged-in student spent about 3 h playing 150 times with the models.
The last row in
Table 3 represents the number of incomplete records. These are log records, which are incomplete either because the students closed the browser window before the models managed to send back the data; or because of hacking attempts.
Future studies of the log data may analyze these parameters with respect to the models, thus identifying what model requires more time, clicks and taps, what models are easier to get high scores, and so forth.
5.2. Students’ Survey
In addition to logging end-user tests, we conducted a simple survey, where students expressed in a free form their observations about the models. The survey contained 10 questions (one for each of the 10 models) of the same pattern: “Describe in a free form your experience with the model. What did you like or did not like about it with respect to visual appearance, implementation, gameplay, difficulty and evaluation?” The survey included an upload form, so that students may attach images if they need to illustrate a problem.
The survey was implemented as a quiz activity in Moodle. It was available only to logged-in students. The evaluation was based on the completeness and importance of provided answers, rather than on whether they are positive or negative.
Every semester the students at Faculty of Mathematics and Informatics, Sofia University, fill anonymous optional surveys about their courses. These surveys are used for quality assessment of the educational activities. The average participation rate for the course Fundamentals of Computer Graphics was 22% in 2017, 16% in 2018 and 13% in 2019. As the survey about the 3D models was also optional, but not anonymous, we did expect that just a few students will complete it. To our surprise, we received 125 filled surveys about the 3D models, which is 83% student’s activity.
Table 4 shows general data about the survey answers. Model 1 is the CMY reservoir, model 4 is the Euler’s grill, model 5 is the Cohen-Sutherland’s thimble and model 7 is the Matrix carousel.
In total, we received 794 comments of 34 k words worth 68 pages of text. This prompted us to try Natural Language Processing methods to analyze the text using different methods for sentiment analysis. The results show that only a small proportion of students used more expressive opinions and the majority used neutral vocabulary. In general, positives for all models prevail.
The survey was configured in a way that all answers are open for edits during the whole end-user test period, thus students could use the survey as a memo and update their answers as much as they need. The students actively used this option—for example, the CMY Reservoir got 91 answers, that were edited 104 times.
The main expectations of the survey were to get answers to four questions and more or less we got all of them answered. The questions are:
Are there any technical issues with using mobile devices?
Are there any difficulties caused by the user interface?
Are gaming evaluations suitable for university students?
Are there any suggestions for improvement of the models?
We asked the students to test the models with their personal computers and mobile devices (usually smartphones). The goal was to find whether the technology, used in the models (mobile 3D graphics) works well on students’ devices of various hardware and software configurations. Only a few problems were reported, mostly related to the initial configuration of the devices.
As for the user interface, we got some really nice suggestions for improvement. Currently, the models inherit the orbiting navigational mode from the Meiro maze—that is, the model is always in the center of the screen and the player orbits around it and zooms in or out. According to survey answers, students would prefer a free navigational mode, which would allow getting closer to specific areas of the model, not necessarily its center. This would help users of smartphones, which screen area is relatively small.
The majority of answers clearly expressed students’ enthusiasm for using a 3D gaming environment instead of traditional quiz-shaped tests. Of course, different students liked different aspects of the models—some liked the visual appearance, others liked the sound effects, and there were students, who liked how academic content is transformed into something that could be played.
Valuable elements of students’ answers are their ideas of modifications. Students suggested some improvements of the models with respect to the user interface or the evaluation scheme. For example, they wanted more control over the camera, clearer identification of interactive elements and better support for touch screens. As for the evaluation, they would like to have a better understanding of the temporal average, as it is a new scoring technique for them and they are not accustomed to it.
During the test period we opened an online forum for all students. We asked them to share their experience that could help the other students to work with the models. The reason for this was that we gave the models to the students with very limited information and guideline. We asked them to explore the models and find by themselves what do they do and how to operate them. Thus this forum acted as mutual aid for the students.
We also encouraged them to share tricks. Some of the students’ findings are particularly helpful for the future development of the models. For example, the students found a problem with the Matrix carousel. The easier configuration of the carousel used easier matrices (like translation and scaling). However, the most difficult configuration used a mixture of all matrix types …and this actually made the solving much easier. Students suggested the following trick—find the easiest matrix and match it to the coordinate system. Then all the other matrices will naturally match.
A further detailed study is needed to analyze the impact on computer graphics soft skills—these are skills, which are not explicitly taught in the course, but nevertheless, they are essential for the domain. Well developed soft skills could make solving the 3D models much easier. This is the reason we deliberately added some modifications in the models, so that to enforce the development of soft skills as a side effect of solving computer graphics problems. As expected, some students treated these modifications as disadvantages in the models. Some of the computer graphics soft skills and their implementation in the models are listed in
Table 5.
Author Contributions
Conceptualization, P.B. and S.B.; methodology, P.B.; software, P.B.; validation, P.B. and S.B.; formal analysis, S.B.; investigation, P.B. and S.B.; resources, P.B.; data curation, P.B.; writing—original draft preparation, P.B. and S.B.; visualization, P.B.; supervision, P.B.; project administration, P.B.; funding acquisition, P.B. All authors have read and agreed to the published version of the manuscript.
Funding
The research is partially funded by Sofia University “St. Kliment Ohridski” Research Science Fund project N80-10-18/18.03.2020 “Use of high-tech tools for development of competency models in training” and by the National Scientific Program “Information and Communication Technologies in Science, Education and Security” (ICTinSES) financed by the Ministry of Education and Science.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CMY | Cyan, magenta, yellow |
| CS | Computer Sciences |
| FCG | Fundamentals of Computer Graphics |
| FMI | Faculty of Mathematics and Informatics |
| GBL | Game-Based Learning |
| GPU | Graphical Processing Unit |
| IBL | Instruction-Based Learning |
| LMS | Learning Management System |
| PBL | Project-Based Learning |
| STEAM | Science, Technology, Engineering, the Arts and Mathematics |
| STEM | Science, Technology, Engineering and Mathematics |
| WebGL | Web Graphics Library |
References
- Ortiz Rojas, M.E.; Chiluiza, K.; Valcke, M. Gamification in higher education and stem: A systematic review of literature. In Proceedings of the 8th International Conference on Education and New Learning Technologies (EDULEARN), Barcelona, Spain, 4–6 July 2016; IATED—International Academy of Technology, Education and Development: Valencia, Spain, 2016; pp. 6548–6558. [Google Scholar]
- Dicheva, D.; Dichev, C.; Agre, G.; Angelova, G. Gamification in Education: A Systematic Mapping Study. J. Educ. Technol. Soc. 2015, 18, 75–88. [Google Scholar]
- Kim, S.; Song, K.; Lockee, B.; Burton, J. Gamification Cases in Education. In Gamification in Learning and Education; Springer: Berlin, Germany, 2018; pp. 117–123. [Google Scholar]
- Fotaris, P.; Mastoras, T.; Leinfellner, R.; Rosunally, Y. Climbing up the Leaderboard: An Empirical Study of Applying Gamification Techniques to a Computer Programming Class. Electron. J. E-Learn. 2016, 14, 94–110. [Google Scholar]
- Piteira, M.; Costa, C.J. Gamification: Conceptual framework to online courses of learning computer programming. In Proceedings of the 2017 12th Iberian Conference on Information Systems and Technologies (CISTI), Lisbon, Portugal, 14–17 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Ibáñez, M.B.; Di-Serio, A.; Delgado-Kloos, C. Gamification for engaging computer science students in learning activities: A case study. IEEE Trans. Learn. Technol. 2014, 7, 291–301. [Google Scholar] [CrossRef]
- de Almeida Souza, M.R.; Constantino, K.F.; Veado, L.F.; Figueiredo, E.M.L. Gamification in software engineering education: An empirical study. In Proceedings of the 2017 IEEE 30th Conference on Software Engineering Education and Training (CSEE&T), Savannah, GA, USA, 7–9 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 276–284. [Google Scholar]
- Iosup, A.; Epema, D. An experience report on using gamification in technical higher education. In Proceedings of the 45th ACM Technical Symposium on Computer Science Education, Atlanta, GA, USA, 5–8 March 2014; ACM: New York, NY, USA, 2014; pp. 27–32. [Google Scholar]
- Villagrasa, S.; Duran, J. Gamification for learning 3D computer graphics arts. In Proceedings of the First International Conference on Technological Ecosystem for Enhancing Multiculturality, Salamanca, Spain, 14–15 November 2013; ACM: New York, NY, USA, 2013; pp. 429–433. [Google Scholar]
- O’Donovan, S.; Gain, J.; Marais, P. A case study in the gamification of a university-level games development course. In Proceedings of the South African Institute for Computer Scientists and Information Technologists Conference; ACM: New York, NY, USA, 2013; pp. 242–251. [Google Scholar]
- van Roy, R.; Zaman, B. Why gamification fails in education and how to make it successful: Introducing nine gamification heuristics based on self-determination theory. In Serious Games and Edutainment Applications; Springer: Berlin, Germany, 2017; pp. 485–509. [Google Scholar]
- Buckley, P.; Doyle, E. Gamification and student motivation. Interact. Learn. Environ. 2016, 24, 1162–1175. [Google Scholar] [CrossRef]
- Freeman, S.; Eddy, S.L.; McDonough, M.; Smith, M.K.; Okoroafor, N.; Jordt, H.; Wenderoth, M.P. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef] [PubMed]
- Hamari, J.; Eranti, V. Framework for Designing and Evaluating Game Achievements. In Proceedings of the 2011 Digra Conference, Hilversum, The Netherlands, 14–17 September 2011. [Google Scholar]
- Heilbrunn, B.; Herzig, P.; Schill, A. Tools for gamification analytics: A survey. In Proceedings of the 2014 IEEE/ACM 7th International Conference on Utility and Cloud Computing, London, UK, 8–11 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 603–608. [Google Scholar]
- Menezes, C.C.N.; Bortoli, R.d. Potential of gamification as assessment tool. Creat. Educ. 2016, 7, 561–566. [Google Scholar] [CrossRef]
- Gañán, D.; Caballé, S.; Clarisó, R.; Conesa, J.; Bañeres, D. ICT-FLAG: A web-based e-assessment platform featuring learning analytics and gamification. Int. J. Web Inf. Syst. 2017, 13, 25–54. [Google Scholar] [CrossRef]
- Zichermann, G.; Cunningham, C. Gamification by Design: Implementing Game Mechanics in Web and Mobile Apps; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2011. [Google Scholar]
- Winnicka, A.; Kȩsik, K.; Połap, D.; Woźniak, M.; Marszałek, Z. A Multi–Agent Gamification System for Managing Smart Homes. Sensors 2019, 19, 1249. [Google Scholar] [CrossRef] [PubMed]
- Boytchev, P.; Boytcheva, S. Evaluation and assessment in TEL courses. AIP Conf. Proc. 2018, 2048, 020035. [Google Scholar]
- Boytchev, P.; Boytcheva, S. Gamified Evaluation in STEAM. In International Conference on Information and Software Technologies; Springer: Berlin, Germany, 2019; pp. 369–382. [Google Scholar]
Figure 1.
Project-Based Learning and Game-Based Learning approaches.
Figure 2.
Examples of 3D models in Meiro—central projection (left) and multilayered objects (right).
Figure 3.
Extending Meiro to support gamified evaluation.
Figure 4.
Two examples of radar diagrams representing competence profiles.
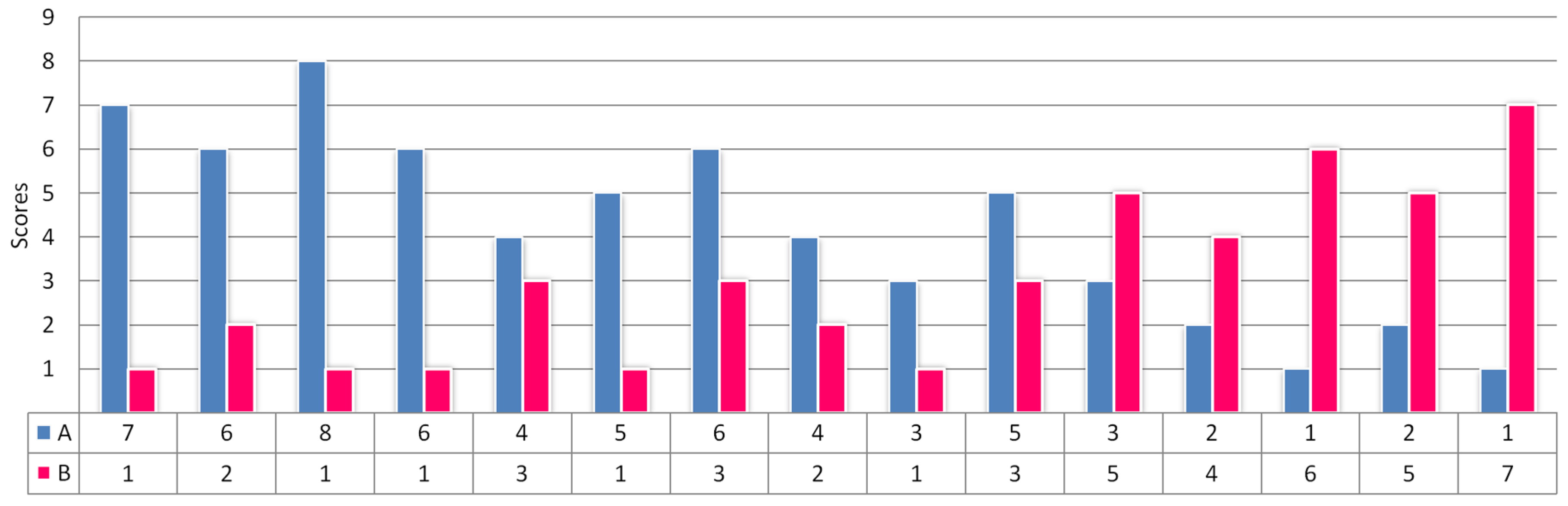
Figure 5.
Scores of students A and B along 15 week semester.
Figure 6.
Blending evaluation and assessment.
Figure 7.
Gallery of developed models.
Figure 8.
A snapshot of the CMY reservoir (left) and disappearing plate reaching a solution (right).
Figure 9.
The cube (left), the dodecahedron (center) and the icosahedron (right) all have .
Figure 10.
A snapshot of the Euler’s grill (left) and examples of different topological complexities (right).
Figure 11.
Bitmasks of the nine areas defined by the framing lines (left), extended approach to convex non-rectangular area with only some of the masks shown (right).
Figure 12.
Snapshots of the Cohen-Sutherland’s thimble.
Figure 13.
Randomly generated interiors with various degrees of complexities.
Figure 14.
Snapshots of the Matrix carousel.
Figure 15.
Transformation of a cube.
Table 1.
Computer graphics competences.
| 1. Mathematics | 2. Computer Sciences | 3. Physics | 4. Art |
|---|
| 1.1. Math objects | 2.1. Rasterization | 3.1. Physics laws | 4.1. Colours |
| 1.2. Equations | 2.2. Geometrical data | 3.2. Simulations | 4.2. Shapes |
| 1.3. Parameters | 2.3. Animation | 3.3. Phenomena | 4.3. Orientation |
| 1.4. Relations | 2.4. Graphical objects | | 4.4. Synchronization |
| 1.5. Approximation | | | 4.5. Graphical effects |
Table 2.
Log data when a model is closed.
| Parameter | Description | Example |
|---|
| ACTION | Type of the log record | END |
| MODEL | Name of the 3D model | T001 |
| DIFFICULTY | Level of difficulty | 2 |
| MAX_SCORE | Maximal score | 0.9 |
| SCORE | Achieved score | 0.84 |
| TIME | Number of seconds | 38 |
| CLICKS | Number of clicks | 14 |
| COMPETENCES | Vectored score | 0.84, 0, 2.53, 0.84, 2.53, 0, 0.84, 0, 0, 0, 1.68, 0, 4.21, 0, 0.84, 0, 2.53 |
| IP | IP address | 188.254.xxx.xxx |
| TIMESTAMP | Local time | 2020-01-05 18:35:00 |
Table 3.
General statistical data retrieved from log files.
| Parameter | Logged-In | Anonymous | Total |
|---|
| Unique users | 121 | 65 | 186 |
| Models played | 17,663 | 1386 | 19,049 |
| Time played (hours) | 342 | 42 | 384 |
| Clicks and taps | 1,048,982 | 89,049 | 1,138,031 |
| Incomplete records | 1543 | 392 | 1935 |
Table 4.
General statistical data from the survey.
Table 5.
Some soft skills and their support in the models.
| Soft Skill | Examples |
|---|
| Seeing similarity of colours | Model 1 (The CMY reservoir) does not provide a numeric representation of the current liquid ink proportions, so students may only inspect the colour visually. |
| Estimating positions in space | Model 8 (The Loop’s torus) requires the students to calculate or guess positions on a curved surface without a detailed coordinate grid to guide them. |
| Using non-visual senses | In model 6 (the Pick’s polygon) students may solve the problem more easily by listening to the sound effects—they resemble a Geiger counter depending on how accurate the solution is. |
| Motion synchronization | Model 2 (The Bouncing balls) requires the students to compare and identify differences in bouncing frequencies of several balls, that bounce at different time offsets. |
| Spacial memory | The interior and exterior of Model 5 (The Cohen-Sutherland’s thimble) cannot be seen at the same time, so students must alternate between two viewpoints and remember objects’ positions in space. |
| Chaining transformations | In model 9 (The flight of the butterfly) students construct a chain of geometrical transformations in order to define motion along a path—they do this by imagining the effect of the transformations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).