Ensemble-Based Online Machine Learning Algorithms for Network Intrusion Detection Systems Using Streaming Data
Abstract
1. Introduction
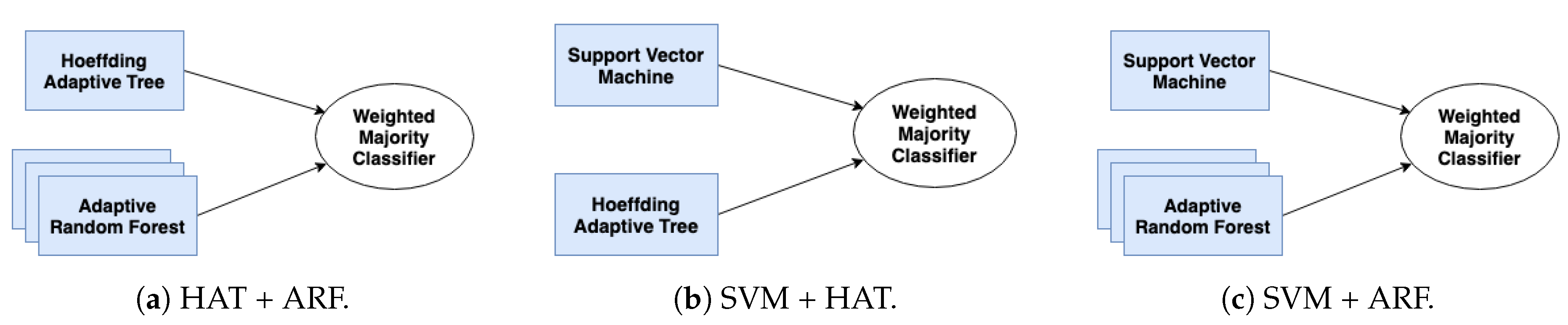
- We explore and compare several stand-alone detectors along with homogeneous and heterogeneous ensembles for malicious traffic detection using the KDDCup99 dataset [9]. Specifically, we investigate stand-alone detectors such as K-nearest neighbor (K-NN), Support Vector Machine (SVM), Hoeffding Adaptive Tree (HAT), and Adaptive Random Forest (ARF). In addition, we investigate homogeneous ensembles based on HAT and ARF. Finally, we propose three heterogeneous ensembles based on HAT + ARF, SVM + HAT, and SVM + ARF.
- We run experiments to investigate the performance of NIDS with streaming data involving multiple protocols, namely, 600,000 HTTP connections and 100,000 SMTP connections. We analyze both the accuracy and run-time of the aforementioned NIDS against these traffic types.
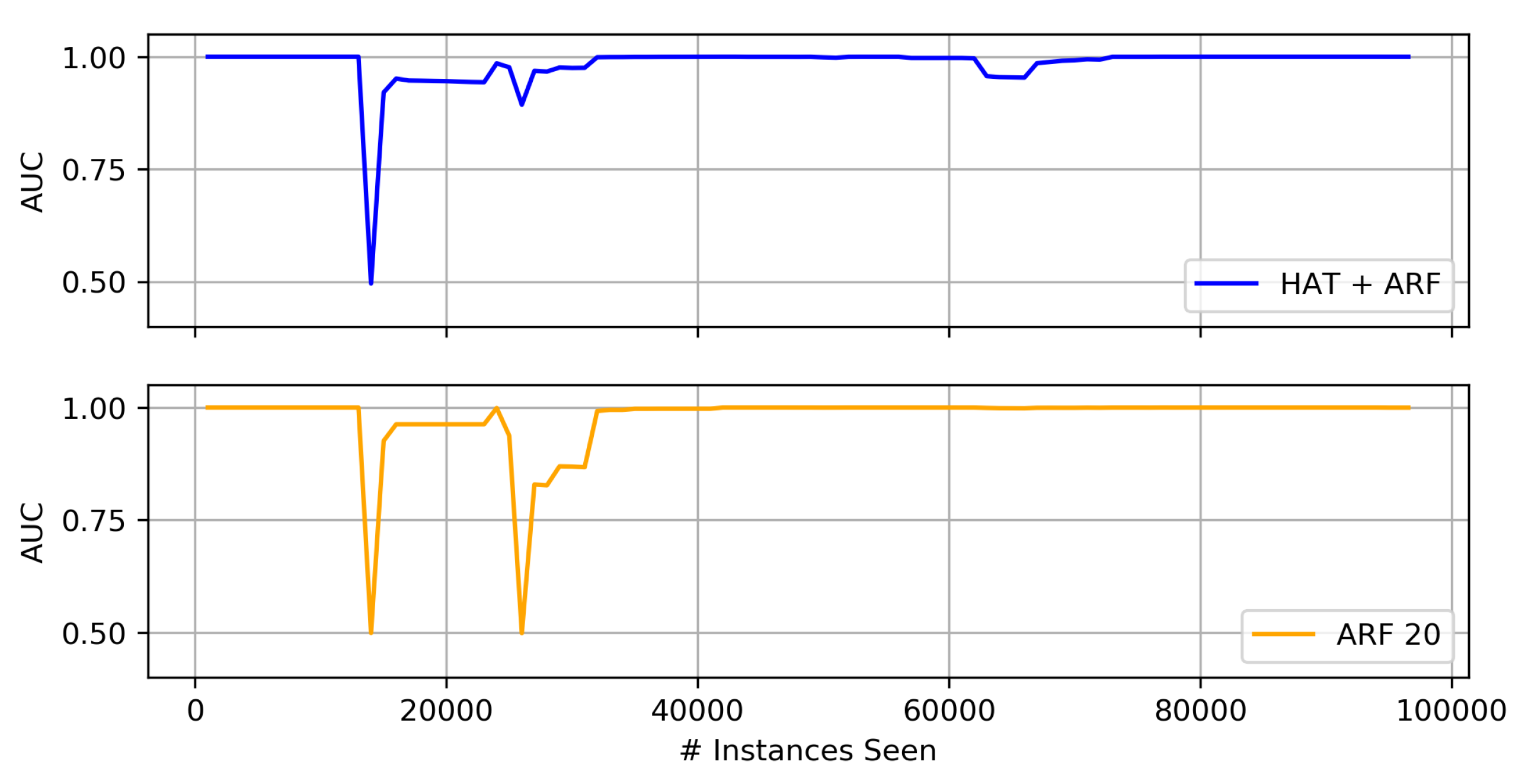
- We investigate the performance of the aforementioned NIDS when concept drift is considered. Through experimental results, we show that the heterogeneous ensemble of HAT + ARF handles concept drift better than the other detectors.
2. Related Work
3. Methodology
3.1. Data Preparation
3.2. Stand-Alone Algorithms
3.2.1. K-Nearest Neighbors
3.2.2. Support Vector Machines
3.2.3. Hoeffding Adaptive Trees
3.3. Homogeneous Ensembles: Adaptive Random Forests
3.4. Proposed Heterogeneous Ensembles
4. Experimental Results
4.1. Evaluation Metrics
4.2. Stand-Alone Models
4.3. Ensemble Algorithms
4.3.1. Accuracy and Run-Time Results
- While stand-alone models offer comparable accuracy results to ensemble models on HTTP and combined connections, ensemble models offer up to improvement in accuracy for SMTP connections. Such improvement is achieved, however, at the cost of increasing the run-time, roughly by three times (except for the K-NN model).
- Since the models presented in Table 1, Table 2 and Table 3 offer close accuracy performance, further experiments are required to investigate if the model’s performance might differ as we plot graphs of the AUC over time, which corresponds to the number of instances the algorithm has trained on. This is presented next.
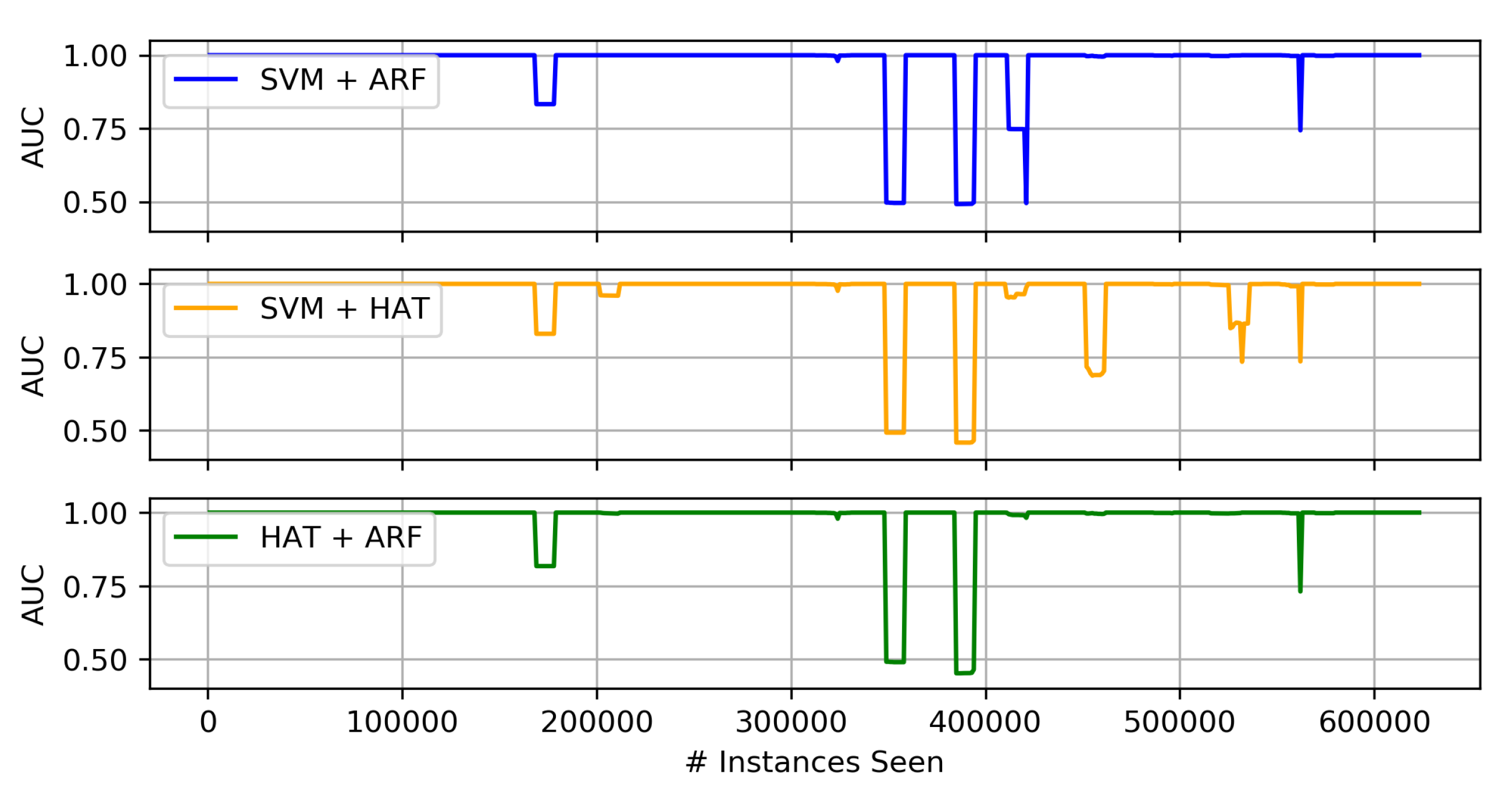
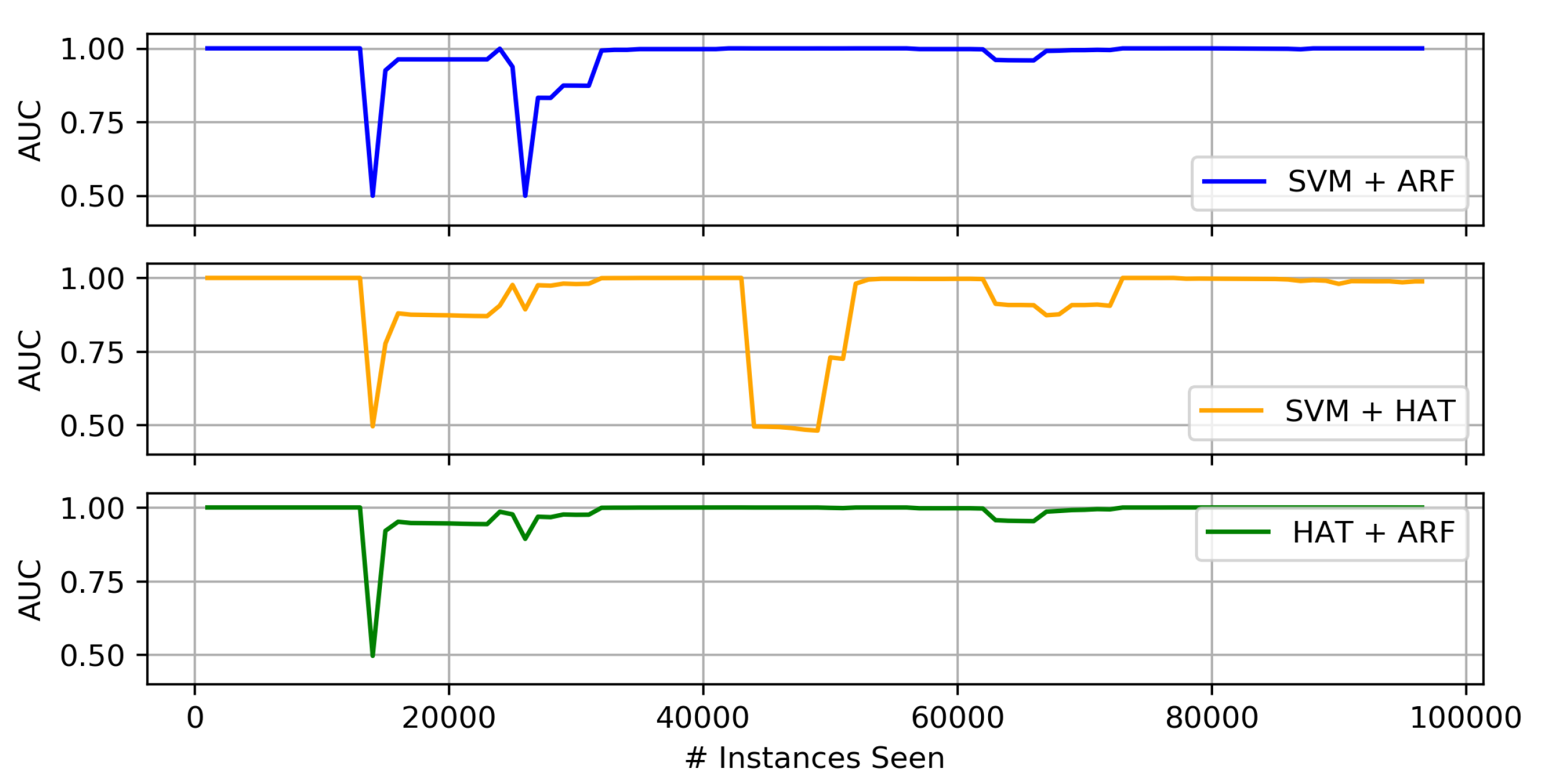
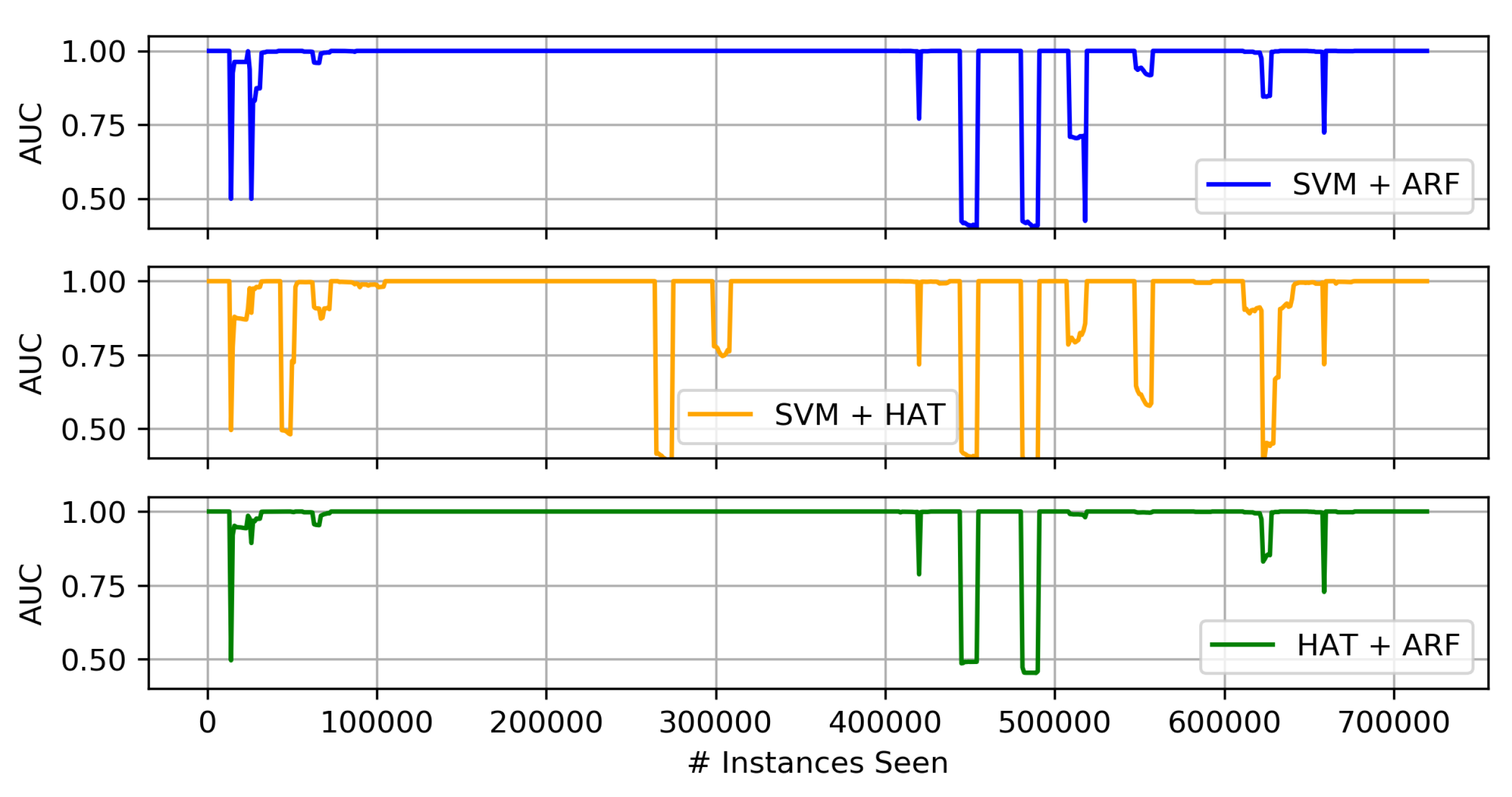
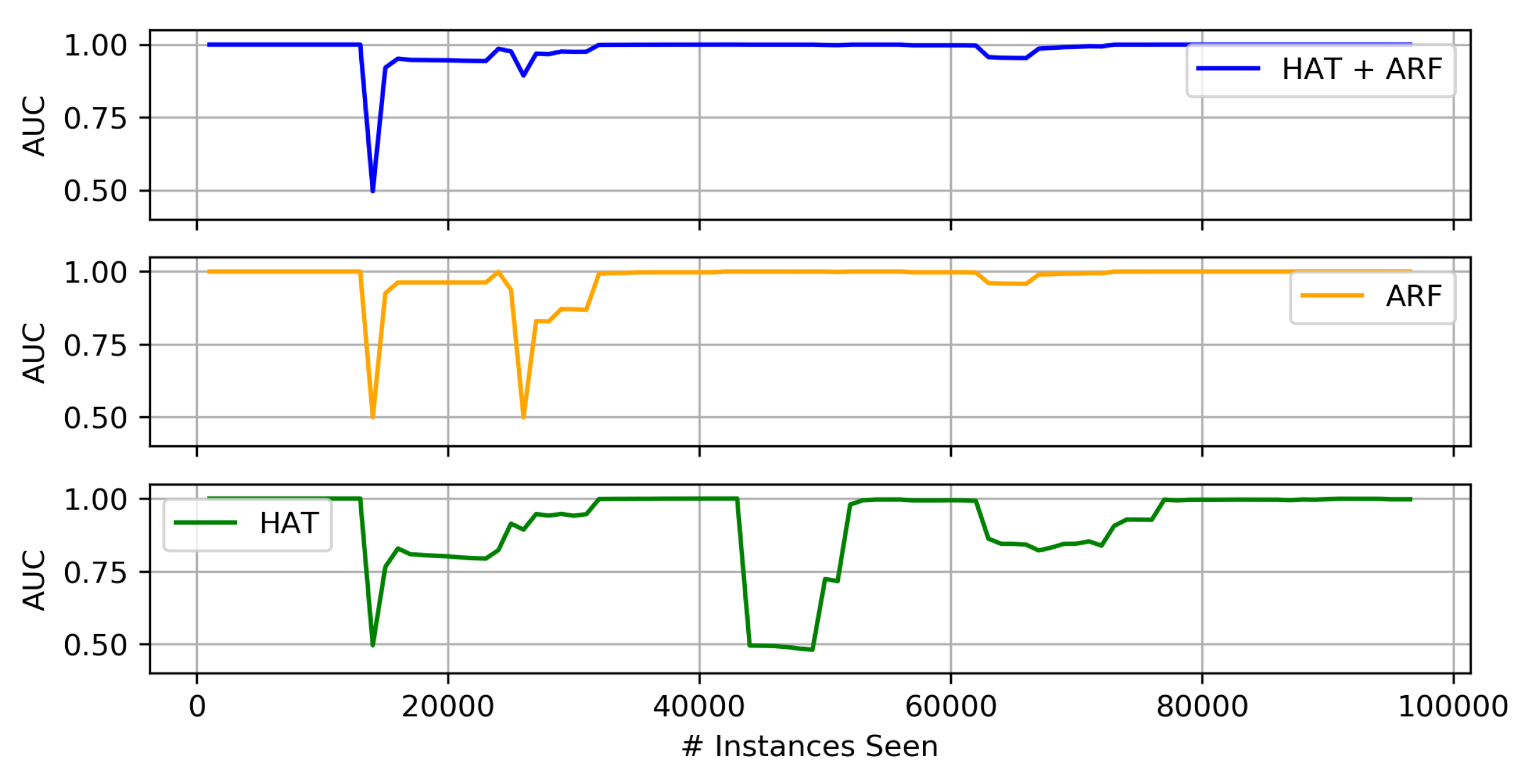
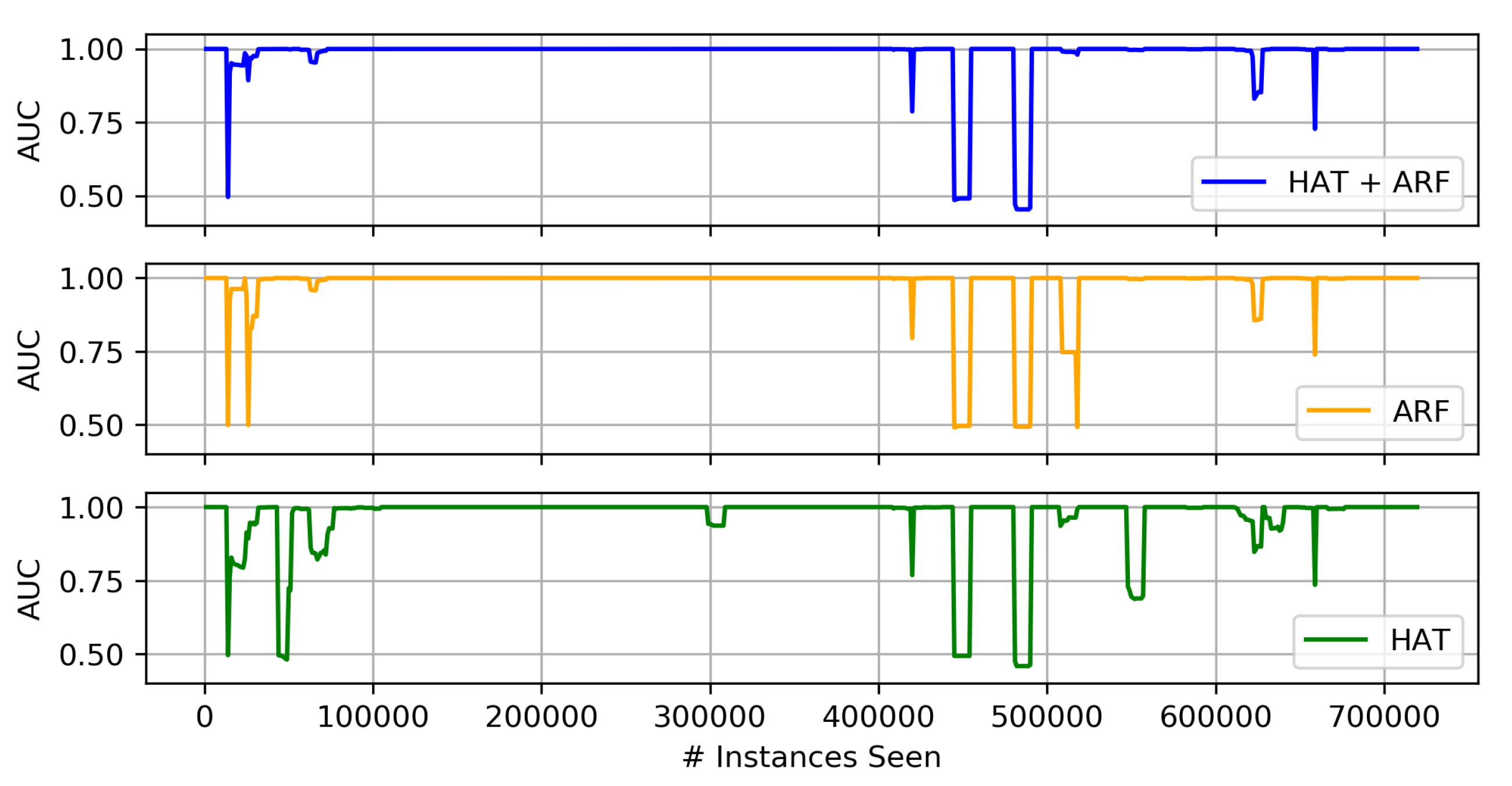
4.3.2. Concept Drift Results
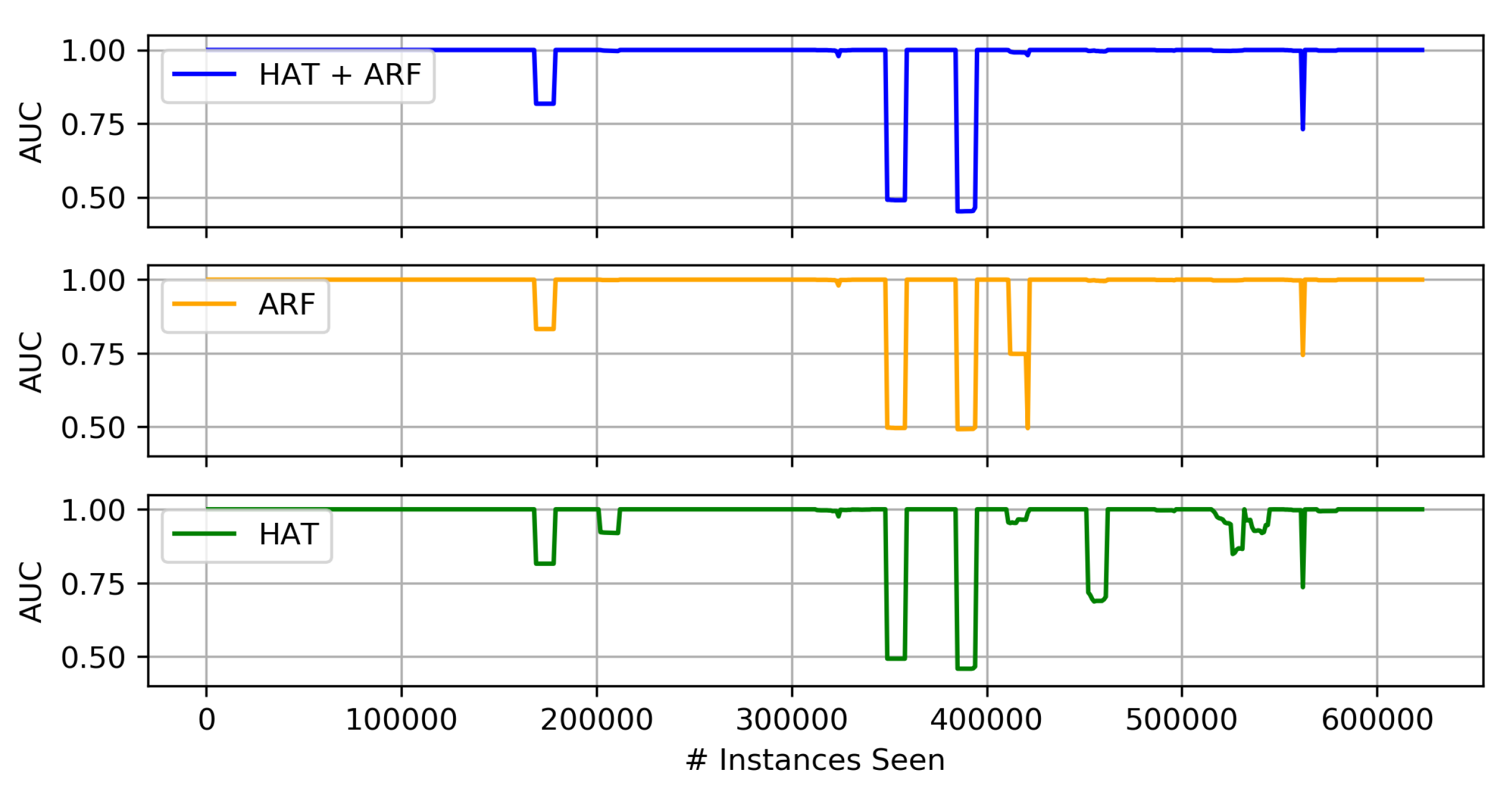
Comparison of Proposed Heterogeneous Ensembles
Comparison of Heterogeneous Ensembles and Their Individual Components
- Almost all of the ensemble techniques, both homogeneous and heterogeneous, lead to higher average AUC than the base (stand-alone) algorithms (i.e., decision trees, SVM, and K-NN). In most cases this comes with at least a slight cost in terms of run-time, and hence, computation resources.
- Of the three proposed heterogeneous ensembles, the HAT + ARF offers the highest accuracy performance. In particular, this approach is obviously better than the two individual algorithms (i.e., HAT and ARF) when looking at the AUC over time, where it recovers or sufficiently handles concept drift in the data stream.
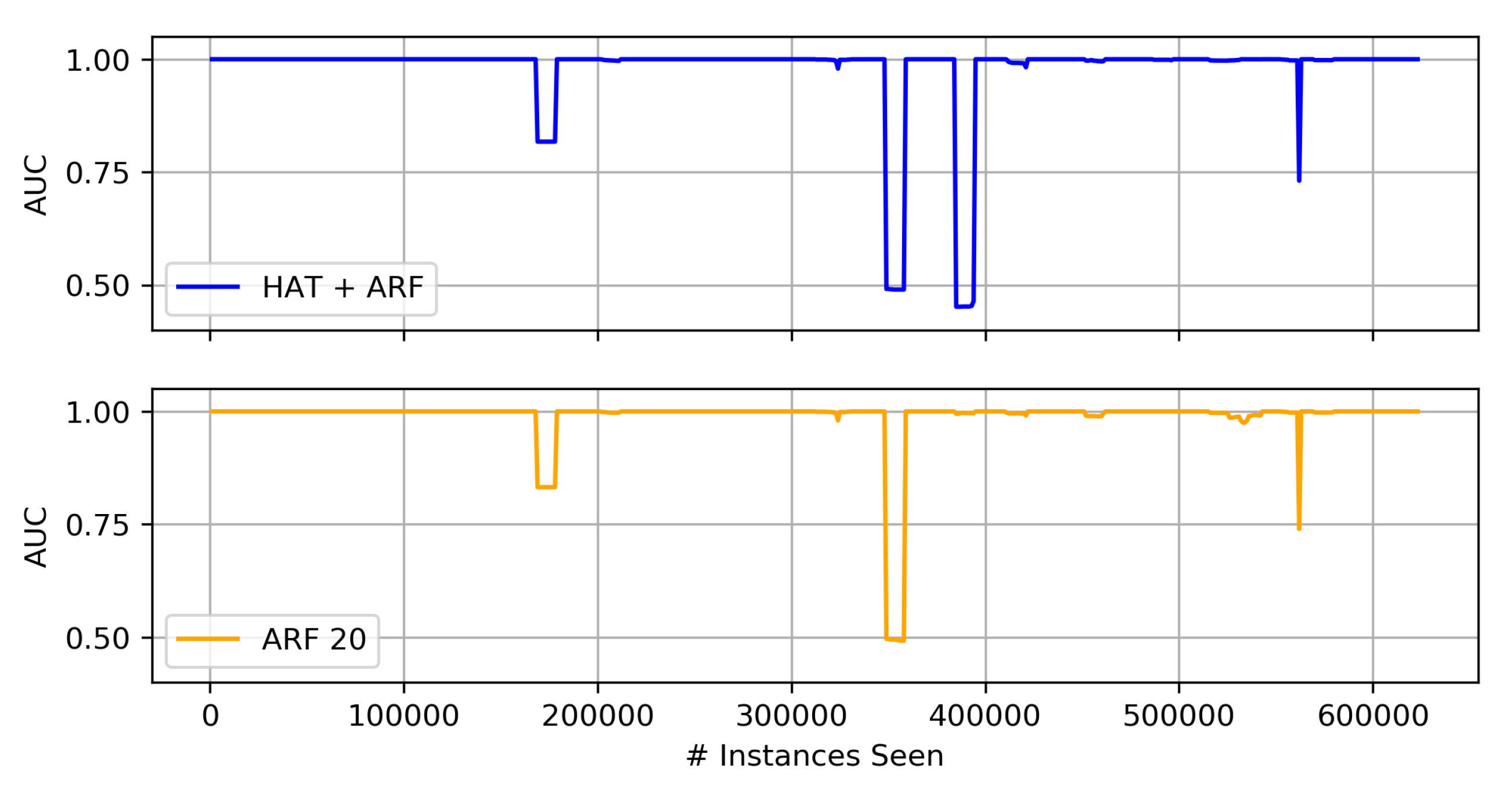
- When comparing HAT + ARF with a larger ARF, close performance is observed, and the larger ARF even performs better in some instances, but with a slightly higher run-time.
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Da Costa, K.A.; Papa, J.P.; Lisboa, C.O.; Munoz, R.; de Albuquerque, V.H.C. Internet of Things: A survey on machine learning-based intrusion detection approaches. Comput. Netw. 2019, 151, 147–157. [Google Scholar] [CrossRef]
- Martínez Torres, J.; Iglesias Comesaña, C.; García-Nieto, P.J. Review: Machine learning techniques applied to cybersecurity. Int. J. Mach. Learn. Cybern. 2019, 10, 2823–2836. [Google Scholar] [CrossRef]
- Srivastava, N.; Chandra Jaiswal, U. Big Data Analytics Technique in Cyber Security: A Review. In Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 27–29 March 2019; pp. 579–585. [Google Scholar]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Whitaker, C.J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy. Mach. Learn. 2003, 51, 181–207. [Google Scholar] [CrossRef]
- Domingos, P.; Hulten, G. Catching up with the data: Research issues in mining data streams. In Proceedings of the Workshop on Research Issues in Data Mining and Knowledge Discovery, Santa Barbara, CA, USA, 20 May 2001. [Google Scholar]
- Hoens, T.R.; Polikar, R.; Chawla, N.V. Learning from streaming data with concept drift and imbalance: An overview. Prog. Artif. Intell. 2012, 1, 89–101. [Google Scholar] [CrossRef]
- Krawczyk, B.; Cano, A. Online ensemble learning with abstaining classifiers for drifting and noisy data streams. Appl. Soft Comput. 2018, 68, 677–692. [Google Scholar] [CrossRef]
- Cup, K. 2007. Available online: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html (accessed on 10 June 2020).
- Bian, S.; Wang, W. On diversity and accuracy of homogeneous and heterogeneous ensembles. Int. J. Hybrid Intell. Syst. 2007, 4, 103–128. [Google Scholar] [CrossRef]
- Hajialian, H.; Toma, C. Network Anomaly Detection by Means of Machine Learning: Random Forest Approach with Apache Spark. Inf. Econ. 2018, 22, 89–98. [Google Scholar] [CrossRef]
- Abd, A.; Hadi, A. Performance Analysis of Big Data Intrusion Detection System over Random Forest Algorithm. Int. J. Appl. Eng. Res. 2018, 13, 1520–1527. [Google Scholar]
- Verma, A.; Ranga, V. Machine Learning Based Intrusion Detection Systems for IoT Applications. In Wireless Personal Communications; Springer: Berlin, Germany, 2019; pp. 1–24. [Google Scholar]
- Rettig, L.; Khayati, M.; Cudre-Mauroux, P.; Piorkowski, M. Online anomaly detection over Big Data streams. In Proceedings of the 2015 IEEE International Conference on Big Data, IEEE Big Data 2015, Santa Clara, CA, USA, 29 October–1 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1113–1122. [Google Scholar]
- Guha, S.; Mishra, N.; Roy, G.; Schrijvers, O. Robust random cut forest based anomaly detection on streams. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 6, pp. 3987–3999. [Google Scholar]
- Mulinka, P.; Casas, P. Stream-based machine learning for network security and anomaly detection. In Proceedings of the Big-DAMA 2018—Proceedings of the 2018 Workshop on Big Data Analytics and Machine Learning for Data Communication Networks, Part of SIGCOMM 2018, Budapest, Hungary, 20 August 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Tan, S.C.; Ting, K.M.; Liu, T.F. Fast anomaly detection for streaming data. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1511–1516. [Google Scholar] [CrossRef]
- Verma, A.; Ranga, V. ELNIDS: Ensemble Learning based Network Intrusion Detection System for RPL based Internet of Things. In Proceedings of the 2019 4th International Conference on Internet of Things: Smart Innovation and Usages, IoT-SIU 2019, San Diego, CA, USA, 18–19 April 2019; pp. 2–7. [Google Scholar] [CrossRef]
- Mirsky, Y.; Doitshman, T.; Elovici, Y.; Shabtai, A. Kitsune: An Ensemble of Autoencoders for Online Network Intrusion Detection. arXiv 2018, arXiv:1802.09089. [Google Scholar]
- Hsu, Y.F.; He, Z.Y.; Tarutani, Y.; Matsuoka, M. Toward an online network intrusion detection system based on ensemble learning. In Proceedings of the IEEE International Conference on Cloud Computing, CLOUD 2019, Milan, Italy, 8–13 July 2019; pp. 174–178. [Google Scholar] [CrossRef]
- Hashmani, M.A.; Jameel, S.M.; Ibrahim, A.M.; Zaffar, M.; Raza, K. An ensemble approach to big data security (Cyber Security). Int. J. Adv. Comput. Sci. Appl. 2018, 9, 75–77. [Google Scholar] [CrossRef]
- Bifet, A.; Holmes, G.; Kirkby, R.; Pfahringer, B. MOA: Massive Online Analysis. J. Mach. Learn. Res. 2010, 11, 1601–1604. [Google Scholar]
- Frank, E.; Mark, A. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Domingos, P.; Hulten, G. Mining high-speed data streams. In Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 71–80. [Google Scholar]
- Bifet, A.; Gavaldà, R. Adaptive learning from evolving data streams. In Proceedings of the 8th International Symposium on Intelligent Data Analysis, IDA 2009, Lyon, France, 31 August–2 September 2009; Springer: Berlin, Germany, 2009; pp. 249–260. [Google Scholar]
- Gomes, H.M.; Bifet, A.; Read, J.; Barddal, J.P.; Enembreck, F.; Pfharinger, B.; Holmes, G.; Abdessalem, T. Adaptive random forests for evolving data stream classification. Mach. Learn. 2017, 106, 1469–1495. [Google Scholar] [CrossRef]
- Brzezinski, D.; Stefanowski, J. Prequential AUC: Properties of the area under the ROC curve for data streams with concept drift. Knowl. Inf. Syst. 2017, 52, 531–562. [Google Scholar] [CrossRef]
| K-NN | SVM | HT | HAT | |
|---|---|---|---|---|
| HTTP | 0.95 ± 0.13 | 0.96 ± 0.13 | 0.99 ± 0.06 | 0.97 ± 0.10 |
| 516.07 s | 4.60 s | 6.59 s | 7.00 s | |
| SMTP | 0.87 ± 0.18 | 0.80 ± 0.28 | 0.90 ± 0.15 | 0.91 ± 0.14 |
| 89.77 s | 1.16 s | 0.87 s | 1.38 s | |
| Combined | 0.94 ± 0.14 | 0.86 ± 0.25 | 0.99 ± 0.07 | 0.96 ± 0.11 |
| 593.32 s | 5.27 s | 9.51 s | 8.74 s |
| BoostHT | BoostHAT | ARF | ARF (20) | |
|---|---|---|---|---|
| HTTP | 0.98 ± 0.08 | 0.98 ± 0.09 | 0.98 ± 0.10 | 0.99 ± 0.07 |
| 25.28 s | 15.62 s | 17.57 s | 29.88 s | |
| SMTP | 0.96 ± 0.09 | 0.97 ± 0.06 | 0.97 ± 0.08 | 0.98 ± 0.08 |
| 3.48 s | 4.74 s | 3.26 s | 5.53 s | |
| Combined | 0.99 ± 0.05 | 0.99 ± 0.06 | 0.98 ± 0.09 | 1.00 ± 0.03 |
| 62.62 s | 41.41 s | 32.72 s | 67.61 s |
| HAT + ARF | SVM + HAT | SVM + ARF | |
|---|---|---|---|
| HTTP | 0.98 ± 0.10 | 0.97 ± 0.10 | 0.98 ± 0.10 |
| 25.2 s | 8.45 s | 19.99 s | |
| SMTP | 0.98 ± 0.05 | 0.93 ± 0.14 | 0.98 ± 0.08 |
| 4.56 s | 1.61 s | 4.17 s | |
| Combined | 0.98 ± 0.09 | 0.94 ± 0.15 | 0.97 ± 0.11 |
| 55.59 s | 11.16 s | 44.39 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martindale, N.; Ismail, M.; Talbert, D.A. Ensemble-Based Online Machine Learning Algorithms for Network Intrusion Detection Systems Using Streaming Data. Information 2020, 11, 315. https://doi.org/10.3390/info11060315
Martindale N, Ismail M, Talbert DA. Ensemble-Based Online Machine Learning Algorithms for Network Intrusion Detection Systems Using Streaming Data. Information. 2020; 11(6):315. https://doi.org/10.3390/info11060315
Chicago/Turabian StyleMartindale, Nathan, Muhammad Ismail, and Douglas A. Talbert. 2020. "Ensemble-Based Online Machine Learning Algorithms for Network Intrusion Detection Systems Using Streaming Data" Information 11, no. 6: 315. https://doi.org/10.3390/info11060315
APA StyleMartindale, N., Ismail, M., & Talbert, D. A. (2020). Ensemble-Based Online Machine Learning Algorithms for Network Intrusion Detection Systems Using Streaming Data. Information, 11(6), 315. https://doi.org/10.3390/info11060315






