Quantitative Evaluation of Dense Skeletons for Image Compression
Abstract
1. Introduction
- What kinds of images does CDMD perform on best?
- What is CDMD’s trade-off between reconstructed quality and compression ratio?
- Which parameter values give best quality and/or compression for a given image type?
- How does CDMD compression compare with JPEG?
2. Related work
2.1. Medial Descriptors and the DMD Method
2.2. Image Simplification Parameters
2.3. Image Compression Quality Metrics
2.4. Image Compression Methods
3. Proposed Compression Method
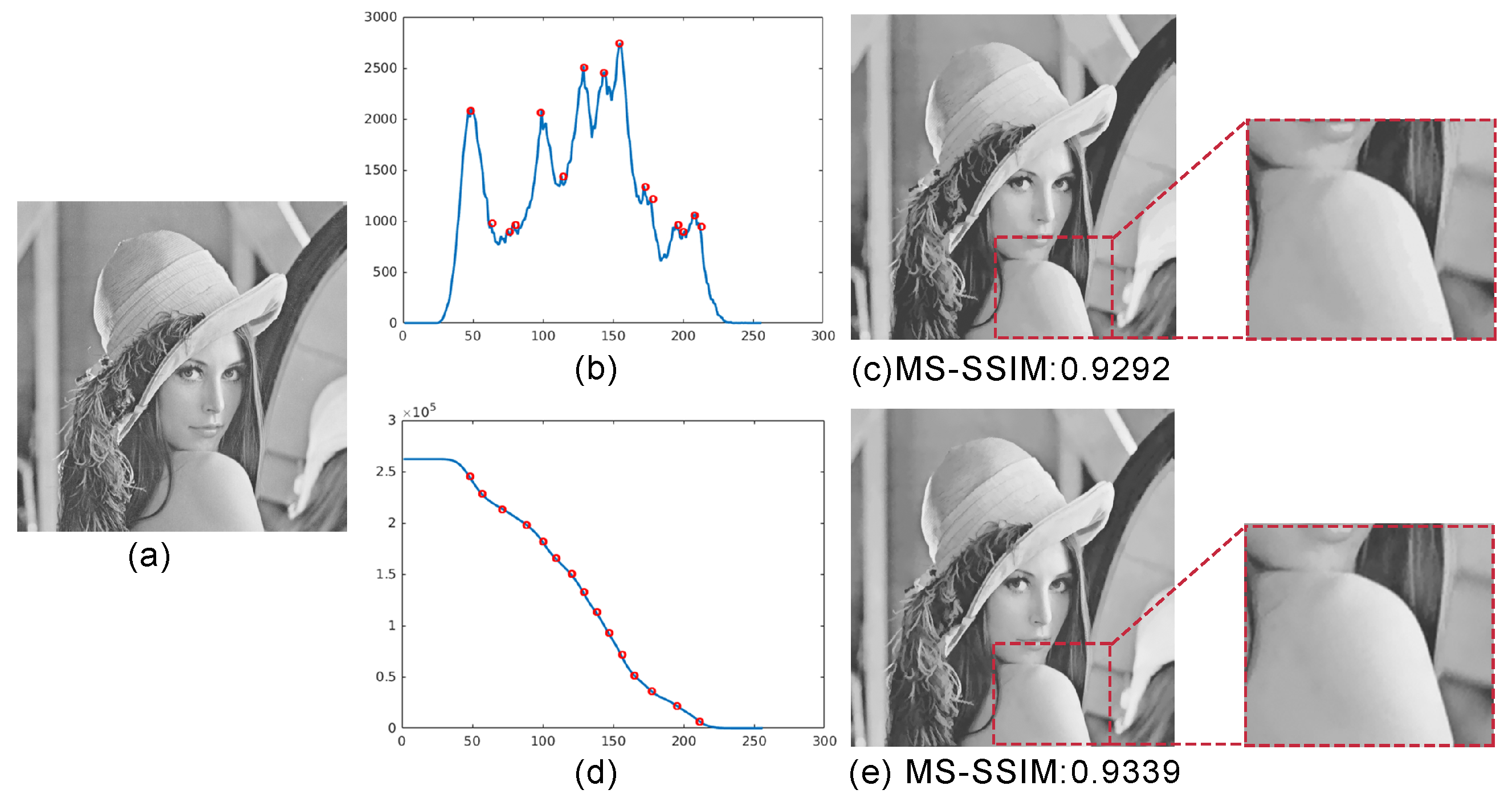
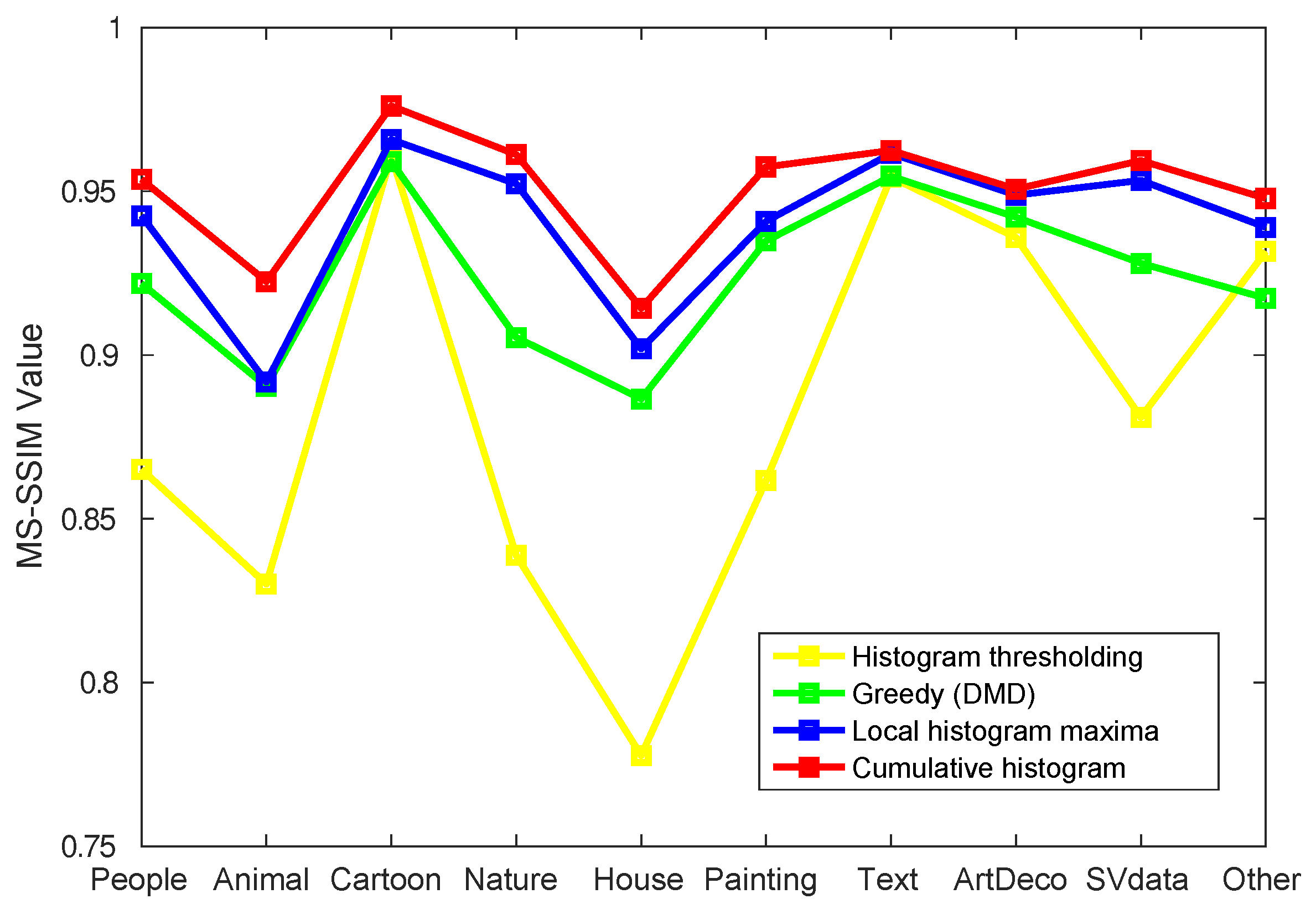
3.1. Layer Selection
3.2. MAT Encoding
4. Evaluation and Optimization
- Layer selection: 3000 times faster and 3.28% higher quality;
- MAT encoding: 20.15% better compression ratio.
4.1. Joint Compression Quality
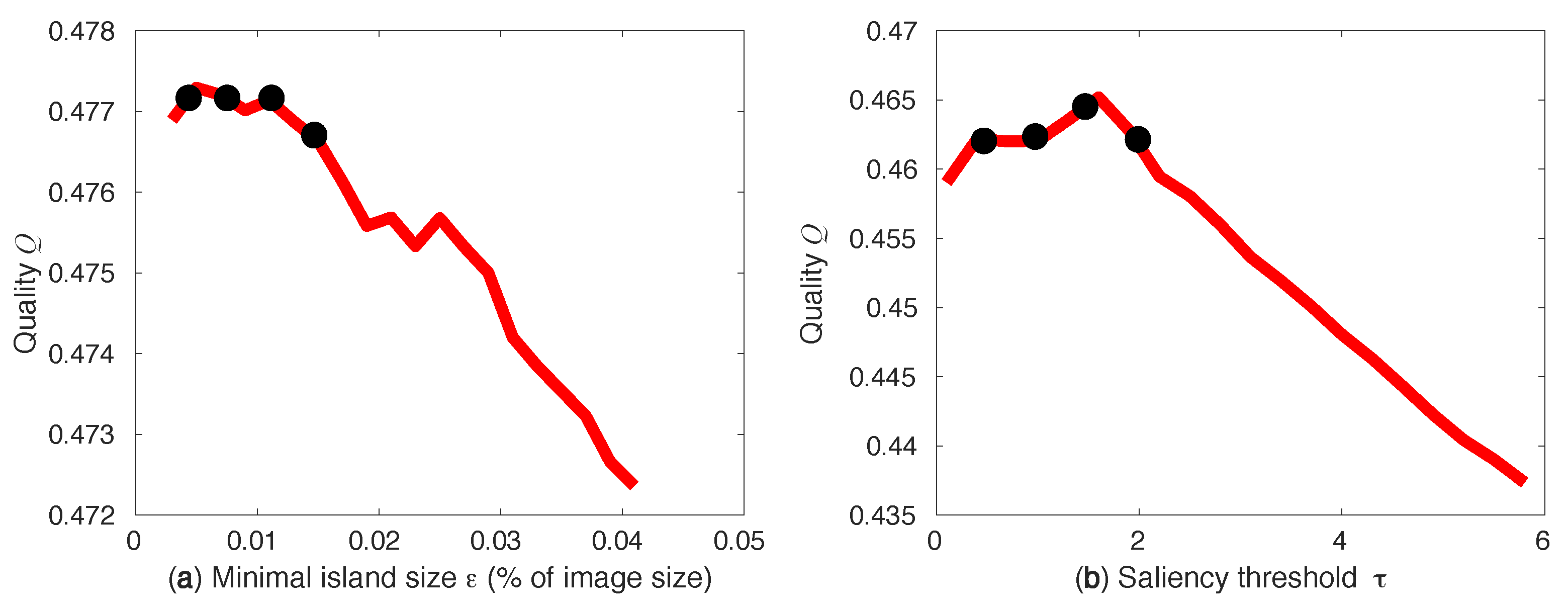
4.2. Optimizing the Joint Compression Quality
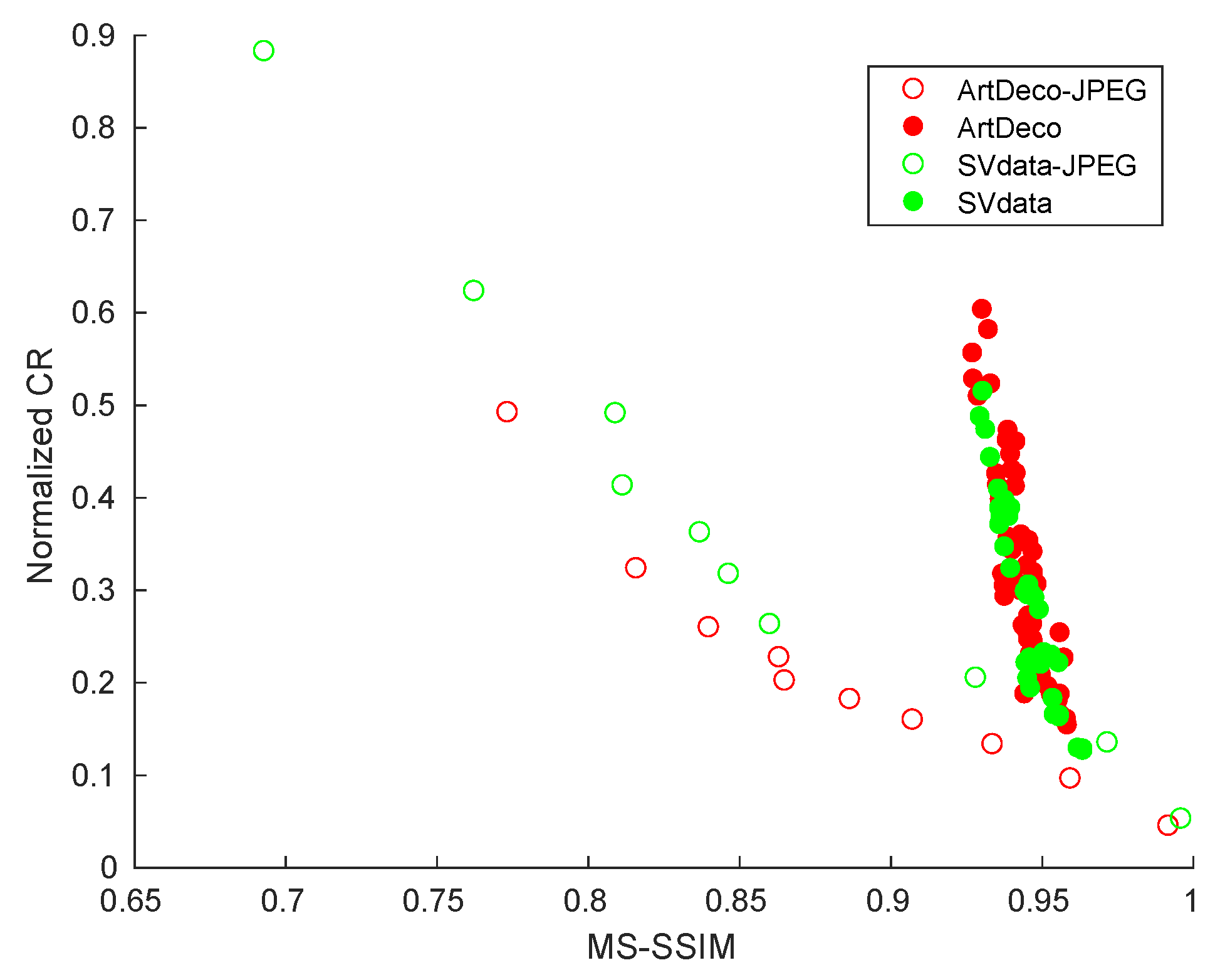
4.3. Trade-Off between MS-SSIM and CR
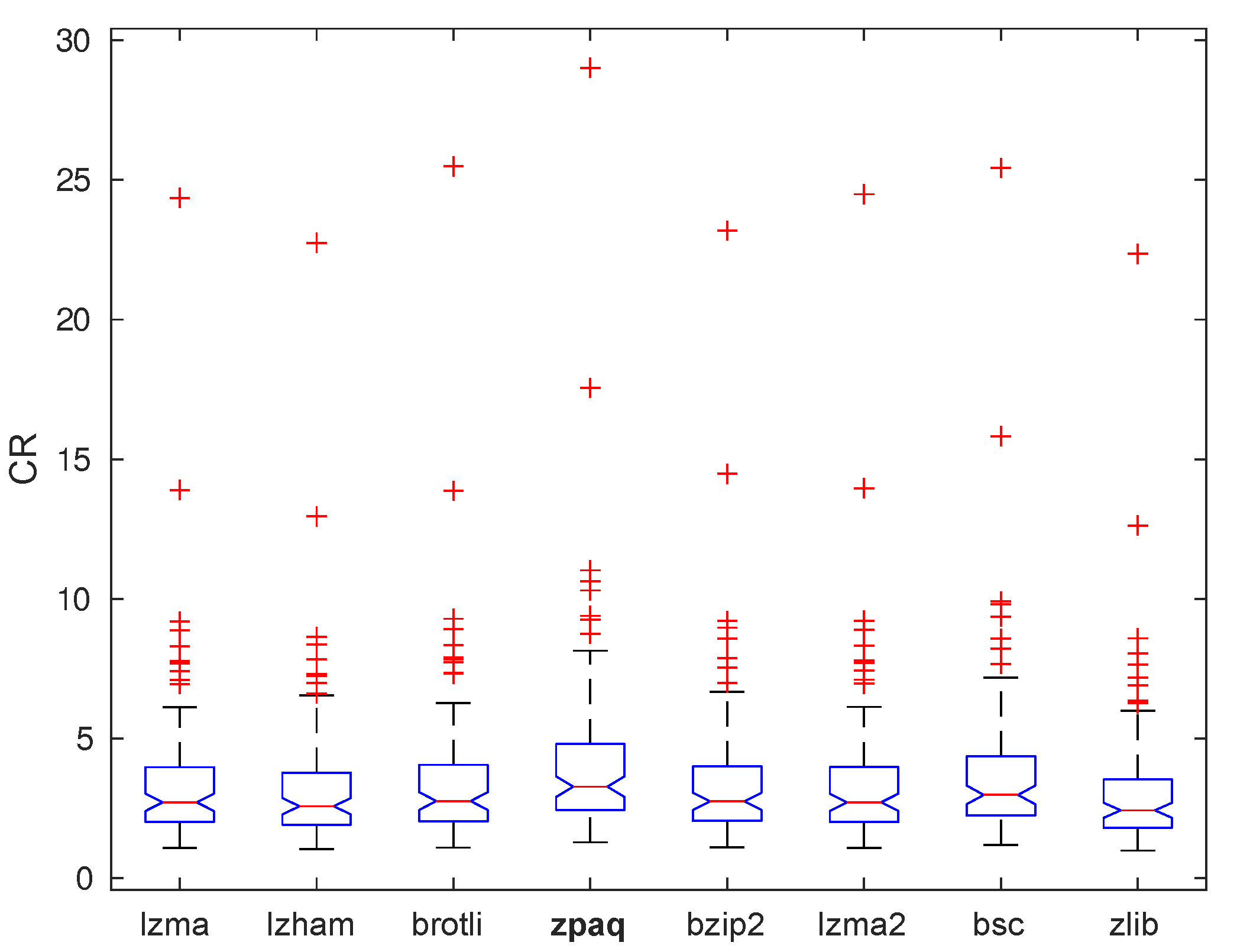
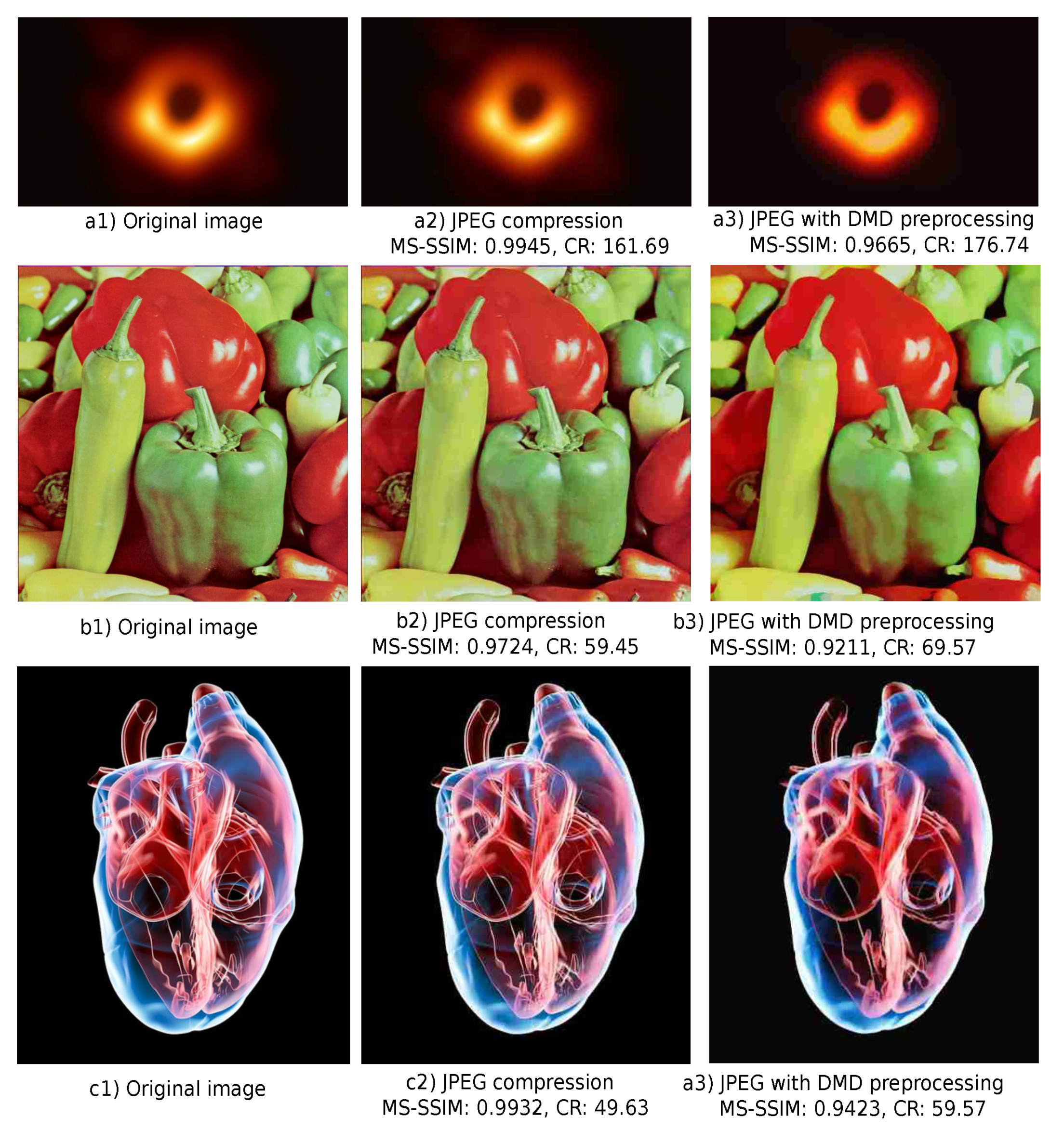
4.4. Comparison with JPEG
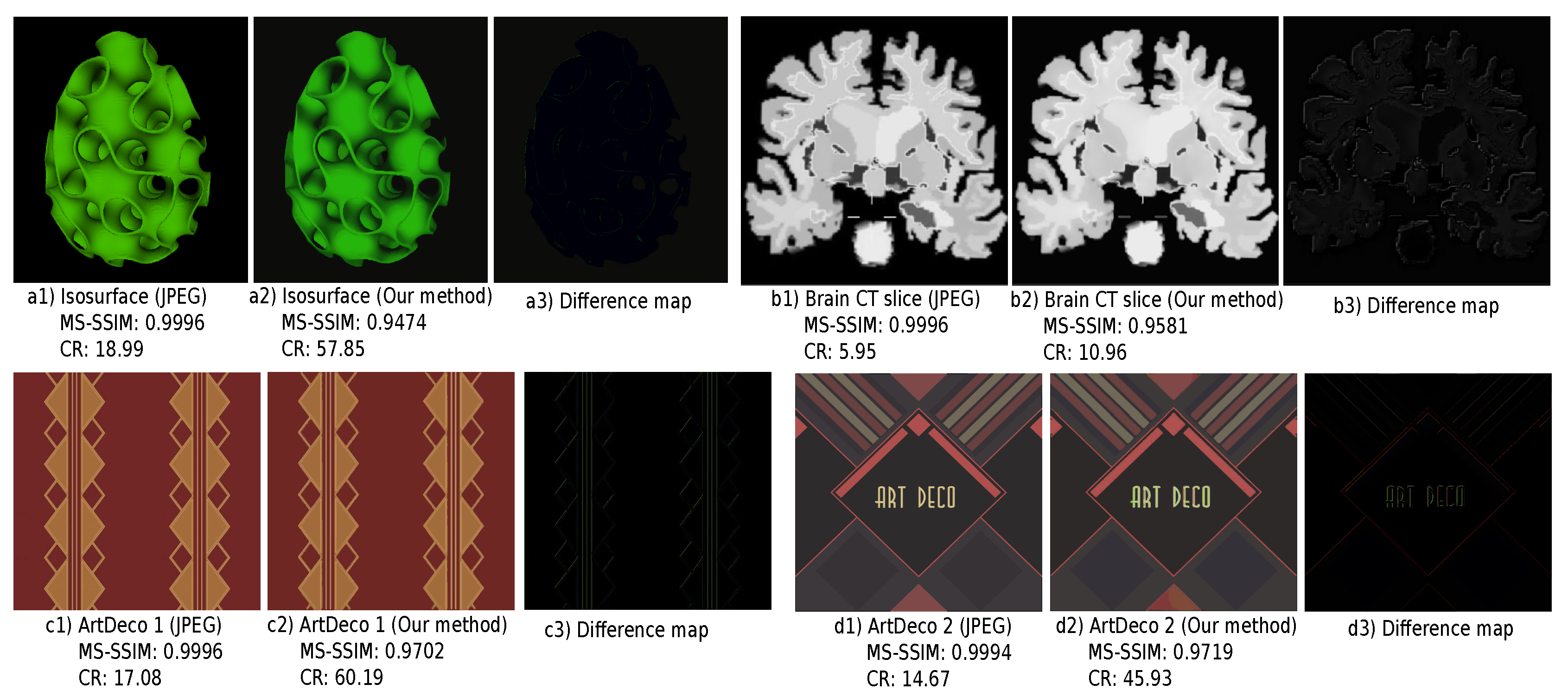
4.5. Handling Noisy Images
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shum, H.Y.; Kang, S.B.; Chan, S.C. Survey of image-based representations and compression techniques. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 1020–1037. [Google Scholar] [CrossRef]
- Wallace, G.K. The JPEG still picture compression standard. IEEE TCE. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Davies, E.R. Machine Vision: Theory, Algorithms, Practicalities; Academic Press: London, UK, 2004. [Google Scholar]
- Siddiqi, K.; Pizer, S. Medial Representations: Mathematics, Algorithms and Applications; Springer: New York, NY, USA, 2008. [Google Scholar]
- Saha, P.K.; Borgefors, G.; di Baja, G.S. A survey on skeletonization algorithms and their applications. Pattern Recognit. Lett. 2016, 76, 3–12. [Google Scholar] [CrossRef]
- Saha, P.K.; Borgefors, G.; di Baja, G.S. Skeletonization—Theory, Methods, and Application; Academic Press: London, UK, 2017. [Google Scholar]
- Van Der Zwan, M.; Meiburg, Y.; Telea, A. A dense medial descriptor for image analysis. In Proceedings of the International Conference on Computer Vision Theory and Applications(VISAPP-2013), Barcelona, Spain, 21–24 February 2013; pp. 285–293. [Google Scholar]
- Koehoorn, J.; Sobiecki, A.; Boda, D.; Diaconeasa, A.; Doshi, S.; Paisey, S.; Jalba, A.; Telea, A. Automated Digital Hair Removal by Threshold Decomposition and Morphological Analysis. In Proceedings of the International Symposium on Mathematical Morphology and Its Applications to Signal and Image (ISMM), Reykjavik, Iceland, 27–29 May 2015. [Google Scholar]
- Sobiecki, A.; Koehoorn, J.; Boda, D.; Solovan, C.; Diaconeasa, A.; Jalba, A.; Telea, A. A New Efficient Method for Digital Hair Removal by Dense Threshold Analysis. In Proceedings of the 4th World Congress of Dermoscopy, Vienna, Austria, 21 April 2015. [Google Scholar]
- Blum, H. A transformation for extracting new descriptors of shape. In Models for the Perception of Speech and Visual Form; Dunn, W.W., Ed.; MIT Press: Cambridge, UK, 1967; pp. 362–381. [Google Scholar]
- Blum, H.; Nagel, R. Shape description using weighted symmetric axis features. Pattern Recognit. 1978, 10, 167–180. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef]
- Telea, A. Feature Preserving Smoothing of Shapes Using Saliency Skeletons. In Visualization in Medicine and Life Sciences II (VMLS); Springer: Basel, Switzerland, 2012; pp. 153–170. [Google Scholar]
- Ogniewicz, R.L.; Kubler, O. Hierarchic Voronoi skeletons. Pattern Recognit. 1995, 28, 343–359. [Google Scholar] [CrossRef]
- Costa, L.; Cesar, R. Shape Analysis and Classification; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Falcão, A.; Stolfi, J.; Lotufo, R. The image foresting transform: Theory, algorithms, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 19–29. [Google Scholar] [CrossRef]
- Telea, A.; van Wijk, J.J. An Augmented Fast Marching Method for Computing Skeletons and Centerlines. In Proceedings of the 2002 Joint Eurographics and IEEE TCVG Symposium on Visualization, VisSym, Barcelona, Spain, 27–29 May 2002. [Google Scholar]
- Kadir, T.; Brady, M. Saliency, Scale and Image Description. Int. J. Comput. Vis. 2001, 45, 83–105. [Google Scholar] [CrossRef]
- Battiato, S.; Farinella, G.M.; Puglisi, G.; Ravi, D. Saliency-based selection of gradient vector flow paths for content aware image resizing. IEEE Trans. Image Process. 2014, 23, 2081–2095. [Google Scholar] [CrossRef]
- Ersoy, O.; Hurter, C.; Paulovich, F.; Cantareiro, G.; Telea, A. Skeleton-based edge bundles for graph visualization. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2364–2373. [Google Scholar] [CrossRef]
- Zhai, X.; Chen, X.; Yu, L.; Telea, A. Interactive Axis-Based 3D Rotation Specification Using Image Skeletons. In Proceedings of the GRAPP, Valletta, Malta, 27–29 February 2020. [Google Scholar]
- Telea, A. Real-Time 2D Skeletonization Using CUDA. Available online: http://www.cs.rug.nl/svcg/Shapes/CUDASkel (accessed on 1 May 2019).
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at Signal Fidelity Measures. IEEE Signal Proc. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Bovik, A.C. Content-weighted video quality assessment using a three-component image model. J. Electron. Imaging 2010, 19, 110–130. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Zhang, C.; Chen, T. A survey on image-based rendering—Representation, sampling and compression. Signal Process Image 2004, 19, 1–28. [Google Scholar] [CrossRef]
- Toderici, G.; O’Malley, S.; Hwang, S.J.; Vincent, D.; Minnen, D.; Baluja, S.; Covell, M.; Sukthankar, R. Variable Rate Image Compression with Recurrent Neural Networks. arXiv 2016, arXiv:1511.06085. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E. End-to-end Optimized Image Compression. arXiv 2017, arXiv:1611.01704. [Google Scholar]
- Toderici, G.; Vincent, D.; Johnston, N.; Hwang, S.J.; Minnen, D.; Shor, J.; Covell, M. Full Resolution Image Compression with Recurrent Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Prakash, A.; Moran, N.; Garber, S.; DiLillo, A.; Storer, J. Semantic Perceptual Image Compression using Deep Convolution Networks. In Proceedings of the Data Compression Conference (DCC), Snowbird, UT, USA, 4–7 April 2017. [Google Scholar]
- Stock, P.; Joulin, A.; Gribonval, R.; Graham, B.; Jégou, H. And the Bit Goes Down: Revisiting the Quantization of Neural Networks. arXiv 2019, arXiv:1907.05686. [Google Scholar]
- Guo, C.; Zhang, L. A novel multi resolution spatiotemporal saliency detection model and its applications in image and video compression. IEEE Trans. Image Process. 2010, 19, 185–198. [Google Scholar]
- Andrushia, A.D.; Thangarjan, R. Saliency-Based Image Compression Using Walsh-Hadamard Transform (WHT). In Biologically Rationalized Computing Techniques For Image Processing Applications; Springer: Cham, Switzerland, 2018; pp. 21–42. [Google Scholar]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Imamoglu, N.; Lin, W.; Fang, Y. A saliency detection model using low-level features based on wavelet transform. IEEE Trans. Multimed. 2013, 15, 96–105. [Google Scholar] [CrossRef]
- Lin, R.J.; Lin, W.S. Computational visual saliency model based on statistics and machine learning. J. Vis. 2014, 14, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Arya, R.; Singh, N.; Agrawal, R. A novel hybrid approach for salient object detection using local and global saliency in frequency domain. Multimed. Tools Appl. 2015, 75, 8267–8287. [Google Scholar] [CrossRef]
- Hecht, S. The visual discrimination of intensity and the Weber-Fechner law. J. Gen. Physiol. 2003, 7, 235–267. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. CDMD-Benchmark. Available online: https://github.com/WangJieying/CDMD-benchmark (accessed on 1 May 2020).
- Cormen, T.H.; Stein, C.; Rivest, R.L.; Leiserson, C.E. Introduction to Algorithms, 3rd ed.; MIT Press: London, UK, 2001; pp. 540–549. [Google Scholar]
- Geelnard, M. Basic Compression Library. Available online: github.com/MariadeAnton/bcl/blob/master/src (accessed on 14 January 2015).
- Roy, A.; Scott, A.J. Unitary designs and codes. Des. Codes Cryptogr. 2009, 53, 13–31. [Google Scholar] [CrossRef]
- Langdon, G.G. An Introduction to Arithmetic Coding. IBM J. Res. Dev. 1984, 28, 135–149. [Google Scholar] [CrossRef]
- Bentley, J.L.; Sleator, D.D.; Tarjan, R.E.; Wei, V.K. A Locally Adaptive Data Compression Scheme. Commun. ACM 1986, 29, 320–330. [Google Scholar] [CrossRef]
- Pavlov, I. LZMA SDK (Software Development Kit). Available online: http://www.7-zip.org/sdk.html (accessed on 1 May 2019).
- Geldreich, R. LAHAM. Available online: https://code.google.com/archive/p/lzham/ (accessed on 1 March 2020).
- Alakuijala, J.; Szabadka, Z. Brotli Compressed Data Format. Available online: https://tools.ietf.org/html/rfc7932 (accessed on 1 March 2020).
- Mahoney, M. The Zpaq Compression Algorithm. Available online: http://mattmahoney.net/dc/zpaq_compression.pdf (accessed on 1 March 2020).
- Seward, J. Bzip2. Available online: http://en.wikipedia.org/wiki/Bzip2 (accessed on 1 March 2020).
- Grebnov, I. Libbsc: A High Performance Data Compression Library. Available online: https://github.com/IlyaGrebnov/libbsc (accessed on 1 March 2020).
- Deutsch, P.; Gailly, J. ZLIB Compressed Data Format Specification Version 3.3. Available online: https://datatracker.ietf.org/doc/rfc1950 (accessed on 1 March 2020).
- Nemerson, E. Squash Library. Available online: http://quixdb.github.io/squash (accessed on 1 March 2020).
- TinyJPG. Smart JPEG and PNG Compression. Available online: https://tinyjpg.com (accessed on 1 March 2020).
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Cao, T.T.; Tang, K.; Mohamed, A.; Tan, T.S. Parallel banding algorithm to compute exact distance transform with the GPU. In Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, Washington, DC, USA, 19–21 February 2010. [Google Scholar]
- Tushabe, F.; Wilkinson, M.H.F. Image preprocessing for compression: Attribute filtering. In Proceedings of the International Conference on Signal Processing and Imaging Engineering (ICSPIE’07), San Francisco, CA, USA, 24–26 October 2007; pp. 1411–1418. [Google Scholar]


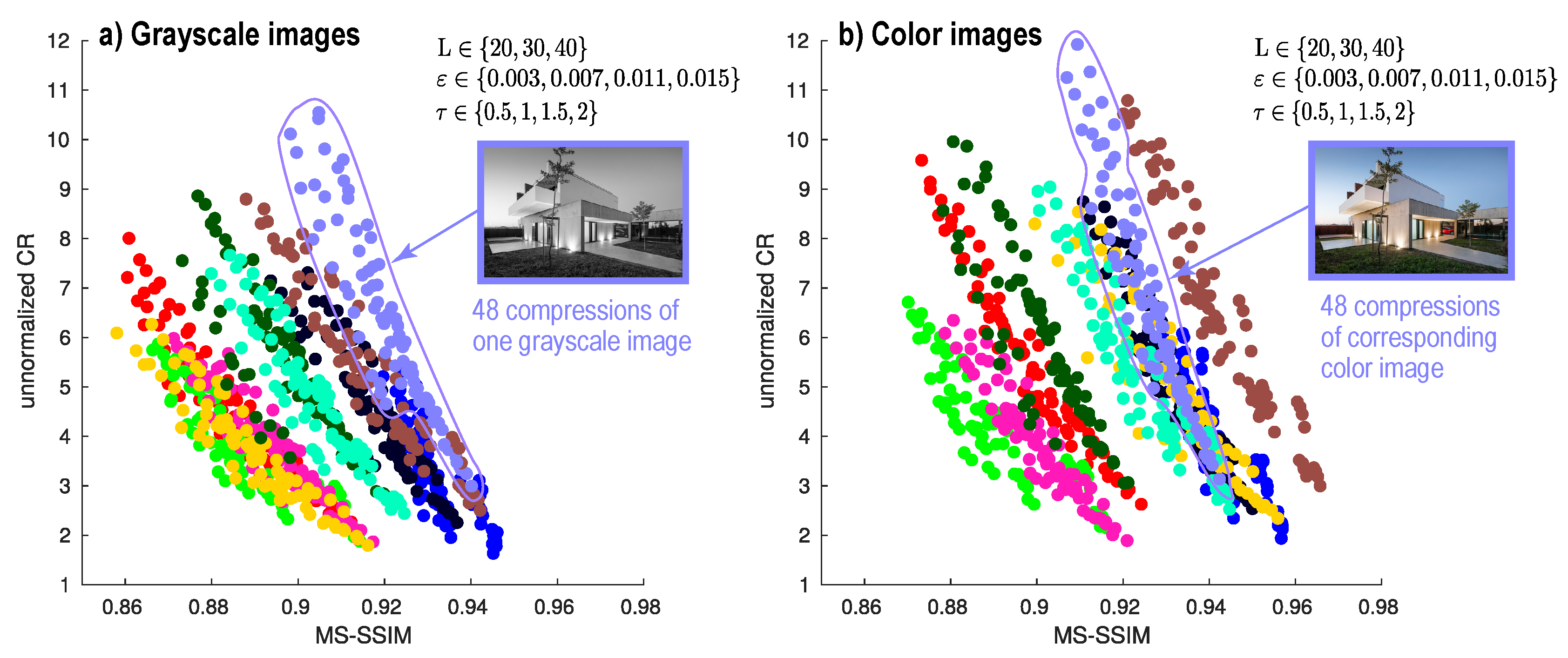
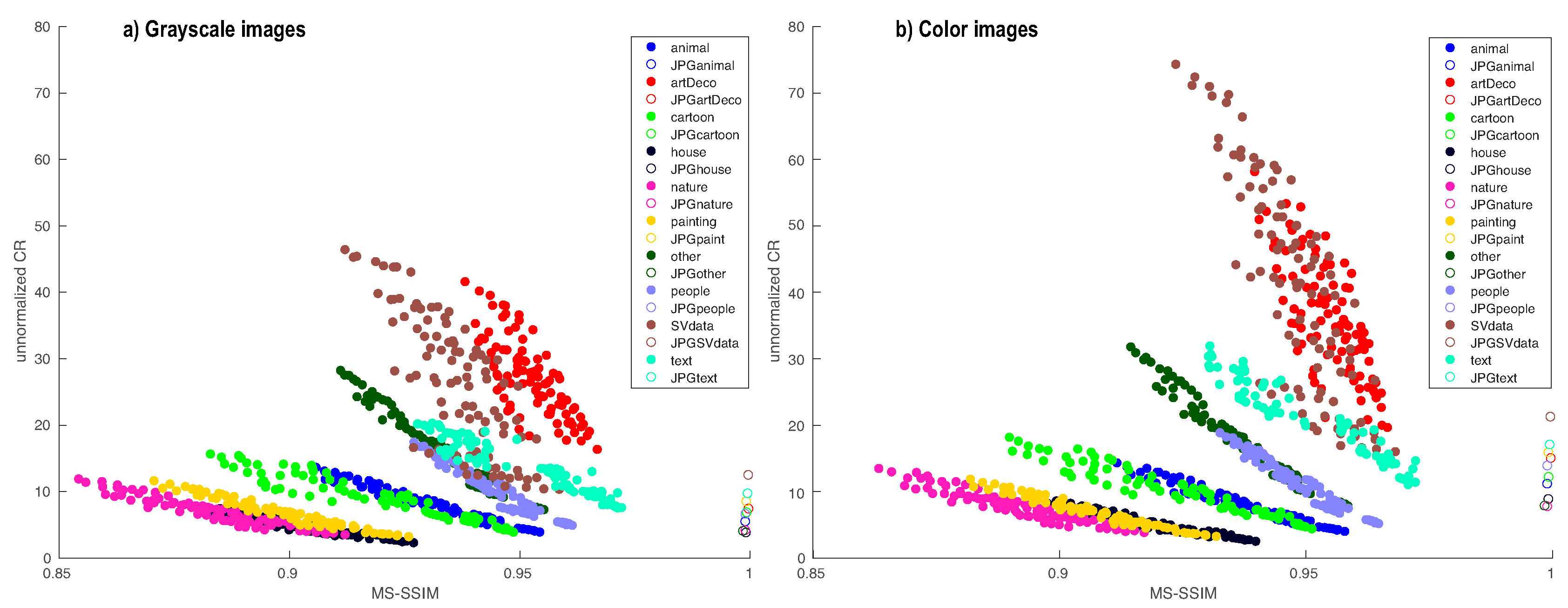
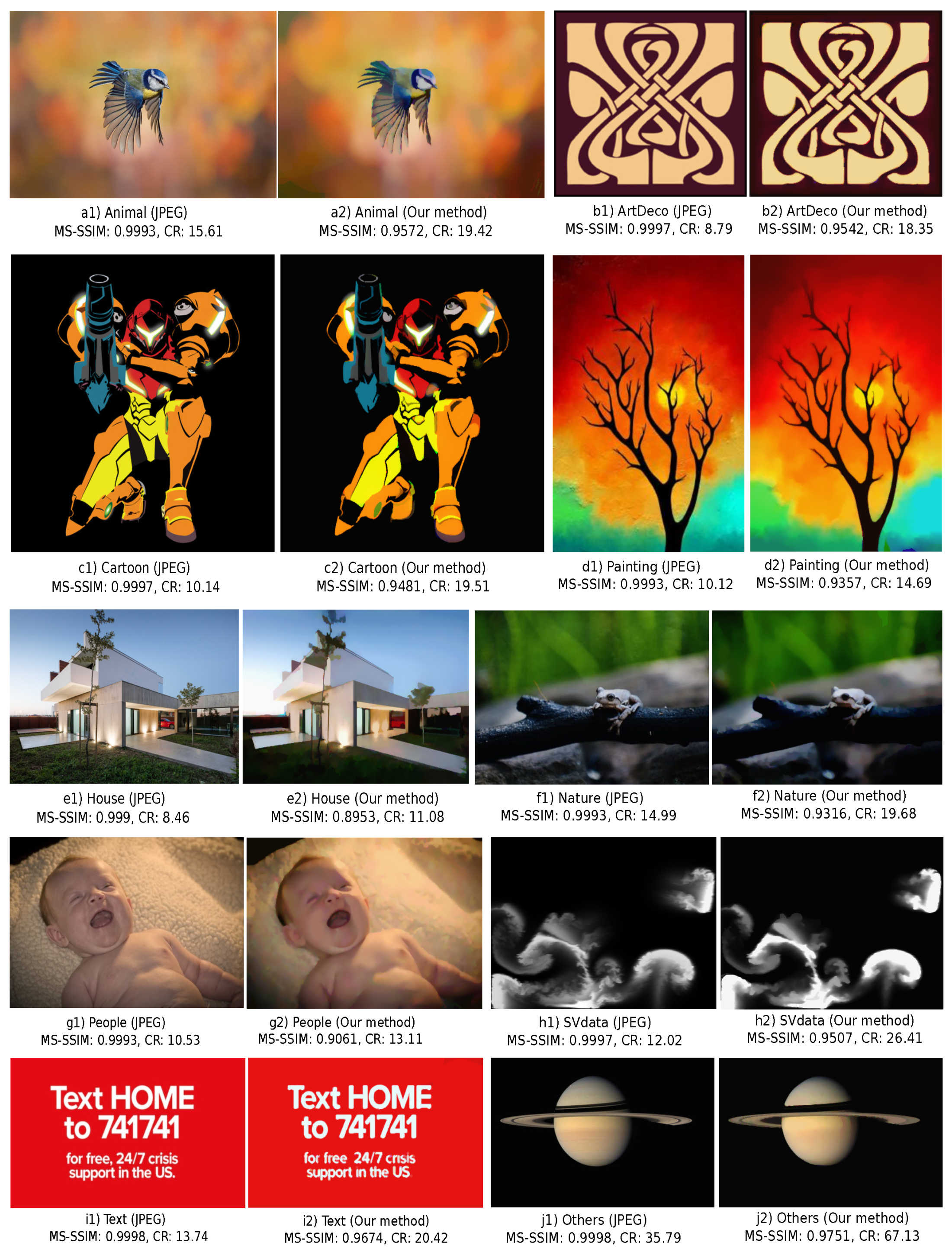
| Type | Description |
|---|---|
| animal | Wild animals in their natural habitat |
| artDeco | Art deco artistic images |
| cartoon | Cartoons and comic strips |
| house | Residential homes surrounded by greenery |
| nature | Panorama landscapes and close-ins of plants |
| other | Miscellaneous (fruit, planets, natural scenery) |
| painting | Classical and modern paintings |
| people | Portrait photos of various people |
| SVdata | Scientific visualizations (scalar and vector fields) |
| text | Typography of various styles and scales |
| Encoding Method | Direct | Huffman | Canonical | Unitary | Exp-Golomb | Arithmetic | Predictive | Compact | Raw | MTF | 40-Case |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Per-layer | 1.672 | 2.464 | 2.464 | 2.074 | 1.799 | 2.673 | 1.865 | 2.121 | 2.418 | 1.865 | 1.67 |
| Inter-layer | 4.083 | 2.727 | 2.751 | 2.912 | 2.9 | 1.692 | 2.874 | 3.155 | 2.816 | 2.46 | 4.358 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Terpstra, M.; Kosinka, J.; Telea, A. Quantitative Evaluation of Dense Skeletons for Image Compression. Information 2020, 11, 274. https://doi.org/10.3390/info11050274
Wang J, Terpstra M, Kosinka J, Telea A. Quantitative Evaluation of Dense Skeletons for Image Compression. Information. 2020; 11(5):274. https://doi.org/10.3390/info11050274
Chicago/Turabian StyleWang, Jieying, Maarten Terpstra, Jiří Kosinka, and Alexandru Telea. 2020. "Quantitative Evaluation of Dense Skeletons for Image Compression" Information 11, no. 5: 274. https://doi.org/10.3390/info11050274
APA StyleWang, J., Terpstra, M., Kosinka, J., & Telea, A. (2020). Quantitative Evaluation of Dense Skeletons for Image Compression. Information, 11(5), 274. https://doi.org/10.3390/info11050274






