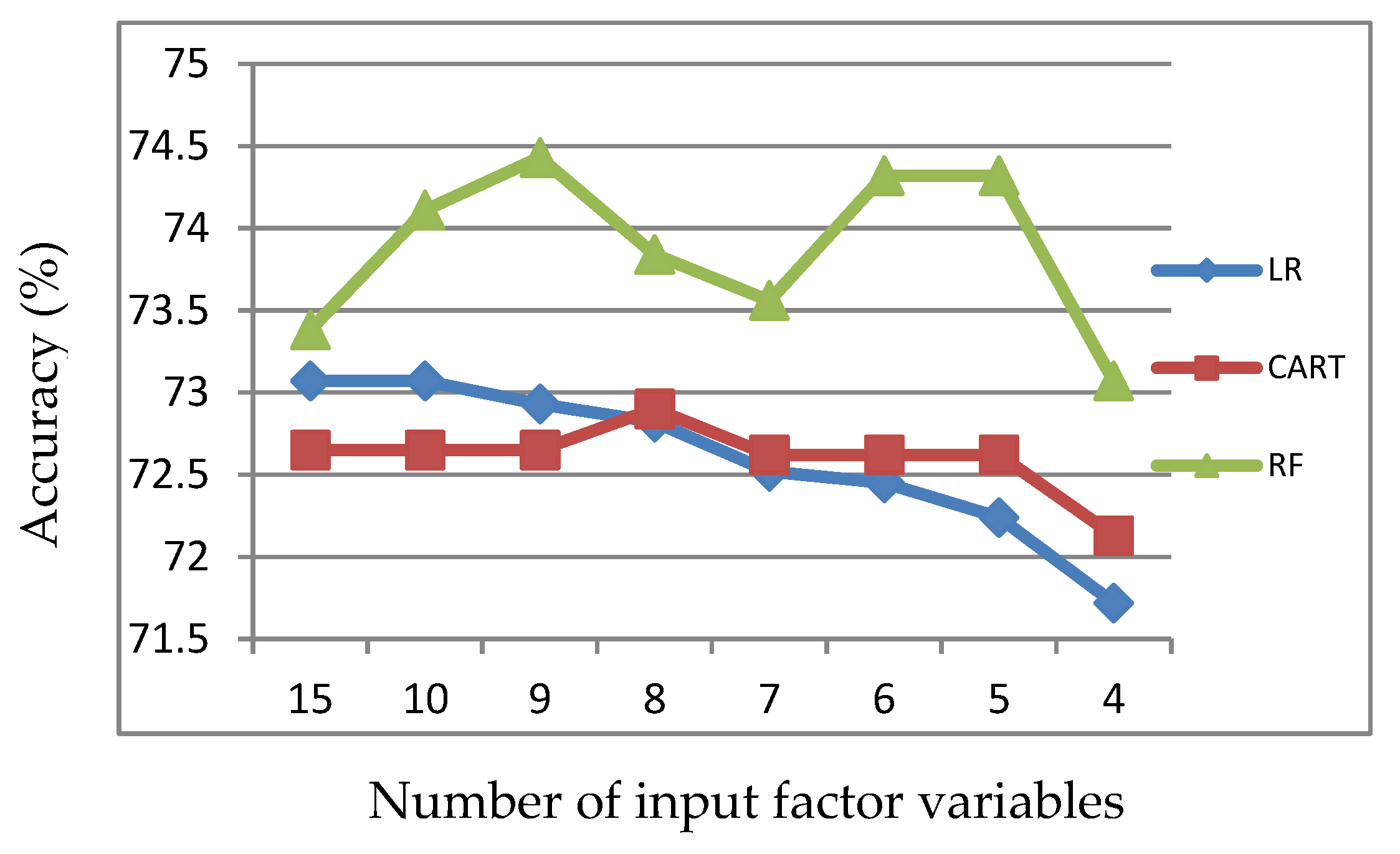
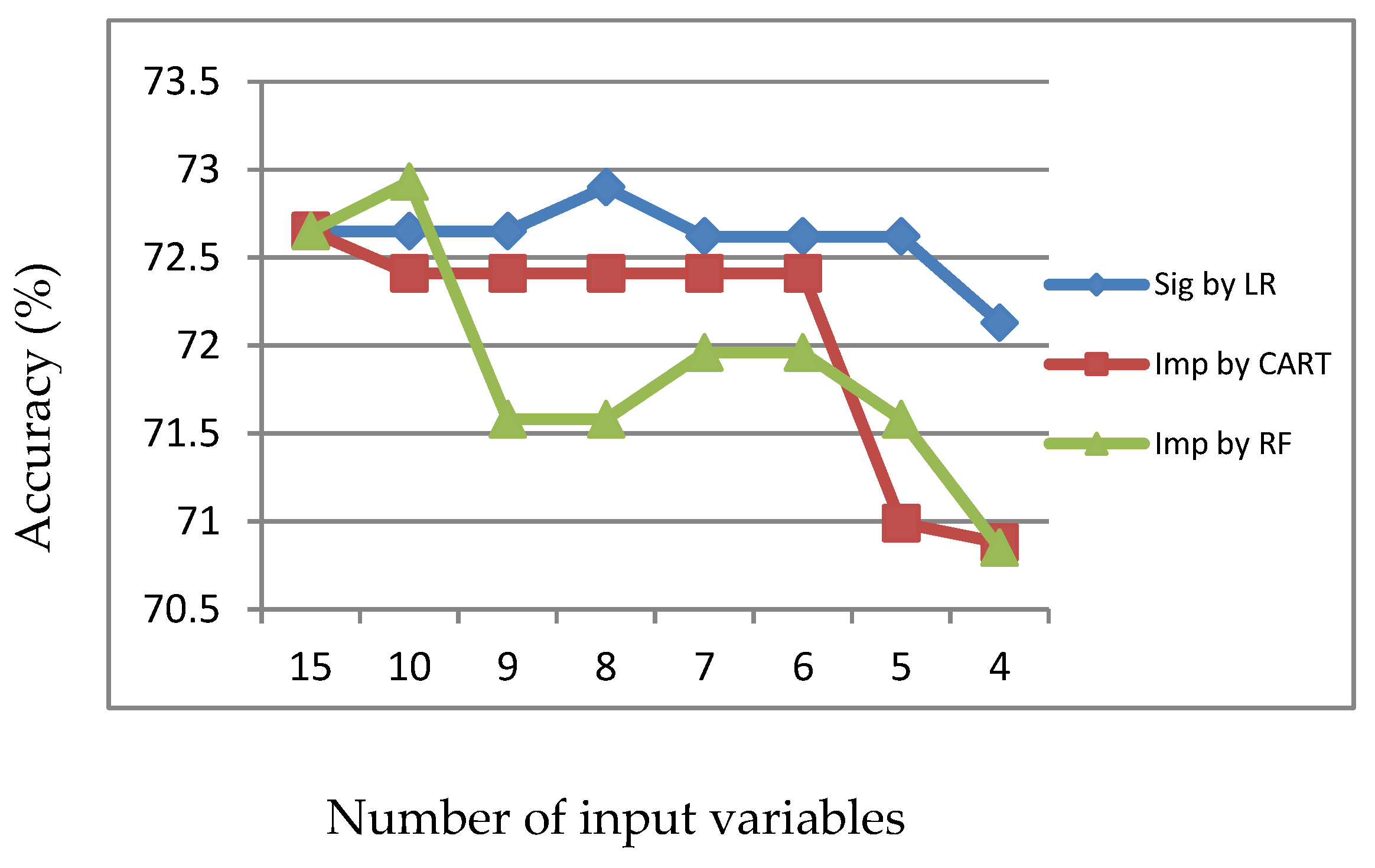
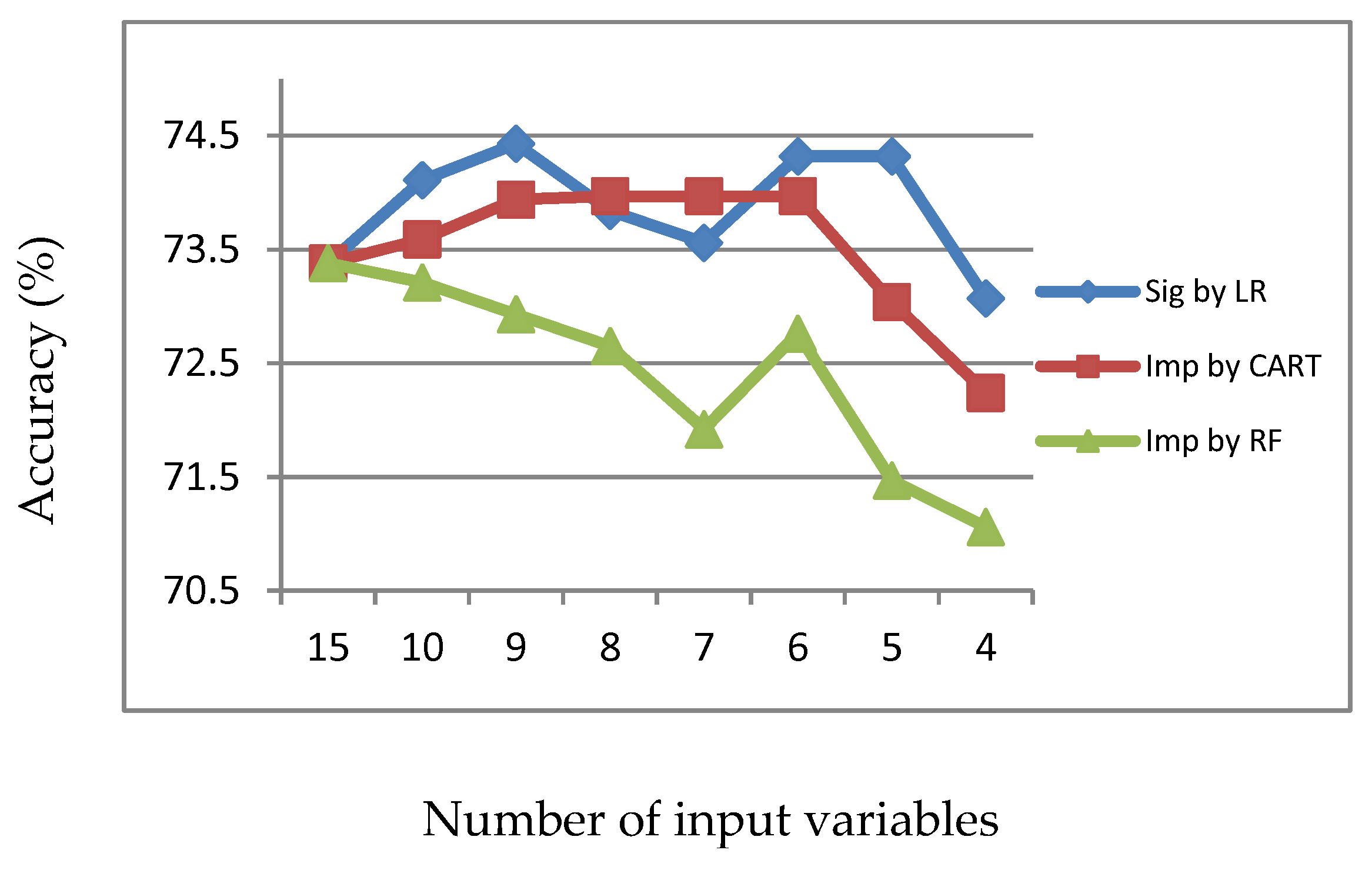
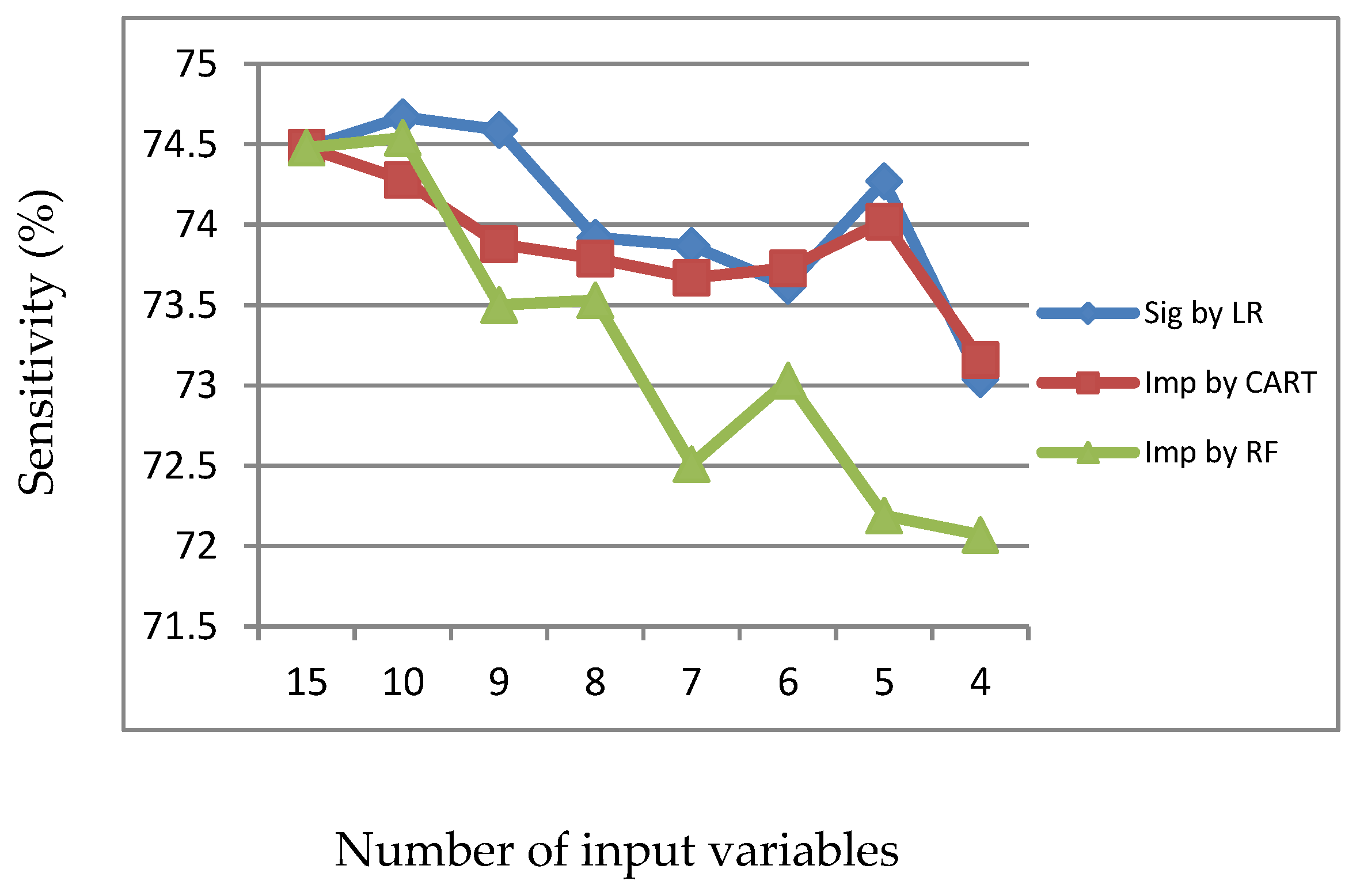
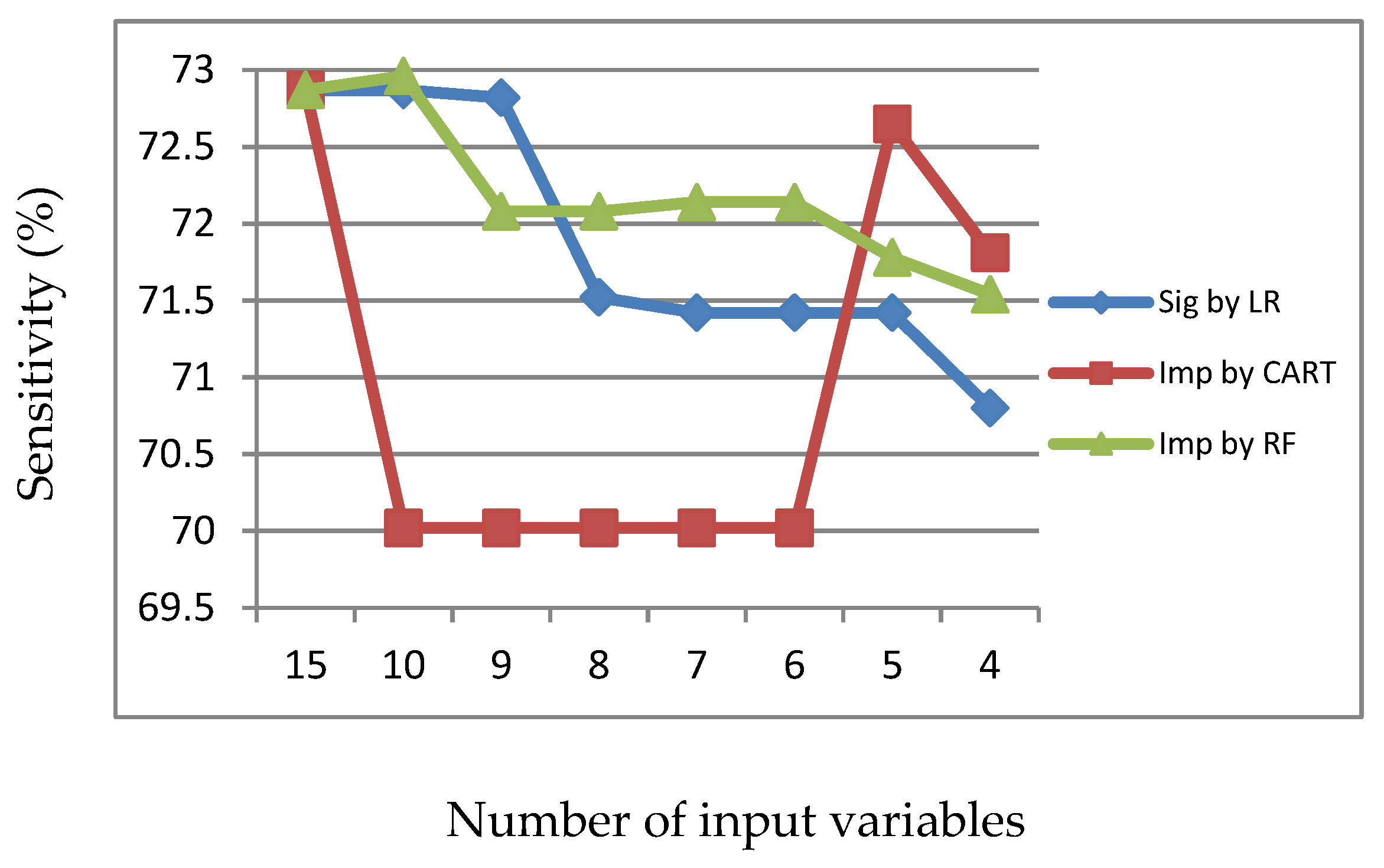
Figure 1.
Accuracy of LR, CART and RF with input of significant variables identified by LR.
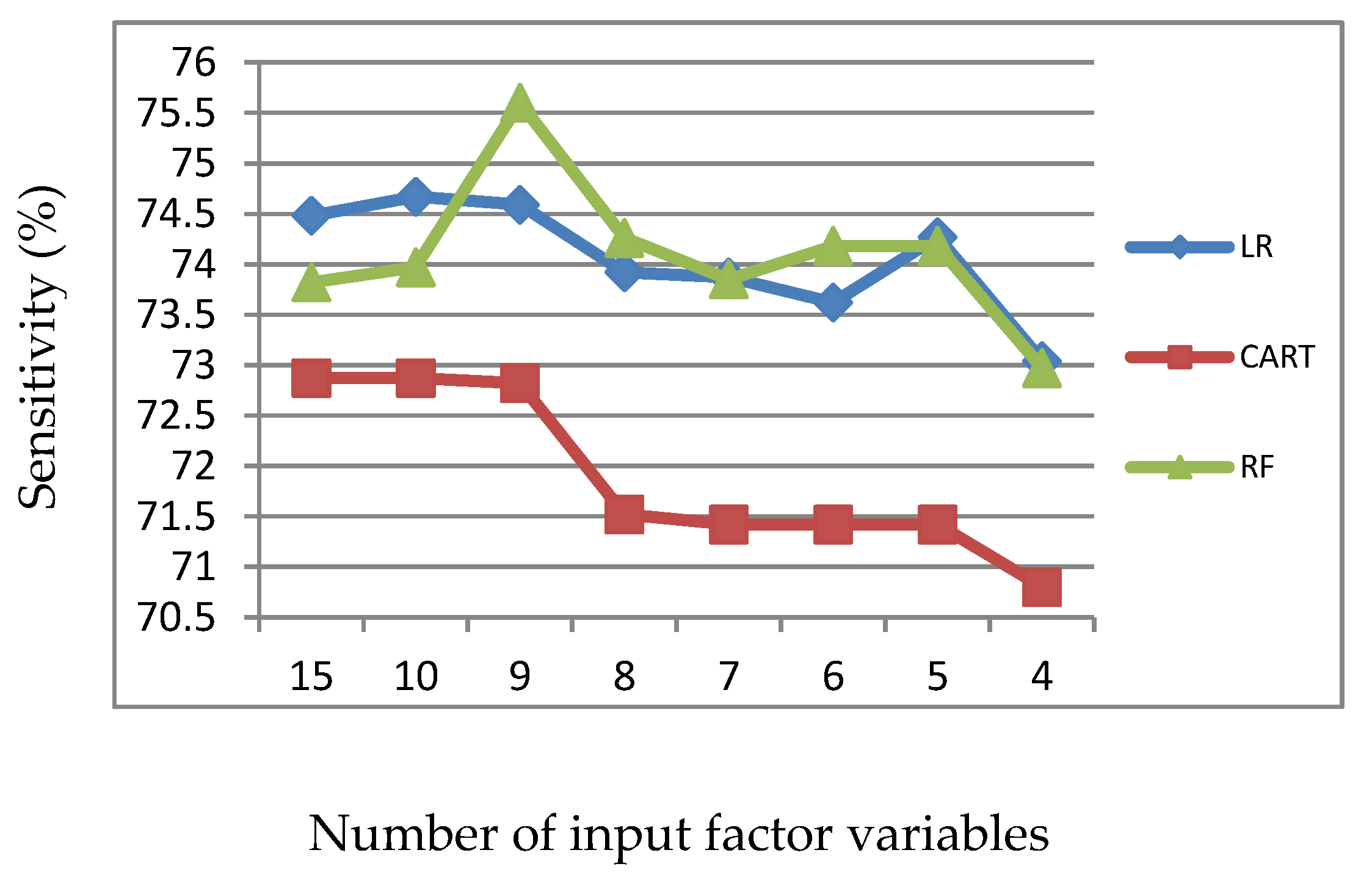
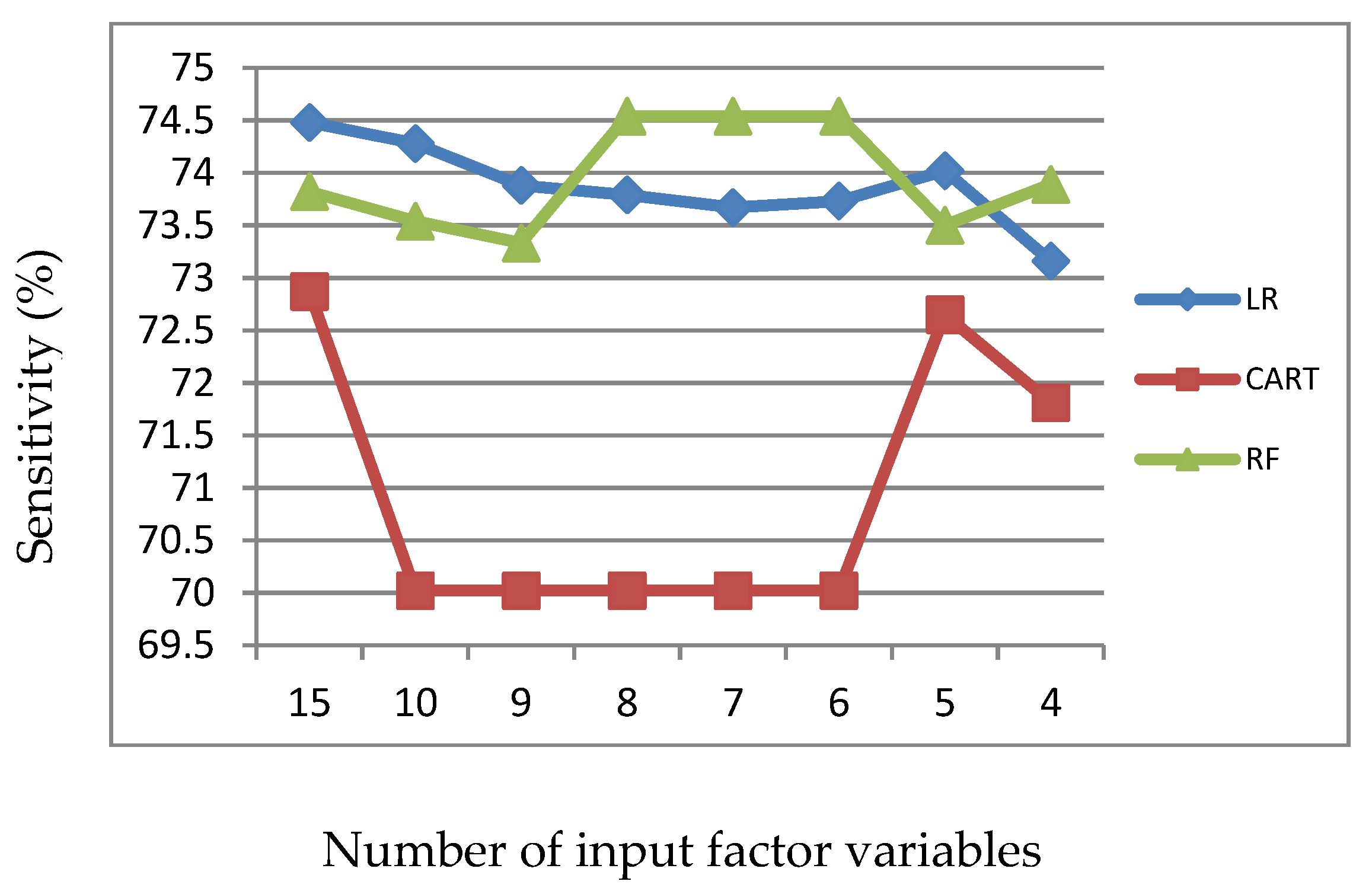
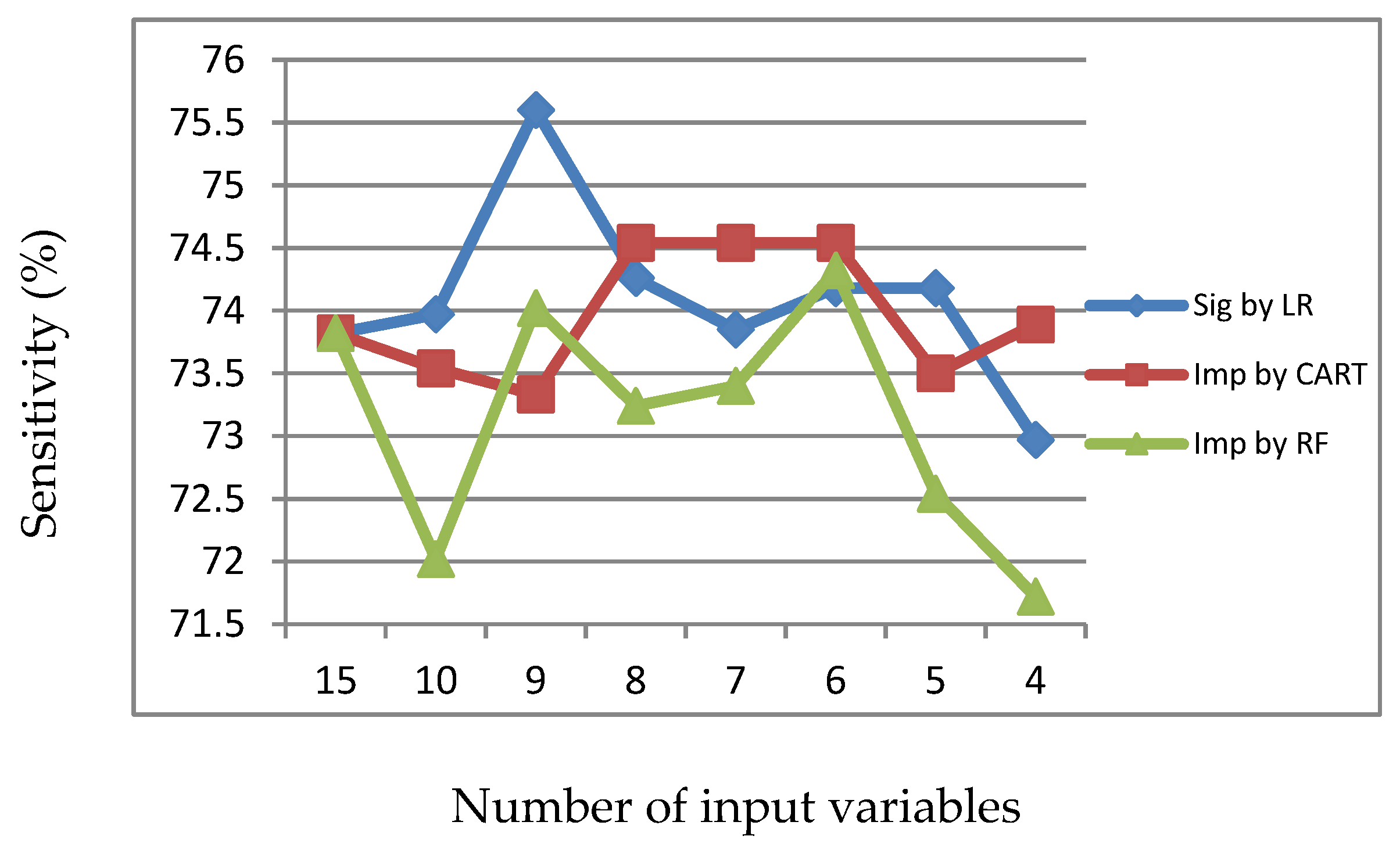
Figure 2.
Sensitivity of LR, CART and RF with input of significant variables identified by LR.
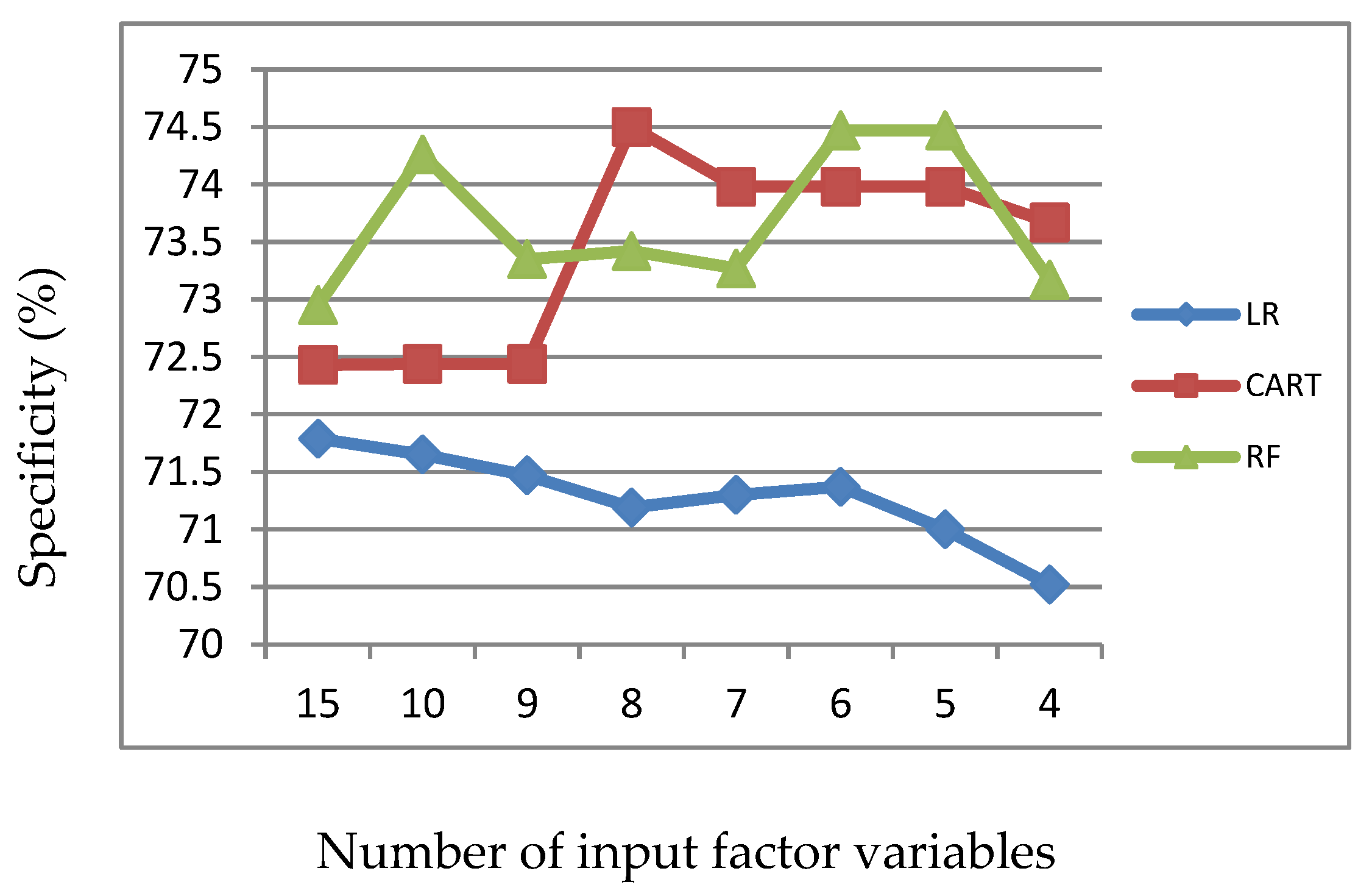
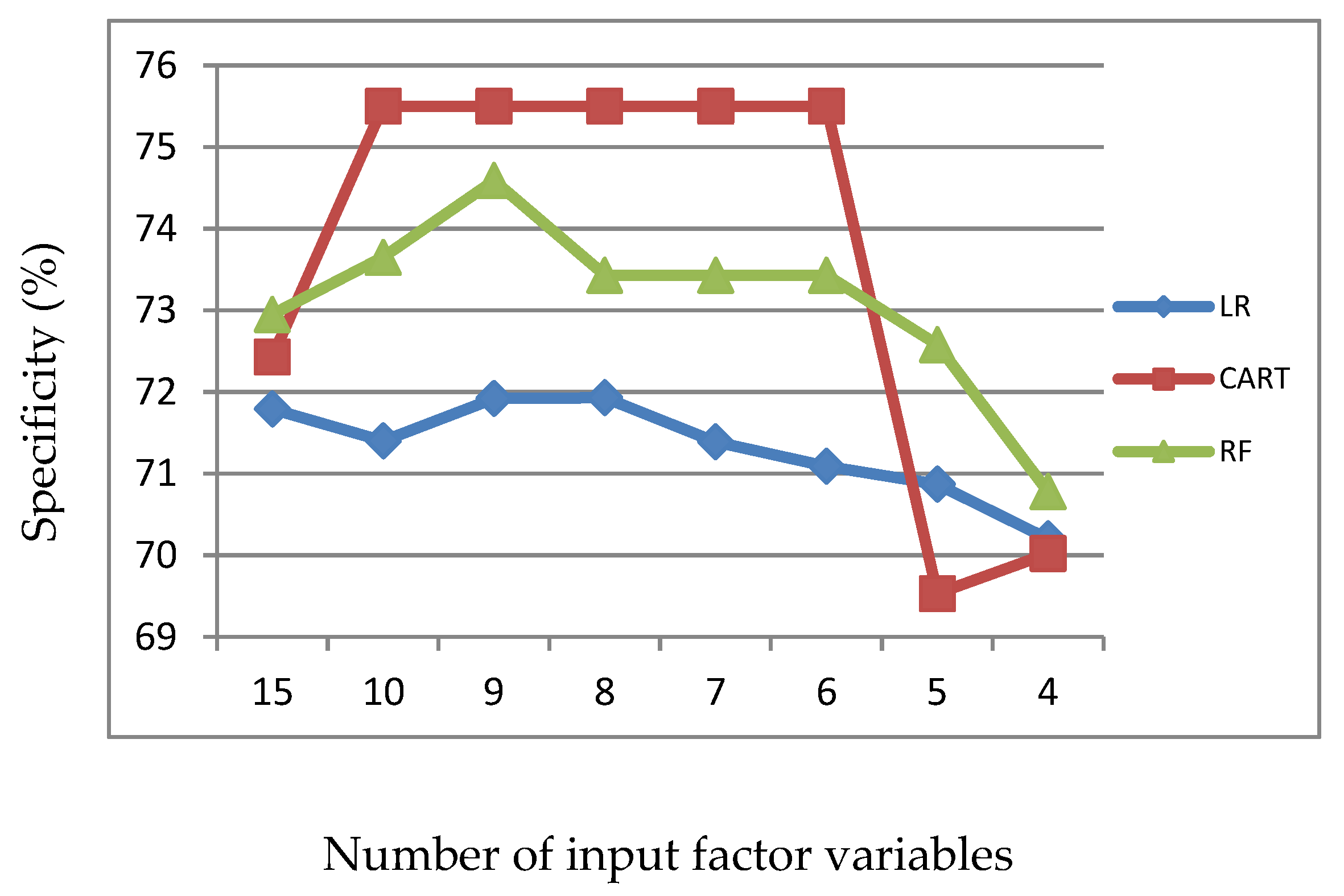
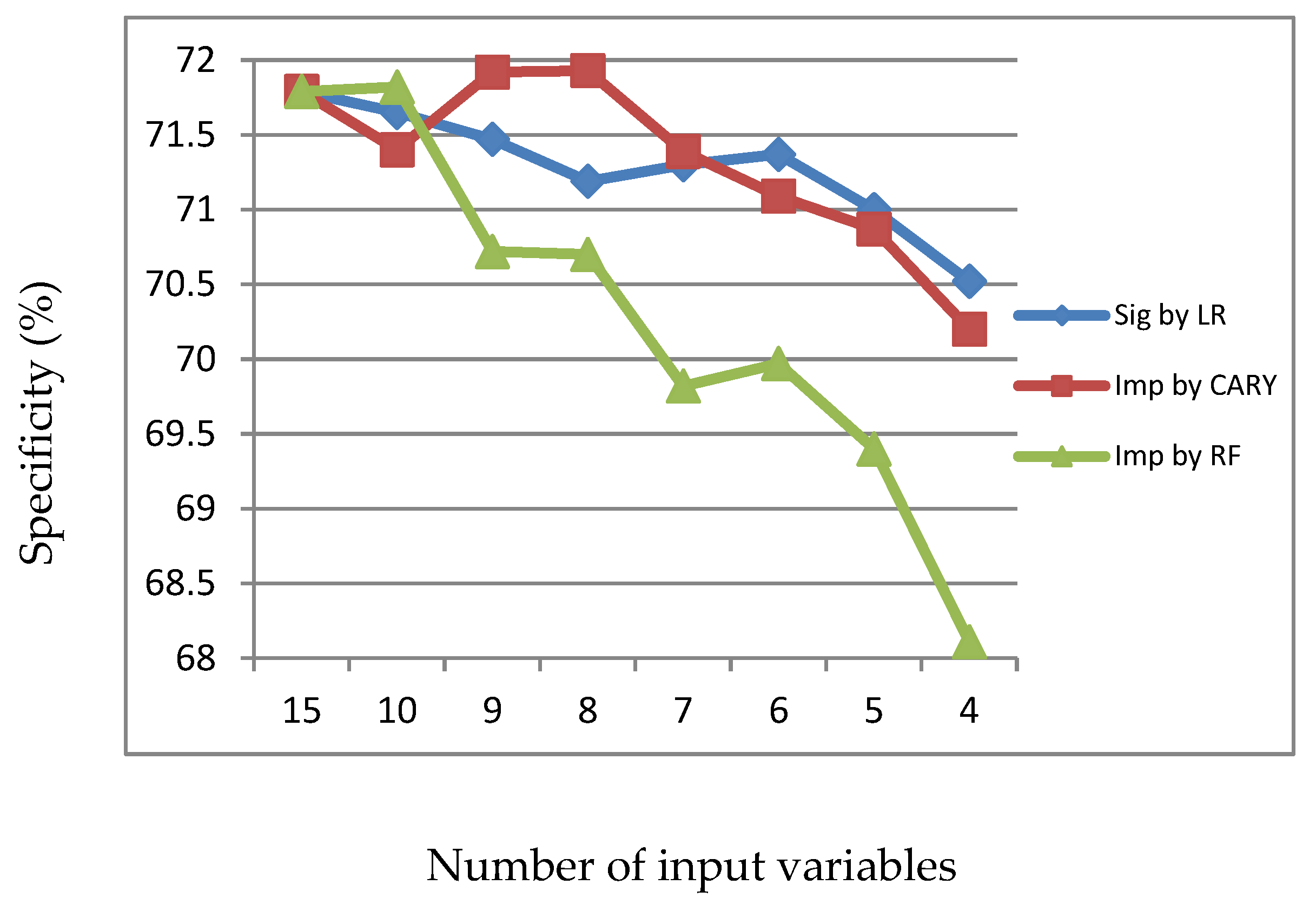
Figure 3.
Specificity of LR, CART and RF with input of significant variables identified by LR.
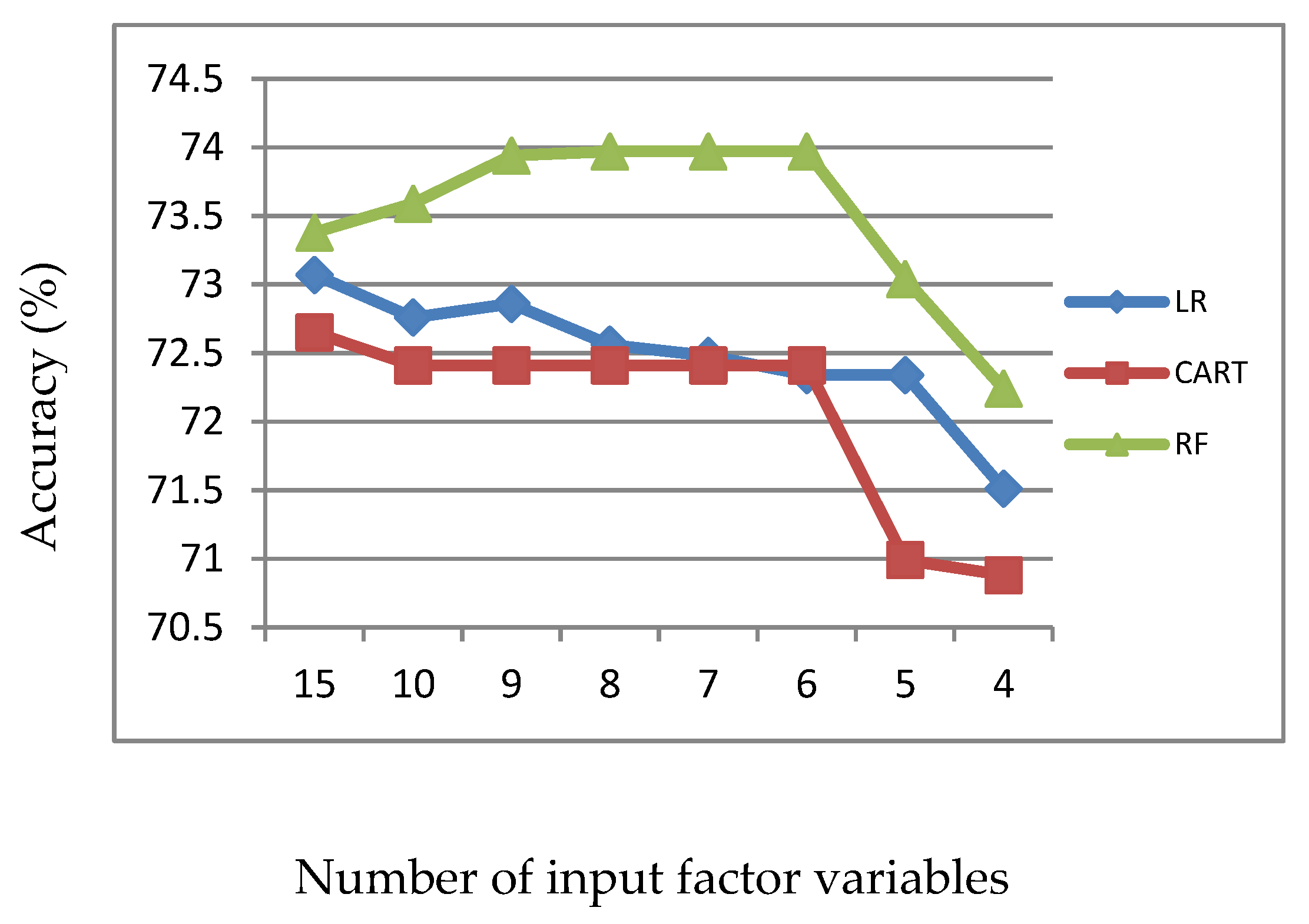
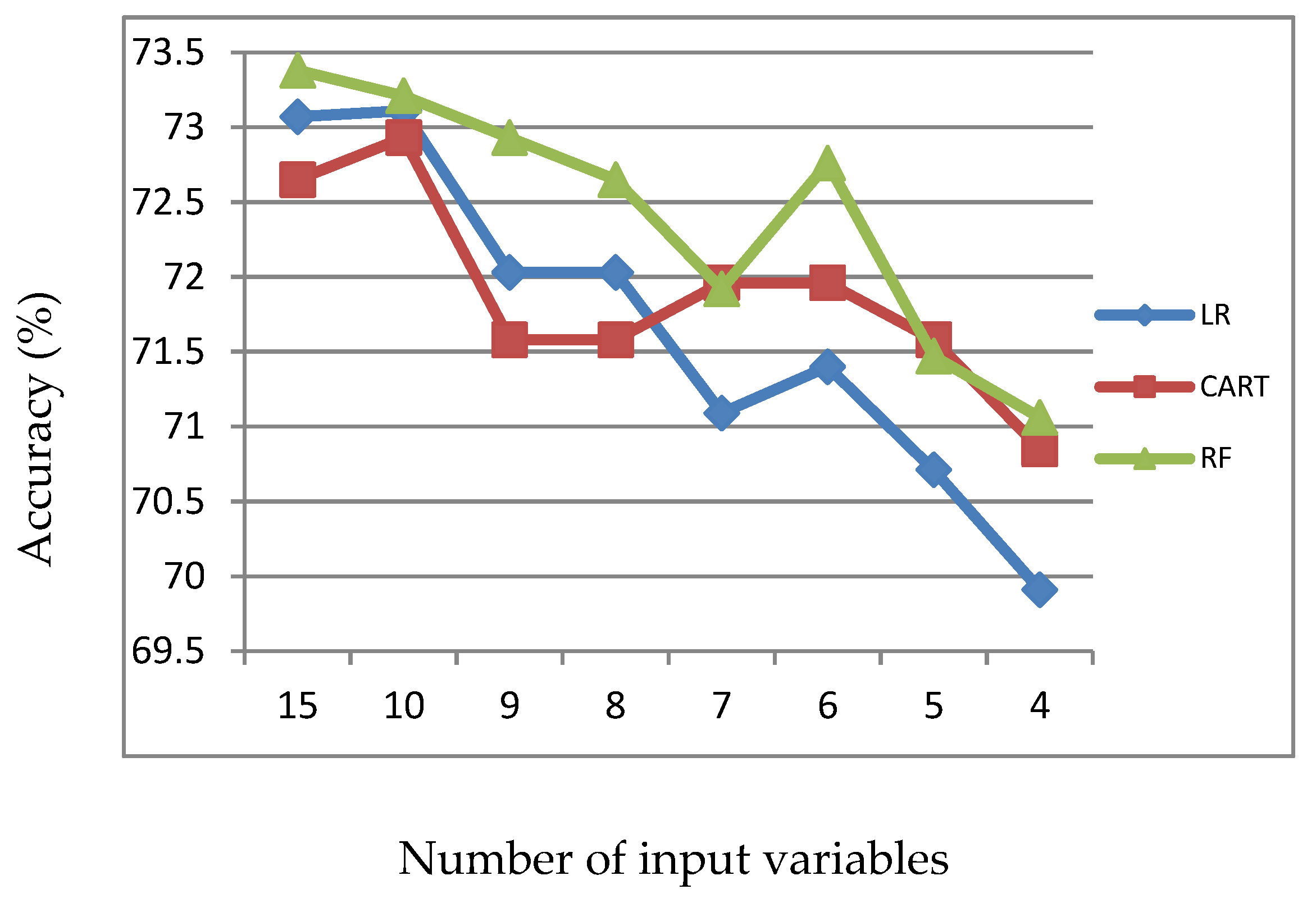
Figure 4.
Accuracy of LR, CART and RF with input of important variables identified by CART.
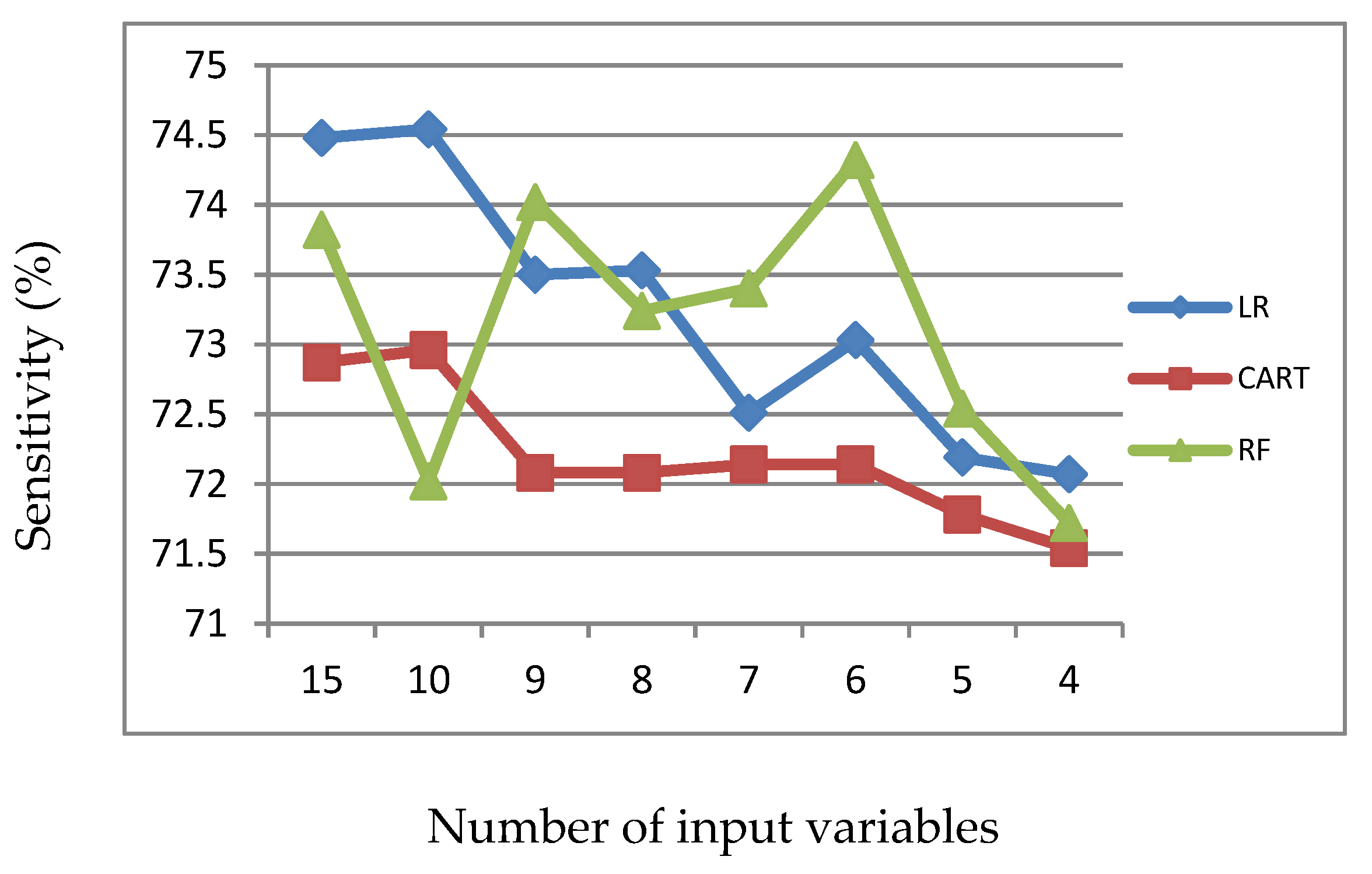
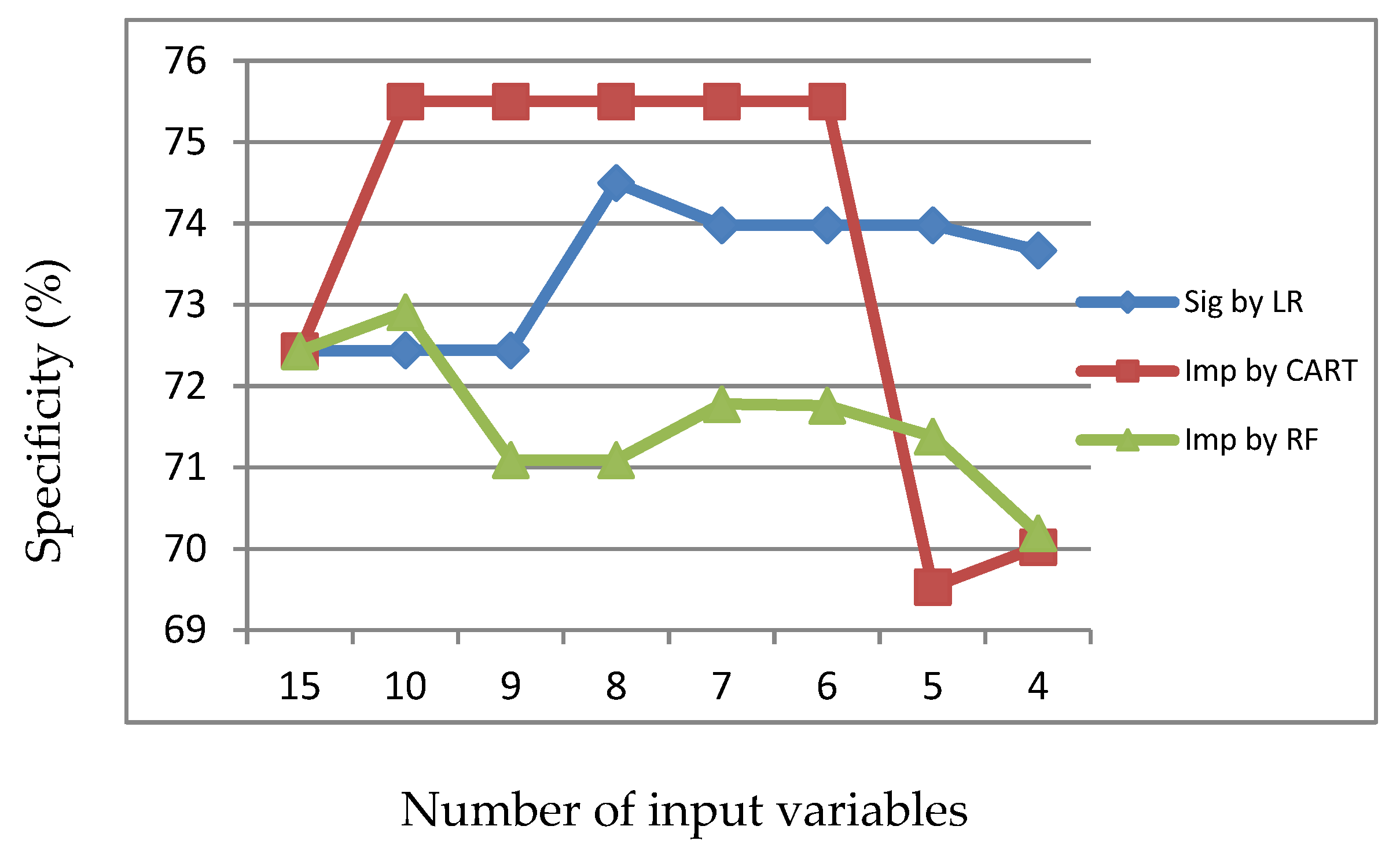
Figure 5.
Sensitivity of LR, CART and RF with input of important variables identified by CART.
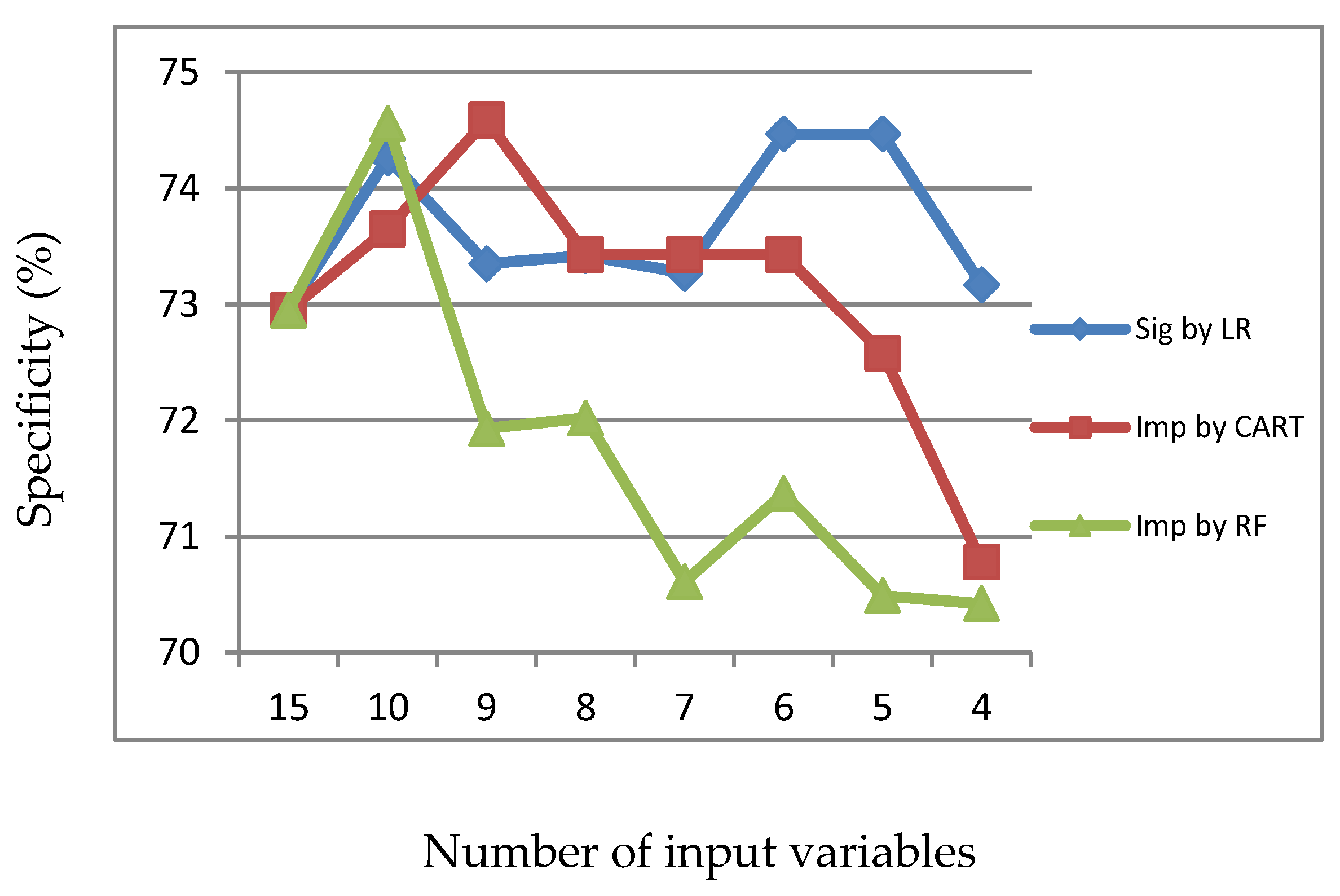
Figure 6.
Specificity of LR, CART and RF with input of important variables identified by CART.
Figure 7.
Accuracy of LR, CART and RF with input of important variables identified by RF.
Figure 8.
Sensitivity of LR, CART and RF with input of important variables identified by RF.
Figure 9.
Specificity of LR, CART and RF with input of important variables identified by RF.
Figure 10.
Accuracy of LR with input of significant or important variables.
Figure 11.
Accuracy of CART with input of significant or important variables.
Figure 12.
Accuracy of RF with input of significant or important variables.
Figure 13.
Sensitivity of LR with input of significant or important variables.
Figure 14.
Sensitivity of CART with input of significant or important variables.
Figure 15.
Sensitivity of RF with input of significant or important variables.
Figure 16.
Specificity of LR with input of significant or important variables.
Figure 17.
Specificity of CART with input of significant or important variables.
Figure 18.
Specificity of RF with input of significant or important variables.
Table 1.
Metric of multicollinearity of 15 correlated variables. GEN: driver gender; AGE: driver age; ALC: alcohol use; LIC: license; VEH: vehicle type; DRI: driver occupation; JOU: journey purpose; ACT: action; MAJ: major cause; WEA: weather condition; LIG: light condition; OBS: obstacle; CRA: crash position; LOC: location; SPE: speed limit.
| | GEN | AGE | ALC | LIC | VEH | DRI | JOU | ACT | MAJ | WEA | LIG | OBS | CRA | LOC | SPE |
|---|
| GEN | 1 | −0.064 | −0.057 | −0.009 | 0.061 | 0.120 | 0.074 | 0.009 | 0.051 | −0.006 | −0.016 | −0.014 | −0.004 | −0.010 | −0.062 |
| AGE | −0.064 | 1 | −0.021 | −0.033 | −0.044 | 0.012 | 0.010 | 0.007 | 0.021 | −0.025 | −0.075 | −0.004 | 0.018 | 0.028 | 0.059 |
| ALC | −0.057 | −0.021 | 1 | 0.219 | 0.065 | 0.047 | 0.100 | 0.011 | 0.034 | −0.032 | 0.189 | −0.010 | 0.043 | 0.034 | 0.003 |
| LIC | −0.009 | −0.033 | 0.219 | 1 | 0.105 | 0.039 | 0.058 | 0.033 | 0.028 | −0.005 | 0.089 | −0.006 | 0.065 | 0.008 | −0.015 |
| VEH | 0.061 | −0.044 | 0.065 | 0.105 | 1 | 0.176 | 0.103 | 0.032 | 0.087 | 0.020 | 0.009 | −0.028 | 0.056 | −0.011 | −0.086 |
| DRI | 0.120 | 0.012 | 0.047 | 0.039 | 0.176 | 1 | 0.288 | 0.041 | 0.055 | 0.011 | 0.025 | −0.020 | 0.010 | 0.006 | −0.077 |
| JOU | 0.074 | 0.010 | 0.100 | 0.058 | 0.103 | 0.288 | 1 | 0.044 | 0.059 | −0.004 | 0.079 | −0.030 | −0.004 | 0.002 | −0.066 |
| ACT | 0.009 | 0.007 | 0.011 | 0.033 | 0.032 | 0.041 | 0.044 | 1 | 0.013 | −0.026 | 0.034 | 0.013 | 0.105 | 0.073 | 0.039 |
| MAJ | 0.051 | 0.021 | 0.034 | 0.028 | 0.087 | 0.055 | 0.059 | 0.013 | 1 | 0.107 | 0.020 | 0.059 | 0.186 | 0.125 | −0.122 |
| WEA | −0.006 | −0.025 | −0.032 | −0.005 | 0.020 | 0.011 | −0.004 | −0.026 | 0.107 | 1 | 0.026 | 0.002 | −0.035 | 0.015 | −0.092 |
| LIG | −0.016 | −0.075 | 0.189 | 0.089 | 0.009 | 0.025 | 0.079 | 0.034 | 0.020 | 0.026 | 1 | 0.028 | −0.011 | −0.058 | −0.105 |
| OBS | −0.014 | −0.004 | −0.010 | −0.006 | −0.028 | −0.020 | −0.030 | 0.013 | 0.059 | 0.002 | 0.028 | 1 | 0.031 | −0.027 | −0.034 |
| CRA | −0.004 | 0.018 | 0.043 | 0.065 | 0.056 | 0.010 | −0.004 | 0.105 | 0.186 | −0.035 | −0.011 | 0.031 | 1 | 0.047 | −0.043 |
| LOC | −0.010 | 0.028 | 0.034 | 0.008 | −0.011 | 0.006 | 0.002 | 0.073 | 0.125 | 0.015 | −0.058 | −0.027 | 0.047 | 1 | 0.289 |
| SPE | −0.062 | 0.059 | 0.003 | −0.015 | −0.086 | −0.077 | −0.066 | 0.039 | −0.122 | −0.092 | −0.105 | −0.034 | −0.043 | 0.289 | 1 |
Table 2.
Descriptive statistics of accident data.
| Variable | Value | Total Number of Accidents = 9472 |
|---|
| Count | Percent (%) |
|---|
| Dependent variable: | | | |
| | | |
| Accident severity | 1. serious accident | 4736 | 50 |
| 2. minor accident | 4736 | 50 |
| Independent variable: | | | |
| | | |
| Driver gender | 1. male | 8180 | 86.4 |
| 2. female | 1292 | 13.6 |
| Driver age | 1. under 30 years old | 3121 | 32.9 |
| 2. 30–39 years old | 2853 | 30.1 |
| 3. 40–49 years old | 2170 | 22.9 |
| 4. 50–65 years old | 1201 | 12.7 |
| 5. above 65 years old | 127 | 1.3 |
| Alcohol use | 1. nondrunken driving | 8164 | 86.2 |
| 2. drunken driving | 1016 | 10.7 |
| 3. unknown | 292 | 3.1 |
| License | 1. with license | 9016 | 95.2 |
| 2. without license | 407 | 4.3 |
| 3. unknown | 49 | 0.5 |
| Vehicle type | 1. bus | 286 | 3.0 |
| 2. heavy truck or tractor-trailer | 1520 | 16.0 |
| 3. passenger car | 5859 | 61.9 |
| 4. light truck | 1688 | 17.8 |
| 5. motorcycle or bicycle | 119 | 1.3 |
| Driver occupation | 1. in job | 6575 | 69.2 |
| 2. student | 202 | 2.1 |
| 3. jobless | 547 | 5.8 |
| 4. unknown | 2148 | 22.7 |
| Journey purpose | 1. commuting trip | 1301 | 13.7 |
| 2. business trip | 446 | 4.7 |
| 3. transportation activity | 1487 | 16.2 |
| 4. visiting, shopping or touring trip | 939 | 9.7 |
| 5. others | 5299 | 55.9 |
| Action | 1. forward | 6876 | 72.6 |
| 2. leftward lane change | 655 | 6.9 |
| 3. rightward lane change | 831 | 8.8 |
| 4. overtaking | 22 | 0.2 |
| 5. abrupt deceleration | 590 | 6.2 |
| 6. others | 498 | 5.3 |
| Major cause | 1. improper lane change | 986 | 10.2 |
| 2. speeding | 189 | 2.0 |
| 3. failure to keep a safe distance | 4002 | 42.3 |
| 4. driving disability | 877 | 9.3 |
| 5. failure to pay attention to the front | 645 | 6.8 |
| 6. brake failure or tire puncture | 613 | 6.5 |
| 7. reverse driving a | 35 | 0.4 |
| 8. others | 2125 | 22.4 |
| Weather condition | 1. sunny | 6643 | 70.1 |
| 2. cloudy | 836 | 8.8 |
| 3. rainy, stormy or foggy | 1993 | 21.0 |
| Light condition | 1. daytime | 5340 | 56.4 |
| 2. dawn or dusk | 279 | 2.9 |
| 3. nighttime with illumination | 2372 | 25.0 |
| 4. nighttime without illumination | 1481 | 15.6 |
| Obstacle | 1. none | 9037 | 95.4 |
| 2. work zone | 272 | 2.9 |
| 3. broken down vehicle on road | 61 | 0.6 |
| 4. others | 102 | 1.1 |
| Crash position | 1. car front | 5233 | 55.2 |
| 2. car rear | 212 | 2.2 |
| 3. car right side | 1870 | 19.7 |
| 4. car left side | 1868 | 19.7 |
| 5. others | 289 | 3.1 |
| Location | 1. traffic lane | 7002 | 73.9 |
| 2. ramp | 1229 | 13.0 |
| 3. acceleration and deceleration lane | 222 | 2.3 |
| 4. shoulder | 489 | 5.2 |
| 5. others | 530 | 5.6 |
| Speed limit | 1. 110 km/h | 2186 | 23.1 |
| 2. 100 km/h | 4054 | 42.8 |
| 3. 90–70 km/h | 1367 | 14.4 |
| 4. 60–40 km/h | 1865 | 19.7 |
Table 3.
Comparisons between significant variables and important variables. LR: logistic regression; CART: classification and regression tree; RF: and random forest.
| Significant Variables by LR | Important Variables by CART | Important Variables by RF |
|---|
| Variable | p-Value | Variable | Importance Score | Variable | Importance Score |
|---|
| Major cause | 0.000 | Major cause | 0.61 | Driver age | 21.15 |
| Vehicle type | 0.000 | Alcohol use | 0.06 | Major cause | 15.10 |
| Speed limit | 0.000 | Location | 0.05 | Journey purpose | 14.25 |
| Alcohol use | 0.000 | Speed limit | 0.04 | Crash position | 12.20 |
| Crash position | 0.000 | Crash position | 0.03 | Light condition | 11.35 |
| License | 0.000 | Vehicle type | 0.03 | Vehicle type | 10.65 |
| Journey purpose | 0.000 | Obstacle | 0.03 | Action | 10.50 |
| Light condition | 0.000 | License | 0.03 | Location | 9.85 |
| Location | 0.000 | Driver occupation | 0.03 | Weather condition | 9.50 |
| Action | 0.001 | Journey purpose | 0.03 | Speed limit | 8.80 |
Table 4.
Accuracy, sensitivity and specificity of LR, CART and RF with input of the 15 original variables.
| Input Variables | | LR (%) | CART (%) | RF (%) |
|---|
| 15 original variables | Accuracy | 73.07 | 72.65 | 73.38 |
| Sensitivity | 74.48 | 72.87 | 73.82 |
| Specificity | 71.79 | 72.43 | 72.95 |
Table 5.
Accuracy, sensitivity and specificity of LR, CART and RF with input of significant variables identified by LR.
| Input Variables | | LR (%) | CART (%) | RF (%) |
|---|
| 15 original variables | Accuracy | 73.07 | 72.65 | 73.38 |
| Sensitivity | 74.48 | 72.87 | 73.82 |
| Specificity | 71.79 | 72.43 | 72.95 |
| 10 significant variables by LR | Accuracy | 73.07 | 72.65 | 74.11 |
| Sensitivity | 74.67 | 72.87 | 73.97 |
| Specificity | 71.65 | 72.44 | 74.26 |
| 9 significant variables by LR | Accuracy | 72.93 | 72.65 | 74.43 |
| Sensitivity | 74.59 | 72.82 | 75.60 |
| Specificity | 71.47 | 72.44 | 73.35 |
| 8 significant variables by LR | Accuracy | 72.82 | 72.9 | 73.84 |
| Sensitivity | 73.92 | 71.52 | 74.26 |
| Specificity | 71.19 | 74.50 | 73.42 |
| 7 significant variables by LR | Accuracy | 72.52 | 72.62 | 73.56 |
| Sensitivity | 73.87 | 71.42 | 73.85 |
| Specificity | 71.30 | 73.98 | 73.27 |
| 6 significant variables by LR | Accuracy | 72.45 | 72.62 | 74.32 |
| Sensitivity | 73.62 | 71.42 | 74.18 |
| Specificity | 71.37 | 73.98 | 74.47 |
| 5 significant variables by LR | Accuracy | 72.24 | 72.62 | 74.32 |
| Sensitivity | 74.27 | 71.42 | 74.18 |
| Specificity | 71.00 | 73.98 | 74.47 |
| 4 significant variables by LR | Accuracy | 71.72 | 72.13 | 73.07 |
| Sensitivity | 73.04 | 70.80 | 72.97 |
| Specificity | 70.52 | 73.67 | 73.17 |
Table 6.
Accuracy, sensitivity and specificity of LR, CART and RF with input of important variables identified by CART.
| Input Variables | | LR (%) | CART (%) | RF (%) |
|---|
| 15 original variables | Accuracy | 73.07 | 72.65 | 73.38 |
| Sensitivity | 74.48 | 72.87 | 73.82 |
| Specificity | 71.79 | 72.43 | 72.95 |
| 10 important variables by CART | Accuracy | 72.76 | 72.41 | 73.59 |
| Sensitivity | 74.28 | 70.02 | 73.54 |
| Specificity | 71.40 | 75.50 | 73.65 |
| 9 important variables by CART | Accuracy | 72.86 | 72.41 | 73.94 |
| Sensitivity | 73.88 | 70.02 | 73.33 |
| Specificity | 71.92 | 75.50 | 74.59 |
| 8 important variables by CART | Accuracy | 72.56 | 72.41 | 73.97 |
| Sensitivity | 73.79 | 70.02 | 74.54 |
| Specificity | 71.93 | 75.50 | 73.43 |
| 7 important variables by CART | Accuracy | 72.48 | 72.41 | 73.97 |
| Sensitivity | 73.67 | 70.02 | 74.54 |
| Specificity | 71.39 | 75.50 | 73.43 |
| 6 important variables by CART | Accuracy | 72.34 | 72.41 | 73.97 |
| Sensitivity | 73.73 | 70.02 | 74.54 |
| Specificity | 71.09 | 75.50 | 73.43 |
| 5 important variables by CART | Accuracy | 72.34 | 70.99 | 73.04 |
| Sensitivity | 74.02 | 72.65 | 73.50 |
| Specificity | 70.87 | 69.53 | 72.58 |
| 4 important variables by CART | Accuracy | 71.51 | 70.88 | 72.24 |
| Sensitivity | 73.16 | 71.81 | 73.89 |
| Specificity | 70.20 | 70.02 | 70.78 |
Table 7.
Accuracy, sensitivity and specificity of LR, CART and RF with input of important variables identified by RF.
| Input Variables | LR (%) | CART (%) | RF (%) |
|---|
| 15 original variables | Accuracy | 73.07 | 72.65 | 73.38 |
| Sensitivity | 74.48 | 72.87 | 73.82 |
| Specificity | 71.79 | 72.43 | 72.95 |
| 10 important variables by RF | Accuracy | 73.11 | 72.93 | 73.21 |
| Sensitivity | 74.54 | 72.96 | 72.02 |
| Specificity | 71.82 | 72.91 | 74.56 |
| 9 important variables by RF | Accuracy | 72.03 | 71.58 | 72.93 |
| Sensitivity | 73.50 | 72.08 | 74.02 |
| Specificity | 70.72 | 71.09 | 71.93 |
| 8 important variables by RF | Accuracy | 72.03 | 71.58 | 72.65 |
| Sensitivity | 73.53 | 72.08 | 73.24 |
| Specificity | 70.70 | 71.09 | 72.02 |
| 7 important variables by RF | Accuracy | 71.09 | 71.96 | 71.92 |
| Sensitivity | 72.51 | 72.14 | 73.40 |
| Specificity | 69.82 | 71.78 | 70.61 |
| 6 important variables by RF | Accuracy | 71.4 | 71.96 | 72.76 |
| Sensitivity | 73.03 | 72.14 | 74.32 |
| Specificity | 69.97 | 71.76 | 71.37 |
| 5 important variables by RF | Accuracy | 70.71 | 71.58 | 71.47 |
| Sensitivity | 72.19 | 71.78 | 72.54 |
| Specificity | 69.40 | 71.38 | 70.49 |
| 4 important variables by RF | Accuracy | 69.91 | 70.85 | 71.06 |
| Sensitivity | 72.07 | 71.54 | 71.72 |
| Specificity | 68.11 | 70.19 | 70.42 |
Table 8.
Estimation result of variable “major cause” and “action”.
| Variable | Value | B | p-Value | Exp(B) |
|---|
| Major cause | 1. improper lane change | –1.078 | 0.000 | 0.340 |
| 2. speeding | 0.685 | 0.001 | 1.984 |
| 3. failure to keep a safe distance | –1.855 | 0.000 | 0.157 |
| 4. driving disability | –0.034 | 0.809 | 0.967 |
| 5. failure to pay attention to the front | –0.584 | 0.000 | 0.557 |
| 6. brake failure or tire puncture | 0.121 | 0.298 | 1.128 |
| 7. reverse driving | 1.780 | 0.019 | 5.931 |
| 8. others | 0 b | 0 | 0 |
| Action | 1. forward | 0.164 | 0.170 | 1.178 |
| 2. left lane change | 0.189 | 0.250 | 1.208 |
| 3. right lane change | 0.425 | 0.008 | 1.529 |
| 4. overtaking | 1.571 | 0.006 | 4.810 |
| 5. abrupt deceleration | –0.009 | 0.956 | 0.991 |
| 6. others | 0 b | 0 | 0 |
Table 9.
Rules converted from tree graph as the output of CART.
| ID | Rule | S% | C% | L |
|---|
| | Antecedent | Consequent | | | |
| 1 | Vehicle type = (BS, HT) | Severity = MIN | 1.17 | 85.56 | 1.72 |
| and major cause = (ILC, FKS) |
| and location = (RP) |
| 2 | Vehicle type = (PC, LT) | Severity = MIN | 0.95 | 79.75 | 1.60 |
| and major cause = (ILC) |
| and speed limit = (60–40) |
| 3 | Major cause = (SP, DDA, FPF, BRF, RD, OR) | Severity = SER | 10.05 | 86.23 | 1.72 |
| and alcohol use = (DRD, UNK) |
| 4 | Major cause = (SP, DDA, FPF, BRF, RD, OR) | Severity = SER | 20.90 | 71.08 | 1.42 |
| and alcohol use = (NDR) |
| and speed limit = (110, 100, 90–70) |