MNCE: Multi-Hop Node Localization Algorithm for Wireless Sensor Network Based on Error Correction
Abstract
1. Introduction
- Range-based localization algorithms require additional physical measurement techniques to complete the localization calculation. Physical measurement techniques, such as RSSI, TOA and AOA, are often used in the localization process of range-based localization algorithms [8];
- Range-free localization algorithms usually use multi-hop routing information directly obtained by sensor nodes in the network to achieve node localization [9].
2. Range-Free Localization Algorithms
3. MNCE Algorithm
- Distance estimation: We can get the estimated distance between nodes by the information that can be directly obtained by sensor nodes such as arrival time, hop number information and connected information;
- Initial localization: According to the estimated distance of the previous stage, the corresponding estimation algorithm is selected to complete the initial localization of the target node;
- Calibration localization: According to the information of the first two stages, the redundant information is eliminated, and the corresponding optimization algorithm is selected to optimize and calibrate the estimated location of target nodes.
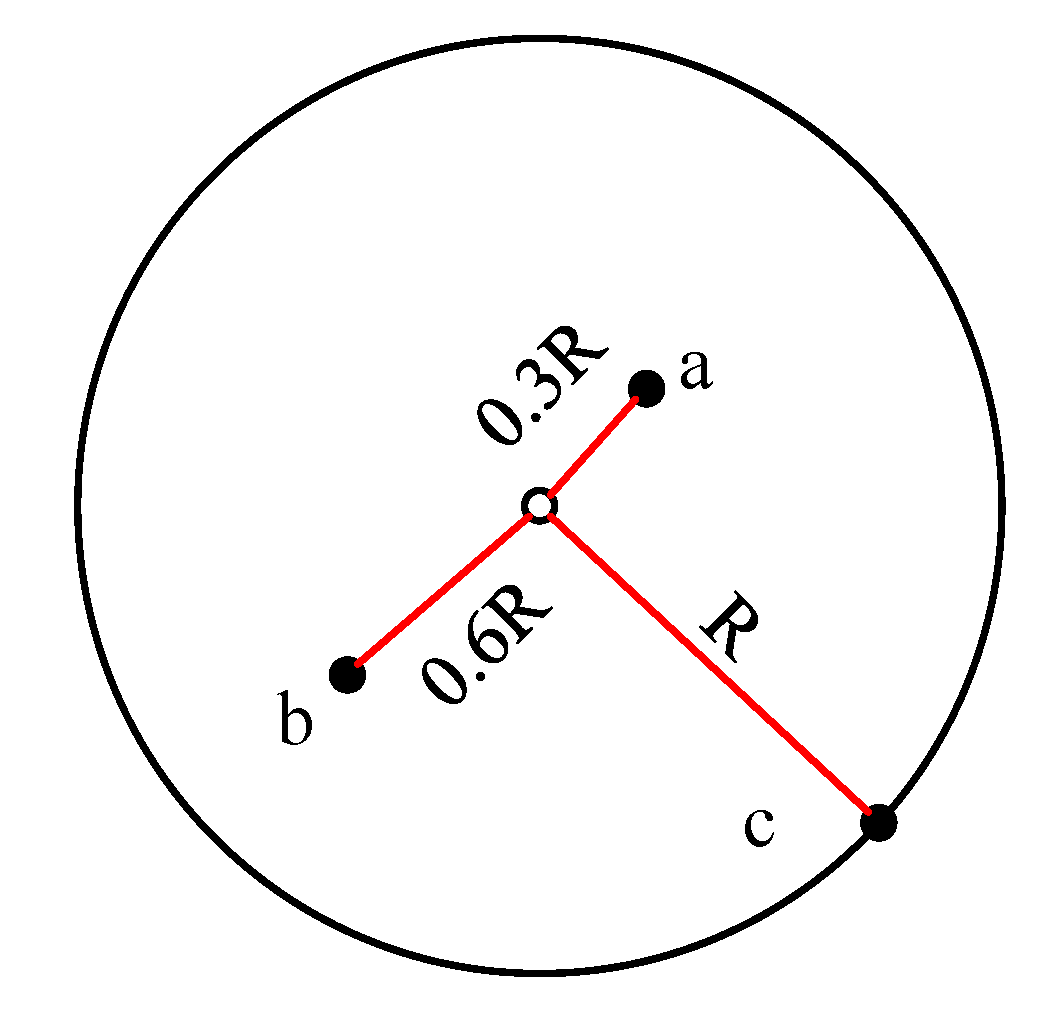
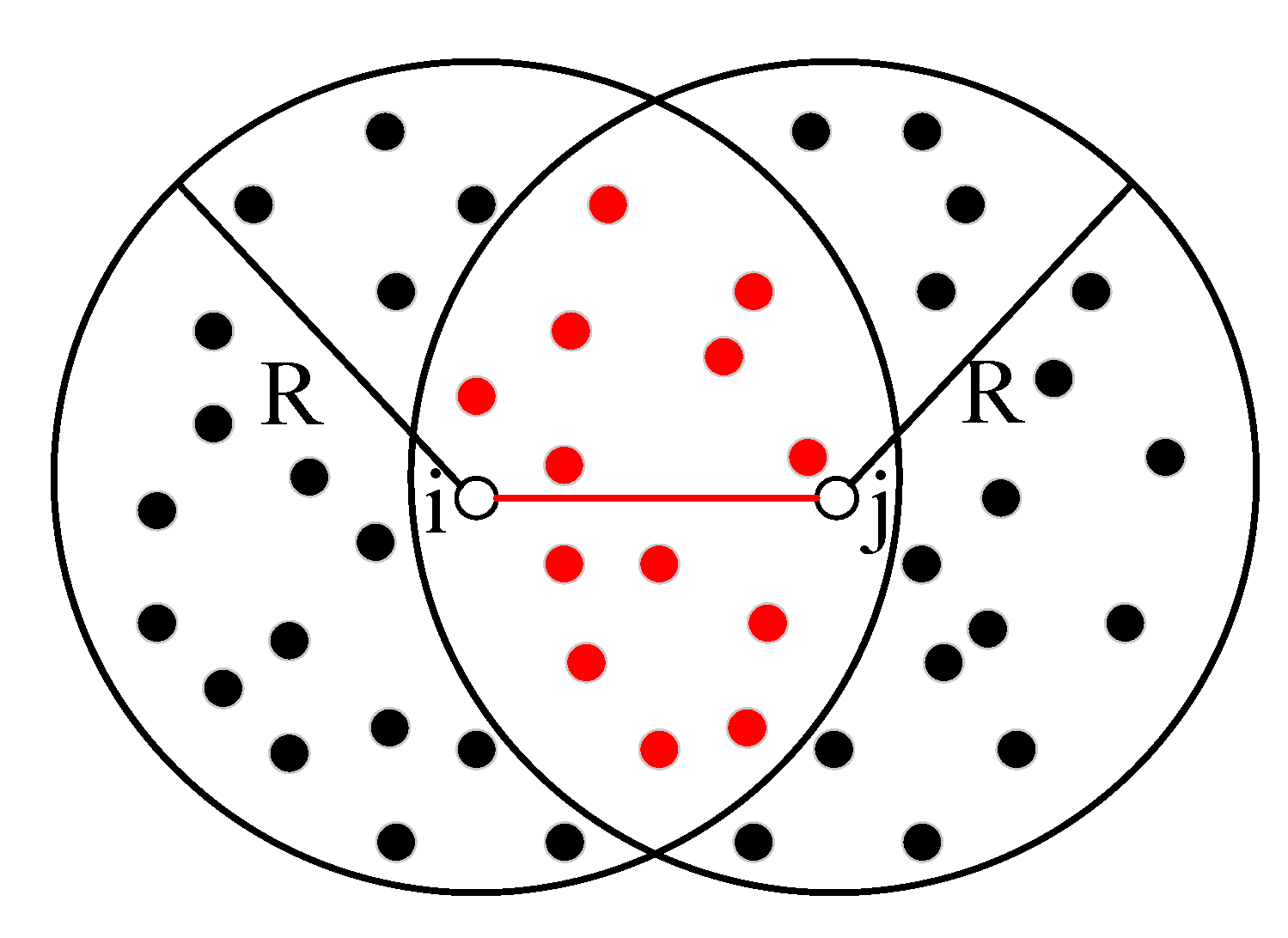
3.1. Distance Estimation
3.2. Error-Correction Rate for the Estimated Distance
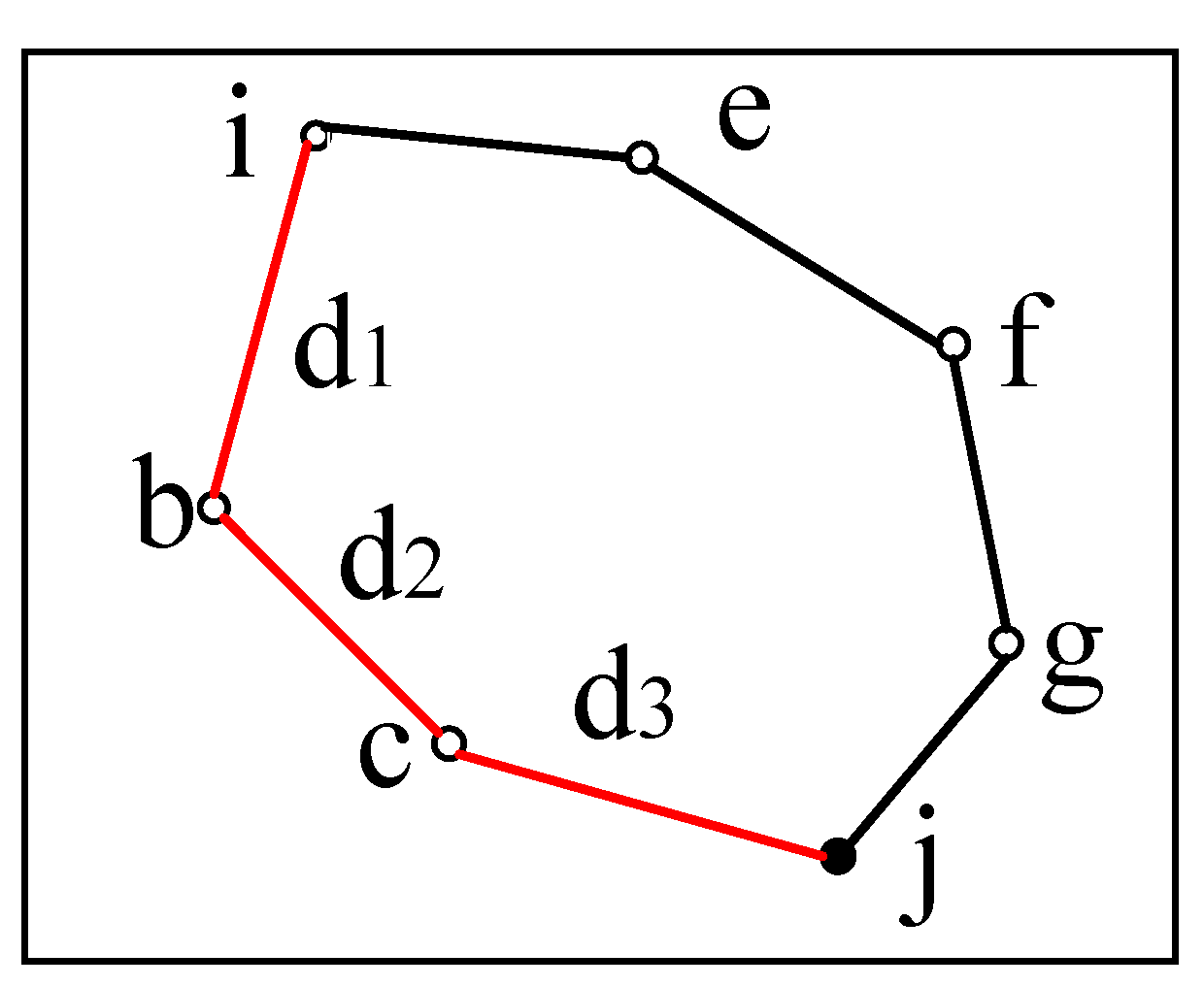
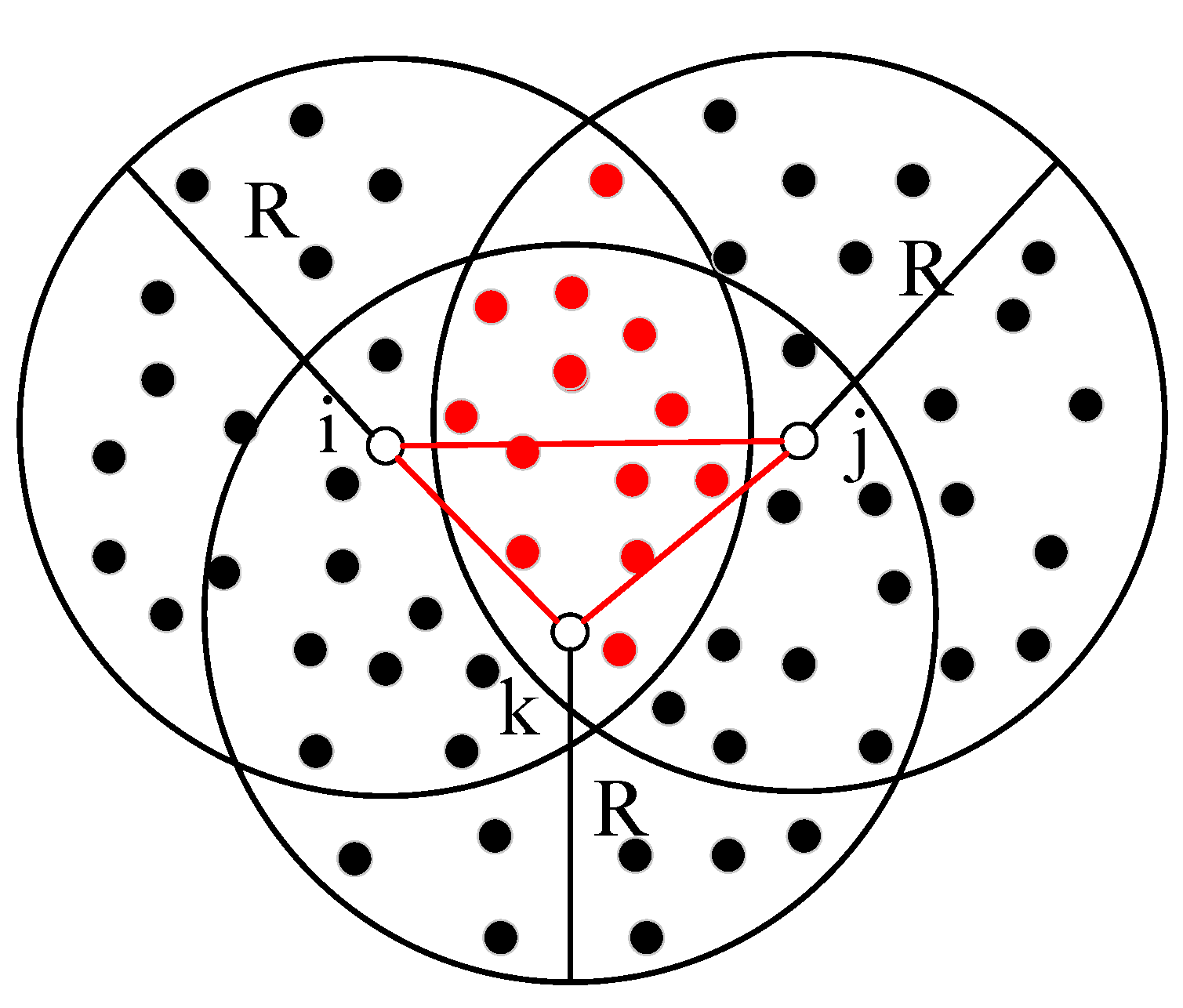
3.3. Node Location Method Based on Total Least Squares
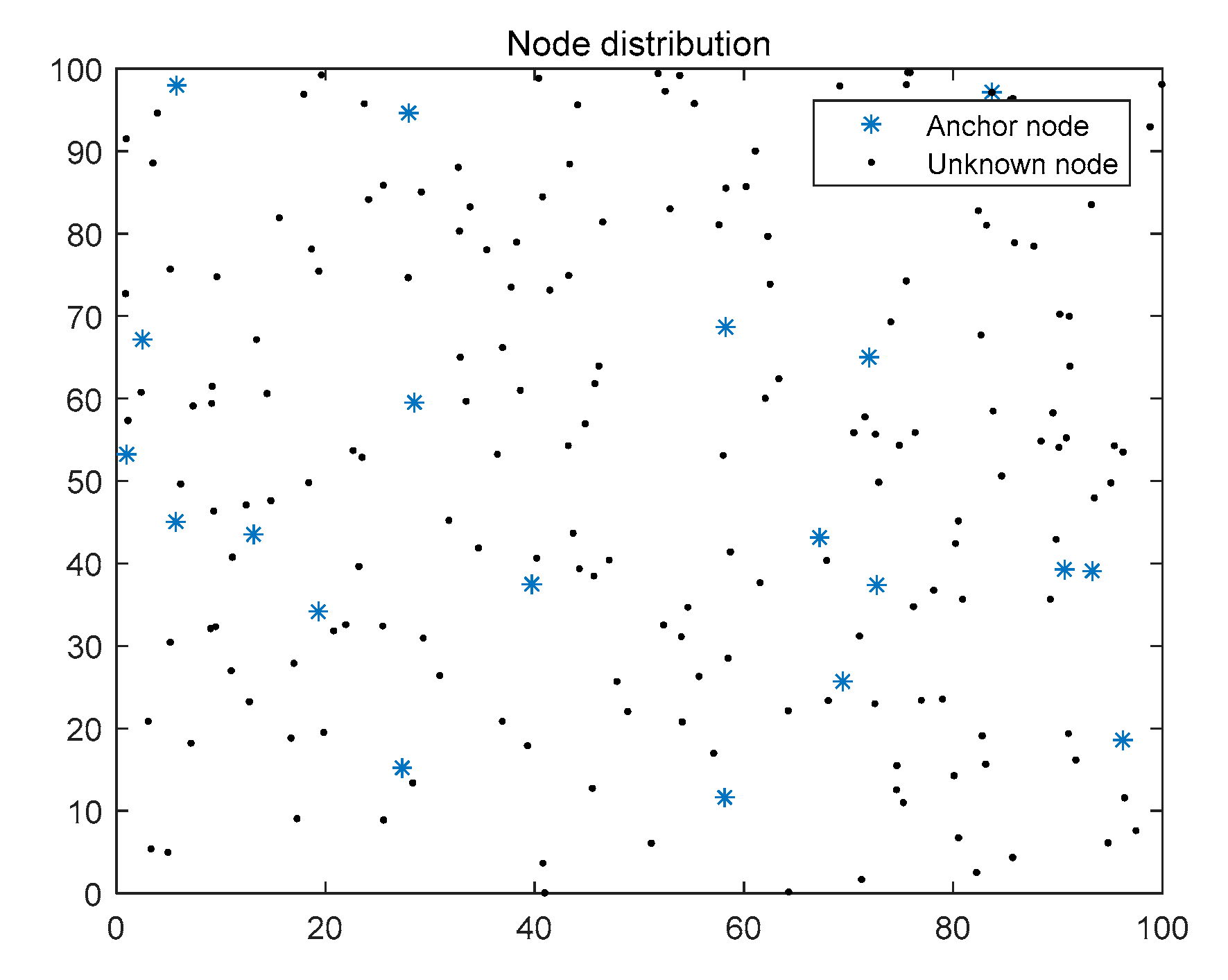
4. Simulation Experiment
4.1. Performance Indicators
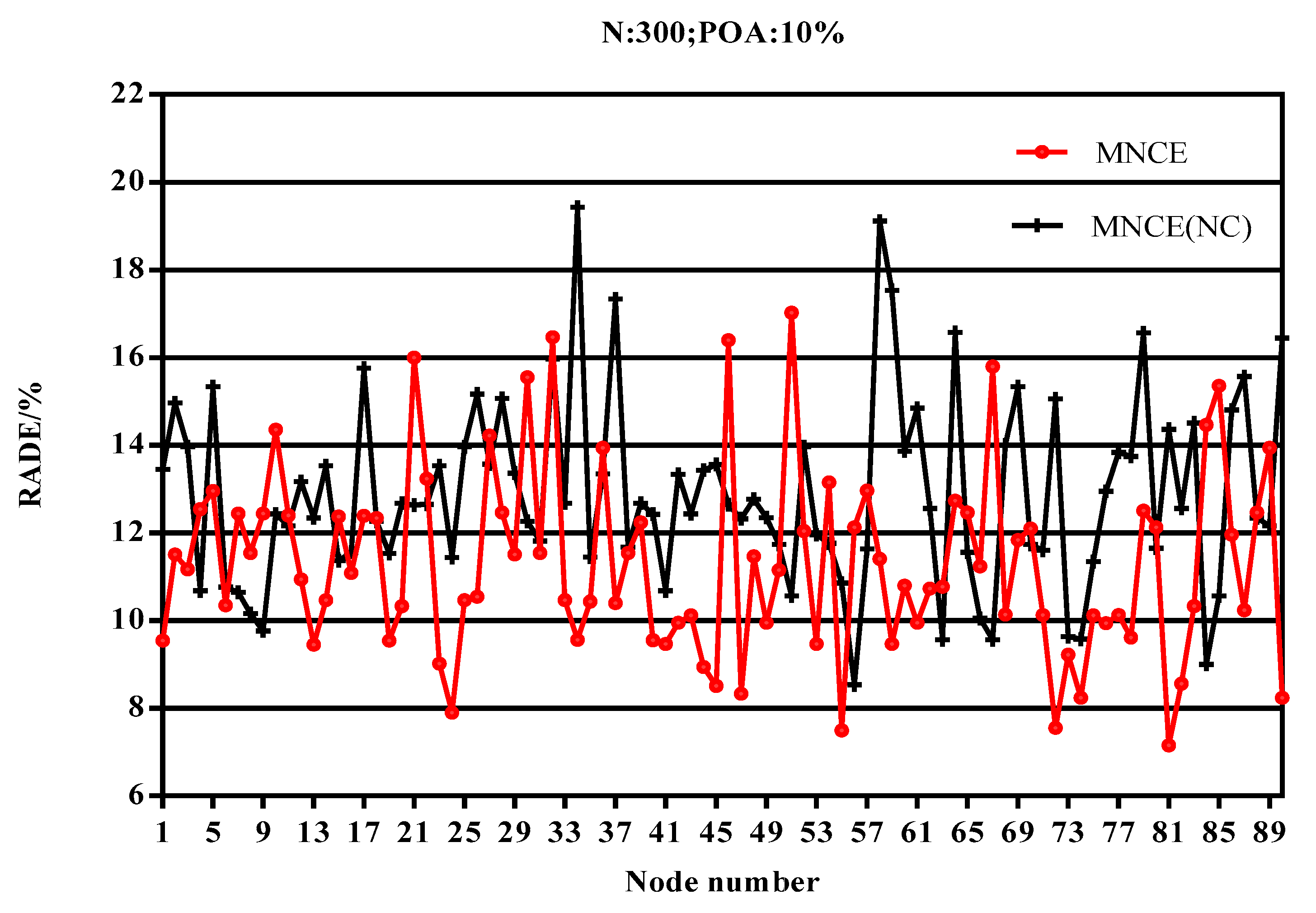
4.2. Impact of the Error Correction Rate on RADE
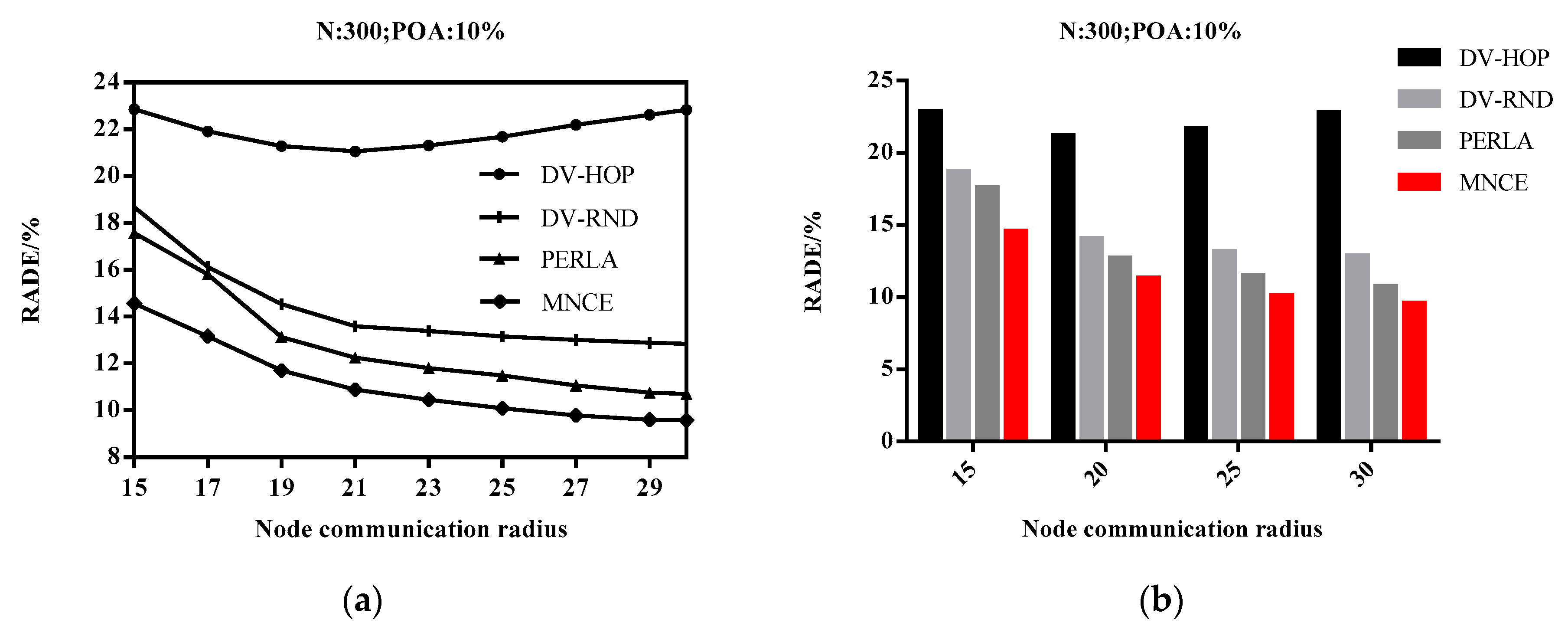
4.3. Impact of Node Communication Radius on RADE
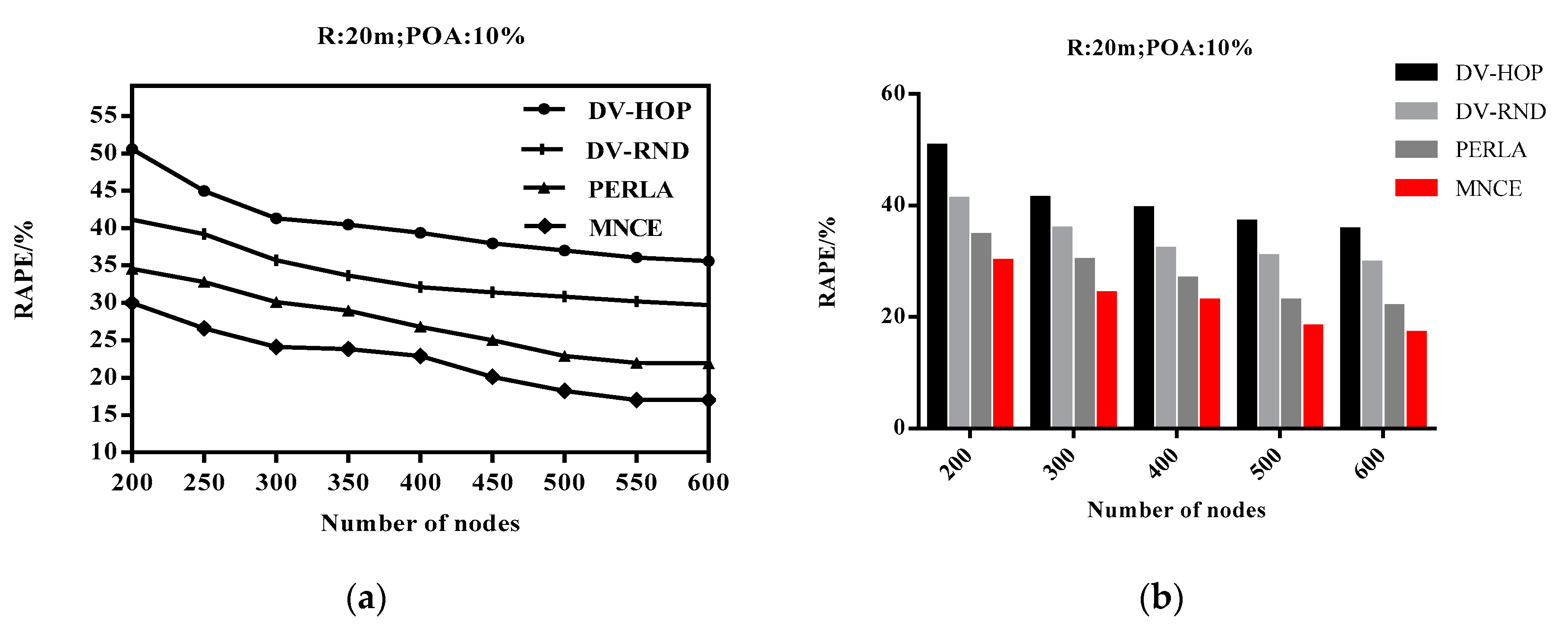
4.4. Impact of the Total Number of Nodes on RAPE
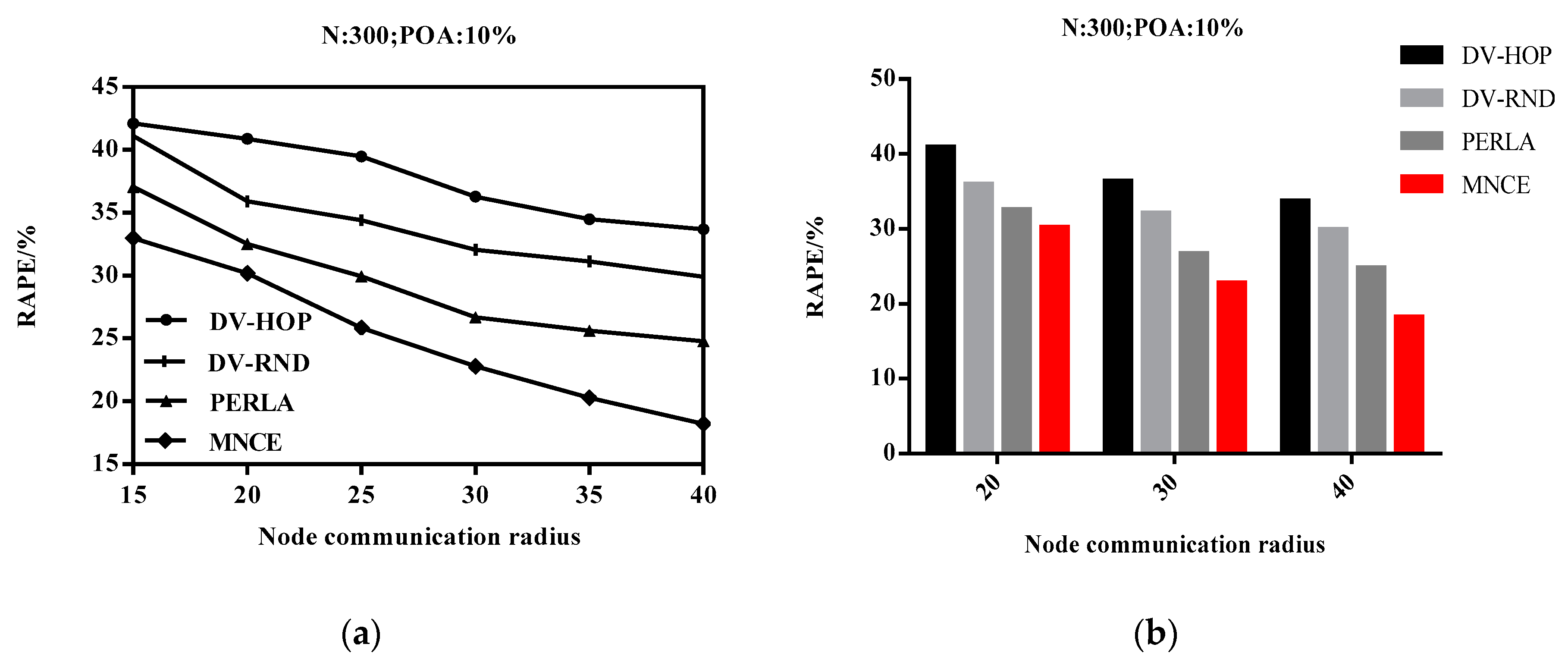
4.5. Impact of Node Communication Radius on RAPE
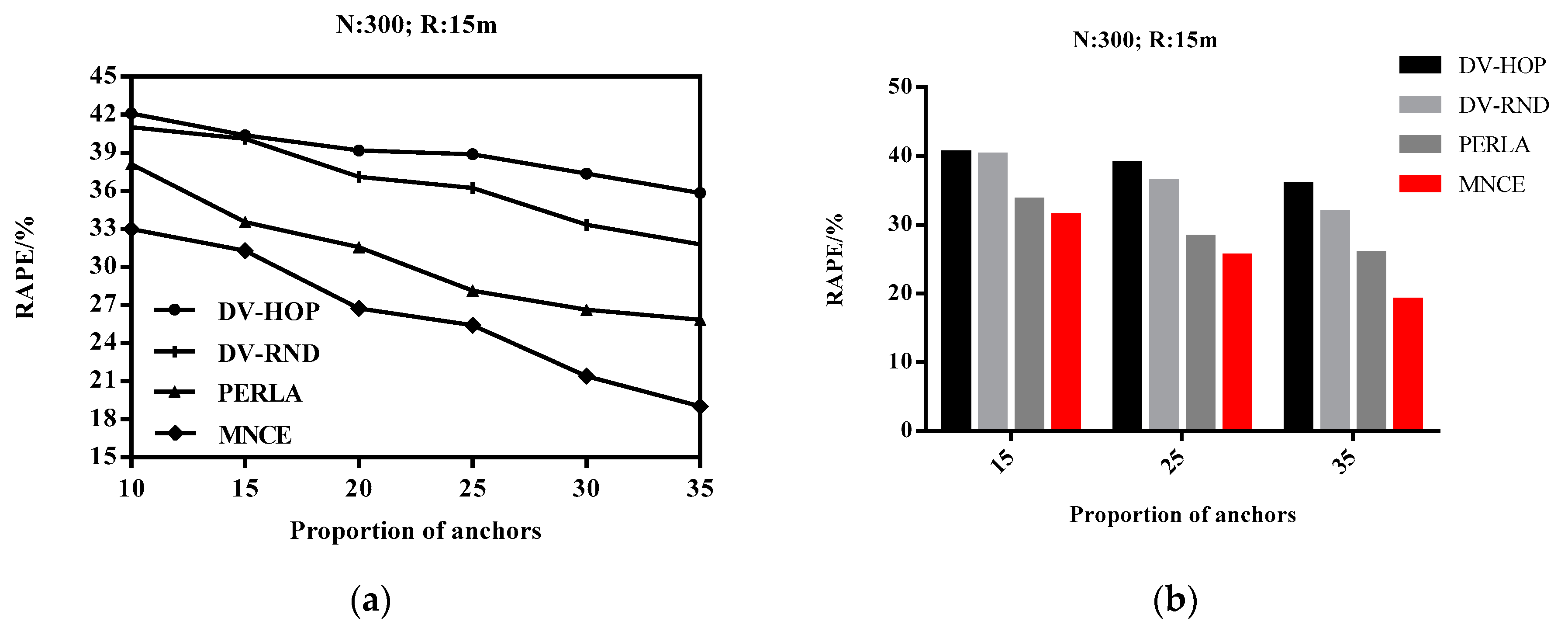
4.6. Impact of the Proportion of Anchor Nodes on RAPE
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hadir, A.; Zine-Dine, K.; Bakhouya, M.; El Kafi, J.; El Ouadghiri, D. Performance Evaluation of DV-Hop Localization Algorithm for Geographical Routing in Wireless Sensor Networks. Procedia Comput. Sci. 2017, 113, 261–266. [Google Scholar] [CrossRef]
- Li, W.; Portilla, J.; Moreno, F.; Liang, G.; Riesgo, T. Multiple feature points representation in target localization of wireless visual sensor networks. J. Netw. Comput. Appl. 2015, 57, 119–128. [Google Scholar] [CrossRef]
- Wang, X.; Sun, T.; Sun, C.; Wang, J. Distributed networked localization using neighboring distances only through a computational topology control approach. Int. J. Distrib. Sens. Netw. 2020, 16, 16. [Google Scholar] [CrossRef]
- Amri, S.; Khelifi, F.; Bradai, A.; Rachedi, A.; Kaddachi, M.L.; Atri, M. A new fuzzy logic based node localization mechanism for Wireless Sensor Networks. Future Gener. Comput. Syst. 2019, 93, 799–813. [Google Scholar] [CrossRef]
- Phoemphon, S.; So-In, C.; Leelathakul, N. A hybrid localization model using node segmentation and improved particle swarm optimization with obstacle-awareness for wireless sensor networks. Expert Syst. Appl. 2020, 143, 113044. [Google Scholar] [CrossRef]
- Velimirovic, A.S.; Djordjevic, G.L.; Velimirovic, M.M.; Jovanovic, M.D. Fuzzy ring-overlapping range-free (FRORF) localization method for wireless sensor networks. Comput. Commun. 2012, 35, 1590–1600. [Google Scholar] [CrossRef]
- Samayveer, S. Sustainable data gathering technique based on nature inspired optimization in WSNs. Sustain. Comput. Inform. Syst. 2019, 24, 100354. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. Distributed algorithm for target localization in wireless sensor networks using RSS and AoA measurements. Pervasive Mob. Comput. 2017, 37, 63–77. [Google Scholar] [CrossRef]
- Li, Q.; Liu, N. Monitoring area coverage optimization algorithm based on nodes perceptual mathematical model in wireless sensor networks. Comput. Commun. 2020, 155, 227–234. [Google Scholar] [CrossRef]
- Poornima, I.G.A.; Paramasivan, B. Anomaly detection in wireless sensor network using machine learning algorithm. Comput. Commun. 2020, 151, 331–337. [Google Scholar] [CrossRef]
- Kaur, A.; Kumar, P.; Gupta, G.P. A weighted centroid localization algorithm for randomly deployed wireless sensor networks. J. King Saud Univ. Comput. Inf. Sci. 2019, 31, 82–91. [Google Scholar] [CrossRef]
- Anindya, I.; Manzur, M. A hybrid wireless sensor network framework for range-free event localization. Ad Hoc Netw. 2015, 27, 81–98. [Google Scholar]
- Darakeh, F.; Mohammad-Khani, G.-R.; Azmi, P. DCRL-WSN: A distributed cooperative and range-free localization algorithm for WSNs. AEU Int. J. Electron. Commun. 2018, 93, 289–295. [Google Scholar] [CrossRef]
- Nagaraju, A. Dipanshu WITHDRAWN: Energy-Efficient Routing Technique for Wireless Sensor Networks Using Multiple Mobile Sink Nodes. Parallel Comput. 2020, 102623. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, B.; Mouftah, H. Distributed robust time-efficient broadcasting algorithms for multi-channel wireless multi-hop networks with channel disruption. Comput. Commun. 2020, 152, 252–265. [Google Scholar] [CrossRef]
- Molaei, A.M.; Hoseinzade, M. High-performance 2D DOA estimation and 3D localization for mixed near/far-field sources using fourth-order spatiotemporal algorithm. Digit. Signal Process. 2020, 100, 102696. [Google Scholar] [CrossRef]
- Zaidi, S.; El Assaf, A.; Affes, S.; Kandil, N. Accurate Range-Free Localization in Multi-Hop Wireless Sensor Networks. IEEE Trans. Commun. 2016, 64, 3886–3900. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, K. An improved DV-HOP positioning algorithm based on Hop distance correction. China Commun. 2014, 1, 415–418. [Google Scholar] [CrossRef]
- Gui, L.; Val, T.; Wei, A.; Dalce, R. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks. Ad Hoc Netw. 2015, 24, 55–73. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Wang, D.; Agrawal, D. Range-Free Localization Using Expected Hop Progress in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1540–1552. [Google Scholar] [CrossRef]
- Wu, G.; Wang, S.; Wang, B.; Dong, Y.; Yan, S. A novel range-free localization based on regulated neighborhood distance for wireless ad hoc and sensor networks. Comput. Netw. 2012, 56, 3581–3593. [Google Scholar] [CrossRef]
- Kumar, S.; Lobiyal, D.K. Power efficient range-free localization algorithm for wireless sensor networks. Wirel. Netw. 2013, 20, 681–694. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Wang, X.; Jin, X.-B.; Bai, Y.-T. Improvements of Multihop Localization Algorithm for Wireless Sensor Networks. IEEE Syst. J. 2019, 13, 365–376. [Google Scholar] [CrossRef]
- Wang, P.; Tu, G. Localization algorithm of wireless sensor network based on matrix reconstruction. Comput. Commun. 2020, 154, 216–222. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Shi, W.; Zhao, Z.; He, Z.; Xia, T. Target localization and tracking based on improved Bayesian enhanced least-squares algorithm in wireless sensor networks. Comput. Netw. 2020, 167, 106968. [Google Scholar] [CrossRef]
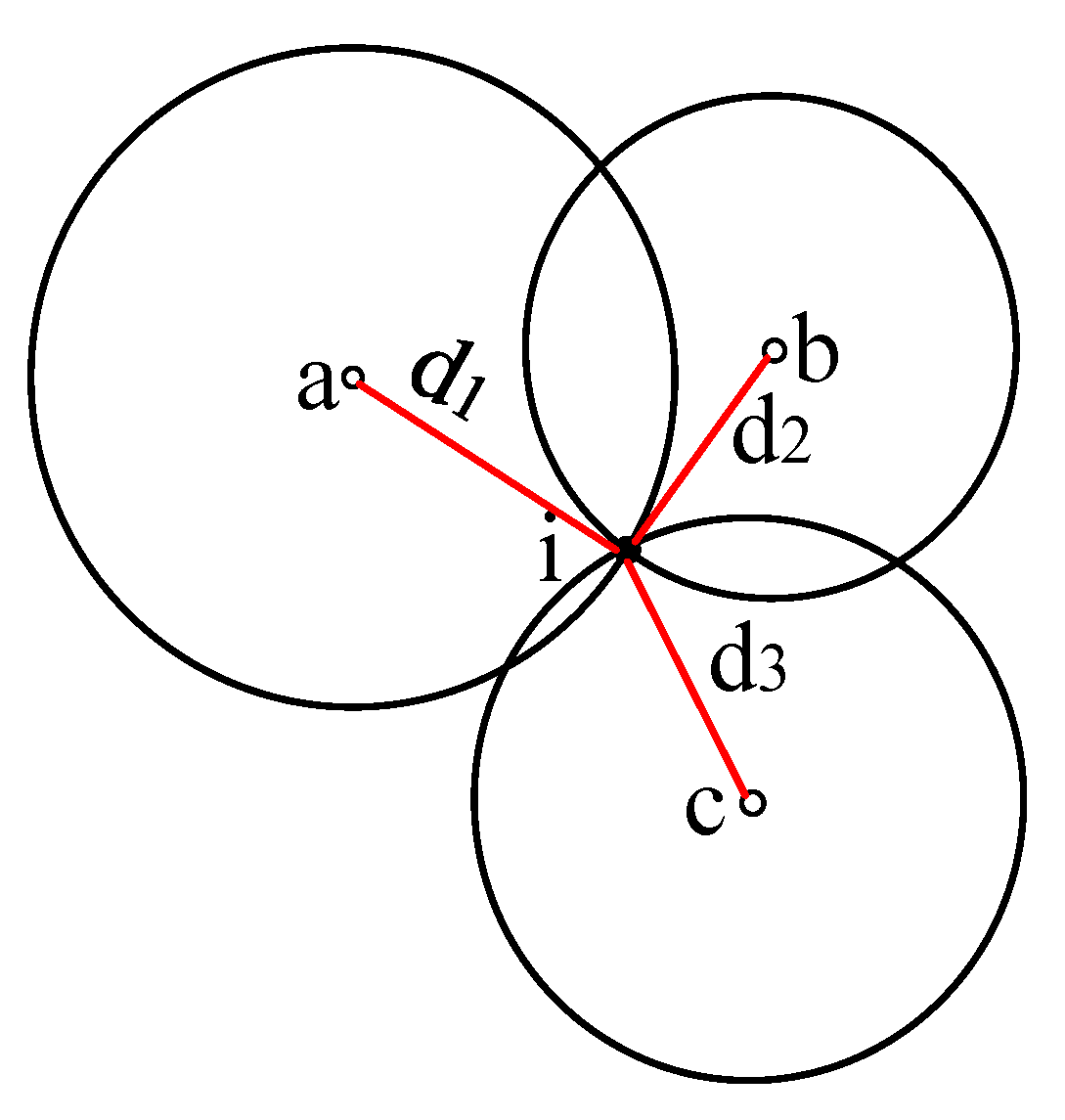
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Chen, Y.; Zhang, Q.; Zhang, W. MNCE: Multi-Hop Node Localization Algorithm for Wireless Sensor Network Based on Error Correction. Information 2020, 11, 269. https://doi.org/10.3390/info11050269
Meng Y, Chen Y, Zhang Q, Zhang W. MNCE: Multi-Hop Node Localization Algorithm for Wireless Sensor Network Based on Error Correction. Information. 2020; 11(5):269. https://doi.org/10.3390/info11050269
Chicago/Turabian StyleMeng, Yinghui, Yuewen Chen, Qiuwen Zhang, and Weiwei Zhang. 2020. "MNCE: Multi-Hop Node Localization Algorithm for Wireless Sensor Network Based on Error Correction" Information 11, no. 5: 269. https://doi.org/10.3390/info11050269
APA StyleMeng, Y., Chen, Y., Zhang, Q., & Zhang, W. (2020). MNCE: Multi-Hop Node Localization Algorithm for Wireless Sensor Network Based on Error Correction. Information, 11(5), 269. https://doi.org/10.3390/info11050269



