Toward Effective Medical Image Analysis Using Hybrid Approaches—Review, Challenges and Applications
Abstract
1. Introduction: Medical Image Analysis Challenges
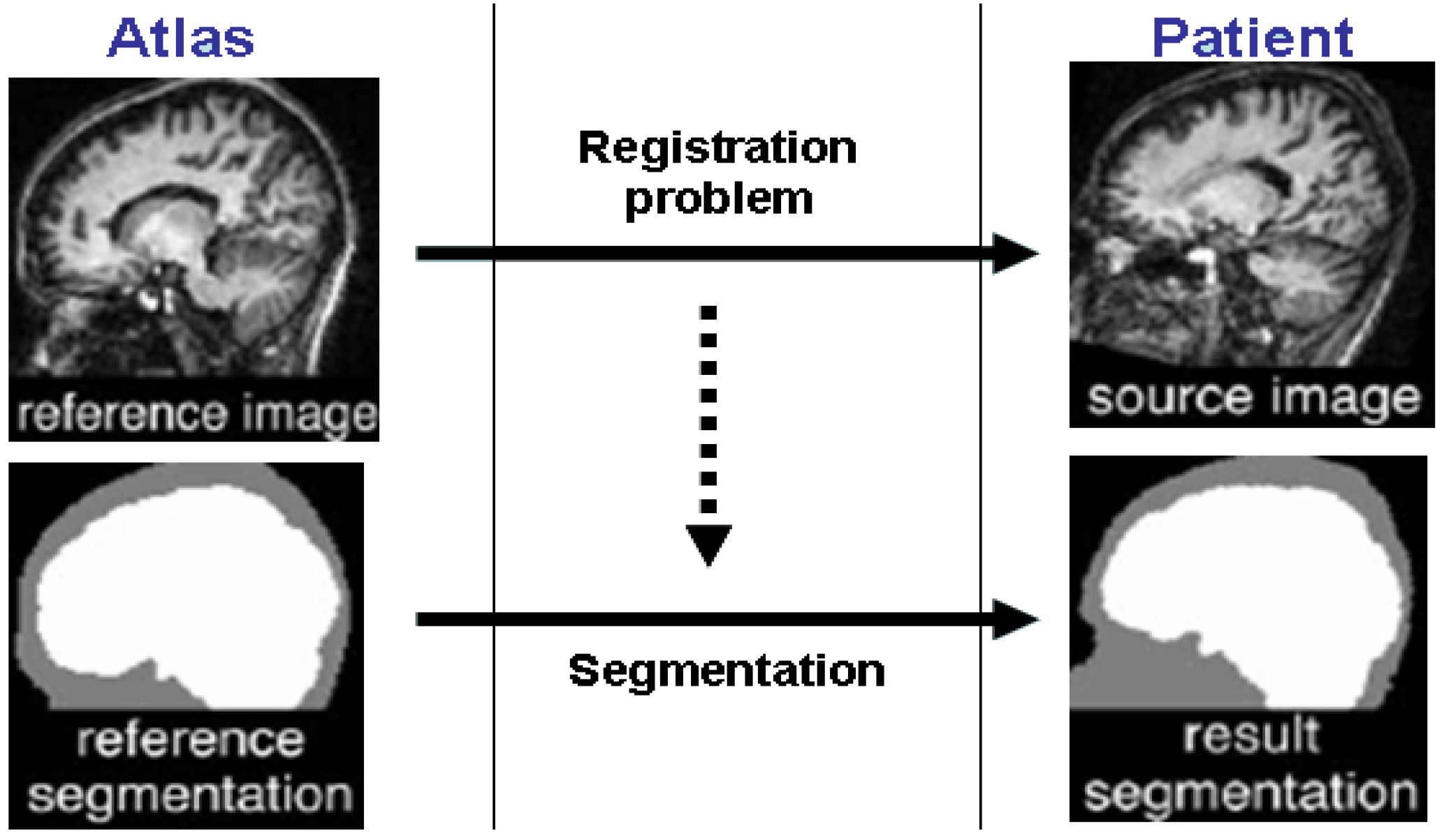
2. Atlas-Guided Methods
3. Variational Deformable Models
4. Statistical Classification and Segmentation of Medical Images
Linear and Non-Linear Support Vector Machines(SVM)
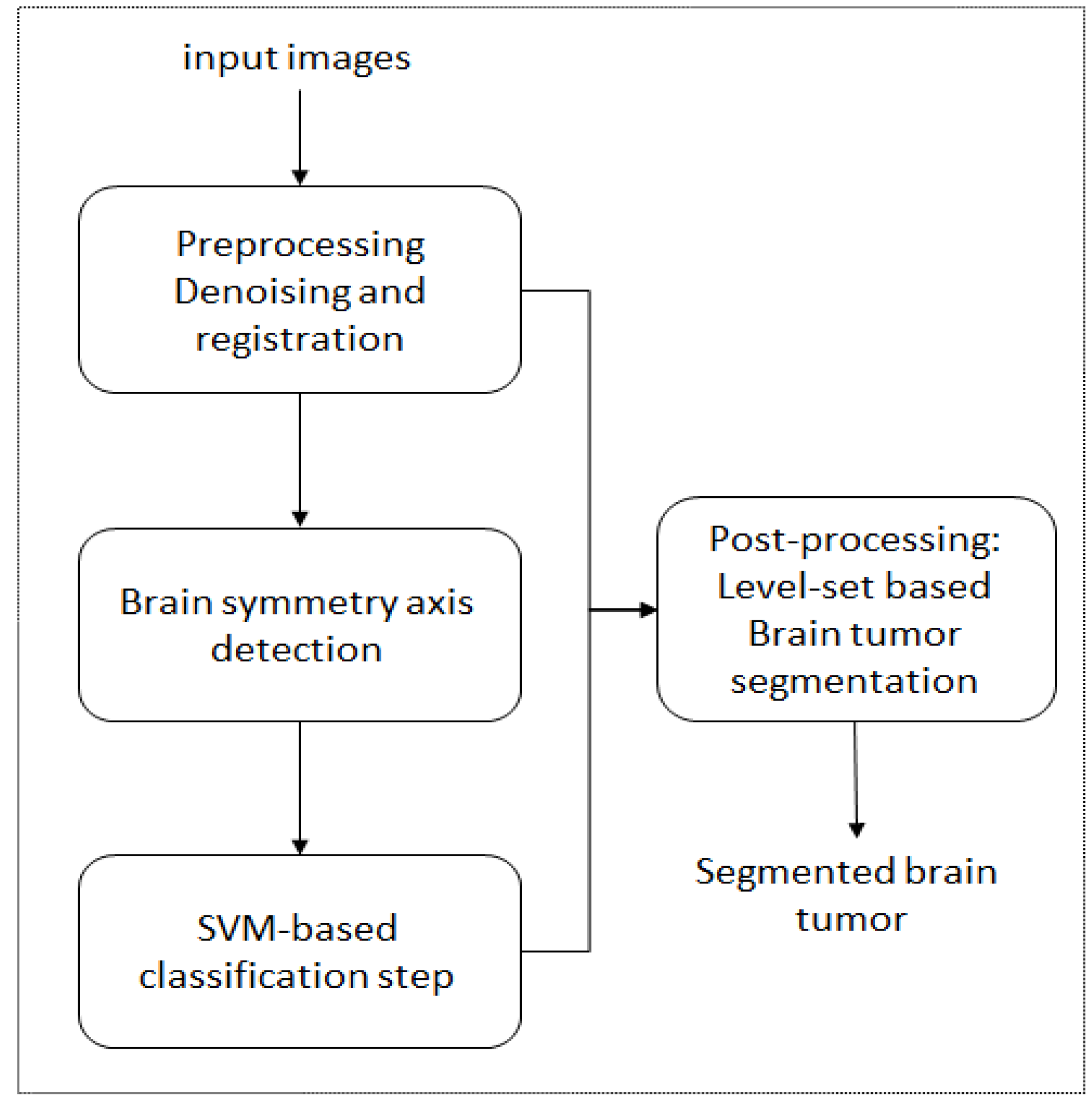
5. A Unified Framework for Brain Tumor Segmentation
- Sensitivity =
- Specificity =
- Similarity index (SI) = ,
6. Conclusions and Discussion
7. Data Availability
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, T.; Thung, K.; Liu, M.; Shi, F.; Zhang, C.; Shen, D. Multi-modal latent space inducing ensemble SVM classifier for early dementia diagnosis with neuroimaging data. Med. Image Anal. 2020, 60, 101630. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Cao, X.; Yap, P.; Shen, D. BIRNet: Brain image registration using dual-supervised fully convolutional networks. Med. Image Anal. 2019, 54, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Q.; Peng, J.; Nie, D.; Zhao, F.; Kim, M.; Zhang, H.; Wee, C.Y.; Wang, S.; Shen, D. Multi-task diagnosis for autism spectrum disorders using multi-modality features: A multi-center study. Hum. Brain Mapp. 2017, 38, 3081–3097. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, H.; Chen, X.; Liu, M.; Zhu, X.; Lee, S.; Shen, D. Strength and similarity guided group-level brain functional network construction for MCI diagnosis. Pattern Recognit. 2019, 88, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Maintz, J.; Viergever, M. Medical Image Analysis. Surv. Med. Image Registr. 1998, 2, 1–36. [Google Scholar]
- Talairach, J.; Tournoux, P. Co-Planar Stereotaxic Atlas of the Human Brain; Georg Thieme Verlag: Stuttgart, Germany, 1988. [Google Scholar]
- Collins, D.; Holmes, C.; Peters, T.; Evans, A. Automatic 3D model-based neuroanatomical segmentation. Hum. Brain Mapp. 1995, 3, 190–208. [Google Scholar] [CrossRef]
- Pohl, K.M.; Fisher, J.; Grimson, W.E.L.; Kikinis, R.; Wells, W.M. A Bayesian model for joint segmentation and registration. NeuroImage 2006, 31, 228–239. [Google Scholar] [CrossRef]
- Warfield, S.; Kaus, M.; Jolesz, F.; Kikinis, R. Adaptive, Template Moderated, Spatially Varying Statistical Classification. Med. Image Anal. 2000, 4, 43–55. [Google Scholar] [CrossRef]
- Clark, M. Knowledge-Guided Processing of Magnetic Resonance Images of the Brain. Ph.D. Thesis, Department of Computer Science and Engineering, University of South Florida, Tampa, FL, USA, 2000. [Google Scholar]
- Dawant, B.M.; Hartmann, S.L.; Pan, S.; Gadamsetty, S. Brain atlas deformation in the presence of small and large space-occupying tumors. Comput. Aided Surg. 2002, 7, 1–10. [Google Scholar] [CrossRef]
- Cuadra, M.; Pollo, C.; Bardera, A.; Cuisenaire, O.; Villemure, J.; Thiran, J. Atlas-based Segmentation of Pathological MR Brain Using a Model of Lesion Growth. IEEE Trans. Med. Imag. 2004, 23, 1301–1314. [Google Scholar]
- Liew, A.; Yan, H. Current Methods in the Automatic Tissue Segmentation of 3D Magnetic Resonance Brain Images. Curr. Med. Imag. Rev. 2006, 2, 91–103. [Google Scholar] [CrossRef][Green Version]
- Sethian, J. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Geometry, Fluid Mechanics, Computer Vision, and Materials Science, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Osher, S.; Sethian, J. Fronts Propagating with Curvature-Dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Malladi, R.; Sethian, J.A.; Vemuri, B.C. Shape modeling with front propagation: A level set approach. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 158–174. [Google Scholar] [CrossRef]
- Chan, T.; Vese, L. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.; Bullitt, E.; Gerig, G. Level set evolution with region competition: Automatic 3-D segmentation of brain tumors. Int. Conf. Pattern Recog. ICPR 2002, 20, 532–535. [Google Scholar]
- Lefohn, A.; Cates, J.; Whitaker, R. Interactive, GPU-based level sets for 3D brain tumor segmentation. Med. Image Comput. Comput. Assisted Intervent. 2003, 2003, 564–572. [Google Scholar]
- Ciofolo, C.; Barillot, C. Brain segmentation with competitive level sets and fuzzy control. Inf. Process. Med. Imag. 2005, 19, 333–344. [Google Scholar] [CrossRef]
- Leventon, M.E.; Grimson, W.E.L.; Faugeras, O. Statistical shape influence in geodesic active contours. CVPR 2000, 316–323. [Google Scholar] [CrossRef]
- Cremers, D.; Kohlberger, T.; Schnörr, C. Shape statistics in kernel space for variational image segmentation. Pattern Recog. 2003, 36, 1929–1943. [Google Scholar] [CrossRef]
- Charpiat, G.; Faugeras, O.; Keriven, R. Approximations of Shape Metrics and Application to Shape Warping and Empirical Shape Statistics. Found. Comput. Math. 2005, 5, 1–58. [Google Scholar] [CrossRef]
- Cremers, D.; Osher, S.J.; Soatto, S. Kernel Density Estimation and Intrinsic Alignment for Shape Priors in Level Set Segmentation. Int. J. Comput. Vis. 2006, 69, 335–351. [Google Scholar] [CrossRef]
- Kim, J.; Çetin, M.; Willsky, A.S. Nonparametric Shape Priors for Active Contour-Based Image Segmentation. Signal Process. 2007, 87, 3021–3044. [Google Scholar] [CrossRef]
- Cootes, T.F.; Edwards, G.J.; Taylor, C.J. Active Appearance Models. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 23, 484–498. [Google Scholar]
- Alroobaea, R.; Alsufyani, A.; Ansari, M.A.; Rubaiee, S.; Algarni, S. Supervised Machine Learning of KFCG Algorithm and MBTC features for efficient classification of Image Database and CBIR Systems. Int. J. Appl. Eng. Res. 2018, 13, 6795–6804. [Google Scholar]
- Zhang, Y.; Brady, M.; Smith, S. Segmentation of brain mr images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imag. 2001, 20, 45–57. [Google Scholar] [CrossRef]
- Bourouis, S.; Hamrouni, K. An efficient framework for brain tumor segmentation in magnetic resonance images. In Proceedings of the IEEE 2008 First Workshops on Image Processing Theory, Tools and Applications, Sousse, Tunisia, 23–26 November 2008; pp. 1–5. [Google Scholar]
- Bourouis, S.; Zaguia, A.; Bouguila, N. Hybrid Statistical Framework for Diabetic Retinopathy Detection. In Proceedings of the Image Analysis and Recognition—15th International Conference, ICIAR 2018, Póvoa de Varzim, Portugal, 27–29 June 2018; pp. 687–694. [Google Scholar]
- Prastawa, M.; Bullitt, E.; Ho, S.; Gerig, G. A brain tumor segmentation framework based on outlier detection. Med. Image Anal. (MedIA) 2004, 8, 275–283. [Google Scholar] [CrossRef]
- Liu, J.; Udupa, J.; Odhner, D.; Hackney, D.; Moonis, G. A system for brain tumor volume estimation via mr imaging and fuzzy connectedness. Comput. Med. Imag. Graph. 2005, 29, 21–34. [Google Scholar] [CrossRef]
- Channoufi, I.; Najar, F.; Bourouis, S.; Azam, M.; Halibas, A.S.; Alroobaea, R.; Al-Badi, A. Flexible Statistical Learning Model for Unsupervised Image Modeling and Segmentation. In Mixture Models and Applications; Springer: Berlin, Germany, 2020; pp. 325–348. [Google Scholar]
- Alhakami, W.; ALharbi, A.; Bourouis, S.; Alroobaea, R.; Bouguila, N. Network Anomaly Intrusion Detection Using a Nonparametric Bayesian Approach and Feature Selection. IEEE Access 2019, 7, 52181–52190. [Google Scholar] [CrossRef]
- Corso, J.; Sharon, E.; Dube, S.; El-Saden, S.; Sinha, U.; Yuille, A. Efficient multilevel brain tumor segmentation with integrated bayesian model classification. IEEE Trans. Med. Imag. 2008, 27, 629–640. [Google Scholar] [CrossRef]
- Bourouis, S.; Hamrouni, K.; Betrouni, N. Automatic MRI Brain Segmentation with Combined Atlas-Based Classification and Level-Set Approach. In Proceedings of the Image Analysis and Recognition, 5th International Conference, ICIAR 2008, Póvoa de Varzim, Portugal, 25–27 June 2008; pp. 770–778. [Google Scholar]
- Fitton, I.; Cornelissen, S.A.P.; Duppen, J.C.; Steenbakkers, R.J.H.M.; Peeters, S.T.H.; Hoebers, F.J.P.; Kaanders, J.H.A.M.; Nowak, P.J.C.M.; Rasch, C.R.N.; van Herk, M. Semi-automatic delineation using weighted CT-MRI registered images for radiotherapy of nasopharyngeal cancer. Int. J. Med. Phys. Res. Pract. 2011, 38, 4662–4666. [Google Scholar] [CrossRef]
- Channoufi, I.; Bourouis, S.; Bouguila, N.; Hamrouni, K. Color image segmentation with bounded generalized Gaussian mixture model and feature selection. In Proceedings of the 4th International Conference on Advanced Technologies for Signal and Image Processing, ATSIP 2018, Sousse, Tunisia, 21–24 March 2018; pp. 1–6. [Google Scholar]
- Seim, H.; Kainmueller, D.; Heller, M.; Lamecker, H.; Zachow, S.; Hege, H.C. Automatic Segmentation of the Pelvic Bones from CT Data based on a Statistical Shape Model. Eur. Worksh. Visual Comput. Biomed. 2008, 8, 224–230. [Google Scholar]
- Vincent, G.; Wolstenholme, C.; Scott, I.; Bowes, M. Fully automatic segmentation of the knee joint using active appearance models. Proc. Med. Image Anal. Clin. 2010, 1, 224. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks, Machine Learning. Comput. Secur. 1995, 20, 273–297. [Google Scholar]
- Bourouis, S.; Zaguia, A.; Bouguila, N.; Alroobaea, R. Deriving Probabilistic SVM Kernels From Flexible Statistical Mixture Models and its Application to Retinal Images Classification. IEEE Access 2019, 7, 1107–1117. [Google Scholar] [CrossRef]
- Najar, F.; Bourouis, S.; Bouguila, N.; Belghith, S. Unsupervised learning of finite full covariance multivariate generalized Gaussian mixture models for human activity recognition. Multimed. Tools Appl. 2019, 78, 18669–18691. [Google Scholar] [CrossRef]
- Byun, H.; Lee, S.W. A survey on pattern recognition applications of support vector machines. Int. J. Pattern Recognit. Artif. Intell. 2003, 17, 459–486. [Google Scholar] [CrossRef]
- Hu, W. Robust Support Vector Machines for Anomaly Detection. In Proceedings of the 2003 International Conference on Machine Learning and Applications (ICMLA 03), Los Angeles, CA, USA, 23–24 June 2003; pp. 23–24. [Google Scholar]
- John, P. Fast training of support vector machines using sequential minimal optimization. In Proceedings of the 2008 3rd International Conference on Intelligent System and Knowledge Engineering, Xiamen, China, 17–19 November 1998. [Google Scholar]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images. IEEE Trans. Med. Imag. 2016, 35, 1240–1251. [Google Scholar] [CrossRef]
- Bourouis, S. Adaptive Variational Model and Learning-based SVM for Medical Image Segmentation. In Proceedings of the ICPRAM 2015—Proceedings of the International Conference on Pattern Recognition Applications and Methods, Lisbon, Portugal, 10–12 January 2015; Volume 1, pp. 149–156. [Google Scholar]
- Cobzas, D.; Birkbeck, N.; Schmidt, M.; Jagersand, M.; Murtha, A. A 3d variational brain tumor segmentation using a high dimensional feature set. In Proceedings of the IEEE 11th International Conference on Computer Vision (ICCV), Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Bourouis, S.; Hamrouni, K. 3D segmentation of MRI brain using level set and unsupervised classification. Int. J. Image Graph. (IJIG) 2010, 10, 135–154. [Google Scholar] [CrossRef]
- Ilunga-Mbuyamba, E.; Aviña-Cervantes, J.G.; Cepeda-Negrete, J.; Ibarra-Manzano, M.A.; Chalopin, C. Automatic selection of localized region-based active contour models using image content analysis applied to brain tumor segmentation. Comput. Biol. Med. 2017, 91, 69–79. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.V.; Dalca, A.V. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE Trans. Med. Imag. 2019, 38, 1788–1800. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015—18th International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Litjens, G.J.S.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Shen, D.; Wu, G.; Suk, H.I. Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef]
- Lundervold, A.S.; Lundervold, A. An overview of deep learning in medical imaging focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef] [PubMed]
- Ker, J.; Wang, L.; Rao, J.; Lim, T. Deep learning applications in medical image analysis. IEEE Access 2017, 6, 9375–9389. [Google Scholar] [CrossRef]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imag. 2018, 9, 611–629. [Google Scholar] [CrossRef]
- Lin, W.; Tong, T.; Gao, Q.; Guo, D.; Du, X.; Yang, Y.; Guo, G.; Xiao, M.; Du, M.; Qu, X.; et al. Convolutional neural networks-based MRI image analysis for the alzheimer’s disease prediction from mild cognitive impairment. Front. Neurosci. 2018, 12, 777. [Google Scholar] [CrossRef]
- Deepak, S.; Ameer, P.M. Brain tumor classification using deep CNN features via transfer learning. Comput. Biol. Med. 2019, 111, 103345. [Google Scholar] [CrossRef]
- Akkus, Z.; Galimzianova, A.; Hoogi, A.; Rubin, D.L.; Erickson, B.J. Deep Learning for Brain MRI Segmentation: State of the Art and Future Directions. J. Digit. Imag. 2017, 30, 449–459. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Tuzikov, A.V.; Colliot, O.; Bloch, I. Evaluation of the symmetry plane in 3D MR brain images. Pattern Recognit. Lett. 2003, 24, 2219–2233. [Google Scholar] [CrossRef]
- Prastawa, M.; Bullitt, E.; Gerig, G. Simulation of Brain Tumors in MR Images for Evaluation of Segmentation Efficacy. Med. Image Anal. (MedIA) 2009, 13, 297–311. [Google Scholar] [CrossRef] [PubMed]
- Zijdenbos, A.; Dawant, B.; Margolin, R.; Palmer, A. Morphometric Analysis of White Matter Lesions in MR Images: Method and Validation. IEEE Trans. Med. Imag. 1994, 13, 716–724. [Google Scholar] [CrossRef]
- Anitha, V.; Murugavalli, S. Brain tumour classification using two-tier classifier with adaptive segmentation technique. IET Comput. Vis. 2016, 10, 9–17. [Google Scholar] [CrossRef]
- Zikic, D.; Glocker, B.; Konukoglu, E.; Criminisi, A.; Demiralp, C.; Shotton, J.; Thomas, O.M.; Das, T.; Jena, R.; Price, S.J. Decision forests for tissue-specific segmentation of high-grade gliomas in multi-channel MR. In International Conference on Medical Image Computing And Computer-Assisted Intervention; Springer: Berlin, Germany, 2012; pp. 369–376. [Google Scholar]
- Bauer, S.; Nolte, L.; Reyes, M. Fully Automatic Segmentation of Brain Tumor Images Using Support Vector Machine Classification in Combination with Hierarchical Conditional Random Field Regularization. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2011—14th International Conference, Toronto, CA, USA, 18–22 September 2011; pp. 354–361. [Google Scholar]
- Njeh, I.; Sallemi, L.; Ayed, I.B.; Chtourou, K.; Lehéricy, S.; Galanaud, D.; Hamida, A.B. 3D multimodal MRI brain glioma tumor and edema segmentation: A graph cut distribution matching approach. Comput. Med. Imag. Graph. 2015, 40, 108–119. [Google Scholar] [CrossRef] [PubMed]
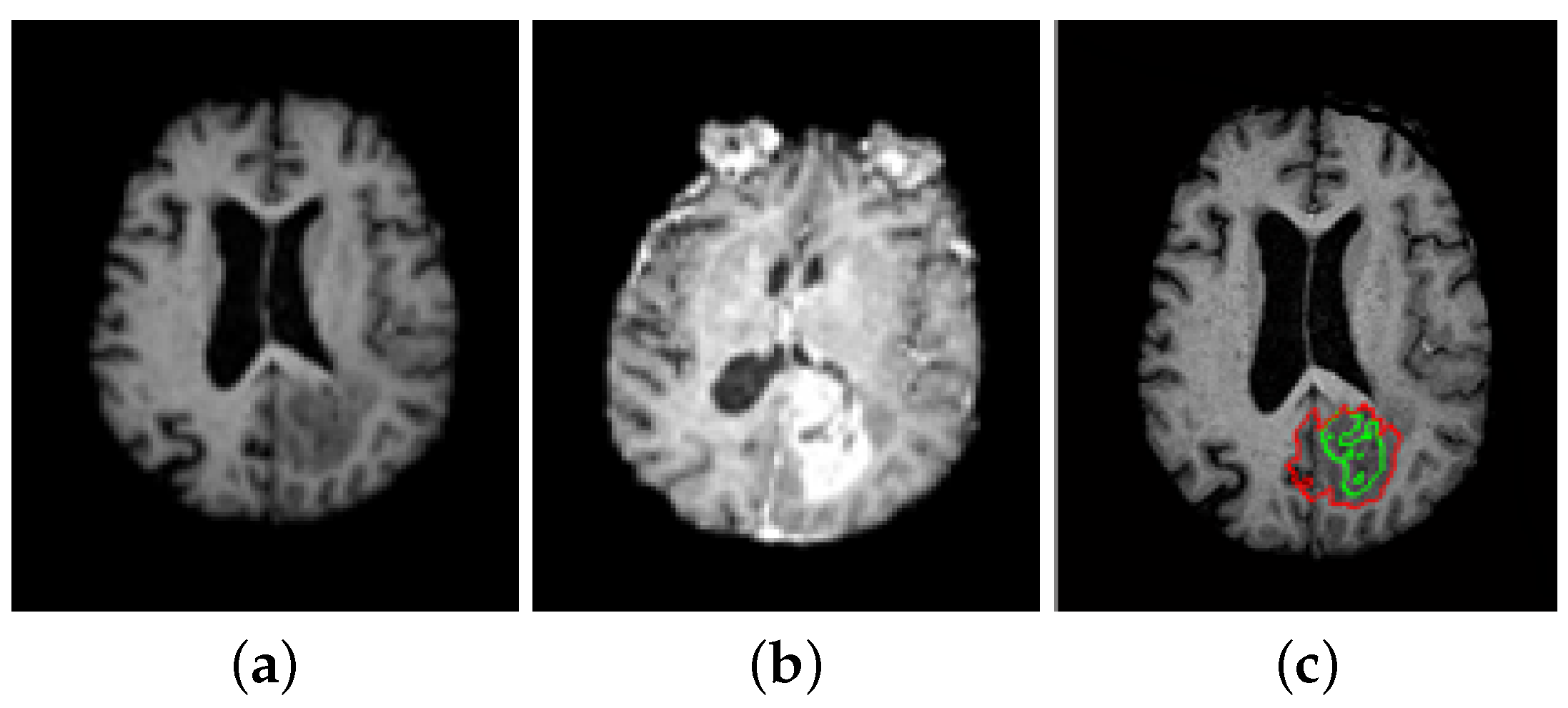
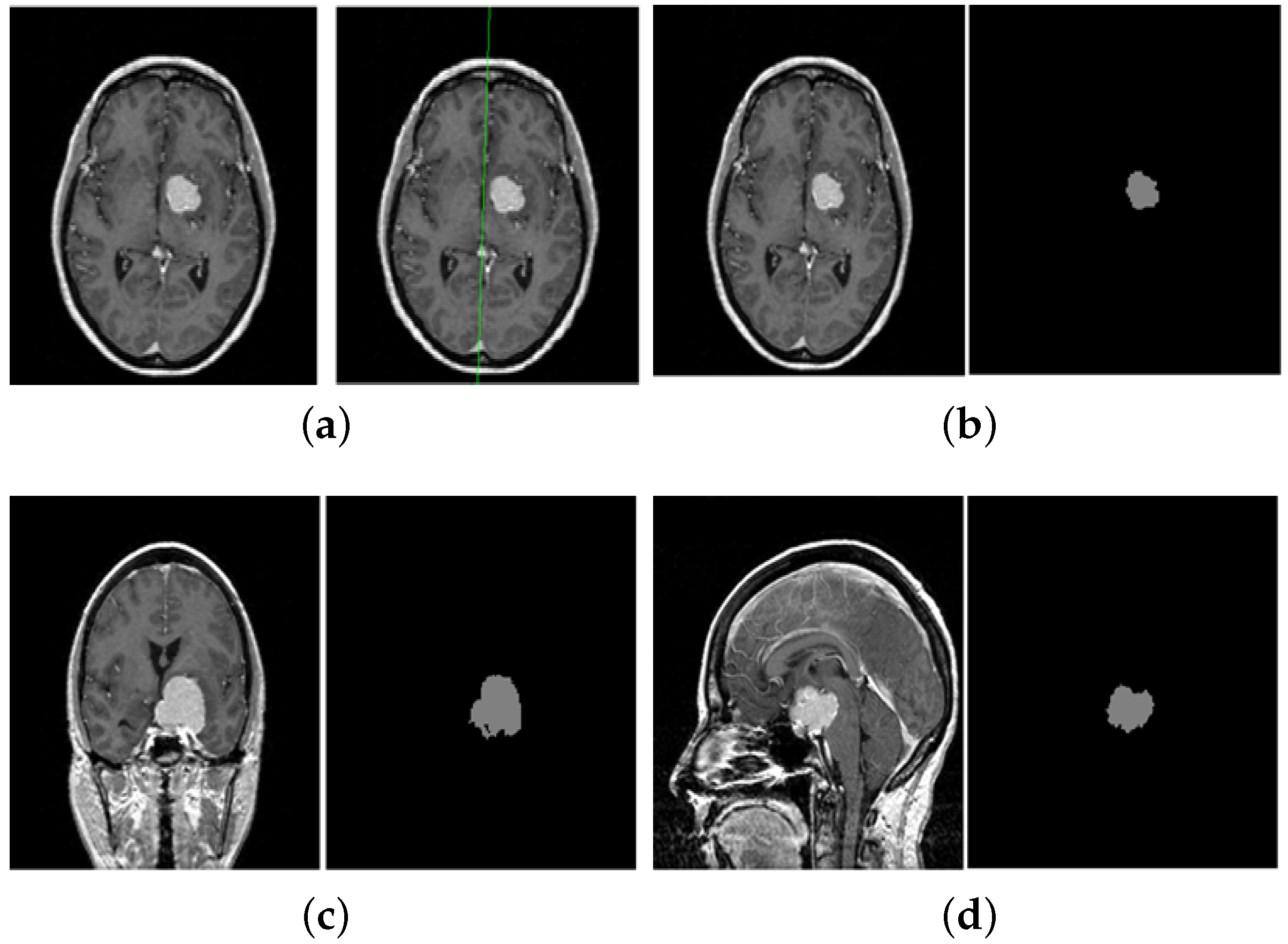
| Slice index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| SI | 0.758 | 0.790 | 0.813 | 0.803 | 0.829 | 0.813 | 0.801 | 0.820 | 0.772 | 0.803 |
| Slice index | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| SI | 0.842 | 0.833 | 0.797 | 0.789 | 0.809 | 0.812 | 0.761 | 0.773 | 0.819 | 0.792 |
| Slice index | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| SI | 0.829 | 0.823 | 0.811 | 0.820 | 0.822 | 0.803 | 0.822 | 0.813 | 0.827 | 0.789 |
| Slice index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Sensitivity | 0.861 | 0.877 | 0.889 | 0.884 | 0.897 | 0.889 | 0.882 | 0.893 | 0.868 | 0.884 |
| Slice index | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Sensitivity | 0.904 | 0.899 | 0.881 | 0.877 | 0.887 | 0.888 | 0.862 | 0.868 | 0.892 | 0.878 |
| Slice index | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Sensitivity | 0.897 | 0.894 | 0.888 | 0.893 | 0.894 | 0.884 | 0.894 | 0.889 | 0.896 | 0.877 |
| Slice index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Specificity | 0.925 | 0.934 | 0.941 | 0.938 | 0.946 | 0.941 | 0.937 | 0.943 | 0.929 | 0.938 |
| Slice index | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Specificity | 0.950 | 0.947 | 0.936 | 0.934 | 0.9402 | 0.9410 | 0.926 | 0.929 | 0.943 | 0.935 |
| Slice index | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Specificity | 0.946 | 0.944 | 0.940 | 0.943 | 0.944 | 0.938 | 0.944 | 0.941 | 0.945 | 0.934 |
| Similarity Index (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|
| 80.9 | 88.7 | 94.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourouis, S.; Alroobaea, R.; Rubaiee, S.; Ahmed, A. Toward Effective Medical Image Analysis Using Hybrid Approaches—Review, Challenges and Applications. Information 2020, 11, 155. https://doi.org/10.3390/info11030155
Bourouis S, Alroobaea R, Rubaiee S, Ahmed A. Toward Effective Medical Image Analysis Using Hybrid Approaches—Review, Challenges and Applications. Information. 2020; 11(3):155. https://doi.org/10.3390/info11030155
Chicago/Turabian StyleBourouis, Sami, Roobaea Alroobaea, Saeed Rubaiee, and Anas Ahmed. 2020. "Toward Effective Medical Image Analysis Using Hybrid Approaches—Review, Challenges and Applications" Information 11, no. 3: 155. https://doi.org/10.3390/info11030155
APA StyleBourouis, S., Alroobaea, R., Rubaiee, S., & Ahmed, A. (2020). Toward Effective Medical Image Analysis Using Hybrid Approaches—Review, Challenges and Applications. Information, 11(3), 155. https://doi.org/10.3390/info11030155







