Robust Beamforming Design for SWIPT-Based Multi-Radio Wireless Mesh Network with Cooperative Jamming
Abstract
1. Introduction
- In this paper, both SWIPT and cooperative jamming technics were adopted in the multi-radio WMN to enhance its power consumption and physical layer security performance, respectively. While [20,21,22,23,24] only adopted the SWIPT, [25,26,27] only adopted the cooperative jamming. Although [28,29,30,31] proposed some beamforming method, considering both SWIPT and cooperative jamming, all of them were designed for the cognitive radio system.
- Both imperfect channel state information and non-linear EH model were considered in this paper, making our system model more practical. Moreover, the imperfect channel state information led to the unknown channel estimate error. We utilized the S-procedure method to relax the channel estimate error constraints.
- The transmit power consumption optimization constrained by the SINR threshold, EH threshold, channel estimate error, and total transmit power was a non-convex problem. We transformed it into a standard SDP format, which was a convex problem.
2. Related Works
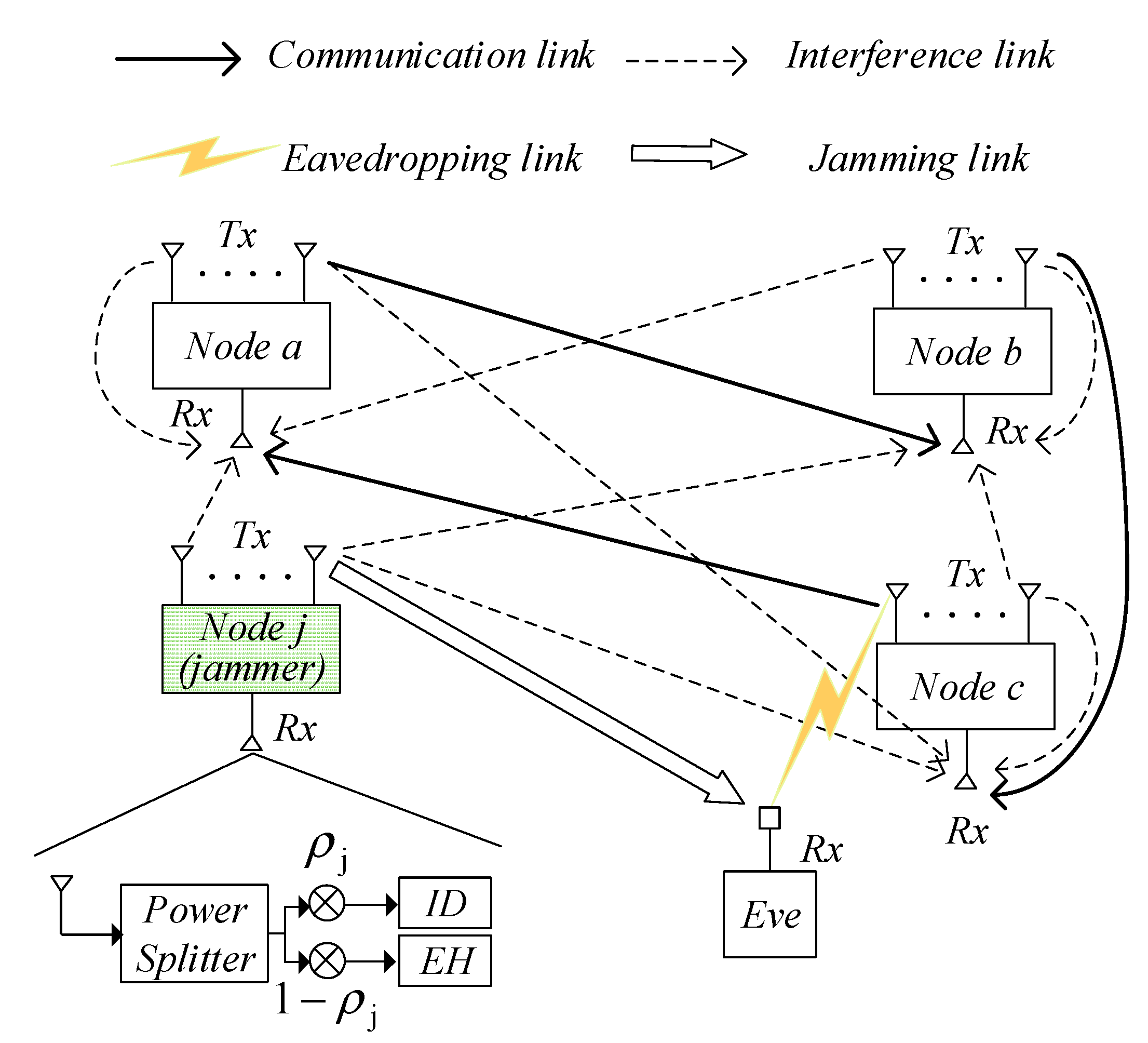
3. System Model
4. Robust Beamforming Design
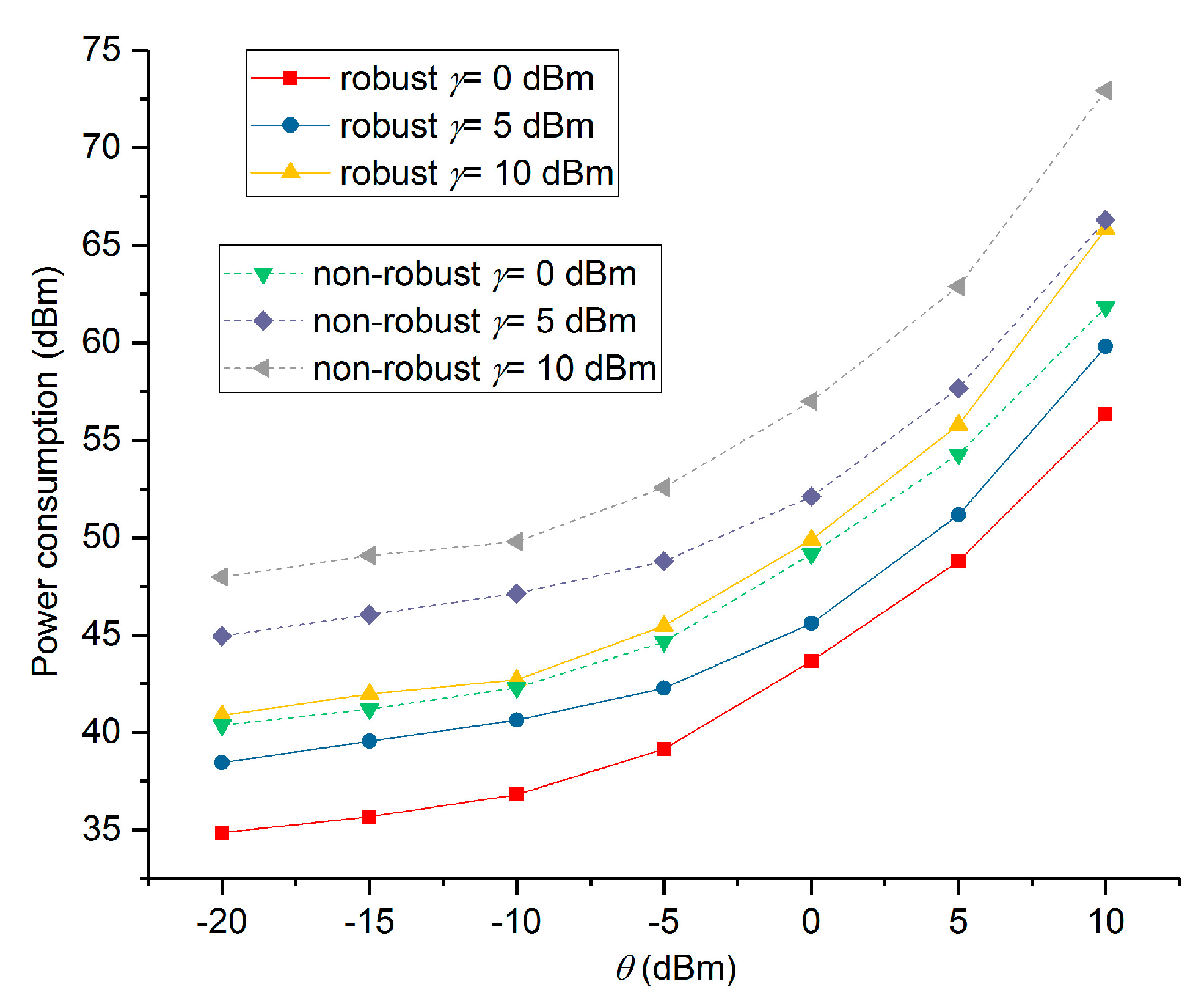
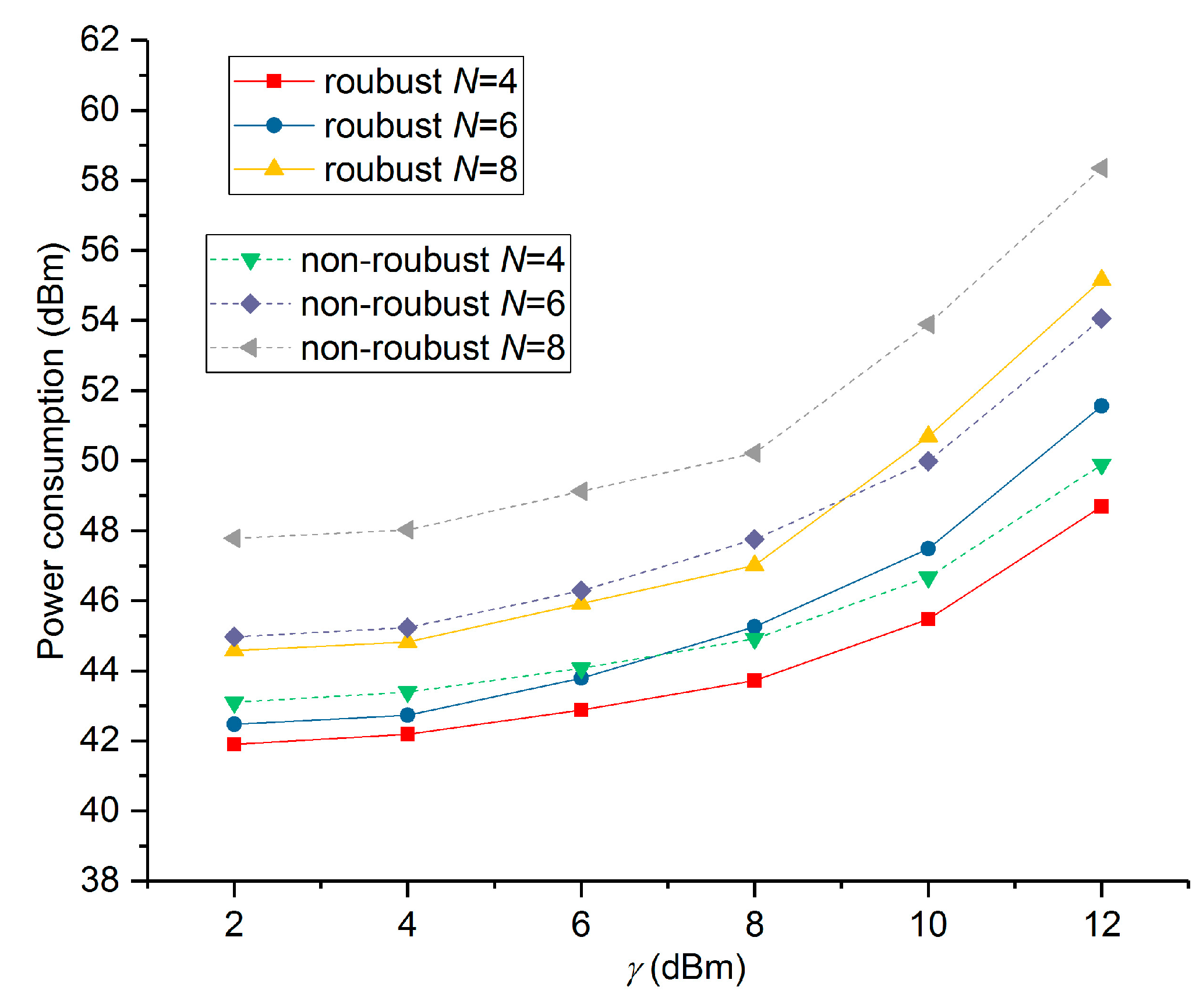
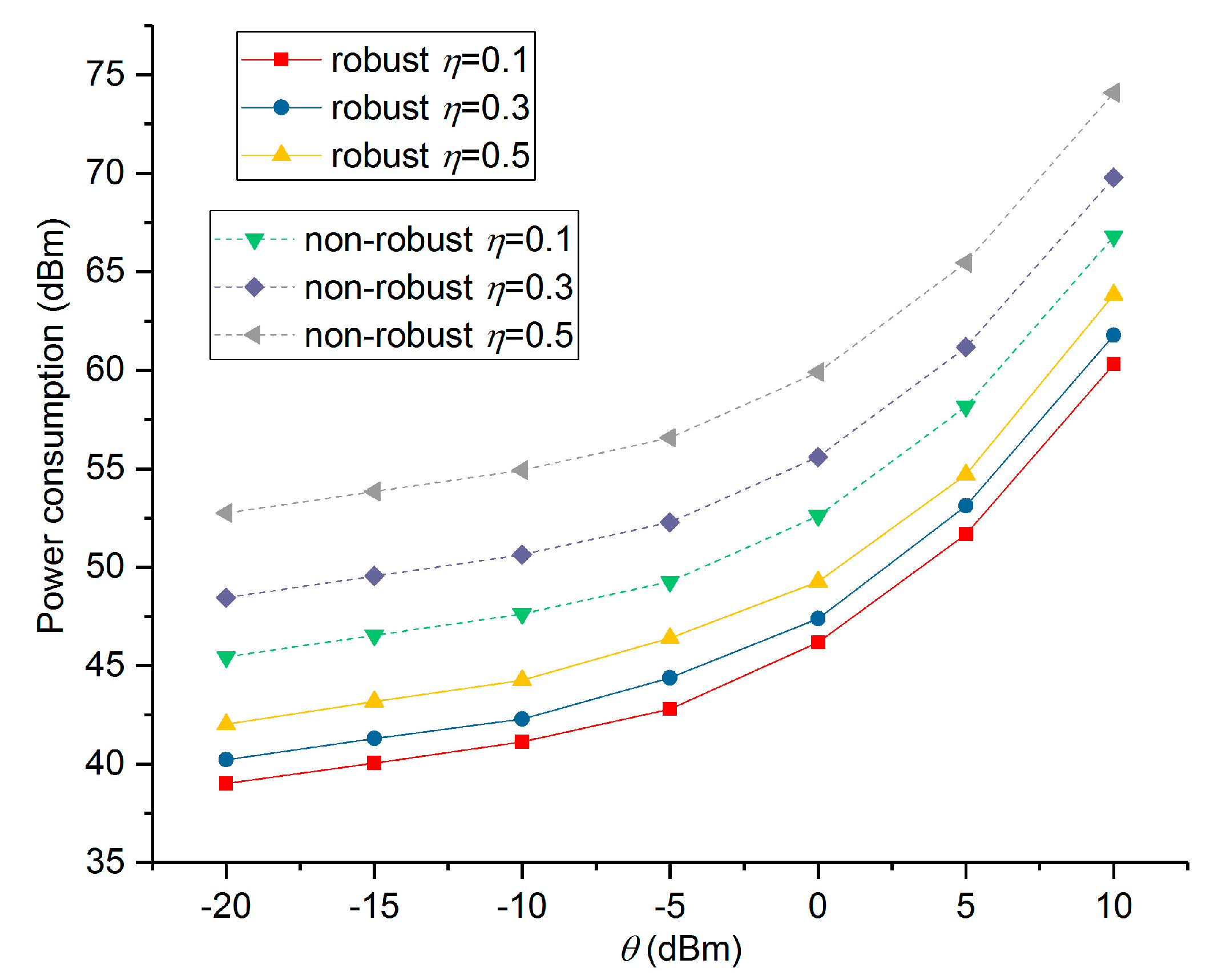
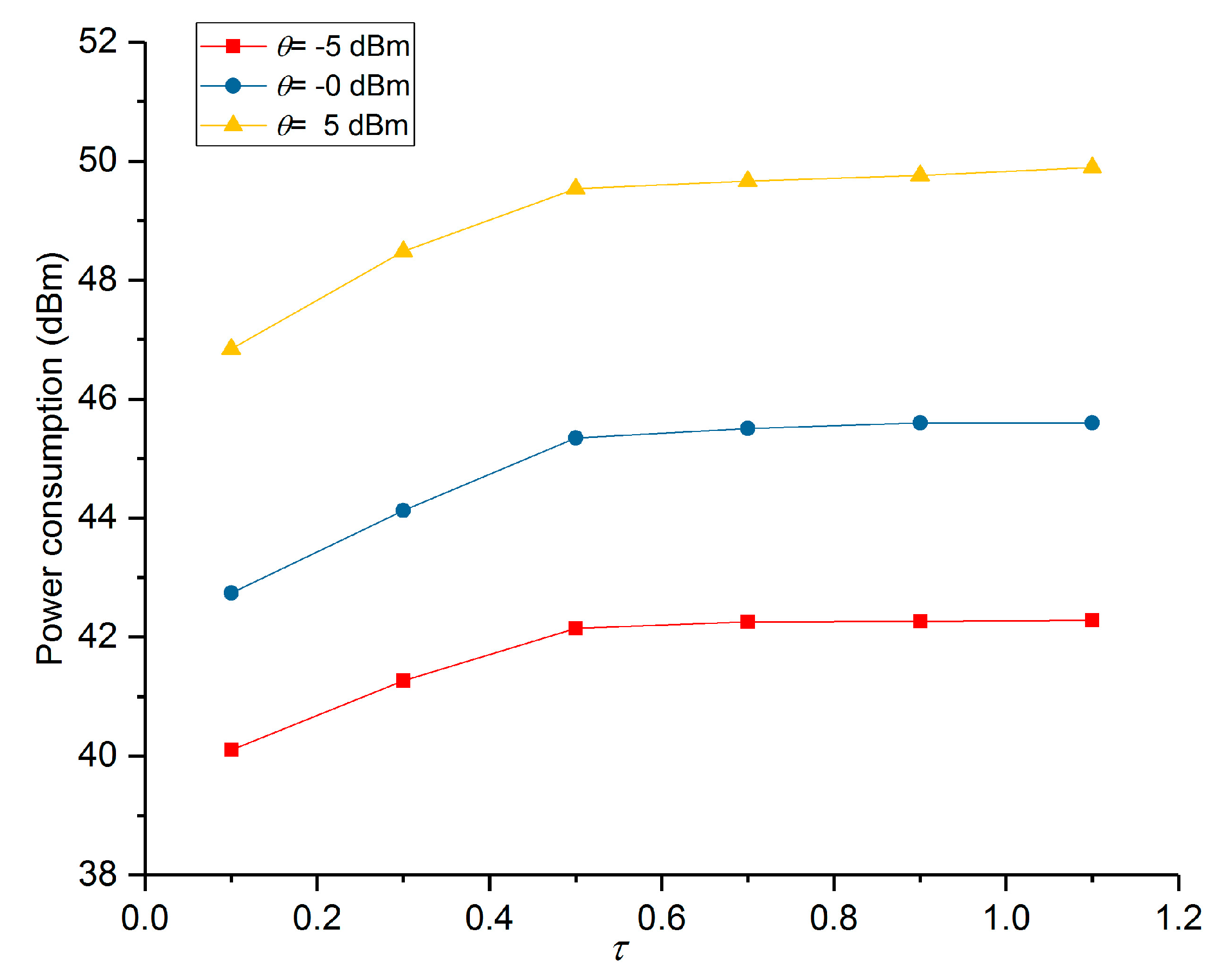
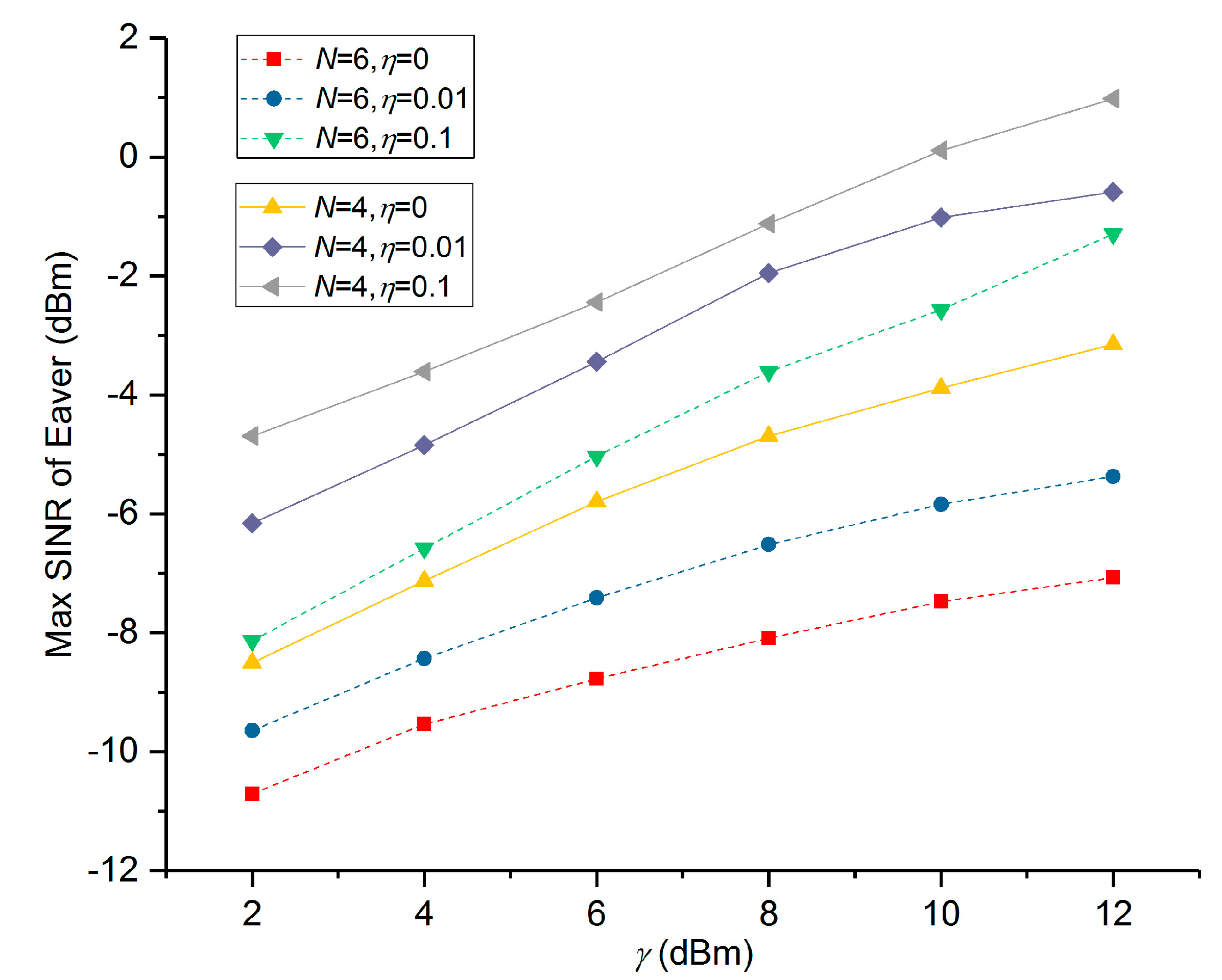
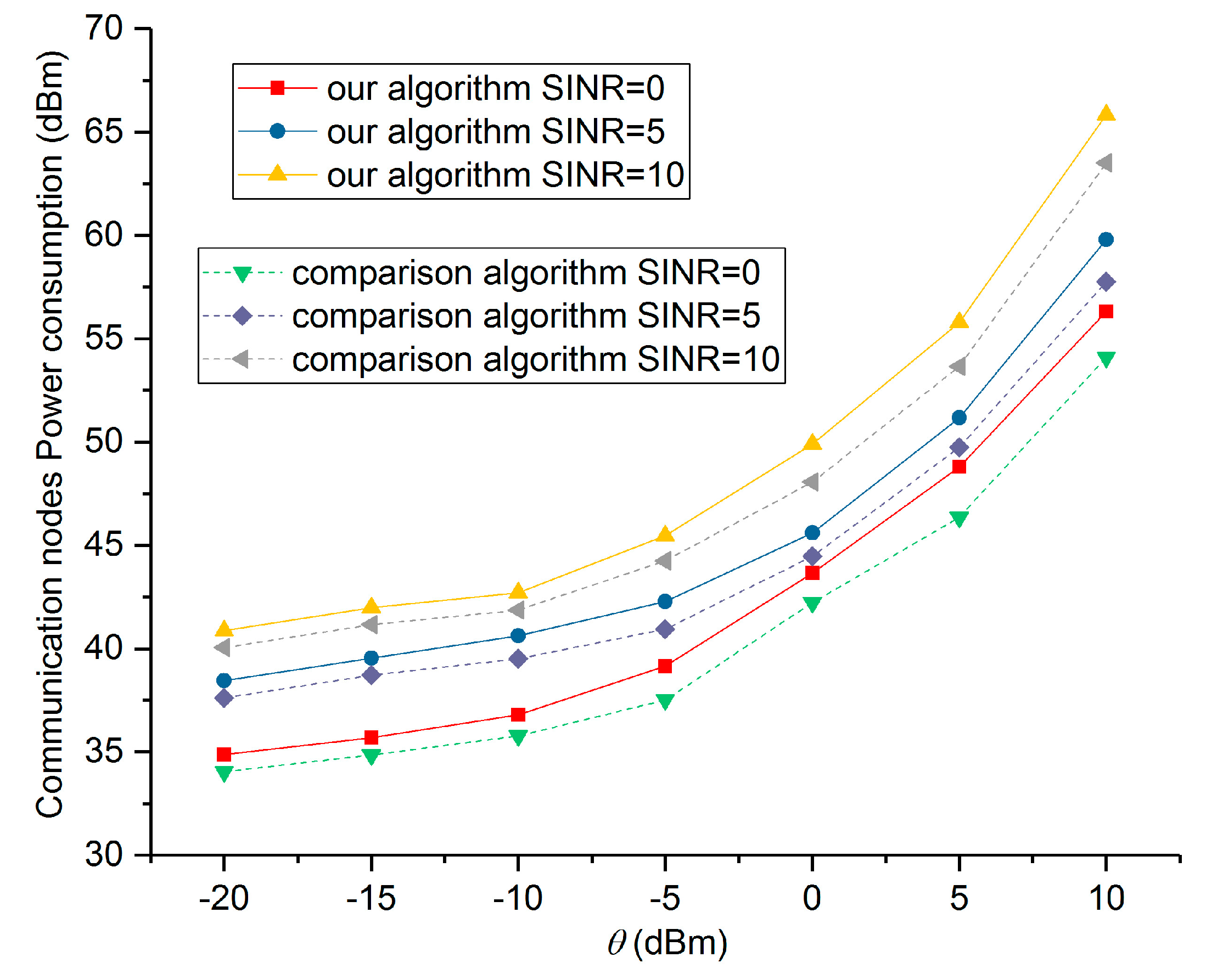
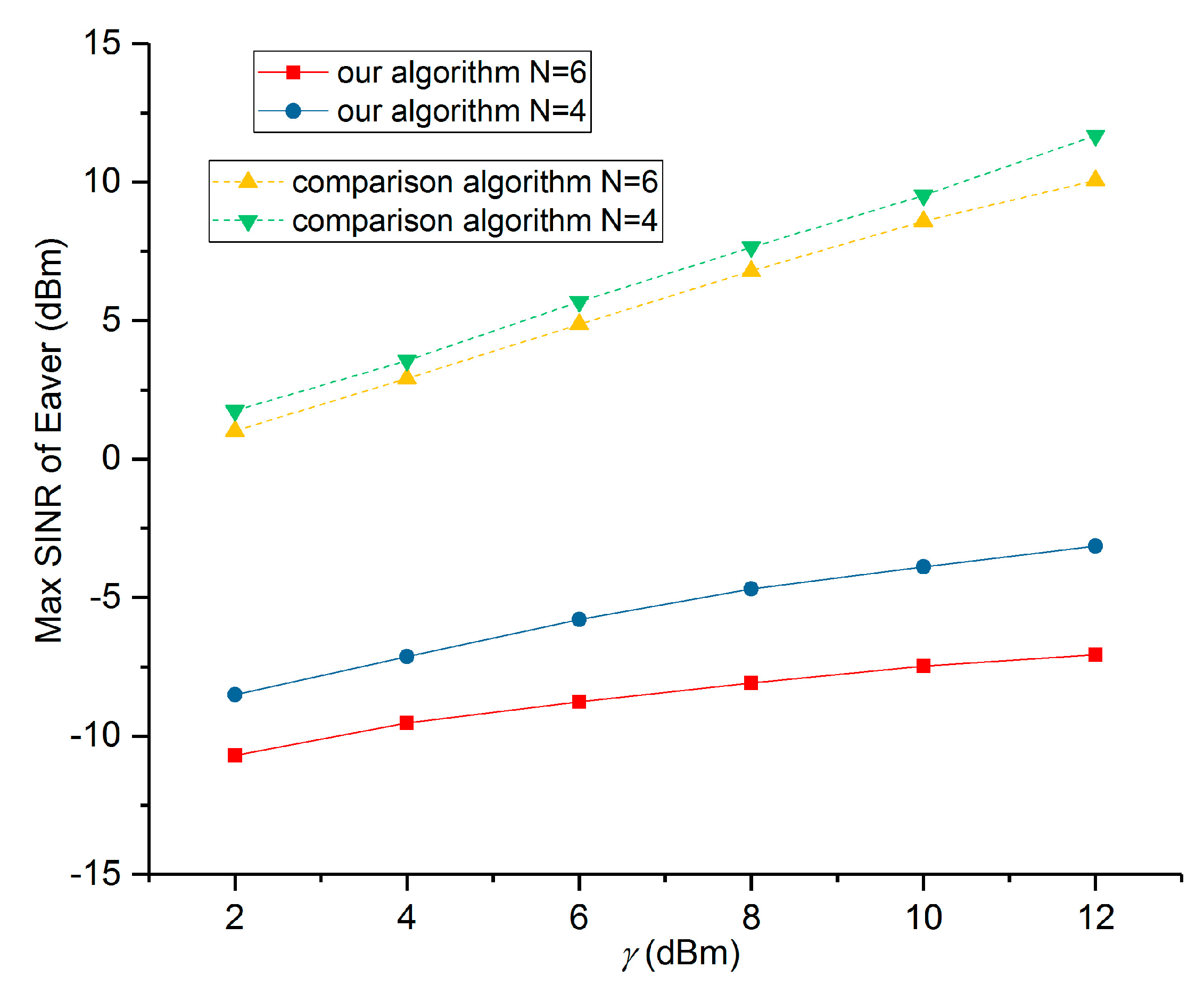
5. Numerical Results and Performance Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cheng, Y.; Li, H.; Shila, D.M.; Cao, X. A Systematic Study of Maximal Scheduling Algorithms in Multiradio Multichannel Wireless Networks. IEEE/ACM Trans. Netw. 2015, 23, 1342–1355. [Google Scholar] [CrossRef]
- Campbell, C.; Khan, S.; Singh, D.; Loo, K. Multi-Channel Multi-Radio Using 802.11 Based Media Access for Sink Nodes in Wireless Sensor Networks. Sensors 2011, 11, 4917–4942. [Google Scholar] [CrossRef]
- Lam, J.; Lee, S.; Tan, W. Performance Evaluation of Multi-Channel Wireless Mesh Networks with Embedded Systems. Sensors 2012, 12, 500–517. [Google Scholar] [CrossRef] [PubMed]
- Santana, J.; Marrero, D.; Macías, E.; Mena, V.; Suárez, Á. Interference Effects Redress over Power-Efficient Wireless-Friendly Mesh Networks for Ubiquitous Sensor Communications across Smart Cities. Sensors 2017, 17, 1678. [Google Scholar] [CrossRef] [PubMed]
- Moayad, A.; Safa, O.; Ismaeel, A.R.; Yaser, J. An Intrusion Detection System for Connected Vehicles in Smart Cities. Ad Hoc Netw. 2019, 10, 1016. [Google Scholar]
- Zaeema, I.; Sobia, J.; Hassaan, Q.; Moayad, A. Resource Efficient Allocation and RRH Placement for Backhaul of Moving Small Cells. IEEE Access. 2019, 7, 47379–47389. [Google Scholar]
- Alim Al Islam, A.B.M.; Islam, M.J.; Nurain, N.; Raghunathan, V. Channel Assignment Techniques for Multi-Radio Wireless Mesh Networks: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 988–1017. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, H.; Wan, P. A theoretical framework for optimal cooperative networking in multiradio multichannel wireless networks. IEEE Wirel. Commun. 2012, 19, 66–73. [Google Scholar] [CrossRef]
- Xie, K.; Wang, X.; Liu, X.; Wen, J.; Cao, J. Interference-Aware Cooperative Communication in Multi-Radio Multi-Channel Wireless Networks. IEEE Trans. Comput. 2016, 5, 1528–1542. [Google Scholar] [CrossRef]
- Park, S.; Kim, B.; Yoon, H.; Choi, S. RA-eV2V: relaying systems for LTE-V2V communications. J. Commun. Netw. 2018, 20, 396–405. [Google Scholar] [CrossRef]
- Ponnimbaduge, P.T.D.; Jayakody, D.N.; Sharma, K.S.K.; Chatzinotas, S.; Li, J. Simultaneous Wireless Information and Power Transfer (SWIPT): Recent Advances and Future Challenges. IEEE Commun. Surv. Tutor. 2018, 1, 264–302. [Google Scholar] [CrossRef]
- Muhammad, S.K.; Sobia, J.; Moayad, A.; Yaser, J.; Thar, B. EPS-TRA: Energy efficient Peer Selection and Time switching Ratio Allocation for SWIPT-enabled D2D Communication. Available online: https://ieeexplore.ieee.org/document/8952654 (accessed on 29 February 2020).
- Haythem, B.S.; Safa, O.; Moayad, A.; Rawan, D.; Ismaeel, A.R.; Yaser, J. Intelligent jamming-aware routing in multi-hop IoT-based opportunistic cognitive radio networks. Ad Hoc Netw. 2020, 98, 102035. [Google Scholar]
- Bruno, R.; Conti, M.; Gregori, E. Mesh networks: commodity multihop ad hoc networks. IEEE Commun. Mag. 2005, 43, 123–131. [Google Scholar] [CrossRef]
- Wang, X.; Yi, P. Security Framework for Wireless Communications in Smart Distribution Grid. IEEE Trans. Smart Grid. 2011, 4, 809–818. [Google Scholar] [CrossRef]
- Glass, S.; Portmann, M.; Muthukkumarasamy, V. Securing Wireless Mesh Networks. IEEE Internet Comput. 2008, 4, 30–36. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, L.; Wong, K.; Heath, R.W. Secure Communications in Millimeter Wave Ad Hoc Networks. IEEE Trans. Wirel. Commun. 2017, 5, 3205–3217. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; McKay, M.R. Enhancing Secrecy With Multi-Antenna Transmission in Wireless Ad Hoc Networks. IEEE Trans. Inf. Forensics Secur. 2013, 11, 1802–1814. [Google Scholar] [CrossRef]
- Alcaraz, C.; Lopez, J. A Security Analysis for Wireless Sensor Mesh Networks in Highly Critical Systems. IEEE Trans. Syst. 2010, 4, 419–428. [Google Scholar] [CrossRef]
- Zhu, G.; Zhong, C.; Suraweera, H.A.; Karagiannidis, G.K.; Zhang, Z.; Tsiftsis, T.A. Wireless information and power transfer in relay systems with multiple antennas and interference. IEEE Trans. Commun. 2015, 4, 1400–1418. [Google Scholar] [CrossRef]
- Liu, D.; Wen, Z.; Liu, X.; Li, S.; Zou, J. Joint Source-Relay Optimization for MIMO Full-Duplex Bidirectional Wireless Sensor Networks with SWIPT. Sensors 2019, 19, 1827. [Google Scholar] [CrossRef]
- Park, J.; Clerckx, B. Joint wireless information and energy transfer in a two-user MIMO interference channel. IEEE Trans. Wirel. Commun. 2013, 8, 4210–4221. [Google Scholar] [CrossRef]
- Xue, L.; Wang, J.; Li, J.; Wang, Y.; Guan, X. Precoding Design for Energy Efficiency Maximization in MIMO Half-Duplex Wireless Sensor Networks with SWIPT. Sensors 2019, 19, 4923. [Google Scholar] [CrossRef] [PubMed]
- Avallone, S.; Banchs, A. A Channel Assignment and Routing Algorithm for Energy Harvesting Multiradio Wireless Mesh Networks. IEEE J. Sel. Areas Commun. 2016, 5, 1463–1476. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 8, 1355–1387. [Google Scholar] [CrossRef]
- Gao, Q.; Huo, Y.; Ma, L.; Xing, X.; Cheng, X.; Jing, T.; Liu, H. Joint design of jammer selection and beamforming for securing MIMO cooperative cognitive radio networks. IET Commun. 2017, 8, 1264–1274. [Google Scholar]
- Wen, Y.; Huo, Y.; Ma, L.; Jing, T.; Gao, Q. A Scheme for Trustworthy Friendly Jammer Selection in Cooperative Cognitive Radio Networks. IEEE Trans. Veh. Technol. 2019, 4, 3500–3512. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.; Li, Q.; Qin, J. Cooperative jamming aided robust secure transmission for wireless information and power transfer in MISO channels. IEEE Trans. Commun. 2015, 3, 906–915. [Google Scholar] [CrossRef]
- Xing, H.; Liu, L.; Zhang, R. Secrecy wireless information and power transfer in fading wiretap channel. IEEE Trans. Veh. Technol. 2016, 1, 180–190. [Google Scholar] [CrossRef]
- Xing, H.; Chu, Z.; Ding, Z.; Nallanathan, A. Harvest-and-jam: Improving security for wireless energy harvesting cooperative networks. In Proceedings of the IEEE Global Communication (GLOBECOM), Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Li, Q.; Zhang, Q.; Qin, J. Secure Relay Beamforming for Simultaneous Wireless Information and Power Transfer in Nonregenerative Relay Networks. IEEE Transactions on Vehicular Technology. 2014, 5, 2462–2467. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Toronto, CA, USA, 6–11 July 2008. [Google Scholar]
- Grover, P.; Sahai, A. Shannon meets Tesla: Wireless information and power transfer. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Austin, TX, USA, 13–18 June 2010. [Google Scholar]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 11, 4754–4767. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.-C. Wireless information and power transfer: A dynamic power splitting approach. IEEE Trans. Commun. 2013, 9, 3990–4001. [Google Scholar] [CrossRef]
- Ding, Z.; Zhong, C.; Ng, D.W.K.; Peng, M.; Suraweera, H.A.; Schober, R.; Poor, H.V. Application of smart antenna technologies in simultaneous wireless information and power transfer. IEEE Commun. Mag. 2015, 4, 86–93. [Google Scholar]
- Xu, J.; Liu, L.; Zhang, R. Multiuser MISO beamforming for simultaneous wireless information and power transfer. IEEE Trans. Signal Process. 2014, 18, 4798–4810. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C.K. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 5, 1989–2001. [Google Scholar] [CrossRef]
- Wen, Y.; Jing, T.; Huo, Y.; Li, Z.; Gao, Q. Secrecy Energy Efficiency Optimization for Cooperative Jamming in Cognitive Radio Network. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018. [Google Scholar]
- Hua, Y.; Ma, Y.; Gholian, A.; Li, Y.; Cirik, A.C.; Liang, P. Radio self-interference cancellation by transmit beamforming, all-analog cancellation and blind digital tuning. Signal Process. 2015, 4, 322–340. [Google Scholar] [CrossRef]
- Boshkovska, E.; Ng, D.W.K.; Zlatanov, N.; Koelpin, A.; Schober, R. Robust resource allocation for MIMO wireless powered communication networks based on a non-linear EH model. IEEE Trans. Commun. 2017, 5, 1984–1999. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, M.; Do, D.; Voznak, M. Enabling Non-Linear Energy Harvesting in Power Domain Based Multiple Access in Relaying Networks: Outage and Ergodic Capacity Performance Analysis. Electronics 2019, 8, 817. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhou, F.; Al-Dhahir, N.; Deng, X. Robust Resource Allocation for MISO Cognitive Radio Networks Under Two Practical Non-Linear Energy Harvesting Models. IEEE Commun. Lett. 2018, 9, 1874–1877. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Y.; Geng, S.; Du, F.; Zhou, Z.; Yang, L. Hybrid Precoding for an Adaptive Interference Decoding SWIPT System with Full-Duplex IoT Devices. IEEE Internet Things J. press. 2020, 7, 1164–1177. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Xue, J.; Biswas, S.; Cirik, A.C.; Du, H.; Yang, Y.; Ratnarajah, T.; Sellathurai, M. Transceiver Design of Optimum Wirelessly Powered Full-Duplex MIMO IoT Devices. IEEE Trans. Commun. 2018, 5, 1955–1969. [Google Scholar] [CrossRef]
- Wen, Z.; Guo, Z.; Beaulieu, N.C.; Liu, X. Robust Beamforming Design for Multi-User MISO Full-Duplex SWIPT System with Channel State Information Uncertainty. IEEE Trans. Veh. Technol. 2019, 2, 1942–1947. [Google Scholar] [CrossRef]
- Chae, S.H.; Jeong, C.; Lim, S.H. Simultaneous Wireless Information and Power Transfer for Internet of Things Sensor Networks. IEEE Internet Things J. 2018, 4, 2829–2843. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, W.; Chang, T.H.; Wang, Y.; Song, E. Joint beamforming and power splitting for MISO interference channel with SWIPT: An SOCP relaxation and decentralized algorithm. IEEE Trans. Signal Process. 2014, 23, 6194–6208. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. Graph Implementations for Non-smooth Convex Programs. Lect. Notes Control Inf. Sci. 2008, 37, 95–110. [Google Scholar]
- Luo, Z.Q.; Ma, W.K.; So, A.M.C.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process. Mag. 2010, 3, 20–34. [Google Scholar] [CrossRef]
- Yu, H.; Lau, V.K.N. Rank-constrained Schur-convex optimization with multiple trace/log-det constraints. IEEE Trans. Signal Process. 2011, 1, 304–314. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Jafar, S.A. Degrees of freedom of wireless networks with relays, feedback, cooperation, and full duplex operation. IEEE Trans. Inf. Theory. 2009, 5, 2334–2344. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Lectures on Modern Convex Optimization: Analysis, Algorithms, Engineering Applications; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhao, X.; Geng, S.; Zhang, Y.; Zhang, L. Robust Beamforming Design for SWIPT-Based Multi-Radio Wireless Mesh Network with Cooperative Jamming. Information 2020, 11, 138. https://doi.org/10.3390/info11030138
Li L, Zhao X, Geng S, Zhang Y, Zhang L. Robust Beamforming Design for SWIPT-Based Multi-Radio Wireless Mesh Network with Cooperative Jamming. Information. 2020; 11(3):138. https://doi.org/10.3390/info11030138
Chicago/Turabian StyleLi, Liang, Xiongwen Zhao, Suiyan Geng, Yu Zhang, and Lei Zhang. 2020. "Robust Beamforming Design for SWIPT-Based Multi-Radio Wireless Mesh Network with Cooperative Jamming" Information 11, no. 3: 138. https://doi.org/10.3390/info11030138
APA StyleLi, L., Zhao, X., Geng, S., Zhang, Y., & Zhang, L. (2020). Robust Beamforming Design for SWIPT-Based Multi-Radio Wireless Mesh Network with Cooperative Jamming. Information, 11(3), 138. https://doi.org/10.3390/info11030138





