Null Models for Formal Contexts †
Abstract
:1. Introduction
2. FCA Basics and Problem Description
3. Related Work
4. Stochastic Modelling
4.1. Coin-Toss—Direct Model
4.2. Coin-Toss: Indirect Model
4.3. Dirichlet Model
| Algorithm 1: Dirichlet Approach |
 |
5. Experiments
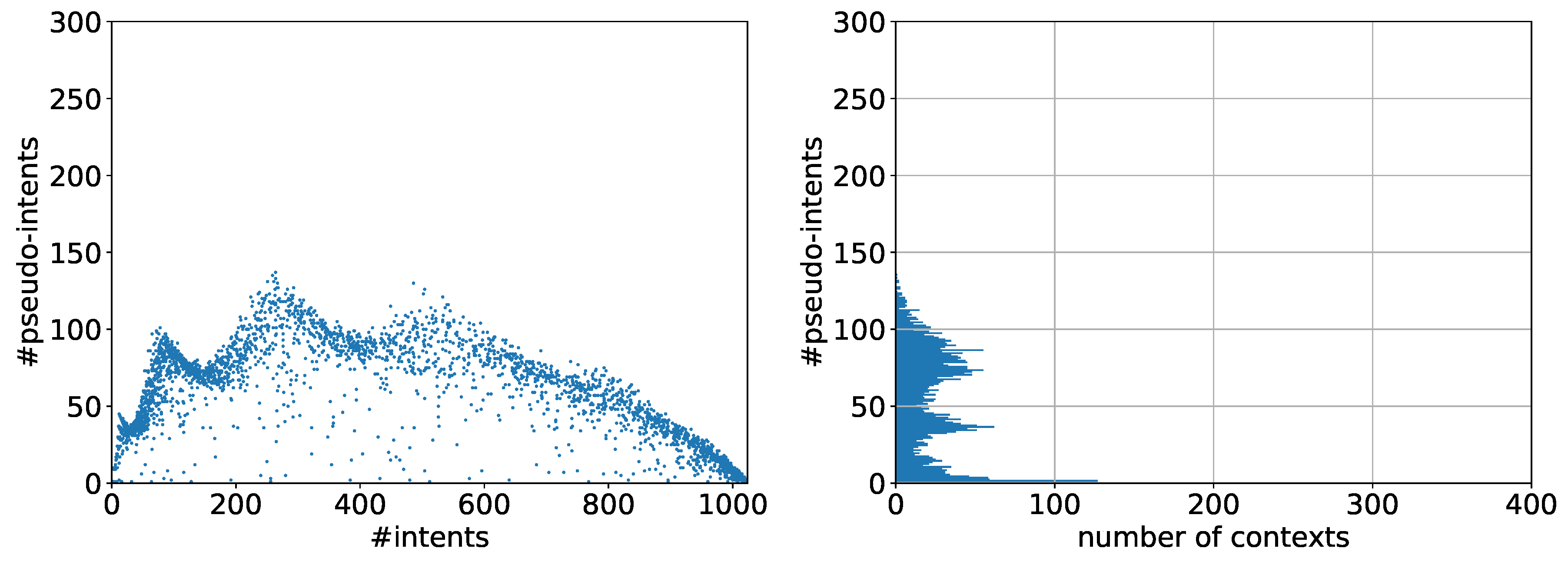
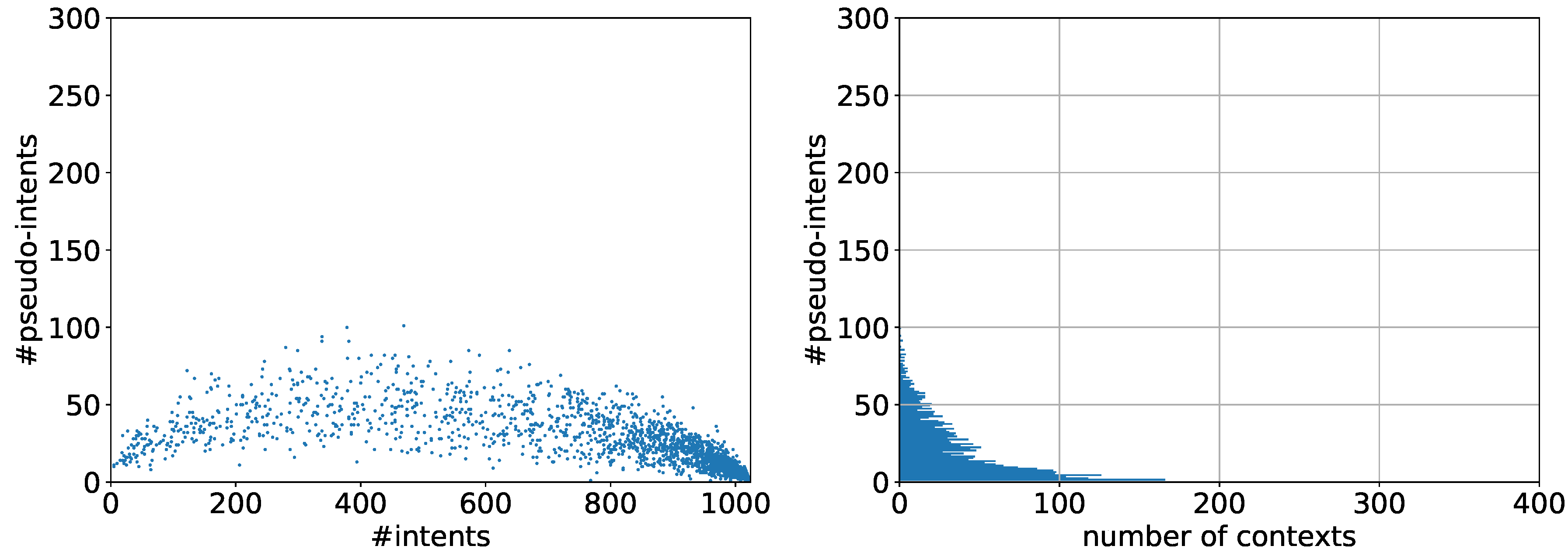
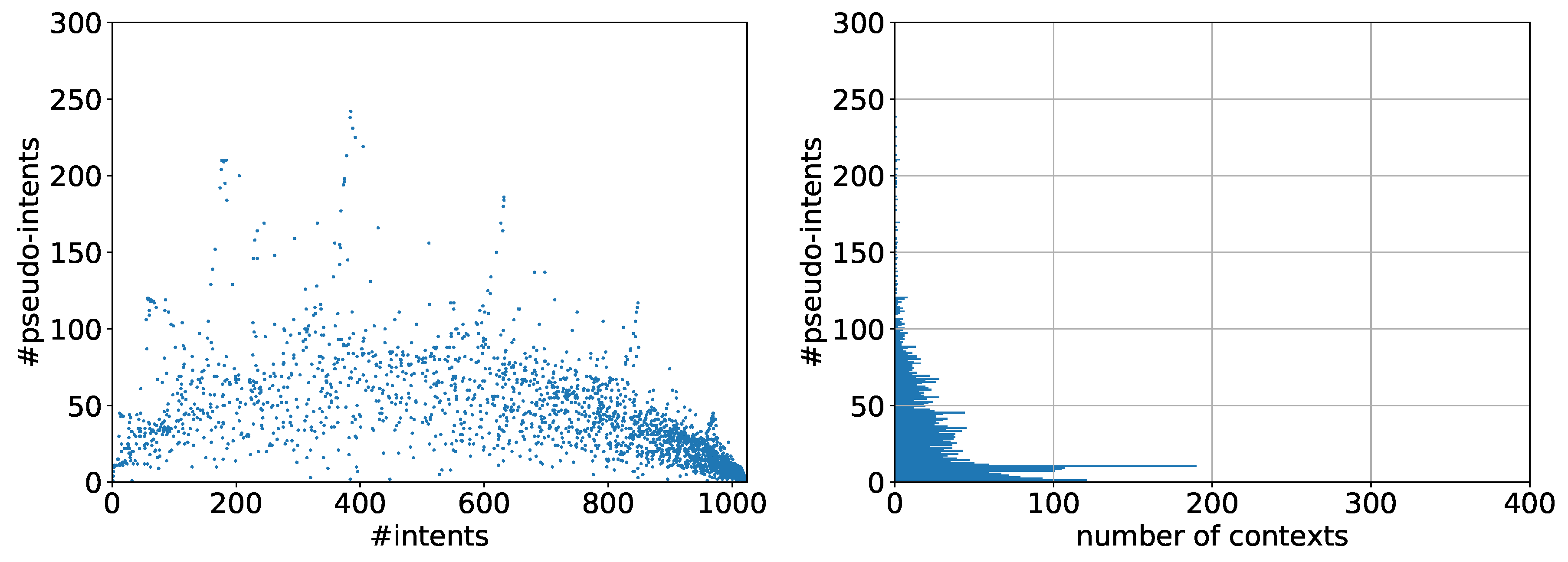
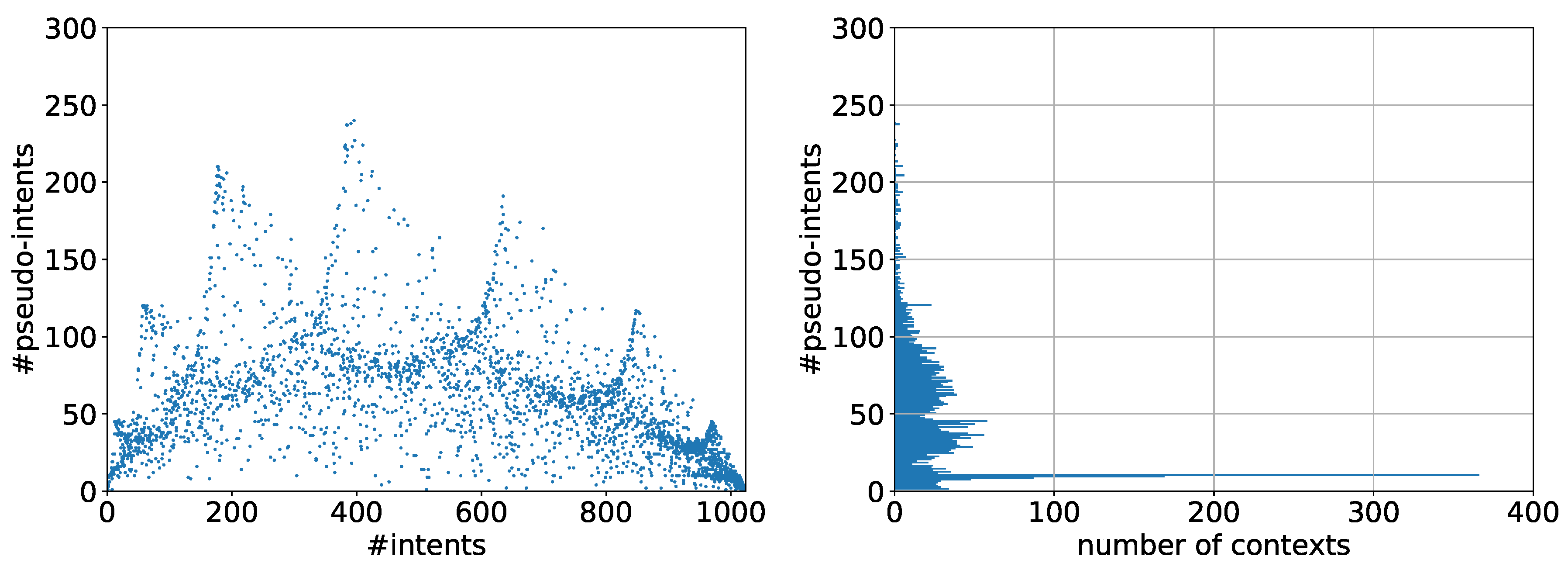
5.1. Observations
5.2. Discussion
5.3. The Problem with Contranominal Scales
6. Applications
6.1. Null Models for Formal Contexts
The Dirichlet Null Model for Formal Contexts
6.2. Evaluation of the Dirichlet Approach for Null Model Generation
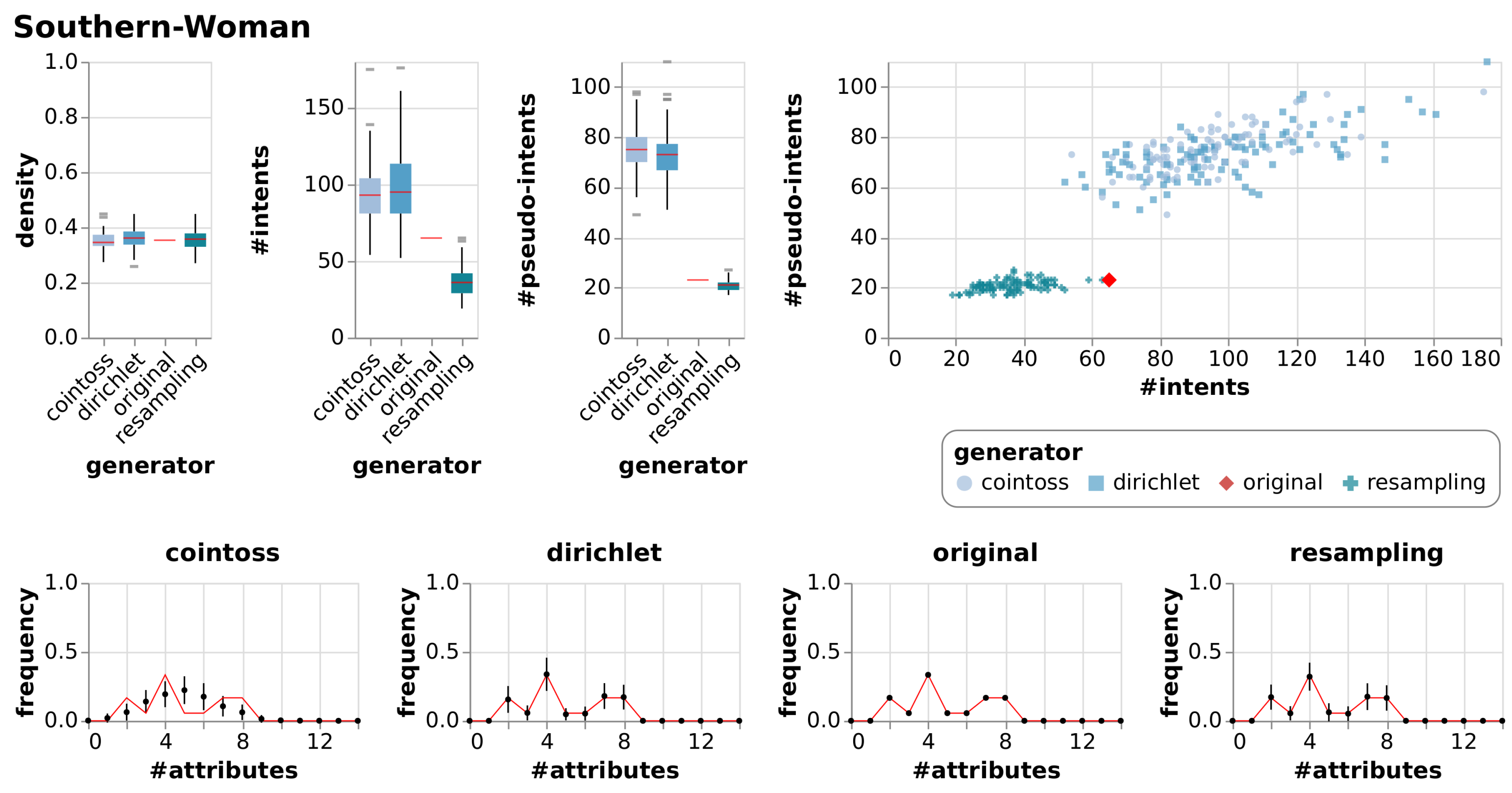
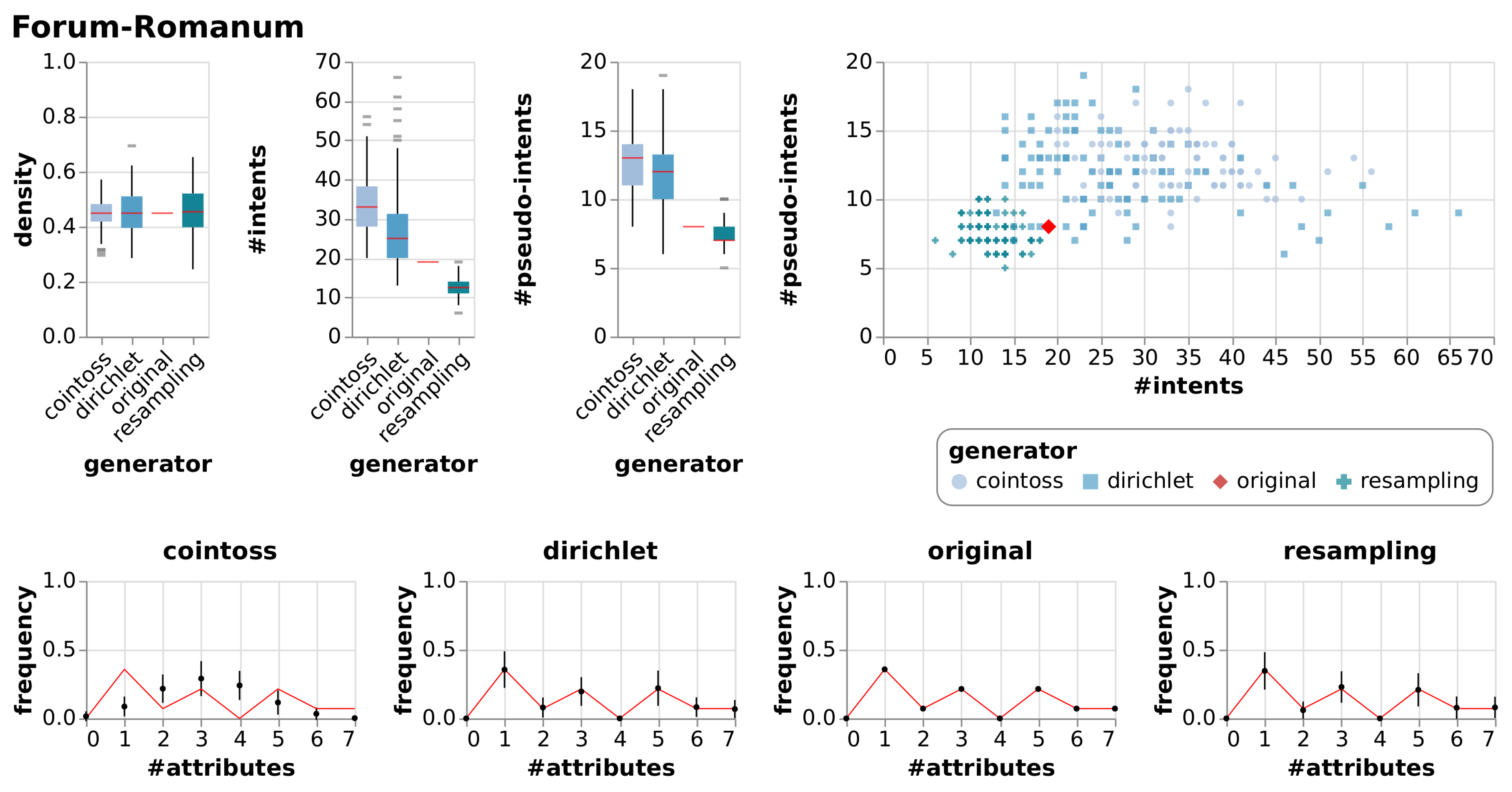
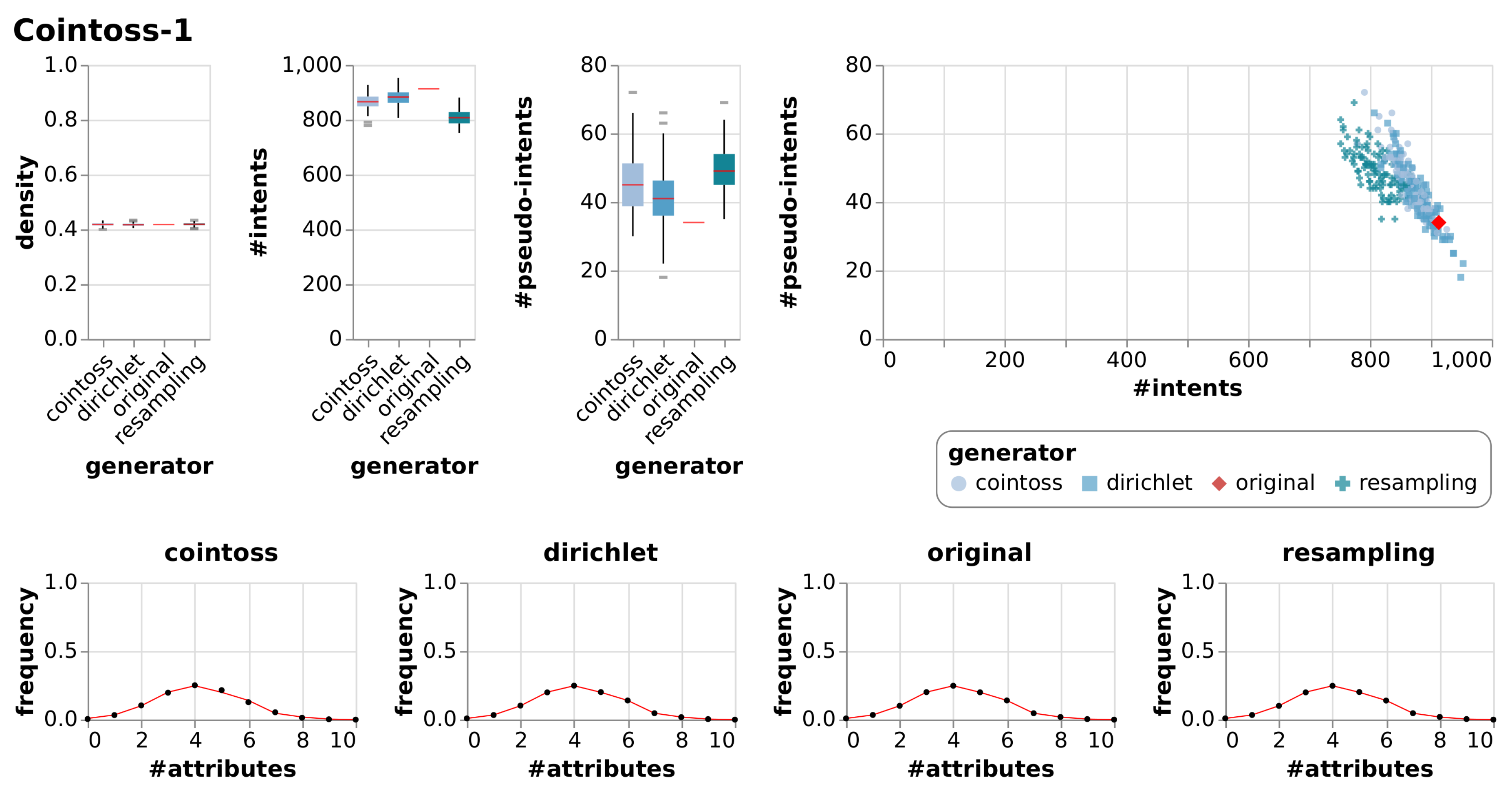
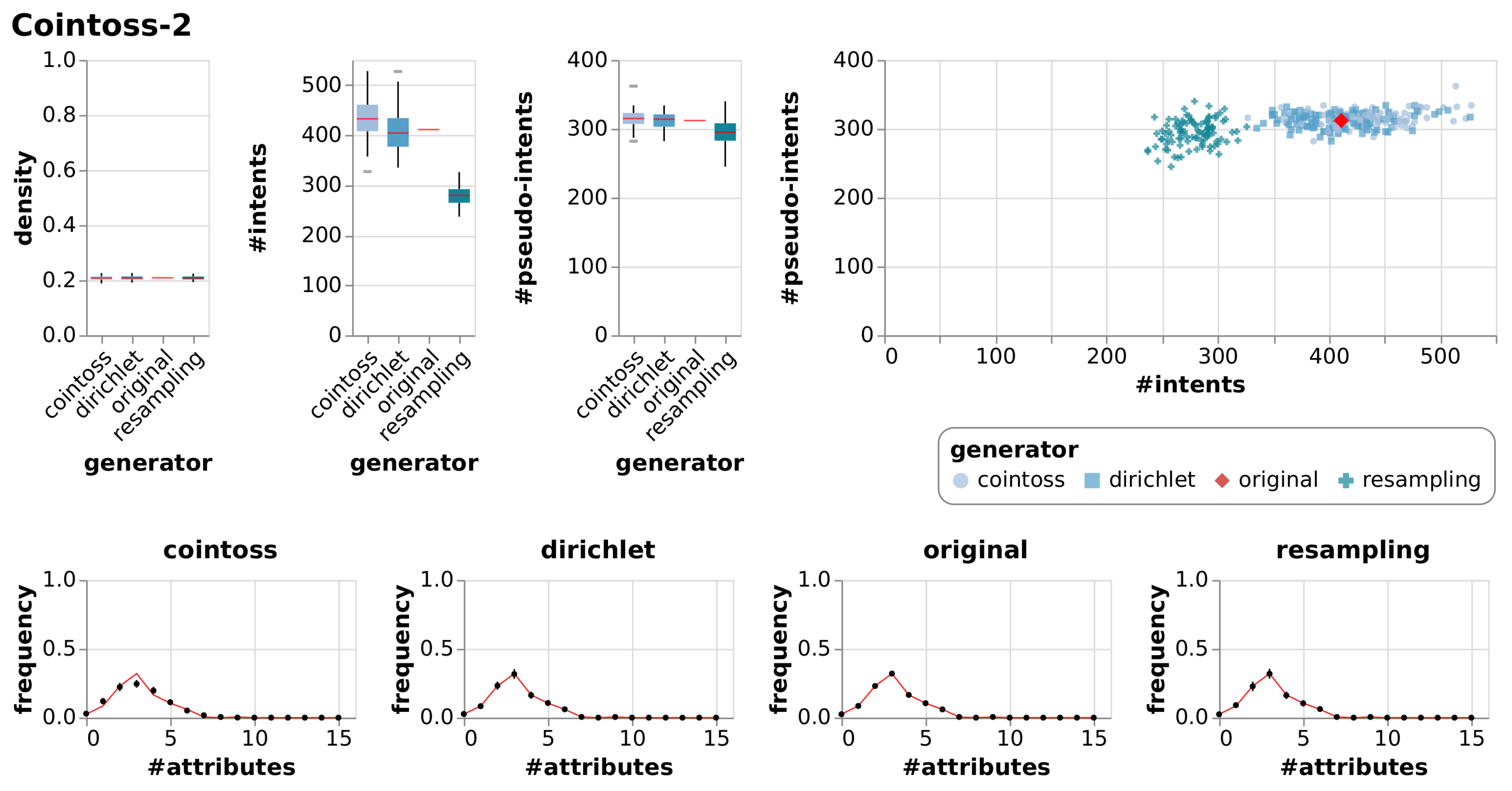
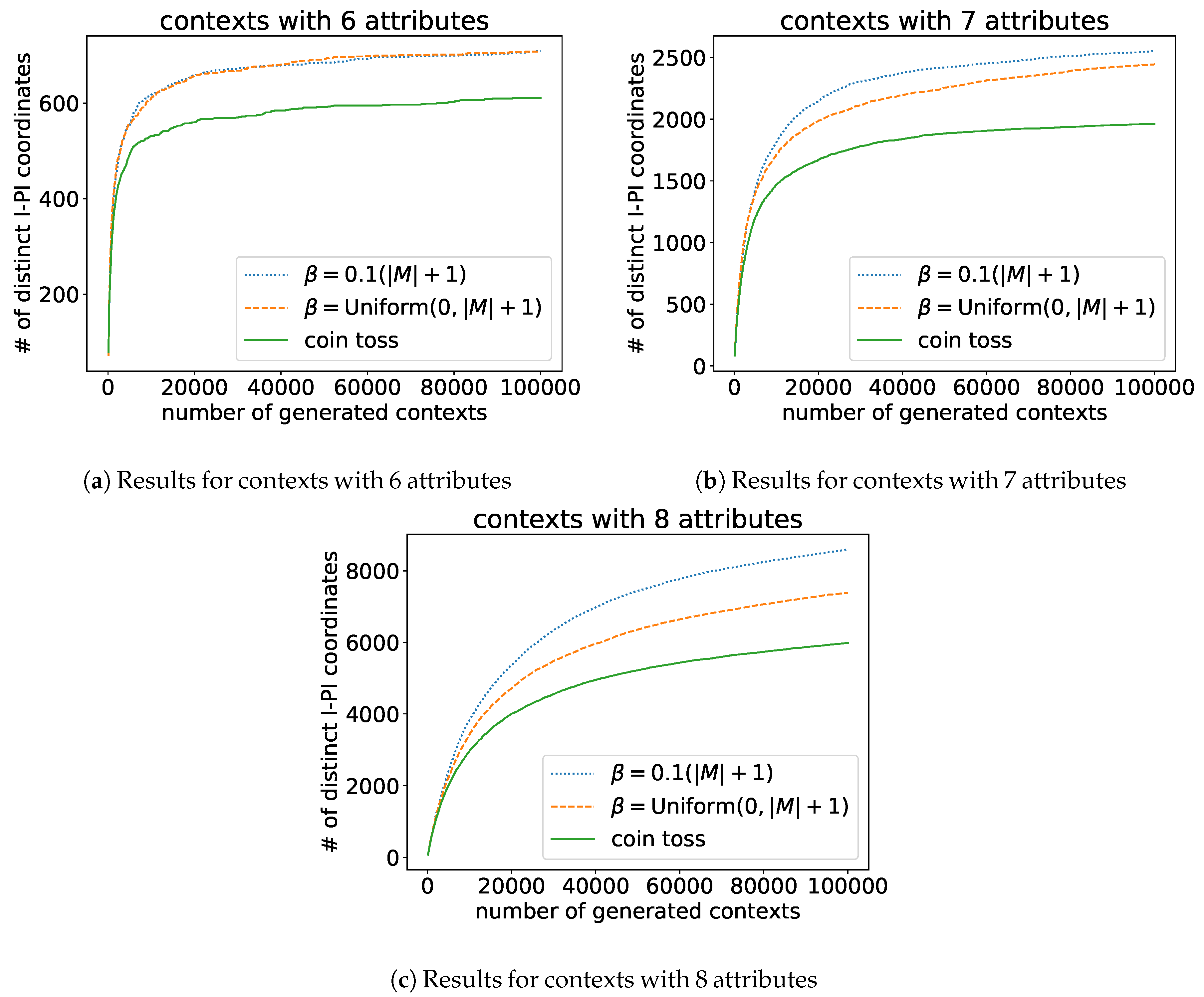
6.2.1. Observations
6.2.2. Evaluation
7. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Felde, M.; Hanika, T. Formal Context Generation Using Dirichlet Distributions. In Graph-Based Representation and Reasoning; Endres, D., Alam, M., Şotropa, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 57–71. [Google Scholar]
- Ganter, B.; Wille, R. Formal Concept Analysis: Mathematical Foundations; Springer: Berlin, Germany, 1999; pp. x+284. [Google Scholar]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ulrich, W.; Gotelli, N.J. Pattern detection in null model analysis. Oikos 2013, 122, 2–18. [Google Scholar] [CrossRef] [Green Version]
- Gotelli, N.J. Null Model Analysis of Species Co-occurrence Patterns. Ecology 2000, 81, 2606–2621. [Google Scholar] [CrossRef]
- Kuznetsov, S.O.; Obiedkov, S.A. Comparing performance of algorithms for generating concept lattices. J. Exp. Theor. Artif. Intell. 2002, 14, 189–216. [Google Scholar] [CrossRef]
- Bazhanov, K.; Obiedkov, S.A. Comparing Performance of Algorithms for Generating the Duquenne-Guigues Basis. In Proceedings of the Eighth International Conference on Concept Lattices and Their Applications, Nancy, France, 17–20 October 2011; Napoli, A., Vychodil, V., Eds.; CEUR-WS.org: Aachen, Germany, 2011; Volume 959, pp. 43–57. [Google Scholar]
- Borchmann, D.; Hanika, T. Some Experimental Results on Randomly Generating Formal Contexts. In Proceedings of the Thirteenth International Conference on Concept Lattices and Their Applications, Moscow, Russia, 18–22 July 2016; Huchard, M., Kuznetsov, S.O., Eds.; CEUR-WS.org: Aachen, Germany, 2016; Volume 1624, pp. 57–69. [Google Scholar]
- Ganter, B. Random Extents and Random Closure Systems. In CLA; Napoli, A., Vychodil, V., Eds.; CEUR-WS.org: Aachen, Germany, 2011; Volume 959, pp. 309–318. [Google Scholar]
- Colomb, P.; Irlande, A.; Raynaud, O. Counting of Moore Families for n=7. In Formal Concept Analysis; Kwuida, L., Sertkaya, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 72–87. [Google Scholar]
- Borchmann, D. Decomposing Finite Closure Operators by Attribute Exploration. In Contributions to ICFCA 2011; Domenach, F., Jäschke, R., Valtchev, P., Eds.; Univ. of Nicosia: Nicosia, Cyprus, 2011; pp. 24–37. [Google Scholar]
- Rimsa, A.; Song, M.A.J.; Zárate, L.E. SCGaz—A Synthetic Formal Context Generator with Density Control for Test and Evaluation of FCA Algorithms. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Manchester, SMC 2013, Manchester, UK, 13–16 October 2013; pp. 3464–3470. [Google Scholar] [CrossRef]
- Ferguson, T.S. A Bayesian Analysis of Some Nonparametric Problems. Ann. Stat. 1973, 1, 209–230. [Google Scholar] [CrossRef]
- Hanika, T.; Hirth, J. Conexp-Clj—A Research Tool for FCA. In Proceedings of the Supplementary Proceedings of ICFCA 2019 Conference and Workshops, Frankfurt, Germany, 25–28 June 2019; CEUR-WS.org: Aachen, Germany, 2019; Volume 2378, pp. 70–75. [Google Scholar]
- Dawkins, B. Siobhan’s Problem: The Coupon Collector Revisited. Am. Stat. 1991, 45, 76–82. [Google Scholar]
- Onnela, J.P.; Arbesman, S.; González, M.C.; Barabási, A.L.; Christakis, N.A. Geographic constraints on social network groups. PLoS ONE 2011, 6, e16939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karsai, M.; Kivelä, M.; Pan, R.K.; Kaski, K.; Kertész, J.; Barabási, A.L.; Saramäki, J. Small but slow world: How network topology and burstiness slow down spreading. Phys. Rev. E 2011, 83, 025102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, F.; Lu, L. Connected Components in Random Graphs with Given Expected Degree Sequences. Ann. Comb. 2002, 6, 125–145. [Google Scholar] [CrossRef]
- Kunegis, J. KONECT: The Koblenz network collection. In Proceedings of the 22nd International World Wide Web Conference, WWW ’13, Rio de Janeiro, Brazil, 13–17 May 2013; Companion Volume; Carr, L., Laender, A.H.F., Lóscio, B.F., King, I., Fontoura, M., Vrandecic, D., Aroyo, L., De Oliveira, J.P.M., Lima, F., Wilde, E., Eds.; International World Wide Web Conferences Steering Committee/ACM: New York, NY, USA, 2013; pp. 1343–1350. [Google Scholar] [CrossRef]
- Faust, K. Centrality in Affiliation Networks. Soc. Netw. 1997, 19, 157–191. [Google Scholar] [CrossRef]
- Czerniak, J.; Zarzycki, H. Application of rough sets in the presumptive diagnosis of urinary system diseases. In Artificial Intelligence and Security in Computing Systems; Sołdek, J., Drobiazgiewicz, L., Eds.; Springer US: Boston, MA, USA, 2003; pp. 41–51. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California: Irvine, CA, USA, 2017. [Google Scholar]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The Bottlenose Dolphin Community of Doubtful Sound Features a Large Proportion of Long-Lasting Associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Felde, M.; Stumme, G. Interactive Collaborative Exploration using Incomplete Contexts. arXiv 2019, arXiv:1908.08740. [Google Scholar]
- Davis, A.; Gardner, B.B.; Gardner, M.R. Deep South; a Social Anthropological Study of Caste and Class; The University of Chicago Press: Chicago, IL, USA, 1941. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
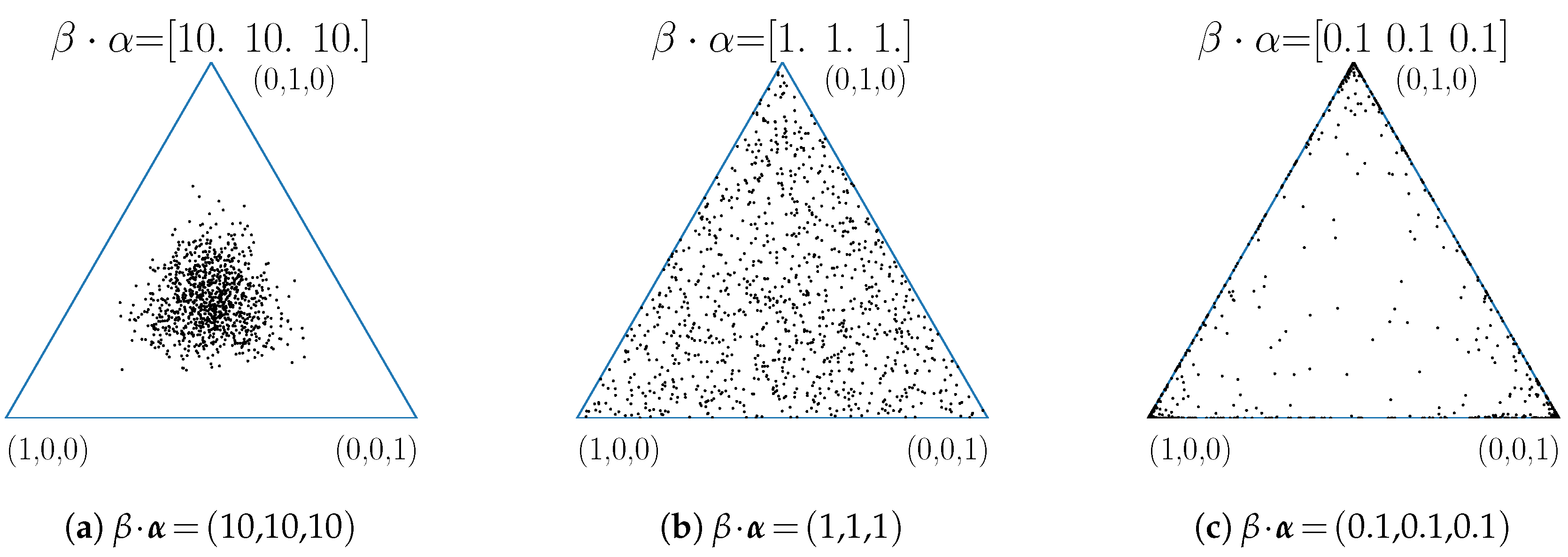

| Constraint | Randomization Method(s) for Null Models |
|---|---|
| keep G-dist and M-dist | pairwise swapping of incidences |
| keep G-dist or M-dist | shuffling of rows or columns |
| keep (G-dist) or (M-dist) | Dirichlet approach based on the row sum distribution as base measure and a high precision parameter. |
| keep (density) | coin-toss based on density, Dirichlet approach |
| keep all implications | resampling of objects |
| Context | Source | Description |
|---|---|---|
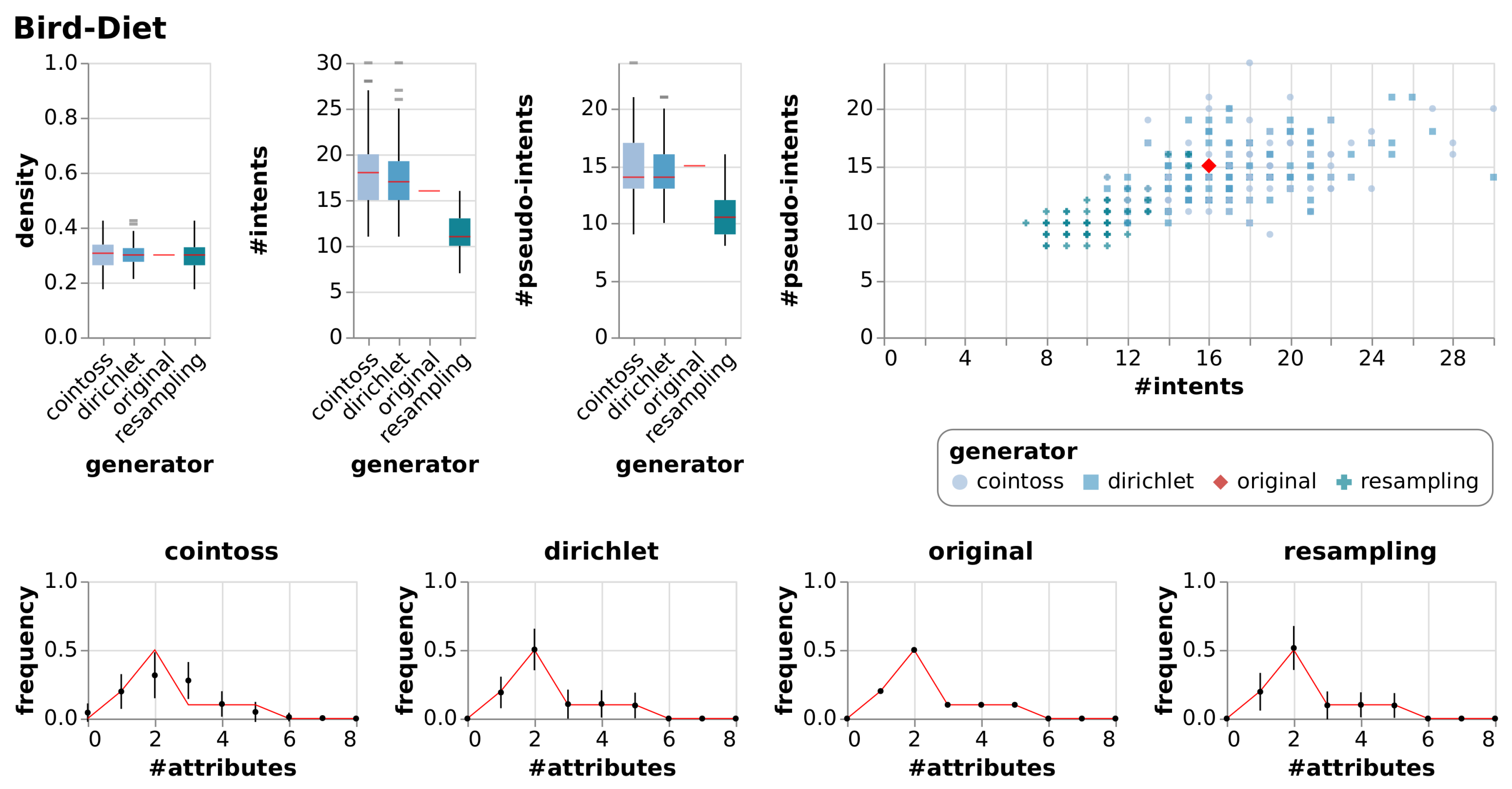
| Bird-Diet | [14] | A context of birds and what they eat. |
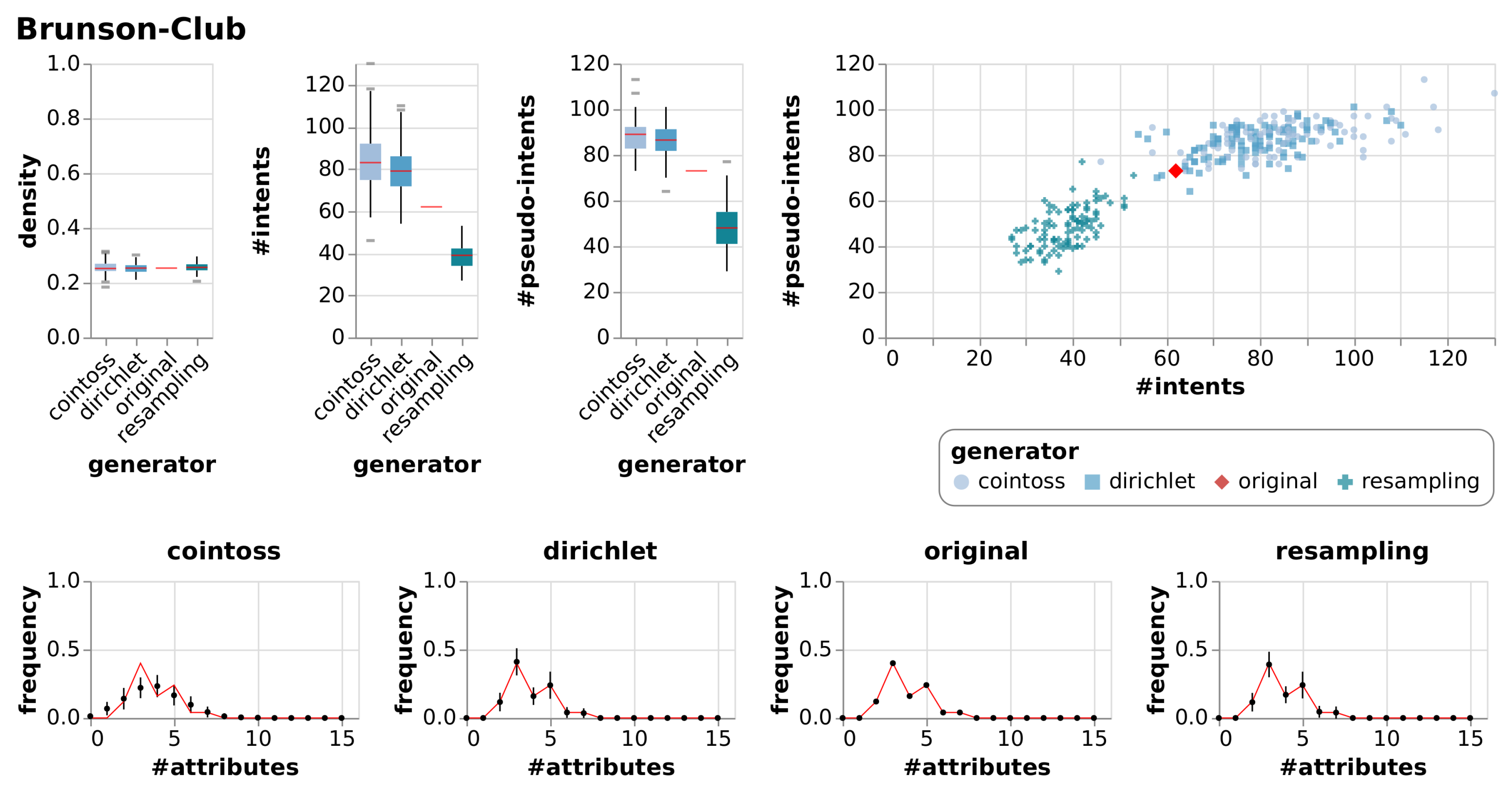
| Brunson-Club | [20,21] | Membership information of corporate executive officers in social organisations. |
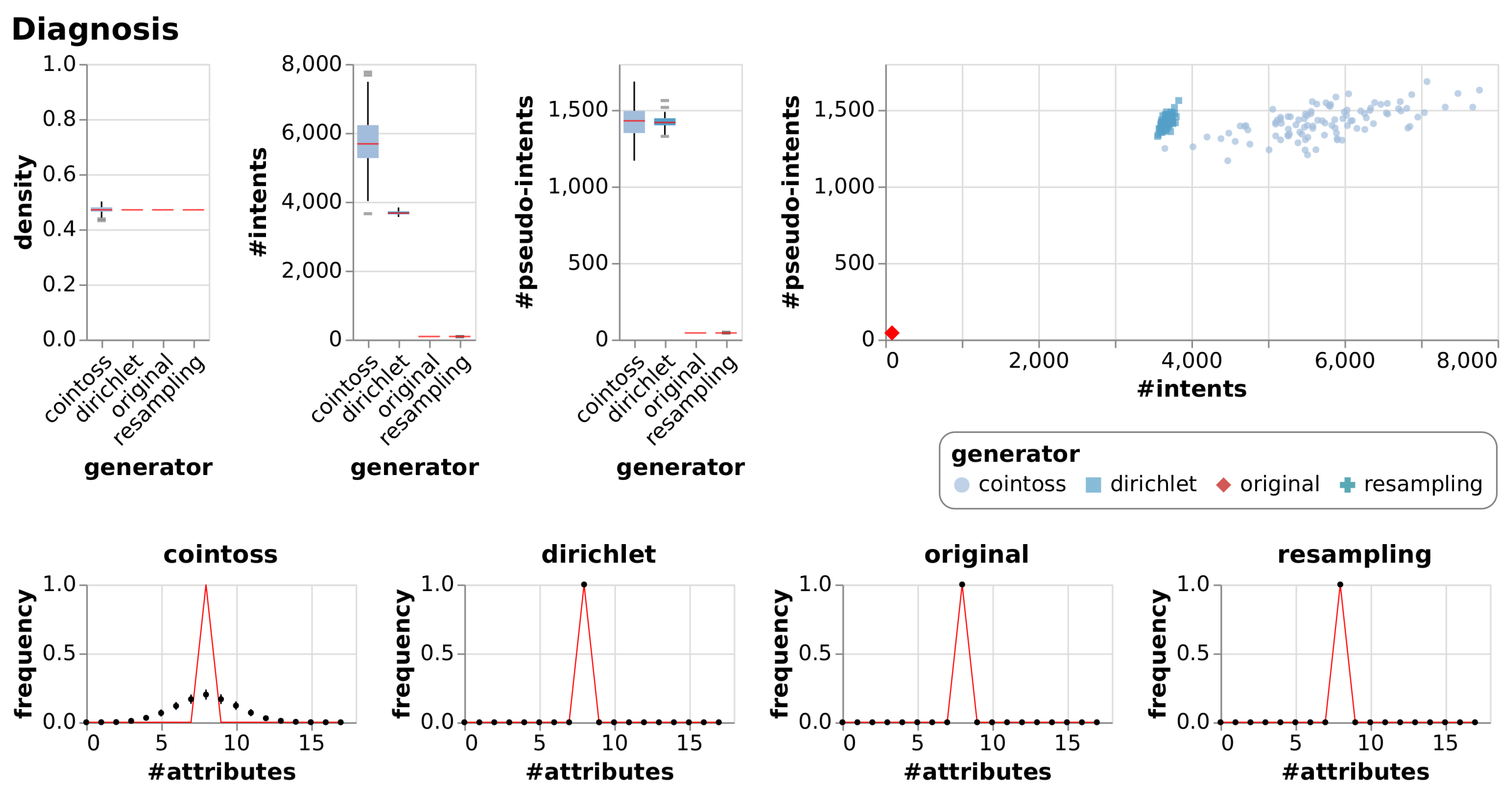
| Diagnosis | [22,23] | The data was created by a medical expert as a data set to test the expert system, which will perform the presumptive diagnosis of two diseases of the urinary system. The temperature attribute is interval-scaled. |
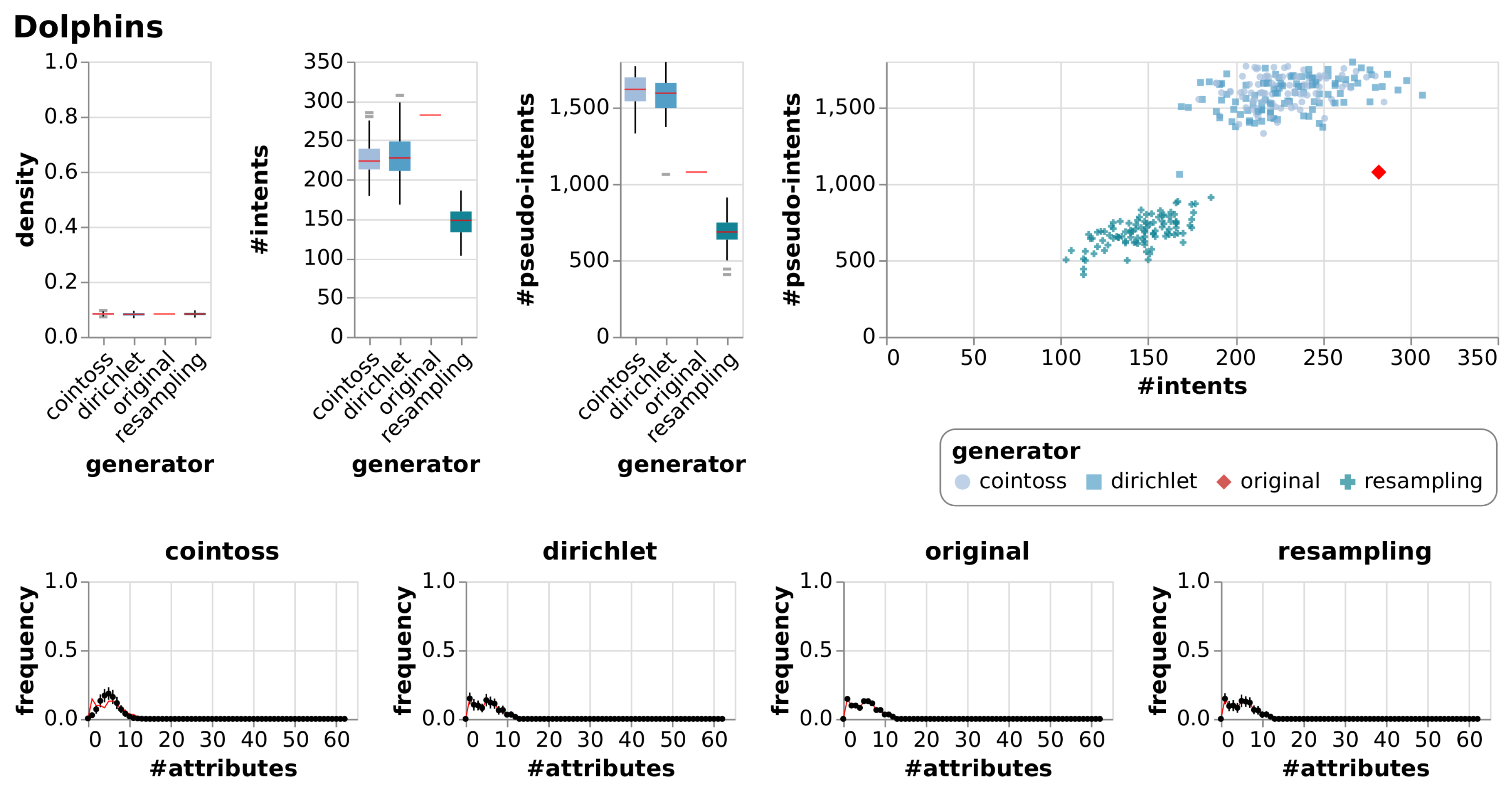
| Dolphins | [20,24] | A formal context created from a directed social network of bottlenose dolphins living in a fjord in New Zealand. A relation indicates frequent association based on observations between 1994 and 2001. |
| Forum-Romanum | [2] | A context based on ratings of monuments on the Forum Romanum in different travel guides and scaled ordinally. This context can be found in the standard work on FCA. |
| Living-Beings-and-Water | [2] | The first formal context in the standard work on FCA (the yellow book) by Ganter and Wille. |
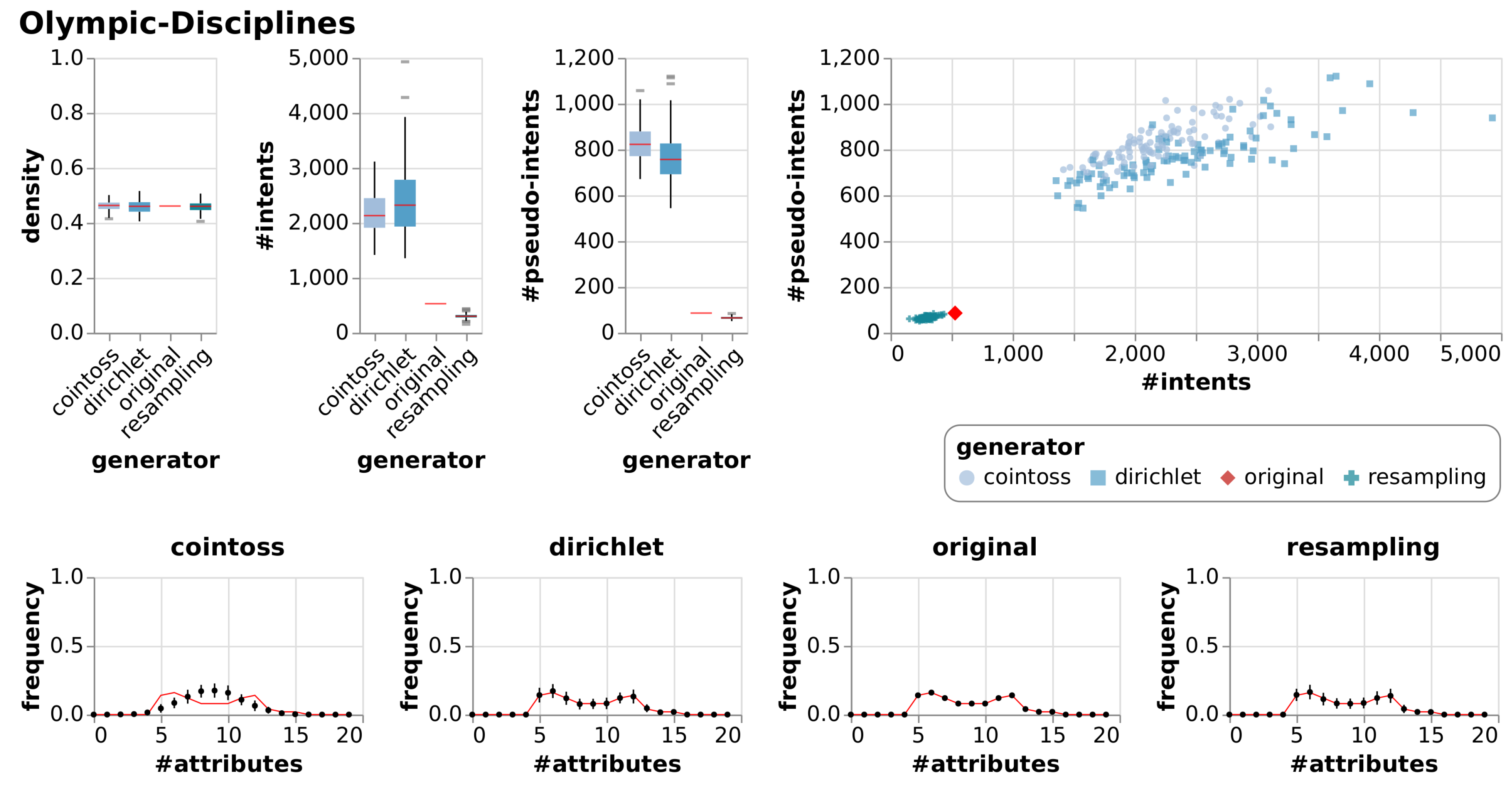
| Olympic-Disciplines | [25] | This context is about the disciplines of the Summer Olympic Games 2020. |
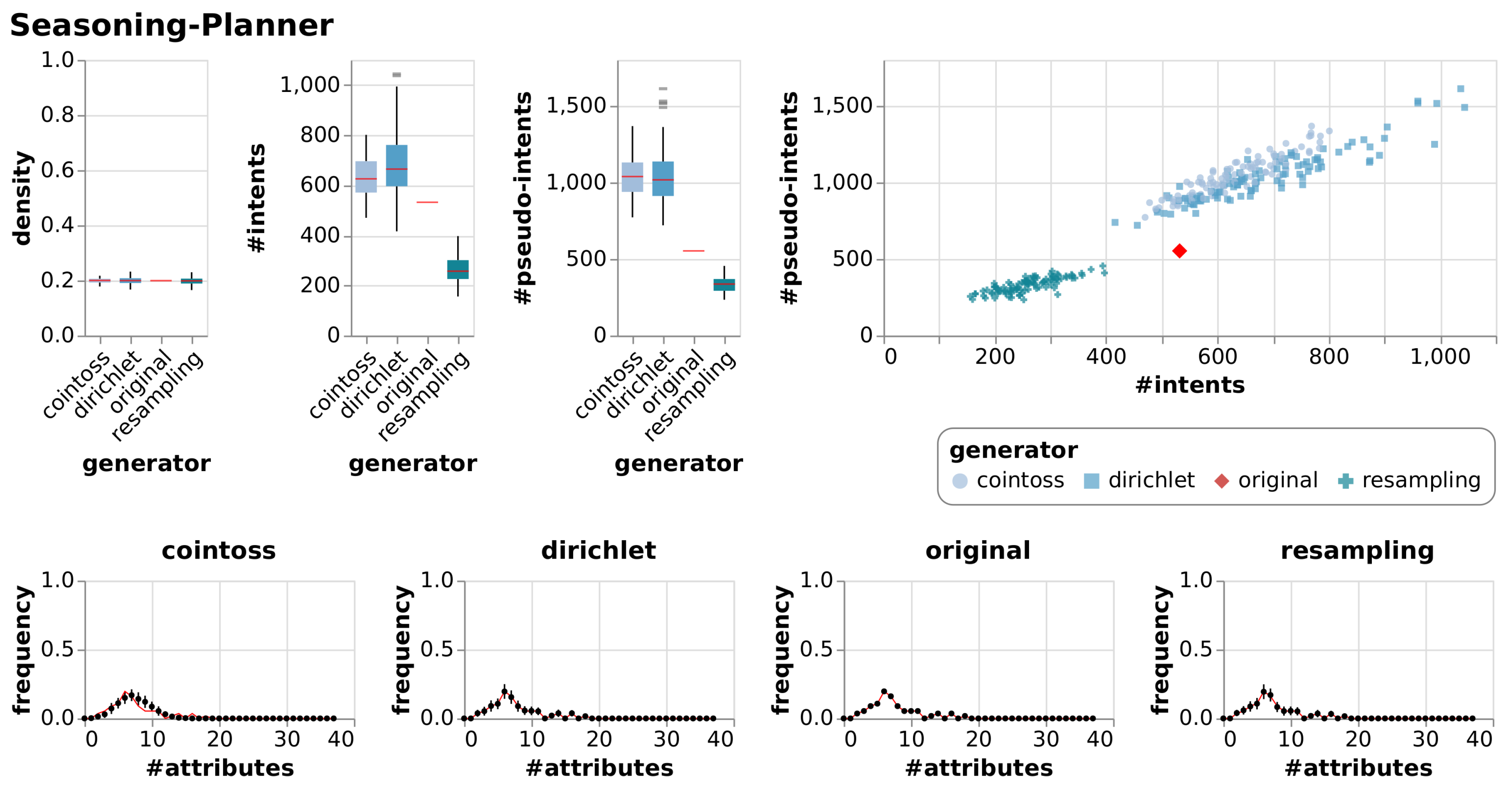
| Seasoning-Planner | [14] | This context contains foods that are related to recommended seasonings based on a chart published by the spice company Fuchs Group. |
| Southern-Woman | [20,26] | Participation of 18 white women in 14 social events over a nine-month period, collected in the Southern United States of America in the 1930s. |
| Wood-Properties | [14] | A context about properties of different kinds of wood. |
| Cointoss-1 | artificial | Artificially generated with the coin-toss approach. |
| Cointoss-2 | artificial | Artificially generated with the coin-toss approach. |
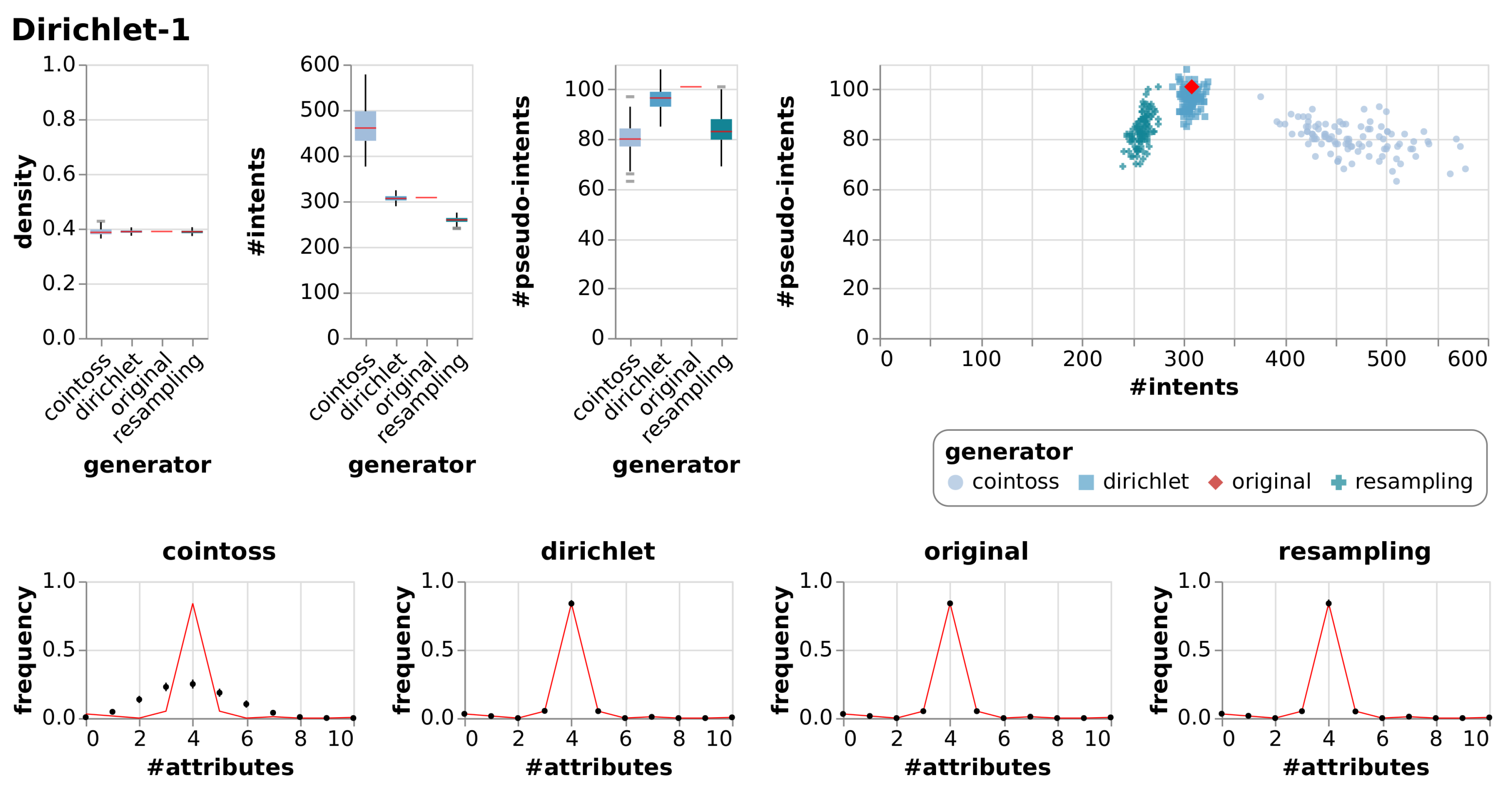
| Dirichlet-1 | artificial | Artificially generated with the Dirichlet approach. |
| Dirichlet-2 | artificial | Artificially generated with the Dirichlet approach. |
| Context | Method | #Attributes | #Objects | ()-Density | -Density | ()-#Intents | -#Intents | ()-#Pseudo-Intents | -#Pseudo-Intents |
|---|---|---|---|---|---|---|---|---|---|
| Bird-Diet | True Context | 8 | 10 | 0.30 | 16 | 15 | |||
| Cointoss | 0.30 | 0.05 | 18 | 3.87 | 15 | 2.85 | |||
| Dirichlet | 0.30 | 0.04 | 18 | 3.50 | 15 | 2.49 | |||
| Resample | 0.30 | 0.05 | 11 | 2.01 | 11 | 1.81 | |||
| Brunson-Club | True Context | 15 | 25 | 0.25 | 62 | 73 | |||
| Cointoss | 0.25 | 0.02 | 84 | 14.18 | 88 | 7.41 | |||
| Dirichlet | 0.25 | 0.02 | 79 | 10.86 | 86 | 7.17 | |||
| Resample | 0.26 | 0.02 | 39 | 5.73 | 48 | 8.94 | |||
| Diagnosis | True Context | 17 | 120 | 0.47 | 88 | 43 | |||
| Cointoss | 0.47 | 0.01 | 5749 | 779.98 | 1422 | 100.19 | |||
| Dirichlet | 0.47 | 0.00 | 3677 | 55.04 | 1420 | 38.12 | |||
| Resample | 0.47 | 0.00 | 87 | 1.94 | 43 | 0.74 | |||
| Dolphins | True Context | 62 | 62 | 0.08 | 282 | 1077 | |||
| Cointoss | 0.08 | 0.00 | 227 | 21.15 | 1611 | 97.30 | |||
| Dirichlet | 0.08 | 0.01 | 231 | 29.73 | 1580 | 117.76 | |||
| Resample | 0.08 | 0.01 | 146 | 18.26 | 685 | 97.01 | |||
| Forum-Romanum | True Context | 7 | 14 | 0.45 | 19 | 8 | |||
| Cointoss | 0.45 | 0.05 | 33 | 7.29 | 13 | 1.92 | |||
| Dirichlet | 0.45 | 0.08 | 27 | 10.84 | 12 | 2.79 | |||
| Resample | 0.46 | 0.09 | 13 | 2.48 | 8 | 1.10 | |||
| Living-Beings-and-Water | True Context | 9 | 8 | 0.47 | 19 | 10 | |||
| Cointoss | 0.46 | 0.06 | 28 | 6.71 | 18 | 3.23 | |||
| Dirichlet | 0.47 | 0.02 | 29 | 4.34 | 19 | 3.57 | |||
| Resample | 0.47 | 0.03 | 12 | 2.47 | 10 | 0.78 | |||
| Olympic-Disciplines | True Context | 19 | 50 | 0.46 | 529 | 86 | |||
| Cointoss | 0.46 | 0.02 | 2178 | 380.38 | 831 | 83.09 | |||
| Dirichlet | 0.46 | 0.02 | 2414 | 674.88 | 773 | 114.78 | |||
| Resample | 0.46 | 0.02 | 301 | 47.00 | 65 | 6.51 | |||
| Seasoning-Planner | True Context | 37 | 56 | 0.20 | 532 | 553 | |||
| Cointoss | 0.20 | 0.01 | 631 | 83.08 | 1045 | 133.45 | |||
| Dirichlet | 0.20 | 0.01 | 688 | 131.33 | 1044 | 172.95 | |||
| Resample | 0.20 | 0.01 | 260 | 52.03 | 331 | 49.12 | |||
| Southern-Woman | True Context | 14 | 18 | 0.35 | 65 | 23 | |||
| Cointoss | 0.35 | 0.03 | 94 | 18.59 | 75 | 8.57 | |||
| Dirichlet | 0.36 | 0.04 | 99 | 25.07 | 73 | 10.09 | |||
| Resample | 0.35 | 0.04 | 36 | 9.00 | 21 | 2.15 | |||
| Wood-Properties | True Context | 28 | 29 | 0.28 | 315 | 275 | |||
| Cointoss | 0.28 | 0.01 | 362 | 54.30 | 432 | 42.88 | |||
| Dirichlet | 0.28 | 0.02 | 361 | 61.43 | 427 | 45.90 | |||
| Resample | 0.29 | 0.02 | 154 | 31.96 | 153 | 31.68 | |||
| Cointoss-1 | True Context | 10 | 793 | 0.42 | 913 | 34 | |||
| Cointoss | 0.42 | 0.01 | 866 | 27.40 | 45 | 8.39 | |||
| Dirichlet | 0.42 | 0.01 | 880 | 29.42 | 42 | 8.97 | |||
| Resample | 0.42 | 0.01 | 808 | 28.68 | 49 | 6.40 | |||
| Cointoss-2 | True Context | 15 | 200 | 0.21 | 411 | 312 | |||
| Cointoss | 0.21 | 0.01 | 434 | 39.18 | 315 | 12.16 | |||
| Dirichlet | 0.21 | 0.01 | 408 | 40.04 | 312 | 11.37 | |||
| Resample | 0.21 | 0.01 | 278 | 19.39 | 294 | 18.59 | |||
| Dirichlet-1 | True Context | 10 | 198 | 0.39 | 308 | 101 | |||
| Cointoss | 0.39 | 0.01 | 467 | 42.57 | 80 | 6.24 | |||
| Dirichlet | 0.39 | 0.01 | 307 | 7.04 | 96 | 4.40 | |||
| Resample | 0.39 | 0.01 | 259 | 7.21 | 84 | 6.61 | |||
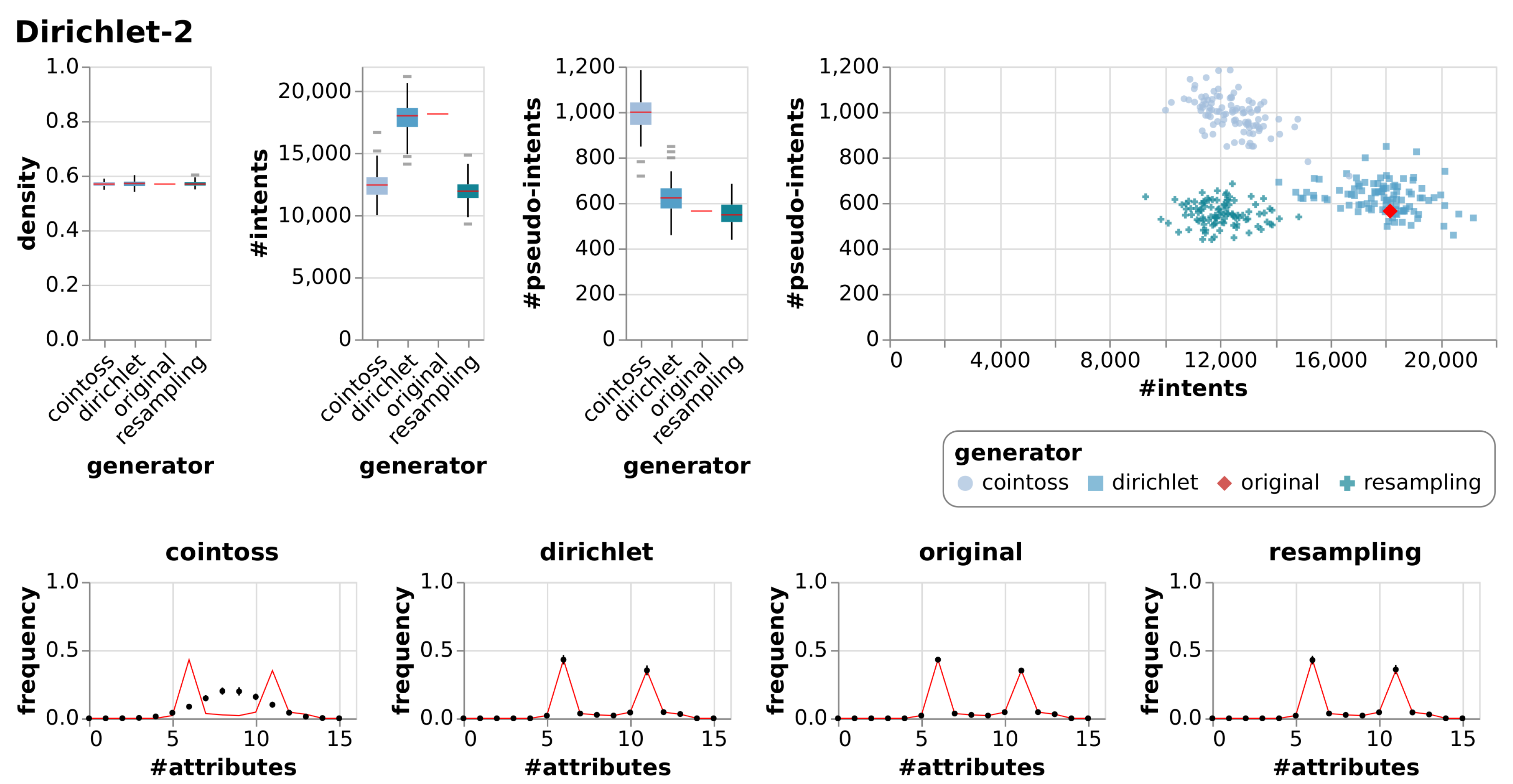
| Dirichlet-2 | True Context | 15 | 200 | 0.57 | 18,166 | 564 | |||
| Cointoss | 0.57 | 0.01 | 12,451 | 1053.37 | 989 | 80.60 | |||
| Dirichlet | 0.57 | 0.01 | 17,894 | 1342.92 | 625 | 68.66 | |||
| Resample | 0.57 | 0.01 | 12,018 | 976.22 | 552 | 51.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felde, M.; Hanika, T.; Stumme, G. Null Models for Formal Contexts. Information 2020, 11, 135. https://doi.org/10.3390/info11030135
Felde M, Hanika T, Stumme G. Null Models for Formal Contexts. Information. 2020; 11(3):135. https://doi.org/10.3390/info11030135
Chicago/Turabian StyleFelde, Maximilian, Tom Hanika, and Gerd Stumme. 2020. "Null Models for Formal Contexts" Information 11, no. 3: 135. https://doi.org/10.3390/info11030135





