Abstract
This paper proposes an improved Harmony Search algorithm, and gives the definition of the Global Sharing Factor of the Harmony Search (HS) algorithm. In the definition, the number of creations of the HS algorithm is applied to the sharing factor and calculated. In this algorithm, the natural harmony encoding method is used to encode the initial harmony, and the total path length of all vehicles is taken as the optimization objective function. A new harmony generation strategy is proposed as follows: each tone component in an evolution is calculated separately using the new learning strategy and update strategy. In the calculation process, the tone component is judged by whether it needs to be adjusted according to the adjustment strategy. In this way, the problems of singularity and randomness of the new harmony generation strategy of basic HS are solved to improve the diversity of algorithm solutions. Then, a new Harmony Search method with Global Sharing Factor based on natural number coding and decoding for the Vehicle Routing Problem (GSF-HS-VRP) is proposed. The improved Global Sharing Factor-Harmony Search-Vehicle Routing Problem (GSF-HS-VRP) algorithm is applied to capacity-limited vehicle path optimization problems compared with the HS, Improved Harmony Search (IHS), Global-best Harmony Search (GHS), and Self-adaptive Global Best Harmony Search (SGHS) algorithms. The small-scale data and Solomon examples were adopted as the experimental data. Compared with the other four algorithms, the GSF-HS-VRP algorithm has the shortest running time, more rapid convergence speed, and higher efficiency. In the multi-vehicle test, with the increase of the number of vehicles, the optimized path of the vehicle is more satisfied in relation to the actual needs of customers. The results showed that this method could effectively improve the optimization performance of the capacity-limited vehicle routing problem.
1. Introduction
The vehicle routing problem (VRP) is an important part of logistics mode and logistics management [1]. Proper selection of the vehicle’s driving route is extremely important to improve the economic efficiency of the logistics model [1]. The vehicle routing problem is a typical Non-deterministic Polynomial-Complete (NPC) problem [2,3,4,5], which are usually solved with heuristic algorithms such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), etc. However, these algorithms all have the disadvantages that it is easy for them to fall into the local minimum and generate a lot of useless loops, which leads to the long running time of GA and premature convergence of PSO [6]. Swarm intelligence optimization algorithms mainly include the Artificial Bee Colony (ABC) algorithm [7], Locust Swarm (LS) Algorithm [8], Moth-Flame Optimization (MFO) [9] Algorithm, Shuffled Frog Leaping Algorithm (SFLA) [10], Fruit Fly Optimization Algorithm (FOA) [11], Harmony Search (HS) algorithm [12], etc. Various swarm intelligence optimization algorithms have their own characteristics and advantages. The ABC Algorithm [7] simulates the characteristics of swarm bees. Through the cooperation of three kinds of bees, the random and targeted evolution of swarms gradually converges to the optimum. Locust Swarms (LS) are a new multi-optima search technique explicitly designed for non-globally convex search spaces [8]. Ldquosmartrdquo is used by LS to start points to scout for promising new areas of the search space before using particle swarms and a greedy local search technique to find a local optimum [8,13]. The Moth-Flame optimization (MFO) algorithm is an optimization algorithm generated by simulating the biological behavior of a moth using the transverse orientation to find a light source [9]. However, the MFO algorithm itself does not have the ability to jump out of the local optimum, and it has the defects of being easily trapped in the local optimum and insufficient convergence speed in the later stage [14]. The Shuffled Frog Leaping Algorithm (SFLA) [10] is a swarm intelligence algorithm that simulates the characteristics of information sharing and communication during frog foraging. The evolutionary idea of the Fruit Fly Optimization Algorithm (FOA) [11] originated from the simulation of the foraging behavior of the fruit fly, which is a global optimization evolutionary algorithm.
The Harmony Search (HS) algorithm [12] is a swarm intelligence algorithm that simulates the process of music players’ repeated tuning of the pitch of each musical instrument through memory to achieve a wonderful harmony process. It has been successfully applied to many engineering problems. The HS algorithm has the advantages of simple concept, fast convergence, easy implementation, a novel generation of solutions, and a few parameters to adjust. It shows better performance than the Genetic Algorithm, Simulated Annealing algorithm, and Tabu Search algorithm on related issues [15,16]. The HS algorithm has been successfully applied in different fields. A new block-matching (BM) algorithm that combines HS with a fitness approximation model is proposed in the literature [17], and the set of motion vectors is evolved through HS operators until the best possible motion vector is identified. In the literature [18], a new dynamic clustering algorithm based on the hybridization of Harmony Search (HS) and fuzzy c-means to automatically segment MRI brain images in an intelligent manner was presented. Improvements to Harmony Search (HS) in circle detection were proposed that enable the algorithm to robustly find multiple circles in larger data sets and still work on realistic images that are heavily corrupted by noisy edges [19]. A new approach to estimate the vanishing point using a harmony search (HS) algorithm was proposed in [20]. Ref. [21] presents a simple mathematical analysis of the explorative search behavior of the Harmony Search (HS) algorithm.
Aiming at the singularity and randomness of the new harmony generation strategy, from the perspective of improving the diversity of algorithm solutions, the global sharing factor is introduced to improve the new harmony generation strategy, and an improved HS algorithm is proposed. The new algorithm is applied to solve the capacity-limited vehicle routing optimization problem. Then, a new Harmony Search method with Global Sharing Factor based on natural number coding and decoding for the Vehicle Routing Problem (GSF-HS-VRP) is proposed to improve the optimization performance.
2. Theory Basis
2.1. Capacity-Limited Vehicle Routing Problem
There are many variants of the VRP problems, of which the Capacity-limited Vehicle Routing Problem (CVRP) is more common [1]. In a CVRP, all customers have the same service type of delivery or receipt. All vehicles carry the same weight of load, each customer’s demand is not greater than the vehicle’s load, and the vehicle starts off and returns to the distribution center [1].
2.2. Mathematical Description of Optimization of VRPs
The definition of the Capacity-limited Vehicle Routing Problem (CVRP) is shown in Equation (1) [1].
Here, represents the total path length of all vehicles, and represents the transportation distance between customer i and customer j. represents the transportation demand of customer i, and represents the load capacity of vehicle s. N is the total amount of customers, in which represents the customer number, and i = 0 and j = 0 represent the number of the distribution center. K is the total amount of vehicles, in which represents the vehicle number, and represents a directly connected path of the vehicle s between the customer i and the customer j; otherwise, . and respectively represent that the needs of customer i and customer j are satisfied by the vehicles.
2.3. Basic HS Algorithm
The basic concept of the basic HS algorithm can be described as follows. It randomly generates harmonies such as to form harmony memory (HM), whose size is HMS. Each harmony is composed of W different tone components, i.e., if the harmony number is , the harmony is represented as . The initial form of HM is as expressed in Equation (2), where HMCR is the probability that takes values from the harmony memory, PAR is the probability of pitch fine-tuning, and BW is the bandwidth of pitch fine-tuning, is the maximum number of algorithm evolutions. r1, r2, and r are random numbers generated by the rand () function when running in the basic harmony search algorithm, and .
According to Equation (3), set the new harmony to be ; then, each tone component of the new harmony is generated by three rules: learning harmony memory, fine-tuning tone components, and the random selection of tone components. refers to randomly generating a new harmonic tone component.
Then, the tone component produced by Equation (3) is judged by the probability PAR whether fine-toning adjustment is required, which is described as Equation (4).
Then, the harmony memory is updated according to the following update strategy described in Equation (5), where represents the value of the objective function or fitness.
The above process is repeated until the number of evolutions is reached.
3. GSF-HS-VRP Algorithm
Similar to other swarm intelligence algorithms, the HS algorithm also has problems such as premature convergence and stagnant convergence, which are mainly caused by its own search mechanism. Firstly, the HS algorithm is a single-body evolutionary algorithm [16] in which a new harmony is randomly generated through learning harmony memory (HM), and then adjusted by the tone fine-tuning mechanism and bandwidth. This generated method has obvious defects such as certain singularity, poor search ability, and requiring a long number of evolutions to converge. Once the generated harmony is near the optimal harmony, it is easy to fall into local optimum and cause premature convergence. Secondly, the HS algorithm provides a mechanism to introduce a new harmony, i.e., to generate a new harmony by randomly selecting the tone just based on the value of the harmony memory value probability (HCMR) parameter. Since most of the parameters including BW and HCMR are chosen from the fixed experience value, the accuracy of the HS algorithm is not particularly high [22].
The paper addresses the singularity and randomness of the new harmony generation strategy; from the perspective of improving the diversity of algorithm solutions, the global sharing factor of the harmony search method is introduced to improve the new harmony generation strategy, and a new Harmony Search method with Global Sharing Factor based on natural number coding and decoding for the Vehicle Routing Problem (GSF-HS-VRP) is proposed and applied to solve the capacity-limited vehicle routing optimization problem.
3.1. Concept Definition
3.1.1. Global Sharing Factor of the Harmony Search Algorithm
The concept of global sharing factor was proposed in the literature [23,24]. It is a sharing factor that changes nonlinearly only along with the number of trials, and it increases rapidly from a small initial value to a steady-state value. Thus, it can be used to suppress the randomness of tone fine-tuning.
In this paper, the global sharing factor is adopted to the HS algorithm to improve the efficiency of the tone generation and fine-tuning mechanism.
The global share factor is shown in Equation (6).
Here, is the global sharing factor, and is a parameter for calculating the global sharing factor, which is denoted in Equation (7). and are the initial value and final value of the parameters, respectively, and their values are set by experience as = 0.1 and = 1.2 [22,23]. T is the number of trials, and in Equation (7), t is the number of trials .
3.1.2. Coding Method
In our algorithm, the initial harmony is encoded using a natural number encoding method. Assuming that the dimension of the tone component is W, then a tone component represents each customer number in the routing optimization natural number encoding, and each customer number should be unique. For example, using an eight-digit integer coding (W = 8), i.e., the total number of customers is N = 8, then the number from 1 to 8 represents each unique customer number, and 0 represents the number of the distribution center. Therefore, in the encoding, each tone component must be different and unique. In the improved routing optimization method in this paper, represents the total path length D of all vehicles, which is the final optimization objective function.
3.1.3. Learning Strategy
In the algorithm, the harmony memory whose size is HMS is randomly generated to find out the global optimal harmony in one harmony evolution. Each tone component of each harmony in the harmony memory adaptively evolves through the learning strategy, which is shown in Equation (8).
3.1.4. Updating Strategy
In a harmony evolution, if the objective function value obtained by learning strategy evolution is slightly lower than , i.e., exists. Then, every tone component of each harmony in the harmony memory adaptively evolves through the update strategy, which is shown in Equation (9).
3.1.5. Randomly Generating Strategy
In a harmony evolution, if the objective function value obtained by updating the strategy evolution is slightly lower than , i.e., exists, use Equation (10) to randomly generate the non-repeating harmony tone.
The learning strategy, updating strategy, and randomly generating strategy are all calculated for each tone component of the harmony. In Equations (8)–(10), represents each tone component in the last evolution, and represents the new value of the corresponding tone component obtained by learning strategy, updating strategy, and randomly generation strategy after evolution.
3.1.6. Adjusting Strategy
When using the global sharing factor to calculate the learning strategy and updating strategy for the tone component, there are two situations that need to be considered for adjustment.
The first case is whether the evolved still belongs to the correct coding range. represents a newly generated customer number whose value should belong to the range of natural number coding. If it exceeds the range, a random value calculated by the formula (int)((rand()%W)) to adjust its value to the right encoding range.
The second case is whether the evolved is the same as the value of other newly generated . The newly generated customer number should be unique; thus, if the situation of duplicate values occurs, they need to be compared one by one and modified with the method of randomly generating harmony tones.
3.1.7. Decoding Method
The arrangement of the vehicles is mainly based on the order of the customer number and the maximum load of the vehicle, i.e., the vehicle is arranged in the first vehicle path according to the customer’s coding order until the maximum load limit of the vehicle is exceeded, and then the second vehicle path is arranged in turn, and so on until the customer is completely arranged. In this paper, the decoding method of [1] was adopted, in which the encoding order of the customer is decoded into the vehicle path sequence of each vehicle in accordance with the maximum load limit per vehicle.
3.1.8. Objective Function
The objective function, i.e., the fitness, refers to the sum of the path lengths according to the total number of vehicles. There are several vehicles with several paths, and the sum length of the paths is taken as the objective function. The calculation method for the objective function is shown in Equation (11). In this paper, each harmony is used as the input of the objective function. Thus, the value of objective function is the total length of the vehicle path generated by the W integer-encoded harmony tones, each of the harmony is composed of N customers, where W = N.
Among them, represents the transportation demand of customer i, represents each unique customer number, and represents the number of the distribution center. The path corresponding to the s-th () vehicle always starts from the distribution center () and then returns to it (). represents the load capacity of the s-th vehicle. represents the transportation distance between customer i and customer i+1 when the s-th vehicle is satisfied, and therefore, represents the sum length of the total paths of K vehicles.
3.2. Theory of Algorithm
The theory of algorithm was described as follows. Set the maximum number of music creations to be . After initializing the harmony memory, the harmony fitness is sorted in descending order to find the optimal harmony in one harmony creation evolution. The global sharing factor is calculated, and each tone component of each harmony in the harmony memory adaptively evolves through the learning strategy according to Equation (8). If , replace with respectively. Otherwise, each tone component evolves through the updating strategy according to Equation (9). If still , use Equation (10) to randomly generate harmony tone.
The above-mentioned harmony tone generation method is repeated until the number of evolution times reaches ; then, the optimal harmony and optimized path sequence are output.
3.3. Algorithm Process
Algorithm: GSF-HS-VRP
Input: the maximum number of evolutions , the size of the harmony memory HMS, and the number of tone component W.
Output: global optimal harmony and optimized path sequence.
Step 1: Randomly generate initial harmony individuals whose number is HMS, which is marked as. . The harmony memory is initialized according to Equation (1). Calculate the fitness of the j-th () harmony according to Equation (11).
Step 2: Each tone component of each harmony is updated.
Begin
Sort each harmony by fitness in descending order to determine .
Calculate according to Equations (6) and (7).
For ()
Update through the learning strategy according to Equation (8).
End
if ()
For ()
End
else
For ()
Update through the update strategy according to Equation (9).
End
if ()
For ()
End
else
For ()
Randomly generate harmony tone according to Equation (10).
End
End
Step 3: Determine whether the number of evolutions has reached . If not, go to Step 2. Otherwise, the algorithm stops and outputs and the optimized path sequence.
3.4. Algorithm Flowchart
The algorithm flowchart of GSF-HS-VRP is shown in Figure 1.
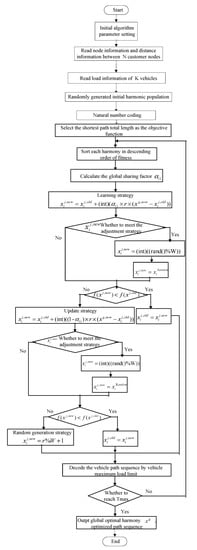
Figure 1.
Flowchart of Harmony Search method with Global Sharing Factor based on natural number coding and decoding for Vehicle Routing Problem (GSF-HS-VRP) algorithm.
3.5. Algorithm Efficiency Analysis
From the efficiency analysis of the HS algorithm in the literature, the time complexity of the HS algorithm is , and the space complexity is . According to the previous descriptions of the improvements of the new algorithm, it can be concluded that the time complexity of the GSF-HS-VRP algorithm is , and the space complexity is . The time complexity and space complexity of GSF-HS-VRP varies with the values of W and K, which are dependent on the size of the small-scale data and Solomon example dataset.
4. Experiment Design and Results Analysis
4.1. Experiment Design
Experiments were carried out on the HS algorithm Improved Harmony Search (IHS) algorithm [25], Global-best Harmony Search (GHS) algorithm [26], Self-adaptive Global Best Harmony Search (SGHS) Algorithm [27], and GSF-HS-VRP algorithm to optimize the vehicle routing problem. The computer processor of the personal computer used in the experiment was Intel Core i5 2.6 GHz and it had a memory of 4.0 GB. The experiment’s programs were programmed by Visual C++ 2010. The final test results were averaged after 30 runs independently.
The experimental parameters were set as follows: HMS = 20, HMCR = 0.9, PAR = 0.3, BW = 0.01, = 20. In the IHS algorithm, the minimum value of pitch tune probability PARmin = 0.01, the maximum value of pitch tune probability PARmax = 0.99, the minimum value of pitch tune bandwidth BWmin = 0.0001, and the maximum value of pitch tune bandwidth BWmax = [25]. In the GHS algorithm, PARmin = 0.01, PARmax = 0.99 [22]. In the SGHS algorithm, the initial probability value of the harmony memory is HMCRm = 0.98, the standard deviation of the value of the harmony memory HMCRs = 0.01, and the probability of the harmony memory is normally distributed within [0.9,1.0], the average initial value of bandwidth PARm = 0.9, the standard deviation of pitch tune bandwidth PARs = 0.05, the pitch tune bandwidth is normally distributed within [0.0,1.0], the specific evolution numbers Learning Period (LP) = 10, minimum value of the pitch tune bandwidth BWmin = 0.0001, the maximum value of the pitch tune bandwidth BWmax = [27]. UB and LB are the maximum value and minimum value of the search range of the algorithm, respectively. In the GSF-HS-VRP algorithm of this paper, according to sharing factor theory and experimental analyses in the literature [22,23], is set to 0.1, and is set to 1.2.
According to the natural number coding method, adjusting strategy, and encoding strategies, the HS, IHS, GHS, and SGHS algorithms in the experiments have been modified to solve the vehicle routing problem, which is to ensure the consistency of the parameters and optimization results of all the five algorithms in the experimental tests.
4.2. Results Analysis
4.2.1. Experiment Results and Analysis of Small-Scale Data
Firstly, the experiment was tested using small-scale data [1]. The distance between customer i and customer i+1 and the demand of customer i are shown in Table 1. The experimental parameters were set as follows: the number of customer nodes is N = 8, i.e., the number of harmony tone components is W = 8, where 1–8 represents each unique customer number, and 0 represents the number of the distribution center. The number of vehicles is K = 2, and the capacity of each car is = 8. The comparison of the results of fixed iterations and average runtime are shown in Table 2, and the average optimum of each algorithm is shown in Figure 2. The comparison results of vehicle routing optimization for each algorithm are shown in Table 3.

Table 1.
Table of customer distance and demand.

Table 2.
Comparison of the results of fixed iterations. HS: Harmony Search, IHS: Improved Harmony Search, GHS: Global-best Harmony Search, SGHS: Self-adaptive Global Best Harmony Search.
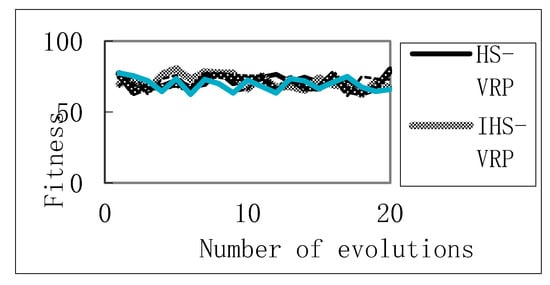
Figure 2.
Average optimum of each algorithm.

Table 3.
Comparison of vehicle routing optimization for each algorithm.
4.2.2. Experiment Results and Analysis of Standard Test Data
Then, the standard test data in the famous Solomon example [28] is used for the experiment, and the C101 dataset is selected as the test set. Experimental parameters were set as follows: the number of customer nodes is N = 100, i.e., the number of harmony tone components is W = 100, where 1 to 100 represents each unique customer number and 0 represents the number of the distribution center. The tests are conducted according to the number of vehicles K = 2, 3, and 10, respectively, and the vehicle capacity of each vehicle is 200.
Results and Comparison of Two Vehicles
In the case of two vehicles, i.e., K = 2, the comparison results of fixed iteration times and average runtime are shown in Table 4. The average optimum iteration curves of four algorithms were drawn in Figure 3. The comparison results of vehicle routing optimization of each algorithm are shown in Table 5.

Table 4.
Comparison results at fixed iteration times.
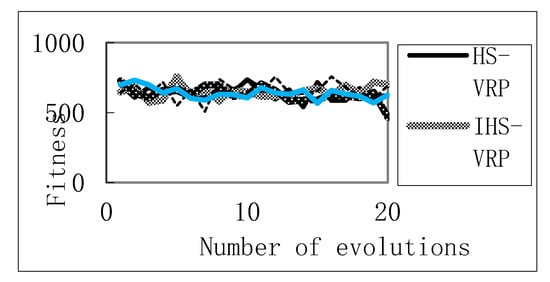
Figure 3.
Average optimum iteration curve of each algorithm.

Table 5.
Comparison results of vehicle routing optimization of each algorithm.
Results and Comparison of Three Vehicles
In the case of three vehicles, i.e., K = 3, the comparison results of fixed iteration times and average runtime are shown in Table 6. The average optimum iteration curves of five algorithms are drawn in Figure 4. The comparison results of vehicle routing optimization of each algorithm are shown in Table 7.

Table 6.
Comparison results of fixed iteration times.
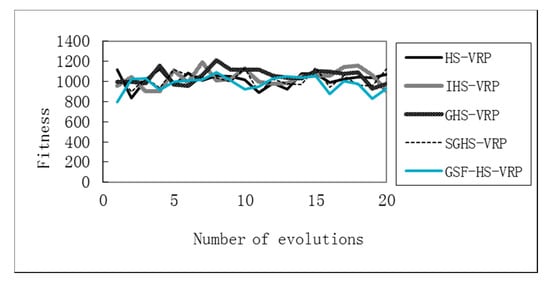
Figure 4.
Average optimum iteration curve of each algorithm.

Table 7.
Comparison results of vehicle routing optimization of each algorithm.
Results and Comparison of Ten Vehicles
In the case of 10 vehicles, i.e., K = 10, the comparison results of fixed iteration times and average runtime are shown in Table 8. The average optimum iteration curves of five algorithms are shown in Figure 5. The comparison results of the vehicle routing optimization of each algorithm are shown in Table 9.

Table 8.
Comparison results at fixed iteration times.
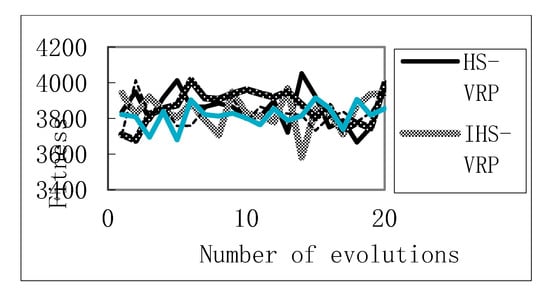
Figure 5.
Average optimum iteration curve of each algorithm.

Table 9.
Comparison optimization path results of the vehicle routing optimization of each algorithm.
4.2.3. Wilcoxon’s Test
Wilcoxon’s test can be used to perform individual comparisons between two algorithms (pairwise comparisons), and the p-value in a pairwise comparison is independent from another one [13,29]. We conducted the behaviors of the five algorithms by means of Wilcoxon’s rank sum test, which known as a non-parametric statistical significance proof for independent samples. The p-values produced by Wilcoxon’s test in the experiments are shown in Table 10. Through the comparison of the computed p-values, we can draw the conclusion that the results of the GSF-HS-VRP algorithm are better than the ones acquired by the other four algorithms, especially for the problem of the Solomon example (K = 3).

Table 10.
p-Values produced by Wilcoxon’s test for the different datasets.
4.2.4. Analysis of Results
It can be seen from the above test results that the GSF-HS-VRP algorithm shows a better average optimum for both small-scale data and standard test data. Compared with the other four algorithms, the GSF-HS-VRP algorithm has the shortest runtimes, achieves the effect of rapid convergence, and improves the efficiency of the algorithm. The algorithm’s average optimum iteration curve also shows that under the condition of fixed evolution times, the GSF-HS-VRP algorithm has a relatively stable evolutionary curve, making it less prone to premature convergence. In the multi-vehicle test, with the increase of the number of vehicles, the optimized path of the vehicle can satisfy the actual needs of more customers. The above results demonstrated that the GSF-HS-VRP algorithm has higher efficiency and reliability than the other four algorithms, which can effectively improve the optimization performance of the capacity limited-vehicle routing problem.
5. Conclusions
In this paper, a new Harmony Search method with Global Sharing Factor based on natural number coding for the Vehicle Routing Problem is proposed. From the perspective of improving the diversity of algorithm solutions, the number of creations of the harmony search algorithm is applied to the sharing factor, and the global sharing factor of the HS algorithm is proposed to improve the new harmony generation strategy. This method adopts natural number coding with high efficiency. The test results show that the optimal path results of this method are significantly improved compared with other HS, IHS, GHS, and SGHS algorithms in solving the problem of capacity-limited vehicle path optimization.
Author Contributions
L.L. conceived and designed the Harmony Search Method and the experiments, and wrote the paper; J.H., F.X. and Y.D. performed the experiments and analyzed the experiments. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Gansu Agricultural University Discipline Construction Fund Project (Grant No. GAU-XKJS-2018-253, GAU-XKJS-2018-255, GAU-XKJS-2018-251), Gansu Province Higher Education Research Project (Grant No. 2019B-086, 2019A-056), Development Foundation Project of College of Information Science and Technology of Gansu Agricultural University (Grant No. GAU-XKFZJJ-2020-11), Young Advisor Fund of Gansu Agricultural University (Grant No. GAU-QDFC-2019-02), National Nature Science Foundation of China (Grant No. 61741201), 2019 General Planning Project of the 13th Five-Year Plan for Education Science in Gansu Province (Grant No. GS[2019]GHB2152), National Higher Education for Basic Computer Education Research Project (Grant No. 2018-AFCEC-214, 2018-AFCEC-213).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, T. Research on Improved Harmony Search Algorithms for VRP. Master’s Thesis, Zhejiang Normal University, Hangzhou, China, 25 March 2015. [Google Scholar]
- Hu, L.; Wang, Z.; Zhao, F. Gaussian harmony search algorithm for driver satisfaction based logistics distribution path optimization. Appl. Res. Comput. 2015, 32, 3622–3625, 3676. [Google Scholar]
- Lau, H.; Chan, T.; Tsui, W.; Pang, W. Application of genetic algorithms to solve the multidepot vehicle routing problem. IEEE Trans. Autom. Sci. Eng. 2010, 7, 383–392. [Google Scholar] [CrossRef]
- Murray, C.; Park, W. Incorporating human factor considerations in unmanned aerial vehicle routing. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 860–869. [Google Scholar] [CrossRef]
- Pavone, M.; Frazzoli, E.; Bullo, F. Adaptive and distributed algorithms for vehicle routing in a stochastic and dynamic environment. IEEE Trans. Autom. Control 2011, 56, 1259–1269. [Google Scholar] [CrossRef]
- Zhao, Z.; Wan, F. The solving of Vehicle Routing Problem based on hybrid harmony search algorithm. In Proceedings of the 3rd International Conference on Computational Intelligence and Industrial Application (PACIIA), Wuhan, China, 6–7 November 2010; pp. 379–382. [Google Scholar]
- Karaboga, D.; Basturk, B. On the Performance of Artificial Bee Colony Algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Chen, S.; Locust, S. A new multi-optima search technique. In Proceedings of the Eleventh Conference on Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. J. Water Sources Planning Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Pan, W. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 29, 69–74. [Google Scholar] [CrossRef]
- Geem, Z.; Kim, J.; Loganathan, G. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Cuevas, E.; González, A.; Zaldívar, D.; Pérez-Cisneros, M. An optimisation algorithm based on the behaviour of locust swarms. Int. J. Bio-Inspir. Comput. 2015, 7, 402–407. [Google Scholar] [CrossRef]
- Wang, G.; Jin, J. Moth-flame optimization algorithm fused on refraction principle and opposite-based learning. Comput. Eng. Appl. 2019, 55, 46–51. [Google Scholar]
- Han, H.; Pan, Q.; Liang, J. Application of improved harmony search algorithm in function optimization. Comput. Eng. 2010, 36, 245–247. [Google Scholar]
- Zhao, P.; Liu, S. Novel intelligent optimization algorithm and its improvement. J. Chin. Comput. Syst. 2010, 31, 955–958. [Google Scholar]
- Cuevas, E. Block-matching algorithm based on harmony search optimization for motion estimation. Appl. Intell. 2013, 39, 165–183. [Google Scholar] [CrossRef]
- Alia, O.; Mandava, R.; Aziz, M. A hybrid harmony search algorithm for MRI brain segmentation. Evol. Intell. 2011, 4, 31–49. [Google Scholar] [CrossRef]
- Fourie, J. Robust circle detection using Harmony Search. J. Optim. 2017, 2017. [Google Scholar] [CrossRef]
- Moon, Y.; Zong, W.; Han, G. Vanishing point detection for self-driving car using harmony search algorithm. Swarm Evol. Comput. 2018, 41, 111–119. [Google Scholar] [CrossRef]
- Das, S.; Mukhopadhyay, A.; Roy, A.; Abraham, A.; Panigrahi, B. Exploratory power of the Harmony Search Algorithm: Analysis and improvements for global numerical optimization. IEEE Trans. Syst. Man Cybern. 2011, 41, 89–106. [Google Scholar] [CrossRef]
- Liu, L.; Huo, J.; Wang, L.; Han, J. Harmony search algorithm based on shuffled frog leaping and bacterial foraging and its application in image. J. Front. Comput. Sci. Technol. 2015, 9, 119–128. [Google Scholar]
- Liu, L.; Huo, J.; Wang, L. Harmony search algorithm with global sharing factor. J. Chongqing Univ. Technol. (Nat. Sci.) 2014, 28, 82–86. [Google Scholar]
- Liu, L.; Wang, L.; Han, J. Shuffled frog leaping algorithm based on global sharing factor. Comput. Eng. 2013, 39, 162–166, 171. [Google Scholar]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Omran, M.; Mahdavi, M. Global-best harmony search. Appl. Math. Comput. 2008, 198, 634–656. [Google Scholar] [CrossRef]
- Pan, Q.K.; Suganthan, P.N.; Tasgetiren, M.F.; Liang, J.J. A self-adaptive global best harmony search algorithm for continuous optimization problems. Appl. Math. Comput. 2010, 216, 830–848. [Google Scholar] [CrossRef]
- Available online: http://web.cba.neu.edu/~msolomon/problems.htm (accessed on 4 February 2020).
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).