Evolutionary Game for Confidentiality in IoT-Enabled Smart Grids
Abstract
1. Introduction
- the formulation of the AMI evolutionary game and the derivation of a numerical scheme for this game,
- the simulations of the evolutionary game on realistic AMI cases for confidentiality,
- the identification of constraints, and
- analysis of the confidentiality evolutionary game allowing the defender to explore the space of strategies and to select the optimal set of solutions.
2. Related Work
3. Evolutionary Game Theory
- mutation mechanism that is represented by the Evolutionary Stable Strategy (ESS) concept; and
- selection mechanism that is represented by the replicator dynamics.
4. Models and Numerical Scheme Development
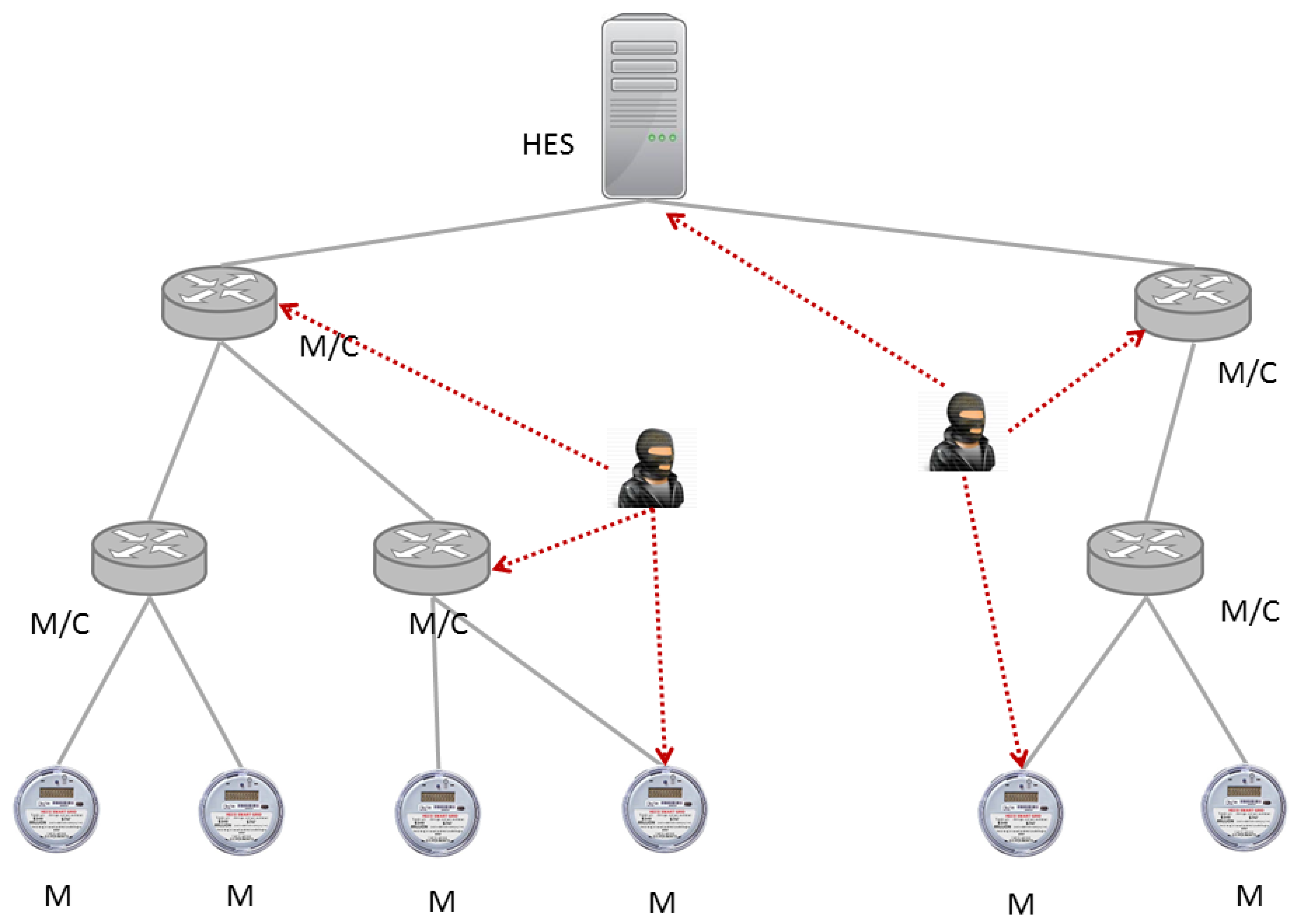
4.1. System and Threat Model
4.2. Game Model
4.3. Evolutionary Game Formulation
4.4. Numerical Scheme
5. AMI Case Study
5.1. Simulation Setup
5.2. Evaluation Metrics
6. Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMI | Advanced Metering Infrastructure |
| CAGR | Compound Annual Growth Rate |
| CPS | Cyber-Physical Systems |
| IoT | Internet of Things |
| FDI | False Data Injection |
| DDoS | Distributed Denial-of-Service |
| EGT | Evolutionary game theory |
| ESS | Evolutionary Stable Strategy |
| APTs | Advanced Persistent Threats |
| NE | Nash equilibrium |
| HES | head-end system |
| C | collector |
| M | meter |
References
- Noll, J.; Garitano, I.; Fayyad, S.; Asberg, E.; Abie, H. Measurable Security, Privacy and Dependability in Smart Grids. J. Cyber Secur. Mobil. 2014, 3, 371–398. [Google Scholar] [CrossRef]
- Ericson, A.B. Ericsson Mobility Report 2020. Available online: https://www.ericsson.com/4adc87/assets/local/mobility-report/documents/2020/november-2020-ericsson-mobility-report.pdf (accessed on 11 December 2020).
- Sadeghi, A.R.; Wachsmann, C.; Waidner, M. Security and Privacy Challenges in Industrial Internet of Things. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 8–12 June 2015; ACM: New York, NY, USA, 2015; pp. 54:1–54:6. [Google Scholar] [CrossRef]
- He, H.; Maple, C.; Watson, T.; Tiwari, A.; Mehnen, J.; Jin, Y.; Gabrys, B. The security challenges in the IoT enabled cyber-physical systems and opportunities for evolutionary computing amp; other computational intelligence. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1015–1021. [Google Scholar] [CrossRef]
- Mavroeidakos, T.; Chaldeakis, V. Threat Landscape of Next Generation IoT-Enabled Smart Grids. In Artificial Intelligence Applications and Innovations, Proceedings of the AIAI 2020 IFIP WG 12.5 International Workshops, Neos Marmaras, Greece, 5–7 June 2020; Maglogiannis, I., Iliadis, L., Pimenidis, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 116–127. [Google Scholar]
- Abie, H.; Balasingham, I. Risk-based Adaptive Security for Smart IoT in eHealth. In Proceedings of the 7th International Conference on Body Area Networks, Oslo, Norway, 24–26 February 2012; pp. 269–275. [Google Scholar]
- Zeitz, K.; Cantrell, M.; Marchany, R.; Tront, J. Designing a Micro-Moving Target IPv6 Defense for the Internet of Things. In Proceedings of the Second International Conference on Internet-of-Things Design and Implementation, Pittsburgh, PA, USA, 18–21 April 2017; ACM: New York, NY, USA, 2017; pp. 179–184. [Google Scholar] [CrossRef]
- Deng, R.; Xiao, G.; Lu, R.; Liang, H.; Vasilakos, A.V. False Data Injection on State Estimation in Power Systems Attacks, Impacts, and Defense: A Survey. IEEE Trans. Ind. Inform. 2017, 13, 411–423. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, L.; Liu, N. Coordinated attacks on electric power systems in a cyber-physical environment. Electr. Power Syst. Res. 2017, 149, 156–168. [Google Scholar] [CrossRef]
- Alabdel Abass, A.A.; Xiao, L.; Mandayam, N.B.; Gajic, Z. Evolutionary Game Theoretic Analysis of Advanced Persistent Threats Against Cloud Storage. IEEE Access 2017, 5, 8482–8491. [Google Scholar] [CrossRef]
- Xu, S. Collaborative Attack vs. Collaborative Defense. In Collaborative Computing: Networking, Applications and Worksharing; Bertino, E., Joshi, J.B.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 217–228. [Google Scholar]
- Sanjab, A.; Saad, W. Data Injection Attacks on Smart Grids with Multiple Adversaries: A Game-Theoretic Perspective. IEEE Trans. Smart Grid 2016, 7, 2038–2049. [Google Scholar] [CrossRef]
- Hoffman, M.; Suetens, S.; Gneezy, U.; Nowak, M.A. An experimental investigation of evolutionary dynamics in the Rock-Paper-Scissors game. Sci. Rep. 2015, 5, 8817. [Google Scholar] [CrossRef]
- Tellbach, D.; Li, Y.F. Cyber-Attacks on Smart Meters in Household Nanogrid: Modeling, Simulation and Analysis. Energies 2018, 11, 316. [Google Scholar] [CrossRef]
- Boudko, S.; Abie, H. An Evolutionary Game for Integrity Attacks and defenses for Advanced Metering Infrastructure. In Proceedings of the 12th European Conference on Software Architecture: Companion Proceedings, Madrid, Spain, 24–28 September 2018. [Google Scholar] [CrossRef]
- Hansen, A.; Staggs, J.; Shenoi, S. Security Analysis of an Advanced Metering Infrastructure. Int. J. Crit. Infrastruct. Prot. 2017, 18, 3–19. [Google Scholar] [CrossRef]
- Foreman, J.C.; Gurugubelli, D. Cyber Attack Surface Analysis of Advanced Metering Infrastructure. arXiv 2016, arXiv:1607.04811. [Google Scholar]
- Cleveland, F.M. Cyber security issues for Advanced Metering Infrasttructure (AMI). In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Goel, S.; Hong, Y. Security Challenges in Smart Grid Implementation. In Smart Grid Security; Springer: London, UK, 2015; pp. 1–39. [Google Scholar] [CrossRef]
- Li, F.; Luo, B.; Liu, P. Secure and Privacy-Preserving Information Aggregation for Smart Grids. Int. J. Secur. Netw. 2011, 6, 28–39. [Google Scholar] [CrossRef]
- Li, H.; Gong, S.; Lai, L.; Han, Z.; Qiu, R.C.; Yang, D. Efficient and Secure Wireless Communications for Advanced Metering Infrastructure in Smart Grids. IEEE Trans. Smart Grid 2012, 3, 1540–1551. [Google Scholar] [CrossRef]
- Baig, Z.A.; Amoudi, A.R. An Analysis of Smart Grid Attacks and Countermeasures. J. Commun. 2013, 8, 473–479. [Google Scholar] [CrossRef]
- Sayin, M.O.; Başar, T. Secure Sensor Design for Cyber-Physical Systems Against Advanced Persistent Threats. In Proceedings of the Decision and Game Theory for Security: 8th International Conference, GameSec 2017, Vienna, Austria, 23–25 October 2017; Rass, S., An, B., Kiekintveld, C., Fang, F., Schauer, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 91–111. [Google Scholar] [CrossRef]
- He, H.; Yan, J. Cyber-physical attacks and defenses in the smart grid: A survey. IET Cyber Phys. Syst. Theory Appl. 2016, 1, 13–27. [Google Scholar]
- Ismail, Z.; Leneutre, J.; Bateman, D.; Chen, L. A game theoretical analysis of data confidentiality attacks on smart-grid AMI. IEEE J. Sel. Areas Commun. 2014, 32, 1486–1499. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Wang, Z. Testability of evolutionary game dynamics based on experimental economics data. Physica A 2017, 486, 455–464. [Google Scholar] [CrossRef]
- Santos, F.; Encarnação, S.; Santos, F.C.; Portugali, J.; Pacheco, J.M. An Evolutionary Game Theoretic Approach to Multi-Sector Coordination and Self-Organization. Entropy 2016, 18, 152. [Google Scholar] [CrossRef]
- Quijano, N.; Ocampo-Martinez, C.; Barreiro-Gomez, J.; Obando, G.; Pantoja, A.; Mojica-Nava, E. The Role of Population Games and Evolutionary Dynamics in Distributed Control Systems: The Advantages of Evolutionary Game Theory. IEEE Control Syst. 2017, 37, 70–97. [Google Scholar] [CrossRef]
- Ficici, S.G.; Melnik, O.; Pollack, J.B. A game-theoretic investigation of selection methods used in evolutionary algorithms. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 2, pp. 880–887. [Google Scholar] [CrossRef]
- Bouhaddi, M.; Adi, K.; Radjef, M.S. Evolutionary Game-Based Defense Mechanism in the MANETs. In Proceedings of the 9th International Conference on Security of Information and Networks, New York, NY, USA, 20–22 July 2016; pp. 88–95. [Google Scholar]
- Vejandla, P.; Dasgupta, D.; Kaushal, A.; Nino, F. Evolving Gaming Strategies for Attacker-Defender in a Simulated Network Environment. In Proceedings of the 2010 IEEE Second International Conference on Social Computing, Minneapolis, MN, USA, 20–22 August 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 889–896. [Google Scholar] [CrossRef]
- Akyazı, U.; Uyar, A.Ş. Detection of DDoS Attacks via an Artificial Immune System-Inspired Multiobjective Evolutionary Algorithm. In Applications of Evolutionary Computation; Di Chio, C., Brabazon, A., Di Caro, G.A., Ebner, M., Farooq, M., Fink, A., Grahl, J., Greenfield, G., Machado, P., O’Neill, M., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–10. [Google Scholar]
- Essaddi, N.; Hamdi, M.; Habib, S.; Boudriga, N. Evolutionary strategies for non-uniform deployment in wireless sensor networks. Int. J. Commun. Netw. Distrib. Syst. 2011, 7, 331–354. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Liu, K.J.R. Distributed Adaptive Networks: A Graphical Evolutionary Game-Theoret View. arXiv 2012, arXiv:1212.1245. [Google Scholar] [CrossRef]
- John, D.J.; Smith, R.W.; Turkett, W.H.; Cañas, D.A.; Fulp, E.W. Evolutionary Based Moving Target Cyber Defense. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 1261–1268. [Google Scholar] [CrossRef]
- Li, Y.; Xu, H.; Cao, Q.; Li, Z.; Shen, S. Evolutionary Game-Based Trust Strategy Adjustment among Nodes in Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2015, 11, 818903. [Google Scholar] [CrossRef]
- Shivshankar, S.; Jamalipour, A. An Evolutionary Game Theory-Based Approach to Cooperation in VANETs Under Different Network Conditions. IEEE Trans. Veh. Technol. 2015, 64, 2015–2022. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Ren, Y.; Feng, R.; Yu, N.; Wan, J. An Evolutionary Game-Based Trust Cooperative Stimulation Model for Large Scale MANETs. Int. J. Distrib. Sens. Netw. 2013, 9, 245017. [Google Scholar] [CrossRef]
- Smith, J.M. Game theory and the evolution of fighting. In On Evolution; Edinburgh University Press: Edinburgh, UK, 1972; pp. 8–28. [Google Scholar]
- Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Foster, D.P.; Young, P. Stochastic Evolutionary Game Dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Ismail, Z.; Kiennert, C.; Leneutre, J.; Chen, L. A Game Theoretical Model for Optimal Distribution of Network Security Resources. In Proceedings of the International Conference on Decision and Game Theory for Security, Vienna, Austria, 23–25 October 2017; pp. 234–255. [Google Scholar]


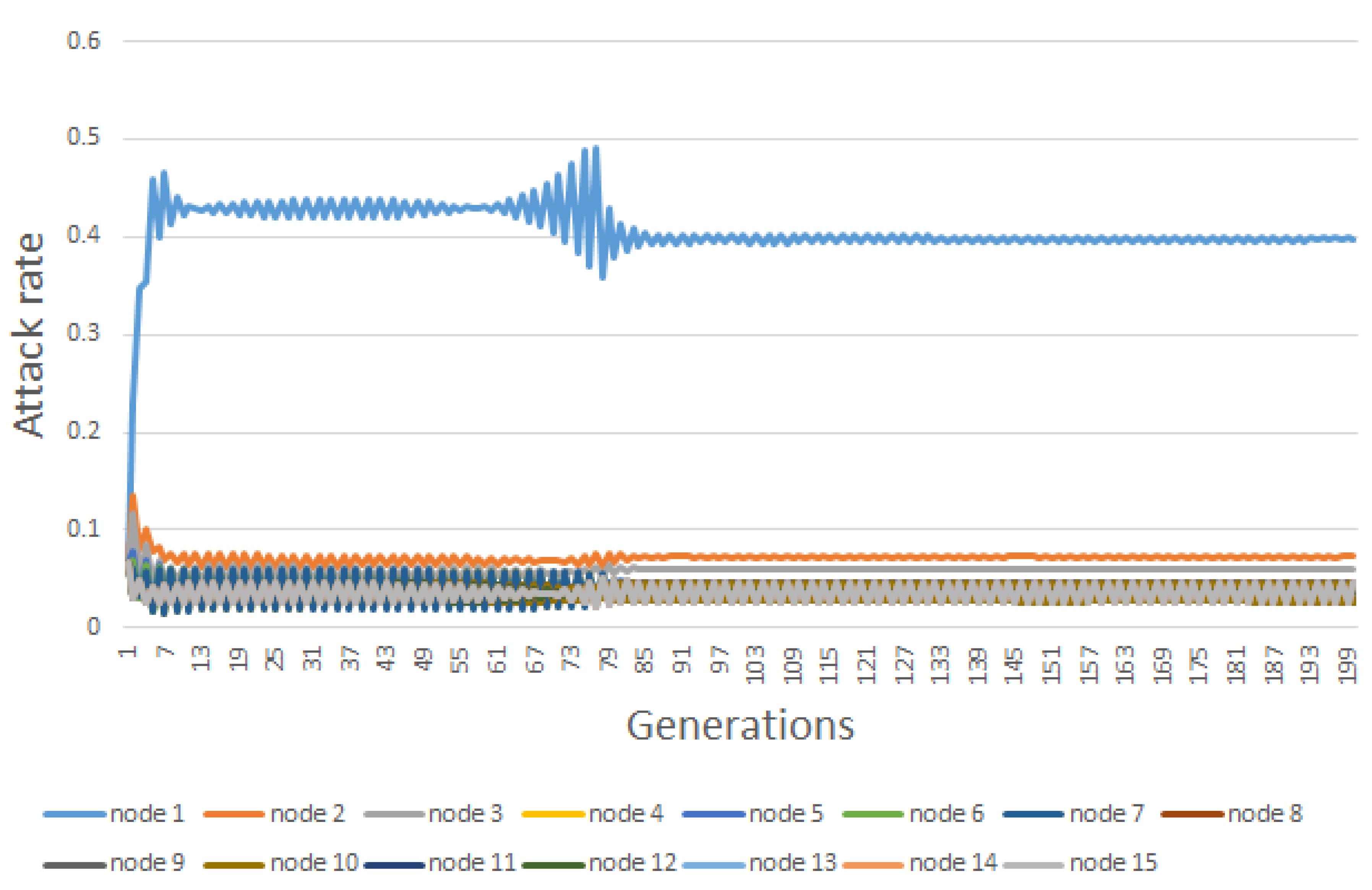
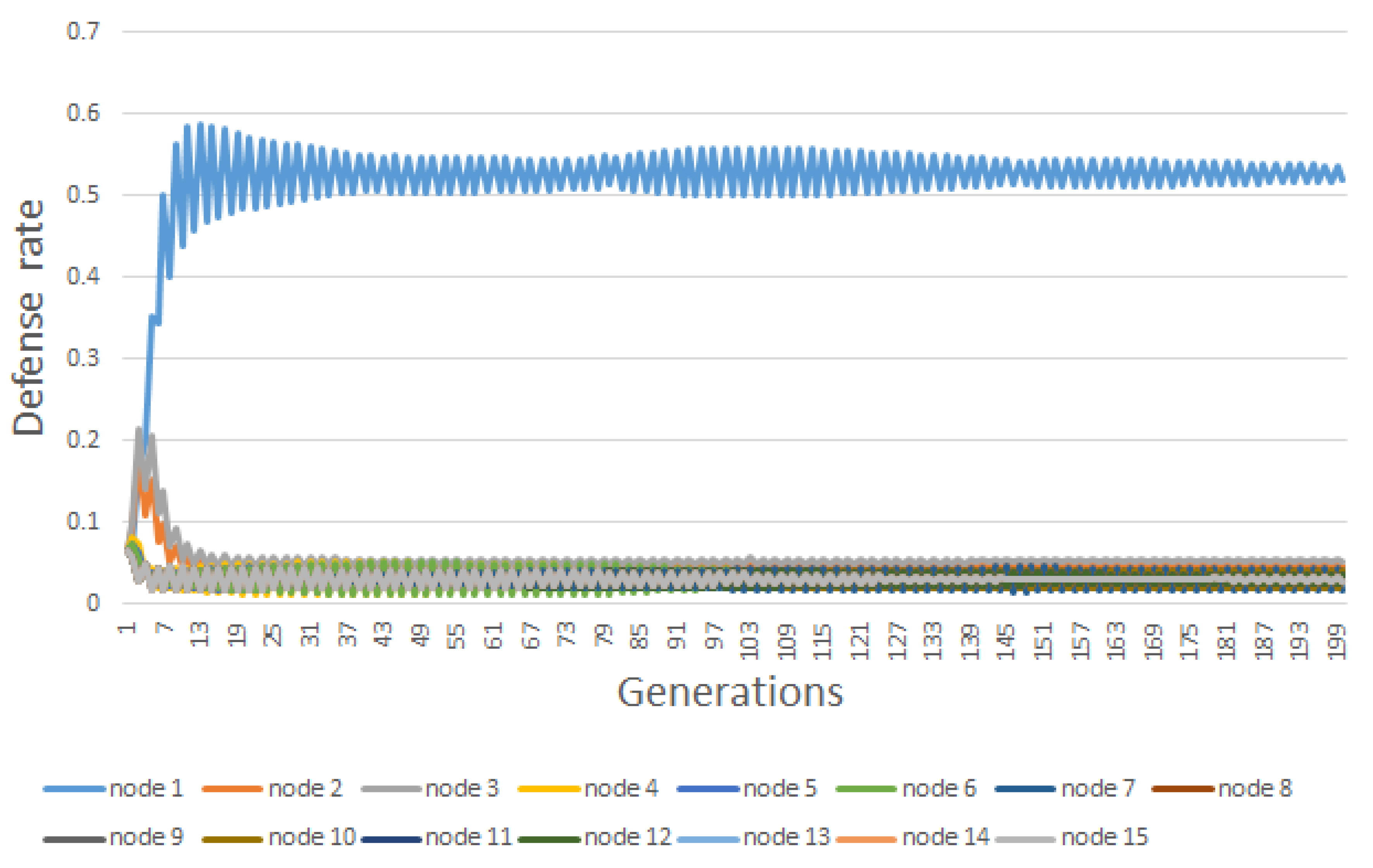
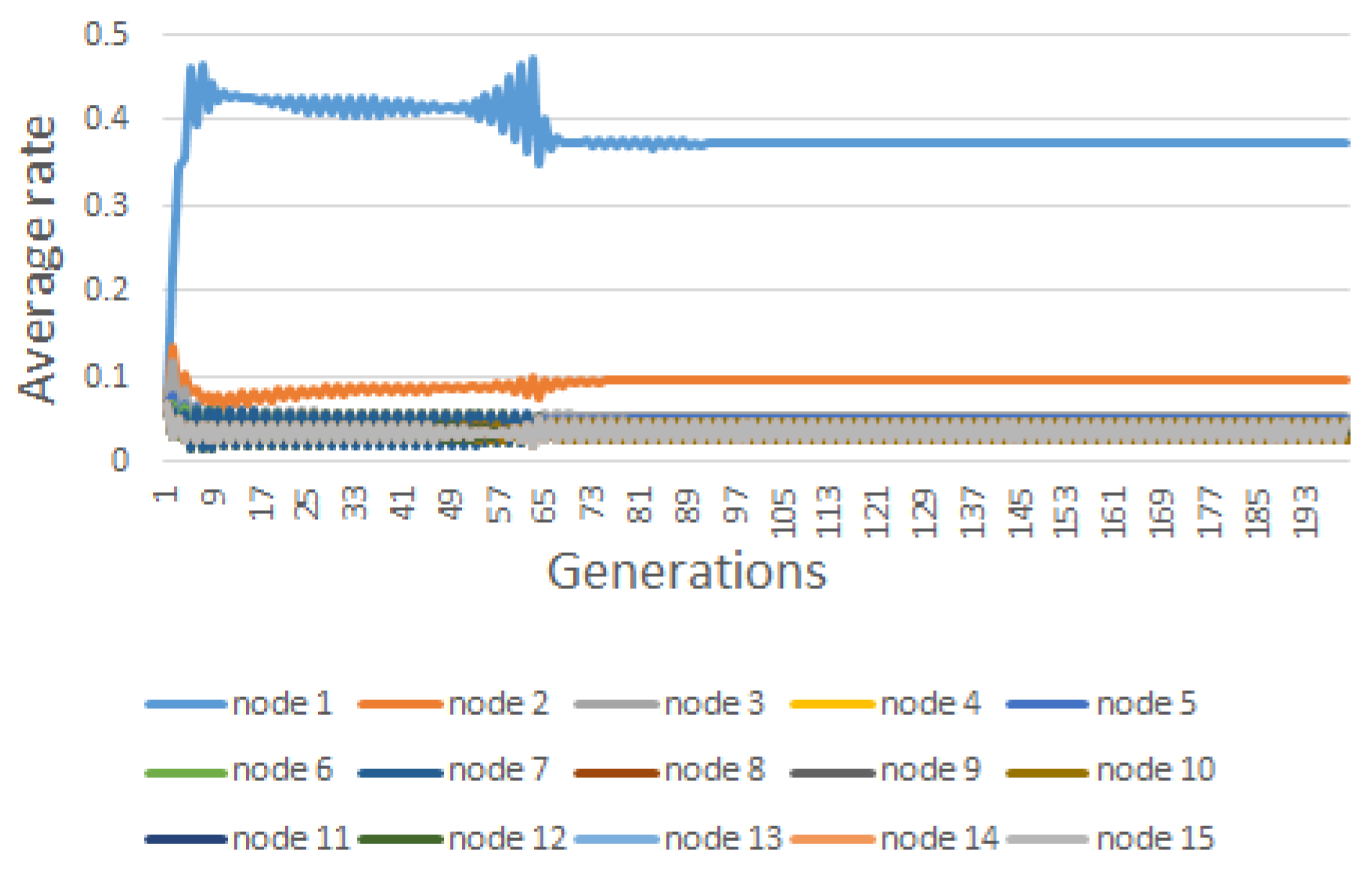
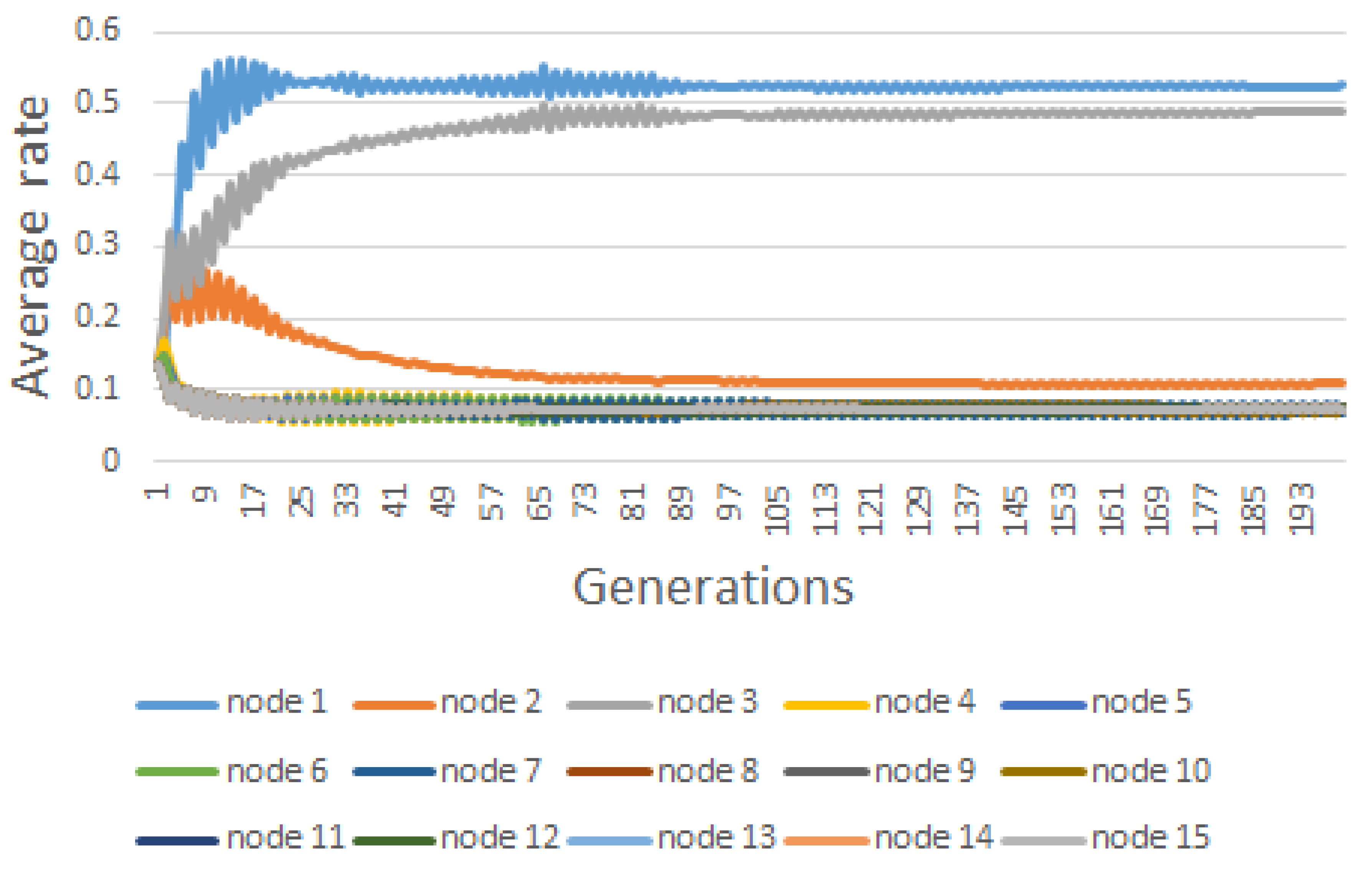
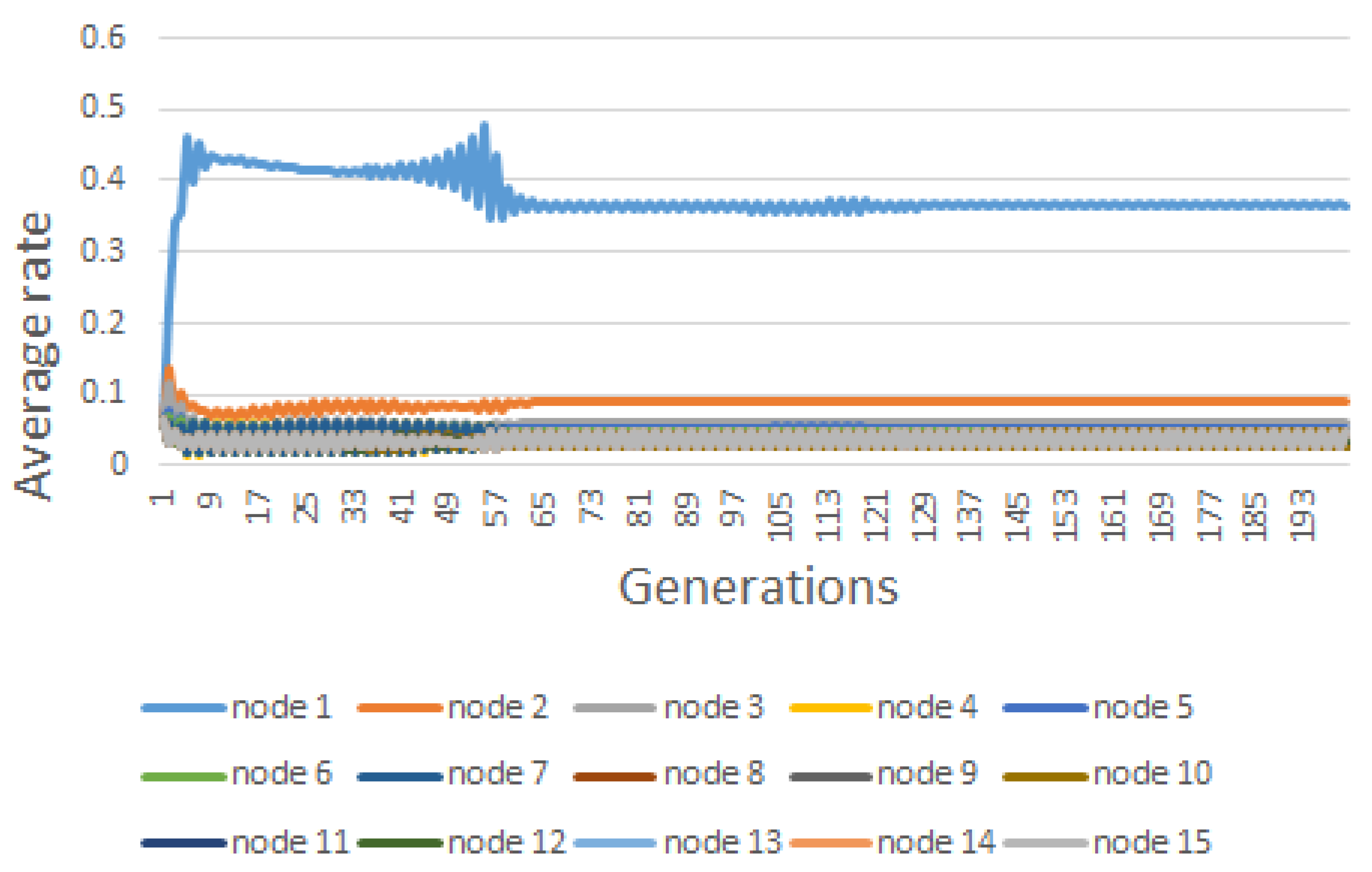
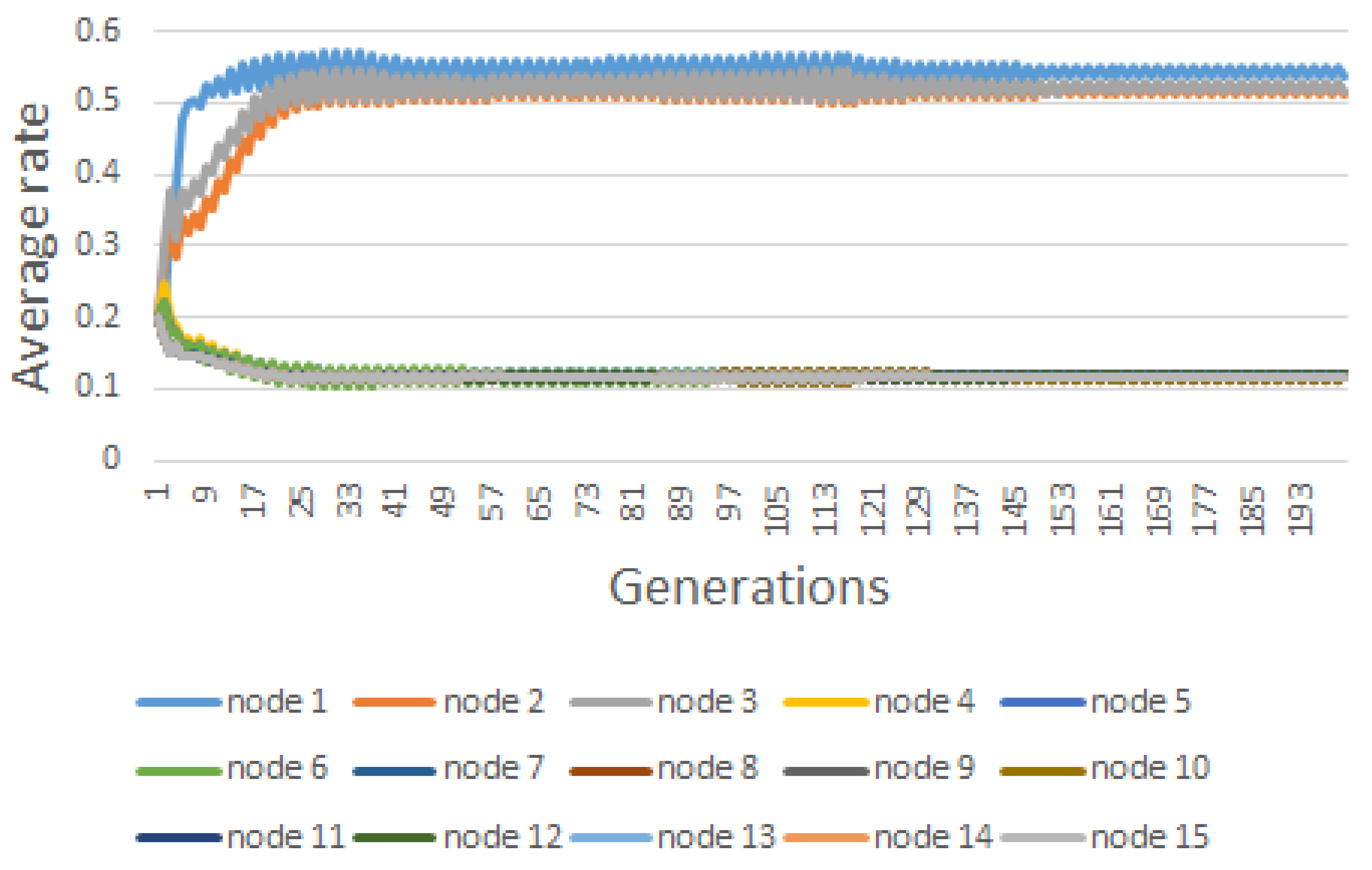
| Node | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| #1 | 33.00 | 6.60 | 1.65 | 0.396246 | 0.51805 | 0.373106 | 0.524613 | 0.364412 | 0.536942 |
| #2 | 15.00 | 3.00 | 0.75 | 0.072595 | 0.04662 | 0.09603 | 0.107789 | 0.089545 | 0.511544 |
| #3 | 18.00 | 3.60 | 0.90 | 0.060055 | 0.05209 | 0.054538 | 0.48788 | 0.060831 | 0.515485 |
| #4 | 3.00 | 0.60 | 0.15 | 0.042049 | 0.03001 | 0.043214 | 0.074903 | 0.045137 | 0.12042 |
| #5 | 12.00 | 2.40 | 0.60 | 0.046897 | 0.029263 | 0.049434 | 0.07387 | 0.053685 | 0.119965 |
| #6 | 9.00 | 1.80 | 0.45 | 0.044304 | 0.028329 | 0.046061 | 0.071233 | 0.049054 | 0.119792 |
| #7 | 9.00 | 1.80 | 0.45 | 0.041939 | 0.018402 | 0.043156 | 0.065708 | 0.045231 | 0.119011 |
| #8 | 3.00 | 0.60 | 0.15 | 0.026952 | 0.04108 | 0.026954 | 0.077835 | 0.026961 | 0.121616 |
| #9 | 3.00 | 0.60 | 0.15 | 0.026952 | 0.04108 | 0.026954 | 0.077835 | 0.026961 | 0.121616 |
| #10 | 3.00 | 0.60 | 0.15 | 0.026952 | 0.04108 | 0.026954 | 0.077835 | 0.026961 | 0.121616 |
| #11 | 3.00 | 0.60 | 0.15 | 0.037328 | 0.035544 | 0.036896 | 0.074586 | 0.036151 | 0.119706 |
| #12 | 3.00 | 0.60 | 0.15 | 0.037328 | 0.035544 | 0.036896 | 0.074586 | 0.036151 | 0.119706 |
| #13 | 3.00 | 0.60 | 0.15 | 0.046802 | 0.027631 | 0.046602 | 0.070442 | 0.046307 | 0.117527 |
| #14 | 3.00 | 0.60 | 0.15 | 0.046802 | 0.027631 | 0.046602 | 0.070442 | 0.046307 | 0.117527 |
| #15 | 3.00 | 0.60 | 0.15 | 0.046802 | 0.027631 | 0.046602 | 0.070442 | 0.046307 | 0.117527 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudko, S.; Aursand, P.; Abie, H. Evolutionary Game for Confidentiality in IoT-Enabled Smart Grids. Information 2020, 11, 582. https://doi.org/10.3390/info11120582
Boudko S, Aursand P, Abie H. Evolutionary Game for Confidentiality in IoT-Enabled Smart Grids. Information. 2020; 11(12):582. https://doi.org/10.3390/info11120582
Chicago/Turabian StyleBoudko, Svetlana, Peder Aursand, and Habtamu Abie. 2020. "Evolutionary Game for Confidentiality in IoT-Enabled Smart Grids" Information 11, no. 12: 582. https://doi.org/10.3390/info11120582
APA StyleBoudko, S., Aursand, P., & Abie, H. (2020). Evolutionary Game for Confidentiality in IoT-Enabled Smart Grids. Information, 11(12), 582. https://doi.org/10.3390/info11120582






