Abstract
One of the significant challenges in machine learning is the classification of imbalanced data. In many situations, standard classifiers cannot learn how to distinguish minority class examples from the others. Since many real problems are unbalanced, this problem has become very relevant and deeply studied today. This paper presents a new preprocessing method based on Delaunay tessellation and the preprocessing algorithm SMOTE (Synthetic Minority Over-sampling Technique), which we call DTO-SMOTE (Delaunay Tessellation Oversampling SMOTE). DTO-SMOTE constructs a mesh of simplices (in this paper, we use tetrahedrons) for creating synthetic examples. We compare results with five preprocessing algorithms (GEOMETRIC-SMOTE, SVM-SMOTE, SMOTE-BORDERLINE-1, SMOTE-BORDERLINE-2, and SMOTE), eight classification algorithms, and 61 binary-class data sets. For some classifiers, DTO-SMOTE has higher performance than others in terms of Area Under the ROC curve (AUC), Geometric Mean (GEO), and Generalized Index of Balanced Accuracy (IBA).
1. Introduction
Imbalanced data sets [] are among the pattern classification problems. To illustrate some applications in recent years, methods for dealing with class imbalance were applied in different areas, such as: Medicine [], Agriculture [], Computer Networks Protection [], analysis of social media [], and Financial Risks [,]. Although researchers and professionals have intensely studied this problem, today, this challenge is still open-ended. Most of the real-world data sets are naturally imbalanced [], and classifiers have difficulties learning from them. Different techniques to solve or mitigate this problem emerge all the time [,,,]. Nevertheless, this problem is far from being addressed entirely.
Synthetic Minority Oversampling Technique (SMOTE) [] is one of the most used preprocessing methods. It works by synthetically generating instances in the line segment joining two examples. SMOTE has several variations in the literature. However, they also follow the same procedure for synthetic instance generation. This procedure leads to a bias of SMOTE (and its variants) to generate a chain trail pattern. This preference is discussed further in Section 3.2. As far as we know, this bias was unnoticed in the literature. We argue that this undesirable tendency may limit the effective use of SMOTE in some domains.
To overcome this problem, we propose a new preprocessing method that relies on constructing a proximity graph based on Delaunay Tessellation. The Delaunay Tessellation (also known as triangulation in the plane) is a fundamental computational geometry structure. The Voronoi diagram’s dual and provides a connection graph for closer points in the space, forming a tessellation composed of a simplex set that completely covers the space. The Delaunay graph is interesting in data analysis, as it can represent the geometry of a point set or approximate its density []. We can use the fact that any point inside the simplex can be described as a linear combination of its vertices to generate new synthetic samples.
We name this new method Delaunay Tessellation Oversampling SMOTE (DTO-SMOTE). Like SMOTE [], the main idea of Delaunay-Oversampling is to synthetically generate new instances, aiming to balance the training data distribution before applying the learning algorithms. The main difference is that, instead of creating synthetic examples in the line segment joining two instances, we generate synthetic examples inside a simplex selected from the Delaunay tessellation. The vertices of the simplex are instances of the data set. The creation of synthetic instances follows a Dirichlet distribution, and we can use the distribution parameters to manipulate where instances can be generated according to the classes of the vertices. This approach makes it possible to avoid SMOTE’s chain trail pattern, allowing artificial instances to cover the input space better.
This paper substantially extends our previous research [] by introducing a simplex selection step based on quality measures and data generation and widely extends the empirical evaluation, including other learning algorithms, baselines, and data sets. The main contributions of this paper are:
- We point out (for the first time) the chain trail pattern formed by the artificial instances that SMOTE generates.
- We propose a new preprocessing technique, named Delaunay Tessellation Oversampling SMOTE (DTO-SMOTE), which uses Delaunay Tessellation to build a simplex mesh. Then, we use simplex quality measures to select candidates (our previous study draws a simplex at random) for instance generation and use a Dirichlet distribution to control where synthetic instances creation inside a simplex (our former study uses the barycenter of the simplex).
- We conduct an extensive experimental evaluation with 61 bi-class data sets (our previous study only considers 15 binary data sets). This empirical comparison includes five preprocessing methods and ten learning algorithms (our former analysis only compares with SMOTE and uses kNN as the learning algorithm). It shows our approach’s appropriateness in many situations, with better average performance on binary data sets.
The remaining of this paper is organized as follows: Section 2 presents issues related to class imbalance and some methods for dealing with them and performance measures. Section 3 discusses the SMOTE family of preprocessing algorithms and their bias in generating synthetic examples in a chain trail pattern. Section 4 presents our new method, DTO-SMOTE, in detail. Section 5 presents the experiments and results. Section 6 discusses the achieved results and describes insights, comments, and future work directions.
2. The Imbalanced Data Set Classification Problem
Classification problems in which one of the classes have more instances than the others are called Imbalanced Classification problems. In practice, although a strict imbalance ratio threshold does not exist, when there is a significant difference in the number of cases in each class, it is considered a matter of a Class Imbalanced Problem. Several authors in the literature acknowledge that this imbalance may degrade classification performance []. Learning from imbalanced data is an important issue as these data sets frequently occur in real-life problems, where practical problems are rarely balanced. This problem occurs in areas like Engineering, Information Technology, Bioinformatics, Medicine, Security, Business Management, among others [].
Facing these problems, researchers have proposed some techniques to deal with imbalanced data set classification problems. There are three primary directives in this area: Preprocessing methods, Cost-Sensitive Learning, and Ensembles []. Section 2.2 briefly describes these three approaches, and Section 2.1 discusses the evaluation of classification problems. Based on these measures, we can assess if specific methods are working or not to solve imbalanced problems.
2.1. Performance Evaluation
Choosing adequate performance metrics to evaluate imbalanced data set classification problems is crucial to select the right preprocessing method and classifier’s algorithm []. In sequence, we review the most used measures for imbalanced classification problems [,]. Without loss of generality, here, we consider two-class classification problems to present these measures.
Figure 1 shows a Confusion Matrix in which the two classes are generally named Class 0 (Negative class or Majority class) and Class 1 (Positive class or Minority class). In this confusion matrix, corresponds to the actual number of majority class instances, and corresponds to the actual number of minority class instances. Furthermore, corresponds to the number of instances predicted as the majority class, and corresponds to the number of instances predicted as the minority class. True Positive values, or , means that a classifier correctly classified majority class samples. False Positive, or , means that examples of which correct label is the minority class misclassified as majority class. False Negative, or , means that a real majority class instance is misclassified as belonging to the minority class. Finally, True Negative, or , means that an actual minority class example is correctly classified as belonging to the minority class.
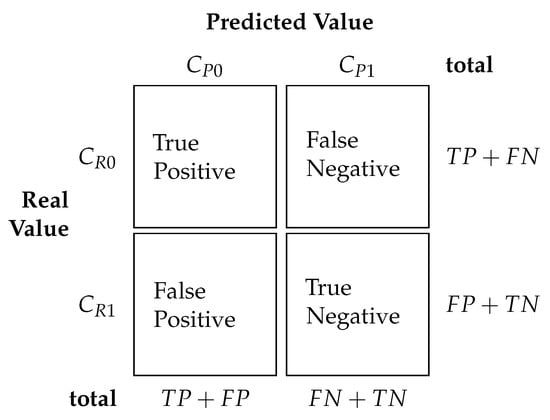
Figure 1.
Confusion Matrix.
Based on this table, accuracy is defined as a rate between the total samples classified correctly by the total test samples submitted to the classifier. Equation (1) presents or Accuracy.
Considering that, in real-life applications, the positive class is the most important, is generally inadequate for imbalanced classifications problems. For instance, a trivial classifier could achieve accuracy in a classification problem where the majority (negative) class instances account for 95%. Nevertheless, it could mispredict all positive class instances. To compromise with these issues, Sensitivity or Recall, , and Specificity, , Equations (2) and (3), respectively, consider the correct classification in each class separately. Here, True Positive Rate, or , is equal to Recall, or , and True Negative rate, or , is equal to , like in Equations (2) and (3), respectively.
Recall or True Positive Rate (—Equation (2)) is the percentage of positive instances correctly classified, whereas Specificity or True Negative Rate (—Equation (3)) is the percentage of negative cases correctly classified.
False Positive Rate (—Equation (4)) is the percentage of misclassified negative instances, and False Negative Rate (—Equation (5)) is the percentage of misclassified positive instances.
There are situations where the focal point is to achieve high assertiveness for positive class. In this case, precision (—Equation (6)) is more suitable. Precision is the percentage of instances predicted as positive and correctly classified as positive.
Precision and Recall are two conflicting factors, where improving one may imply in degrading the other. One measure that relates to Precision and Recall is called . Equation (7) shows the score, which is the weighted harmonic mean between Precision and Recall.
A measure that tries to capture the trade-offs between errors in both classes for imbalanced problems is Geometric Mean (—Equation (8)). This measure is associated with the ROCcurve []. Note that, when and have high values, also has a high value. On the other hand, when one of them has a low value, diminishes.
or Area Under Curve is related to the (Receiver Operating Characteristic) curve []. This curve plots and when for various thresholds of the positive class likelihood. For a single threshold, could be calculated by Equation (9). For multiple thresholds, the trapezoidal rule [].
Generalized Index of Balanced Accuracy (—Equation (10)), described in Reference [], quantifies an arrangement between and a ratio of how balanced the two-class precision in each class is in the data set []. The parameter trades-off the influence dominance of and the . The authors recommend that , and, when is set to 0, .
In this present work, we adopted , as recommended by the authors who proposed the metric [].
2.2. Methods for Dealing with Class Imbalance
Dealing with imbalanced data is a challenging task. Real-world problems are imbalanced, and, to overcome this problem, several techniques have been proposed in the literature. In this section, we review some of them.
2.2.1. Preprocessing
Preprocessing occurs before the data set is submitted to the classifier training process [,]. The main advantage of these methods is that they are algorithm agnostic, and it does not necessarily alter the original classifier algorithm. Therefore, they can be used together with any classifier. On the other hand, preprocessing could be cost-intensive in terms of processing time. Main techniques for preprocessing imbalanced data sets are resampling algorithms []. Resampling works to achieve a balanced data set as a result. There are three resampling categories: Oversampling, Undersampling, and Hybrid methods.
- Oversampling Oversampling creates synthetic or duplicate minority class samples [,] to match the same number of samples from the majority class. As a result, the training data set becomes balanced before the training phase. The Synthetic Minority Oversampling Technique [,], discussed in Section 3, is the primary method in this category.
- Undersampling Undersampling discards some majority class instances to matches the number of samples from the minority class. The primary method in this category is Random Under-Sampling (RUS) [,,]. Nevertheless, there are some issues regarding these techniques. When some data suffer deletion, important information could be discarded, leading to a weak classifier’s training due to the lack of relevant information. To deal with the lost of information, some strategies were proposed in the literature. In Evolutionary Undersampling [], the undersampling is framed as a search problem for prototypes. This process reduces the number of instances from a data set, aiming not to lose a significant accuracy classification rate, using an evolutionary algorithm. Another interesting method is ACOSampling []. This method is based on ant colony optimization [] in the search phase. It adopts this strategy to determine the best subset of majority class instances to keep in the training set.
- Hybrid The hybrid method’s main idea is to minimize drawbacks from undersampling and oversampling, while taking into account their benefits, to achieve a balanced data set. To illustrate this combination, we can cite some methods, like SMOTE + Tomek Link [], SMOTE + ENN [], SMOTE-RSB [], and SMOTE-IPF [], which combine the SMOTE oversampling technique with different data cleaning, to remove some spurious artificial instances introduced in the oversampling phase, and data clustering followed by oversampling [].
2.2.2. Cost-Sensitive Learning
The main idea about this strategy is that misclassification costs are uneven for the majority and minority classes. It is necessary to alter the original classifier’s algorithm to implement this strategy so that the algorithm considers the different misclassification costs. [] present a recent review of cost-sensitive approaches.
2.2.3. Ensemble Learning
Ensemble methods combine two or more classifiers resulting in one classifier with (potentially) more performance than if they were used separately []. However, only using standard ensembles cannot solve imbalanced problems [,]. The reason is that ensembles aim mainly to improve accuracy, and, for imbalanced data classification, accuracy is not adequate due to the prevalence of the majority class. So, the most common technique to apply ensemble in imbalanced classification problems are variations of Bagging [] and Boosting [] especially developed for imbalanced data:
Bagging
Bagging [] consists of training several classifiers with different sampled data sets, randomly drawn from the original one with replacement. The final classification uses a majority or weighted vote from the pool of classifiers [,]. One way to extend Bagging to imbalanced data is to train different classifiers with bootstrapped replicas of the original data set. To ensure that minority class instances are present in each sampled data set, stratified sampling is performed. Within each data set, oversampling methods are used to balance the classes [].
Boosting
Boosting [] differs from Bagging as Boosting weights samples to measure classification difficulty in the learning phase. At the beginning of the process, all instances have the same weight, and classifiers are trained iteratively, changing their weights. Difficult examples receive higher weights than simpler ones. To extend boosting to imbalanced scenarios, oversampling methods are introduced in the process to balance the original data set in each iteration [].
3. The SMOTE Family of Oversampling
As our method was developed to relieve bias of the SMOTE oversampling method (and many variations that uses the procedure of SMOTE for generating a synthetic instance based on the interpolation within the line segment of two instances in the data set) suffers; in this section, we review the SMOTE family of oversampling methods.
The preprocessing technique SMOTE [,] is an oversampling technique in which the main goal is to artificially generate new instances of the minority class interpolating pairs of neighbor instances. The target is to achieve a balanced distribution among all the classes in the data set. To do that, SMOTE selects one minority class instance i and calculates its k minority class nearest-neighbors. The generation of a new synthetic instance consists of interpolating in a line segment formed by selected sample i and a random instance j, which lies in the k minority nearest neighborhood of i. In the original paper [], the parameter k is set to 5. The generation of a new instance follows Equation (11).
where:
- is the new instance vector;
- is the feature vector of instance i;
- is the feature vector of instance j;
- r is a random number between 0 and 1.
In 2018, SMOTE was 15 years old [], and an extensive overview of its applicability and variants based on it are surveyed. We briefly describe some of these methods next.
3.1. SMOTE Variations
3.1.1. Borderline-SMOTE
Borderline-SMOTE [] is a variation that considers samples of the minority class that are far from the majority class boundary may contribute less than samples on the border to build the classifier. Thus, the Borderline-SMOTE preferentially generates synthetic instances that lie near to the decision border. Han describes in his paper [] that data set examples on the borderline and nearby are more misclassified than cases in other regions. Here, borderline means a region where minority class examples are close to the majority ones.
3.1.2. SMOTE-SVM
SMOTE-SVM [] generates artificial samples along the decision boundary. Like Borderline-Smote, SMOTE-SVM assumes that the decision boundary is the best place to create new synthetic samples, as this region is the most critical one for the training process. However, SMOTE-SVM uses support vectors to determine the decision boundaries in SMOTE-SVM.
3.1.3. ADASYN
The basic idea of ADASYN [] is to use a density distribution of each class’s instances as a criterion to automatically choose the number of synthetic minority samples that need to be generated. Considering a binary class data set, and lets and be the number of the minority class and the majority class samples. The degree of class imbalance d is calculated by Equation (12).
The number of minority class samples to be generated is calculated using Equation (13), G is the number of artificial minority class instances to be created, and is a desired balanced coefficient parameter. When , the target is a fully balanced data set.
The ratio around each minority class instance in Equation (14) is defined by the distance of the K nearest neighbor calculated in Euclidean distance, and is the number of examples in K nearest neighbors of which belongs to the majority class.
Normalizing result in calculated by Equation (15).
After that, for each minority class instance , the number of synthetic data samples that needs to be generated is calculated by Equation (16).
Finally, for each , generate new synthetic samples by Equation (17), where is a new synthetic sample, is a randomly chosen minority class sample, and is a random number between 0 and 1.
After all these steps, the output is a balanced data set.
3.1.4. Geometric SMOTE
Geometric SMOTE [] generates synthetic samples in a geometric region called hyperspheroid. There are three main steps in this method. First, it creates new synthetic examples in the surface of a hypersphere centered at an original minority class example covering only minority class instances, ensuring that new examples are not noise. Second, it increases the variety of generated examples by expanding the respective hyperspheroid around the minority class instances applying hyper-sphere expansion factors. Finally, Geometric SMOTE has the options to use geometric transformations, such as translation, deformations, and truncation of the hyperspheroids, to cover other areas of the space.
3.1.5. Manifold-Based Synthetic Oversampling
Manifold-based synthetic oversampling [] transforms the original data set into a manifold structure and generates instances in the manifold space. Finally, the algorithm maps the synthetic artificial samples to feature space. Aiming to improve SMOTE, the manifold oversampling method requires that the data set conform to the manifold property []. If this requirement is fulfilled, a manifold embedding method can be used to induce a manifold representation of the minority class. Then, oversampling is applied in this embedded space. The most common manifold methods are Principal Component Analysis (PCA) and Denoising Autoencoders (DAE), according to Bellinger [].
3.2. The SMOTE Chain Trail Pattern Bias
In general, SMOTE variants differ where the synthetic instances are generated. However, they are similar to how these synthetic instances are created. In this section, we argue that SMOTE and other methods based on its artificial instance generation process have an undesirable bias. The synthetic instances follow a chain trail pattern. The reason is related to the pairwise interpolation process, in which artificial examples are generated in the line segment joining two examples. For highly imbalanced data sets, the interpolation process has a high likelihood to select the same pair, as the selection procedure uses the neighborhood of the instances, and an instance can be selected as a seed several times. Therefore, the generation process creates synthetic examples within the same line segment, and a chain trail pattern emerges. Recently, Reference [] noticed that the SMOTE has a bias where instances are inward-placed diverging from the original class distribution. Still, they did not correlate this with the synthetic data generation process. As far as we knew, this chain trail pattern is unnoticed in the literature.
Figure 2 illustrates this bias. This figure is a two-dimensional projection for a binary class (thyroid) data set(a), alongside their over-sampled versions using SMOTE (b), Borderline SMOTE with its two versions (c) and (d), SMOTE-SVM (e), and Geometric SMOTE (f), as well as our proposed DTO-SMOTE algorithm (g). Observe that the synthetic instances generated by SMOTE, Borderline SMOTE, and SMOTE-SVM follow a chain trail. For Borderline and SMOTE-SVM, these trails concentrate near class boundaries.
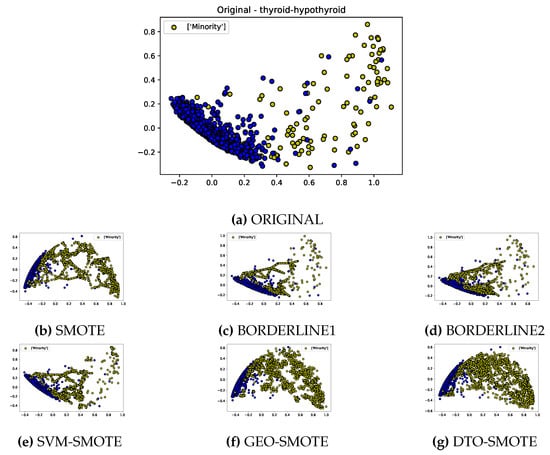
Figure 2.
SMOTE trail path patterns, thyroid-hypothyroid data set.
On the other hand, although the chain trail pattern is not present in Geometric SMOTE, its synthetic data generation also leads to an undesirable bias. The artificial data generation process considers hyper-spheres centered in some instances, where the radii may grow. Furthermore, the seed candidates are instances far from the decision boundary, and the bias pattern follows these hyper-spheres. Therefore, Geometric SMOTE also has a bias related to the synthetic data generation procedure.
As we will discuss in the next section, our approach can interpolate over a simplex from a simplex mesh, and thus is not restricted to a line segment, avoiding the chain trail pattern (as can be seen in the Figure 2g. We also use simplex mesh quality measures to spread the synthetic generated data over the instance space.
4. Delaunay Tessellation Oversampling—DTO-SMOTE
4.1. Simplex Geometry
In computation geometry, triangulation is one of the main primitives in two-dimensional space. It is often used to determine the vicinity of a point by forming triangles with other nearby points. For higher-dimensional spaces, the analogous to triangulation is a tessellation, and to a triangle is a simplex, respectively.
The Delaunay triangulation of a set of points P in the two-dimensional Euclidean space is defined as follows: the Delaunay triangulation is a triangulation such that no point in P is inside the circumscribed spheres of other triangles in . The definition extends to higher-dimensional spaces, where no point in P is inside the circumscribed hyper-spheres of other simplices in .
The Delaunay tessellation has some interesting properties. In the plane, the triangulation is a maximum planar graph and completely divides the space by triangles (if no four points are co-linear). The center of the circumsphere of a Delaunay polyhedron is a vertex of the Voronoi cells. Figure 3 shows an example of a Voronoi diagram (in grey) and a Delaunay tessellation (in orange) for a two-dimensional space. The closest neighbor to any point lies on edge in the Delaunay triangulation, as the nearest neighbor graph is a subgraph of the Delaunay triangulation. This unique set of neighboring points defines the neighborhood of the point and represents a parameter-free definition of a point’s surroundings. The triangulation maximizes the minimum angle of the triangles, avoiding the occurrence of silver triangles. A silver triangle is a triangle with one or two extremely acute angles, hence with a long/thin shape. Intuitively, the Delaunay tessellation is a group of simplices that are most regularized in shape, compared to any other triangulation type. Delaunay tessellation may be used to approximate a manifold by a simple mesh [,], in computational geometry [,], and planning in automated driving [], among others.
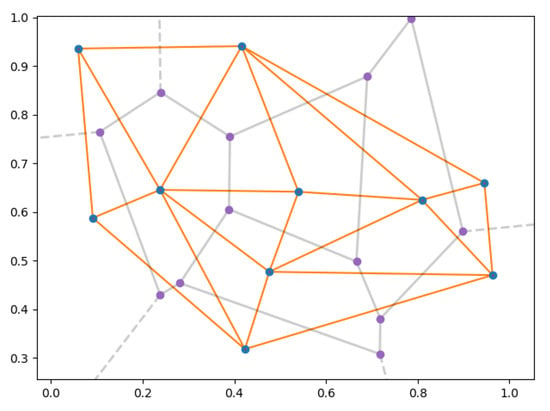
Figure 3.
Delaunay triangulation (orange) and Voronoi diagram.
For a D-dimensional space, a simplex has points. For instance, in the plane, a simplex has three points (a triangle), while, in a three-dimensional space, a simplex has four points (a tetrahedron).
Each point from a simplex is called a simplex’s vertex. Another simplex description is a convex hull of its vertices, or S is the set of all points that can be expressed as a convex combination of its vertices . S boundaries consist of faces, which are simplices of lower dimensions composed by a subset of the simplex vertices. Furthermore, any point inside a simplex can be expressed as a combination of its vertices as . The vector x is called the barycentric coordinates of the point p concerning the simplex S [].
For a set P of points, different algorithms can be used to compute . A reasonably general approach for computing the tessellation in a D-dimensional space consists of converting the tessellation problem into finding the convex hull of P in -dimensional space, by giving each point p a new coordinate equal to . The computational complexity of this approach is . This paper uses the Delaunay tessellation algorithm implemented in the Python SciPy package [].
4.2. Mesh Generation
Given a data set composed by a set of instances (,), where is an n-dimensional feature matrix, and is the vector of class labels. Each represents the feature values, and corresponds to the class value of instance i. The number of instances of the data set is m.
The first step to applying Delaunay Tetrahedral Oversampling (DTO-SMOTE) is to perform a dimensionality reduction. This operation reduces the n-dimensional features matrix to a three-dimensional space . The reasons for using a dimensionality reduction are twofold: first, for m points and n dimensions, a generic mesh contains simplices, and points compose each simplex. Thus, we will have many simplices to interpolated, and many vertices will compose each simplex. Second, the computational complexity of mesh building will increase with large data dimensions. Hence, projecting the high-dimensional data to a lower dimension space is a way to make the mesh building more manageable. As we project into 3D space, the mesh is formed by tetrahedrons, and the interpolation process is carried out within four instances. However, the process is generic and other dimensions (including not applying a feature reduction). Any dimensionality reduction technique can be used for this reduction. However, it should be kept in mind that this dimensionality reduction is only used for the mesh generation, and the artificial instances are generated into the original space. Therefore, the classifiers’ training is also performed using the original space. A similar procedure was used in Reference [] to immerse the data into a manifold space with lower dimension.
The next step consists of running the Delaunay tessellation algorithm using . In other words, we calculate , where . The result of this process is a set of tetrahedrons, in which the vertices lie in . The method of synthetically generate a new instance corresponds to an interpolation using the vertices of a tetrahedron. To this end, our algorithm randomly selects a tetrahedron and a point p inside this tetrahedron in barycentric coordinates and uses p for interpolation. As there is a one-to-one mapping between the barycentric coordinates the Euclidean coordinates, the new instance’s generation corresponds to an interpolation of the points of the selected tetrahedron in the original n-dimensional X-space.
For selecting a tetrahedron for interpolation, our algorithm computes some quality indices for each tetrahedron. Furthermore, to consider the class neighborhood of the instance, we use the ratio of vertices of the tetrahedron associated with a minority class to weight the quality indices and associate them with probabilities. These probabilities are then used to randomly select tetrahedrons with replacement. (It is necessary because some data sets do not produce enough tetrahedrons to generate the adequate numbers of artificial samples.)
The generation of the point p inside the tetrahedrons follows a Dirichlet Distribution. The algorithm adjusts the distribution parameters according to the class associated with a vertex for tetrahedrons with vertices belonging to majority class instances. This step assigns higher probabilities to vertices and facets related to the minority class, similar to Reference [,]. These steps will be explained in detail in the next sections.
4.3. Tetrahedral Quality Evaluation
Given a Delaunay tessellation , our approach selects a tetrahedron from to generate a new instance. In principle, we can randomly choose a tetrahedron of . However, the tetrahedrons have different shapes. Furthermore, the tetrahedrons have different class labels associated with their vertices. Our method uses the shape and class distribution to guide the selection of the tetrahedrons.
The shapes of the tetrahedrons are generally associated with the quality of the tessellation []. Smaller tetrahedrons with a regular shape usually emerge from dense areas of the input space []. On the other hand, bigger tetrahedrons or very acute angles appear near boundaries.
Maur [] proposes different tetrahedral quality measures. The main idea is how far a new tetrahedron is from the equilateral tetrahedron. The answer to this question, the following quality measures are proposed: Relative Volume, Radius Ratio, Solid Angle, Minimum Solid Angle, Maximum Solid Angle, Edge Ratio, and Aspect Ratio, explained next.
- Relative Volume: The relative volume of the current tetrahedron is computed as its real volume divided by the value of maximal volume in the tessellation [].
- Radius Ratio: The radius ratio is the weighed ratio between the radius of the inscribed sphere (r) to the radius of the circumscribed sphere (R), as shown in Equation (18).
- Solid Angle: The solid angle is the area of a spherical triangle created on the unit sphere in which the center is in the tetrahedron vertex []. We compute the sum of four solid angles of the tetrahedron.
- Minimum Solid Angle: This returns the minimum solid angle instead of their sum.
- Maximum Solid Angle: This returns the maximum solid angle instead of their sum.
- Edge Ratio: The edge ratio computes the ratio between the length of the most prolonged edge E to the length of the shortest edge of the tetrahedron, as shown in Equation (19).
- Aspect Ratio: The aspect ration computes the ratio between the radius of the sphere that circumscribes the tetrahedron (R) to the length of the longest edge (E), as shown in Equation (20).
The selection of tetrahedron quality measure to use is a hyperparameter of our algorithm. For each tetrahedron from the tesselation, we compute the selected quality measure and weight it by the proportion of the minority class examples we want to generate the new synthetic instance. If all four vertices belong to the majority class, the tetrahedron quality measure is multiplied by zero and will not be taken into account for synthetic instance creation. On the other hand, if all four vertices belong to the minority class, the quality measure is multiplied by one. Tetrahedrons with mixed class vertices are weighed accordingly. For instance, if two out of the four vertices belong to the minority class, the calculated quality measure is multiplied by 0.5.
These weighed tetrahedron quality measures are then normalized, to sum up to 1 and represent a probability distribution. Therefore, to select tetrahedrons for interpolation, we use a weighted sampling with replacement, where probabilities came from the tetrahedrons’ quality measures, as described earlier.
4.4. Synthetic Instance Generation
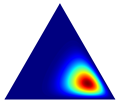
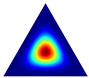
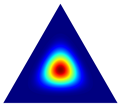
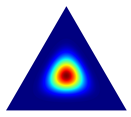
Once a tetrahedron has been selected, the synthetic instance generation process requires a draw of a random point inside the tetrahedron. To this end, we use a Dirichlet distribution. A p-dimensional vector of positive reals parametrizes this distribution. A random draw of a Dirichlet distribution returns a p-dimensional vector , where , and . For the symmetric Dirichlet distribution, when , each point inside the simplex has an equal probability of being chosen. On the other hand, when is a positive constant greater than 1, the distribution favors points near the simplex center. For nonsymmetric distribution, different values of can be used to control the likelihood of where points can be generated (see Table 1), where, for the sake of visualization, we show density plots of three-dimensional Dirichlet distribution for different values of .

Table 1.
Dirichlet distribution.
Given a tetrahedron, we use the parameter vector to establish the likelihood region where the new point will be generated. If all the tetrahedron’s vertices are associated with minority class instances, then we use a symmetric Dirichlet distribution to draw the new instance. Therefore, depending on the value of , we can draw a point uniformly in the simplex () or closer to the tetrahedron barycenter (). However, suppose not all tetrahedron vertices are associated with the minority class. In that case, the distribution is asymmetric, where if the class of the vertex i is the majority, and , where c is a hyperparameter that can be set by the user.
In summary, let be the index set of the instances a tetrahedron k selected as described in Section 4.3. We draw a random vector , where is defined as
Then, a new instance
where can be interpreted as the weighted mean of the instances that are vertices of the tetrahedron , where the weights are drawn from the Dirichlet distribution.
4.5. Method Description
Here, we present steps to build DTO-SMOTE. Algorithm 1 presents the algorithm. The main steps are outlined next.
| Algorithm 1: DTO-SMOTE |
 |
- The algorithm takes as input an imbalanced data set, a data compression algorithm, some tetrahedron quality measure (Section 4.3), and the Dirichlet hyperparameter c (Section 4.4);
- Using the compression technique, reduce feature space to a three-dimensional space resulting in ;
- Construct the Delaunay tessellation using the compressed data set
- For all simplex from , compute a simplex quality measure (Section 4.3);
- After that, we calculate weights for all simplex in this way: where is the vertex’s proportion of instances belonging to the minority class in the simplex and is the quality index calculated for the simplex, according to quality measure selected; The weights are normalized to sum 1, for representing probabilities.
- Randomly choose with replacement a simplex (tetrahedron) from , according to the probabilities calculated from step 5.
- Once a simplex was selected, generate a new sample using a Dirichlet distribution, as described in Section 4.4.
- Steps 6 and 7 are repeated until the number of samples in Minority Class matches the number of instances of the Majority Class.
5. Experiments and Results
This section describes the experimental evaluation carried out for evaluating our new preprocessing techniques. The experimental protocol is depicted in Figure 4. Experiments are conducted using 5-fold cross-validation. We opt to execute 5-fold cross-validation instead of 10-fold cross-validation as in imbalanced data sets because using 10-fold may lead to a test set with very few instances from the minority class. As suggested in Reference [], preprocessing methods are only applied to the training set. Considering the random nature of DTO-SMOTE and other oversampling methods to build artificial data, we repeat the entire process three times, i.e., we ran -fold cross-validation.
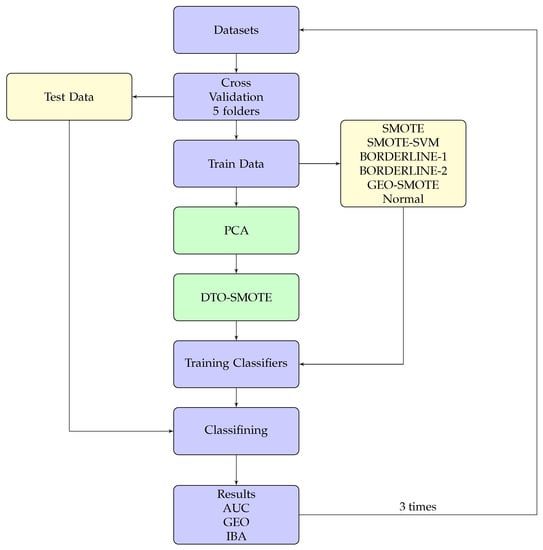
Figure 4.
Delaunay Tessellation Oversampling Synthetic Minority Over-sampling Technique (DTO-SMOTE) flowchart.
We compare our method with the preprocessing techniques: SMOTE [], SMOTESVM [], BORDERLINE SMOTE 1 [], BORDERLINE SMOTE 2 [], and GEOMETRIC SMOTE []. All these methods are executed with the default parameters. For running SMOTE, SMOTESVM, BORDERLINE SMOTE 1, and BORDERLINE SMOTE 2, we use the imbalanced-learn package []. For GEOMETRIC SMOTE, we use the implementation of the author, available at https://geometric-smote.readthedocs.io/. Furthermore, we also compare results without any preprocessing. Table 2 presents the alias used for showing the results.

Table 2.
Oversampling techniques.
To evaluate our methods’ effectiveness, we compare the original and oversampled data sets with eight different learning algorithms, as presented in Table 3. All classifiers are available in the SciKit–Learn package and Intel Python Distribution, at http://scikit-learn.org/ and https://software.intel.com/en-us/distribution-for-python, respectively, and were used with default parameters, as described in Table 3.

Table 3.
Machine learning algorithms.
Experiments were performed with 61 bi-class data sets. Table 4 show the characteristics of the bi-class Data sets used in our experiments. For each data set, the tables present the Imbalance Ratio (IR), the number of samples (Samples), and the number of features (Features).

Table 4.
Bi-class data sets.
We use the Principal Component Analysis (PCA) algorithm to compress the data sets before applying the Delaunay Tessellation. This choice was motivated due to its simplicity and extensive use. However, any method that compresses the data to a lower dimension can be used instead of PCA. Furthermore, PCA was also used in Reference [] for dimensionality reduction for manifold embedding.
Source Code for DTO-SMOTE can be found at https://github.com/carvalhoamc/DTOSMOTE. Furthermore, all results are available at https://github.com/carvalhoamc/DTO-SMOTE and scripts to reproduce the analysis are at https://github.com/carvalhoamc/dtosmote_performance.
5.1. Influence of Parameters
Our method has two parameters: the tetrahedral quality metric and the Dirichlet parameter . The quality metric influences the selection of tetrahedral for interpolation, while the influences where the interpolation will occur in a particular tetrahedral. We have experimented with all the tetrahedral quality metrics described in Section 4.3. For the parameter , we experiment with the parameter ranging from 1 to 9.5 with step size 0.5. In total, we made runs for bi-class data sets for each of the eight classifiers used in the experiments.
Figure 5 depicts the influence of this parameter. The graphs show the variation in rank as a function of the parameter for each tetrahedral quality measure, averaged over all the data sets. Results are homogeneous among the different metrics (AUC, GEO, and IBA for binary data sets). As can be seen, the quality measure based on the solid angle produces better results. Furthermore, larger than four also produces good average results.
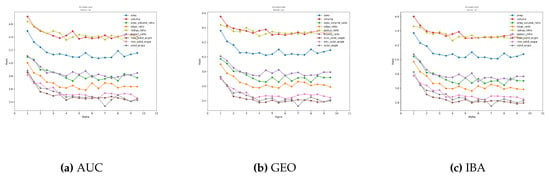
Figure 5.
Bi-class DTO-SMOTE rank by Dirichlet .
With these results, we choose the default values for and geometry for the DTO-SMOTE algorithm. The selected values for bi-class is 7, and the quality measure set is the solid angle. Therefore, we use the solid angle as the tetrahedron quality measure and for bi-class problems for comparison with other SMOTE methods.
5.2. Experimental Results for Bi-Class Data Sets
For binary class data sets, we evaluate three performance measures: Area Under de ROC curve (AUC), Geometric Mean (GEO), and Index of Balanced Accuracy (IBA). In this work, we adopted the parameter for IBA to 0, as recommended by the authors.
Due to space limitations, we did not include in the paper numerical results for each data set. However, all the results are publicly available at https://github.com/carvalhoamc/DTO-SMOTE. To draw general conclusions about the our method’s performance, we present average rank performance and statistical analysis.
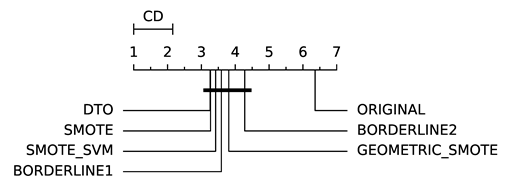
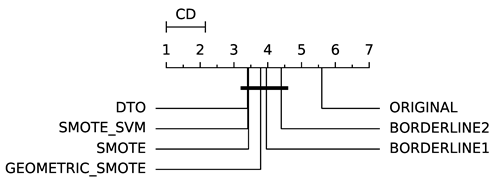
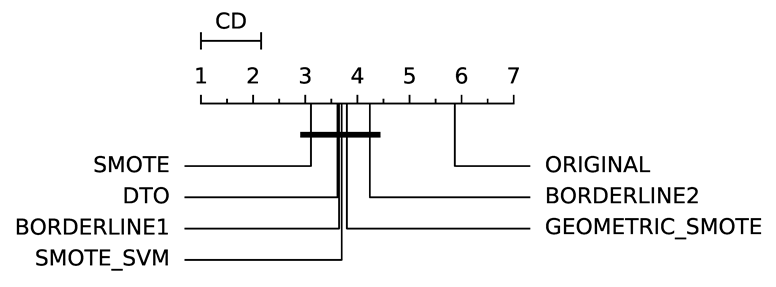
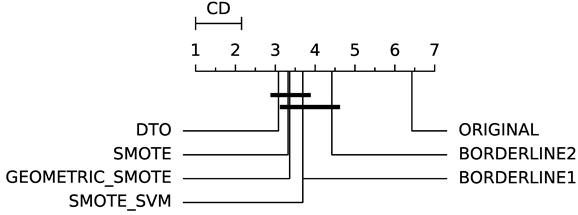
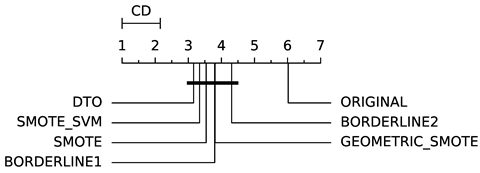
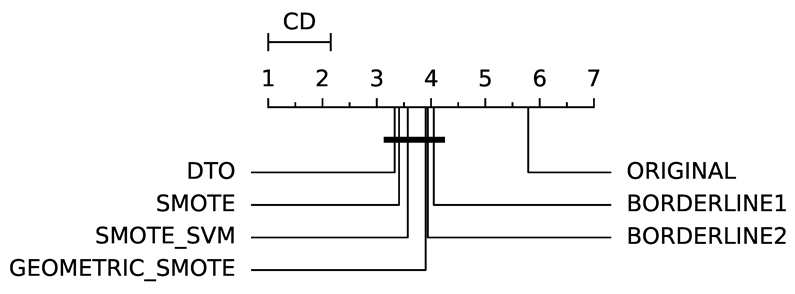
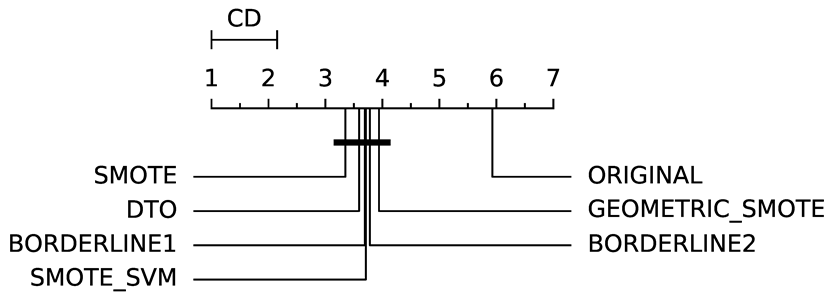
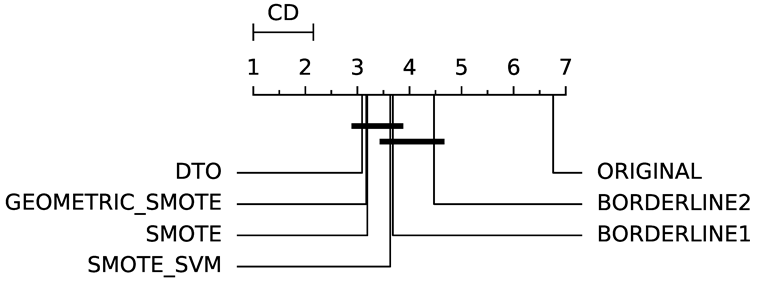
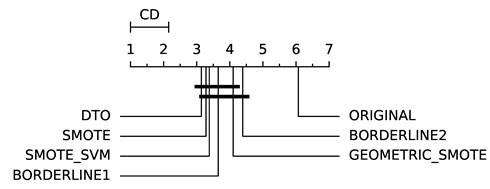
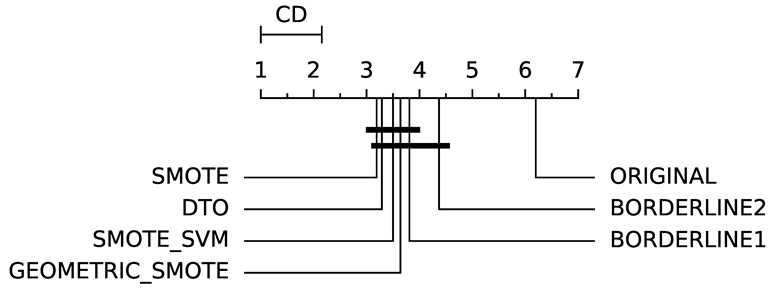
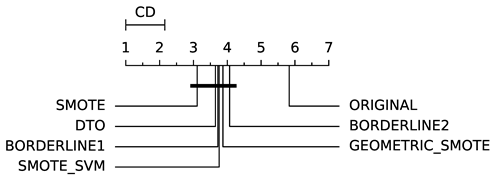
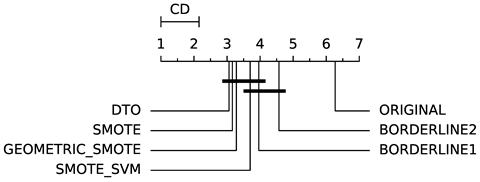
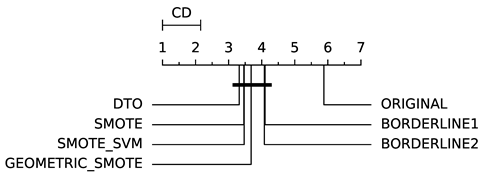
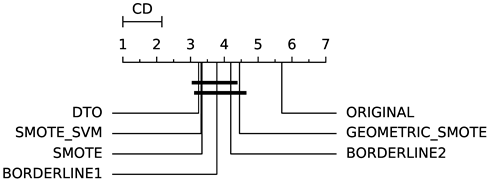
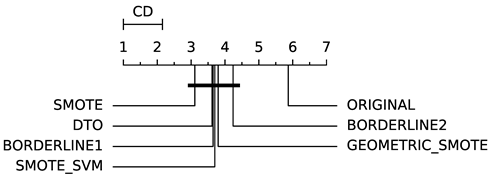
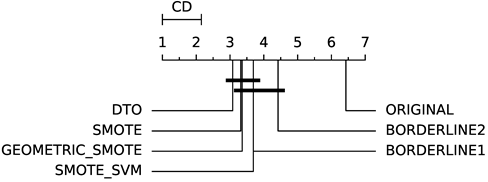
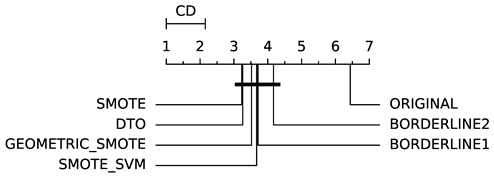
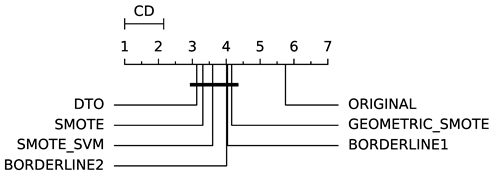
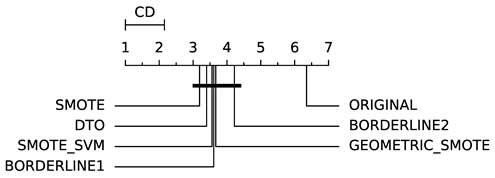
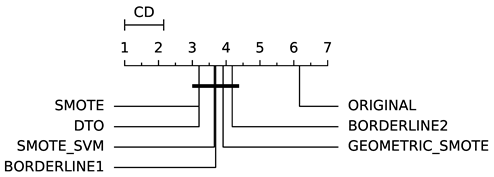
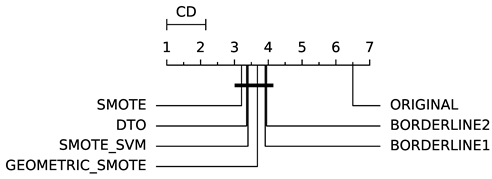
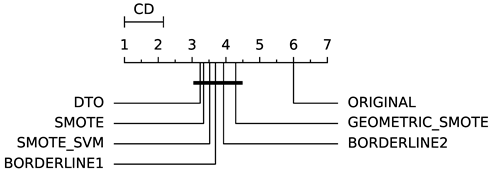
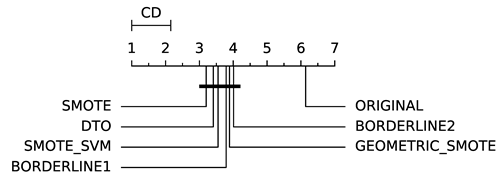
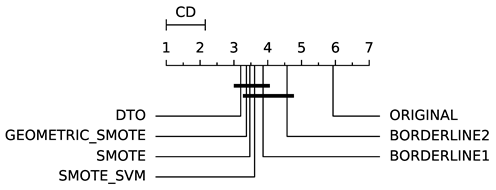
To evaluate whether the differences among methods are statistically significant, we use a non-parametric Friedman multiple comparison testing (Table 5). The Friedman test is the non-parametric equivalent of the two-way ANOVA. Under the null hypothesis, it states that all the algorithms are equivalent, so rejecting this hypothesis implies significant differences among all algorithms. When the Friedman test rejects the null hypothesis, we can proceed with a post-hoc test to detect the significant differences among the methods. For this, we used Shaffer post-hoc multiple comparisons for controlling the family-wise error.

Table 5.
Diagram of significance differences.
The results of the statistical tests are presented in the form of a diagram of significant differences. In these diagrams, results were ordered by decreasing performance, where the best algorithms are placed to the left in the graph. A thick line joining two methods indicates that there is no statistical significance among them. All the results are based on the average performance of 3 runs of 5-fold cross-validation.
In terms of AUC (Table 6), DTO-SMOTE performed better in terms of global rank in 7 of the eight classification algorithms (Table 3). Only the KNN algorithm, our method did not obtain the best average performance with DTO-SMOTE. However, for KNN, DTO-SMOTE was in second place, little after the SMOTE algorithm. Regarding the critical differences diagram (Table 5) DTO-SMOTE is in the first place in 7 of 8 algorithms, significantly outperforming the data set without treatment.

Table 6.
Area Under the ROC curve (AUC) rank (solid angle and ); see Table 5.
In terms of GEO (Table 7), DTO-SMOTE performed better in terms of rank with ABC, DTREE, LRG, and RF (Table 3). There was a tie between DTO-SMOTE and SMOTE for the SVM algorithm. For KNN, MLP, and SGD, SMOTE presented better performance. The winner in terms of global rank for bi-class problems under the GEO measure was the DTO-SMOTE algorithm. Again, DTO-SMOTE significantly outperforms the data set without treatment in terms of GEO Table 5.

Table 7.
Geometric Mean (GEO) rank (solid angle and ); see Table 5.
Regarding IBA (Table 8), DTO-SMOTE has a better average rank with ABC, LRG, RF and SVM classifiers (Table 3). With DTREE, KNN, MLP, and SGD, SMOTE had the best rank performance. In terms of average rank, SMOTE is in first place, followed by DTO-SMOTE in second place. DTO-SMOTE is significantly better than no treating, as can be seen in Table 5.

Table 8.
Index of Balanced Accuracy (IBA) rank (solid angle and ); see Table 5.
In general, our method (DTO-SMOTE) showed a better average performance when used as a preprocessing technique for several classifiers. For all learning algorithms, it was ranked first or second in at least one performance measure for all eight learning algorithms. Furthermore, it has better overall rank performance in terms of AUC and GEO, and second (with a lower standard deviation) in IBA. These results are a strong indicator of the utility of our proposed method for imbalanced bi-class classification problems. Table 5 shows all the pairwise comparisons of the data methods evaluated in bi-class data sets in terms of AUC, GEO, and IBA. Although there are a few statistical differences between our proposed method (DTO-SMOTE) and the other SMOTE variants, our approach is ranked firstly with ABC, RF, LRG, and RF for all three performance measures AUC, GEO, and IBA. It is ranked firstly with DTREE for AUC and GEO, and it is ranked firstly with SVM for AUC and IBA. For KNN, it is ranked in second place for all three measures and, for MLP and SGD, it is ranked in second place for GEO and IBA. Furthermore, DTO-SMOTE is statistically better than Original for all classifiers.
6. Conclusions
This paper presents DTO-SMOTE, an oversampling algorithm that generates synthetic instances based on the Delaunay tessellation. DTO-SMOTE is an evolution of our previous work, presented in Reference []. In that study, we evaluated an initial version of our preprocessing method considering only the KNN learning algorithm. Furthermore, our previous version does not consider the shape of the tetrahedrons and uses their barycenters for interpolation. This new version uses tetrahedron quality indices to select tetrahedrons, and a Dirichlet distribution to randomly choose a point for interpolation. We conduct a sizeable experimental study comparing our method with five SMOTE variations evaluated with eight learning algorithms, 61 binary data sets, and three different performance measures.
Results indicate a better average performance when the method is used for class imbalanced classification problems. Besides that, we plan to study the imbalanced data set complexity by analyzing the simplex mesh and its quality indexes. The main advantage is that DTO-SMOTE proved to be more efficient than the other oversampling algorithms on average, according to the results presented. In comparison to the other algorithms, DTO-SMOTE can be a little slower as it needs to create a three-dimensional mesh. In future work, we intend to assess whether the refinement of the mesh can lead to better results in terms of performance in the classification.
Our goal is to better understand the data set characteristics that lead to an increase in performance, as the simplex geometry could be linked to the data’s local density []. We also plan to investigate the SMOTE bias theoretically in the future. This procedure could reduce efforts in selecting a proper method and parameters for specific data sets. Our implementation, and all results and scripts for analysis, are publicly available on the Internet.
Author Contributions
A.M.d.C. and R.C.P. conceived the main idea of the algorithm and designed the tests; R.C.P. supervised the design of the system; A.M.d.C. designed the system and ran the experiments and collected data; All authors contributed in writing the original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prati, R.C.; Batista, G.E.A.P.A.; Silva, D.F. Class imbalance revisited: A new experimental setup to assess the performance of treatment methods. Knowl. Inf. Syst. 2015, 45, 247–270. [Google Scholar] [CrossRef]
- Krawczyk, B.; Galar, M.; Jeleń, Ł.; Herrera, F. Evolutionary undersampling boosting for imbalanced classification of breast cancer malignancy. Appl. Soft Comput. J. 2016, 38, 714–726. [Google Scholar] [CrossRef]
- Troncoso, A.; Ribera, P.; Asencio-Cortés, G.; Vega, I.; Gallego, D. Imbalanced classification techniques for monsoon forecasting based on a new climatic time series. Environ. Model. Softw. 2018, 106, 48–56. [Google Scholar] [CrossRef]
- Yan, B.; Han, G. LA-GRU: Building Combined Intrusion Detection Model Based on Imbalanced Learning and Gated Recurrent Unit Neural Network. Secur. Commun. Netw. 2018, 2018. [Google Scholar] [CrossRef]
- Farías, D.I.H.; Prati, R.; Herrera, F.; Rosso, P. Irony detection in Twitter with imbalanced class distributions. J. Intell. Fuzzy Syst. 2020, 39, 2147–2163. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.Z.; Yuan, J. Predicting Extreme Financial Risks on Imbalanced Dataset: A Combined Kernel FCM and Kernel SMOTE Based SVM Classifier. Comput. Econ. 2020, 56, 187–216. [Google Scholar] [CrossRef]
- Roumani, Y.F.; Nwankpa, J.K.; Tanniru, M. Predicting firm failure in the software industry. Artif. Intell. Rev. 2020, 53, 4161–4182. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Kotagiri, R.; Wu, L.; Tari, Z.; Cheriet, M. KRNN: K Rare-class Nearest Neighbour classification. Pattern Recognit. 2017, 62, 33–44. [Google Scholar] [CrossRef]
- Sawangarreerak, S.; Thanathamathee, P. Random Forest with Sampling Techniques for Handling Imbalanced Prediction of University Student Depression. Information 2020, 11, 519. [Google Scholar] [CrossRef]
- Oksuz, K.; Cam, B.C.; Kalkan, S.; Akbas, E. Imbalance problems in object detection: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef]
- Fiorentini, N.; Losa, M. Handling imbalanced data in road crash severity prediction by machine learning algorithms. Infrastructures 2020, 5, 61. [Google Scholar] [CrossRef]
- Patel, H.; Singh Rajput, D.; Thippa Reddy, G.; Iwendi, C.; Kashif Bashir, A.; Jo, O. A review on classification of imbalanced data for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2020, 16, 1550147720916404. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic Minority Over-sampling Technique Nitesh. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Schaap, W.E.; van de Weygaert, R. Continuous fields and discrete samples: Reconstruction through Delaunay tessellations. Astron. Astrophys. 2000, 363, L29–L32. [Google Scholar]
- Carvalho, A.M.D.; Prati, R.C. Improving kNN classification under Unbalanced Data. A New Geometric Oversampling Approach. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Japkowicz, N.; Shah, M. Evaluating Learning Algorithms: A Classification Perspective; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- García, V.; Sánchez, J.; Mollineda, R. On the effectiveness of preprocessing methods when dealing with different levels of class imbalance. Knowl.-Based Syst. 2012, 25, 13–21. [Google Scholar] [CrossRef]
- Prati, R.C.; Batista, G.E.A.P.A.; Monard, M.C. A Survey on Graphical Methods for Classification Predictive Performance Evaluation. IEEE Trans. Knowl. Data Eng. 2011, 23, 1601–1618. [Google Scholar] [CrossRef]
- Haixiang, G.; Yijing, L.; Shang, J.; Mingyun, G.; Yuanyue, H.; Bing, G. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar] [CrossRef]
- Fernandez, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-year Anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- García, S.; Herrera, F. Evolutionary undersampling for classification with imbalanced datasets: Proposals and taxonomy. Evol. Comput. 2009, 17, 275–306. [Google Scholar] [CrossRef]
- Yu, H.; Ni, J.; Zhao, J. ACOSampling: An ant colony optimization-based undersampling method for classifying imbalanced DNA microarray data. Neurocomputing 2013, 101, 309–318. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Sun, Y.; Castellano, C.G.; Robinson, M.; Adams, R.; Rust, A.G.; Davey, N. Using pre & post-processing methods to improve binding site predictions. Pattern Recognit. 2009, 42, 1949–1958. [Google Scholar]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM Sigkdd Explor. Newsl. 2004, 6, 20. [Google Scholar] [CrossRef]
- Ramentol, E.; Caballero, Y.; Bello, R.; Herrera, F. SMOTE-RSB *: A hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-sets using SMOTE and rough sets theory. Knowl. Inf. Syst. 2012, 33, 245–265. [Google Scholar] [CrossRef]
- Sáez, J.A.; Luengo, J.; Stefanowski, J.; Herrera, F. SMOTE-IPF: Addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering. Inf. Sci. 2015, 291, 184–203. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, J.; Wu, C.A. Imbalanced learning based on data-partition and SMOTE. Information 2018, 9, 238. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Cost-Sensitive Learning. In Learning from Imbalanced Data Sets; Springer: New York, NY, USA, 2018; pp. 63–78. [Google Scholar]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Ensemble Learning. In Learning from Imbalanced Data Sets; Springer: New York, NY, USA, 2018; pp. 147–196. [Google Scholar]
- Galar, M.; Fernández, A.; Barrenechea, E.; Sola, H.; Herrera, F. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. Syst. Man Cybern. Part C Appl. Rev. IEEE Trans. 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Leo, B. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. In Advances in Intelligent Computing; Huang, D.S., Zhang, X.P., Huang, G.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Nguyen, H.M.; Cooper, E.W.; Kamei, K. Borderline over-sampling for imbalanced data classification. Int. J. Knowl. Eng. Soft Data Paradig. 2011, 3, 4. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1322–1328. [Google Scholar]
- Douzas, G.; Bacao, F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE. Inf. Sci. 2019, 501, 118–135. [Google Scholar] [CrossRef]
- Bellinger, C.; Drummond, C.; Japkowicz, N. Manifold-based synthetic oversampling with manifold conformance estimation. Mach. Learn. 2018, 107, 605–637. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F. A Comprehensive Analysis of Synthetic Minority Oversampling TEchnique (SMOTE) for Handling Class Imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Gao, Z.; Yu, Z.; Holst, M. Feature-preserving surface mesh smoothing via suboptimal Delaunay triangulation. Graph. Model. 2013, 75, 23–38. [Google Scholar] [CrossRef]
- Samat, A.; Gamba, P.; Liu, S.; Du, P.; Abuduwaili, J. Jointly Informative and Manifold Structure Representative Sampling Based Active Learning for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 6803–6817. [Google Scholar] [CrossRef]
- Kolluri, R.; Shewchuk, J.R.; O’Brien, J.F. Spectral surface reconstruction from noisy point clouds. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Nice, France, 8–10 July 2004; pp. 11–21. [Google Scholar]
- De Kok, T.; Van Kreveld, M.; Löffler, M. Generating realistic terrains with higher-order Delaunay triangulations. Comput. Geom. 2007, 36, 52–65. [Google Scholar] [CrossRef][Green Version]
- Anderson, S.J.; Karumanchi, S.B.; Iagnemma, K. Constraint-based planning and control for safe, semi-autonomous operation of vehicles. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium (IV), Madrid, Spain, 3–7 June 2012; pp. 383–388. [Google Scholar]
- Devriendt, K.; Van Mieghem, P. The simplex geometry of graphs. J. Complex Netw. 2019, 7, 469–490. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.scipy.org/ (accessed on 5 November 2020).
- Maur, P. Delaunay Triangulation in 3D. Ph.D. Thesis, University of West Bohemia in Pilsen, Pilsen, Czech Republic, 2002. [Google Scholar]
- Santos, M.S.; Soares, J.P.; Abreu, P.H.; Araujo, H.; Santos, J. Cross-validation for imbalanced datasets: Avoiding overoptimistic and overfitting approaches [research frontier]. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Abou-Moustafa, K.; Ferrie, F.P. Local generalized quadratic distance metrics: Application to the k-nearest neighbors classifier. Adv. Data Anal. Classif. 2018, 12, 341–363. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and regression trees. Classif. Regres. Trees 2017, 1, 1–358. [Google Scholar]
- Pearlmutter, B.A. Fast Exact Multiplication by the Hessian. Neural Comput. 1994, 6, 147–160. [Google Scholar] [CrossRef]
- Utkin, L.V.; Zhuk, Y.A. Robust boosting classification models with local sets of probability distributions. Knowl.-Based Syst. 2014, 61, 59–75. [Google Scholar] [CrossRef]
- Shen, H. Towards a Mathematical Understanding of the Difficulty in Learning with Feedforward Neural Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 811–820. [Google Scholar]
- Chang, C.C.; Lin, C.j.; Tieleman, T. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. (TIST) 2008, 307, 1–39. [Google Scholar] [CrossRef]
- Zhang, T.; Damerau, F.; Johnson, D. Text chunking based on a generalization of winnow. J. Mach. Learn. Res. 2002, 2, 615–637. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).