Ensemble Classification through Random Projections for Single-Cell RNA-Seq Data
Abstract
:1. Introduction
2. Background Material
2.1. The Random Projection Method
2.2. Random Projections for Ensemble Classification
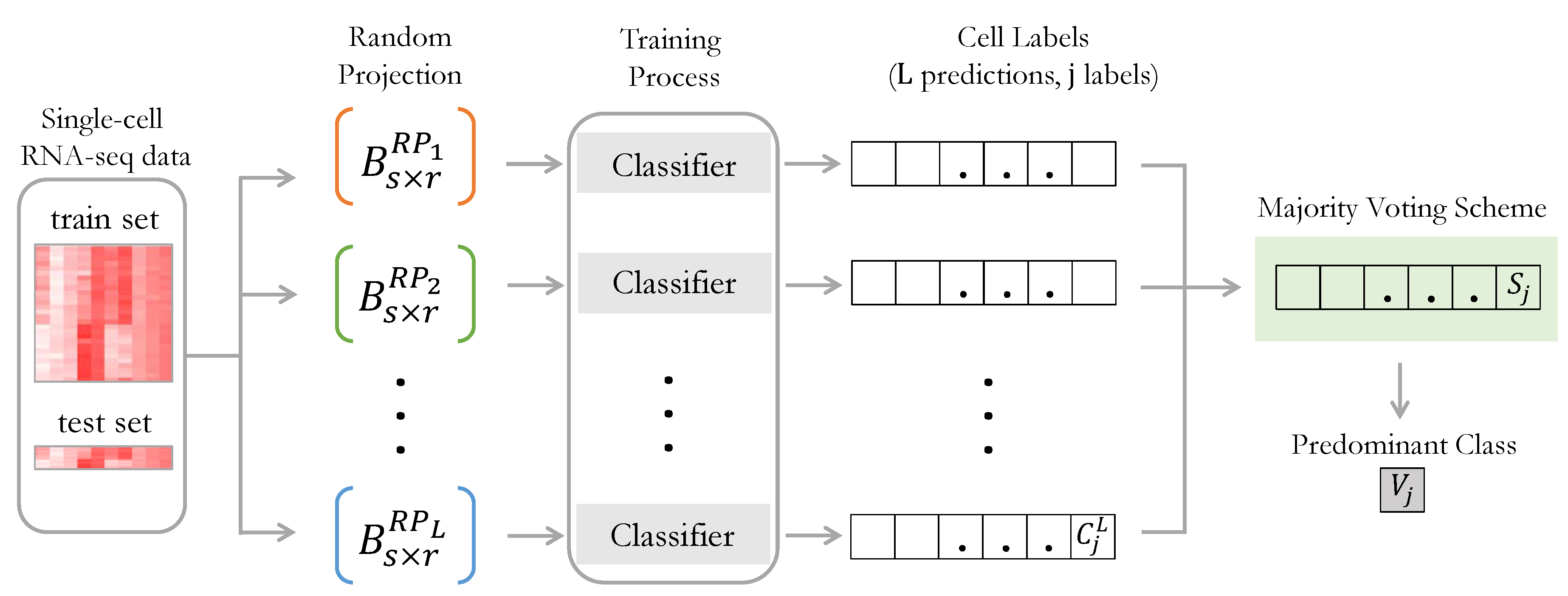
3. The Multiple Random Projection and Voting Methodology
| Algorithm 1 MRPV Pseudocode |
Input: Data (A), RP spaces number (L), RP spaces dimensions (r), Classifier selection Output: The class assignment V for each test point
|
4. Experimental Analysis
4.1. Dataset Description
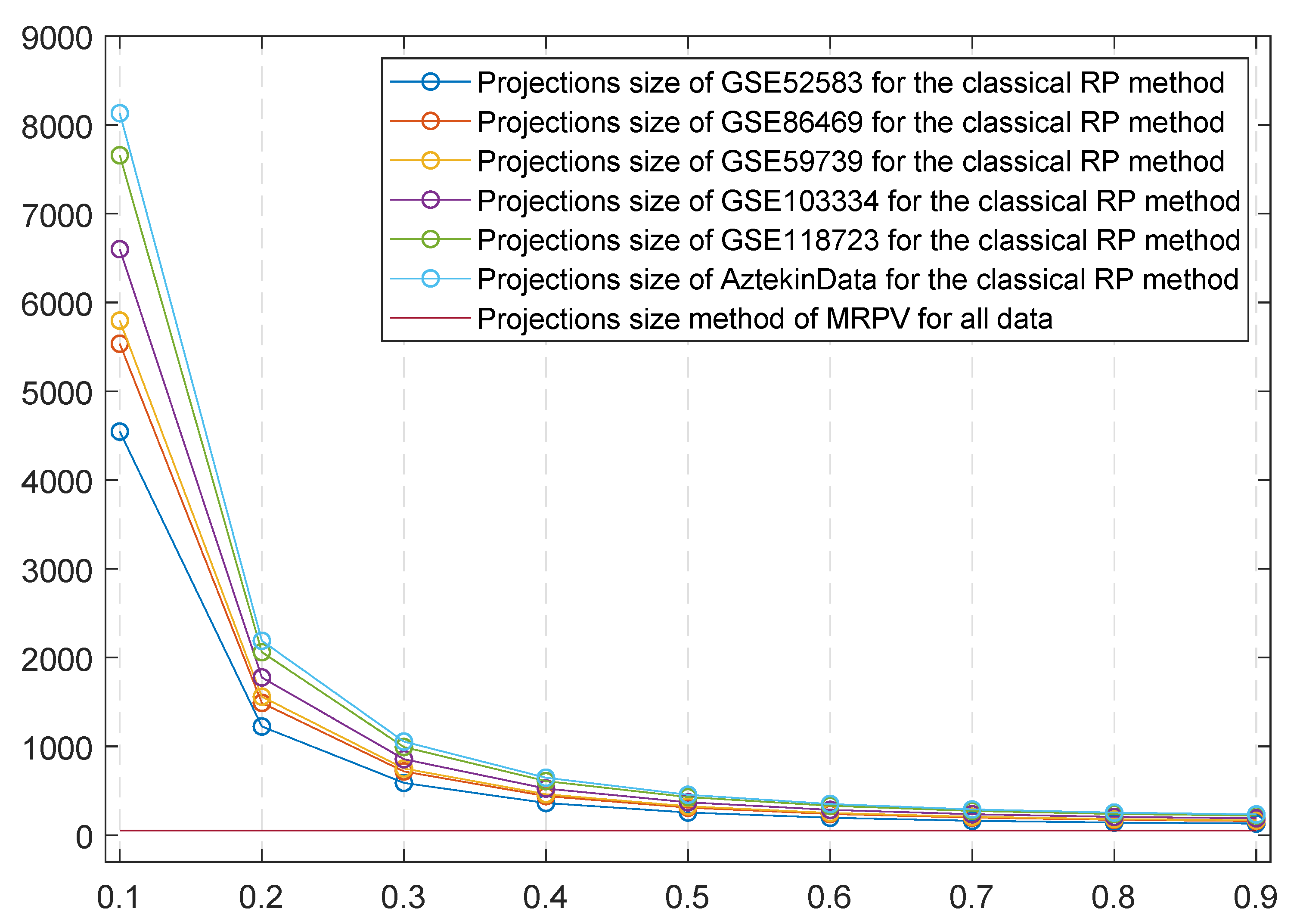
4.2. MRPV Performance Evaluation
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, X.W.; Lin, X. Big data deep learning: Challenges and perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Luo, J.; Wu, M.; Gopukumar, D.; Zhao, Y. Big data application in biomedical research and health care: A literature review. Biomed. Inform. Insights 2016, 8, BII-S31559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reuter, J.A.; Spacek, D.V.; Snyder, M.P. High-throughput sequencing technologies. Mol. Cell 2015, 58, 586–597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wetterstrand, K. DNA Sequencing Costs: Data-National Human Genome Research Institute (NHGRI). Available online: https://www.genome.gov/about-genomics/fact-sheets/DNA-Sequencing-Costs-Data (accessed on 27 October 2020).
- Tan, Y.; Cahan, P. SingleCellNet: A computational tool to classify single cell RNA-Seq data across platforms and across species. Cell Syst. 2019, 9, 207–213. [Google Scholar] [CrossRef]
- Vrahatis, A.G.; Tasoulis, S.K.; Maglogiannis, I.; Plagianakos, V.P. Recent Machine Learning Approaches for Single-Cell RNA-seq Data Analysis. In Advanced Computational Intelligence in Healthcare-7; Springer: Berlin/Heidelberg, Germany, 2020; pp. 65–79. [Google Scholar]
- Tasoulis, S.K.; Vrahatis, A.G.; Georgakopoulos, S.V.; Plagianakos, V.P. Biomedical Data Ensemble Classification using Random Projections. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 166–172. [Google Scholar]
- Achlioptas, D. Database-friendly random projections. In Proceedings of the Twentieth ACM Symposium on Principles of Database Systems, New York, NY, USA, 21–23 May 2001; pp. 274–281. [Google Scholar]
- Bingham, E.; Mannila, H. Random projection in dimensionality reduction: Applications to image and text data. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 26–29 August 2001; pp. 245–250. [Google Scholar]
- Papadimitriou, C.H.; Raghavan, P.; Tamaki, H.; Vempala, S. Latent semantic indexing: A probabilistic analysis. In Proceedings of the 17th ACM Symp. on the Principles of Database Systems, Seattle, WA, USA, 1–3 June 1998; pp. 159–168. [Google Scholar]
- Dasgupta, S. Learning Mixtures of Gaussians. Found. Comput. Sci. Annu. IEEE Symp. 1999, 634. [Google Scholar] [CrossRef]
- Dasgupta, S. Experiments with Random Projection. In Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 30 June–3 July 2000; pp. 143–151. [Google Scholar]
- Cannings, T.I.; Samworth, R.J. Random-projection ensemble classification. J. R. Stat. Soc. Ser. B Stat. Methodol. 2017, 79, 959–1035. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Context vectors: General purpose approximate meaning representations self-organized from raw data. Comput. Intell. Imitating Life 1994, 3, 43–56. [Google Scholar]
- Schclar, A.; Rokach, L. Random projection ensemble classifiers. In International Conference on Enterprise Information Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 309–316. [Google Scholar]
- Kuncheva, L.I. Diversity in multiple classifier systems. Inf. Fusion 2005, 6, 3–4. [Google Scholar] [CrossRef]
- Dasgupta, S.; Gupta, A. An elementary proof of a theorem of Johnson and Lindenstrauss. Random Struct. Algor. 2003, 22, 60–65. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Risso, D.; Cole, M.; Risso, M.D. BiocStyle; biocViews ExperimentData; SequencingData. Package ‘scRNAseq’ 2020. Available online: https://bioconductor.riken.jp/packages/devel/data/experiment/manuals/scRNAseq/man/scRNAseq.pdf (accessed on 27 October 2020).
- Mathys, H.; Adaikkan, C.; Gao, F.; Young, J.Z.; Manet, E.; Hemberg, M.; De Jager, P.L.; Ransohoff, R.M.; Regev, A.; Tsai, L.H. Temporal tracking of microglia activation in neurodegeneration at single-cell resolution. Cell Rep. 2017, 21, 366–380. [Google Scholar] [CrossRef] [Green Version]
- Lawlor, N.; George, J.; Bolisetty, M.; Kursawe, R.; Sun, L.; Sivakamasundari, V.; Kycia, I.; Robson, P.; Stitzel, M.L. Single-cell transcriptomes identify human islet cell signatures and reveal cell-type–specific expression changes in type 2 diabetes. Genome Res. 2017, 27, 208–222. [Google Scholar] [CrossRef] [PubMed]
- Usoskin, D.; Furlan, A.; Islam, S.; Abdo, H.; Lönnerberg, P.; Lou, D.; Hjerling-Leffler, J.; Haeggström, J.; Kharchenko, O.; Kharchenko, P.V.; et al. Unbiased classification of sensory neuron types by large-scale single-cell RNA sequencing. Nat. Neurosci. 2015, 18, 145. [Google Scholar] [CrossRef] [PubMed]
- Treutlein, B.; Brownfield, D.G.; Wu, A.R.; Neff, N.F.; Mantalas, G.L.; Espinoza, F.H.; Desai, T.J.; Krasnow, M.A.; Quake, S.R. Reconstructing lineage hierarchies of the distal lung epithelium using single-cell RNA-seq. Nature 2014, 509, 371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarkar, A.K.; Tung, P.Y.; Blischak, J.D.; Burnett, J.E.; Li, Y.I.; Stephens, M.; Gilad, Y. Discovery and characterization of variance QTLs in human induced pluripotent stem cells. PLoS Genet. 2019, 15, e1008045. [Google Scholar] [CrossRef] [Green Version]
- Aztekin, C.; Hiscock, T.; Marioni, J.; Gurdon, J.; Simons, B.; Jullien, J. Identification of a regeneration-organizing cell in the Xenopus tail. Science 2019, 364, 653–658. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.; Lo, K.; Geddes, T.A.; Kim, H.J.; Yang, J.Y.H.; Yang, P. scReClassify: Post hoc cell type classification of single-cell rNA-seq data. BMC Genom. 2019, 20, 1–10. [Google Scholar] [CrossRef]
- Alquicira-Hernandez, J.; Sathe, A.; Ji, H.P.; Nguyen, Q.; Powell, J.E. scPred: Accurate supervised method for cell-type classification from single-cell RNA-seq data. Genome Biol. 2019, 20, 1–17. [Google Scholar]




| GEO Dataset | Type | Dimensions | Samples | Classes | References |
|---|---|---|---|---|---|
| GSE103334 | scRNA-seq | 23,951 | 2208 | 4 | [20] |
| GSE86469 | scRNA-seq | 26,616 | 638 | 2 | [21] |
| GSE59739 | scRNA-seq | 25,333 | 854 | 3 | [22] |
| GSE52583 | scRNA-seq | 23,228 | 201 | 4 | [23] |
| GSE118723 | scRNA-seq | 20,151 | 7584 | 6 | [24] |
| AztekinData | scRNA-seq | 31,535 | 13,199 | 5 | [25] |
| GSE103334 | GSE52583 | GSE59739 | GSE86469 | GSE118723 | AztekinData | |
|---|---|---|---|---|---|---|
| MEAN (Sth) | MEAN (Sth) | MEAN (Sth) | MEAN(Sth) | MEAN (Sth) | MEAN (Sth) | |
| MRPV-LDA | 1.2 × 10 (0.47) | 6.8 × 10 (0.01) | 8.9 × 10 (0.02) | 8.0 × 10 (0.01) | 5.7 × 10 (1.13) | 1.1 × 10 (13.0) |
| MRPV-KNN | 1.3 × 10 (0.13) | 4.3 × 10 (0.01) | 7.2 × 10 (0.00) | 6.7 × 10 (0.02) | 1.0 × 10 (1.10) | 2.9 × 10 (2.32) |
| MRPV-RLDA | 8.3 × 10 (0.46) | 6.5 × 10 (0.13) | 8.1 × 10 (0.04) | 7.7 × 10 (0.03) | 6.1 × 10 (1.20) | 1.1 × 10 (3.18) |
| RP-LDA | 3.7 × 10 (10.1) | 2.1 × 10 (0.03) | 9.1 × 10 (0.1) | 6.2 × 10 (0.05) | 6.8 × 10 (5.32) | 1.1 × 10 (14.9) |
| RP-KNN | 8.3 × 10 (3.58) | 1.1 × 10 (0.02) | 3.4 × 10 (0.09) | 2.8 × 10 (0.03) | 4.8 × 10 (7.12) | 1.5 × 10 (12.4) |
| RP-RLDA | 3.6 × 10 (0.48) | 3.3 × 10 (0.30) | 9.6 × 10 (0.29) | 5.6 × 10 (1.95) | 7.5 × 10 (15.2) | 1.3 × 10 (22.4) |
| KNN | 5.9 × 10 (17.6) | 1.0 × 10 (0.01) | 1.2 × 10 (0.03) | 7.8 × 10 (0.03) | 1.0 × 10 (65.2) | 2.4 × 10 (78.9) |
| LDA | 4.4 × 10 (16.2) | 6.0 × 10 (0.49) | 1.9 × 10 (1.80) | 1.3 × 10 (4.68) | 6.8 × 10 (45.5) | 1.7 × 10 (55.6) |
| BAGGING | 3.1 × 10 (2.18) | 3.1 × 10 (0.22) | 1.2 × 10 (0.47) | 9.7 × 10 (0.19) | 4.2 × 10 (39.2) | 1.5 × 10 (95.3) |
| RF | 9.5 × 10 (25.2) | 2.4 × 10 (0.05) | 2.2 × 10 (1.58) | 1.6 × 10 (0.43) | 1.7 × 10 (95.6) | 5.4 × 10 (25.2) |
| DeepNN | 9.2 × 10 (85.5) | 5.0 × 10 (40.2) | 7.6 × 10 (47.4) | 6.2 × 10 (68.8) | 6.9 × 10 (34.3) | 2.2 × 10 (31.4) |
| scReClassify | 1.5 × 10 (13.5) | 1.8 × 10 (0.10) | 8.1 × 10 (1.44) | 4.4 × 10 (1.18) | 3.0 × 10 (51.2) | Ν/Α |
| scPred | 7.9 × 10 (5.15) | 6.1 × 10 (1.21) | 1.3 × 10 (2.30) | 7.1 × 10 (1.48) | 1.8 × 10 (23.6) | Ν/Α |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrahatis, A.G.; Tasoulis, S.K.; Georgakopoulos, S.V.; Plagianakos, V.P. Ensemble Classification through Random Projections for Single-Cell RNA-Seq Data. Information 2020, 11, 502. https://doi.org/10.3390/info11110502
Vrahatis AG, Tasoulis SK, Georgakopoulos SV, Plagianakos VP. Ensemble Classification through Random Projections for Single-Cell RNA-Seq Data. Information. 2020; 11(11):502. https://doi.org/10.3390/info11110502
Chicago/Turabian StyleVrahatis, Aristidis G., Sotiris K. Tasoulis, Spiros V. Georgakopoulos, and Vassilis P. Plagianakos. 2020. "Ensemble Classification through Random Projections for Single-Cell RNA-Seq Data" Information 11, no. 11: 502. https://doi.org/10.3390/info11110502
APA StyleVrahatis, A. G., Tasoulis, S. K., Georgakopoulos, S. V., & Plagianakos, V. P. (2020). Ensemble Classification through Random Projections for Single-Cell RNA-Seq Data. Information, 11(11), 502. https://doi.org/10.3390/info11110502







