Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications
Abstract
:1. Introduction
- We introduce two types of binary non-uniform scalar quantizers, named binary quantizer type 1 and binary quantizer type 2, and provide detailed descriptions of the design methods. Furthermore, we investigate the effect of clipping with the aim of reducing the quantization noise. Quantizers are designed for the memoryless Laplacian source with zero-mean and unit variance.
- We conduct a detailed analysis of both binary quantizers and provide recommendations for quantizer selection in applications where the non-optimal design is required.
- We analyze the performance of both quantizers in a wide range of input data variances and investigate the robustness property.
- We propose a method to improve the performance in a wide dynamic range that is based on the forward adaption technique.
- We verify the correctness of the theoretical quantizer models by applying them to several real data, including speech, image, and neural network parameters.
2. Previous Work
3. Design Methods of Binary Quantizer
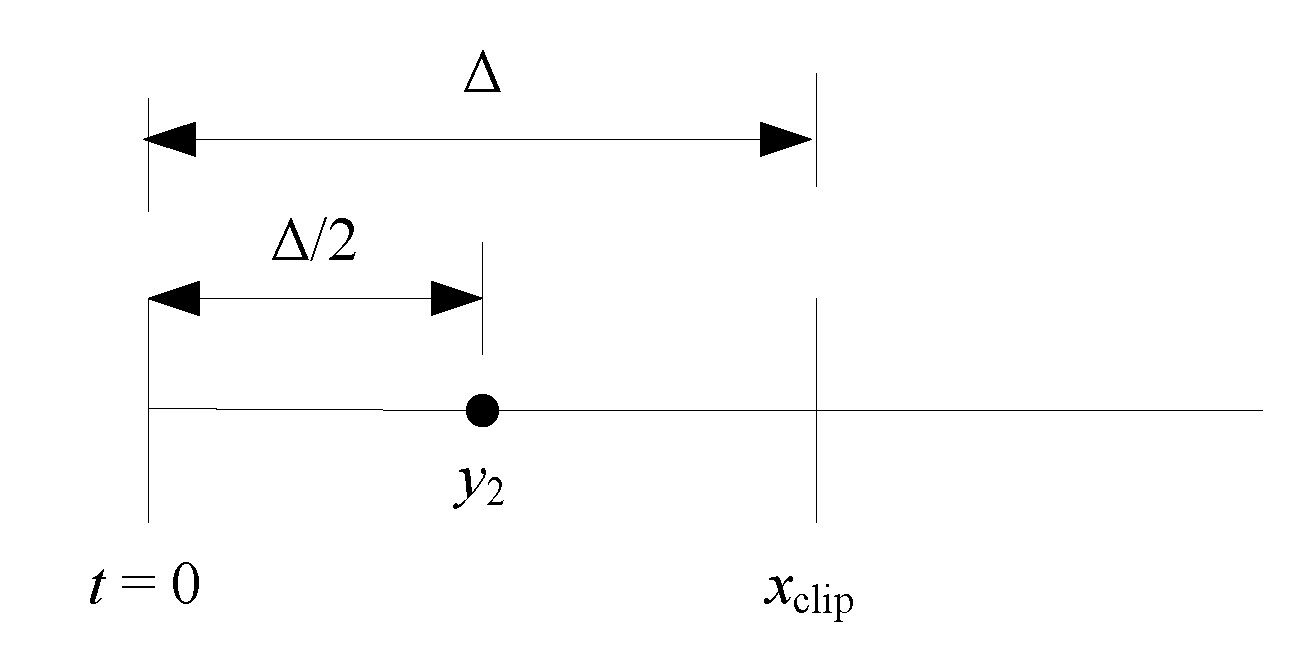
3.1. Binary Quantizer Type 1
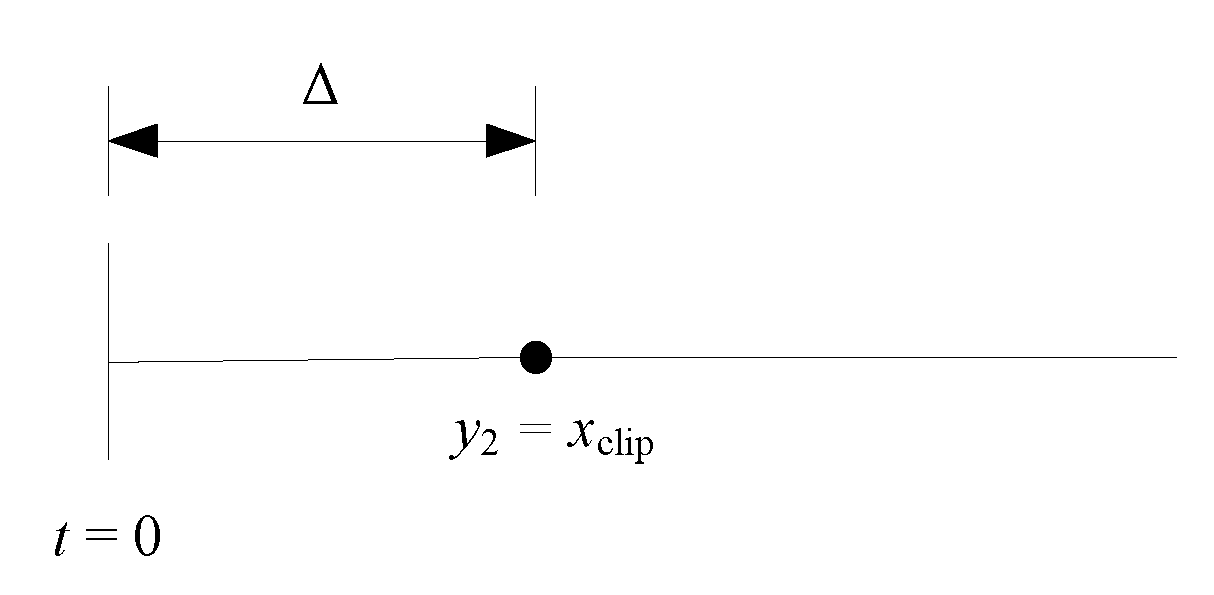
3.2. Binary Quantizer Type 2
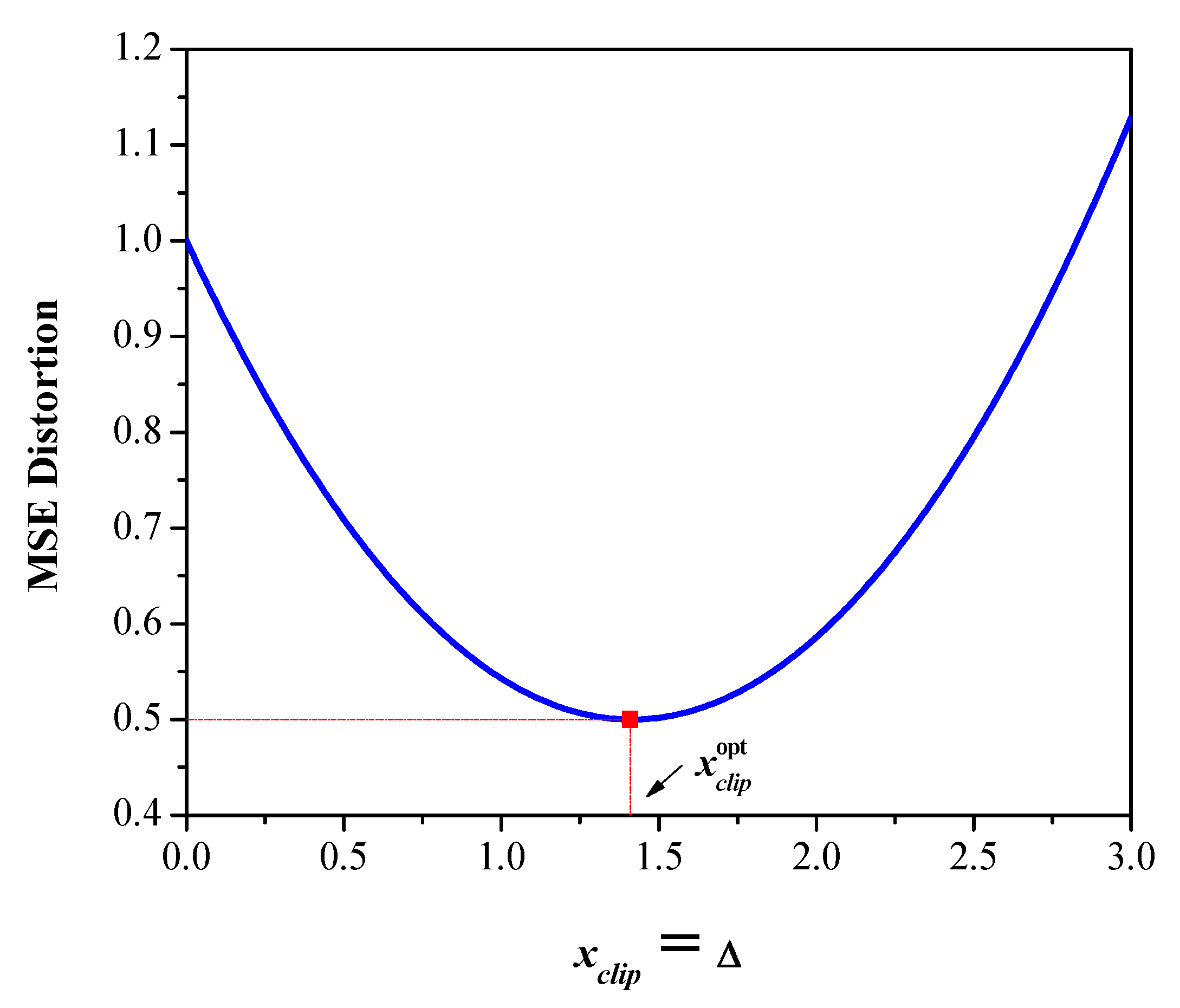
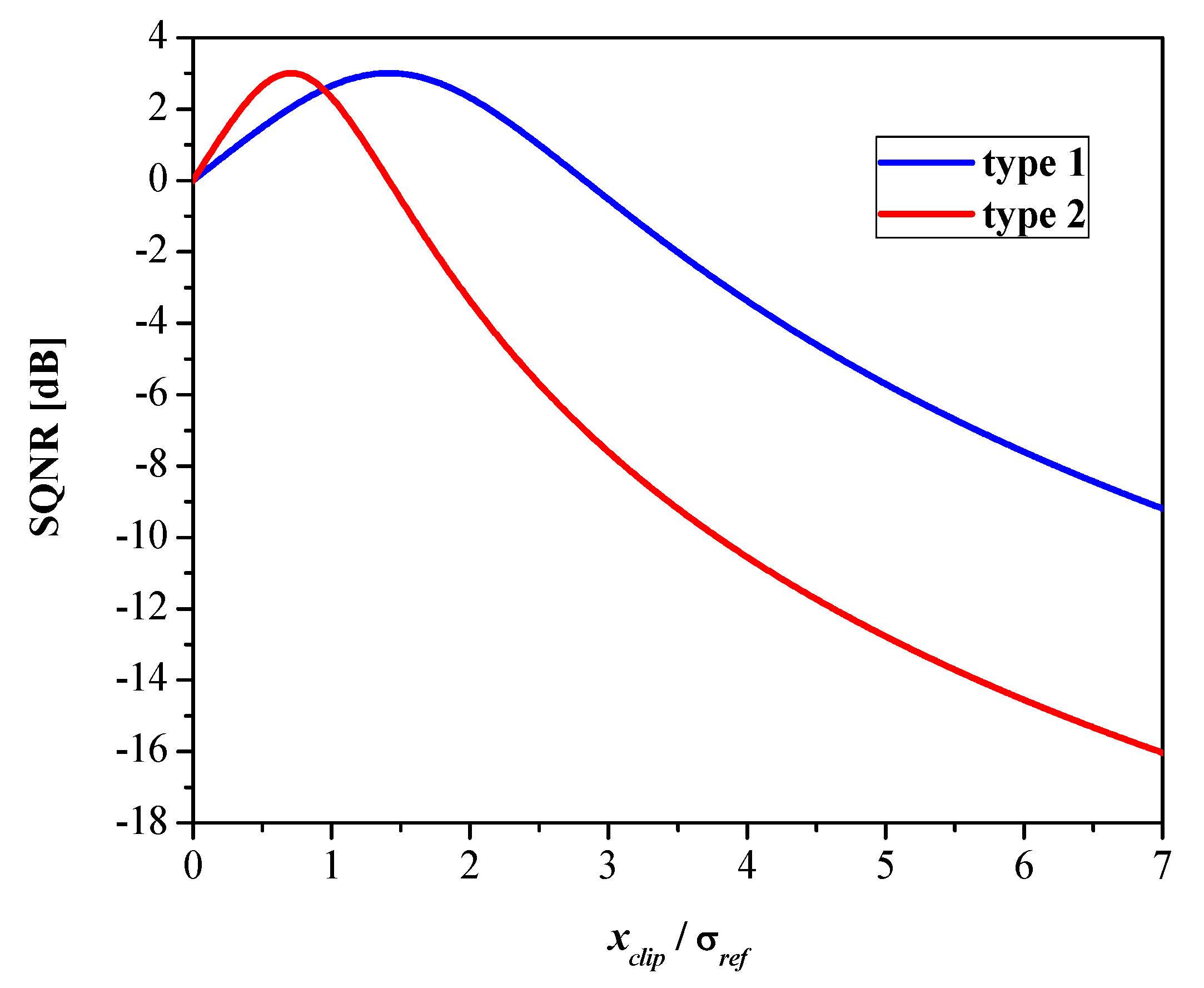
3.3. Quantizer Performance Evaluation
4. Analysis in a Wide Dynamic Range
5. Applications of Binary Quantizer
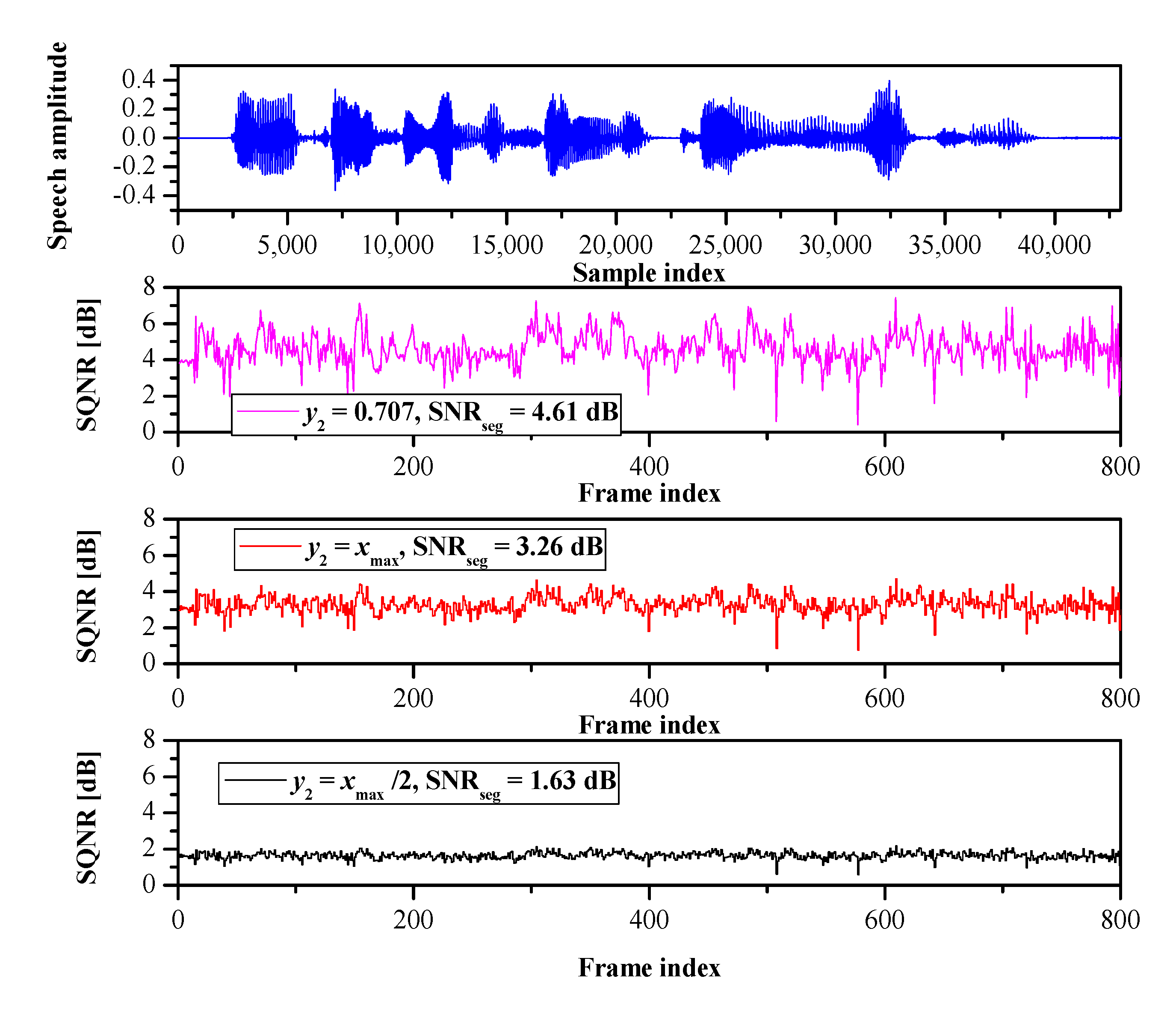
5.1. Speech Coding
5.1.1. PCM
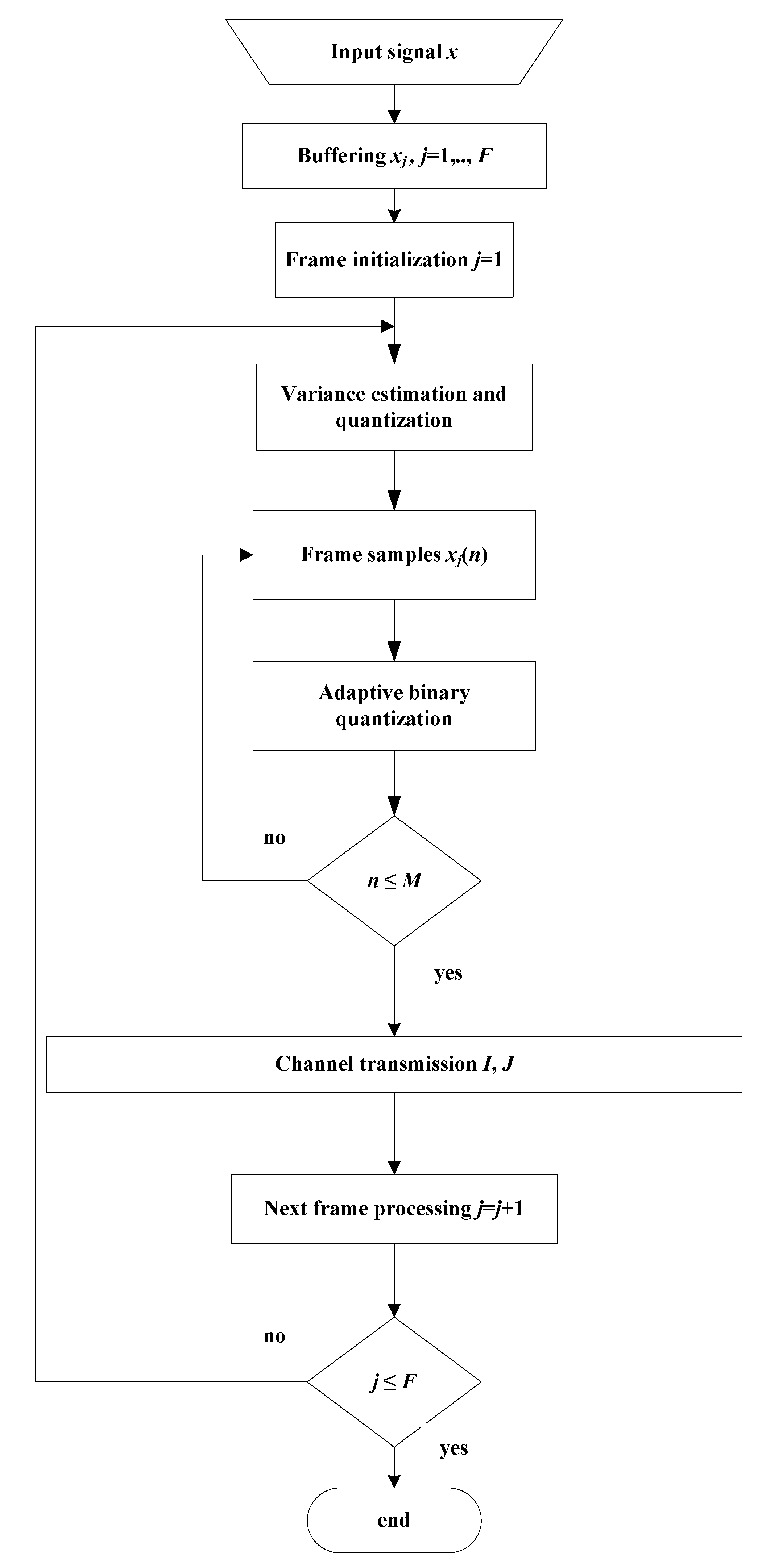
- Step 1. Buffering. A group of M consecutive samples (i.e., one frame, xj(n), n = 1, …, M, j = 1, ..., F), is stored within the buffer, where j is the frame index and F is the total number of frames.
- Step 2. Variance estimation and quantization. For the stored frame, the variance is estimated by the following equation [1,3,4,5]:The log-uniform quantizer is used for variance quantization, which performs uniform quantization in the logarithmic domain [3,4,5]. In particular, it quantizes the variance Vj (dB) = 10 logσj2 to one of L allowed values, defined aswhere ΔL = Vmax − Vmin /L denotes the step size and Vmax and Vmin denote the maximal and minimal estimated variance values. As this information is required at the decoder side, it has to be transmitted once per frame by the index J with log2L bits.
- Step 3. Adaptive binary quantization. An adaptive binary quantizer is obtained by multiplying the parameter of the binary quantizer designed for the reference variance value by factor g:where g is defined asEach frame sample is quantized using the adaptive binary quantizer, and the output is encoded with a one-bit codeword (index I).
- Step 4. Repeat all previous steps until all frames are processed.
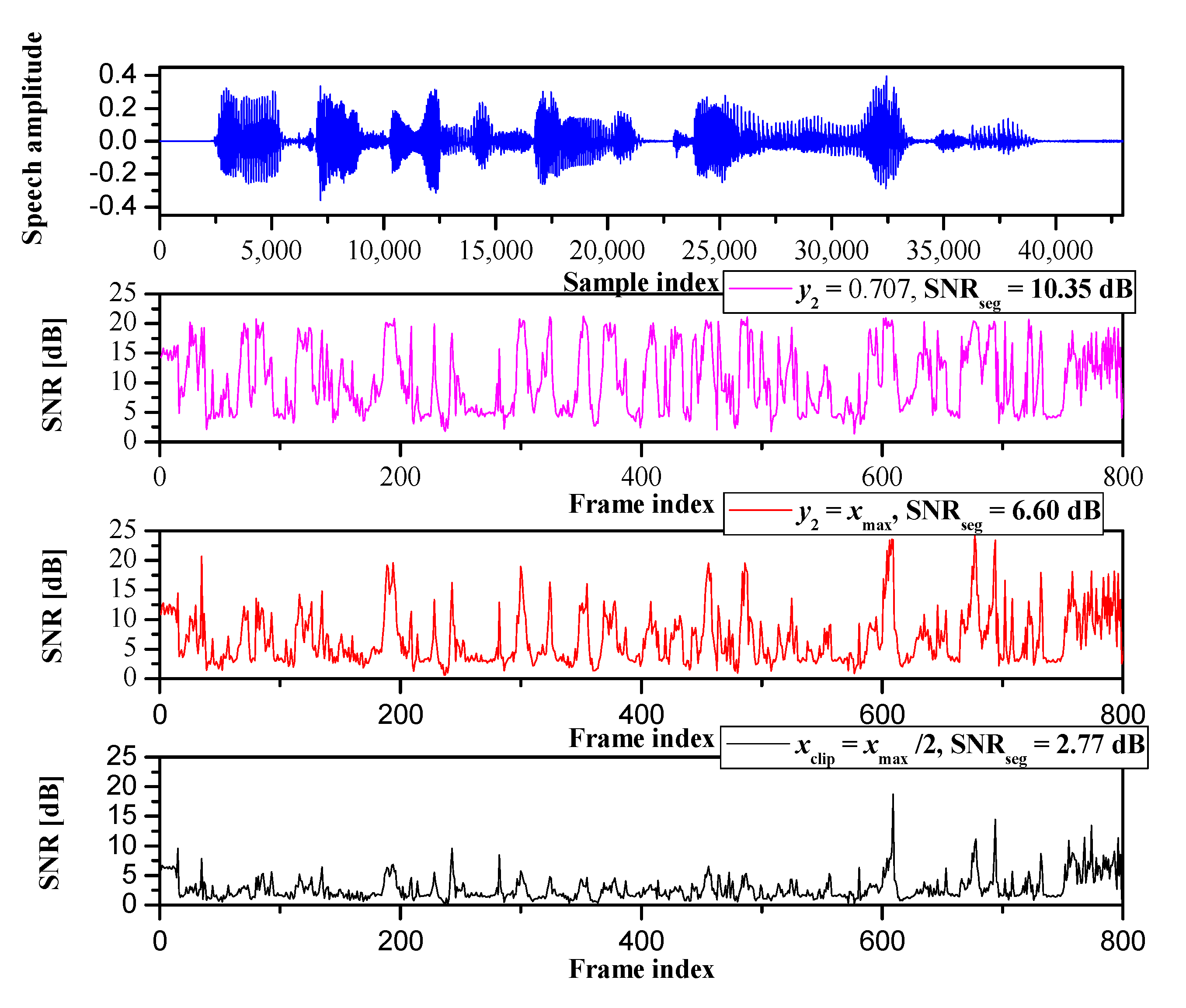
5.1.2. Delta Modulation
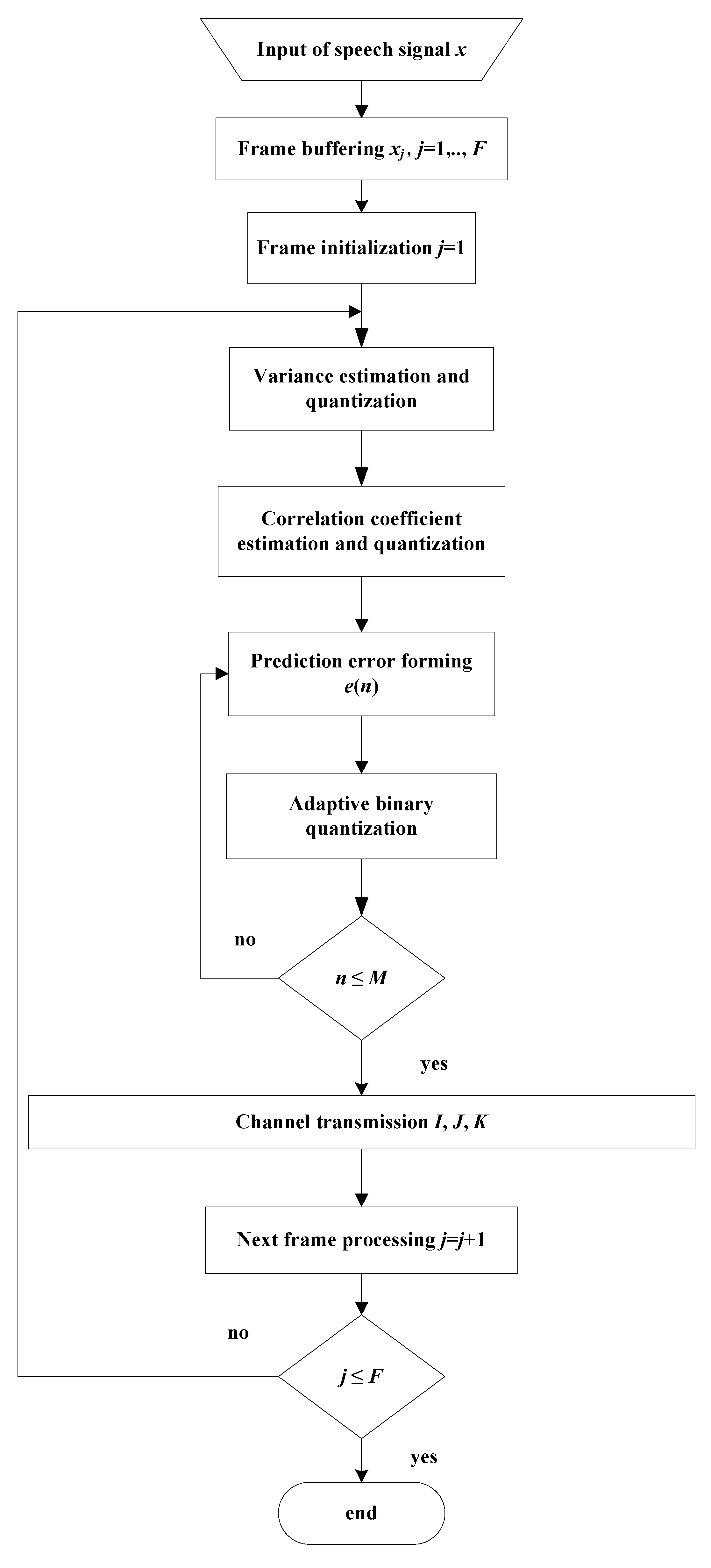
- Step 1. Buffering. This is the same as in Step 1 of the algorithm in Section 5.1.1.
- Step 2. Variance estimation and quantization. This is the same as in Step 2 of the algorithm in Section 5.1.1.
- Step 3. Estimation of the correlation coefficient and quantization. The correlation coefficient, denoted as ρ, for the current jth frame is estimated as [1,7,8,9]It is uniformly quantized to one of S available values, given bywhere Δρ = ρmax − ρmin/S denotes the step size and ρmax and ρmin denote the maximal and minimal estimated values of the correlation coefficient. This information is also required at the decoder side, and it has to be transferred once per frame by the index K with log2S bits.
- Step 4. Determination of the prediction error. For the jth frame, the prediction error can be determined according towhere xp(n) = ρk ∙ yj(n − 1) is the predicted sample value and yj(n) is the reconstructed value:where eq(n) is the quantized value of ej(n).
- Step 5. Adaptive binary quantization. For the jth frame, the scaling factor is given bywhere g is defined by Equation (17) and ρk is given by Equation (19). The adaptive representative level is obtained as in Equation (16).The prediction error signal was quantized using the adaptive binary quantizer and the output was encoded with a one-bit codeword (index I).
- Step 6. Repeat all previous steps until all frames are processed.
5.2. Image Coding
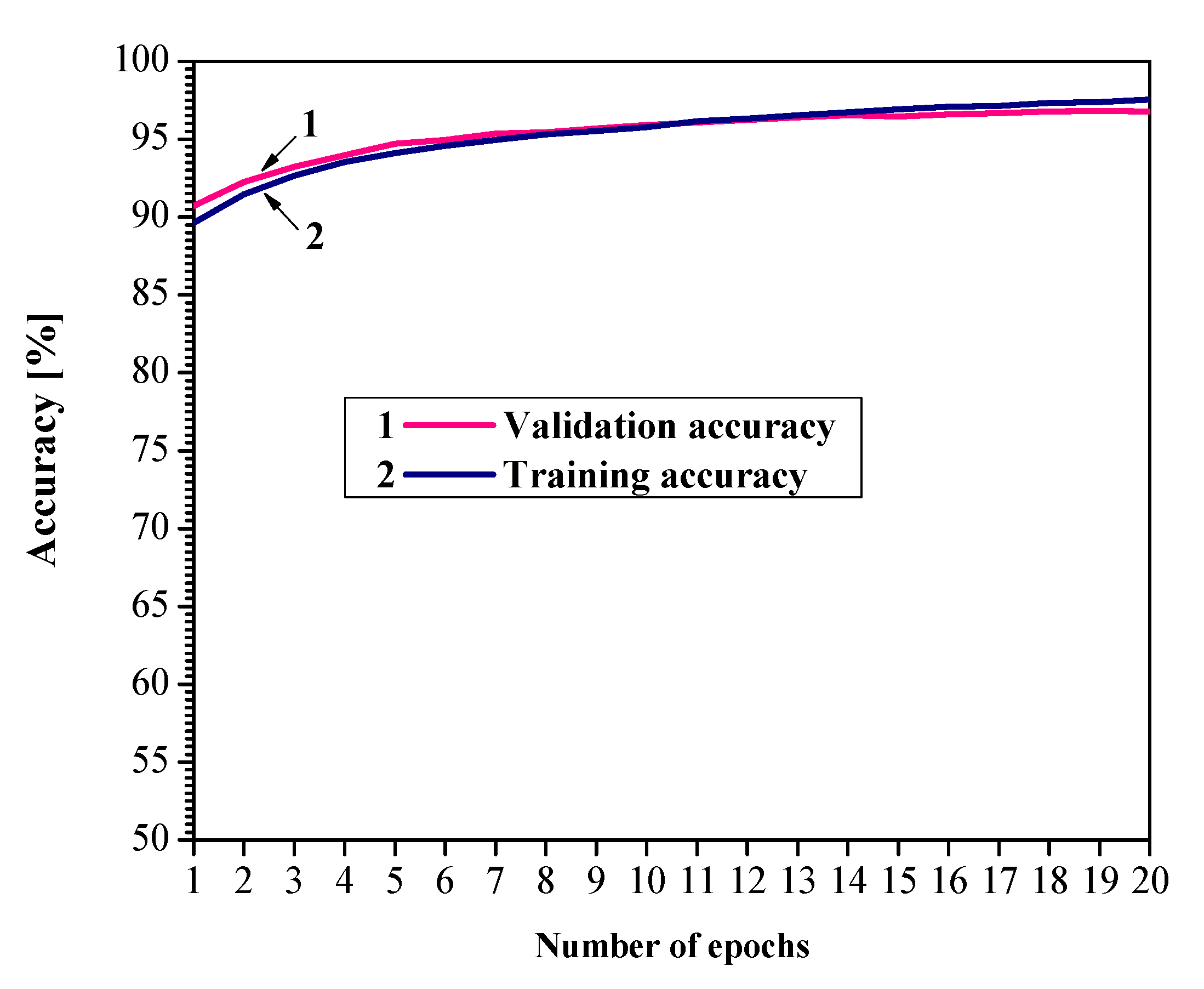
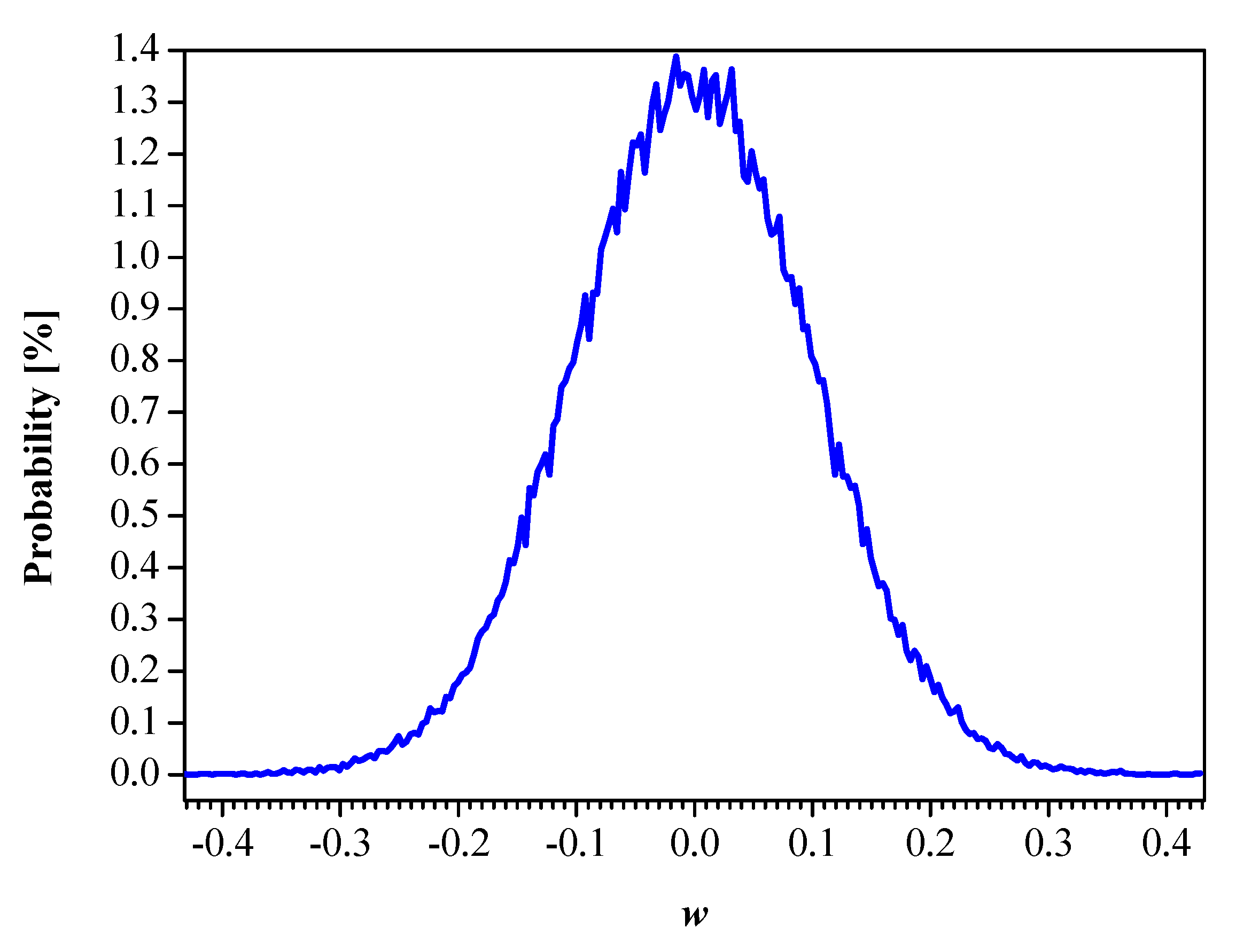
5.3. Neural Networks Compression
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jayant, N.C.; Noll, P. Digital Coding of Waveforms: Principles and Applications to Speech and Video; Prentice Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Gersho, A.; Gray, R. Vector Quantization and Signal Compression; Kluwer Academic Publishers: New York, NY, USA, 1992. [Google Scholar]
- Chu, W.C. Speech Coding Algorithms: Foundation and Evolution of Standardized Coders; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Peric, Z.; Nikolic, J.; Denic, B.; Despotovic, V. Forward adaptive dual-mode quantizer based on the first-degree spline approximation and embedded G.711 codec. Radioengineering 2019, 28, 729–739. [Google Scholar] [CrossRef]
- Nikolic, J.; Peric, Z. Lloyd-Max’s algorithm implementation in speech coding algorithm based on forward adaptive technique. Informatica 2008, 19, 255–270. [Google Scholar] [CrossRef]
- Prosalentis, E.A.; Tombras, G.S. 2-bit adaptive delta modulation system with improved performance. EURASIP J. Adv. Signal Proc. 2007, 2006, 16286. [Google Scholar] [CrossRef] [Green Version]
- Peric, Z.; Denic, B.; Despotovic, V. Novel two-bit adaptive delta modulation algorithms. Informatica 2019, 30, 117–134. [Google Scholar] [CrossRef]
- Peric, Z.; Denic, B.; Despotovic, V. An efficient two-digit adaptive delta modulation for Laplacian source coding. Int. J. Elect. 2019, 106, 1085–1100. [Google Scholar] [CrossRef]
- Denic, B.; Peric, Z.; Despotovic, V. Three-level delta modulation for Laplacian source coding. Adv. Elect. Comp. Eng. 2017, 17, 95–102. [Google Scholar] [CrossRef]
- Delp, E.J.; Saenz, M.; Salama, P. Block Truncation Coding (BTC). In Handbook of Image and Video Processing; Elsevier Academic Press: San Diego, CA, USA, 2005; pp. 661–670. [Google Scholar]
- Jiang, M.; Yang, H. Secure outsourcing algorithm of BTC feature extraction in cloud computing. IEEE Access 2020, 8, 106958–106967. [Google Scholar] [CrossRef]
- Simic, N.; Peric, Z.; Savic, M. Coding algorithm for grayscale images—Design of piecewise uniform quantizer with Golomb-Rice code and novel analytical model for performance analysis. Informatica 2017, 28, 703–724. [Google Scholar] [CrossRef]
- Savic, M.; Peric, Z.; Dincic, M. Coding algorithm for grayscale images based on piecewise uniform quantizers. Informatica 2012, 23, 125–140. [Google Scholar] [CrossRef]
- Huang, K.; Ni, B.; Yang, X. Efficient quantization for neural networks with binary weights and low bitwidth activations. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (AAAI-19), Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Nia, V.P.; Belbahr, M. Binary quantizer. J. Comput. Vis. Imaging Syst. 2018, 4, 3. [Google Scholar]
- Qina, H.; Gonga, R.; Liu, X.; Baie, X.; Songc, J.; Sebed, N. Binary neural networks: A survey. arXiv 2020, arXiv:2004.03333. [Google Scholar] [CrossRef] [Green Version]
- Pouransari, H.; Tu, Z.; Tuzel, O. Least squares binary quantization of neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14−19 June 2020. [Google Scholar]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks: Training neural networks with weights and activations constrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5−10 December 2016. [Google Scholar]
- Simons, T.; Lee, D.J. A review of binarized neural networks. Electronics 2019, 8, 661. [Google Scholar] [CrossRef] [Green Version]
- Darabi, S.; Belbahri, M.; Courbariaux, M.; Nia, V.P. Regularized binary network training. arXiv 2018, arXiv:1812.11800. [Google Scholar]
- Gazor, S.; Zhang, W. Speech probability distribution. IEEE Signal Proc. Lett. 2003, 10, 204–207. [Google Scholar] [CrossRef]
- Banner, R.; Nahshan, Y.; Hoffer, E.; Soudry, D. ACIQ: Analytical clipping for integer quantization of neural networks. arXiv 2018, arXiv:1810.05723. [Google Scholar]
- Banner, R.; Nahshan, Y.; Soudry, D. Post training 4-bit quantization of convolutional networks for rapid-deployment. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8−10 December 2019. [Google Scholar]
- Zrilic, D.G. Circuits and Systems Based on Delta Modulation; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gibson, J.D. Speech compression. Information 2016, 7, 32. [Google Scholar] [CrossRef] [Green Version]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-onlyinference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18−23 June 2018. [Google Scholar]
- Gong, J.; Shen, H.; Zhang, G.; Liu, X.; Li, S.; Jin, G.; Maheshwari, N.; Fomenko, E.; Segal, E. Highly efficient 8-bit low precision inference of convolutional neural networks with IntelCaffe. arXiv 2018, arXiv:1805.08691. [Google Scholar]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: Awhitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar]
- McKinstry, J.L.; Esser, S.K.; Appuswamy, R.; Bablani, D.; Arthur, J.V.; Yildiz, I.B.; Modha, D.S. Discovering low-precision networks close to full-precision networks for efficient embedded inference. arXiv 2018, arXiv:1809.04191. [Google Scholar]
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.I.; Srinivasan, V.; Gopalakrishnan., K. Pact: Parameterized clipping activation for quantized neural networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Ullah, I.; Manzo, M.; Shah, M.; Madden, M. Graph Convolutional Networks: Analysis, improvements and results. arXiv 2019, arXiv:1912.09592. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized neural networks: Training neural networks with low precision weights and activations. J. Mach. Learn. Res. 2018, 18, 1–30. [Google Scholar]
- Tkachenko, R.; Izonin, I.; Kryvinska, N.; Dronyuk, I.; Zub, K. An approach towards increasing prediction accuracy for the recovery of missing IoT data based on the GRNN-SGTM ensemble. Sensors 2020, 20, 2625. [Google Scholar] [CrossRef] [PubMed]
- Tkachenko, R.; Izonin, I. Model and principles for the implementation of neural-like structures based on geometric data transformations. In Proceedings of the International Conference on Computer Science (ICCSEEA 2018) AISC Series; Springer: Cham, Switzerland, 2019; Volume 754, pp. 578–587. [Google Scholar]
- Na, S. Asymptotic formulas for mismatched fixed-rate minimum MSE Laplacian quantizers. IEEE Signal Proc. Lett. 2008, 15, 13–16. [Google Scholar]
- Demonte, P.; HARVARD Speech Corpus—Audio Recording 2019. University of Salford Collection. 2019. Available online: https://doi.org/10.17866/rd.salford.c.4437578.v1 (accessed on 1 September 2020).
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database (accessed on 1 September 2020).
- Lecun, Y.; Cortez, C.; Burges, C. The MNIST Handwritten Digit Database. Available online: yann.lecun.com (accessed on 1 September 2020).





| Block | Block | |||||
|---|---|---|---|---|---|---|
| 4 × 4 | 8 × 8 | |||||
| rσ | 8 | 5 | 4 | 8 | 5 | 4 |
| rsr | 8 | 5 | 4 | 8 | 5 | 4 |
| PSQNR (dB) | 32.06 | 31.84 | 31.37 | 28.59 | 28.47 | 28.18 |
| R (bpp) | 2 | 1.5 | 1.625 | 1.25 | 1.16 | 1.125 |
| Block | 4 × 4 | ||
|---|---|---|---|
| rσ | 8 | 8 | 8 |
| rsr | 8 | 8 | 8 |
| y2 | 1.5 | 3 | |
| PSQNR (dB) | 32.06 | 28.69 | 20.87 |
| R (bpp) | 2 | 2 | 2 |
| Y2 | Full Precision | |||
|---|---|---|---|---|
| xmax/2 (Type 1) | xmax (Type 2) | |||
| Accuracy (%) | 91.28 | 81.66 | 89.96 | 96.70 |
| SQNR (dB) | 4.287 | 1.636 | 3.205 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peric, Z.; Denic, B.; Savic, M.; Despotovic, V. Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications. Information 2020, 11, 501. https://doi.org/10.3390/info11110501
Peric Z, Denic B, Savic M, Despotovic V. Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications. Information. 2020; 11(11):501. https://doi.org/10.3390/info11110501
Chicago/Turabian StylePeric, Zoran, Bojan Denic, Milan Savic, and Vladimir Despotovic. 2020. "Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications" Information 11, no. 11: 501. https://doi.org/10.3390/info11110501
APA StylePeric, Z., Denic, B., Savic, M., & Despotovic, V. (2020). Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications. Information, 11(11), 501. https://doi.org/10.3390/info11110501







