A GARCH Model with Artificial Neural Networks
Abstract
1. Introduction
2. GARCH–ANN Construction
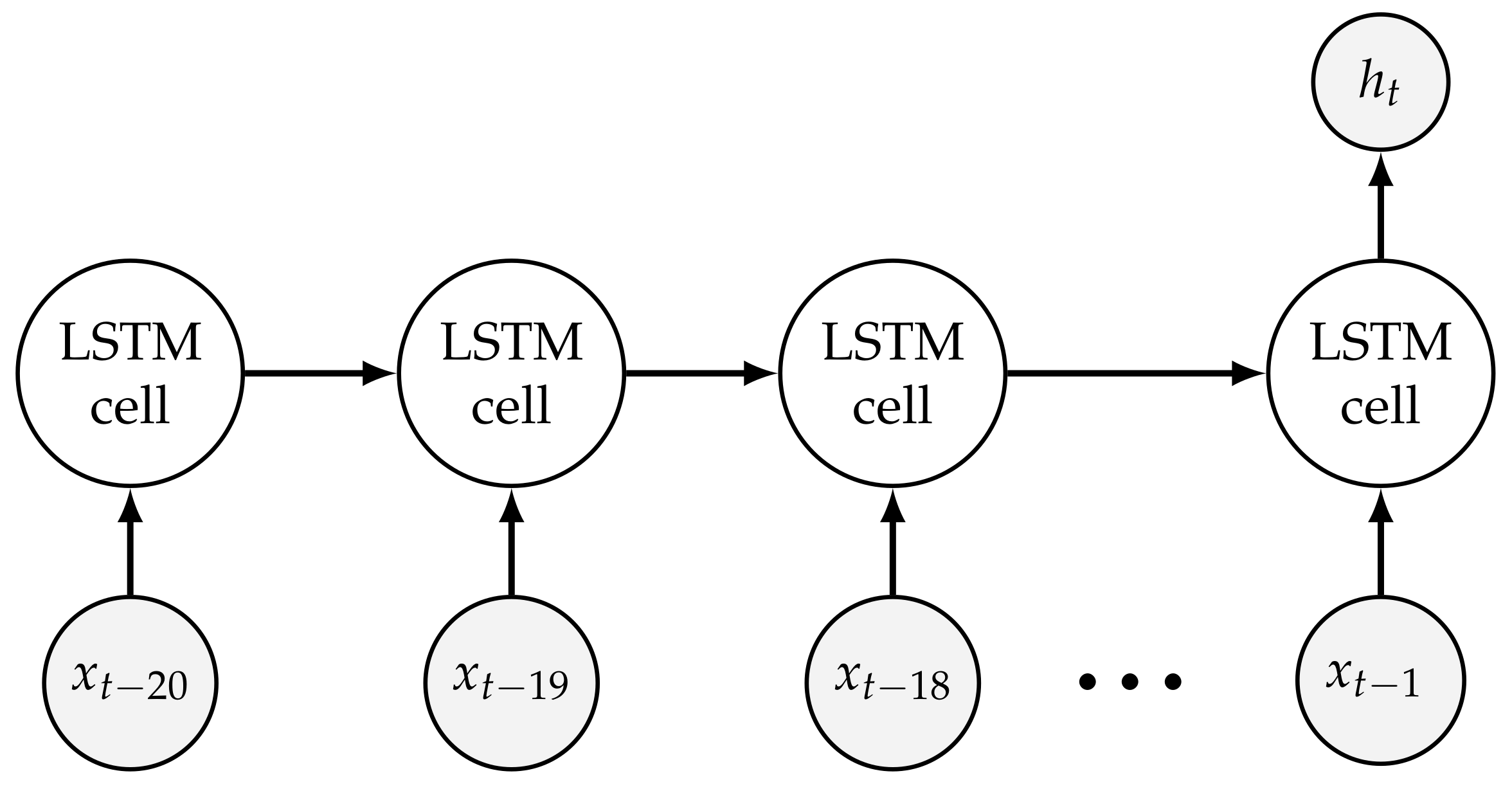
2.1. Network Architecture
2.2. Objective Function
3. Data Processing
- Read the data by pandas in Python.
- Normalize the data set. Assume that x is a vector. We normalize it by
- Create the instances by labeling the data on the previous 20 days as the input and labeling the current return as the target variable.
- Create the training instances (90%) and testing instances (10%).
- Shuffle the training instances.
4. Training
- The instances during training are split into batches with size 500 for optimization.
- The optimization algorithm is Adam [30].
- The number of epochs it can tolerate for no improvement is 10.
- The maximum number of epochs is 1000.
5. Empirical Results
- Forecast one-step ahead .
- Out-of-the-sample mean absolute error (MAE) is computed by the equation:
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bollerslev, T. A conditionally heteroskedastic time series model for speculative prices and rates of return. Rev. Econ. Stat. 1987, 69, 542. [Google Scholar] [CrossRef]
- Nikolaev, N.; Tino, P.; Smirnov, E. Time-dependent series variance learning with recurrent mixture density networks. Neurocomputing 2013, 122, 501–512. [Google Scholar] [CrossRef]
- So, M.K.P.; Yu, P.L.H. Empirical analysis of GARCH models in value at risk estimation. J. Int. Financ. Mark. Inst. Money 2006, 16, 180–197. [Google Scholar] [CrossRef]
- So, M.K.P.; Wong, C.M. Estimation of multiple period expected shortfall and median shortfall for risk management. Quant. Financ. 2012, 12, 739–754. [Google Scholar] [CrossRef]
- Chen, C.W.S.; So, M.K.P. On a threshold heteroscedastic model. Int. J. Forecast. 2006, 22, 73–89. [Google Scholar] [CrossRef]
- Chen, C.W.S.; So, M.K.P.; Lin, E.M.H. Volatility forecasting with double Markov switching GARCH models. J. Forecast. 2009, 28, 681–697. [Google Scholar] [CrossRef]
- So, M.; Xu, R. Forecasting intraday volatility and value-at-risk with high-frequency Data. Asia Pac. Financ. Mark. 2013, 20, 83–111. [Google Scholar] [CrossRef]
- Efimova, O.; Serletis, A. Energy markets volatility modelling using GARCH. Energy Econ. 2014, 43, 264–273. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Gold price volatility: A forecasting approach using the Artificial Neural Network–GARCH model. Expert Syst. Appl. 2015, 42, 7245–7251. [Google Scholar] [CrossRef]
- Zhipeng, Y.; Shenghong, L. Hedge ratio on Markov regime-switching diagonal Bekk–Garch model. Financ. Res. Lett. 2018, 24, 199–220. [Google Scholar] [CrossRef]
- Escobar-Anel, M.; Rastegari, J.; Stentoft, L. Option pricing with conditional GARCH models. Eur. J. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Mercuri, L. Option pricing in a Garch model with tempered stable innovations. Financ. Res. Lett. 2008, 5, 172–182. [Google Scholar] [CrossRef]
- Nikolaev, N.; Tino, P.; Smirnov, E. Time-dependent series variance estimation via recurrent neural networks. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Taiyuan, China, 24–25 September 2011; Volume 6791, pp. 176–184. [Google Scholar]
- Kristjanpoller, W.; Minutolo, M.C. Forecasting volatility of oil price using an artificial neural network-GARCH model. Expert Syst. Appl. 2016, 65, 233–241. [Google Scholar] [CrossRef]
- Liu, H.; Li, R.; Yuan, J. Deposit insurance pricing under GARCH. Financ. Res. Lett. 2018, 26, 242–249. [Google Scholar] [CrossRef]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Ardia, D.; Bluteau, K.; Rüede, M. Regime changes in Bitcoin GARCH volatility dynamics. Financ. Res. Lett. 2019, 29, 266–271. [Google Scholar] [CrossRef]
- Cheikh, N.B.; Zaied, Y.B.; Chevallier, J. Asymmetric volatility in cryptocurrency markets: New evidence from smooth transition GARCH models. Financ. Res. Lett. 2020, 35, 101293. [Google Scholar] [CrossRef]
- Heaton, J.B.; Polson, N.G.; Witte, J.H. Deep Learning in Finance. arXiv 2016, arXiv:1602.06561. [Google Scholar]
- Chen, L.; Pelger, M.; Zhu, J. Deep Learning in Asset Pricing. SSRN Electron. J. 2019. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Chen, R.; Li, X.; Hao, C.; Liu, S.; Zhang, G.; Jiang, B. Online At-Risk Student Identification Using RNN-GRU Joint Neural Networks. Information 2020, 11, 474. [Google Scholar] [CrossRef]
- Feng, G.; He, J.; Polson, N.G. Deep learning for predicting asset returns. IDEAS Working Paper Series from RePEc. arXiv 2018, arXiv:1804.09314. [Google Scholar]
- Dugas, C.; Bengio, Y.; Bélisle, F.; Nadeau, C.; Garcia, R. Incorporating second-order functional knowledge for better option pricing. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Senior, A.; Lei, X. Fine context, low-rank, softplus deep neural networks for mobile speech recognition. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 7644–7648. [Google Scholar] [CrossRef]
- Shavit, G. Neural Network Including Input Normalization for Use in a Closed Loop Control System. U.S. Patent 6,078,843, 20 June 2000. [Google Scholar]
- Jayalakshmi, T.; Santhakumaran, A. Statistical Normalization and Back Propagationfor Classification. Int. J. Comput. Theory Eng. 2011, 3, 89–93. [Google Scholar] [CrossRef]
- Yin, Z.; Wan, B.; Yuan, F.; Xia, X.; Shi, J. A deep normalization and convolutional neural network for image smoke detection. IEEE Access 2017, 5, 18429–18438. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Yoshua, B.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning. Coursera, video lectures 2012, 265. Available online: https://www.coursera.org/learn/neural-networks-deep-learning (accessed on 3 October 2020).
- Forsberg, L.; Ghysels, E. Why do absolute returns predict volatility so well? J. Financ. Econom. 2007, 5, 31–67. [Google Scholar] [CrossRef]
- Winkelbauer, A. Moments and Absolute Moments of the Normal Distribution. arXiv 2012, arXiv:1209.4340. [Google Scholar]
- Sheppard, K.; Khrapov, S.; Lipták, G.; Mikedeltalima; Capellini, R.; Hugle; Esvhd; Fortin, A.; JPN; Adams, A.; et al. bashtage/arch: Release 4.15. 2020. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Korobov, M.; Lopuhin, K. ELI5. 2016. Available online: https://eli5.readthedocs.io/en/latest/index.html## (accessed on 20 October 2020).
- Pedregosa, F.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
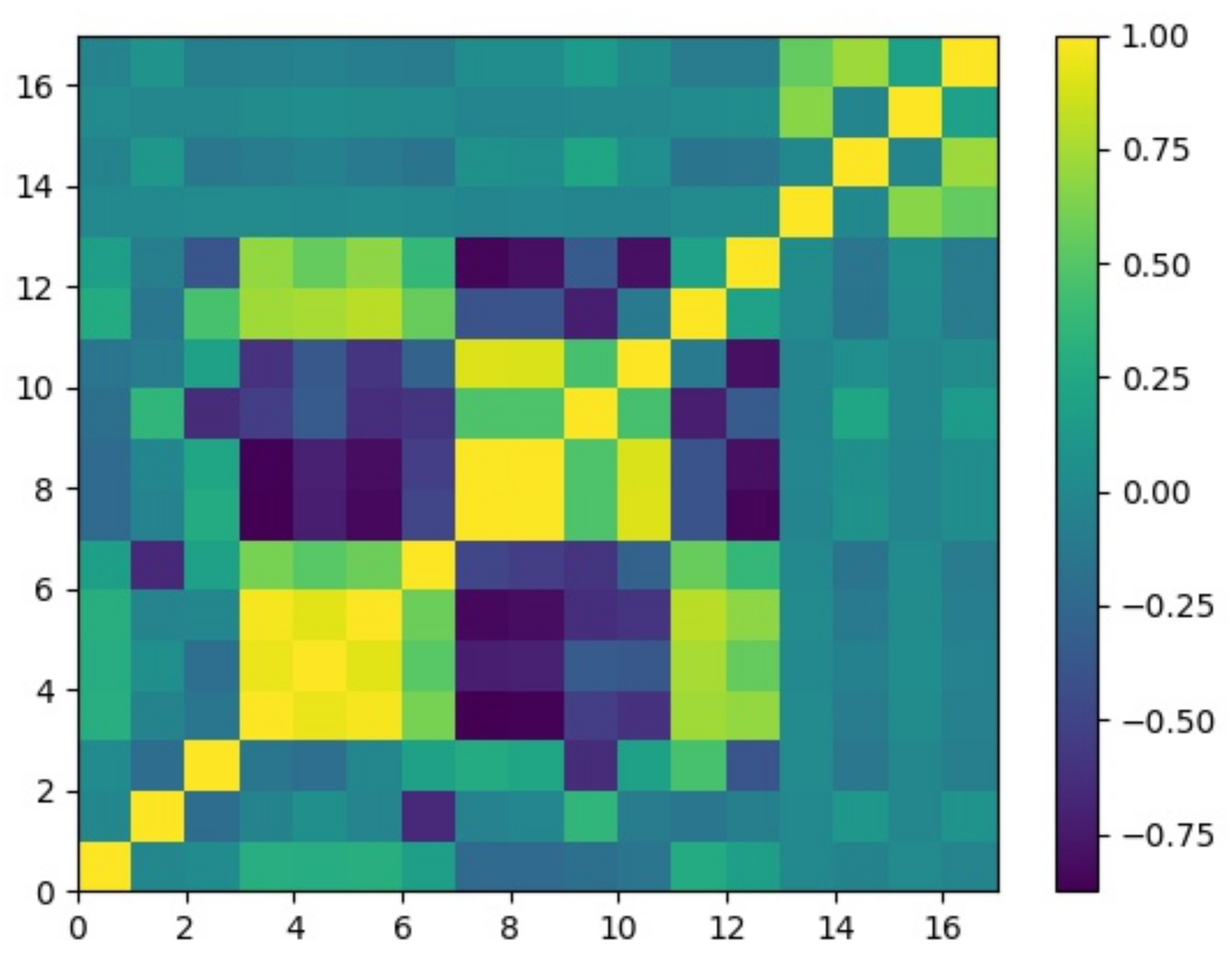

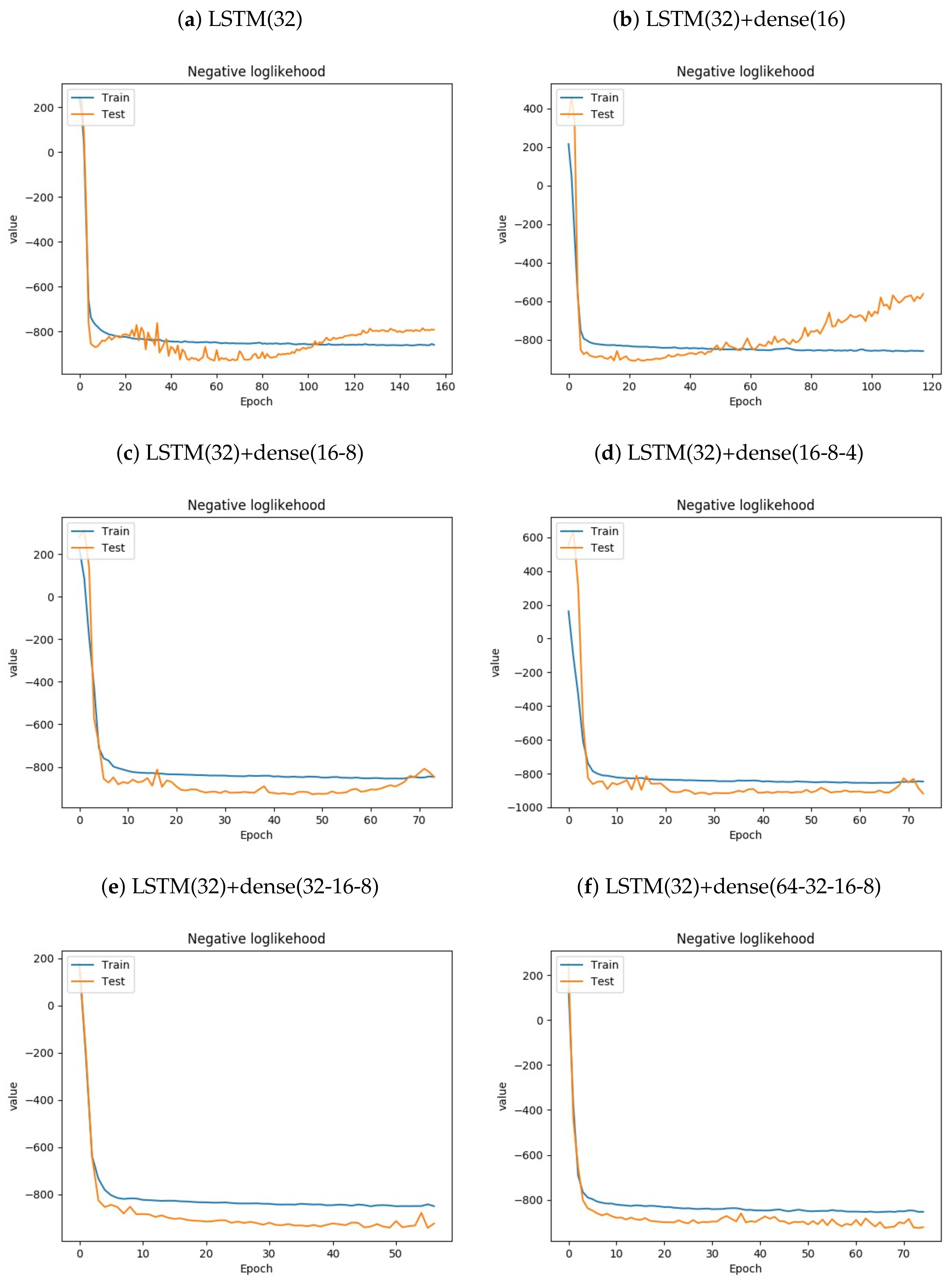


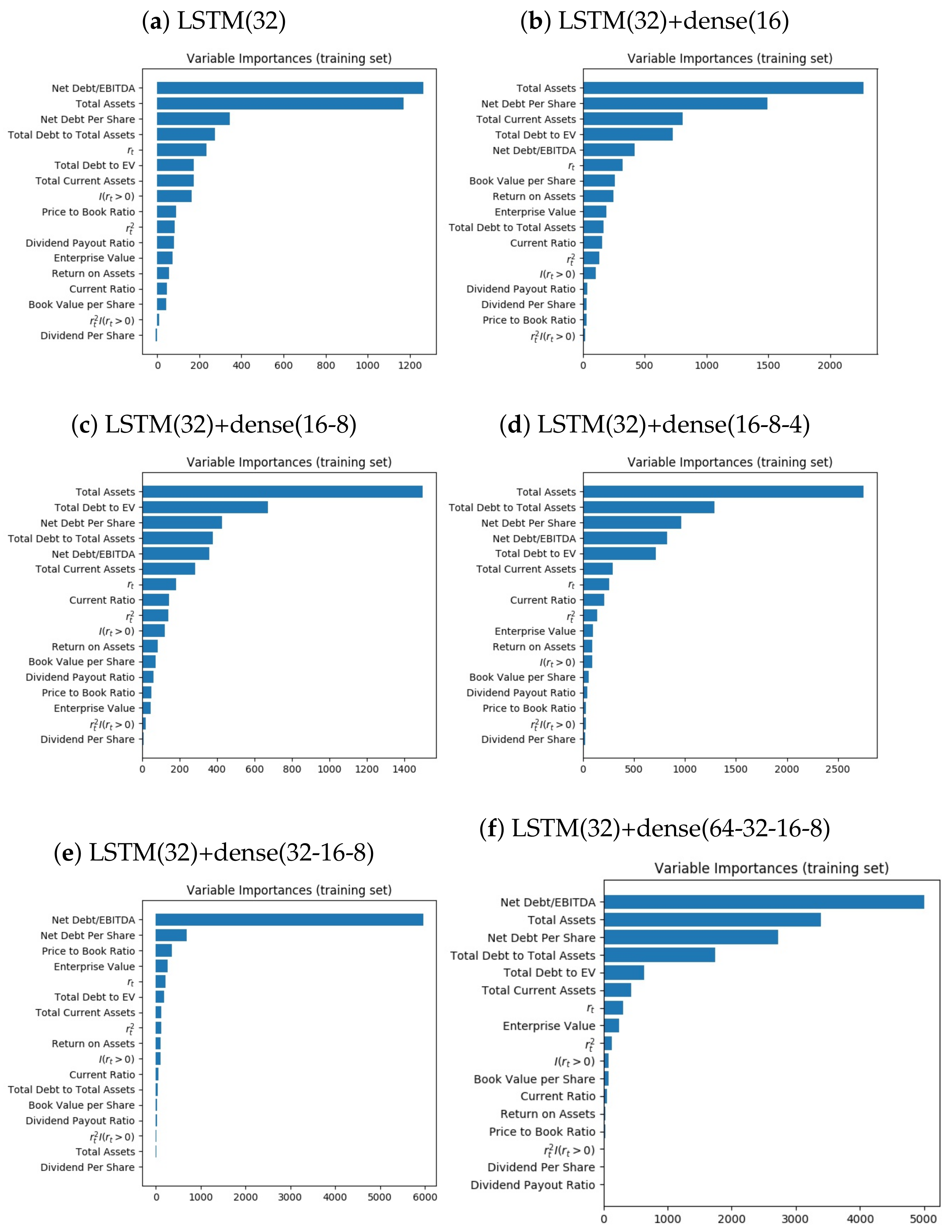
| Variables | Mean | SD | Min | Q1 | Q2 | Q3 | Max |
|---|---|---|---|---|---|---|---|
| Dividend Per Share | 0.12 | 0.17 | 0.00 | 0.01 | 0.05 | 0.17 | 1.48 |
| Dividend Payout Ratio | 47.07 | 17.96 | 31.76 | 37.06 | 40.98 | 50.93 | 149.44 |
| Price to Book Ratio | 2.82 | 0.60 | 1.45 | 2.42 | 2.80 | 3.12 | 5.18 |
| Book Value per Share | 569.11 | 178.44 | 294.92 | 419.68 | 531.66 | 734.31 | 909.82 |
| Total Assets | 2963.16 | 671.13 | 1697.03 | 2490.23 | 2993.91 | 3439.50 | 4289.84 |
| Total Current Assets | 414.51 | 111.10 | 248.15 | 327.81 | 374.38 | 511.33 | 638.52 |
| Return on Assets | 2.48 | 0.79 | 0.47 | 2.23 | 2.79 | 3.06 | 3.46 |
| Total Debt to Total Assets | 31.08 | 6.05 | 23.33 | 25.02 | 29.78 | 37.53 | 39.40 |
| Net Debt/EBITDA | 2.87 | 1.38 | 1.04 | 1.52 | 2.42 | 4.30 | 4.93 |
| Total Debt to EV | 0.45 | 0.11 | 0.28 | 0.35 | 0.46 | 0.51 | 0.84 |
| Net Debt Per Share | 500.11 | 209.89 | 214.27 | 318.64 | 467.07 | 639.34 | 960.83 |
| Enterprise Value | 2074.31 | 587.25 | 1069.78 | 1635.50 | 1935.85 | 2356.26 | 3929.46 |
| Current Ratio | 1.29 | 0.11 | 1.04 | 1.18 | 1.32 | 1.38 | 1.45 |
| 0.02 | 1.19 | −9.03 | −0.47 | 0.06 | 0.57 | 11.58 | |
| 1.41 | 4.65 | 0.00 | 0.05 | 0.28 | 1.10 | 134.10 | |
| 0.53 | 0.50 | 0.00 | 0.00 | 1.00 | 1.00 | 1.00 | |
| 0.70 | 3.51 | 0.00 | 0.00 | 0.00 | 0.32 | 134.10 |
| Architecture | |||
|---|---|---|---|
| LSTM(32) | 0.0293 | 0.0102 | 0.0036 |
| LSTM(32)+dense(16) | 0.1163 | 0.0843 | 0.0702 |
| LSTM(32)+dense(16-8) | 0.0290 | 0.0107 | 0.0042 |
| LSTM(32)+dense(16-8-4) | 0.0204 | 0.0064 | 0.0020 |
| LSTM(32)+dense(32-16-8) | 0.0195 | 0.0060 | 0.0019 |
| LSTM(32)+dense(64-32-16-8) | 0.0209 | 0.0067 | 0.0022 |
| GARCH-t(1,1) | 0.0221 | 0.0073 | 0.0021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.K.; So, M.K.P. A GARCH Model with Artificial Neural Networks. Information 2020, 11, 489. https://doi.org/10.3390/info11100489
Liu WK, So MKP. A GARCH Model with Artificial Neural Networks. Information. 2020; 11(10):489. https://doi.org/10.3390/info11100489
Chicago/Turabian StyleLiu, Wing Ki, and Mike K. P. So. 2020. "A GARCH Model with Artificial Neural Networks" Information 11, no. 10: 489. https://doi.org/10.3390/info11100489
APA StyleLiu, W. K., & So, M. K. P. (2020). A GARCH Model with Artificial Neural Networks. Information, 11(10), 489. https://doi.org/10.3390/info11100489






