Recursive Matrix Calculation Paradigm by the Example of Structured Matrix
Abstract
1. Introduction
- We derive recursive algorithms for calculating the determinant and inverse of the generalized Vandermonde matrix.
- The importance of the recursive algorithms becomes clear when we consider practical implementation of the GVM; they are useful each time we add a new interpolation node or a new root of a given differential equation in question.
- The recursive algorithms, which we propose in this work, can allow avoiding the recalculation of the determinant and/or inverse.
- The main advantage of the recursive algorithms is the fact that the computational complexity of the presented algorithm is of the O(n) class for the computation of the determinant.
- The results of this article do not require any symbolic calculations and, therefore, can be performed by a numerical algorithm implemented in a high-level (like Matlab or Mathematica) or low-level programming language (C, C++, Java, Pascal, Fortran, etc.).
2. Practical Importance of the Generalized Vandermonde Matrix
- ▪
- Linear, ordinary differential equations (ODE): the Jordan canonical form matrix of the ODE in the Frobenius form is a generalized Vandermonde matrix ([8] pp. 86–95).
- ▪
- Control issues: investigating the so-called controllability [9] of the higher-order systems leads to the issue of inverting the classic Vandermonde matrix [10] (in the case of distinct zeros of the system characteristic polynomial) and the generalized Vandermonde matrix [11] (for systems with multiple characteristic polynomial zeros). As the examples of the higher-order models of the physical objects, we can mention Timoshenko’s elastic beam equation [12] (fourth order) and Korteweg-de Vries’s equation of waves on shallow water surfaces [13,14] (third, fifth, and seventh order).
- ▪
- Interpolation: apart from the ordinary polynomial interpolation with single nodes, we consider the Hermite interpolation, allowing multiple interpolation nodes. This issue leads to the system of linear equations, with the generalized Vandermonde matrix ([15] pp. 363–373).
- ▪
- Information coding: the generalized Vandermonde matrix is used in coding and decoding information in the Hermitian code [16].
- ▪
- Optimization of the non-homogeneous differential equation [17].
3. Algorithms for the Generalized Vandermonde Matrix Determinant
- (A)
- Suppose we have the value of the Vandermonde determinant for a given series of roots . How can we calculate the determinant after inserting another root into an arbitrary position in the root series, without the need to recalculate the whole determinant? This problem corresponds to the situation which frequently emerges in practice, i.e., adding a new node (polynomial interpolation) or increasing the order of the characteristic equation (linear differential equation solving, optimization, and control problems).
- (B)
- Contrary to the previous scenario, we have the Vandermonde determinant value for a given root series . We remove an arbitrary root from the series. How can we recursively calculate the determinant in this case? The examples of real applications from the previous point also apply here. The proper solution is given in Section 3.1.
- (C)
- We are searching for the determinant value, when, in the given root series , we change the value of an arbitrarily chosen root (Section 3.1).
- (D)
- We are searching for the determinant value, for the given root series , calculated recursively.
3.1. The Recursive Determinant Formula
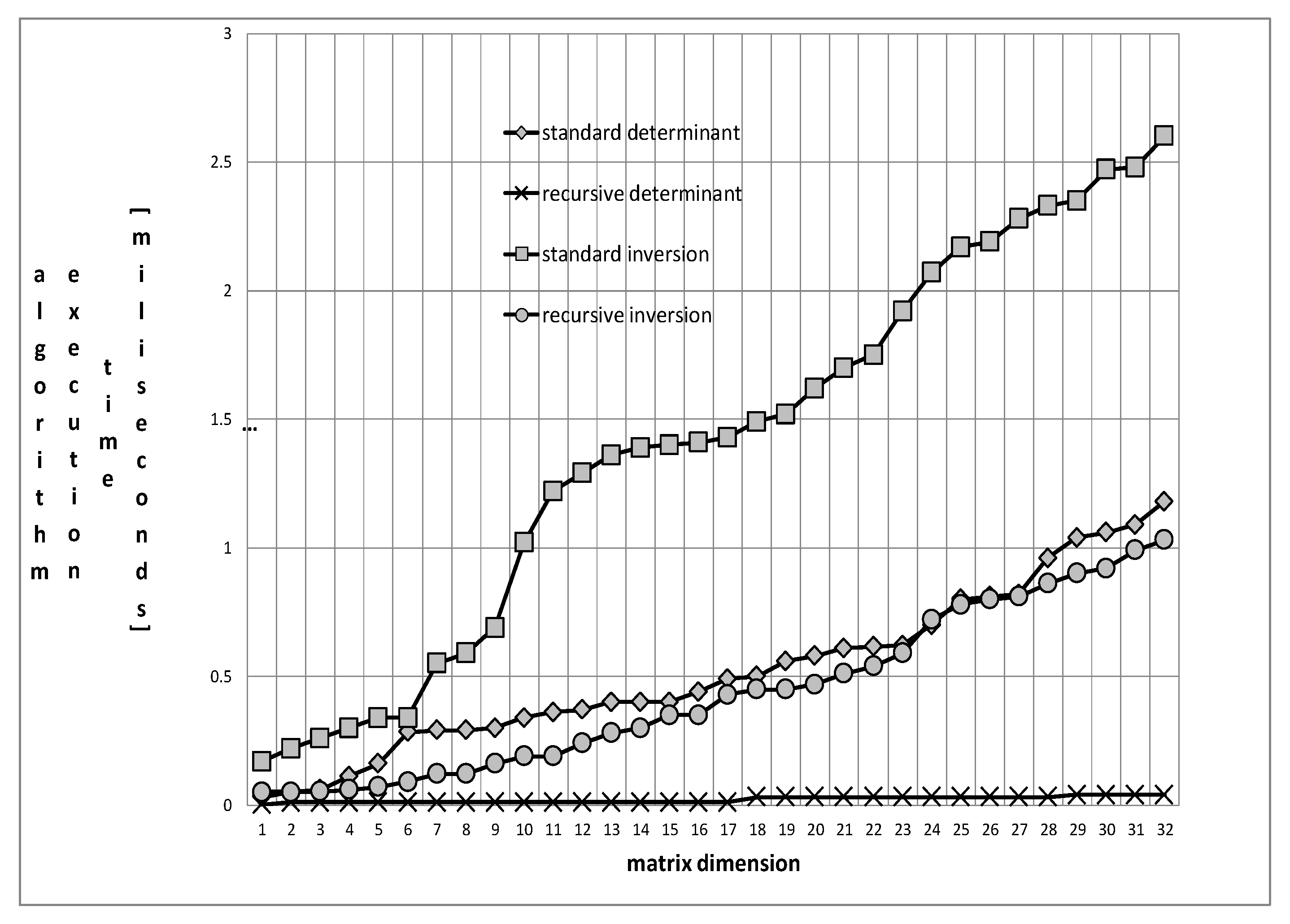
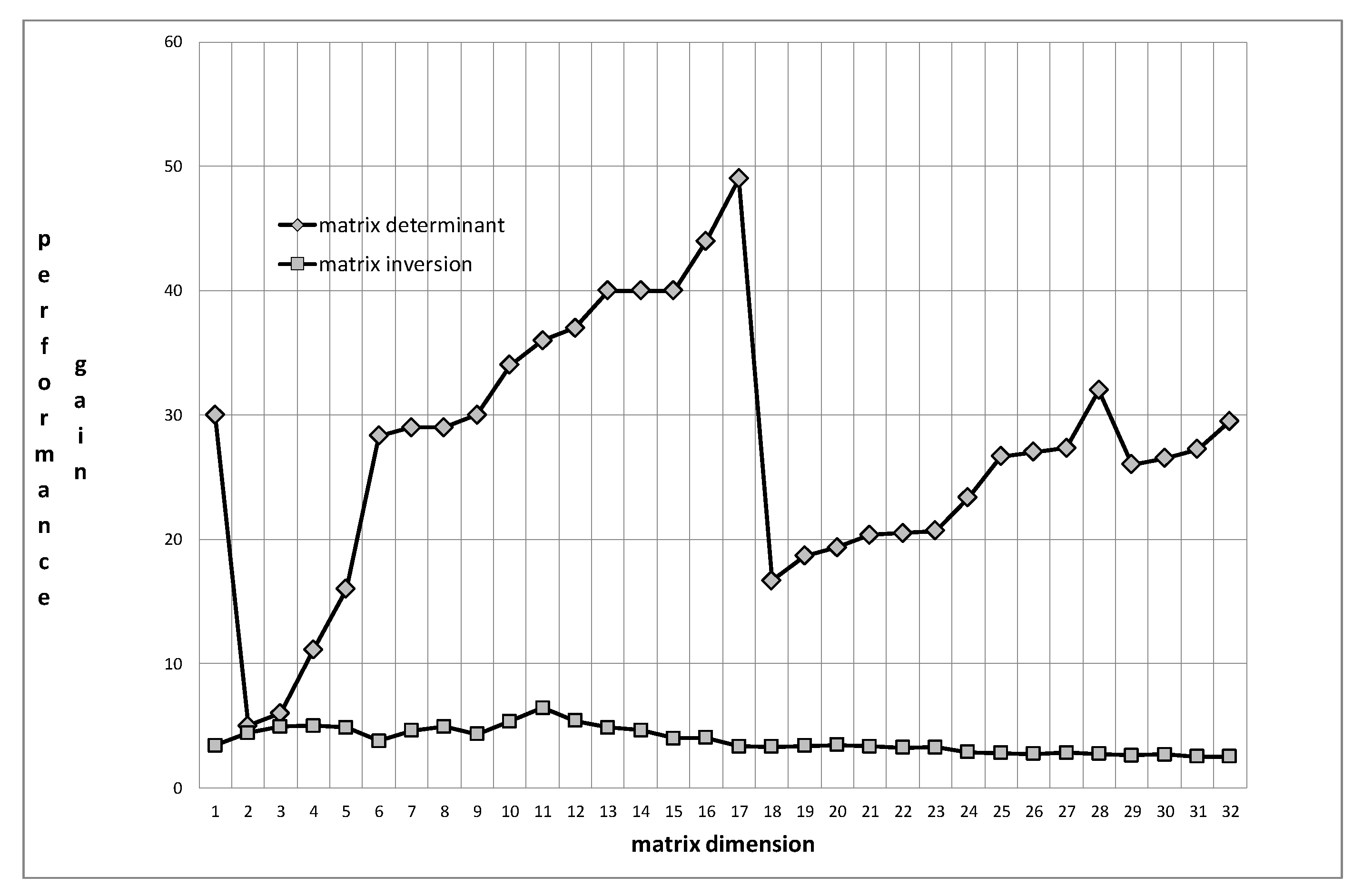
3.2. Computational Complexity of the Proposed Algorithms
- ▪
- The computational complexity of the presented Algorithms A–C is of the O(n) class with respect to the number of floating-point operations necessary to perform. This enables us to efficiently solve the incremental Vandermonde problems, avoiding the quadratic complexity, typical in the Vandermonde field (e.g., References [14,18])
- ▪
- Algorithm D is of the O(n2) class, being, by the linear term, more efficient than the ordinary Gauss elimination method.
3.3. Special Cases
3.3.1. Generalized Vandermonde Matrix with Equidistant Roots
3.3.2. Generalized Vandermonde Matrix with Positive Integer Roots
4. Algorithms for the Generalized Vandermonde Matrix Inverse
4.1. Definition of the Elementary Symmetric Functions
4.2. Theorem of the Recursive Inverse
- The multiplication requires O(n2) operations; as the result, we get the n-element vertical vector.
- The multiplication requires O(n2) operations; as the result, we get the n-element horizontal vector. ☐
4.3. Algorithm 1
| Algorithm 1:Incremental Inverting of the Generalized Vandermonde Matrix |
|
4.4. Computational Complexity
- ▪
- As we analyzed in the point (C), Section 4.2, the computational complexity of the incremental Algorithm 1, which is constructed on the basis of of Equation (12), is of the O(n2) class with respect to the number of floating-point operations which have to be performed. This is possible thanks to the proper multiplication order in Equation (12). This way, we avoid the O(n3) complexity while adding a new root.
- ▪
- The computational complexity of the recursive Algorithm 2 is of the O(n3) class.
| Algorithm 2:For Recursive Inverting the Generalized Vandermonde Matrix. |
|
5. Example
- -
- general exponent: .
- -
- size: .
- -
- roots: .
5.1. Objective
5.2. Recursive Determinant Calculation
5.3. Recursive Inverse Finding
5.4. Summary of the Example
6. Research and Extensions
- ▪
- Construction of the parallel algorithm for the generalized Vandermonde matrices.
- ▪
- Adaptation of the algorithms to vector-oriented hardware units.
- ▪
- Combination of both.
- ▪
- Application on Graphics Hardware Unit architecture.
- ▪
- Application of the results in new branches, like deep learning and artificial intelligence.
- ▪
- Total variation problems and optimization methods;
- ▪
- Power systems networks;
- ▪
- The numerical problem preconditioning;
- ▪
- Fractional order differential equations.
7. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Respondek, J. On the confluent Vandermonde matrix calculation algorithm. Appl. Math. Lett. 2011, 24, 103–106. [Google Scholar] [CrossRef]
- Respondek, J. Numerical recipes for the high efficient inverse of the confluent Vandermonde matrices. Appl. Math. Comput. 2011, 218, 2044–2054. [Google Scholar] [CrossRef]
- Respondek, J. Highly Efficient Recursive Algorithms for the Generalized Vandermonde Matrix. In Proceedings of the 30th European Simulation and Modelling Conference—ESM’ 2016, Las Palmas de Gran Canaria, Spain, 26–28 October 2016; pp. 15–19. [Google Scholar]
- Respondek, J. Recursive Algorithms for the Generalized Vandermonde Matrix Determinants. In Proceedings of the 33rd Annual European Simulation and Modelling Conference—ESM’ 2019, Palma de Mallorca, Spain, 28–30 October 2019; pp. 53–57. [Google Scholar]
- El-Mikkawy, M.E.A. Explicit inverse of a generalized Vandermonde matrix. Appl. Math. Comput. 2003, 146, 643–651. [Google Scholar] [CrossRef]
- Hou, S.; Hou, E. Recursive computation of inverses of confluent Vandermonde matrices. Electron. J. Math. Technol. 2007, 1, 12–26. [Google Scholar]
- Hou, S.; Pang, W. Inversion of confluent Vandermonde matrices. Comput. Math. Appl. 2002, 43, 1539–1547. [Google Scholar] [CrossRef]
- Gorecki, H. Optimization of the Dynamical Systems; PWN: Warsaw, Poland, 1993. [Google Scholar]
- Klamka, J. Controllability of Dynamical Systems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Respondek, J. Approximate controllability of infinite dimensional systems of the n-th order. Int. J. Appl. Math. Comput. Sci. 2008, 18, 199–212. [Google Scholar] [CrossRef]
- Respondek, J. Approximate controllability of the n-th order infinite dimensional systems with controls delayed by the control devices. Int. J. Syst. Sci. 2008, 39, 765–782. [Google Scholar] [CrossRef]
- Timoshenko, S. Vibration Problems in Engineering, D, 3rd ed.; Van Nostrand Company: London, UK, 1955. [Google Scholar]
- Bellman, R. Introduction to Matrix Analysis; Mcgraw-Hill Book Company: New York, NY, USA, 1960. [Google Scholar]
- Eisinberg, A.; Fedele, G. On the inversion of the Vandermonde matrix. Appl. Math. Comput. 2006, 174, 1384–1397. [Google Scholar] [CrossRef]
- Kincaid, D.R.; Cheney, E.W. Numerical Analysis: Mathematics of Scientific Computing, 3rd ed.; Brooks Cole: Florence, KY, USA, 2001. [Google Scholar]
- Lee, K.; O’Sullivan, M.E. Algebraic soft-decision decoding of Hermitian codes. IEEE Trans. Inf. Theory 2010, 56, 2587–2600. [Google Scholar] [CrossRef]
- Gorecki, H. On switching instants in minimum-time control problem. One-dimensional case n-tuple eigenvalue. Bull. Acad. Pol. Sci. 1968, 16, 23–30. [Google Scholar]
- Yan, S.; Yang, A. Explicit Algorithm to the Inverse of Vandermonde Matrix. In Proceedings of the 2009 Internatonal Conference on Test and Measurement, Hong Kong, China, 5–6 December 2009; pp. 176–179. [Google Scholar]
- Dassios, I.; Fountoulakis, K.; Gondzio, J. A preconditioner for a primal-dual newton conjugate gradients method for compressed sensing problems. SIAM J. Sci. Comput. 2015, 37, A2783–A2812. [Google Scholar] [CrossRef]
- Dassios, I.; Baleanu, D. Optimal solutions for singular linear systems of Caputo fractional differential equations. Math. Methods Appl. Sci. 2018. [Google Scholar] [CrossRef]
- Dassios, I. Analytic Loss Minimization: Theoretical Framework of a Second Order Optimization Method. Symmetry 2019, 11, 136. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Respondek, J.S. Recursive Matrix Calculation Paradigm by the Example of Structured Matrix. Information 2020, 11, 42. https://doi.org/10.3390/info11010042
Respondek JS. Recursive Matrix Calculation Paradigm by the Example of Structured Matrix. Information. 2020; 11(1):42. https://doi.org/10.3390/info11010042
Chicago/Turabian StyleRespondek, Jerzy S. 2020. "Recursive Matrix Calculation Paradigm by the Example of Structured Matrix" Information 11, no. 1: 42. https://doi.org/10.3390/info11010042
APA StyleRespondek, J. S. (2020). Recursive Matrix Calculation Paradigm by the Example of Structured Matrix. Information, 11(1), 42. https://doi.org/10.3390/info11010042




