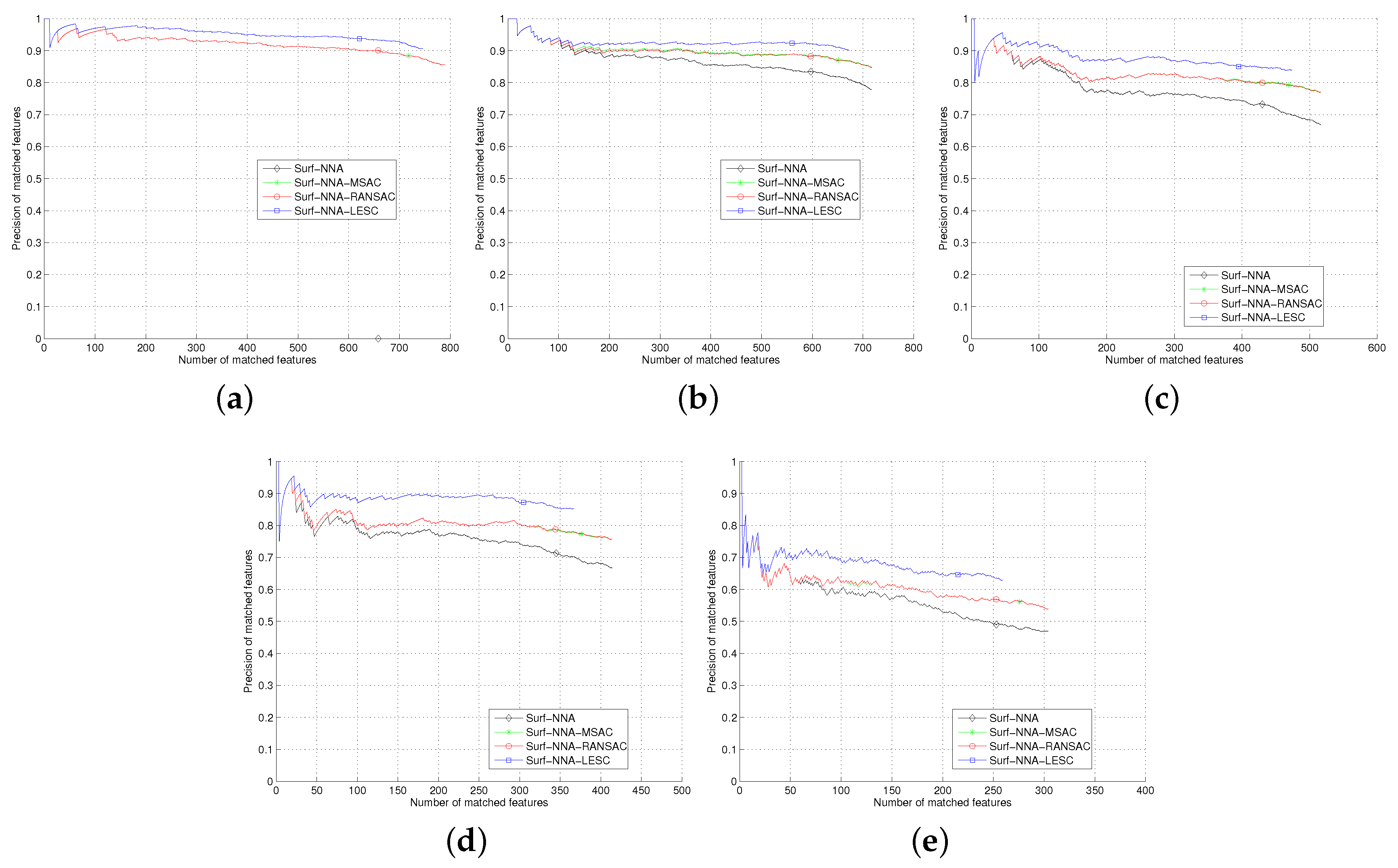
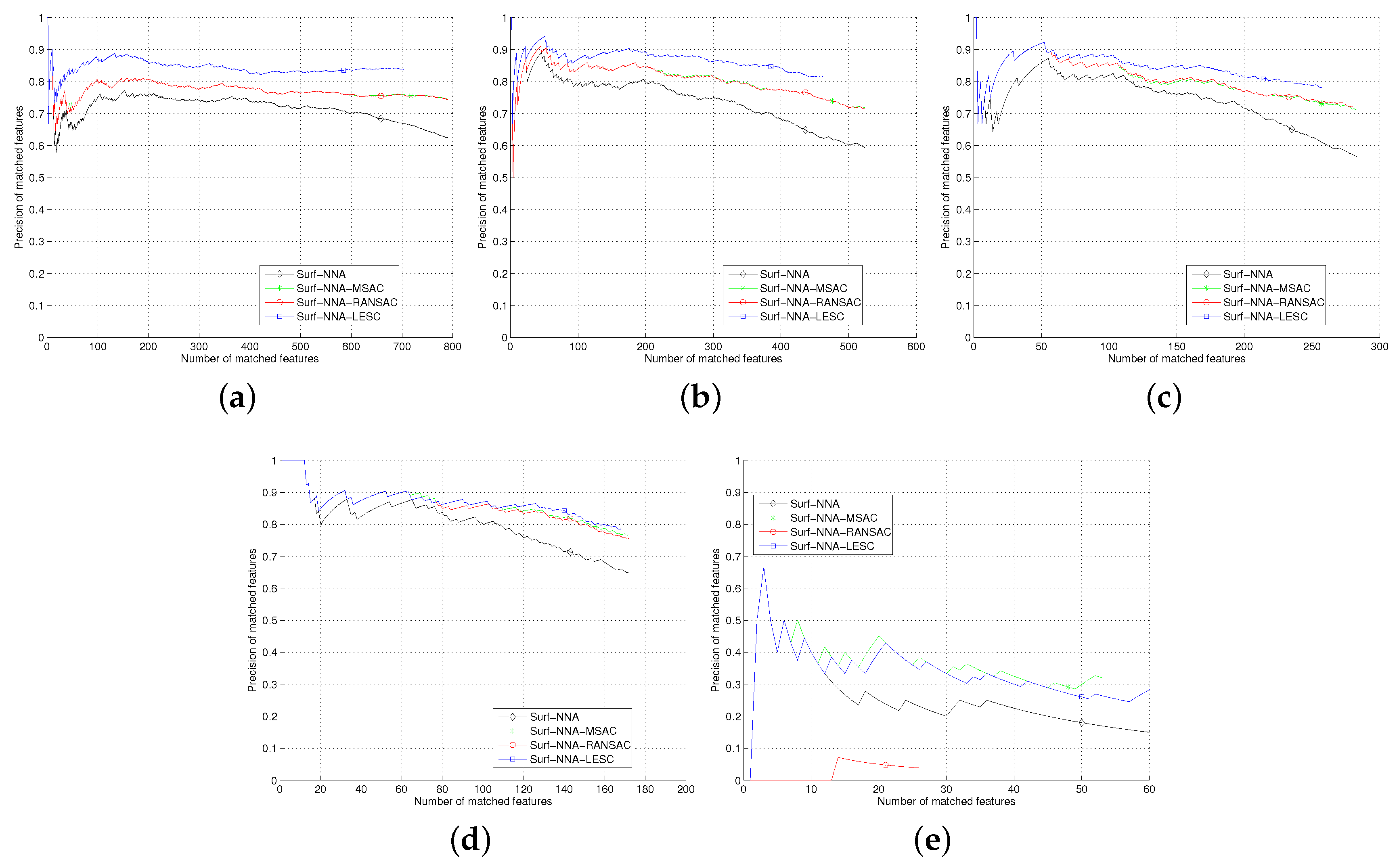
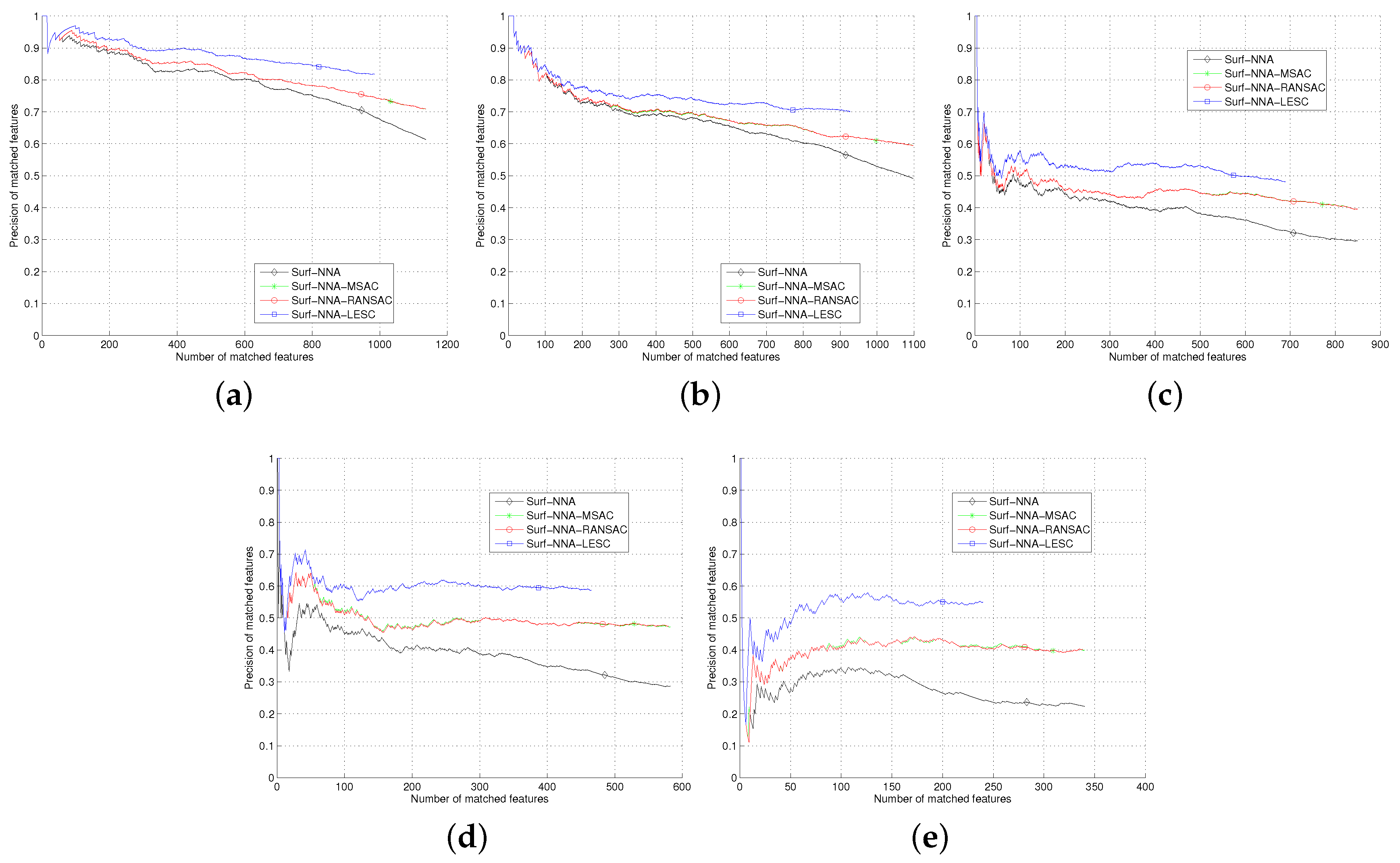
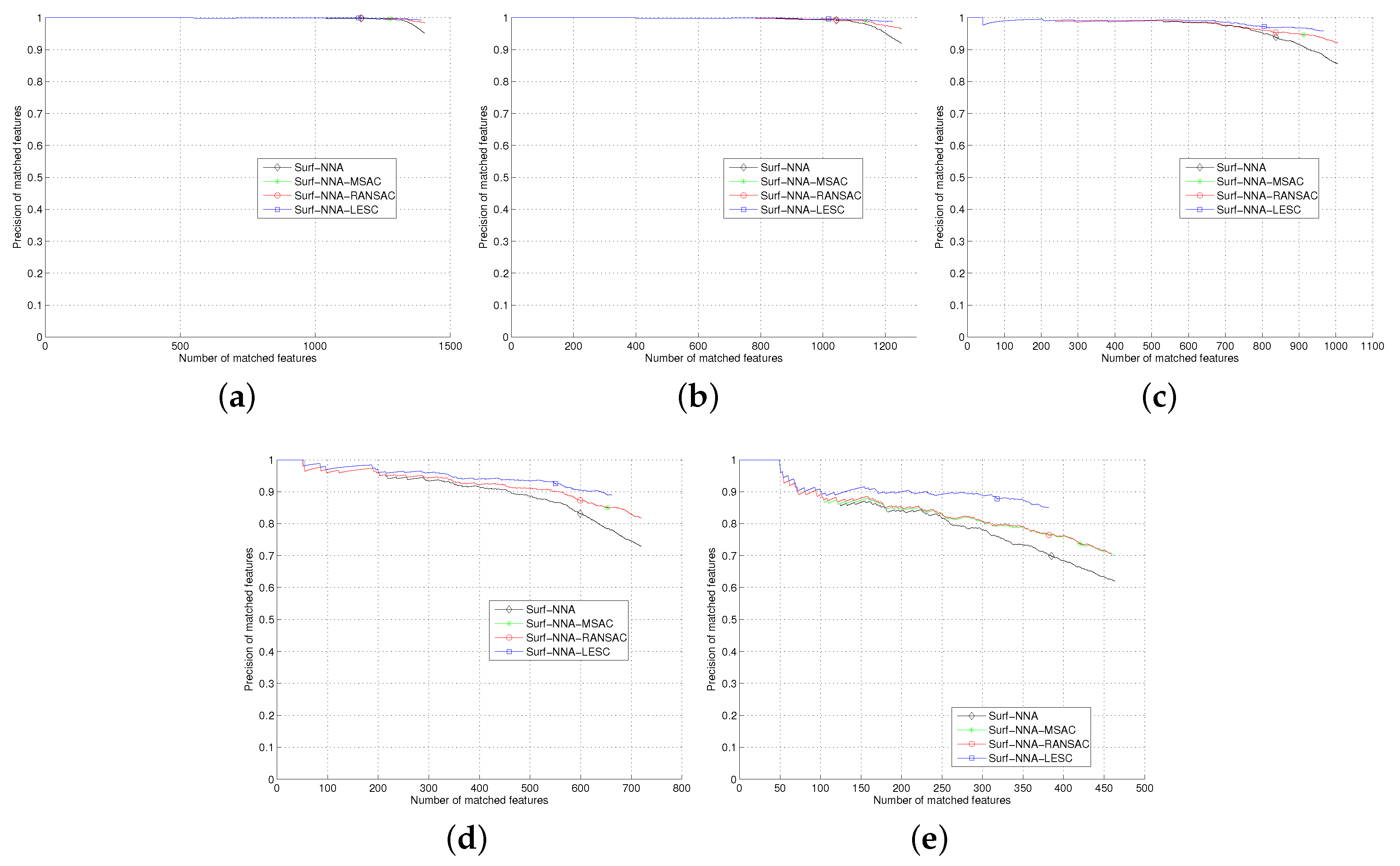
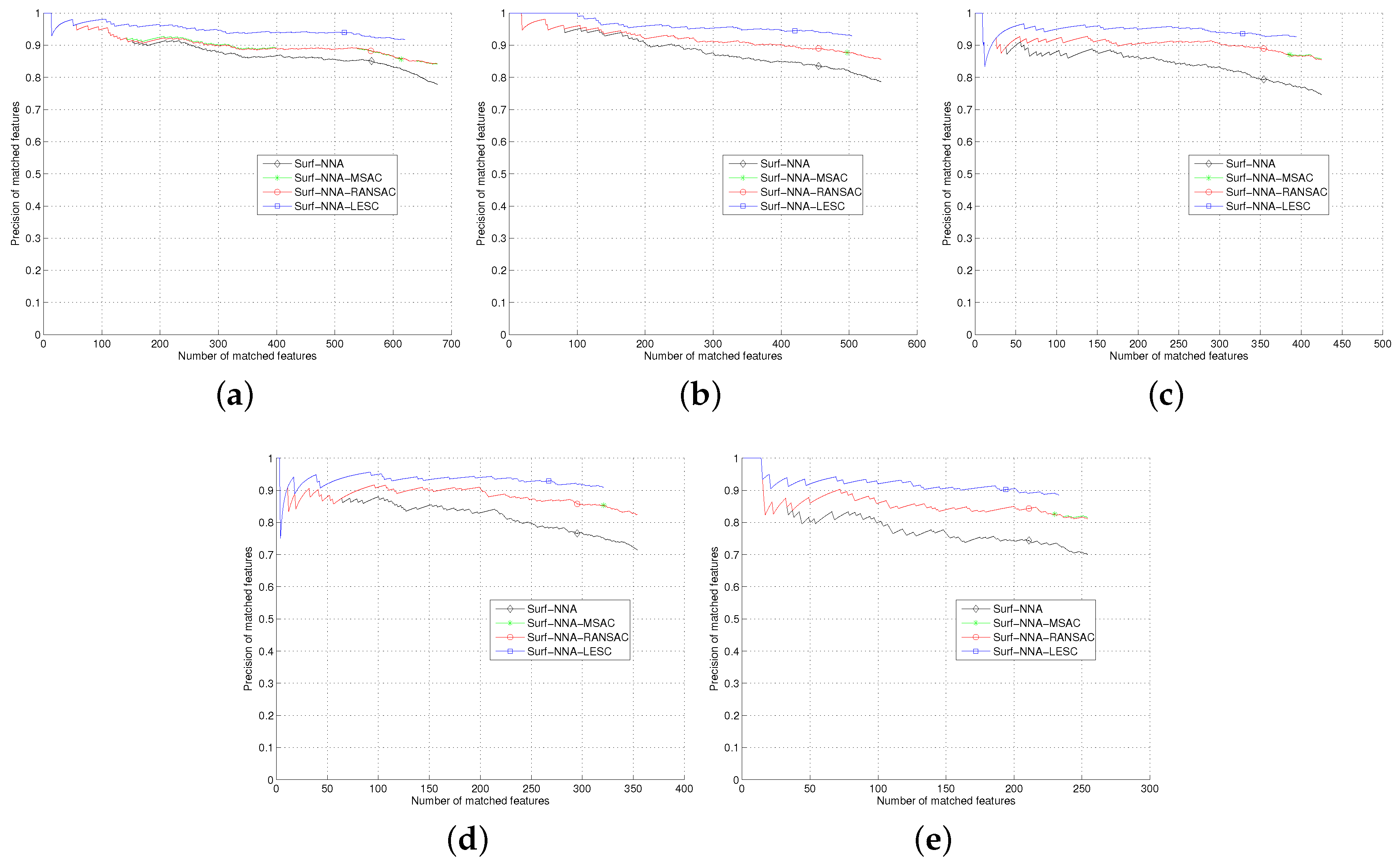
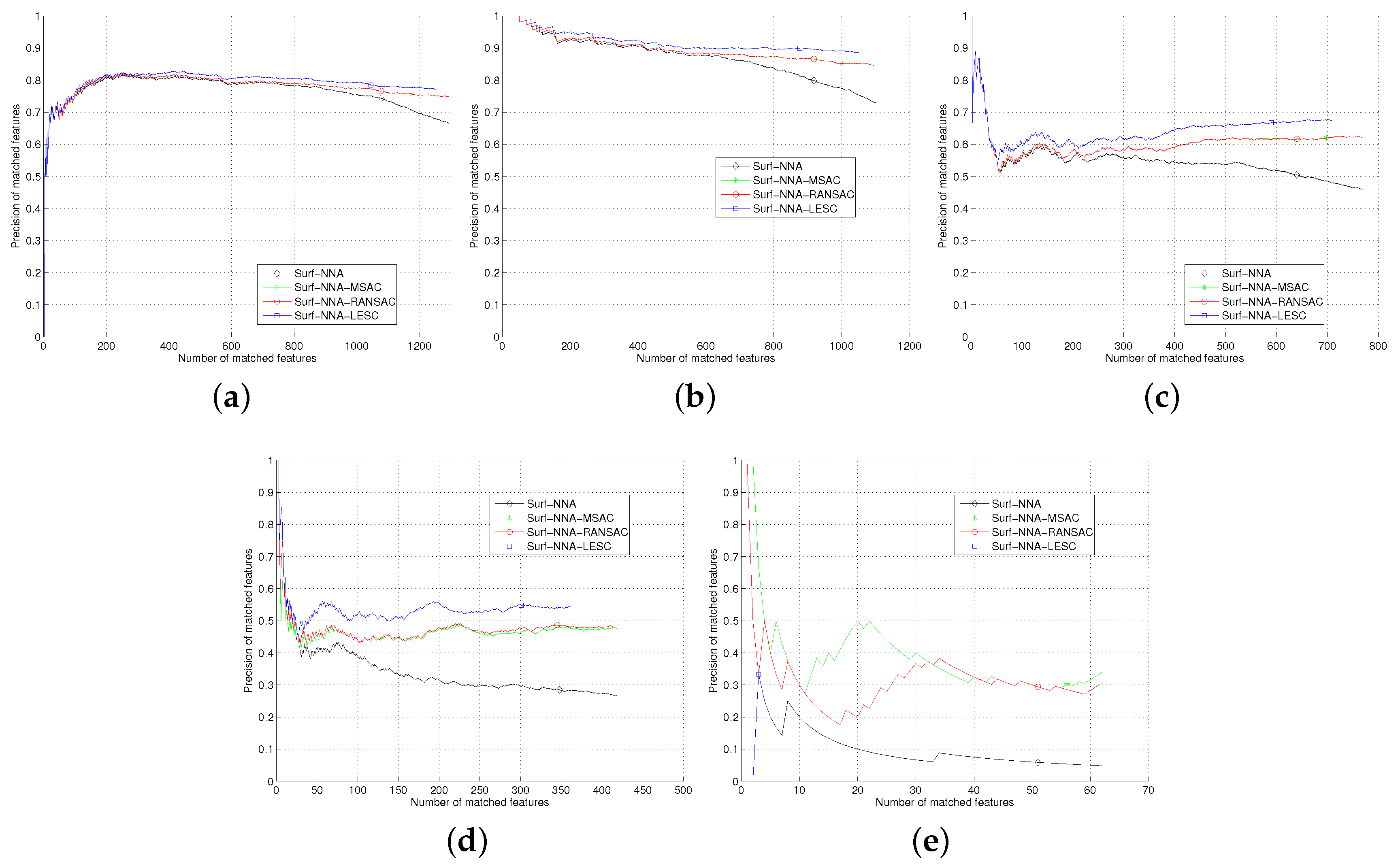
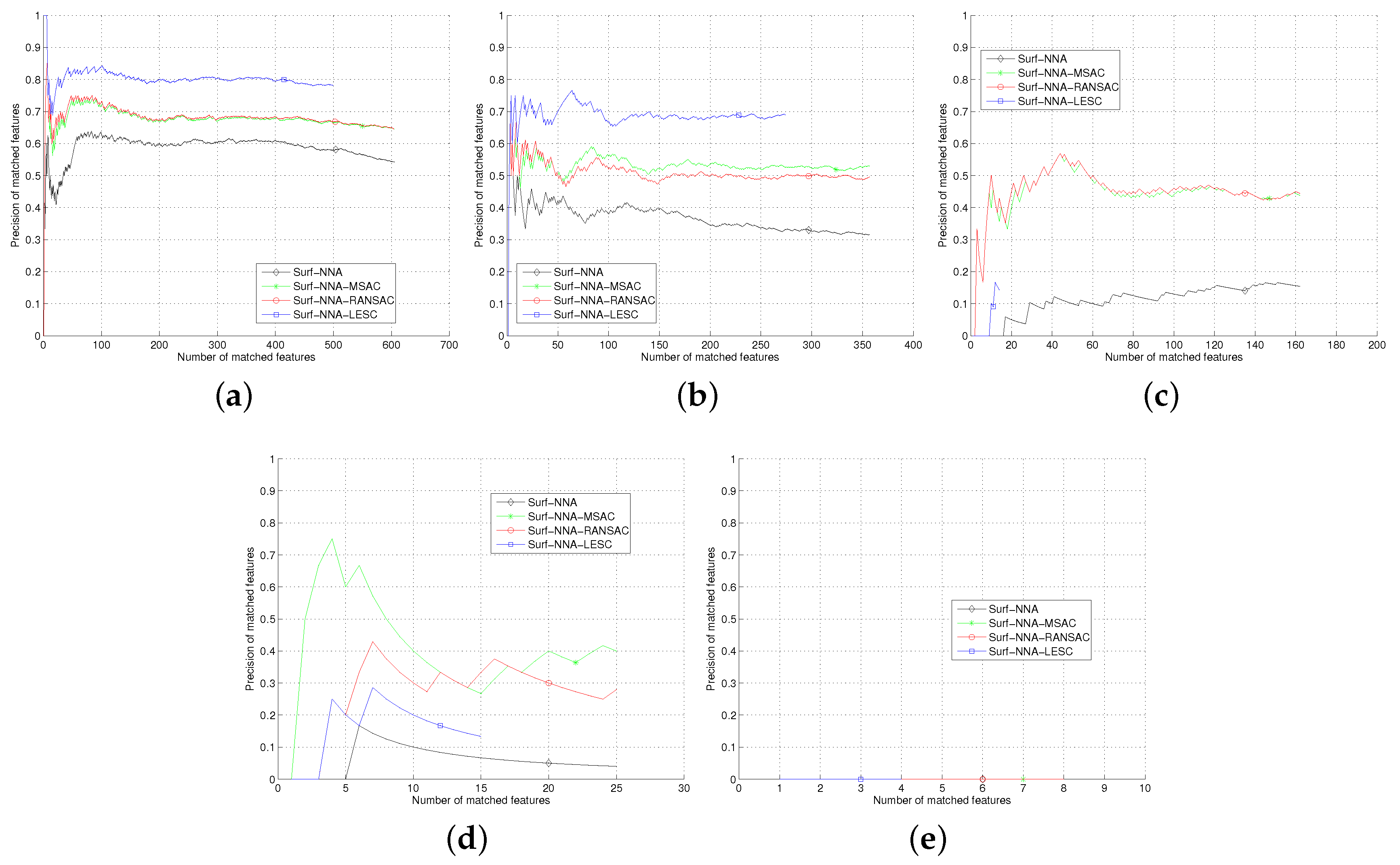
The
random sample consensus (RANSAC) [
1] has been broadly applied to obviate outliers with the
nearest neighbour-based approach (NNA) for matching features. It prominently increases the precision-recall rate of matches. Under the framework of RANSAC, many improved versions have been studied. Using
maximum likelihood estimation (MLE) instead of counting inliers, MLESAC introduces a likelihood function to evaluate a consensus set [
2]. AMLESAC also exploits the MLE technique in consensus estimation but, other than MLESAC, only estimating outlier share in its procedure, AMLESAC estimates outlier share and inlier noise simultaneously [
3]. To speed up the computation of RANSAC, R-RANSAC applies a preliminary test procedure, which evaluates the hypotheses by a small-sized sample to reduce some unnecessary verifications against all data points [
4]. Exploiting
Wald’s sequential probability test (SPRT), the optimal R-RANSAC also employs the preliminary test scheme to improve RANSAC [
5]. Rather than the “depth-first” scheme in RANSAC, the preemptive RANSAC adopts the “breadth-first” strategy, which first generates all hypotheses and then compares them [
6]. Guided-MLESAC uses a distribution constructed by the prior information instead of the uniform distribution, which generates hypotheses with a higher probability for searching the largest consensus set [
7]. Unlike the plain RANSAC uniformly generating hypotheses, PROSAC non-uniformly draws samples from a sequence of monotonically increasing subsets, which are ordered by some “quality” valued by the element with the worst likely score in each subset. This scheme enables uncontaminated correspondences to be drawn as early as possible, thus reducing computational cost [
8]. SEASAC further improves PROSAC through updating samples with only one data point at a time, replacing the worst one, whereas any such points in PROSAC will not be removed [
9]. Cov-RANSAC employs SPRT and covariance test to form a set of potential inliers, on which the standard RANSAC run afterwards [
10]. Before the procedure of RANSAC, DT-RANSAC constructs a refined set from putative matches based on topological information [
11]. Since the scale ratio of correct matches approximates the scale variation of two images, SVH-RANSAC proposes a scale constraint, the scale variation homogeneity, to group data points, and thus the potential correct matches are more probable to be used to generate hypotheses [
12]. SC-RANSAC exploits matching score to produce a set of reliable data points and then generates a hypothesis from these data points [
13].
In the standard RANSAC framework, all inliers are treated as having equal quality for hypothesizing homographies and, by this assumption, the number of times attempting to obtain the largest consensus set is estimated. Then the noise in inliers can affects the precision of estimating homographies and therefore impacts on the estimation of the largest consensus set. To cope with this defect, we study an approach of consensus estimation suppressing the influence from noise. The rest of this work is organized as follows. In
Section 2, we discuss the limitation and some improvements in the standard RANSAC framework on the noise problem. In
Section 3, we present a new approach for consensus estimation, which is based on the least square method. In
Section 4, a new feature matching method built on our new consensus estimator is presented. In
Section 5, we test the least square based consensus estimator and compare it with the plain RANSAC and MSAC. Finally we conclude our work in
Section 6.