Enhanced Grid-Based Visual Analysis of Retinal Layer Thickness with Optical Coherence Tomography †
Abstract
1. Introduction
- Enhanced grid design: We propose an adaptive grid-based reduction of retinal thickness data. New grid layouts are derived by radial and sector-wise subdivision of well-established grids. The representation quality of alternative grids is rated and best options are suggested to the user.
- Grid-based visual analysis: We develop a flexible visual analysis tool for grid-based data exploration. Grids are interactively refined, compared to other grids, and cell-related details are shown on demand. A complementary procedure eases the analysis of ophthalmic study data.
- Evaluation of ophthalmic studies: We apply our tool to investigate localized variations in retinal layer thickness in two cross-sectional studies with patients suffering from diabetes mellitus. The main findings are summarized and compared to results of current analysis procedures.
2. Background
- patient-specific assessments of the retinal condition of individuals and
- group-specific evaluations of experimental and prospective studies.
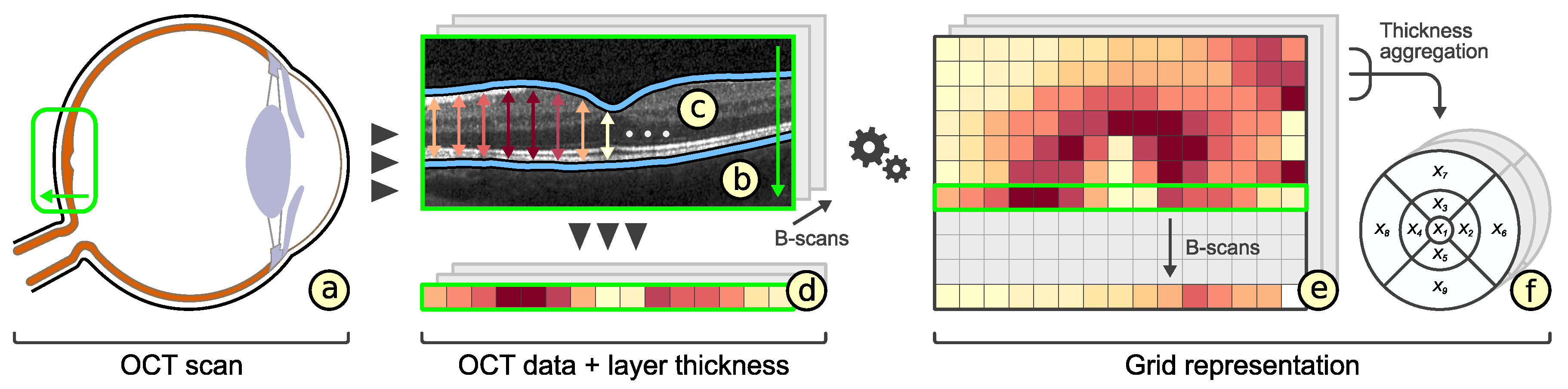
2.1. Visual Analysis of OCT Data
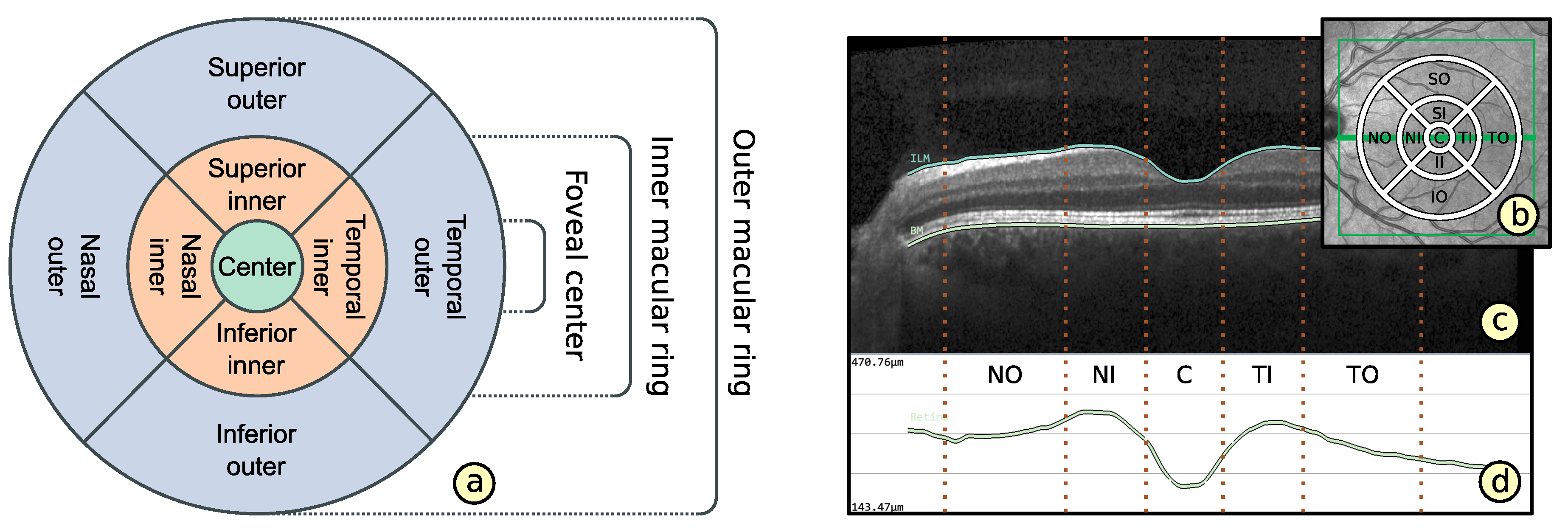
2.2. Representation of Retinal Layer Thickness via ETDRS Grids
3. Grid Design
3.1. Grid-Related Requirements
- Layout based on ETDRS grid (): The basic layout of alternative grids should correspond to the ETDRS grid. This is to maintain the ability to localize anatomically important areas of the macula near the center of the retina.
- Comparability of grid layouts (): Alternative grid layouts should be comparable to both the basic ETDRS grid and other alternative grids. This is to ensure that analysis results from multiple datasets with different grids are relatable.
- Compact data representation (): The number of grid cells should be small and the content of a grid cell should be represented by mainly one descriptive value. Nevertheless, an appropriate representation of thickness data has to be facilitated.
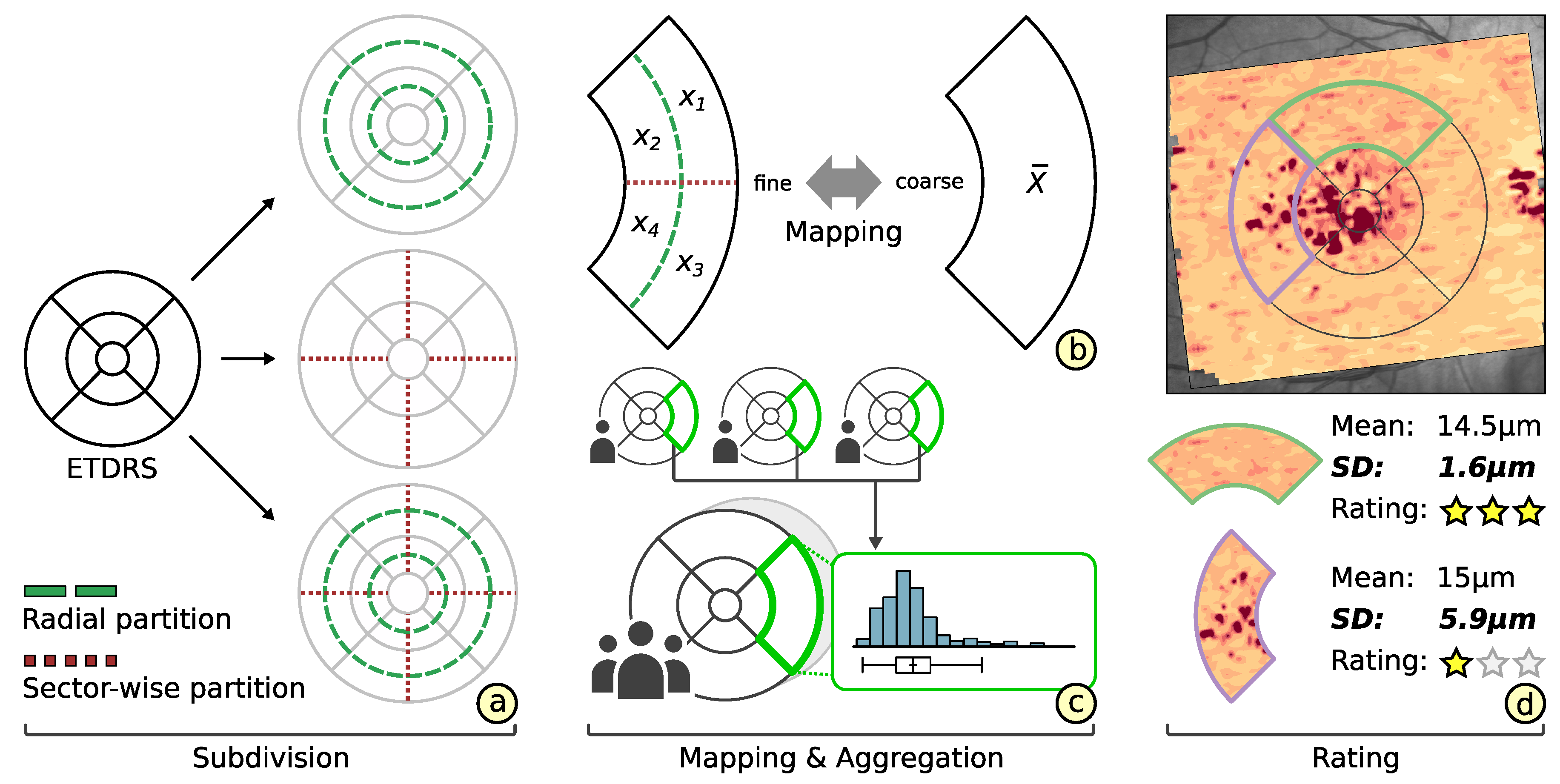
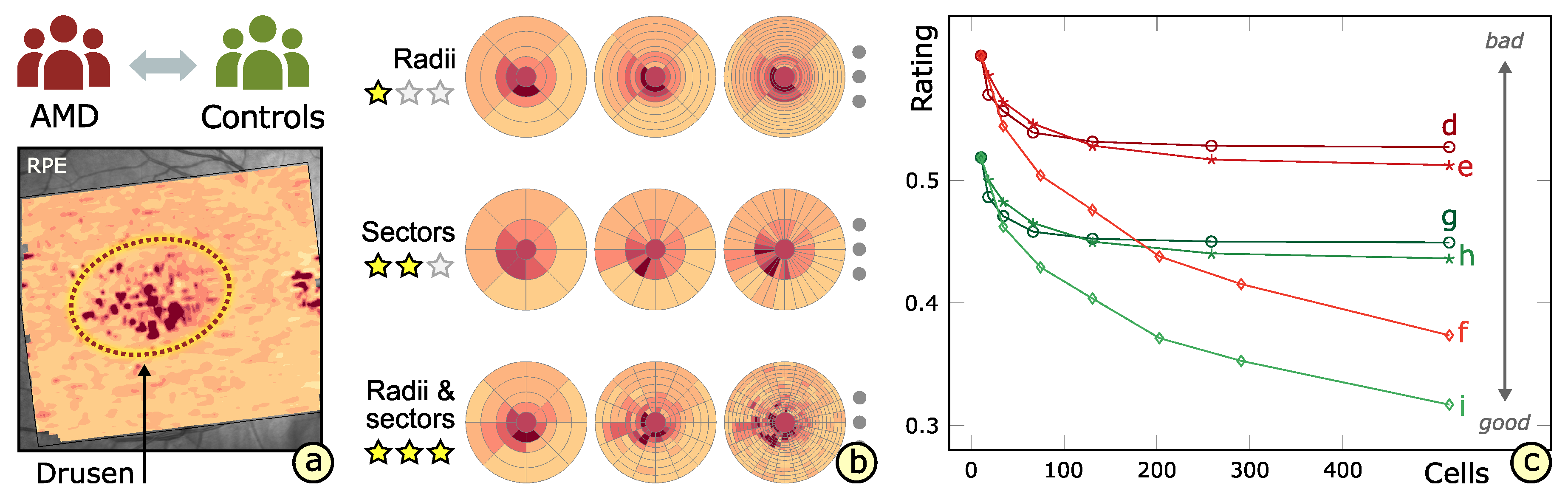
3.2. Subdivision of Grids
3.3. Comparability of Grids
3.4. Rating of Grids
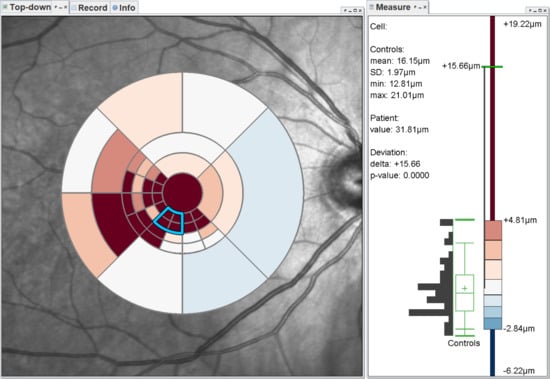
4. Grid Exploration
4.1. Visualization-Related Requirements
- Visualization in spatial context (): The thickness values of grids have to be presented in their underlying spatial frame of reference. This ensures that they are relatable to respective regions within the retina and allows to understand their spatial distribution.
- Grid details on demand (): Details of grids with respect to space, e.g., finer subdivision of cells, and encoded information, e.g., the distribution of underlying thickness values, have to be made visually available upon request. This way, interactive investigations of findings at different levels of granularity are possible.
- Relation of multiple grids (): The thickness differences between multiple grids have to be graphically presented. In connection with the comparability of grid layouts (cf. ), the differences need to be visualized in a common space. In case of ophthalmic studies, statistical quantification on top of a pure comparative display is required.
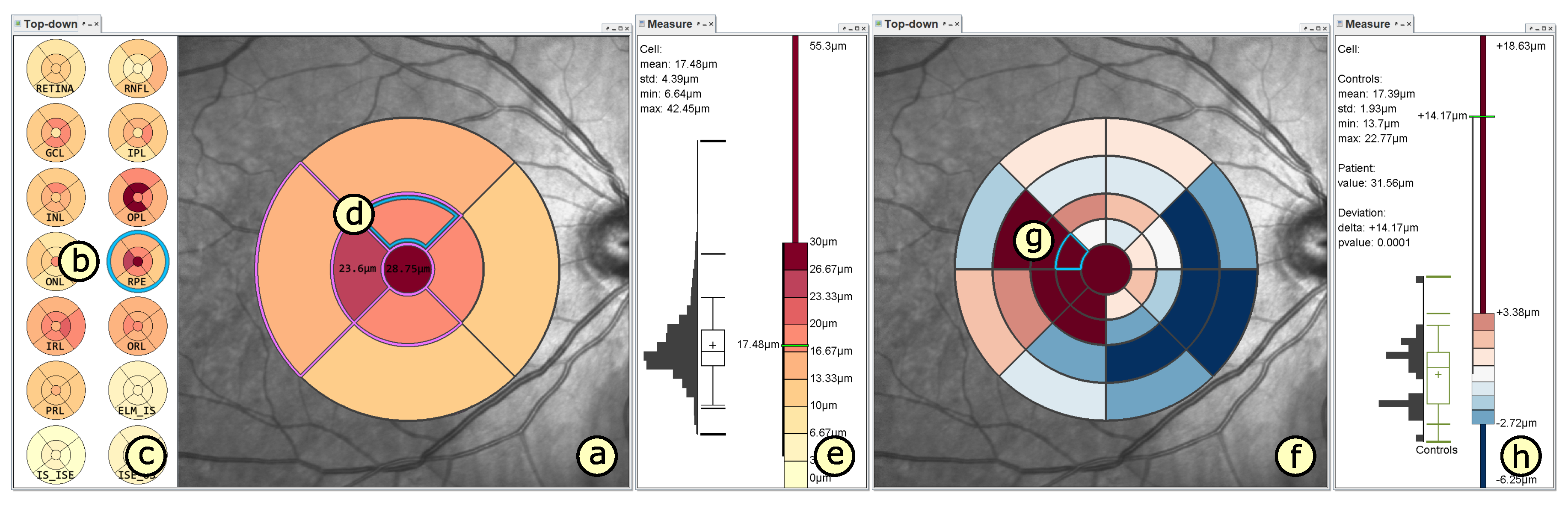
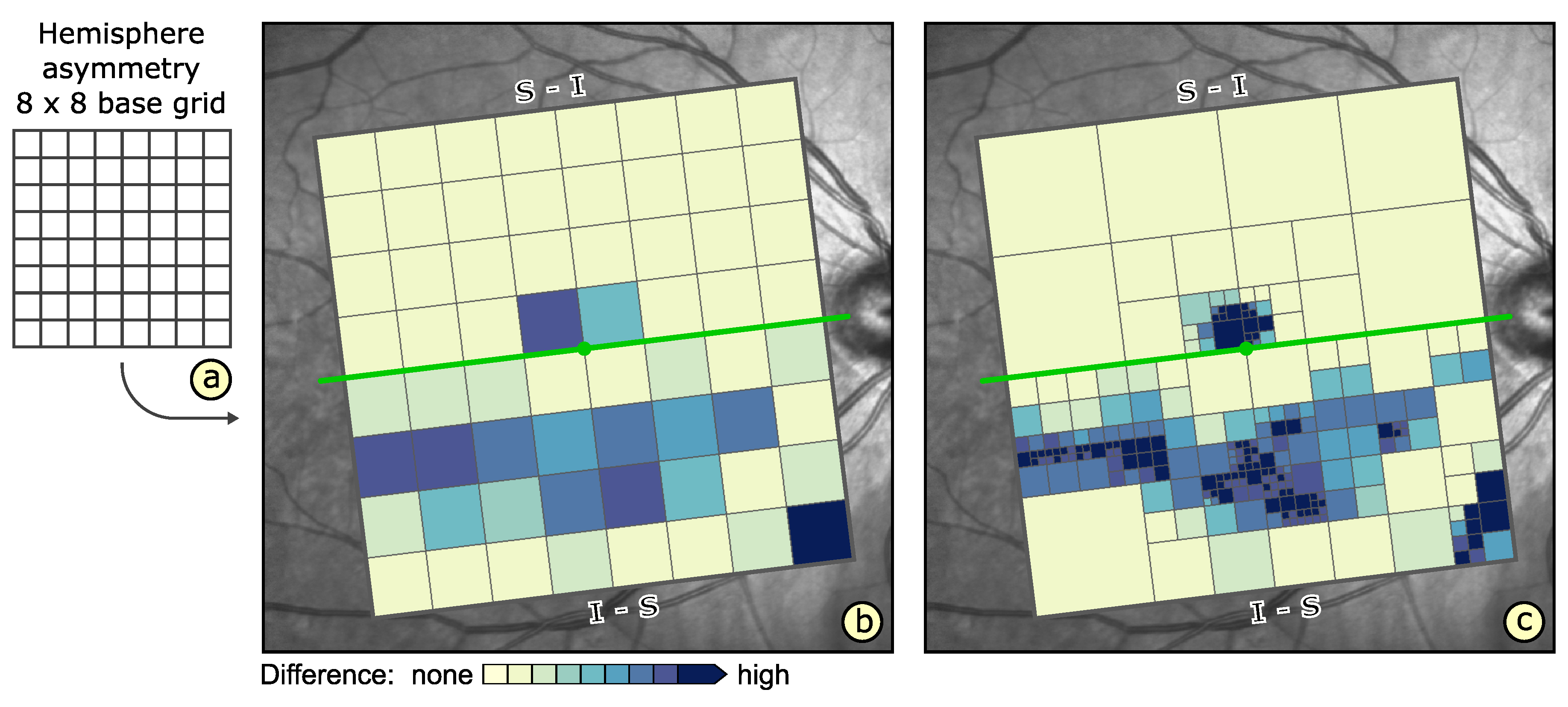
4.2. Presentation of Grids
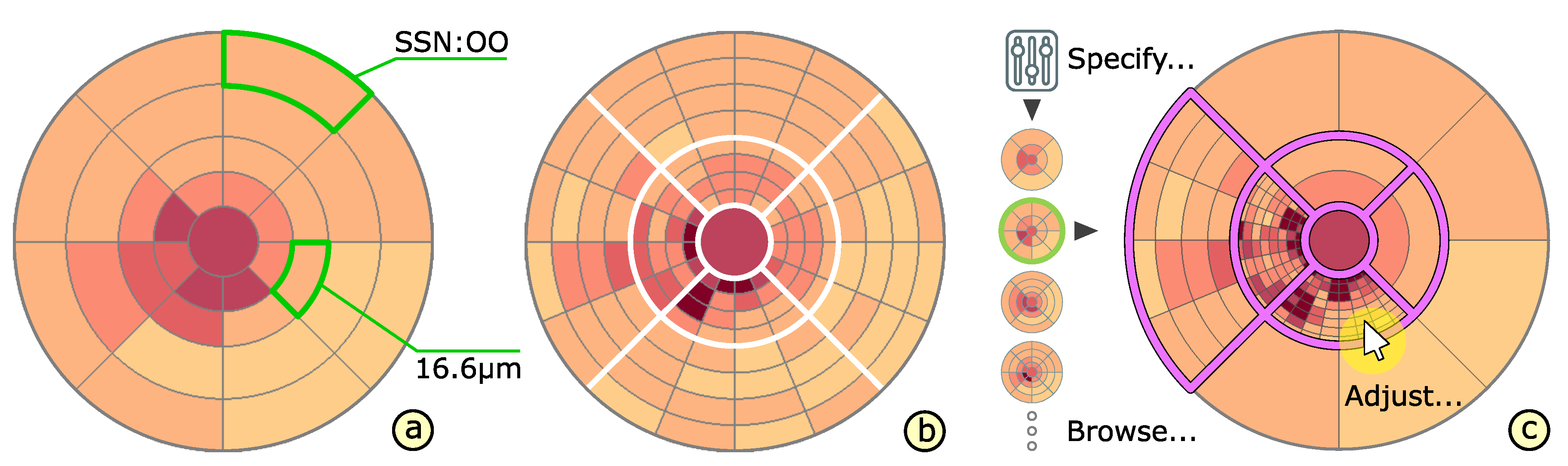
4.3. Adaptation of Grids
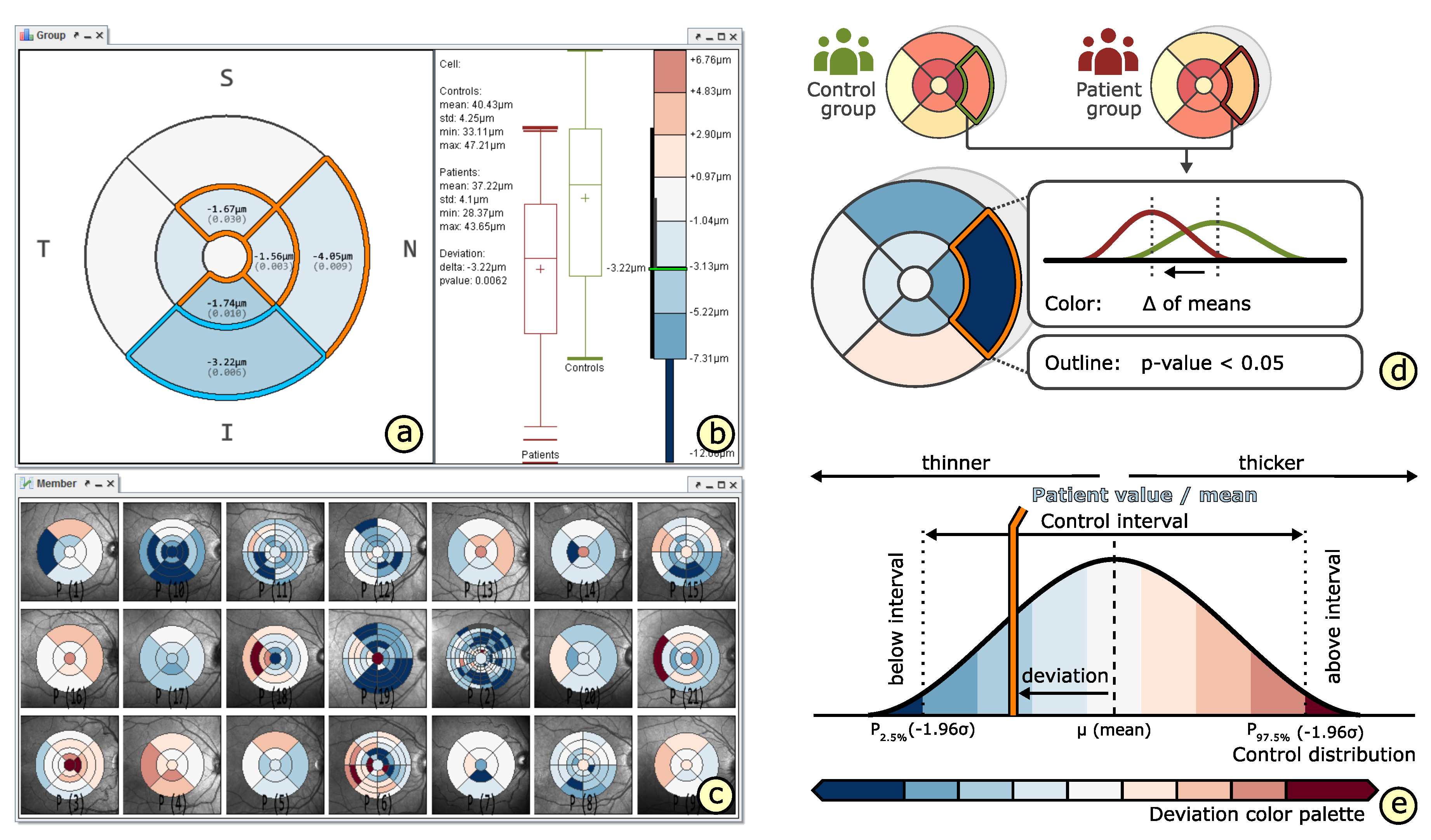
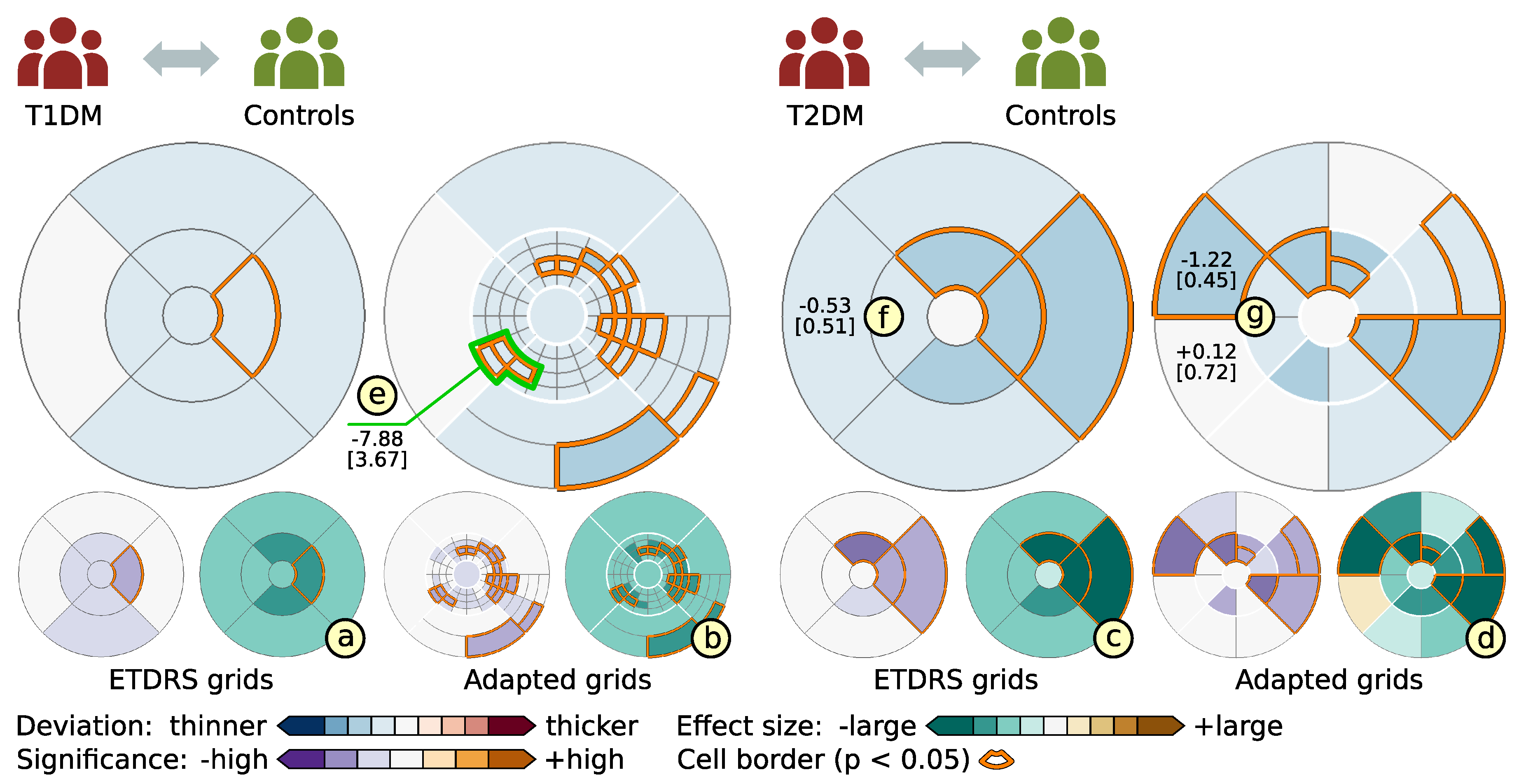
4.4. Comparison of Grids
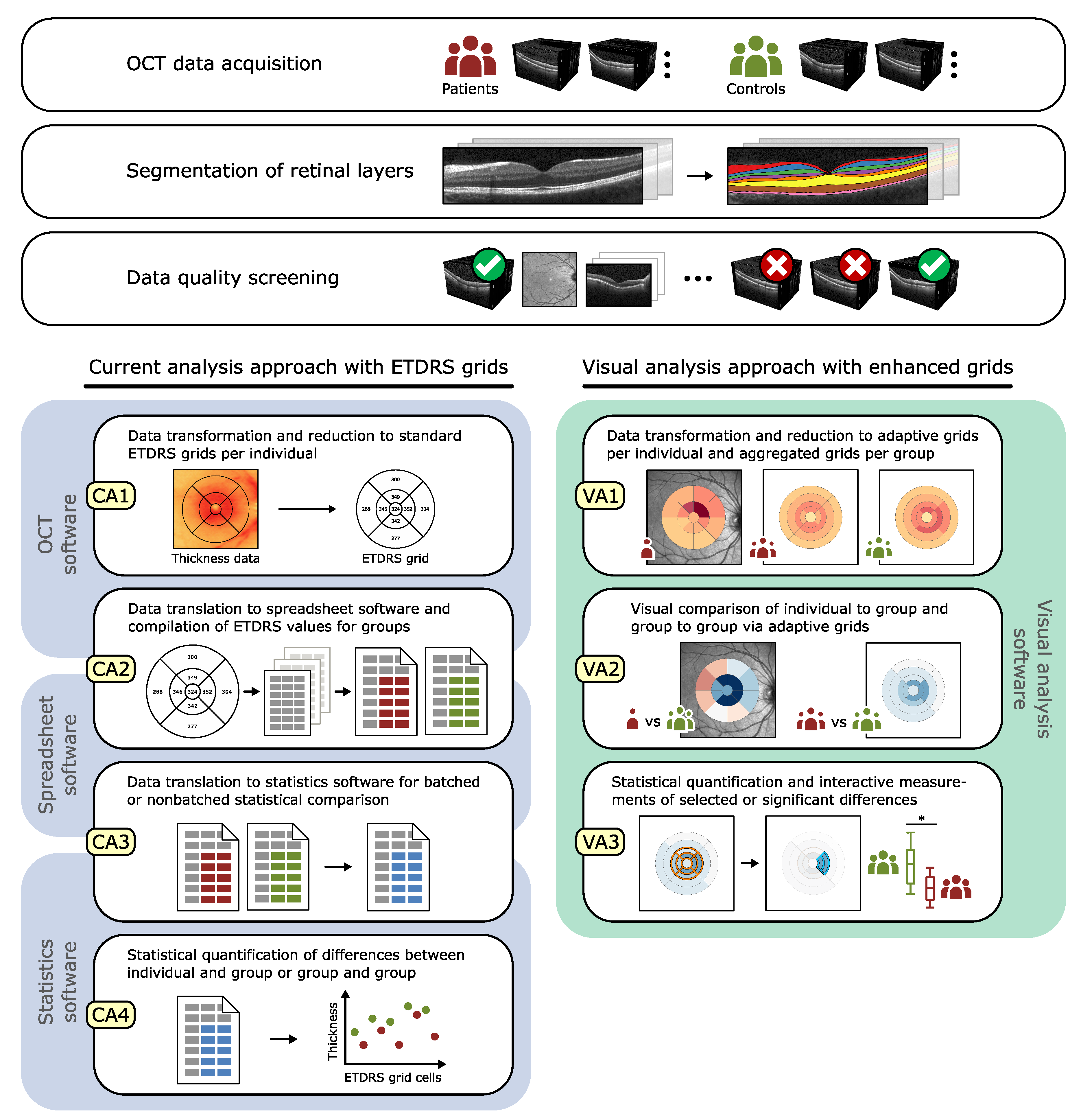
5. Grid-Based Visual Analysis of Retinal Layer Thickness
5.1. A Visual Analysis Tool
5.2. A Visual Analysis Procedure
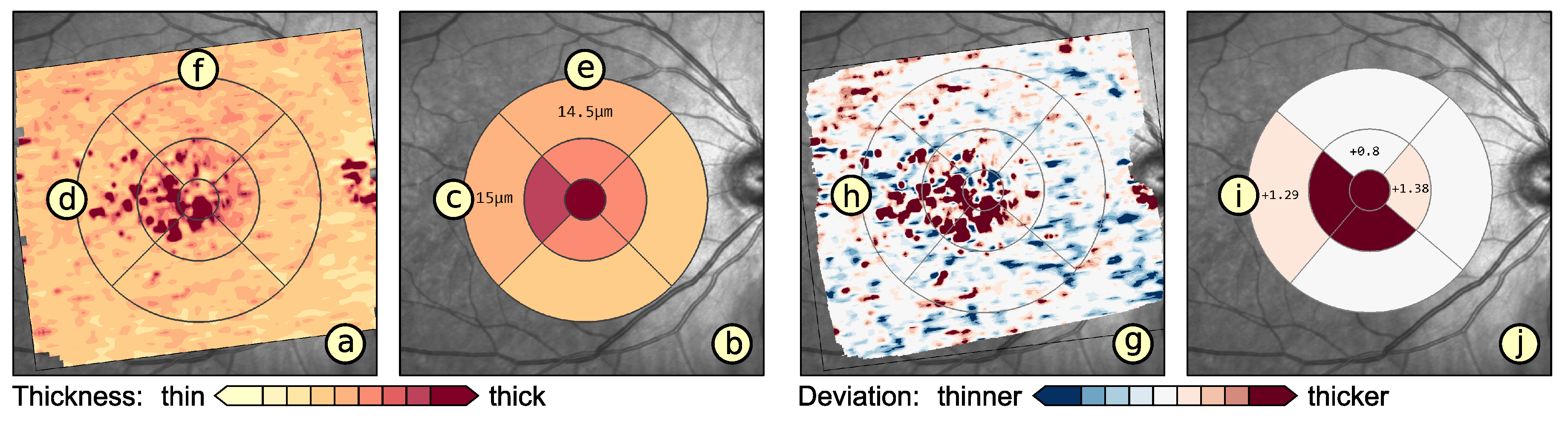
6. Application
6.1. Experimental Evaluation of Patients with Age-Related Macular Degeneration
6.2. Grid-Based Analysis of Retinal Layer Thickness in Patients with Diabetes Mellitus
7. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OCT | Optical coherence tomography |
| B-scan | Cross-sectional tomographic depth-image |
| ETDRS | Early treatment retinopathy study |
| First grid design requirement | |
| Second grid design requirement | |
| Third grid design requirement | |
| First visualization design requirement | |
| Second visualization design requirement | |
| Third visualization design requirement | |
| CA | Current ETDRS grid-based analysis approach |
| VA | Enhanced grid-based visual analysis approach |
| AMD | Age-related macular degeneration |
| T1DM | Type one diabetes mellitus |
| T2DM | Type two diabetes mellitus |
| TR | Total retina |
| RNFL | Retinal nerve fiber layer |
| GCL | Ganglion cell layer |
| IPL | Inner plexiform layer |
| INL | Inner nuclear layer |
References
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical Coherence Tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, N.; Hangai, M. OCT Atlas; Springer: Berlin, Germany, 2014. [Google Scholar]
- Keane, P.A.; Patel, P.J.; Liakopoulos, S.; Heussen, F.M.; Sadda, S.R.; Tufail, A. Evaluation of Age-related Macular Degeneration With Optical Coherence Tomography. Surv. Ophthalmol. 2012, 57, 389–414. [Google Scholar] [CrossRef] [PubMed]
- Virgili, G.; Menchini, F.; Casazza, G.; Hogg, R.; Das, R.R.; Wang, X.; Michelessi, M. Optical coherence tomography (OCT) for detection of macular oedema in patients with diabetic retinopathy. Cochrane Database Syst. Rev. 2015, 1, CD008081. [Google Scholar] [CrossRef] [PubMed]
- Grewal, D.S.; Tanna, A.P. Diagnosis of glaucoma and detection of glaucoma progression using spectral domain optical coherence tomography. Curr. Opin. Ophthalmol. 2013, 24, 150–161. [Google Scholar] [CrossRef] [PubMed]
- Dörr, J.; Wernecke, K.D.; Bock, M.; Gaede, G.; Wuerfel, J.T.; Pfueller, C.F.; Bellmann-Strobl, J.; Freing, A.; Brandt, A.U.; Friedemann, P. Association of Retinal and Macular Damage with Brain Atrophy in Multiple Sclerosis. PLoS ONE 2011, 6, 1–6. [Google Scholar] [CrossRef]
- Kashani, A.H.; Chen, C.L.; Gahm, J.K.; Zheng, F.; Richter, G.M.; Rosenfeld, P.J.; Shi, Y.; Wang, R.K. Optical coherence tomography angiography: A comprehensive review of current methods and clinical applications. Prog. Retin. Eye Res. 2017, 60, 66–100. [Google Scholar] [CrossRef] [PubMed]
- Röhlig, M.; Stüwe, J.; Schmidt, C.; Prakasam, R.K.; Stachs, O.; Schumann, H. Grid-Based Exploration of OCT Thickness Data of Intraretinal Layers. In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications – Volume 3: IVAPP, Prague, Czech Republic, 25–27 February 2019; pp. 129–140. [Google Scholar] [CrossRef]
- Costa, R.A.; Skaf, M.; Melo, L.A.; Calucci, D.; Cardillo, J.A.; Castro, J.C.; Huang, D.; Wojtkowski, M. Retinal assessment using optical coherence tomography. Prog. Retin. Eye Res. 2006, 25, 325–353. [Google Scholar] [CrossRef]
- Hee, M.R.; Izatt, J.A.; Swanson, E.A.; Huang, D.; Schuman, J.S.; Lin, C.P.; Puliafito, C.A.; Fujimoto, J.G. Optical Coherence Tomography of the Human Retina. JAMA Ophthalmol. 1995, 113, 325–332. [Google Scholar] [CrossRef]
- Drexler, W.; Morgner, U.; Ghanta, R.K.; Kärtner, F.X.; Schuman, J.S.; Fujimoto, J.G. Ultrahigh-resolution ophthalmic optical coherence tomography. Nat. Med. 2001, 7, 502–507. [Google Scholar] [CrossRef]
- Choma, M.A.; Sarunic, M.V.; Yang, C.; Izatt, J.A. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 11, 2183–2189. [Google Scholar] [CrossRef]
- Adhi, M.; Duker, J.S. Optical coherence tomography—Current and future applications. Curr. Opin. Ophthalmol. 2013, 24, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Cogliati, A.; Canavesi, C.; Hayes, A.; Tankam, P.; Duma, V.F.; Santhanam, A.; Thompson, K.P.; Rolland, J.P. MEMS-based handheld scanning probe with pre-shaped input signals for distortion-free images in Gabor-domain optical coherence microscopy. Opt. Express 2016, 24, 13365–13374. [Google Scholar] [CrossRef] [PubMed]
- Drexler, W.; Morgner, U.; Kärtner, F.X.; Pitris, C.; Boppart, S.A.; Li, X.D.; Ippen, E.P.; Fujimoto, J.G. In vivo ultrahigh-resolution optical coherence tomography. Opt. Lett. 1999, 24, 1221–1223. [Google Scholar] [CrossRef] [PubMed]
- Baghaie, A.; Yu, Z.; D’Souza, R.M. State-of-the-art in retinal optical coherence tomography image analysis. Quant. Imaging Med. Surg. 2015, 5, 603–617. [Google Scholar] [CrossRef] [PubMed]
- Ehnes, A.; Wenner, Y.; Friedburg, C.; Preising, M.N.; Bowl, W.; Sekundo, W.; zu Bexten, E.M.; Stieger, K.; Lorenz, B. Optical Coherence Tomography (OCT) Device Independent Intraretinal Layer Segmentation. Transl. Vis. Sci. Techn. 2014, 3. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, J.; Swanson, E. The Development, Commercialization, and Impact of Optical Coherence Tomography. Investig. Ophth. Vis. Sci. 2016, 57, OCT1–OCT13. [Google Scholar] [CrossRef] [PubMed]
- Garvin, M.K.; Abramoff, M.D.; Wu, X.; Russell, S.R.; Burns, T.L.; Sonka, M. Automated 3-D Intraretinal Layer Segmentation of Macular Spectral-Domain Optical Coherence Tomography Images. IEEE Trans. Med. Imaging 2009, 28, 1436–1447. [Google Scholar] [CrossRef]
- Mayer, M.A.; Hornegger, J.; Mardin, C.Y.; Tornow, R.P. Retinal Nerve Fiber Layer Segmentation on FD-OCT Scans of Normal Subjects and Glaucoma Patients. Biomed. Opt. Express 2010, 1, 1358–1383. [Google Scholar] [CrossRef]
- Mazzaferri, J.; Beaton, L.; Hounye, G.; Sayah, D.N.; Costantino, S. Open-source algorithm for automatic choroid segmentation of OCT volume reconstructions. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Schindelin, J.; Rueden, C.T.; Hiner, M.C.; Eliceiri, K.W. The ImageJ ecosystem: An open platform for biomedical image analysis. Mol. Reprod. Dev. 2015, 82, 518–529. [Google Scholar] [CrossRef]
- Garrido, M.G.; Beck, S.C.; Mühlfriedel, R.; Julien, S.; Schraermeyer, U.; Seeliger, M.W. Towards a Quantitative OCT Image Analysis. PLoS ONE 2014, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Glittenberg, C.; Krebs, I.; Falkner-Radler, C.; Zeiler, F.; Haas, P.; Hagen, S.; Binder, S. Advantages of Using a Ray-traced, Three-Dimensional Rendering System for Spectral Domain Cirrus HD-OCT to Visualize Subtle Structures of the Vitreoretinal Interface. Ophthalmic Surg. Lasers Imaging 2009, 40, 127–134. [Google Scholar] [CrossRef] [PubMed]
- De Fauw, J.; Ledsam, J.R.; Romera-Paredes, B.; Nikolov, S.; Tomasev, N.; Blackwell, S.; Askham, H.; Glorot, X.; O’Donoghue, B.; Visentin, D.; et al. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat. Med. 2018, 24, 1342–1350. [Google Scholar] [CrossRef] [PubMed]
- Röhlig, M.; Schmidt, C.; Prakasam, R.K.; Schumann, H.; Stachs, O. Visual Analysis of Retinal Changes with Optical Coherence Tomography. Visual Comput. 2018, 34, 1209–1224. [Google Scholar] [CrossRef]
- Prakasam, R.K.; Röhlig, M.; Fischer, D.C.; Götze, A.; Jünemann, A.; Schumann, H.; Stachs, O. Deviation maps for understanding thickness changes of inner retinal layers in children with type 1 diabetes mellitus. Curr. Eye Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Early Treatment Diabetic Retinopathy Study Research Group. Grading Diabetic Retinopathy from Stereoscopic Color Fundus Photographs—An Extension of the Modified Airlie House Classification: ETDRS Report Number 10. Ophthalmology 1991, 98, 786–806. [Google Scholar] [CrossRef]
- Götze, A.; von Keyserlingk, S.; Peschel, S.; Jacoby, U.; Schreiver, C.; Köhler, B.; Allgeier, S.; Winter, K.; Röhlig, M.; Jünemann, A.; et al. The corneal subbasal nerve plexus and thickness of the retinal layers in pediatric type 1 diabetes and matched controls. Sci. Rep. 2018, 8, 14. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Huang, S.; Ma, Q.; Lin, H.; Pan, M.; Liu, X.; Lu, F.; Shen, M. Ultra-high resolution profiles of macular intra-retinal layer thicknesses and associations with visual field defects in primary open angle glaucoma. Sci. Rep. 2017, 7, 41100. [Google Scholar] [CrossRef] [PubMed]
- Asrani, S.; Rosdahl, J.; Allingham, R. Novel software strategy for glaucoma diagnosis: Asymmetry analysis of retinal thickness. Arch. Ophthalmol. 2011, 129, 1205–1211. [Google Scholar] [CrossRef]
- Harrower, M.; Brewer, C.A. ColorBrewer.org: An Online Tool for Selecting Colour Schemes for Maps. Cartogr. J. 2003, 40, 27–37. [Google Scholar] [CrossRef]
- Odell, D.; Dubis, A.M.; Lever, J.F.; Stepien, K.E.; Carroll, J. Assessing errors inherent in OCT-derived macular thickness maps. J. Ophthalmol. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Berufsverband der Augenärzte Deutschlands e.V.; Deutsche Ophthalmologische Gesellschaft; Retinologische Gesellschaft e.V. Quality assurance of optical coherence tomography for diagnostics of the fundus: Positional statement of the BVA, DOG and RG. Ophthalmologe 2017, 114, 617–624. [Google Scholar] [CrossRef]
- Chhablani, J.; Sharma, A.; Goud, A.; Peguda, H.K.; Rao, H.L.; Begum, V.U.; Barteselli, G. Neurodegeneration in Type 2 Diabetes: Evidence From Spectral-Domain Optical Coherence Tomography. Investig. Ophth. Vis. Sci. 2015, 56, 6333–6338. [Google Scholar] [CrossRef] [PubMed]
- Gundogan, F.C.; Akay, F.; Uzun, S.; Yolcu, U.; Çağıltay, E.; Toyran, S. Early Neurodegeneration of the Inner Retinal Layers in Type 1 Diabetes Mellitus. Ophthalmologica 2016, 235, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Tekin, K.; Inanc, M.; Kurnaz, E.; Bayramoglu, E.; Aydemir, E.; Koc, M.; Kiziltoprak, H.; Aycan, Z. Quantitative evaluation of early retinal changes in children with type 1 diabetes mellitus without retinopathy. Clin. Exp. Optom. 2018, 101, 680–685. [Google Scholar] [CrossRef] [PubMed]
- Frydkjaer-Olsen, U.; Hansen, R.S.; Peto, T.; Grauslund, J. Structural neurodegeneration correlates with early diabetic retinopathy. Int. Ophthalmol. 2018, 38, 1621–1626. [Google Scholar] [CrossRef]
- Stachs, O.; Prakasam, R.K.; Fischer, D.C.; Schumann, H.; Matuszewska, A.; Tschöpe, D.; Hettlich, H.J.; Röhlig, M. Visual Analytics of OCT data: Utility of deviation maps in describing retinal layer thickness changes. Investig. Ophth. Vis. Sci. 2019, 60, 1290. [Google Scholar]
- Schulz, H.J.; Röhlig, M.; Nonnemann, L.; Aehnelt, M.; Diener, H.; Urban, B.; Schumann, H. Lightweight Coordination of Multiple Independent Visual Analytics Tools. In Proceedings of the 14th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications – Volume 3: IVAPP, Prague, Czech Republic, 25–27 February 2019; pp. 106–117. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Röhlig, M.; Prakasam, R.K.; Stüwe, J.; Schmidt, C.; Stachs, O.; Schumann, H. Enhanced Grid-Based Visual Analysis of Retinal Layer Thickness with Optical Coherence Tomography. Information 2019, 10, 266. https://doi.org/10.3390/info10090266
Röhlig M, Prakasam RK, Stüwe J, Schmidt C, Stachs O, Schumann H. Enhanced Grid-Based Visual Analysis of Retinal Layer Thickness with Optical Coherence Tomography. Information. 2019; 10(9):266. https://doi.org/10.3390/info10090266
Chicago/Turabian StyleRöhlig, Martin, Ruby Kala Prakasam, Jörg Stüwe, Christoph Schmidt, Oliver Stachs, and Heidrun Schumann. 2019. "Enhanced Grid-Based Visual Analysis of Retinal Layer Thickness with Optical Coherence Tomography" Information 10, no. 9: 266. https://doi.org/10.3390/info10090266
APA StyleRöhlig, M., Prakasam, R. K., Stüwe, J., Schmidt, C., Stachs, O., & Schumann, H. (2019). Enhanced Grid-Based Visual Analysis of Retinal Layer Thickness with Optical Coherence Tomography. Information, 10(9), 266. https://doi.org/10.3390/info10090266