Semantic Information G Theory and Logical Bayesian Inference for Machine Learning
Abstract
1. Introduction
- Fisher’s likelihood method for hypothesis-testing [1];
- Carnap and Bar-Hillel’s semantic information formula with logical probability [9];
- Tarski’s truth theory for the definition of truth and logical probability [28];
- Davidson’s truth-conditional semantics [29];
- Kullback and Leibler’s KL divergence [5];
- Akaike’s proof [4] that the ML criterion is equal to the minimum KL divergence criterion;
- Theil’s generalized KL formula [37];
- the Donsker–Varadhan representation as a generalized KL formula with Gibbs density [38];
- Wittgenstein’s thought: meaning lies in uses (see [39], p. 80);
- making use of the prior knowledge of instances for probability predictions;
- multilabel learning, belonging to supervised learning;
- the Maximum Mutual Information (MMI) classifications of unseen instances, belonging to semi-supervised learning; and,
- mixture models, belonging to unsupervised learning.
2. Methods I: Background
2.1. From Shannon Information Theory to Semantic Information G Theory
2.1.1. From Shannon’s Mutual Information to Semantic Mutual Information
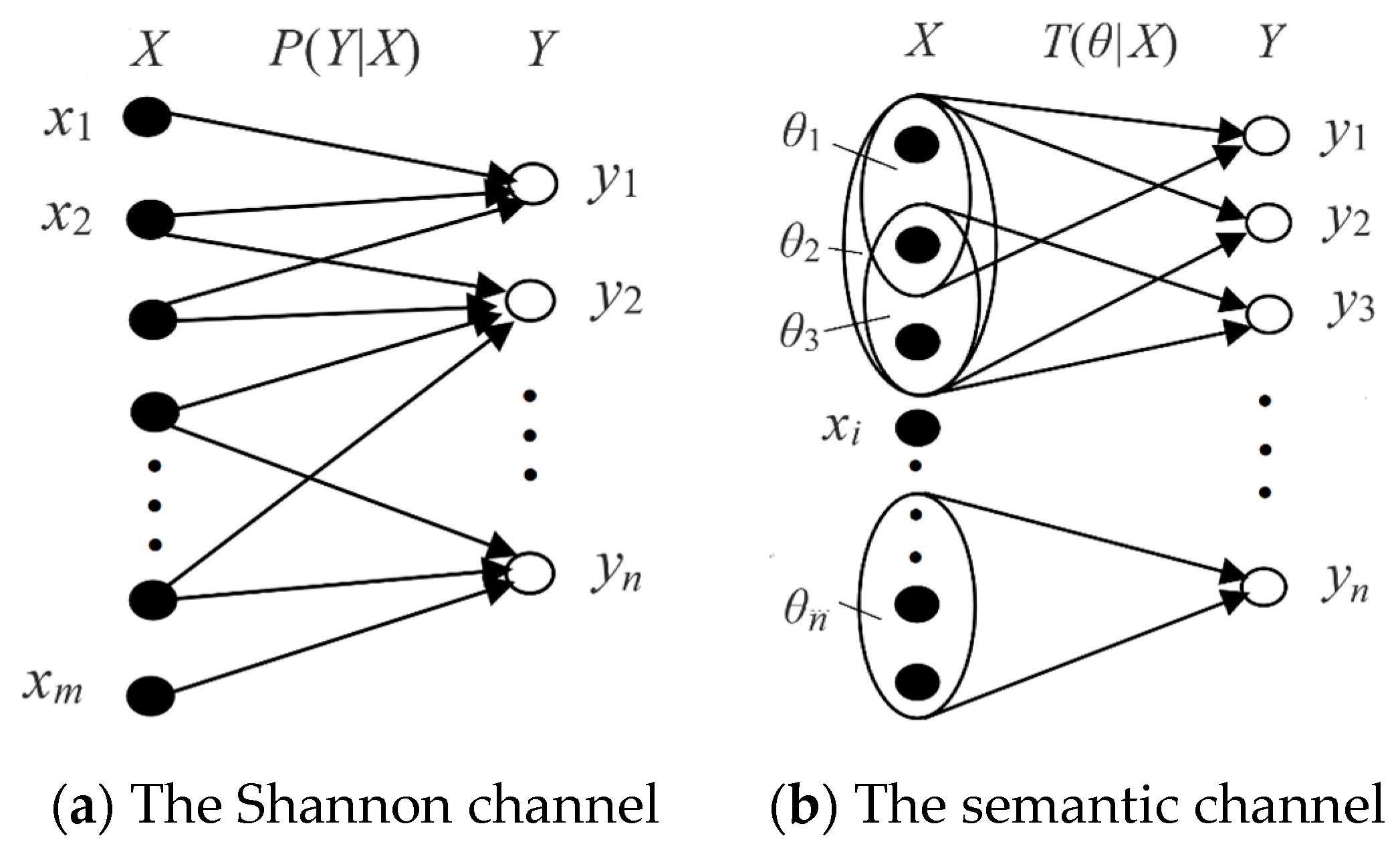
- x: an instance or data point; X: a discrete random variable taking a value x∈U = {x1, x2, …, xm}.
- y: a hypothesis or label; Y: a discrete random variable taking a value y∈V = {y1, y2, …, yn}.
- P(yj|x) (with fixed yj and variable x): a Transition Probability Function (TPF) (named as such by Shannon [7]).
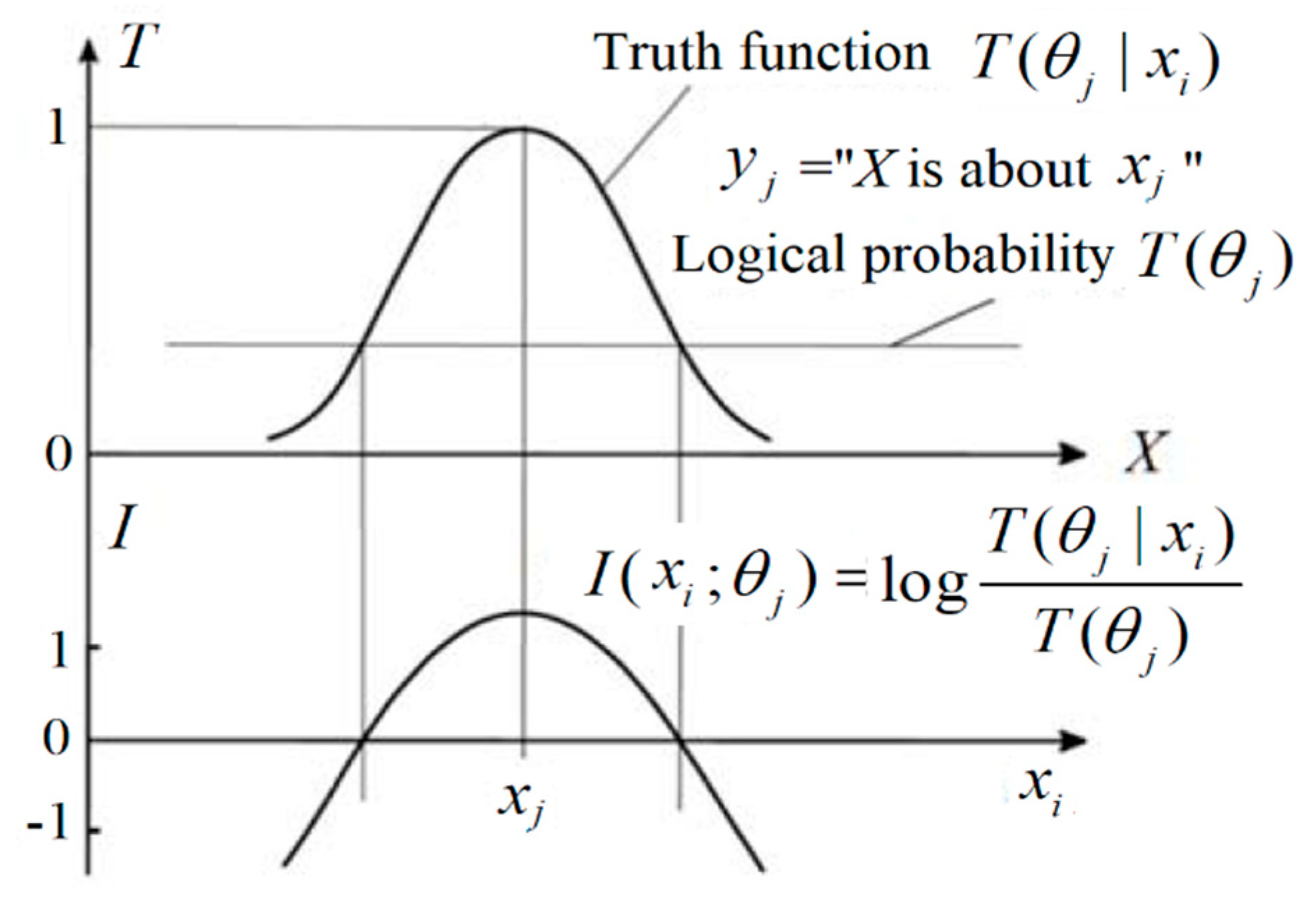
- θj is a fuzzy subset of U which is used to explain the semantic meaning of a predicate yj(X) = “X ϵ θj”. If θj is non-fuzzy, we may replace it with Aj. The θj is also treated as a model or a group of model parameters.
- A probability is defined with “=”, such that P(yj) = P(Y = yj), is a statistical probability; a probability is defined with “∈”, such as P(X∈θj), is a logical probability. To distinguish P(Y = yj) and P(X∈θj), we define T(θj) = P(X∈θj) as the logical probability of yj.
- T(θj|x) = P(x∈θj) = P(X∈θj|X = x) is the conditional logical probability function of yj; this is also called the (fuzzy) truth function of yj or the membership function of θj.
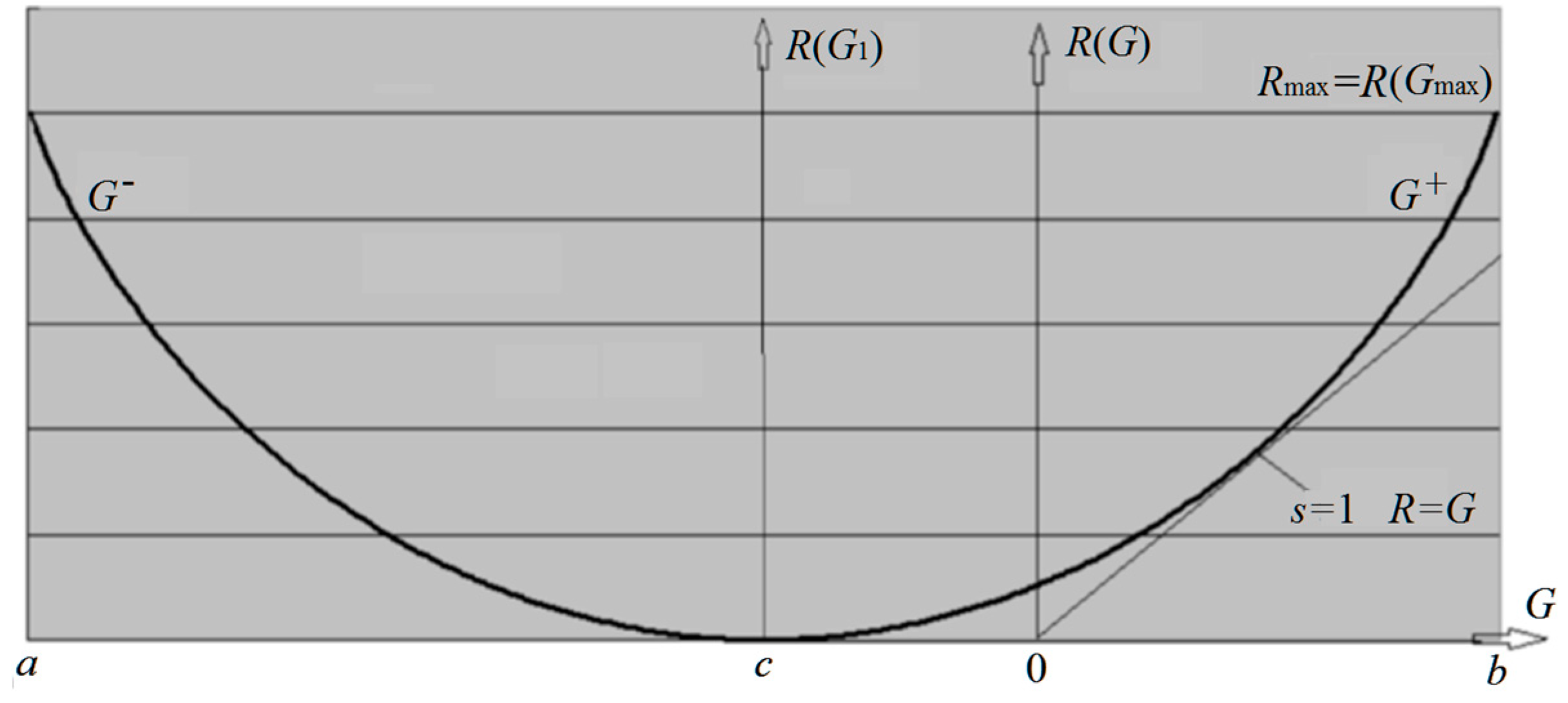
2.1.2. From the Rate-Distortion Function R(D) to the Rate-Verisimilitude Function R(G)
2.2. From Traditional Bayes Prediction to Logical Bayesian Inference
2.2.1. Traditional Bayes Prediction, Likelihood Inference (LI), and Bayesian Inference (BI)
- it is especially suitable to cases where Y is a random variable for a frequency generator, such as a dice;
- as the sample size increases, the distribution P(θ|X) will gradually shrink to some θj* coming from the MLE; and,
- BI can make use of prior knowledge better than LI.
- the probability prediction from BI [3] is not compatible with traditional Bayes prediction;
- P(θ) is subjectively selected; and,
- BI cannot make use of the prior of X.
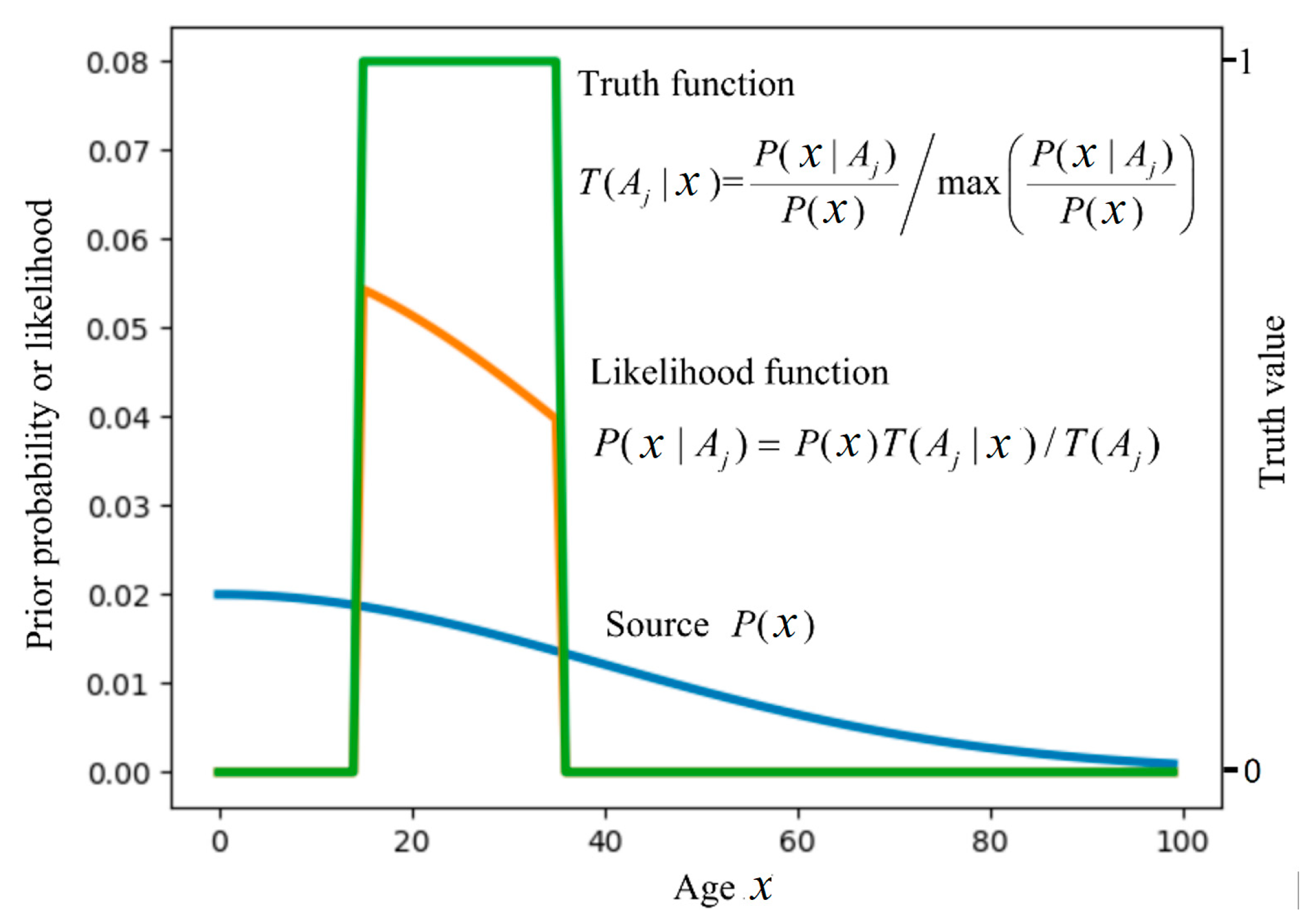
2.2.2. From Fisher’s Inverse Probability Function P(θj|x) to Logical Bayesian Inference (LBI)
- we can use an optimized truth function T*(θj|x) to make probability predictions for different P(x) just as we would use P(yj|x) or P(θj|x);
- we can train a truth function with parameters by a sample with small size, as we would train a likelihood function;
- the truth function indicates the semantic meaning of a hypothesis and, hence, is easy for us to understand;
- it is also the membership function, which indicates the denotation of a label or the range of a class and, hence, is suitable for classification;
- to train a truth function, we only need P(x) and P(x|yj), without needing P(yj) or P(θj); and,
- letting T(θj|x)∝P(yj|x), we construct a bridge between statistics and logic.
3. Methods II: The Channel Matching (CM) Algorithms
3.1. CM1: To Resolve the Multilabel-Learning-for-New-P(x) Problem
3.1.1. Optimizing Truth Functions or Membership Functions
3.1.2. For the Confirmation Measure of Major Premises
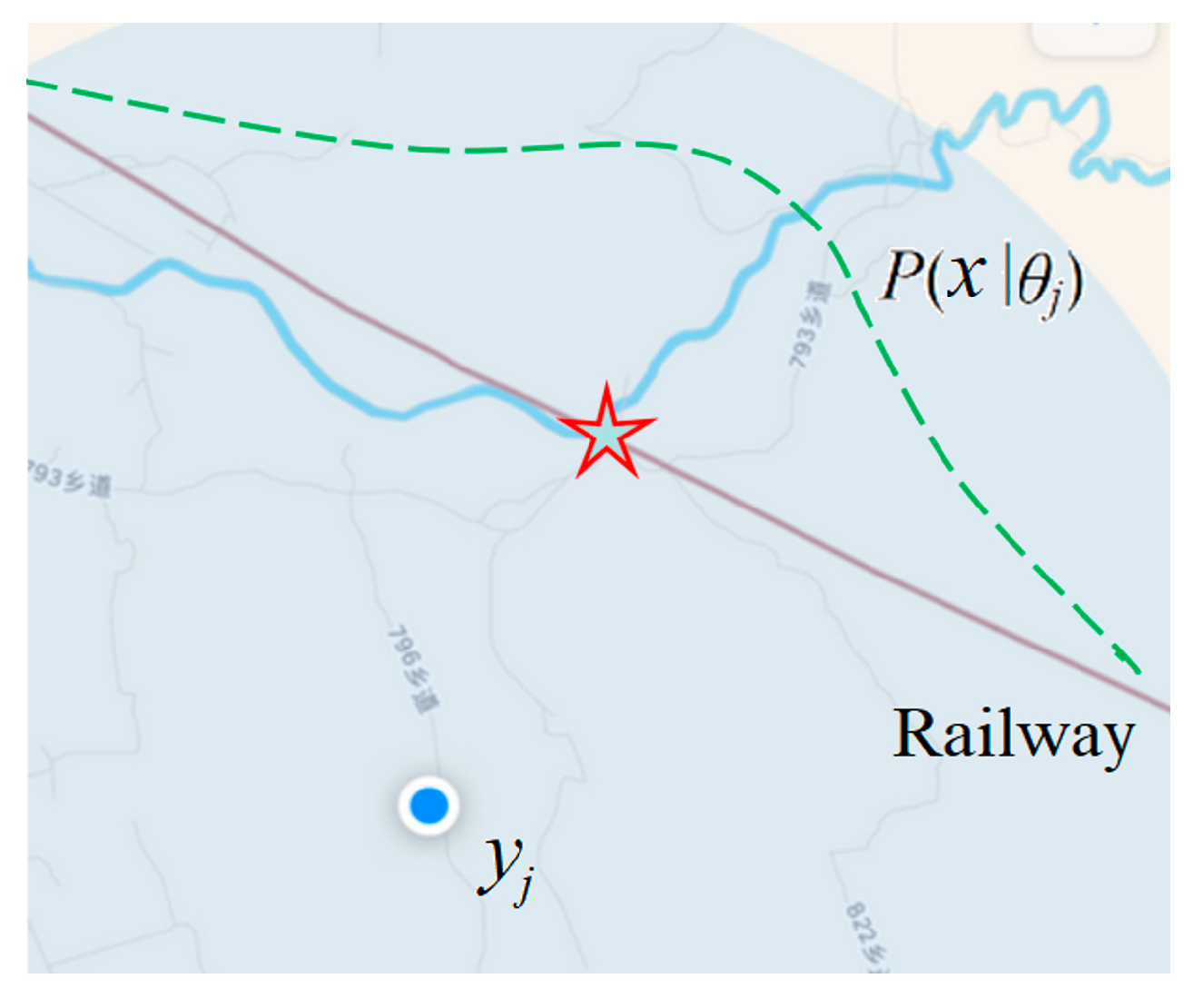
3.1.3. Rectifying the Parameters of a GPS Device
3.2. CM2: The Semantic Channel and the Shannon Channel Mutually Match for Multilabel Classifications
- Matching I: Let the semantic channel match the Shannon channel or use CM1 for multilabel learning; and,
- Matching II: Let the Shannon channel match the semantic channel by using the Maximum Semantic Information (MSI) classifier.
3.3. CM3: the CM Iteration Algorithm for MMI Classification of Unseen Instances
3.4. CM4: the CM-EM Algorithm for Mixture Models
- R(G) − G is close to the relative entropy H(P‖Pθ).
4. Results
4.1. The Results of CM2 for Multilabel Learning and Classification
4.2. The Results of CM3 for the MMI classifications of Unseen Instances
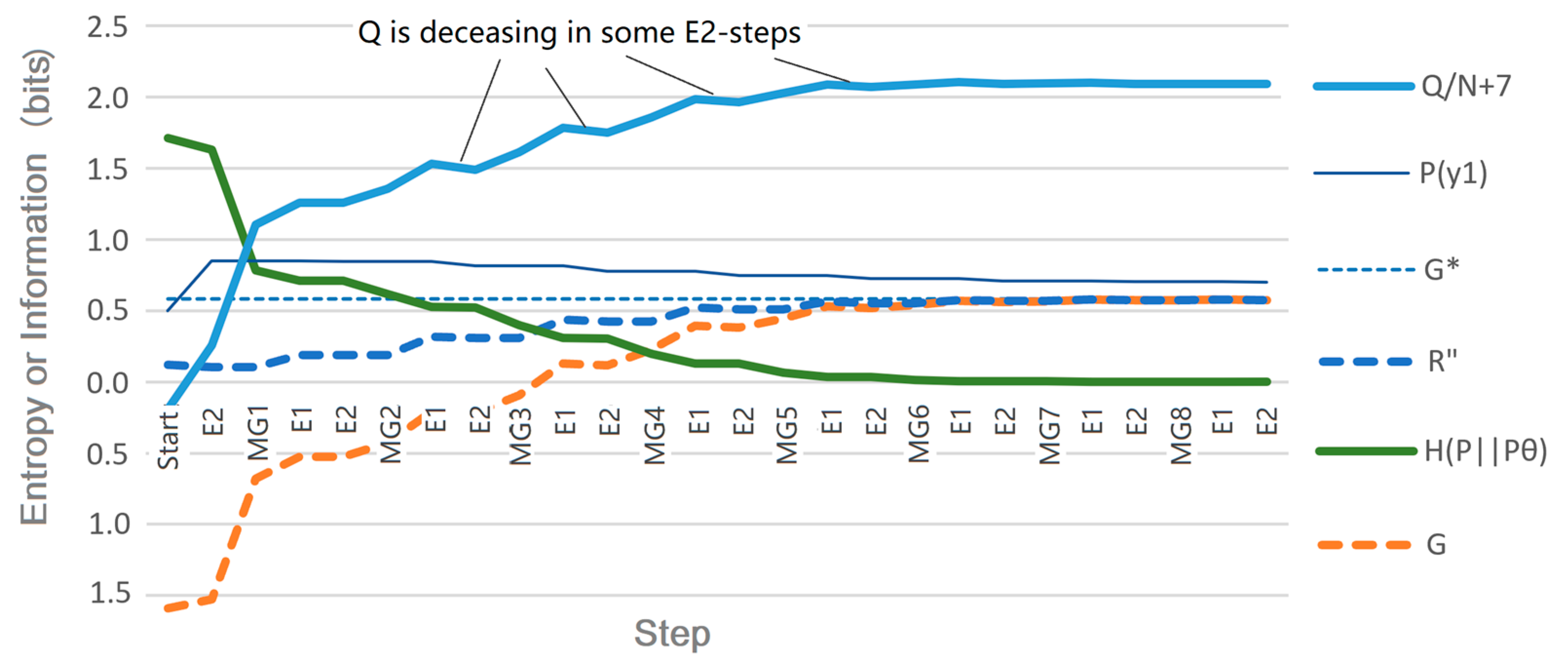
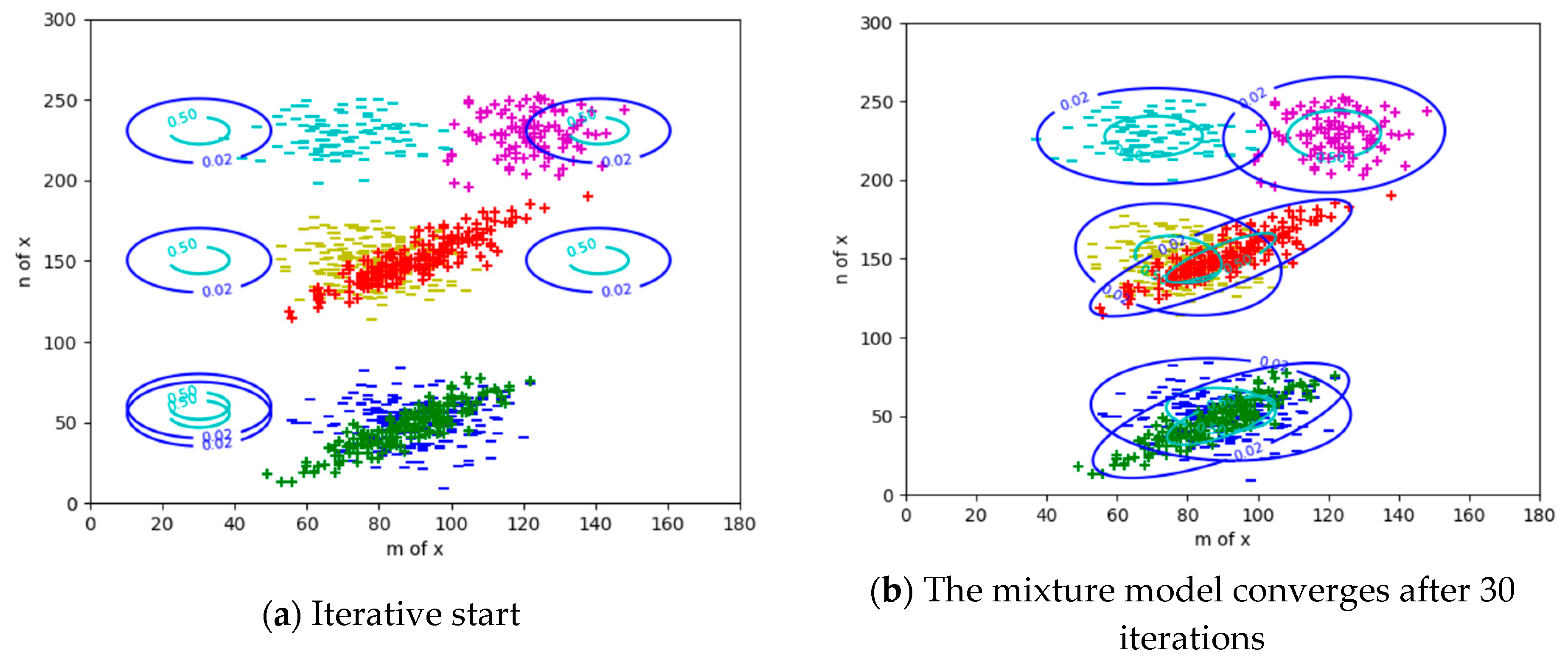
4.3. The Results of CM4 for Mixture Models
5. Discussion
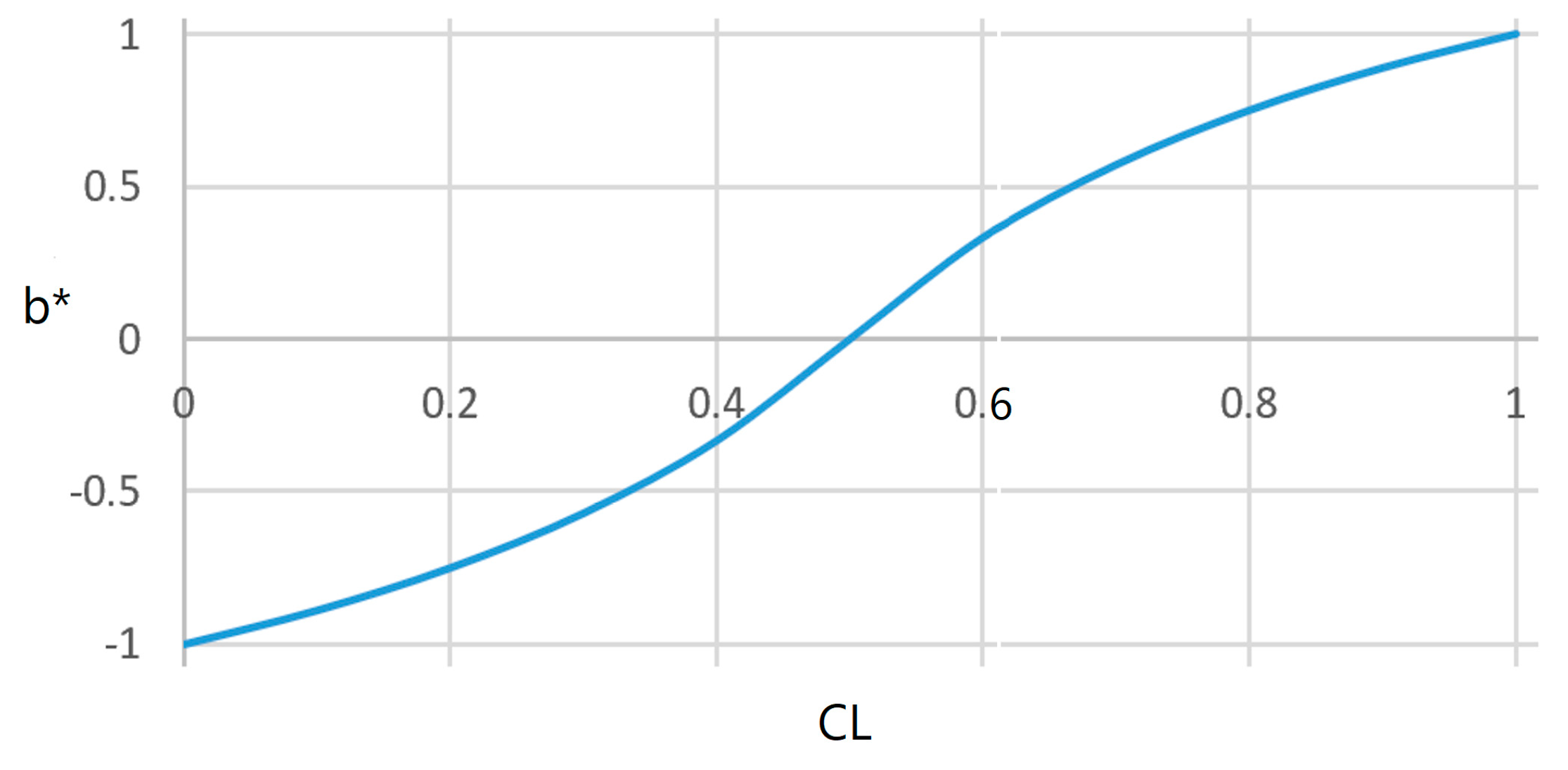
5.1. Discussing Confirmation Measure b*
5.2. Discussing CM2 for the Multilabel Classification
5.3. Discussing CM3 for the MMI Classification of Unseen Instances
5.4. Discussing CM4 for mixture models
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BI | Bayesian Inference |
| CM | Channel Matching |
| CM-EM | Channel Matching Expectation-Maximization |
| EM | Expectation-Maximization |
| G theory | Semantic information G theory |
| GPS | Global Positioning System |
| HIV | Human Immunodeficiency Virus |
| IPF | Inverse Probability Function |
| KL | Kullback-Leibler |
| LBI | Logical Bayesian Inference |
| LI | Likelihood Inference |
| MLE | Maximum Likelihood Estimation |
| MM | Maximum Mutual Information |
| MMI | Maximization-Maximization |
| MPP | Maximum Posterior Probability |
| MSI | Maximum Semantic Information |
| MSIE | Maximum Semantic Information Estimation |
| SMI | Semantic Mutual Information |
| SHMI | Shannon’s Mutual Information |
| TBP | Traditional Bayes Prediction |
| TPF | Transition Probability Function |
Appendix A
| Program Name | Task |
|---|---|
| Bayes Theorem III 2.py | For Figure 9. To show label learning. |
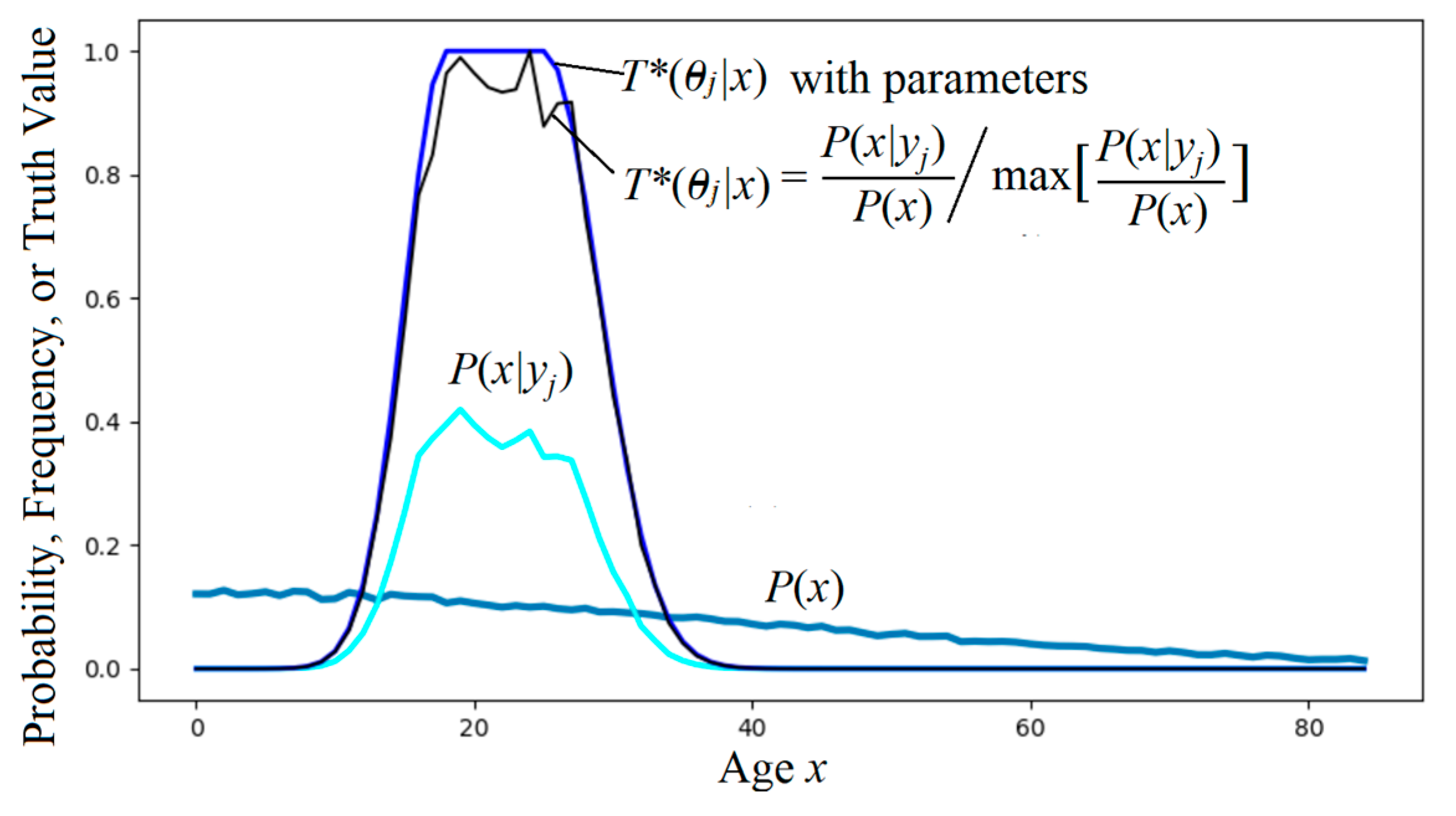
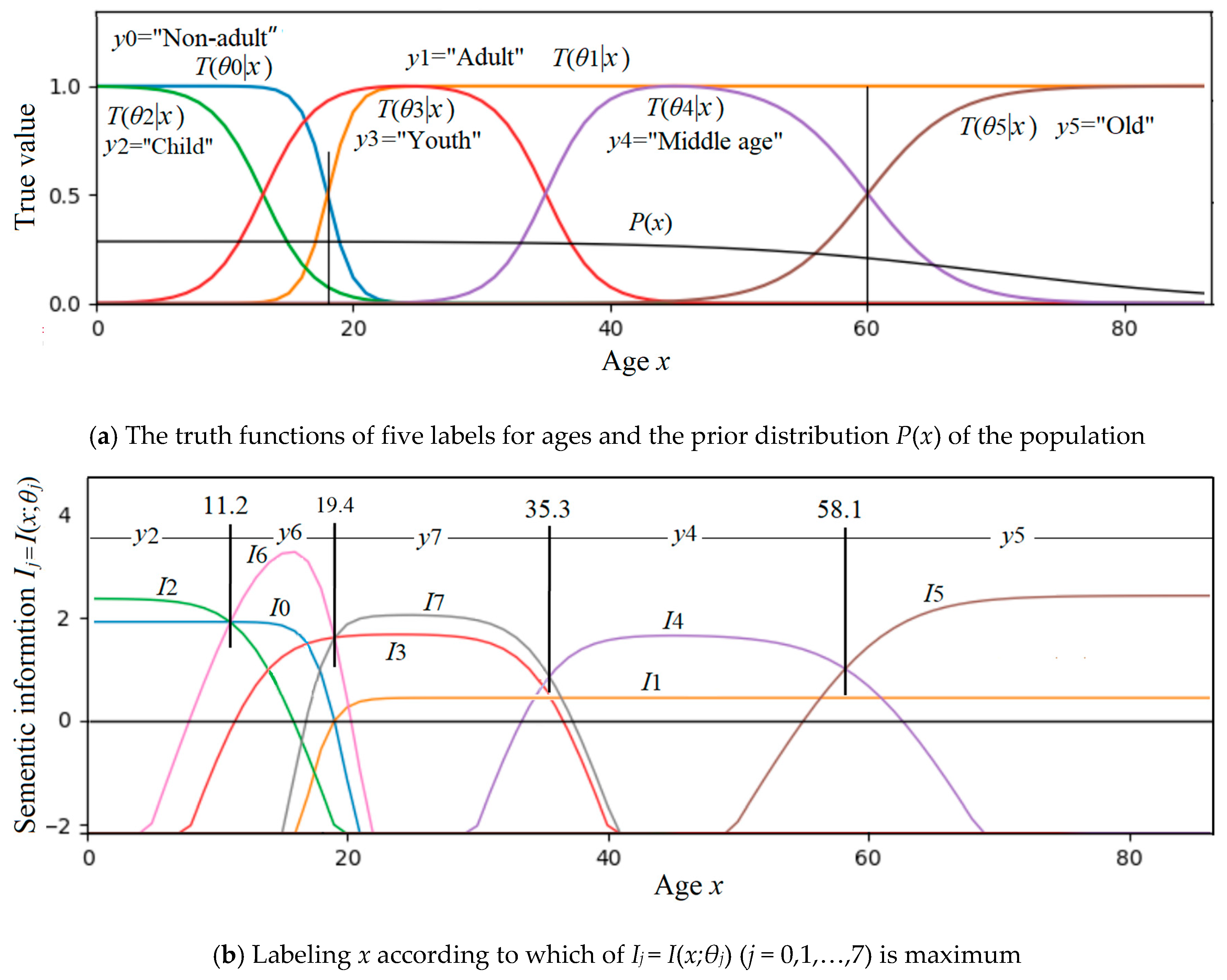
| Ages-MI-classification.py | For Figure 10. To show people classification on ages using maximum semantic information criterion for given membership functions and P(x). |
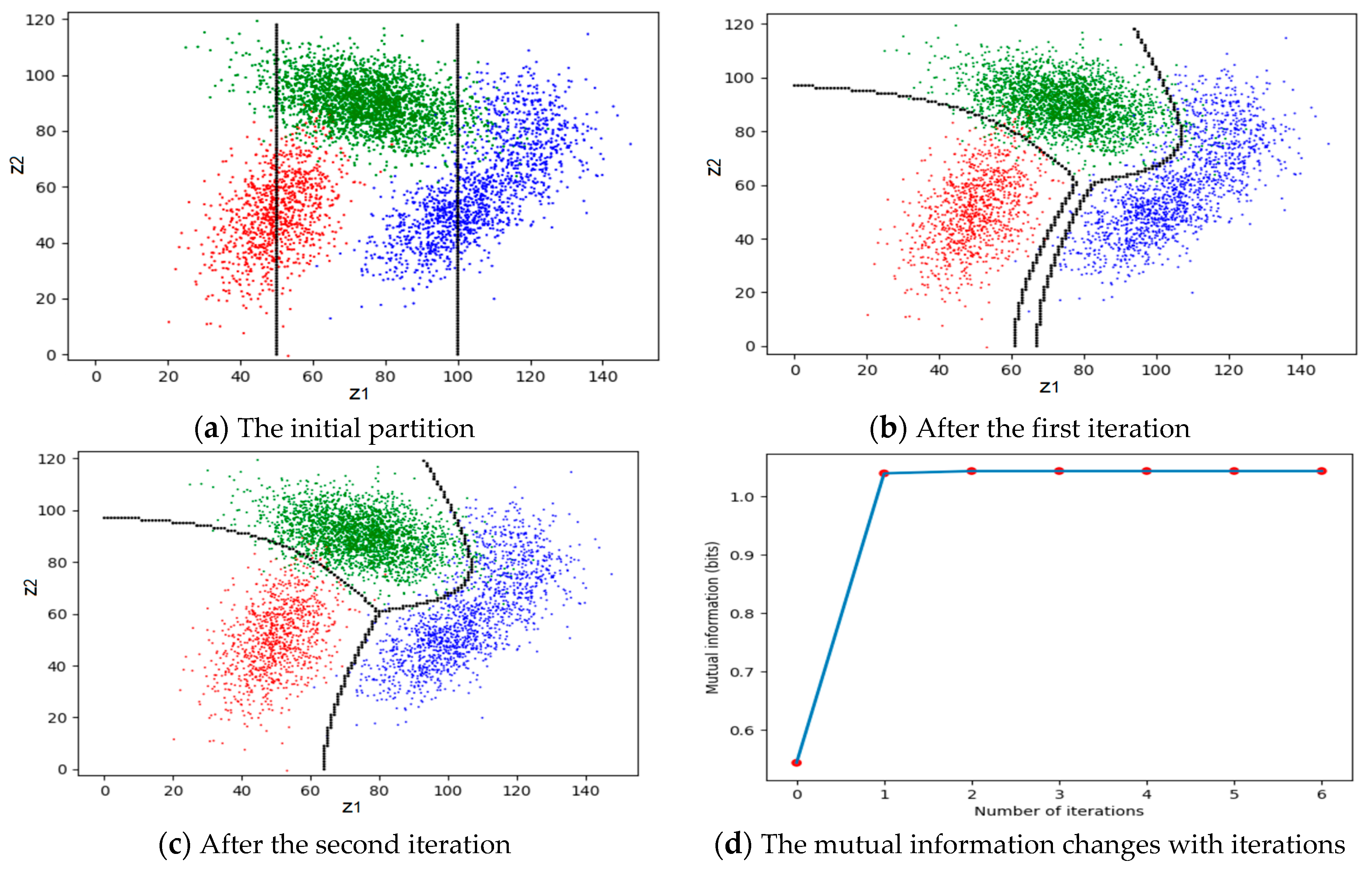
| MMI-v.py | For Figure 11. To show the Channels Matching (CM) algorithm for the maximum mutual information classifications of unseen instances. One can modify parameters or the initial partition in the program for different result. |
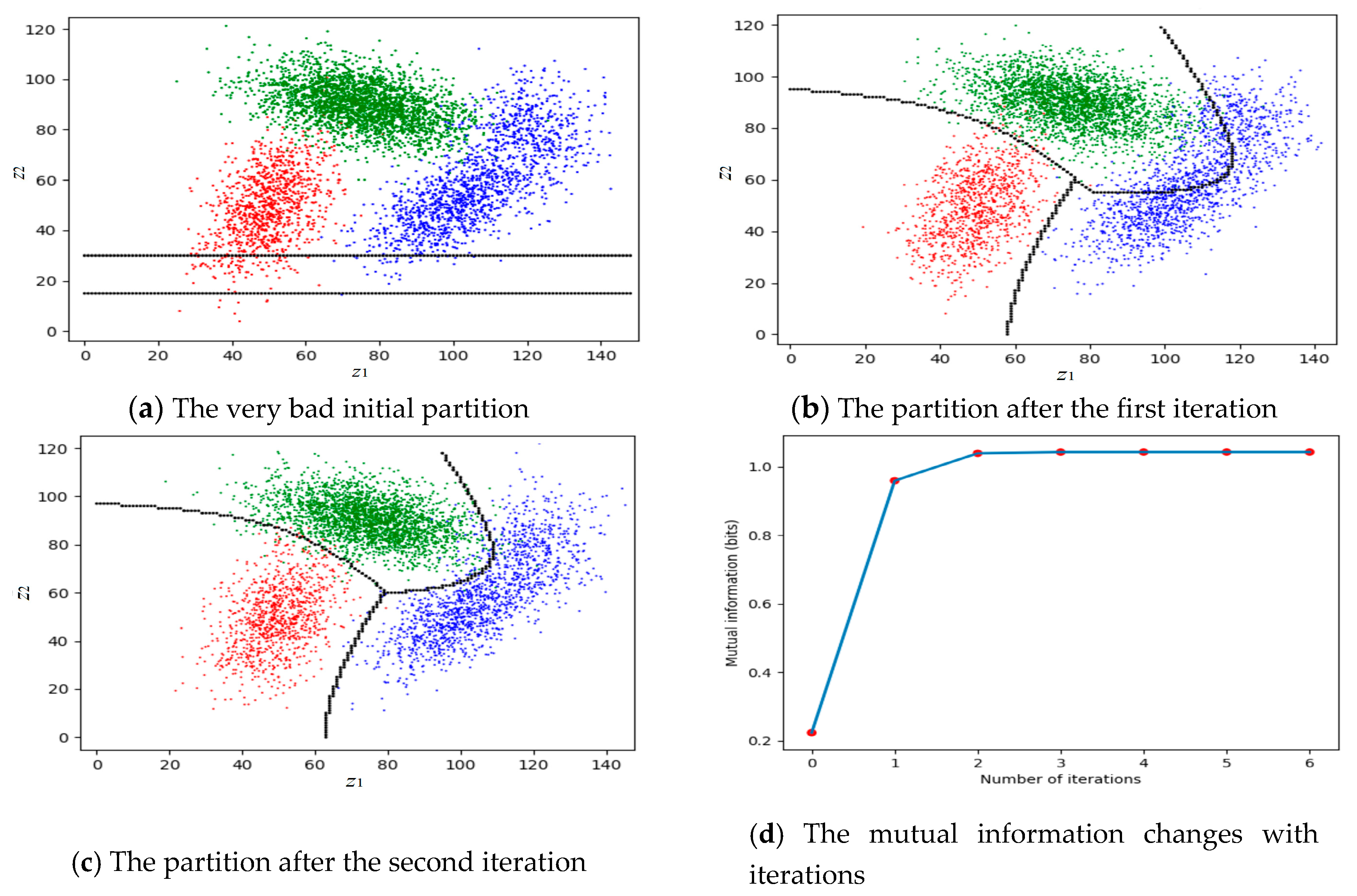
| MMI-H.py | For Figure 12. |
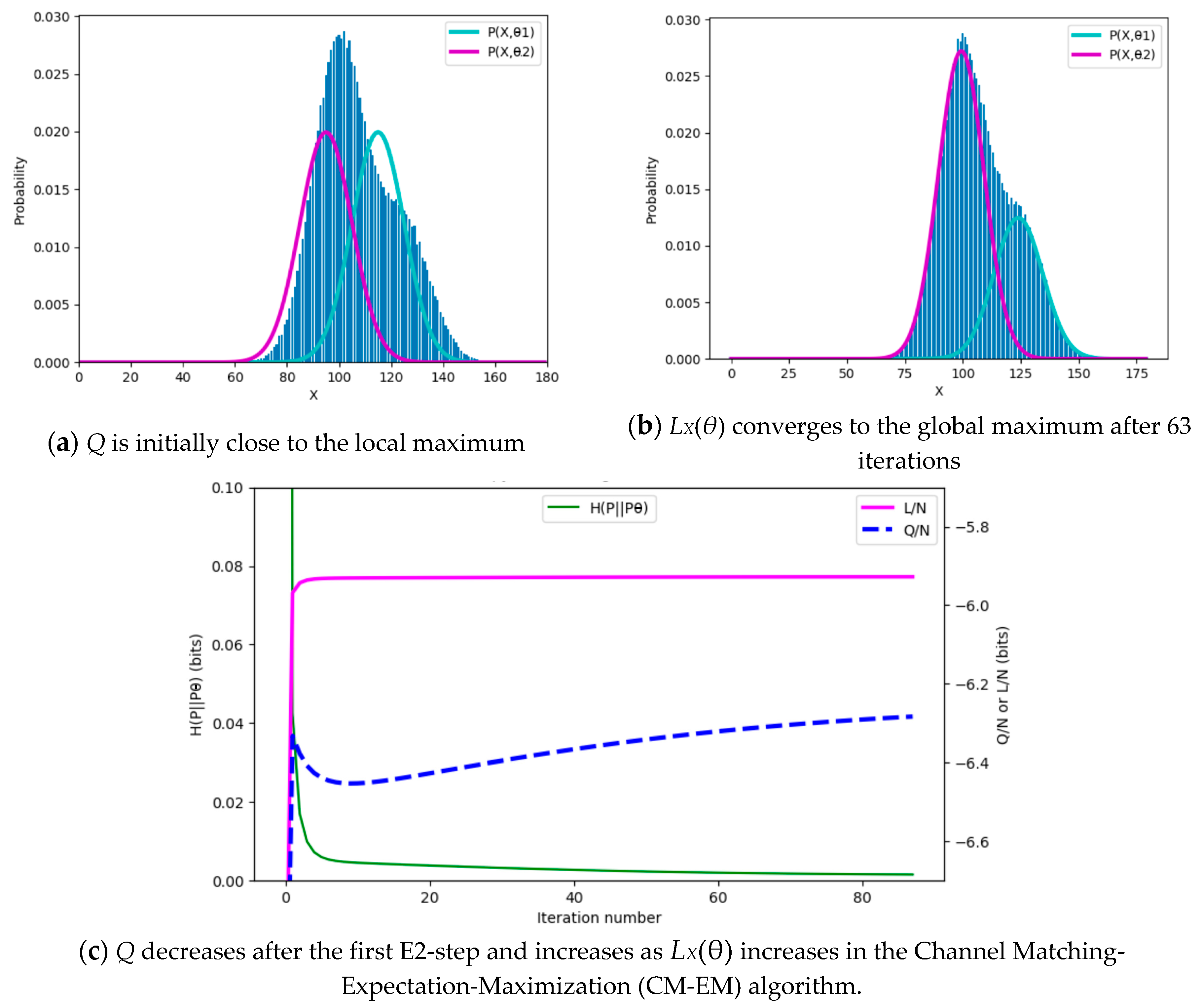
| LocationTrap3lines.py | For Figure 13. To show how the CM-EM algorithm for mixture models avoids local convergence because of the local maximum of Q. |
| Folder ForEx6 (with Excel file and Word readme file) | For Figure 14. To show the effect of every step of the CM-EM algorithm for mixture models. |
| MixModels6-2valid.py | For Figure 15. To show the CM-EM algorithm of for a two-dimensional mixture models with seriously overlapped components. |
References
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Fienberg, S.E. When Did Bayesian Inference Become “Bayesian”? Bayesian Anal. 2006, 1, 1–40. [Google Scholar] [CrossRef]
- Bayesian Inference. In Wikipedia: The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Bayesian_inference (accessed on 3 March 2019).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–429, 623–656. [Google Scholar] [CrossRef]
- Weaver, W. Recent contributions to the mathematical theory of communication. In The Mathematical Theory of Communication, 1st ed.; Shannon, C.E., Weaver, W., Eds.; The University of Illinois Press: Urbana, IL, USA, 1963; pp. 93–117. [Google Scholar]
- Carnap, R.; Bar-Hillel, Y. An Outline of a Theory of Semantic Information; Tech. Rep. No. 247; Research Laboratory of Electronics, MIT: Cambridge, MA, USA, 1952. [Google Scholar]
- Bonnevie, E. Dretske’s semantic information theory and metatheories in library and information science. J. Doc. 2001, 57, 519–534. [Google Scholar] [CrossRef]
- Floridi, L. Outline of a theory of strongly semantic information. Minds Mach. 2004, 14, 197–221. [Google Scholar] [CrossRef]
- Zhong, Y.X. A theory of semantic information. China Commun. 2017, 14, 1–17. [Google Scholar] [CrossRef]
- D’Alfonso, S. On Quantifying Semantic Information. Information 2011, 2, 61–101. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a non-probabilistic entropy in setting of fuzzy sets. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Bhandari, D.; Pal, N.R. Some new information measures of fuzzy sets. Inf. Sci. 1993, 67, 209–228. [Google Scholar] [CrossRef]
- Kumar, T.; Bajaj, R.K.; Gupta, B. On some parametric generalized measures of fuzzy information, directed divergence and information Improvement. Int. J. Comput. Appl. 2011, 30, 5–10. [Google Scholar]
- Klir, G. Generalized information theory. Fuzzy Sets Syst. 1991, 40, 127–142. [Google Scholar] [CrossRef]
- Wang, Y. Generalized Information Theory: A Review and Outlook. Inf. Technol. J. 2011, 10, 461–469. [Google Scholar] [CrossRef][Green Version]
- Belghazi, I.; Rajeswar, S.; Baratin, A.; Hjelm, R.D.; Courville, A. Mine: Mutual information neural estimation. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2018; Available online: https://arxiv.org/abs/1801.04062 (accessed on 1 January 2019).
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Trischler, A.; Bengio, Y. Learning Deep Representations by Mutual Information Estimation and Maximization. Available online: https://arxiv.org/abs/1808.06670 (accessed on 22 February 2019).
- Lu, C. Shannon equations reform and applications. BUSEFAL 1990, 44, 45–52. Available online: https://www.listic.univ-smb.fr/production-scientifique/revue-busefal/version-electronique/ebusefal-44/ (accessed on 5 March 2019).
- Lu, C. B-fuzzy quasi-Boolean algebra and a generalize mutual entropy formula. Fuzzy Syst. Math. 1991, 5, 76–80. (in Chinese). [Google Scholar]
- Lu, C. A Generalized Information Theory; China Science and Technology University Press: Hefei, China, 1993; ISBN 7-312-00501-2. (in Chinese) [Google Scholar]
- Lu, C. Meanings of generalized entropy and generalized mutual information for coding. J. China Inst. Commun. 1994, 15, 37–44. (in Chinese). [Google Scholar]
- Lu, C. A generalization of Shannon’s information theory. Int. J. Gen. Syst. 1999, 28, 453–490. [Google Scholar] [CrossRef]
- Lu, C. GPS information and rate-tolerance and its relationships with rate distortion and complexity distortions. J. Chengdu Univ. Inf. Technol. 2012, 6, 27–32. (In Chinese) [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Tarski, A. The semantic conception of truth: and the foundations of semantics. Philos. Phenomenol. Res. 1994, 4, 341–376. [Google Scholar] [CrossRef]
- Davidson, D. Truth and meaning. Synthese 1967, 17, 304–323. [Google Scholar] [CrossRef]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Nat. Conv. Rec. 1959, 4, 142–163. [Google Scholar]
- Popper, K. The Logic of Scientific Discovery, 1st ed.; Routledge: London, UK, 1959. [Google Scholar]
- Popper, K. Conjectures and Refutations, 1st ed.; Routledge: London, UK, 2002. [Google Scholar]
- Goodfellow, I.; Bengio, Y. Deep Learning, 1st ed.; The MIP Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Carnap, R. Logical Foundations of Probability, 1st ed.; University of Chicago Press: Chicago, IL, USA, 1950. [Google Scholar]
- Zadeh, L.A. Probability measures of fuzzy events. J. Math. Anal. Appl. 1986, 23, 421–427. [Google Scholar] [CrossRef]
- Floridi, L. Semantic conceptions of information. In Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2005; Available online: http://seop.illc.uva.nl/entries/information-semantic/ (accessed on 1 July 2019).
- Theil, H. Economics and Information Theory; North-Holland Pub. Co.: Amsterdam, The Netherlands; Rand McNally: Chicago, IL, USA, 1967. [Google Scholar]
- Donsker, M.; Varadhan, S. Asymptotic evaluation of certain Markov process expectations for large time IV. Commun. Pure Appl. Math. 1983, 36, 183–212. [Google Scholar] [CrossRef]
- Wittgenstein, L. Philosophical Investigations; Basil Blackwell Ltd: Oxford, UK, 1958. [Google Scholar]
- Bayes, T.; Price, R. An essay towards solving a problem in the doctrine of chance. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Lu, C. From Bayesian inference to logical Bayesian inference: A new mathematical frame for semantic communication and machine learning. In Intelligence Science II, Proceedings of the ICIS2018, Beijing, China, 2 October 2018; Shi, Z.Z., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 11–23. [Google Scholar]
- Lu, C. Channels’ matching algorithm for mixture models. In Intelligence Science I, Proceedings of ICIS 2017, Beijing, China, 27 September 2017; Shi, Z.Z., Goertel, B., Feng, J.L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 321–332. [Google Scholar]
- Lu, C. Semantic channel and Shannon channel mutually match and iterate for tests and estimations with maximum mutual information and maximum likelihood. In Proceedings of the 2018 IEEE International Conference on Big Data and Smart Computing, Shanghai, China, 15 January 2018; IEEE Computer Society Press Room: Washington, DC, USA, 2018; pp. 15–18. [Google Scholar]
- Lu, C. Semantic channel and Shannon channel mutually match for multi-label classification. In Intelligence Science II, Proceedings of ICIS 2018, Beijing, China, 2 October 2018; Shi, Z.Z., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 37–48. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy sets and probability: Misunderstandings, bridges and gaps. In Proceedings of the 1993 Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March 1993. [Google Scholar]
- Thomas, S.F. Possibilistic uncertainty and statistical inference. In Proceedings of the ORSA/TIMS Meeting, Houston, TX, USA, 11–14 October 1981. [Google Scholar]
- Wang, P.Z. From the fuzzy statistics to the falling fandom subsets. In Advances in Fuzzy Sets, Possibility Theory and Applications; Wang, P.P., Ed.; Plenum Press: New York, NY, 1983; pp. 81–96. [Google Scholar]
- Berger, T. Rate Distortion Theory; Prentice-Hall: Enklewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Thornbury, J.R.; Fryback, D.G.; Edwards, W. Likelihood ratios as a measure of the diagnostic usefulness of excretory urogram information. Radiology 1975, 114, 561–565. [Google Scholar] [CrossRef]
- OraQuick. Available online: http://www.oraquick.com/Home (accessed on 31 December 2016).
- Zhang, M.L.; Zhou, Z.H. A review on multi-label learning algorithm. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Zhang, M.L.; Li, Y.K.; Liu, X.Y.; Geng, X. Binary relevance for multi-label learning: An overview. Front. Comput. Sci. 2018, 12, 191–202. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B 1997, 39, 1–38. [Google Scholar] [CrossRef]
- Ueda, N.; Nakano, R. Deterministic annealing EM algorithm. Neural Netw. 1998, 11, 271–282. [Google Scholar] [CrossRef]
- Marin, J.-M.; Mengersen, K.; Robert, C.P. Bayesian modelling and inference on mixtures of distributions. In Handbook of Statistics: Bayesian Thinking, Modeling and Computation; Dey, D., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 459–507. [Google Scholar]
- Neal, R.; Hinton, G. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models; Michael, I.J., Ed.; MIT Press: Cambridge, MA, USA, 1999; pp. 355–368. [Google Scholar]
- Lu, C. From the EM Algorithm to the CM-EM Algorithm for Global Convergence of Mixture Models. Available online: https://arxiv.org/abs/18 (accessed on 26 October 2018).
- James, H. Inductive logic. In The Stanford Encyclopedia of Philosophy; Edward, N.Z., Ed.; Stanford University Press: Palo Alto, CA, USA, 2018; Available online: https://plato.stanford.edu/archives/spr2018/entries/logic-inductive/ (accessed on 19 March 2018).
- Tentori, K.; Crupi, V.; Bonini, N.; Osherson, D. Comparison of confirmation measures. Cognition 2007, 103, 107–119. [Google Scholar] [CrossRef]
- Ellery, E.; Fitelson, B. Measuring confirmation and evidence. J. Philos. 2000, 97, 663–672. [Google Scholar]
- Huang, W.H.; Chen, Y.G. The multiset EM algorithm. Stat. Probab. Lett. 2017, 126, 41–48. [Google Scholar] [CrossRef]
- Ueda, N.; Nakano, R.; Ghahramani, Z.; Hinton, G.E. SMEM algorithm for mixture models. Neural Comput. 2000, 12, 2109–2128. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, C.; Yi, X. Competitive EM algorithm for finite mixture models. Pattern Recognit. 2004, 37, 131–144. [Google Scholar] [CrossRef]
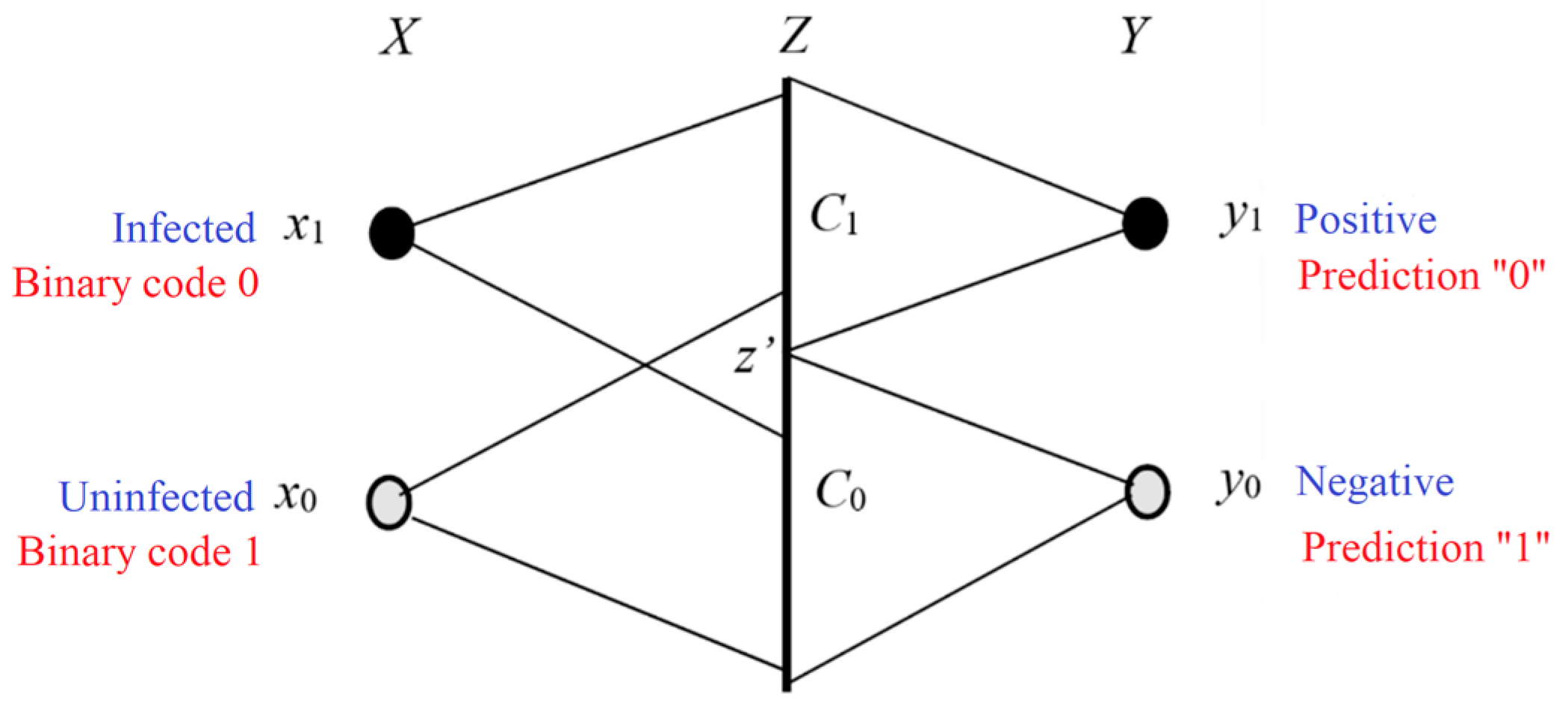

| Infected Subject x1 | Uninfected Subject x0 | |
|---|---|---|
| Positive y1 | P(y1|x1) = sensitivity = 0.917 | P(y1|x0) = 1 − specificity = 0.001 |
| Negative y0 | P(y0|x1) = 1 − sensitivity = 0.083 | P(y0|x0) = specificity = 0.999 |
| Y | Infected x1 | Uninfected x0 |
|---|---|---|
| Positive y1 | T(θ1|x1) = 1 | T(θ1|x0) = b1′ |
| Negative y0 | T(θ0|x1) = b0′ | T(θ0|x0) = 1 |
| μz1 | μz2 | σz1 | σz2 | ρ | P(xi) | |
|---|---|---|---|---|---|---|
| P(z|x0) | 50 | 50 | 75 | 200 | 50 | 0.2 |
| P(z|x1) | 75 | 90 | 200 | 75 | −50 | 0.5 |
| P(z|x21) | 100 | 50 | 125 | 125 | 75 | 0.2 |
| P(z|x22) | 120 | 80 | 75 | 125 | 0 | 0.1 |
| Real Parameters | Starting Parameters H(P‖Pθ) = 0.68 bit | Parameters after 9 E2-Steps H(P‖Pθ) = 0.00072 bit | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| μ* | σ* | P*(Y) | μ | σ | P(Y) | μ | σ | P(Y) | ||
| y1 | 46 | 2 | 0.7 | 30 | 20 | 0.5 | 46.001 | 2.032 | 0.6990 | |
| y2 | 50 | 20 | 0.3 | 70 | 20 | 0.5 | 50.08 | 19.17 | 0.3010 | |
| Algorithm | Sample Size | Iteration Number | Convergent Parameters | ||||
|---|---|---|---|---|---|---|---|
| μ1 | μ2 | σ1 | σ2 | P(y1) | |||
| EM | 1000 | about 36 | 46.14 | 49.68 | 1.90 | 19.18 | 0.731 |
| MM | 1000 | about 18 | 46.14 | 49.68 | 1.90 | 19.18 | 0.731 |
| CM-EM | 1000 | 8 | 46.01 | 49.53 | 2.08 | 21.13 | 0.705 |
| Real parameters | 46 | 50 | 2 | 20 | 0.7 | ||
| About | Gradient Descent | CM3 |
|---|---|---|
| Models for different classes | Optimized together | Optimized separately |
| Boundaries is expressed by | Functions with parameters | Numerical values |
| For complicated boundaries | Not easy | Easy |
| Consider gradient and search | Necessary | Unnecessary |
| Convergence | Not easy | Easy |
| Computation | Complicated | Simple |
| Iterations needed | Many | 2–3 |
| Samples required | Not necessarily big | Big enough |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C. Semantic Information G Theory and Logical Bayesian Inference for Machine Learning. Information 2019, 10, 261. https://doi.org/10.3390/info10080261
Lu C. Semantic Information G Theory and Logical Bayesian Inference for Machine Learning. Information. 2019; 10(8):261. https://doi.org/10.3390/info10080261
Chicago/Turabian StyleLu, Chenguang. 2019. "Semantic Information G Theory and Logical Bayesian Inference for Machine Learning" Information 10, no. 8: 261. https://doi.org/10.3390/info10080261
APA StyleLu, C. (2019). Semantic Information G Theory and Logical Bayesian Inference for Machine Learning. Information, 10(8), 261. https://doi.org/10.3390/info10080261




