Using an Exponential Random Graph Model to Recommend Academic Collaborators
Abstract
1. Introduction
2. Background
2.1. Collaboration and Social Context
2.2. Exponential Random Graph Model
- is the probability of the entire graph being conditional on parameters represented by ;
- is a normalizing constant;
- is a vector of parameters associated with the graph statistics; and
- is a vector of the graph statistics.
3. Related Work
3.1. Recommending Collaborators
3.2. Recommending Collaborators Based on Social Context
3.3. RSs Based on the ERGM
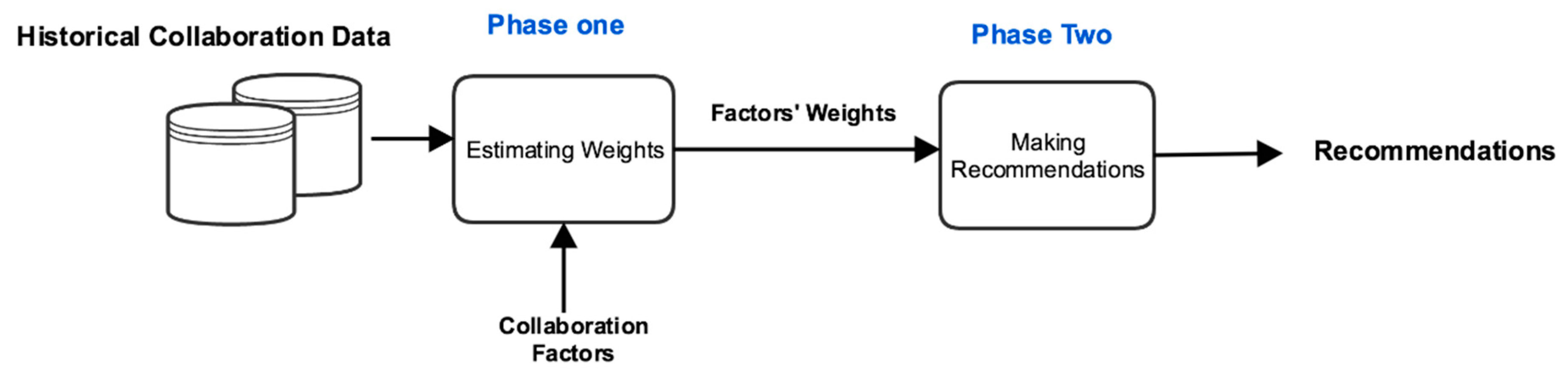
4. Methodology Used
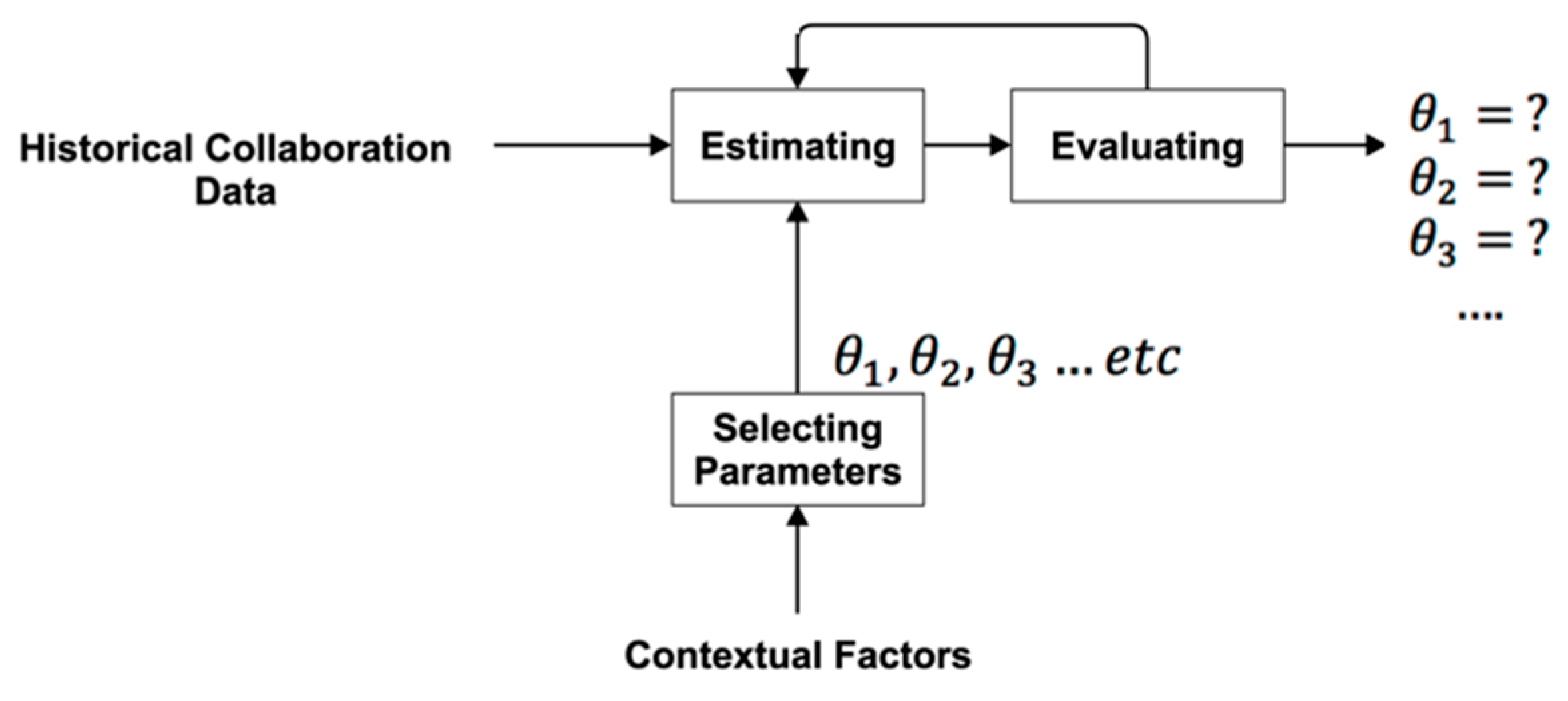
4.1. Phase One: Estimating Weights
- Historical collaboration data: Historical collaboration data play an important role in building and testing context-aware RSs. Historical collaboration data are data related to the collaborations of a group of researchers in a particular scientific community from a previous time period. These data include historical collaboration networks, research areas of individuals in the collaboration network, and centrality scores for these individuals. The observed collaboration network is a historical collaboration network.
- Selecting parameters: Contextual parameters that match the theories about collaboration factors must be selected. For example, because it is assumed that researchers choose to collaborate with similar and influential researchers, the following parameters are selected: research areas; social context parameters used to measure influence, such as degree centrality; betweenness centrality; and eigenvector centrality. These parameters represent different actor attributes. In addition, standard parameters corresponding to network topology can be included [34]. Each parameter corresponds to a network configuration, which in turn corresponds to a network theory.
- Estimating: Estimating can involve systematically searching through possible parameter values until the right estimate is achieved. The outputs are the estimated weights for the chosen parameters. These values are validated through evaluation.
- Evaluating: The estimated parameters are evaluated using goodness of fit (GOF), which is a statistical approach for assessing how well estimated parameters fit the observed data using a t-ratio [33]. This method is included in the ERGM package and involves a simulation of networks using estimated parameters and summary statistics. The statistics of simulated networks are compared with the actual network using a t-ratio.
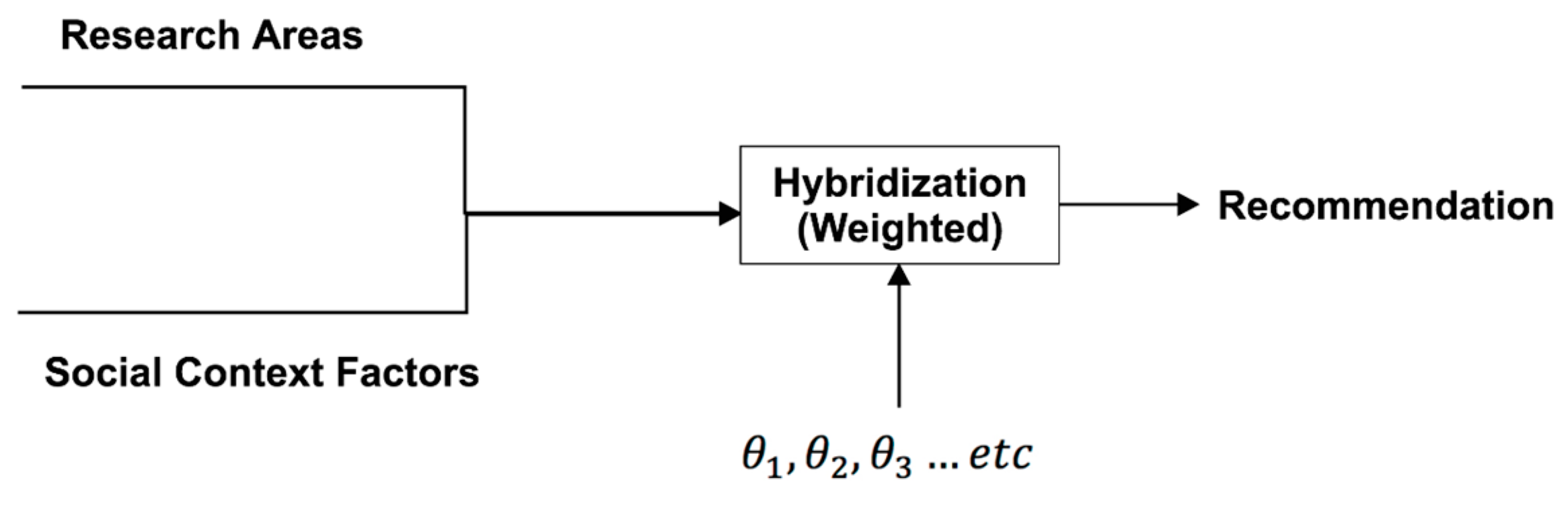
4.2. Phase Two: Making Recommendations
- is a variable that shows whether a given user and collaborator have similar research areas;
- is the weight for the given factor ; and
- is the value of context factor for potential collaborator
5. Implementation
- Scopus: Scopus is one of largest abstract and citation databases for peer-reviewed literature, including scientific journals, books, and conference proceedings. Publications from two years (2013, 2014) were collected for faculty members associated with the College of Computer and Information Sciences (CCIS) that are indexed by Scopus.
- College annual report: The college annual report details the main activities and achievements of students and faculty members each year. This information includes a list of the different types of publications for each faculty member indexed in Scopus and in other citation databases.
- Faculty websites: Every faculty has a webpage hosted on the university server that includes information about each faculty member and their teaching and research activities.
- Research_Match, which demonstrates the significance that similar research areas have on collaboration;
- Degree_Activity, which illustrates the significance that degree centrality has on collaboration;
- Betweenness_Activity, which indicates the significance of betweenness centrality;
- Eigenvector_Activity, which identifies the significance that eigenvector centrality has on collaboration;
- Edges, which is a network topology parameter in ERGM; and
- Alternative Triangulation (AT), which is a network topology parameter that represents transitivity. This parameter demonstrates the significance that a common collaborator has on collaboration.
6. Evaluation
- Group 1—Old: Old users are faculty members who collaborated in 2013 and 2014.
- Group 2—New: New users consist of new members who joined the CCIS network in 2014.
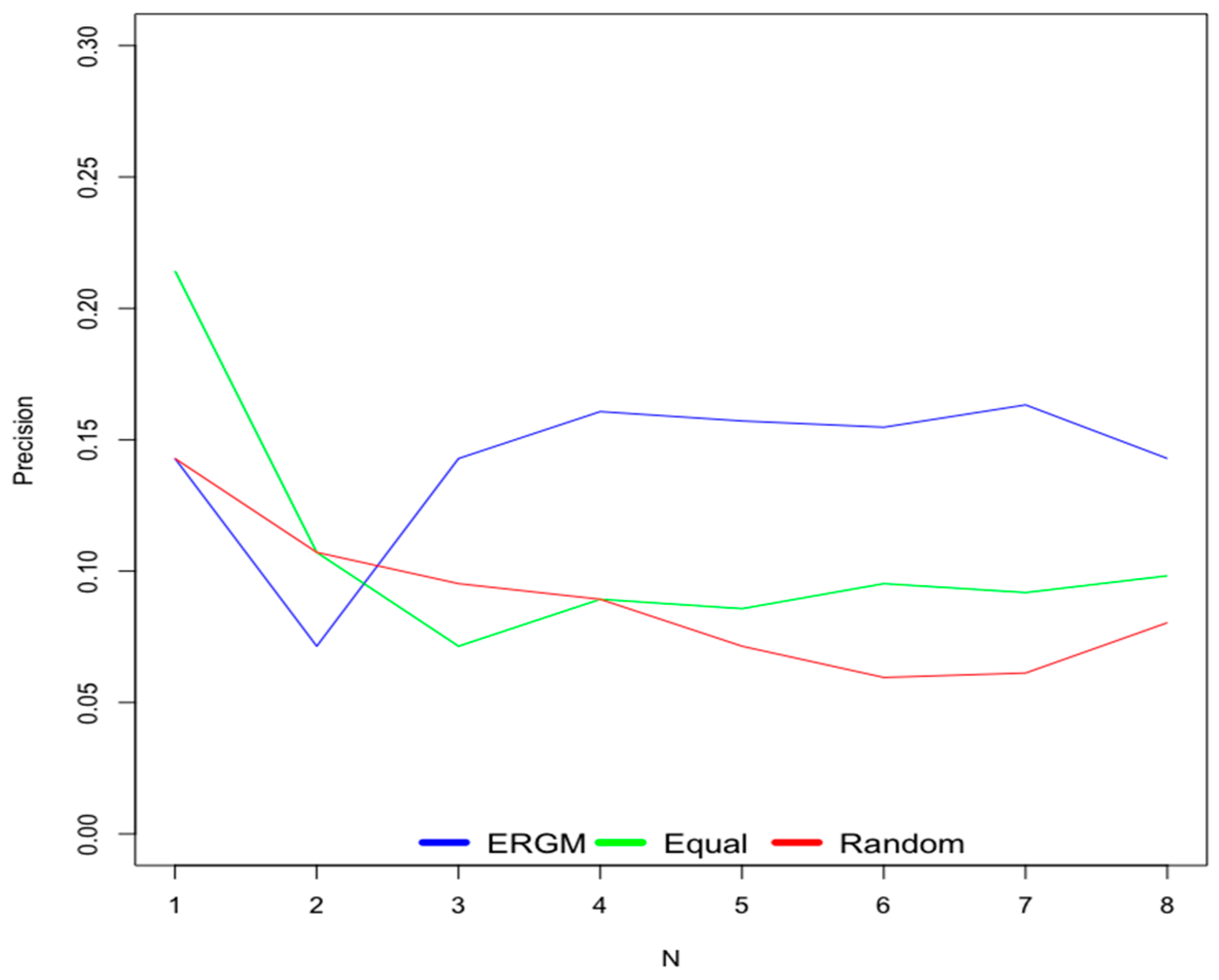
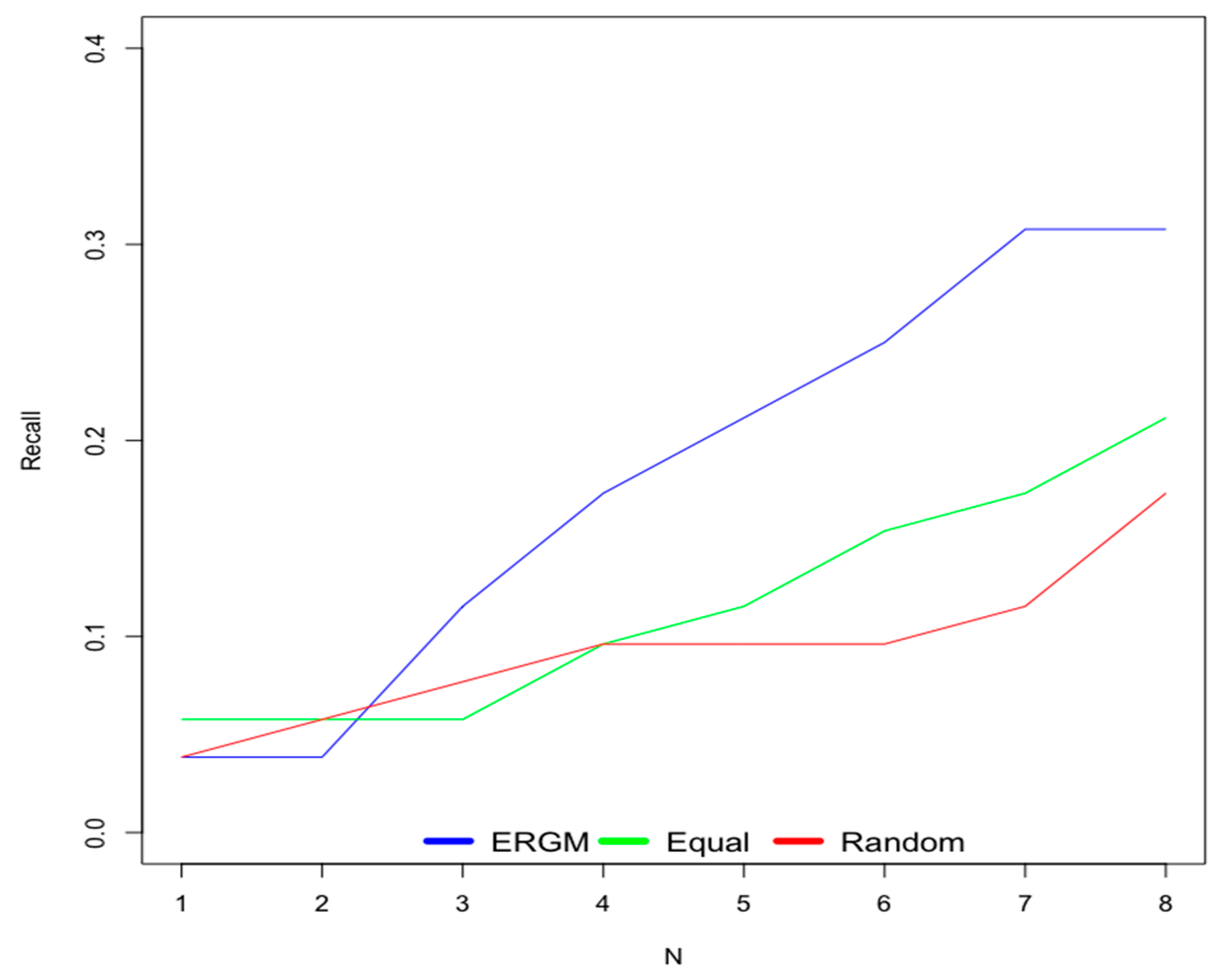
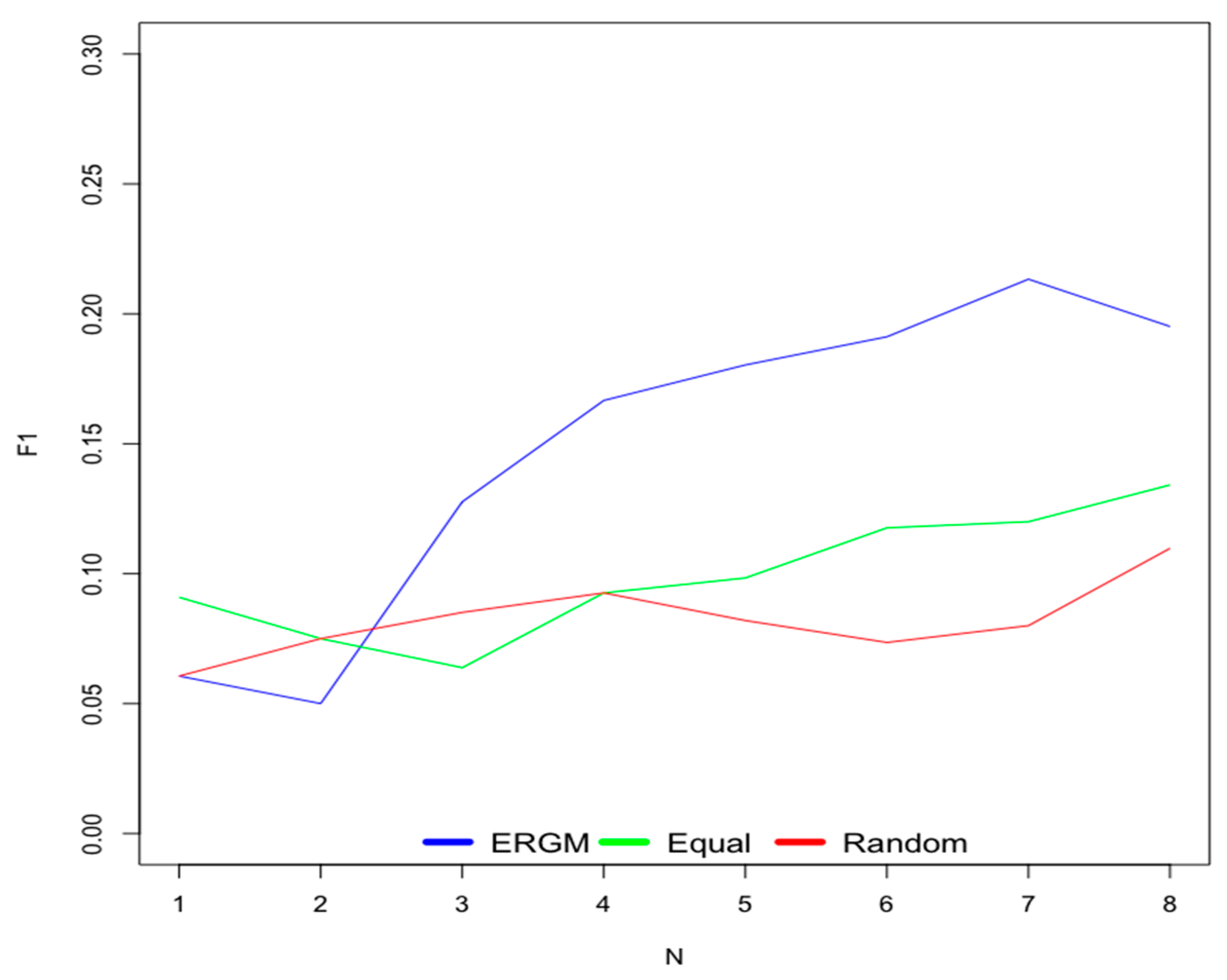
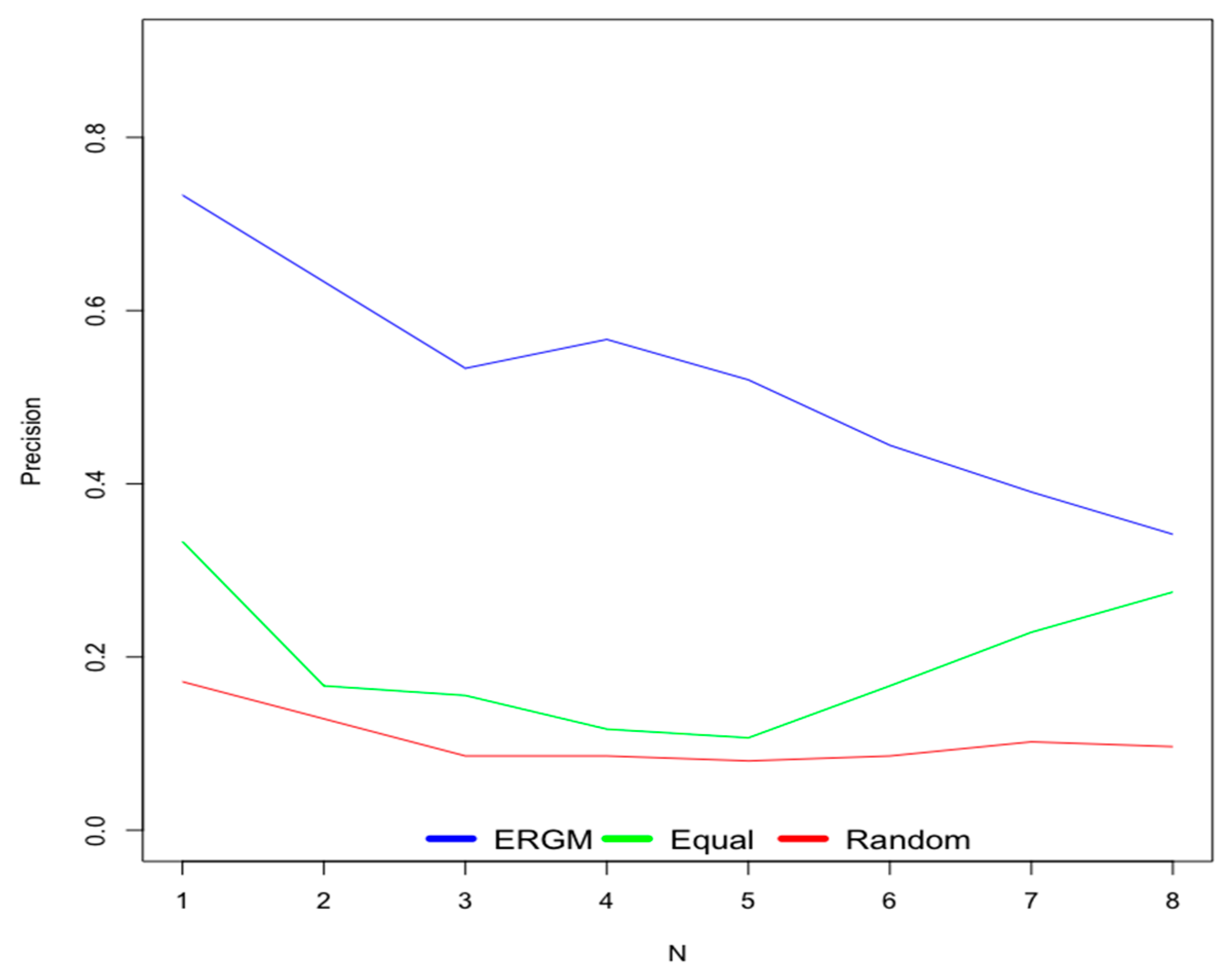
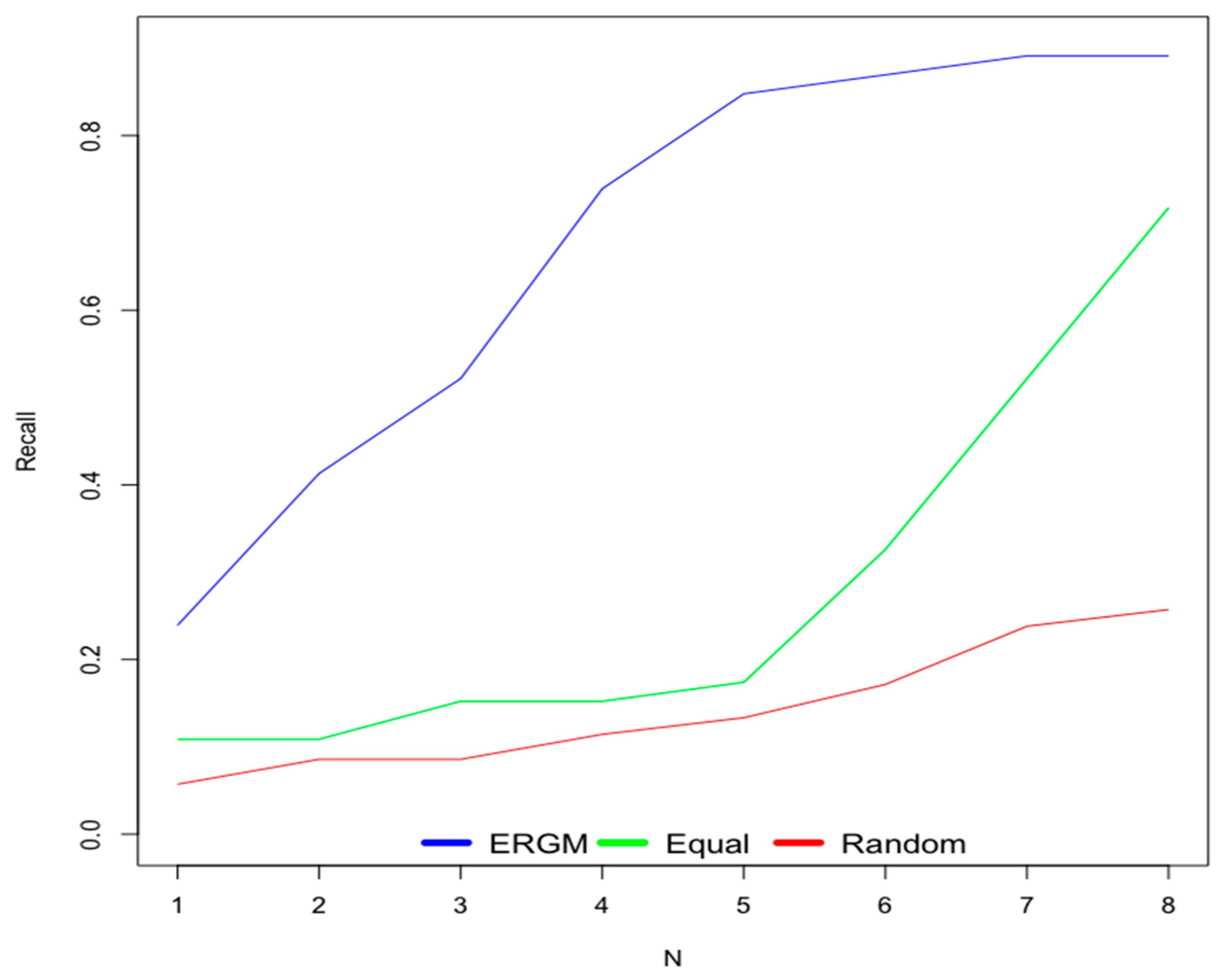
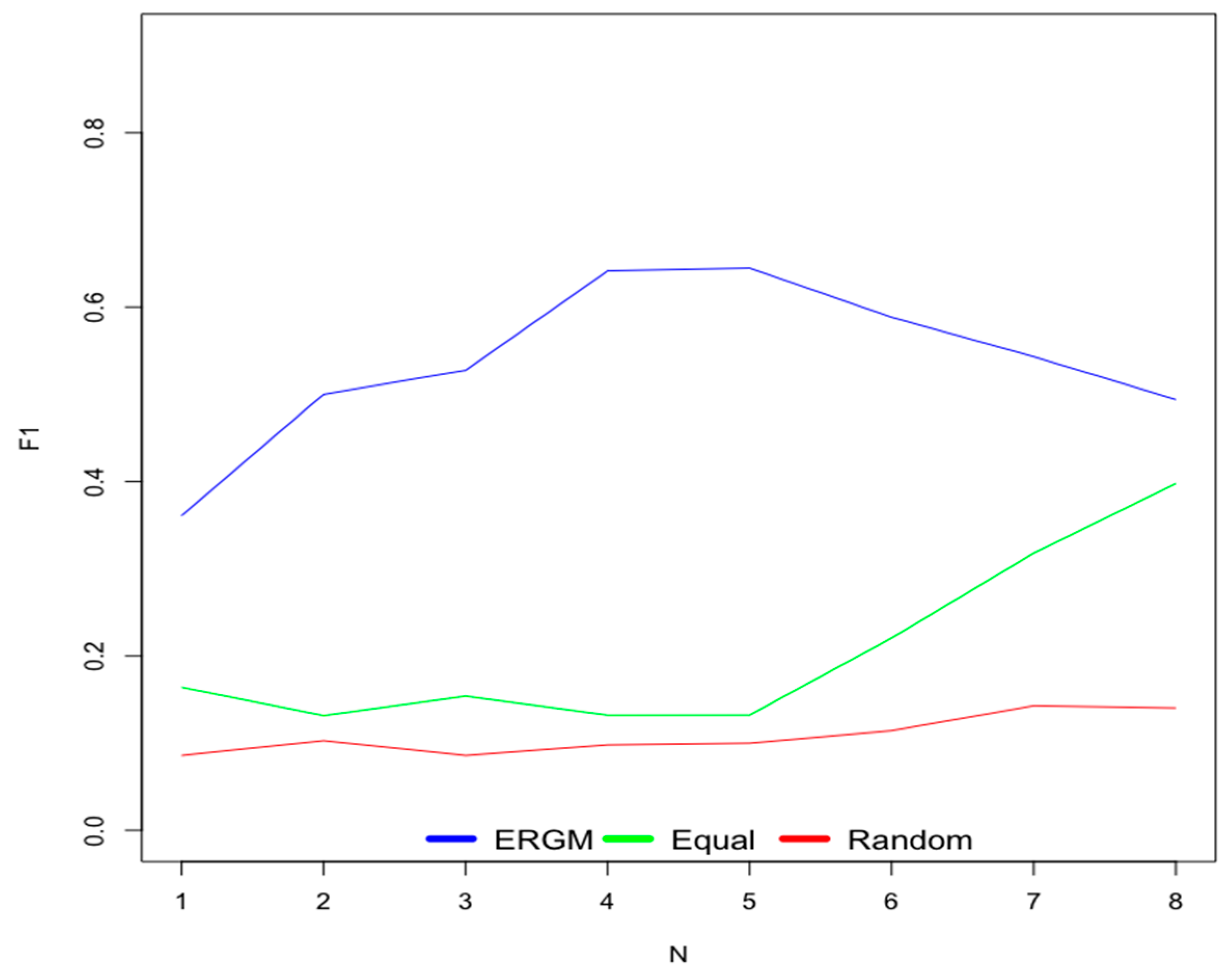
- Scenario 1—ERGM: This scenario uses weights for contextual factors calculated using the ERGM.
- Scenario 2—Equal: This scenario considers equal weights for all contextual factors.
- Scenario 3—Random: This scenario uses random weights for contextual factors.
- true positives (tp): These are the correctly predicted collaborators.
- true negatives (tn): These are the correctly predicted negative values.
- false positives (fp): These occur when a collaborator is predicted but the actual data show this prediction to be false.
- false negatives (fn): These occur when the RS fails to produce an accurate prediction.
6.1. Old Users
6.2. New Users
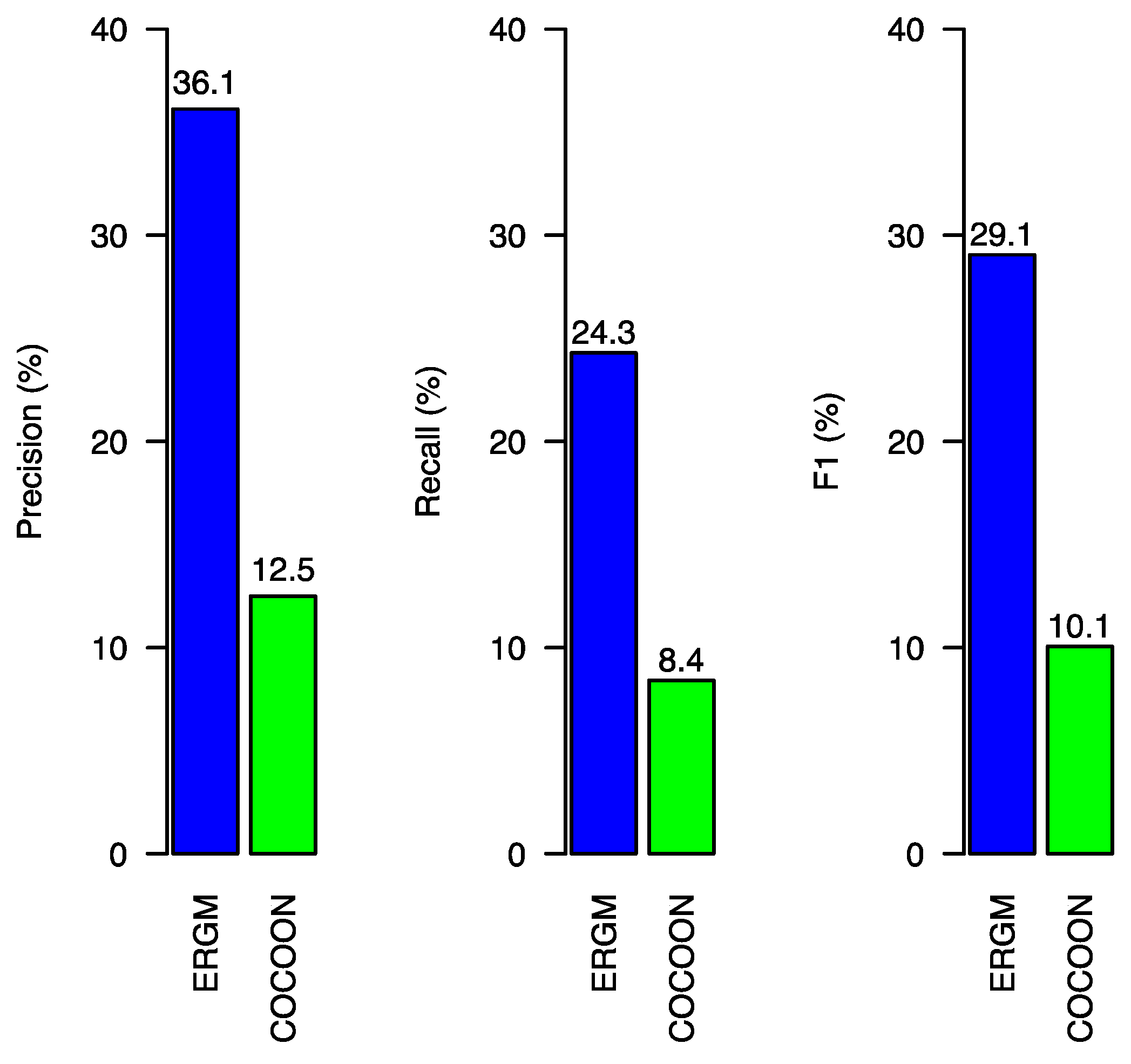
7. Comparison with Other Methods
8. Discussion and Research Limitations
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milojević, S. Modes of collaboration in modern science: Beyond power laws and preferential attachment. J. Am. Soc. Inf. Sci. Technol. 2010, 61, 1410–1423. [Google Scholar] [CrossRef]
- Jain, R.K.; Triandis, H.C.; Weick, C.W. Universities and Basic Research. In Managing Research, Development, and Innovation; John Wiley & Sons, Inc.: New York, NY, USA, 2010; pp. 296–314. [Google Scholar]
- Borgatti, S.P.; Everett, M.G.; Johnson, J.C. Analyzing Social Networks; SAGE Publications Ltd.: Thousand Oaks, CA, USA; London, UK, 2013. [Google Scholar]
- Bozeman, B.; Boardman, C. Research Collaboration and Team Science; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Khalid, N.H.; Ibrahim, R.; Selamat, A.; Kadir, M.R.A. Collaboration patterns of researchers using Social Network Analysis approach. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 1632–1637. [Google Scholar]
- Abowd, G.D.; Dey, A.K.; Brown, P.J.; Davies, N.; Smith, M.; Steggles, P. Towards a Better Understanding of Context and Context-Awareness. In Handheld and Ubiquitous Computing; Springer: Berlin/Heidelberg, Germany, 1999; pp. 304–307. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A. Context-aware recommender systems. In Recommender Systems Handbook; Springer: Berlin, Germany, 2015; pp. 191–226. [Google Scholar]
- Burke, R. Hybrid Recommender Systems: Survey and Experiments. User Model User-Adap Inter. 2002, 12, 331–370. [Google Scholar] [CrossRef]
- Robins, G.; Pattison, P.; Kalish, Y.; Lusher, D. An introduction to exponential random graph (p*) models for social networks. Soc. Netw. 2007, 29, 173–191. [Google Scholar] [CrossRef]
- Pattison, P.E.; Robins, G.L.; Snijders, T.A.B.; Wang, P. Conditional estimation of exponential random graph models from snowball sampling designs. J. Math. Psychol. 2013, 57, 284–296. [Google Scholar] [CrossRef]
- Damiani, E.; Ceravolo, P.; Frati, F.; Bellandi, V.; Maier, R.; Seeber, I.; Waldhart, G. Applying recommender systems in collaboration environments. Comput. Hum. Behav. 2015, 51, 1124–1133. [Google Scholar] [CrossRef]
- Wild, F.; Ochoa, X.; Heinze, N.; Crespo, R.M.; Quick, K. Bringing together what belongs together: A recommender-system to foster academic collaboration. In Proceedings of the 1st STELLAR Alpine Rendez-Vous 2009, Garmisch-Partenkirchen, Germany, 30 November–3 December 2009. [Google Scholar]
- del-Rio, F.; Parra, D.; Kuzmicic, J.; Svec, E. Towards a Recommender System for Undergraduate Research. arXiv 2017, arXiv:1706.06701. [Google Scholar]
- Beel, J.; Dinesh, S. Real-World Recommender Systems for Academia: The Pain and Gain in Building, Operating, and Researching them. In Proceedings of the 5th International Workshop on Bibliometric-enhanced Information Retrieval (BIR2017), Aberdeen, UK, 9 April 2017; pp. 6–17. [Google Scholar]
- Lopes, G.R.; da Silva, R.; de Oliveira, J.P.M. Applying Gini coefficient to quantify scientific collaboration in researchers network. In Proceedings of the International Conference on Web Intelligence, Mining and Semantics, Sogndal, Norway, 25–27 May 2011; p. 68. [Google Scholar]
- Gollapalli, S.D.; Mitra, P.; Giles, C.L. Similar Researcher Search in Academic Environments. In Proceedings of the 12th ACM/IEEE-CS Joint Conference on Digital Libraries, Washington, DC, USA, 10–14 June 2012; pp. 167–170. [Google Scholar] [CrossRef]
- Lee, D.H.; Brusilovsky, P.; Schleyer, T. Recommending collaborators using social features and MeSH terms. Proc. Am. Soc. Info. Sci. Technol. 2011, 48, 1–10. [Google Scholar] [CrossRef]
- Fazel-Zarandi, M.; Devlin, H.J.; Huang, Y.; Contractor, N. Expert Recommendation Based on Social Drivers, Social Network Analysis, and Semantic Data Representation. In Proceedings of the 2nd International Workshop on Information Heterogeneity and Fusion in Recommender Systems, Chicago, IL, USA, 27 October 2011; pp. 41–48. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, X.; Hao, J.; Ma, J.; Lau, R.Y.K.; Xu, W. Combining social network and semantic concept analysis for personalized academic researcher recommendation. Decis. Support Syst. 2012, 54, 564–573. [Google Scholar] [CrossRef]
- Collins, A.M.; Loftus, E.F. A spreading-activation theory of semantic processing. Psychol. Rev. 1975, 82, 407. [Google Scholar] [CrossRef]
- Davoodi, E.; Kianmehr, K.; Afsharchi, M. A semantic social network-based expert recommender system. Appl. Intell. 2013, 39, 1–13. [Google Scholar] [CrossRef]
- Cohen, S.; Ebel, L. Recommending Collaborators Using Keywords. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 959–962. [Google Scholar] [CrossRef]
- Sie, R.L.L.; van Engelen, B.J.; Bitter-Rijpkema, M.; Sloep, P.B. COCOON CORE: CO-author REcommendations Based on Betweenness Centrality and Interest Similarity. In Recommender Systems for Technology Enhanced Learning; Manouselis, N., Drachsler, H., Verbert, K., Santos, O.C., Eds.; Springer: New York, NY, USA, 2014; pp. 267–282. [Google Scholar]
- Huynh, T.; Takasu, A.; Masada, T.; Hoang, K. Collaborator Recommendation for Isolated Researchers. In Proceedings of the 2014 28th International Conference on Advanced Information Networking and Applications Workshops (WAINA), Victoria, BC, Canada, 13–16 May 2014; pp. 639–644. [Google Scholar] [CrossRef]
- Xia, F.; Chen, Z.; Wang, W.; Li, J.; Yang, L.T. MVCWalker: Random Walk-Based Most Valuable Collaborators Recommendation Exploiting Academic Factors. IEEE Trans. Emerg. Topics Comput. 2014, 2, 364–375. [Google Scholar] [CrossRef]
- Rohani, V.A.; Kasirun, Z.M.; Ratnavelu, K. An Enhanced Content-Based Recommender System for Academic Social Networks. In Proceedings of the 2014 IEEE Fourth International Conference on Big Data and Cloud Computing (BDCloud), Sydney, Australia, 3–5 December 2014; pp. 424–431. [Google Scholar]
- Ye, M.; Liu, X.; Lee, W.-C. Exploring social influence for recommendation: A generative model approach. In Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval, Portland, OR, USA, 12–16 August 2012; pp. 671–680. [Google Scholar]
- de Souza Junior, G.; Justel, C.M.; Duarte, J.C. Recommendation System for Social Networks based on the Influence of Actors through Graph Analysis. In Proceedings of the 18th Latin-Iberoamerican Conference on Operations Research, CLAIO 2016, Santiago de Chile, Chile, 2–6 October 2016. [Google Scholar]
- Bozeman, B.; Corley, E. Scientists’ collaboration strategies: Implications for scientific and technical human capital. Res. Policy. 2004, 33, 599–616. [Google Scholar] [CrossRef]
- Bozeman, B.; Gaughan, M.; Youtie, J.; Slade, C.P.; Rimes, H. Research collaboration experiences, good and bad: Dispatches from the front lines. Sci. Public Policy 2015, 43, 226–244. [Google Scholar] [CrossRef]
- Gunawardena, S.; Weber, R.O. Recommending Collaborators for Multidisciplinary Academic Collaboration. Available online: https://idea.library.drexel.edu/islandora/object/idea%3A3637/datastream/OBJ/view (accessed on 23 June 2019).
- Yang, D.H.; Su, Y. A Social Recommender System Based on Exponential Random Graph Model and Sentiment Similarity. Appl. Mech. Mater. 2014, 488–489, 1326–1330. [Google Scholar] [CrossRef]
- Yang, D.; Huang, C.; Wang, M. A social recommender system by combining social network and sentiment similarity: A case study of healthcare. J. Inf. Sci. 2017, 43, 635–648. [Google Scholar] [CrossRef]
- Hunter, D.R.; Goodreau, S.M.; Handcock, M.S. Goodness of fit of social network models. J. Am. Stat. Assoc. 2008, 103, 248–258. [Google Scholar] [CrossRef]
- Wang, P.; Robins, G.L.; Pattison, P.E.; Koskinen, J.H. MPNet: Program for the Simulation and Estimation of (p*) Exponential Random Graph Models for Multilevel Networks; Melbourne School of Psychological Sciences: Melbourne, Australia, 2014. [Google Scholar]
- Said, A. Evaluating the Accuracy and Utility of Recommender Systems. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Moody, J. The structure of a social science collaboration network: Disciplinary cohesion from 1963 to 1999. Am. Sociol. Rev. 2004, 69, 213–238. [Google Scholar] [CrossRef]
- Parada, G.A.; Ceballos, H.G.; Cantu, F.J.; Rodriguez-Aceves, L. Recommending Intra-Institutional Scientific Collaboration Through Coauthorship Network Visualization. In Proceedings of the 2013 Workshop on Computational Scientometrics: Theory & Applications, San Francisco, CA, USA, 28 October 2013; pp. 7–12. [Google Scholar] [CrossRef]
- Soetjipto, R. Automatic Detection of Research Interest Using Topic Modeling. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Osborne, F.; Motta, E. Mining semantic relations between research areas. In Proceedings of the 11th International Semantic Web Conference, Boston, MA, USA, 11–15 November 2012; pp. 410–426. [Google Scholar]
- Shapira, B.; Arazy, O.; Kumar, N. Improving Social Recommender Systems. IT Prof. 2009, 11, 38–44. [Google Scholar]
| Centrality Measure | Definition | Formula |
|---|---|---|
| Closeness centrality | Measure of relative node i distances to the n other nodes. | is the length of the path between i and j. |
| Betweenness Centrality | Measure of extent to which a node lies between other nodes in the network. | is the number of shortest paths between i and j. is the number of shortest paths between i and j that k lies on. |
| Eigenvector Centrality | Measure of node centrality that takes into account neighbors’ centralities. | |
| Kats Centrality | Measures node influence within a network. |
| Parameter | Weight | t-Ratio | |
|---|---|---|---|
| Edge | −7.1686 | −0.012 | * |
| Alternative Triangulation (AT) | 1.1855 | 0.015 | * |
| Betweenness_Activity | −1.5488 | 0.02 | * |
| Degree_Activity | 3.1432 | −0.011 | * |
| Eigenvector_Activity | −0.1549 | −0.035 | |
| Research_Match | 1.3129 | 0.046 | * |
| Parameter | GOF t-Value |
|---|---|
| Edge | −0.039 |
| AT | 0.037 |
| Betweenness_Activity | −0.064 |
| Degree_Activity | −0.062 |
| Eigenvector_Activity | −0.139 |
| Research_Match | 0.253 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ballaa, H.; Al-Dossari, H.; Chikh, A. Using an Exponential Random Graph Model to Recommend Academic Collaborators. Information 2019, 10, 220. https://doi.org/10.3390/info10060220
Al-Ballaa H, Al-Dossari H, Chikh A. Using an Exponential Random Graph Model to Recommend Academic Collaborators. Information. 2019; 10(6):220. https://doi.org/10.3390/info10060220
Chicago/Turabian StyleAl-Ballaa, Hailah, Hmood Al-Dossari, and Azeddine Chikh. 2019. "Using an Exponential Random Graph Model to Recommend Academic Collaborators" Information 10, no. 6: 220. https://doi.org/10.3390/info10060220
APA StyleAl-Ballaa, H., Al-Dossari, H., & Chikh, A. (2019). Using an Exponential Random Graph Model to Recommend Academic Collaborators. Information, 10(6), 220. https://doi.org/10.3390/info10060220




