Latent Feature Group Learning for High-Dimensional Data Clustering
Abstract
1. Introduction
2. Related Work
- Huang et al. [5] proposed W-k-means clustering algorithm which can automatically compute the feature weights in k-means clustering process. W-k-means extends the standard k-means algorithm with one additional step to compute the feature weights at each iteration of clustering process. The feature weight is inversely proportional to the sum of within-cluster variances of feature. As such, noise features can be identified and their effects on the clustering result are significantly reduced. Amorim et al. [22] extended W-k-means algorithm with Minkowski’s metric and assigned the Minkowski’s exponent that coincides with the exponent to feature weights.
- Hoff [17] proposed a multivariate Dirichlet process mixture model, which is based on a Pólya urn cluster model for the multivariate means and variances. The model is learned by a Markov chain Monte Carlo process. However, its computational cost is prohibitive. Fan et al. [23] proposed a variational inference framework for unsupervised non-Gaussian feature selection, in the context of the finite generalized Dirichlet (GD) mixture-based clustering. Under the proposed principled variational framework, it simultaneously estimates all the involved parameters and determines the complexity (i.e., both model and feature selection) of GD mixture.
- Domeniconi et al. [16] proposed the locally adaptive clustering (LAC) algorithm, which assigns a weight for each feature in the cluster. They used an iterative algorithm to minimize the objective function. Cheng et al. [21] proposed another weighting k-means approach very similar to LAC, but allowing for incorporation of further constraints. Jing et al. [4] proposed the entropy weighting K-means (EWKM) algorithm, which also assigns a weight to each feature in each cluster. Different from LAC, EWKM extends the standard k-means algorithm with one additional step to compute the feature weights for each cluster at each iteration. The weight is inversely proportional to the sum of within-cluster variances of feature in the cluster.
- Tsai and Chiu [19] developed a feature weights self-adjustment mechanism for k-means clustering on the relational datasets, in which the feature weights are automatically computed by minimizing the within-cluster discrepancy and maximizing the between-cluster discrepancy simultaneously. Deng et al. [20] proposed an enhanced soft subspace clustering algorithm (ESSC) which employs both within-cluster and between-cluster information in the subspace clustering process. Xia et al. [24] proposed a multi-objective-evolutionary-approach-based soft subspace clustering (MOEASSC) algorithm which optimizes two minimization objective functions simultaneously by using a multi-objective evolutionary approach. They also proposed a two-step method to reduce the difficulty in identifying the subspace of each cluster, the cluster memberships of objects and the number of clusters.
- Chen et al. [7] proposed a two-level weighting method named FG-k-means for multi-view data in which two types of weights are employed: a view weight is assigned to each view to identify the view compactness and a feature weight is also assigned to each feature in a view to identify the feature contribution. Cai et al. [25] used FG-k-means for text clustering. They first used the topic model LDA to partition the words into several groups and then used FG-k-means to cluster the text data. The experimental results show that the word grouping method improves the clustering performance on text data. Gan et al. [26] extended FG-k-means to generate the feature groups automatically by clustering the features weights. The objective function of clustering feature weights is added as a penalty term to the objective function of FG-k-means. This indicates that there is a much higher chance to construct all informative abstract features than all informative individual features.
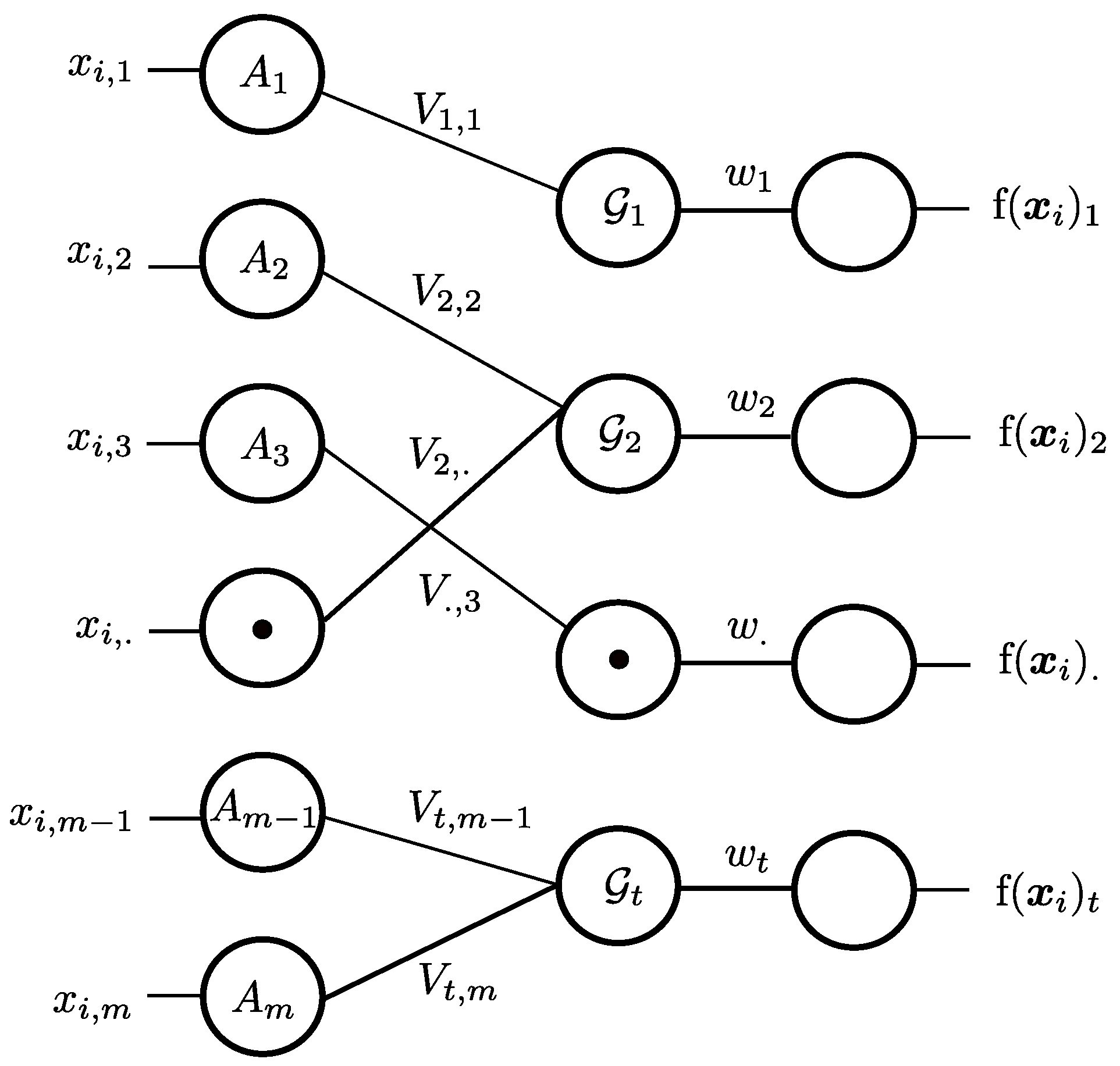
3. Latent Feature Group Projection in Subspace Clustering
4. Latent Feature Group Learning Algorithm
4.1. Revised FG-k-Means
4.2. The Mass-Based Dissimilarity
4.3. Optimization of Equation (6)
- 1.
- Problem : Fix , and , and solve the reduced problem . Problem is solved bywhere .
- 2.
- Problem : Fix , and , and solve the reduced problem . Problem is solved by updating the centers of the clusters by Algorithm 1.
| Algorithm 1 Cluster center updating. |
| Input:U,W,V. |
| Output: The updating cluster centers Z. |
| 1: Generate a similarity matrix , where ; |
| 2: Generate a distance sum matrix , where ; |
| 3: Generate a density matrix , find the smallest value in every column m of and consider the corresponding object as the center of cluster m for . |
| 4: return Z; |
- 3.
- Problem : Fix , , and , and solve the reduced problem . Problem is solved by the following Theorem 1.
- 4.
- Problem : Fix , , and , and solve the reduced problem . Problem is solved as follows. Because of the additivity of objective function in Equation (6), the matrix W can be divided into k subproblems for k clusters, respectively. Letandthen the lth subproblem of original problem can be written as
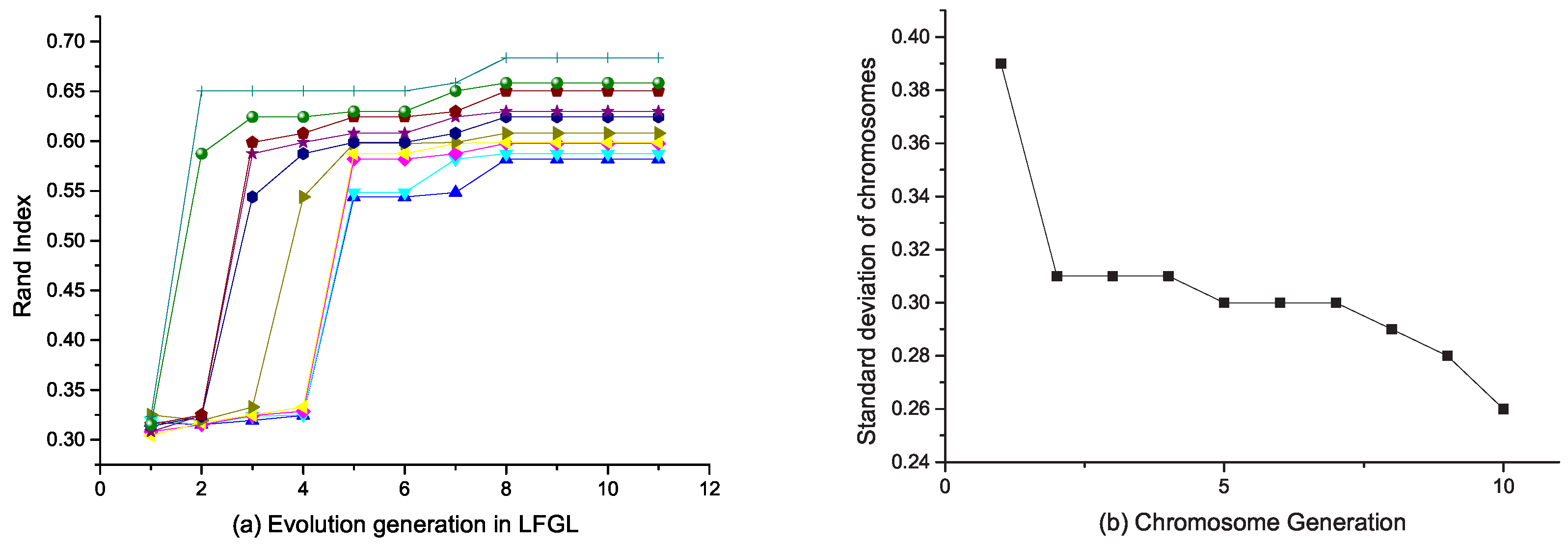
4.4. Evolutionary Method to Select the Best Feature Grouping Structure
- There are 10 strongest chromosomes which are selected with the highest scores.
- The crossover is performed in the following steps. The 10 chromosomes are randomly grouped into five pairs. For each pair of chromosome i and chromosome j, the corresponding binary sequence and are compared. If two sequences are same, the sequence is copied as the new generation of . For the remaining pairs of different binary sequences, we randomly select one sequence from one chromosome to replace the corresponding sequence of another chromosome by the probability . Finally, we encode as a new chromosome in the next generation. The rule to generate is defined aswhere is randomly generated for each .
- For the process of mutation, we randomly choose five chromosomes from 10 alternative chromosomes. For each chromosome , we randomly generate a new chromosome . The rule to generate iswhere is randomly generated for each .
4.5. LFGL Algorithm
| Algorithm 2 LFGL algorithm. |
| Input: The dataset X, the number of clusters k, two positive parameters and , the number of feature groups t. |
| Output: Local optimal values of , , , and . |
| 1: Initialize 20 chromosomes representing 20 different possibilities of feature grouping; |
| 2: For each chromosome, we initialize by sampling the positive values , then normalize so that ; |
| 3: Initialize with the method mentioned in Section 4.4 to build V matrix, then normalize so that the -norm of each row of is 1; |
| 4: Randomly choose k cluster centers ; |
| 5: Update , , and , respectively; |
| 6: The objective function P obtains its local minimum value, then update and go back to Step 9; |
| 7: Calculate BIC of 20 clustering results from 20 chromosomes, choose the best 10 ones and make 10 new chromosomes by crossover and mutation; |
| 8: Repeat ten times and find the best solution of clustering. |
5. Experiments
5.1. Datasets
5.2. Evaluation Measures
- is defined as
- is defined as
- is defined as
- is defined as
- is defined as
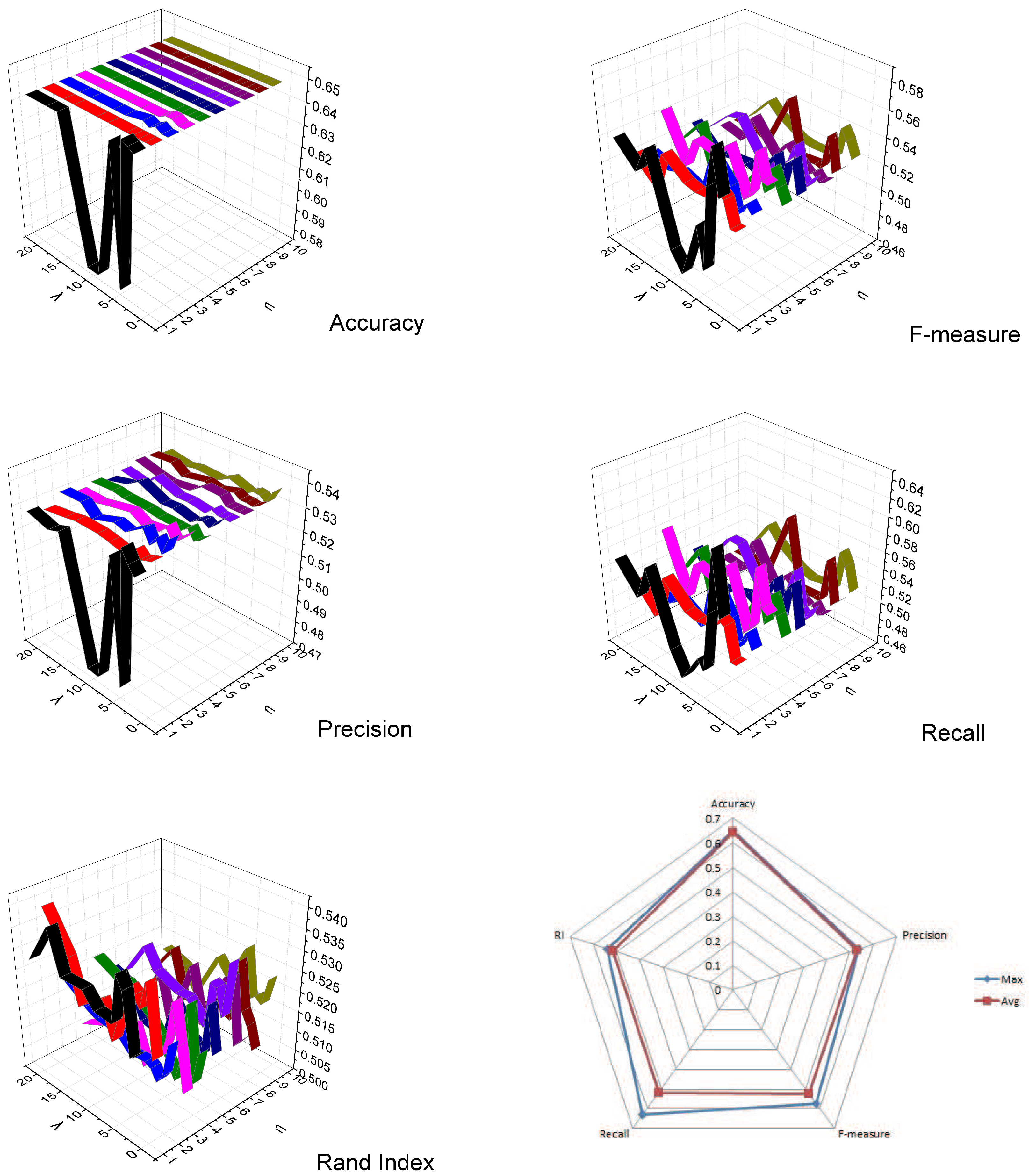
5.3. Parameters Settings
5.4. Clustering Results and Analysis
5.5. Feature Grouping Analysis
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Donoho, D.L. High-dimensional data analysis: The curses and blessings of dimensionality. AMS Math Chall. Lect. 2000, 1, 375. [Google Scholar]
- Parsons, L.; Haque, E.; Liu, H. Subspace clustering for high dimensional data: A review. ACM Sigkdd Explor. Newsl. 2004, 6, 90–105. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Zimek, A. Clustering high-dimensional data: A survey on subspace clustering, pattern-based clustering, and correlation clustering. ACM Trans. Knowl. Discov. Data 2009, 3, 1. [Google Scholar] [CrossRef]
- Jing, L.; Ng, M.K.; Huang, J.Z. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data. IEEE Trans. Knowl. Data Eng. 2007, 8, 1026–1041. [Google Scholar] [CrossRef]
- Huang, J.Z.; Ng, M.K.; Rong, H.; Li, Z. Automated variable weighting in k-means type clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 5, 657–668. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Huang, J.Z.; Ye, Y. TW-k-means: Automated two-level variable weighting clustering algorithm for multiview data. IEEE Trans. Knowl. Data Eng. 2013, 25, 932–944. [Google Scholar] [CrossRef]
- Chen, X.; Ye, Y.; Xu, X.; Huang, J.Z. A feature group weighting method for subspace clustering of high-dimensional data. Pattern Recognit. 2012, 45, 434–446. [Google Scholar] [CrossRef]
- Gnanadesikan, R.; Kettenring, J.R.; Tsao, S.L. Weighting and selection of variables for cluster analysis. J. Classif. 1995, 12, 113–136. [Google Scholar] [CrossRef]
- De Soete, G. Optimal variable weighting for ultrametric and additive tree clustering. Qual. Quant. 1986, 20, 169–180. [Google Scholar] [CrossRef]
- De Soete, G. OVWTRE: A program for optimal variable weighting for ultrametric and additive tree fitting. J. Classif. 1988, 5, 101–104. [Google Scholar] [CrossRef]
- Fowlkes, E.B.; Gnanadesikan, R.; Kettenring, J.R. Variable selection in clustering. J. Classif. 1988, 5, 205–228. [Google Scholar] [CrossRef]
- Makarenkov, V.; Leclerc, B. An algorithm for the fitting of a tree metric according to a weighted least-squares criterion. J. Classif. 1999, 16, 3–26. [Google Scholar] [CrossRef]
- Makarenkov, V.; Legendre, P. Optimal variable weighting for ultrametric and additive trees and K-means partitioning: Methods and software. J. Classif. 2001, 18, 245–271. [Google Scholar]
- Modha, D.S.; Spangler, W.S. Feature weighting in k-means clustering. Mach. Learn. 2003, 52, 217–237. [Google Scholar] [CrossRef]
- Friedman, J.H.; Meulman, J.J. Clustering objects on subsets of attributes (with discussion). J. R. Stat. Soc. B 2004, 66, 815–849. [Google Scholar] [CrossRef]
- Domeniconi, C.; Gunopulos, D.; Ma, S.; Yan, B.; Al-Razgan, M.; Papadopoulos, D. Locally adaptive metrics for clustering high dimensional data. Data Min. Knowl. Discov. 2007, 14, 63–97. [Google Scholar] [CrossRef]
- Hoff, P.D. Model-based subspace clustering. Bayesian Anal. 2006, 1, 321–344. [Google Scholar] [CrossRef]
- Bouveyron, C.; Girard, S.; Schmid, C. High-dimensional data clustering. Comput. Stat. Data Anal. 2007, 52, 502–519. [Google Scholar] [CrossRef]
- Tsai, C.Y.; Chiu, C.C. Developing a feature weight self-adjustment mechanism for a K-means clustering algorithm. Comput. Stat. Data Anal. 2008, 52, 4658–4672. [Google Scholar] [CrossRef]
- Deng, Z.; Choi, K.S.; Chung, F.L.; Wang, S. Enhanced soft subspace clustering integrating within-cluster and between-cluster information. Pattern Recognit. 2010, 43, 767–781. [Google Scholar] [CrossRef]
- Cheng, H.; Hua, K.A.; Vu, K. Constrained locally weighted clustering. Proc. VLDB Endow. 2008, 1, 90–101. [Google Scholar] [CrossRef]
- De Amorim, R.C.; Mirkin, B. Minkowski metric, feature weighting and anomalous cluster initializing in K-Means clustering. Pattern Recognit. 2012, 45, 1061–1075. [Google Scholar] [CrossRef]
- Fan, W.; Bouguila, N.; Ziou, D. Unsupervised hybrid feature extraction selection for high-dimensional non-Gaussian data clustering with variational inference. IEEE Trans. Knowl. Data Eng. 2013, 25, 1670–1685. [Google Scholar] [CrossRef]
- Xia, H.; Zhuang, J.; Yu, D. Novel soft subspace clustering with multi-objective evolutionary approach for high-dimensional data. Pattern Recognit. 2013, 46, 2562–2575. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, X.; Peng, P.X.; Huang, J.Z. A LDA feature grouping method for subspace clustering of text data. In Proceedings of the Pacific-Asia Workshop on Intelligence and Security Informatics, Tainan, Taiwan, 13 May 2014; pp. 78–90. [Google Scholar]
- Gan, G.; Ng, M.K.P. Subspace clustering with automatic feature grouping. Pattern Recognit. 2015, 48, 3703–3713. [Google Scholar] [CrossRef]
- Ting, K.M.; Zhu, Y.; Carman, M.; Zhu, Y.; Zhou, Z.H. Overcoming key weaknesses of distance-based neighbourhood methods using a data dependent dissimilarity measure. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1205–1214. [Google Scholar]
- Gançarski, P.; Blansché, A. Darwinian, Lamarckian, and Baldwinian (Co) Evolutionary Approaches for Feature Weighting in K-means-Based Algorithms. IEEE Trans. Evol. Comput. 2008, 12, 617–629. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, S.; Lin, S.; Wang, S.; Philip, S.Y. Clustering embedded approaches for efficient information network inference. Data Sci. Eng. 2016, 1, 29–40. [Google Scholar] [CrossRef]
- Mai, S.T.; Amer-Yahia, S.; Bailly, S.; Pépin, J.L.; Chouakria, A.D.; Nguyen, K.T.; Nguyen, A.D. Evolutionary active constrained clustering for obstructive sleep apnea analysis. Data Sci. Eng. 2018, 3, 359–378. [Google Scholar] [CrossRef]
- Song, Q.; Ni, J.; Wang, G. A fast clustering-based feature subset selection algorithm for high-dimensional data. IEEE Trans. Knowl. Data Eng. 2013, 25, 1–14. [Google Scholar] [CrossRef]
- García-Torres, M.; Gómez-Vela, F.; Melián-Batista, B.; Moreno-Vega, J.M. High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach. Inf. Sci. 2016, 326, 102–118. [Google Scholar] [CrossRef]
- Ur Rehman, M.H.; Liew, C.S.; Abbas, A.; Jayaraman, P.P.; Wah, T.Y.; Khan, S.U. Big data reduction methods: a survey. Data Sci. Eng. 2016, 1, 265–284. [Google Scholar] [CrossRef]
- Vargas-Solar, G.; Zechinelli-Martini, J.L.; Espinosa-Oviedo, J.A. Big Data Management: What to Keep from the Past to Face Future Challenges? Data Sci. Eng. 2017, 2, 328–345. [Google Scholar] [CrossRef]
| Dataset | Objects | Features | Classes |
|---|---|---|---|
| SRBCT | 63 | 2308 | 4 |
| Lymphoma | 62 | 4026 | 3 |
| Prostate | 102 | 6033 | 2 |
| Adenocarcinoma | 76 | 9868 | 2 |
| Breast2classes | 77 | 4870 | 2 |
| CNS | 60 | 7129 | 2 |
| WebKB texas | 814 | 4029 | 7 |
| Data | Predicted Positive | Predicted Negative |
|---|---|---|
| True condition positive | True Positive () | False Negative () |
| True condition negative | False Positive () | True Negative () |
| Data | Evaluation | k-Means | EWKM | TWKM | LAC | FG-k-Means | LFGL |
|---|---|---|---|---|---|---|---|
| SRBCT | Rand Index | 0.661 | 0.603 | 0.654 | 0.597 | 0.654 | |
| Accuracy | 0.528 | 0.476 | 0.530 | 0.413 | 0.512 | ||
| Precision | 0.304 | 0.366 | 0.296 | 0.375 | 0.351 | ||
| Recall | 0.353 | 0.344 | 0.380 | 0.339 | 0.385 | ||
| F-Measure | 0.293 | 0.163 | 0.293 | 0.287 | 0.339 | ||
| Lymphoma | Rand Index | 0.727 | 0.804 | 0.612 | 0.488 | 0.921 | |
| Accuracy | 0.855 | 0.838 | 0.755 | 0.419 | 0.845 | ||
| Precision | 0.844 | 0.854 | 0.677 | 0.488 | |||
| Recall | 0.563 | 0.736 | 0.441 | 0.336 | |||
| F-Measure | 0.675 | 0.791 | 0.534 | 0.488 | 0.771 | ||
| Prostate | Rand Index | 0.507 | 0.504 | 0.507 | 0.495 | 0.509 | |
| Accuracy | 0.578 | 0.606 | 0.576 | 0.500 | |||
| Precision | 0.503 | 0.49 | 0.502 | 0.491 | 0.500 | ||
| Recall | 0.541 | 0.515 | 0.573 | 0.510 | 0.523 | ||
| F-Measure | 0.521 | 0.507 | 0.532 | 0.491 | |||
| Adenocarcinoma | Rand Index | 0.528 | 0.605 | 0.588 | |||
| Accuracy | 0.842 | 0.842 | 0.832 | 0.615 | |||
| Precision | 0.722 | 0.743 | 0.731 | 0.642 | |||
| Recall | 0.576 | 0.723 | 0.562 | 0.807 | |||
| F-Measure | 0.641 | 0.719 | 0.692 | 0.768 | |||
| Breast2classes | Rand Index | 0.546 | 0.507 | 0.479 | 0.491 | 0.508 | |
| Accuracy | 0.584 | 0.574 | 0.470 | 0.584 | |||
| Precision | 0.507 | 0.452 | 0.404 | 0.523 | |||
| Recall | 0.696 | 0.757 | 0.608 | 0.603 | 0.682 | ||
| F-Measure | 0.607 | 0.608 | 0.527 | 0.481 | 0.599 | ||
| CNS | Rand Index | 0.493 | 0.506 | 0.496 | 0.500 | ||
| Accuracy | 0.661 | 0.661 | 0.661 | 0.615 | |||
| Precision | 0.531 | 0.542 | 0.536 | 0.507 | |||
| Recall | 0.583 | 0.584 | 0.545 | 0.609 | |||
| F-Measure | 0.556 | 0.559 | 0.539 | 0.513 | |||
| WebKB texas | Rand Index | 0.507 | 0.507 | 0.496 | 0.488 | 0.501 | |
| Accuracy | 0.578 | 0.563 | 0.516 | 0.528 | 0.545 | ||
| Precision | 0.502 | 0.502 | 0.492 | 0.509 | 0.496 | ||
| Recall | 0.514 | 0.557 | 0.562 | 0.564 | 0.612 | ||
| F-Measure | 0.508 | 0.520 | 0.513 | 0.496 | 0.507 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; He, Y.; Ma, L.; Huang, J.Z. Latent Feature Group Learning for High-Dimensional Data Clustering. Information 2019, 10, 208. https://doi.org/10.3390/info10060208
Wang W, He Y, Ma L, Huang JZ. Latent Feature Group Learning for High-Dimensional Data Clustering. Information. 2019; 10(6):208. https://doi.org/10.3390/info10060208
Chicago/Turabian StyleWang, Wenting, Yulin He, Liheng Ma, and Joshua Zhexue Huang. 2019. "Latent Feature Group Learning for High-Dimensional Data Clustering" Information 10, no. 6: 208. https://doi.org/10.3390/info10060208
APA StyleWang, W., He, Y., Ma, L., & Huang, J. Z. (2019). Latent Feature Group Learning for High-Dimensional Data Clustering. Information, 10(6), 208. https://doi.org/10.3390/info10060208





