Abstract
Due to the selfishness of vehicles and the scarcity of spectrum resources, how to realize fair and effective spectrum resources allocation has become one of the primary tasks in VANET. In this paper, we propose a hierarchical resource allocation scheme based on Nash bargaining game. Firstly, we analyze the spectrum resource allocation problem between different Road Side Units (RSUs), which obtain resources from the central cloud. Thereafter, considering the difference of vehicular users (VUEs), we construct the matching degree index between VUEs and RSUs. Then, we deal with the spectrum resource allocation problem between VUEs and RSUs. To reduce computational overhead, we transform the original problem into two sub-problems: power allocation and slot allocation, according to the time division multiplexing mechanism. The simulation results show that the proposed scheme can fairly and effectively allocate resources in VANET according to VUEs’ demand.
1. Introduction
With the rapid increase of the number of vehicles, traffic accidents and congestion are becoming more and more serious, which has attracted worldwide attention [1]. The concept of Vehicular Ad-hoc Networks (VANET) is considered to be an effective way to solve this problem. Through modern information and communications technology, the vehicles can access the network and interact with the cloud resource pool in time [2]. In addition, edge cloud computing has been applied to the VANET for data acquisition considering the simple deployment of edge cloud infrastructure [3]. For example, Autonomous Vehicular Clouds was proposed to offer potential applications to VUEs, which ensures the safe operation of autonomous vehicles and provides the services required in the running process of vehicles [4]. VANET clouds usually comprises three types of clouds, which are Central cloud, RSU cloud, and Vehicular cloud [5]. One of the main advantages of VANET clouds is that no additional infrastructure is required. The central cloud is a centralized resource pool that provides the resources needed for RSUs and vehicles. The RSU cloud provides services for vehicle access networks. The vehicular cloud consists of vehicles on the road, providing services for data transmission between vehicles. As seen in Figure 1, the role of central cloud is to achieve centralized scheduling of spectrum resources. Multiple RSUs are connected to the central cloud through the forward link and the management interface, different RSUs’ wireless resources are abstracted into a virtual resource pool. VUEs request resources from RSUs within the communication range of each RSU.
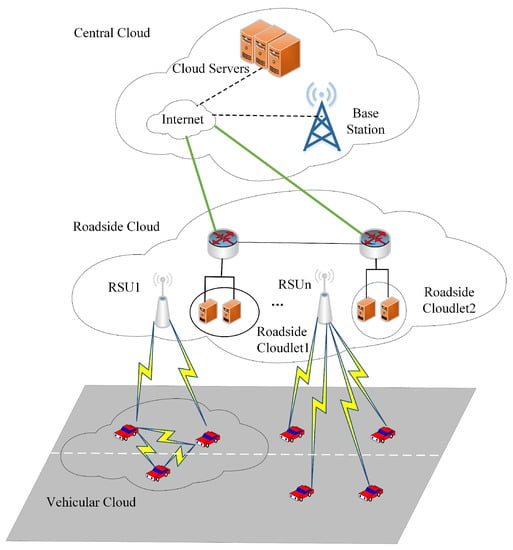
Figure 1.
Network access in Vehicular Ad hoc Network-Cloud.
However, due to the high mobility of vehicles, the topological structure of the VANET is constantly changing, and the number of vehicles within the coverage area of RSU is constantly changing, which increases the difficulty of resource allocation and results in tidal phenomena in VANET [6]. On the other hand, the selfishness of VUEs brings new challenges and difficulties to the rational resource allocation in vehicular networks [7]. For example, the uncertainty of vehicle motion and the selfish behaviors of vehicles may lead to the cloud resource competition among the VUEs and result in network congestion, which occurs in the data access through the RSUs cloud and central cloud. Considering the sparse deployment of RSU, when the number of vehicle users increases rapidly within the coverage of an RSU, the spectrum resources of the RSU can not meet the needs of all vehicle users. Therefore, how to fairly and efficiently allocate spectrum resources to VUEs has become an urgent problem to be solved.
At this stage, some scholars have put forward some resources allocation mechanisms in VANET. A spectrum resource acquisition method based on game theory is proposed, which is modeled as a non-cooperative congestion game to ensure the fair resource allocation [8]. Some research has transformed the problem of spectrum resource allocation into a semi-Markov decision-making process to achieve reasonable and effective resource allocation [9]. In [10], a repeated game scheme based on Gauss-Seidel (G-S) iteration method is proposed to solve the resource allocation problem in VANET. Considering the selfishness of the vehicle, a punishment strategy is proposed to avoid the irrational behavior of the vehicles [11]. However, the above research has some limitations and only considers the spectrum resource allocation within the coverage of a single RSU. Considering the tidal phenomenon caused by vehicle movement [12], the above research fails to realize the reasonable allocation of spectrum resources in the central cloud, resulting in the waste of spectrum resources.
In non-hot spots of cities, considering the deployment cost, RSUs cannot be deployed on a large scale, which means they cannot form a seamless coverage network [13]. When the traffic tends to be congested during rush hours, the network load of a single RSU is bound to increase sharply, resulting in that the Qos of VUEs cannot be guaranteed. In addition, the services that the VUEs request from the RSUs can be divided into safety services and nonsafety services [14]. Safety services are used to send safety messages, for example, various warning messages the assist vehicles to prevent accidents. Nonsafety services are used for entertainment purposes. Obviously, safety services have a higher priority than nonsafety services. Hence, considering the limited resource of RSU, we must first satisfy the requirements of safety services. On the other hand, the services requested by VUEs have different requirements for transmission characteristics provided by RSUs, such as delay, jitter and packet loss rate [15]. Therefore, in order to solve the resource allocation problem in the VANET in a more reasonable way, we must take the differences of services requested by VUEs into account, while ensuring the fair allocation of resources.
In this paper, we proposes a hierarchical resource allocation scheme based on Nash bargaining game to achieve a fair and efficient resource allocation in VANET. In the first layer, we study the resource allocation between the central cloud and the RSUs’ cloud. In the second layer, we study resource allocation between RSUs and VUEs. The major contributions of this paper are as follows:
- Considering the characteristics of VANET, we propose a hierarchical resource allocation architecture based on Nash bargaining game to ensure the proportional fairness and effectiveness of resources allocation in VANET.
- Considering the tidal phenomenon caused by the random movement of vehicles and the limited resources of a single RSU, we study the resource allocation strategy of the central cloud by establishing the Nash bargaining model between RSUs.
- Considering the selfishness of VUEs and the difference of services requested by VUEs, we study the resource allocation of RSUs, by establishing the Nash bargaining game model of VUEs and constructing the matching degree index between VUEs and RSUs.
- To reduce computational overhead, we transform the resources allocation problem between VUEs and RSUs into two sub-problems: power allocation and slot allocation, according to the time division multiplexing mechanism.
2. Hierarchical Resource Allocation Scheme Based on Nash Bargaining Game
In this section, we briefly introduce the bargaining game and Nash bargaining solution. Thereafter, we propose the hierarchical mathematical model of resource allocation in VANET based on Nash bargaining game. Finally, we give the solution of this hierarchical model.
2.1. Bargaining Game and Nash Bargaining Solution
The game theory can effectively solve the problem of competition among the VUEs in the process of resource allocation. Although the selfish characteristics of VUEs in non-cooperative games conform to the actual situation, the rational behaviors of VUEs will damage the overall benefit of the system and restrict the benefit of other VUEs. Therefore, relevant constraints need to be established among the VUEs to enable them to cooperate with each other and to improve the overall efficiency of the system as much as possible.
Bargaining game [16] is a kind of cooperative game in which both players have the opportunity to reach a win-win situation. In this game, there is a conflict of interest among the participants. If either party cannot accept the bargaining scheme, the overall agreement will not be reached. Before the specific definition is given, a simple example of two-person bargaining game is given firstly. We assume participant 1 and participant 2 share the benefits of the system, which is X. Participant 1 first proposes a share of the proceeds, which is x, . In addition, then, participant 2 judges whether to accept the agreement based on the proposal and decision of participant 1. If the agreement is accepted, participant 2 receives the remaining proceeds, which is . Otherwise, participant 2 rejects the agreement, both parties fail to reach an agreement, the benefits will be zero.
The definition of a Nash bargaining game is as follows. represents a game problem with K players. represents the set of all participants’ policies. The set of benefits that participants can obtain in the game is . represents the benefit of the ith participant under the failure agreement. Clearly, participants do not participate in the collaboration when the benefits allocated to the collaboration are less than . Then, game G is called the bargaining game of K participants.
The Nash Bargaining Solution (NBS) is the function mapping that can make the above bargaining game G has the unique optimal return vector, . However, there may be multiple bargaining functions, therefore, the most widely used bargaining function is selected to realize effective and reasonable allocation of resources in VANET. This bargaining solution is subject to the following conditions [17].
- .
- is Pareto optimal.
- As for any linear mapping g, it should satisfy .
- If and , .
- Symmetry.
Conditions 1 and 2 guarantee the validity and rationality of the existence of NBS, condition 2 means the ideal state of resource allocation, in which the bargaining scheme is optimal. Conditions 3 to conditions 5 guarantee the proportional fairness of NBS, and conditions 3 indicates that NBS has zoom invariance. It means that if the benefit function changes linearly, the final NBS stays the same. The condition 4 indicates that the expansion of the domain will not affect the final result of the bargaining game. The bargaining function of NBS meeting the above five conditions is shown below
is a strictly quasiconcave function on a nonempty closed set . This function has a unique maximum value in the maximum solution problem. Considering the selfishness of VUEs and the architectural characteristics of VANET, Nash bargaining game is suitable for solving the resource allocation problem among the central cloud, RSU cloud and VUEs based on the analysis above. A hierarchical resource allocation scheme based on Nash bargaining games will be described in the following paragraphs. Table 1 summarizes the important notations in this paper for easy reference.

Table 1.
The description of variables in hierarchical resource allocation scheme.
2.2. The Formulation of Hierarchical Resource Allocation Scheme in VANET
In this section, a hierarchical resource allocation scheme based on Nash bargaining game is proposed. In the first layer, we analyze the resource allocation between central cloud and RSU cloud. Thereafter, based on the matching degree between VUEs and RSUs, We study the resources allocations problem between them in the second layer.
2.2.1. Resources Allocation Scheme for RSUs in the First Layer
Different RSUs share the centralized spectrum resources of central cloud resources pool, the first layer of the hierarchical resource allocation scheme is the problem of allocating spectrum resources to RSUs from the central cloud. We assume that is the set of RSUs, the spectrum resource requirements of the kth RSU is . According to Shannon theory [18], we use the transmission rate to represent the benefit function of each RSU
where is the white Gaussian noise, and represent the transmission power and channel gain of the kth RSU, respectively. is the modulation factor of orthogonal amplitude modulation [19], which can be denoted as
where , . BER is the maximum error rate that the kth RSU can tolerate. According to the definition of NBS, the cooperative game problem of the first layer centralized resource allocation can be expressed as . is a set of benefits that each RSU gets when participating in the game. The minimum is the disagreement point. We assume the total spectrum resources of the central cloud is , the Nash bargaining game problem can be formulated as
is the target function for resource allocation at the first layer. is the spectrum resources vector assigned to each RSU, which is . The first constraint in Formula (4) is used to guarantee the existence of the optimal allocation vector. The second constraint indicates that the number of spectrum resources shared by RSUs cannot exceed the total spectrum resources in central cloud. According to the properties of logarithmic functions and Lagrange multiplier method, the Lagrange function form of this spectrum allocation problem can be formulated as
is lagrangian multiplier, according to the definition of the KKT condition [20], Formula (5) should satisfy the following three conditions
After formula derivation, we can get and
in Formula (7), . From Formula (6), due to is a nonnegative variable, we can find that . Hence, through formula derivation and calculation, the optimal spectrum resources allocated to the kth RSU can be obtained
After completing the spectrum resources allocation for RSUs in the first layer, we need to continue to study the allocation of spectrum resources for VUEs within the coverage of RSUs.
2.2.2. Resources Allocation for VUEs in the Second Layer
According to the spectrum resources allocated in the first layer, the spectrum resources obtained by the kth RSU is . In order to improve the utilization of spectrum resources, each RSU network adopts the multiuser orthogonal frequency-division multiplexing (OFDM) systems [21]. Hence, continuous spectrum resources are divided into several slices of virtual resources in the form of orthogonal subcarriers in the RSUs cloud. Meanwhile, transmission power is distributed to each VUEs. We assume that each RSU’s subcarrier has the same bandwidth, the subcarrier bandwidth of the kth RSU is . The number of subchannel resources in the kth RSU is
means the integer down. We use to represent the set of VUEs in the kth RSU. We assume that the benefits set of VUEs in bargaining cooperation is . is the disagreement point, which is the minimum benefit set that VUEs are willing to accept. Therefore, the Nash bargaining game of the second layer resource allocation issue can be represented by . In order to guarantee the efficiency and fairness of the resources allocation at the VUEs layer, we formulate the resource allocation optimization problem as
Formula (11) represents the optimization problem of resource allocation to VUEs at the second layer. is the strategy vectors of VUEs in the kth RSU for subcarrier allocation. is the strategy vector of VUEs in the kth RSU for transmission power allocation. denotes whether subchannel j is assigned to VUE i or not (i.e., if subchannel j is assigned to VUE i, ; otherwise, ). and represent the channel gain and transmission distance between RSUs and VUEs, respectively. is the decay coefficient of distance. is the modulation coefficients of subcarriers, we assume that this coefficient is equal to in Formula (2).
According to the above analysis, we can achieve a proportional fairness resources allocation in VANET. However, the above resource allocation analysis does not take into account the differences of VUEs, that means the services requested from RSUs by VUEs are different from each other. On the other hand, the performance of RSUs is different with each other. Different VUEs should have different performance requirements in different RSUs. For example, latency and jitter may be more important than throughput for a VUE requested the online game. A low-latency RSU is more suitable for transmitting voice services, and the low jitter RSU is more suitable for video stream transmission services. However, in most previous studies, the benefit function of VUEs just depend on the power and the number of subcarriers allocated. As shown in formula 11, VUEs obtaining the same amount of resources have the same benefits, which does not take into account differences of VUEs. It is not consistent with the actual situation. In order to solve the above problems, we firstly construct the matching degree index between VUEs and RSUs.
The evaluation of matching degree index is based on computing the L-dimensional Euclidean distance between services features offers and demands, where L is the number of services features. We use binary variables to represent whether the lth services feature can be provided to ith VUEs by the kth RSU, such as low-latency, low-jitter and high-throughput. The value of is 1, which indicates that the kth RSU can provide the ith VUEs with the lth services feature. The value of is 0, which indicates that the kth RSU can not provide the ith VUEs with the lth services feature. On the other hand, we use binary variables to represent whether the lth services feature will be demanded by the ith VUEs from the kth RSU. The value of is 1, which indicates that the lth services feature will be demanded by ith VUEs. To facilitate analysis, we use the variable to represent the ability of the RSU providing service features for the ith VUE
Obviously, as the value of gradually increases, the ability of the kth RSU providing service features for the ith VUEs becomes worse. Therefore, we use exponential function to build the matching degree index between RSUs and VUEs. The matching degree index between the ith VUE and the kth RSU can be formulated as
where is the normalized weight, is a reputation parameter of the kth RSU, which is related to services features provided in the past.
Thereafter, considering the matching degree index between VUEs and RSUs, Equation (11) can be transformed into
The NBS optimization problem in formulation 14 is a mixed integer nonlinear programming problem (MINLP), which is NP-hard. In order to reduce the computation complexity, we adopt the time-sharing relaxation [22] to transform the MINLP problem into a nonlinear real-number programming problem. We introduce allocation time variable , which means the fraction of time when VUE i occupies the all subchannels of the kth RSU. Now, the optimization problem 14 can be transformed into two sub-problems: optimal power allocation and optimal time allocation. we assume that represents the time length occupied by the ith VUE in the kth RSU. We assume . Then, the optimization problem can be formulated as
From [23], we know that necessary and sufficient condition for the optimal allocation solution exists, the sub-problem of the optimal transmission power can be converted to
Obviously, optimization function 16 is log-concave with respect to , and constraint is linear. Thus the optimization power allocation problem is convex. According to the Lagrangian multiplier method, the Lagrangian function can be written as
The Lagrangian multiplier vector is . According to KKT conditions, the following conditions must be satisfied
Then, we can obtain the optimal transmission power for VUE i on subchannel j, which is given as
where .
According to the value of the optimal transmission power , we can get the optimal transmission rate
Then, the sub-problems of optimal time allocation can be formulated as
The Lagrange function is formulated as
is the time vector allocated to VUEs. is the lagrangian multiplier. According to KKT conditions, the following conditions must be satisfied
and then, the optimal transmission time allocation for the ith VUE in the kth RSU is obtained
Thus, we present the algorithm in Algorithm 1. In Algorithm 1, we firstly calculate the spectrum resources obtained by the kth RSU. Then, we obtain the power resource and time slot resource of the VUE i in the kth RSU. Therefore, the time complexity of Algorithm 1 is .
| Algorithm 1 Hierarchical Resource allocation based on Nash bargaining game |
|
3. Algorithm Simulation and Results Analysis
In this section, we use Python 3.5 to evaluate the performance of the proposed method in terms of proportional fairness and effectiveness. We firstly introduced the simulation setup. Then a lot of simulation results are provided and analyzed.
3.1. Simulation Setup
We assume that there are three RSUs in the simulation scenario, namely RSU1, RSU2, RSU3. Then we consider a group of VUEs that are randomly deployed in the OFDMA wireless network within the coverage of RSUs. The total spectrum resources of the resource pool is 15 MHz. The minimum transmission rate requirement for RSUs are Mbps, Mbps, Mbps, respectively. The bit error rate of each RSU is initialized to . The average transmission power of each RSU are 50 mW, 20 mW, 20 mW, respectively. The average communication radius of each RSU are 200 m, 150 m, 100 m, respectively. we assume that the value of the is 3.
For analysis purposes, we assume that there are three types of VUEs within the coverage of RSUs. VUE1 primarily requests voice service from the RSU. VUE2 primarily requests a text service from the RSU. VUE3 mainly requests video services from the RSU. Obviously, different VUEs have different requirements for the service characteristics provided by RSU. Latency and jitter may be more important than throughput for a VUE requesting online game services. In addition, in order to facilitate the calculation, we use the delay, jitter and packet loss rate to measure the performance of RSUs. For example, the minimum requirements for delay, jitter and packet loss rate for VUE1 are 100 ms, 25 ms and 4% respectively, while the best performance of RSU1 for delay, jitter and packet loss rate is 98 ms, 27 ms and 5%, respectively. Hence, according to the analysis above, we can find that , , . Then, we can calculate the matching degree between VUEs and RSUs. The performance parameter values of each RSU are shown in Table 2.

Table 2.
Performance parameter values of RSUs.
As we know, RSU with low latency is better suited to provide voice services, text services should prefer RSU with low packet loss rates, video services should prefer RSU with less jittery. The minimum performance requirements of VUEs for delay, jitter and packet loss rate are shown in Table 3. According to Equation (14), we can get the matching degree between each RSUs and VUEs, as shown in Table 4. Then we can find that RSU1 is suitable for voice transmission services, RSU2 and RSU3 are suitable for text services.

Table 3.
The minimum performance requirements of VUEs.

Table 4.
The matching degree between RSUs and VUEs.
After the spectrum resources allocation to RSUs is completed, we consider the allocation of resources for VUEs in the second layer, including power allocation and subchannel allocation. Consider the space limitation of this paper, we just study the resources allocation problems in RSU2. We assume that there are three types of VUEs within the coverage of RSU2, which are VUE1, VUE2 and VUE3, respectively. The value of minimum rate requirement = 0.1 Mbps, = 0.5 Mbps and = 1.0 Mbps. The subchannel bandwidth kHz. The maximum bit error rate that VUEs can tolerate is .
3.2. Simulation Results
The proposed resources allocation scheme is evaluated through by two measurements: effectiveness and fairness. The effectiveness means that the minimum rate requirements of any VUE can be met by negotiating with other VUEs. The fairness means the proportional fairness considering the individual minimum rate.
Figure 2 and Figure 3 show the impact of BER (the maximum bit error rate that RSU1 can tolerate) on the spectrum allocation. As shown in Figure 2, the spectrum allocated of RSU1 decreases with the increase of BER. It is because that the increase of BER increases the modulation coefficient according to Equation (3). With the minimum transmission rate been satisfied (denoted in Figure 3), when the spectrum resources required by RSU1 are reduced, the additional spectrum resources will be distributed to RSU2 and RSU3 in proportion, so the spectrum resources obtained by the two RSUs will increase with the increase of BER. Then, as for RSU1, the increase of BER eventually leads to the increase of transmission rate for each RSU, which can be concluded from Figure 3.
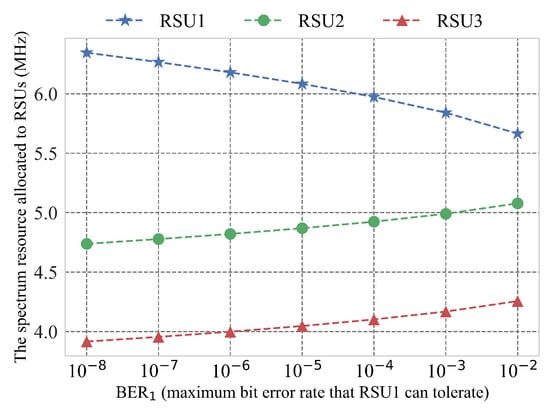
Figure 2.
The spectrum resources allocated to RSUs vary with the BER.
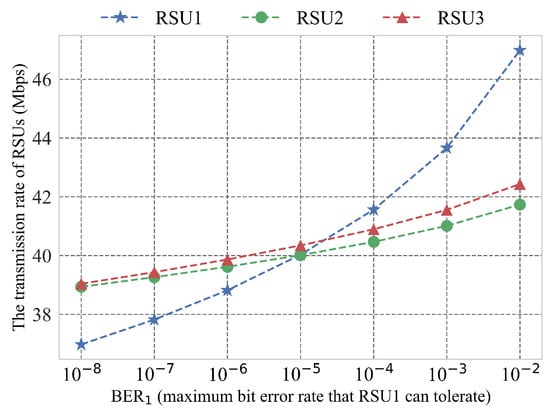
Figure 3.
The transmission rate of RSUs vary with the BER.
Figure 4 shows the impact of RSU1’s minimum rate requirements on spectrum resource allocation. After the minimum spectrum resources requirements of each RSU are satisfied, the rest of the spectrum resources is redistributed fairly to all RSUs in proportion to demand. Therefore, even if the minimum transmission rate requirements of RSU1 is 0 Mbps, RSU1 can still be allocated 4 MHz spectrum resources. To meet the increasing demand for RSU1’s minimum transmission rate, more spectrum resources must be allocated to RSU1, resulting in gradual reduction in spectrum resources allocated to RSU2 and RSU3.
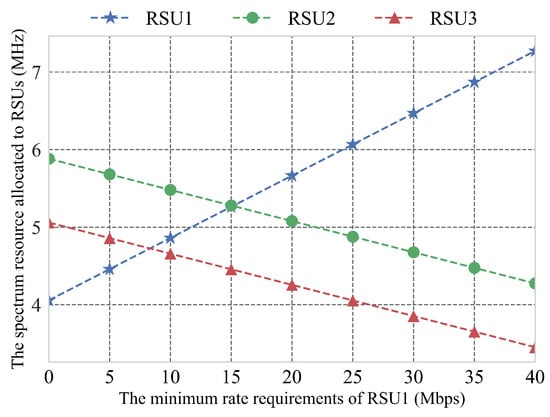
Figure 4.
The spectrum allocation results of RSUs vary with the minimum rate requirements of RSU1.
Figure 5 show the spectrum resources obtained by RSUs under different distribution schemes. After meeting the minimum rate requirements of RSU1 and RSU2, the allocation scheme based on the maximum throughput of the system allocated the remaining spectrum resources to RSU3, which has better average performance than RSU1 and RSU2. On the contrary, after meeting the minimum requirements of each RSU, the Nash bargaining scheme would distribute the remaining spectrum resources equally to all RSUs in proportion to demand. By further observation of the spectrum resources obtained by RSU2 and RSU3, we can be found that RSU2 obtained less spectrum resources in the maximum throughput allocation scheme of the system for its poor average performance, while in the Nash bargaining scheme, it can obtain spectrum resources in proportion to demand.
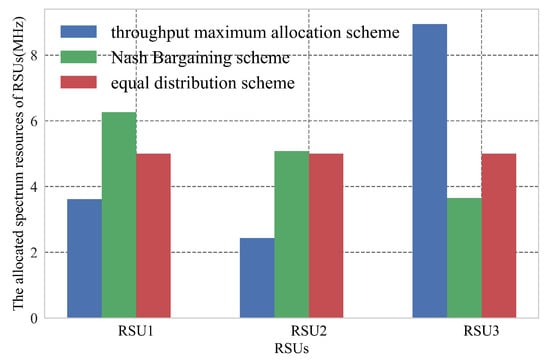
Figure 5.
Spectrum resources obtained by RSUs under different distribution schemes.
Thereafter, we analyze the resource allocation for VUEs in the second layer. If we do not take into account the differences of VUEs and the matching degree between VUEs and RSUs, as long as each VUE has the same resource requirements, each VUE can get the same amount of resources from the RSU. Obviously, this case is unreasonable. Therefore, when researching the resource allocation scheme of the VUE layer, we must consider the matching degree between VUEs and RSUs.
Figure 6 shows the effect of the communication distance between VUEs and RSUs. When the communication distance between each VUE and RSUs is the same, the transmission time slot size obtained by each VUE is determined by the minimum transmission rate requirements of each VUE. Therefore, VUE3 will be allocated to the maximum transmission time slots, which has the maximum transmission rate requirements for requesting the video services. In addition, as the distance between VUE3 and RSU increases gradually, in order to meet the minimum rate demand of VUE3, the transmission time slot size allocated to VUE3 must increase at the same time. On the contrary, the transmission time slots allocated to VUE1 and VUE2 will be reduced appropriately. The rate reduction can be accepted by these VUEs because their rates are still greater than their minimum rates requirements. Therefore, proposed scheme can achieve fair and reasonable allocation of resources according to the minimum needs of VUEs.
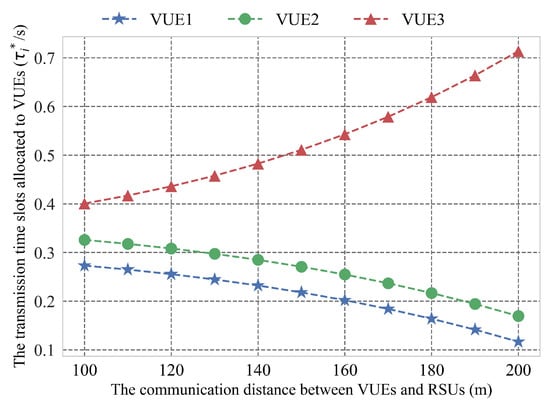
Figure 6.
The time fraction allocation of VUEs when VUE3 moves away from the RSU.
Thereafter, we compare the effectiveness of proposed hierarchical resource allocation scheme with other resource allocation schemes, such as equal distribution scheme and throughput maximum scheme. To prove the advantages of our proposed scheme, we study the trend of VUE3’s transmission rate when the distance between VUE3 and RSU3 increases gradually. In Figure 7, when the distance between VUE3 and RSU3 increases gradually, the path loss of data transmission also increases. Therefore, the transmission rate of the VUE3 will decrease gradually in these three resource allocation schemes. When the distance between VUE3 and RSU3 is greater than 180m, the transmission rate of the VUE3 will be lower than 1 Mbps in equal distribution scheme and throughput maximum scheme. That means the minimum rate requirements of VUE3 cannot be guaranteed. However, in our proposed scheme, when the distance between the VUE3 and the RSU3 is greater than 180 m, the minimum rate demand of the VUE3 can still be met.
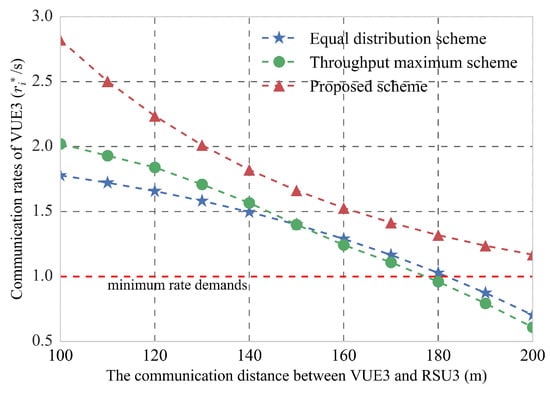
Figure 7.
The comparison between the proposed method with existing methods on effectiveness.
We evaluate the performance of the proposed method in guaranteeing the fairness of VUEs. The fairness index can be mathematically defined as [24]
where . If , the ratios of VUEs’ rates to the corresponding minimum rate are the same, which implies that the resource allocation is perfectly fair. From Figure 8, we can find that the proposed scheme outperforms the equal distribution scheme and the throughput maximum scheme in fairness. This is because the proposed scheme realizes the dynamic allocation of resources based on Nash bargaining game. However, in equal distribution scheme, each VUE is assigned the same resources. When the number of VUEs increases, the resources allocated to each VUE decreases. Then, the minimum rate requirements of some VUEs cannot be met. As a result, the fairness index decreases with the number of VUEs. In throughput maximum scheme, it will first satisfy the minimum demand of the VUEs, who have the poor communication condition. Then, more resources will be allocated to the VUEs with better communication condition. However, when the number of VUEs is large enough, in order to maximize system throughput, the minimum demand of the VUEs who have the poor communication condition cannot be met. Therefore, the fairness index begin to drop. The proposed hierarchical resource allocation scheme provides a better fairness index due to its proportional allocation based on Nash bargain game.
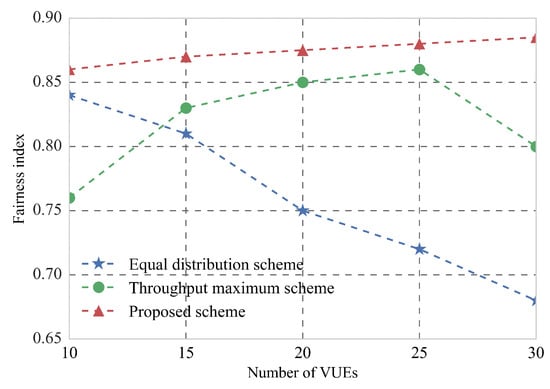
Figure 8.
The comparison between the proposed method with existing methods on fairness.
4. Conclusions
In this paper, a hierarchical resource allocation scheme is proposed to realize fair and effective resource allocation in VANET. In the first layer, the random movement of vehicles brings difficulty for the central cloud to allocate resources to RSUs. Therefore, we use Nash bargaining game to achieve fair and efficient resources allocation between RSUs. In the second layer, considering the selfishness of VUEs and the difference of services requested by VUEs, we construct the matching degree index between RSUs and VUEs. Then, we establish the Nash bargaining game model to achieve fair and effective resources allocation to VUEs. In order to reduce the computation complexity, we transform the original problem into two sub-problems: power allocation and slot allocation. Simulation results show that the proposed hierarchical resource allocation scheme can realize the fairness and effectiveness of resource allocation in VANET.
Author Contributions
All authors contributed to the development and completion of this paper. Conceptualization and Data curation, X.Z. (Xiaoshuai Zhao); Formal analysis, X.Z. (Xiaoshuai Zhao) and Y.L.; Funding acquisition and Investigation, X.Z. (Xiaoshuai Zhao); Validation, X.Z. (Xiaoyong Zhang); Review & Editing, X.Z. (Xiaoyong Zhang) and Y.L. All authors conducted the revisions and approved the publication.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 61873353), the Fundamental Research Funds for the Central Universities of Central South University (Grant No. 2018zzts535).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeadally, S.; Hunt, R.; Chen, Y.S. Vehicular ad hoc networks (VANETS): Status, results, and challenges. Telecommun. Syst. 2012, 50, 217–241. [Google Scholar] [CrossRef]
- Mershad, K.; Artail, H. A Framework for Implementing Mobile Cloud Services in VANETs. In Proceedings of the 2013 IEEE Sixth International Conference on Cloud Computing, Santa Clara, CA, USA, 28 June–3 July 2013; pp. 83–90. [Google Scholar]
- El-Sayed, H.; Sankar, S.; Prasad, M. Edge of things: The big picture on the integration of edge, IoT and the cloud in a distributed computing environment. IEEE Access 2018, 6, 1706–1717. [Google Scholar] [CrossRef]
- Huang, R.; Chang, B.; Tsai, Y.; Liang, Y. Mobile Edge Computing-Based Vehicular Cloud of Cooperative Adaptive Driving for Platooning Autonomous Self Driving. In Proceedings of the 2017 IEEE 7th International Symposium on Cloud and Service Computing (SC2), Kanazawa, Japan, 22–25 November 2017; pp. 32–39. [Google Scholar]
- Lee, E.; Lee, E.K.; Gerla, M. Vehicular cloud networking: Architecture and design principles. IEEE Commun. Mag. 2014, 52, 148–155. [Google Scholar] [CrossRef]
- Shrestha, R.; Bajracharya, R.; Nam, S.Y. Challenges of Future VANET and Cloud-Based Approaches. Wirel. Commun. Mob. Comput. 2018, 2018, 5603518. [Google Scholar] [CrossRef]
- Sou, R.; Shieh, W.C.; Lee, Y. A video frame exchange protocol with selfishness detection mechanism under sparse infrastructure-based deployment in VANET. In Proceedings of the 2011 IEEE 7th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Wuhan, China, 10–12 October 2011; pp. 498–504. [Google Scholar]
- Tao, J.; Zhang, Z.; Feng, F.; He, J.; Xu, Y. Non-cooperative Resource Allocation Scheme for Data Access in VANET Cloud Environment. In Proceedings of the 2015 Third International Conference on Advanced Cloud and Big Data, Yangzhou, China, 30 October–1 November 2015; pp. 190–196. [Google Scholar]
- Li, M.; Zhao, L.; Liang, H. An SMDP-Based Prioritized Channel Allocation Scheme in Cognitive Enabled Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2017, 66, 7925–7933. [Google Scholar] [CrossRef]
- Tao, J.; Xu, Y.; Zhang, Z. A resource allocation game with restriction mechanism in VANET cloud. Concurr. Comput. Pract. Exp. 2017, 29, e4038. [Google Scholar] [CrossRef]
- Shivshankar, S.; Jamalipour, A. Effect of altruism and punishment on selfish behavior for cooperation in Vehicular Networks. In Proceedings of the 2012 1st IEEE International Conference on Communications in China, Beijing, China, 15–17 August 2012; pp. 653–658. [Google Scholar]
- Wang, P.; Wu, Y.Y.; Wang, X.D. The Optimal Designs in Time and Space of Signalized Intersection under Traffic Tide Phenomenon. Appl. Mech. Mater. 2013, 253, 1851–1854. [Google Scholar] [CrossRef]
- Cavalcante, E.S.; Aquino, A.L.L.; Pappa, G.L. Roadside unit deployment for information dissemination in a VANET: An evolutionary approach. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 27–34. [Google Scholar]
- Sivasakthi, M.; Suresh, S.R. Research on vehicular ad hoc networks (VANETs): An overview. Int. J. Appl. Sci. Eng. Res. 2013, 2, 23–27. [Google Scholar]
- Dixit, M.; Kumar, R.; Sagar, A.K. VANET: Architectures, research issues, routing protocols, and its applications. In Proceedings of the 2016 International Conference on Computing, Communication and Automation, Noida, India, 29–30 April 2016; pp. 555–561. [Google Scholar]
- Nash, J.F., Jr. The bargaining problem. Econom. J. Econom. Soc. 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Myerson, R.B. Game Theory; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- IEEE. Sessions: Shannon theory. In Proceedings of the 1988 IEEE International Symposium on Information Theory, Kobe, Japan, 19–24 June 1988; pp. 2–13. [Google Scholar]
- Chung, S.T.; Goldsmith, A.J. Degrees of freedom in adaptive modulation: A unified view. IEEE Trans. Commun. 2001, 49, 1561–1571. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bazzi, A.A.; Zanella, A.; Masini, B.M. An OFDMA-Based MAC Protocol for Next-Generation VANETs. IEEE Trans. Veh. Technol. 2015, 64, 4088–4100. [Google Scholar] [CrossRef]
- Wong, C.Y.; Cheng, R.S.; Lataief, K.B.; Murch, R.D. Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE J. Sel. Areas Commun. 1999, 17, 1747–1758. [Google Scholar] [CrossRef]
- Lee, K.D.; Leung, V.C.M. Fair allocation of subcarrier and power in an OFDMA wireless mesh network. IEEE J. Sel. Areas Commun. 2006, 24, 2051–2060. [Google Scholar] [CrossRef]
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems; ACM: New York, NY, USA, 1984. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).