1. Introduction
Having the world’s largest producer, consumer, and exporter of the textile and apparel industry, China takes more than 50% of the world’s total fiber processing and 40% of global textile and apparel exports (Statistical data of China Textile Economic Research Center in 2016). In recent years, China has raised great awareness of ecological environment protection. Since 2015, China has implemented the new Environmental Protection Law to encourage enterprises to practice green supply chains (GSC). Furthermore, the law aims to enhance supervision responsibility of governments, which poses enormous challenges to the textile industry in China.
In Zhejiang Province, for example, the total annual output of the textile and apparel industry accounts for 16.62% of the province’s total industrial output. The number of textile and apparel enterprises is 58,178, of which 97.56% are small and medium-sized enterprises (2016 Zhejiang Statistical Yearbook). In recent years, efforts in environmental protection have increased year by year. From the official data released by Zhejiang Environmental Protection Bureau, in 2017, more than 1000 environmental cases of this industry were investigated and penalized in Zhejiang. Large-scale and long-term suspension of production has seriously suppressed industrial development. Therefore, how to establish a sustainable development mode of inter-firm cooperation has become a topic of great concern to the industry and the government.
Green supply chain management (GSCM) is an effective way to improve the performance of industrial environment [
1]. Incorporating sustainability into the supply chain is becoming a key priority for many textile and apparel companies. For example, H&M, Patagonia, and The North Face have incorporated various approaches to enhance their levels of sustainable supply chain management [
2]. The prior studies have demonstrated that specific modes of collaboration can both enable effective GSCM and diminish barriers for policy implementation [
3,
4].
The textile and apparel industry in China is geographically clustered [
5]. Based on the views of “2016 China Textile Industry Cluster Development Report” by China National Textile and Apparel Council (CNTAC), industry information inside the cluster is almost completely transparent, and there exists complex game behavior among supply chain partners that maintain complementary, competitive, or cooperative relationships with each other. Brands that occupy a central position are the leaders of the supply chain. The upstream and downstream SMEs act according to the leader’s requirements. Our investigation on the textile and apparel industry in Zhejiang also proved the above judgement. Therefore, it is of great practical significance to analyze the game behavior between suppliers and manufacturers in the GSC and explore the GSC governance mechanism, based on the reality of the textile and apparel industry in China.
The prior literature on a two-level supply chain has focused on the game between one manufacturer and one supplier. Research on group game behavior in GSC needs to be improved. For instance, the game between the manufacturer and the supplier group, and the game between the homogenous or complementary suppliers. Based on the characteristics of the textile and apparel industry clusters, this study develops a novel two-level GSC game model consisting of a single manufacturer and three suppliers and identifies some critical conditions for implementing green improvement in the GSC through equilibrium analysis. In particular, our model assumes that the manufacturer is the leader of the supply chain, and the suppliers are either homogeneous or complementary. Through game analysis, we derive the game equilibrium price and corresponding equilibrium conditions of the GSC. Our game model and findings make significant contributions to the literature by providing the strategic guidance for all parties to participate in the greening process and especially for GSC leader to make managerial decision to promote greening.
The rest of this study is organized as follows. The next section reviews prior related literature.
Section 3 presents a two-level GSC game model consisting of a single manufacturer and multiple suppliers. In
Section 4, through the model optimization analysis, we demonstrate the equilibrium conditions within the GSC and discuss their implications. The last section concludes the paper with practical recommendations.
3. Model of Green Supply Chain
This section presents a two-level GSC game model consisting of a single manufacturer and multiple suppliers. We first describe the model setting and sequence, and then show the basic game model along with the manufacturer and suppliers’ decision before and after green investment.
3.1. Model Setting
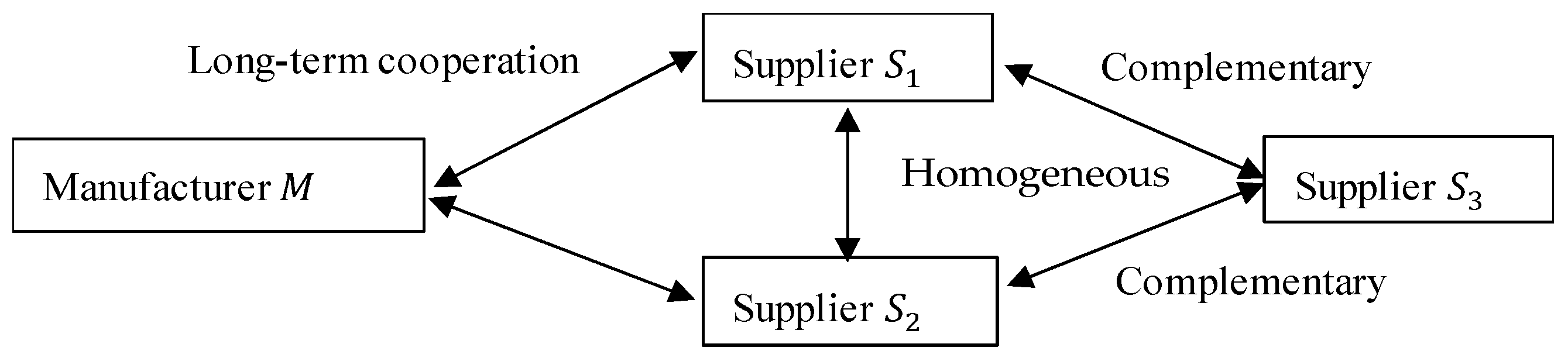
The supply chain of the textile and apparel industry mainly includes raw material suppliers (providing cotton, silk and wool), suppliers of primary products (providing clothing fabric), manufacturer of garments, and retailers. This process is accompanied by a variety of ancillary support links, including auxiliary material suppliers, manufacturing equipment suppliers, and so on. According to the industry, this study abstracts a two-level GSC structure consisting of one manufacturer and three suppliers (two homogeneous suppliers and one complementary supplier). We develop a manufacturer-led game model to explore its multi-party game relationship, and to obtain the equilibrium prices when benefits are maximized. The research assumptions are as follows:
(1) Both the manufacturer and suppliers are risk-neutral, and the goal of their decisions is to maximize profits. Assume that the manufacturer
only involves the operation of two raw materials, the main material
and the auxiliary material
. The supplier
and the supplier
. are homogenous suppliers, providing the raw material
. The supplier
, as a complementary supplier of the supplier
. and the supplier
, provide the raw material
. The manufacturer
. and the supplier
have established a stable cooperative relationship in long-term procurement. The auxiliary material supplier
passively adopts the same decision-making options as the main material suppliers. Relationships between the model’s main players are shown in
Figure 1.
(2) Referring to Jiang and Sui [
23] and Zhu and Dou [
25], the demand
is positively correlated with the total market demand
and the product’s greening level
, and negatively correlated with the unit price
of the product. The demand function is represented as
. Consumers who prefer “cheap and good quality” products tend to buy green products at a low price.
is the price sensitivity coefficient and
. is the coefficient representing the sensitivity of a consumer to a product’s greening level, where
. Referring to Zhu and Dou [
31], it is assumed that the price of ordinary products before greening is
, and its greening level is
.
is the lowest greening level of the admission to the market. The price of products after greening is
, and its greening level is
. Obviously,
, i.e., the higher the greening level of the product, the more environmentally friendly. In the textile and apparel industry, the greening level of the product can usually be measured by the solvent toxicity and recyclability in the production process, the carbon label and the degree of natural degradation of the discarded clothes.
(3) This study focuses on the analysis of game relationships within GSC, and subsequent research can be extended to the analysis of game relationships with external stakeholders. Therefore, we assume that external stakeholders have reached a game equilibrium, that is, consumers are willing to purchase green products produced by manufacturers, and the government will supervise manufacturers to implement green investment. Manufacturers are motivated to develop green products, the costs of which includes production process improving, procurement of related equipment, and R&D of new products. Referring to D’Asprement’s approach [
32], the product R&D cost formula is
, where
is the R&D adjustment factor and
. Supplier
and
are free to decide whether to respond to the manufacturer’s green investment. R&D costs are all borne by the manufacturer, and suppliers only bear additional green processing costs.
3.3. Decisions Before and After Green Investment
(1) Before the implementation of the green investment, the unit price of the main material provided by the supplier and is , and there is a linear relationship of between the price and the sales volume. Here, is the total demand of and is the price sensitivity coefficient, where . The unit price of the auxiliary material provided by the supplier is , and there is a linear relationship of between the price and the sales volume, in which is the total demand of , is the price sensitivity coefficient, and . The processing cost of the manufacturer’s unit product is . The unit price of the manufacturer’s product is , and there is a linear relationship of between the price and the sales volume. Each unit of the product needs units of main material and units of auxiliary material , that is, and .
(2) After the implementation of green investment, the unit price of the manufacturer’s product is . Since the products are improved only in the greening level, the relationship between the price and sales volume still satisfies . The unit price of the main material provided by the supplier and is , and there is a linear relationship of between the price and the sales volume. The unit price of the auxiliary material provided by the supplier is , and there is a linear relationship of between the price and the sales volume. The processing cost of the manufacturer’s unit product is . Each unit of the product still needs units of and units of , that is, . To simplify the analysis, it is assumed that the operating costs, except the processing costs of the suppliers and manufacturers, do not change after the implementation of the green investment.
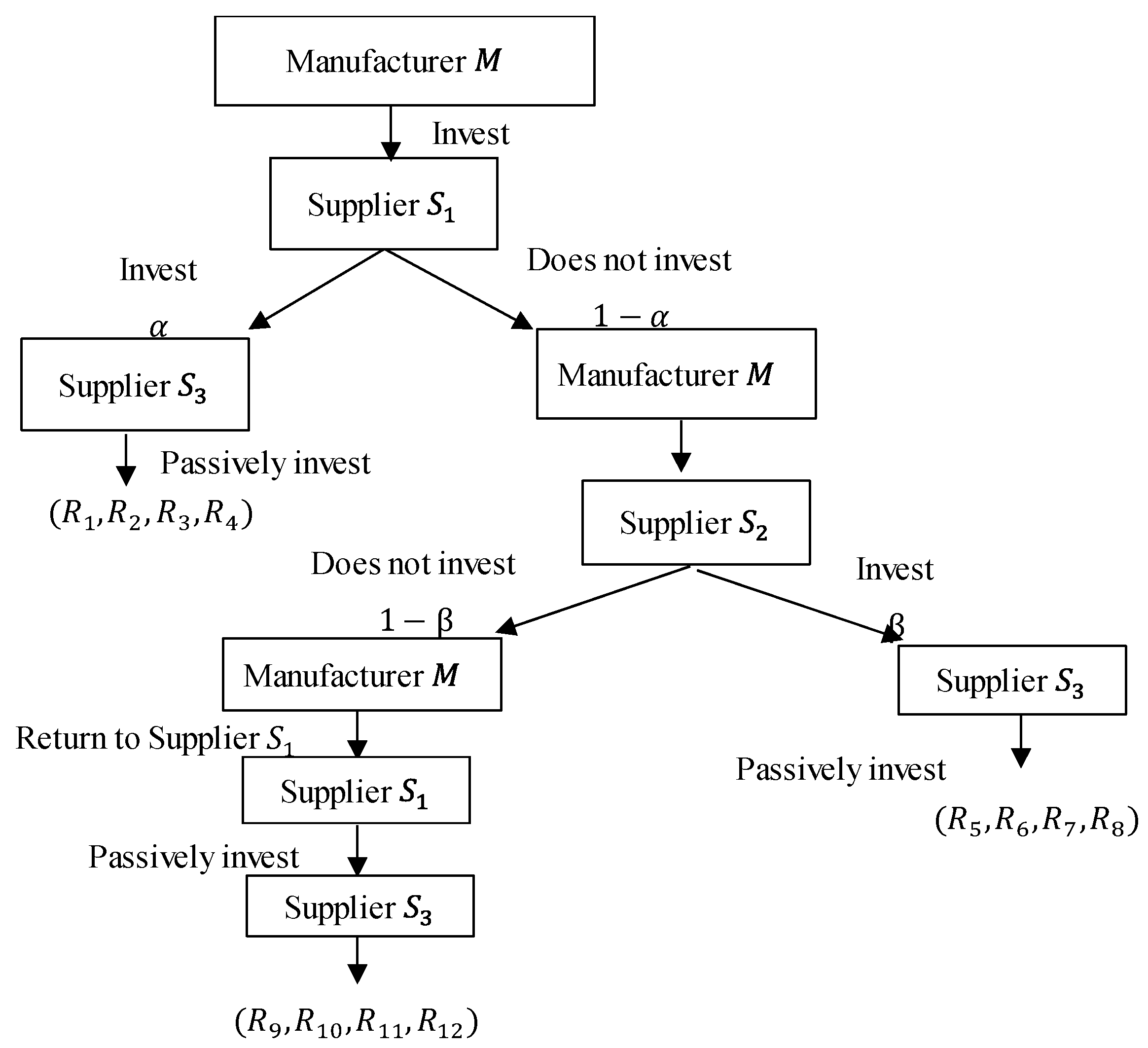
(3) After the manufacturer implements the green investment, if the original supplier does not cooperate, the manufacturer will purchase from the supplier . The purchase price is still , but the manufacturer M has to bear an additional purchase cost . Meantime, the supplier needs to sell the raw materials to other manufacturers, and each unit of material generates additional sales expenses . If the supplier does not cooperate, the manufacturer returns to purchase raw materials from the original supplier . The purchase price is , but the manufacturer needs to pay an additional processing fee per unit product.
(4) After the manufacturer implements the green investment, if the original supplier and the substitute supplier do not respond to the investment, and the manufacturer still purchases the raw materials from the original supplier , the purchase price per unit is still , but it will incur additional processing costs per product for manufacturer .
(5) After the manufacturer implements the green investment, the probability that the supplier cooperates is , where . After the manufacturer implements the green investment, the probability that the supplier cooperates is , where .
The main decision variables before and after green investment are shown in
Table 1.
3.4. Basic Game Model
In the game between the manufacturer
and its suppliers
,
,
, the decision-making behavior of the participants has a sequence and all participants can obtain the historical information of the game, then making their own decisions optimal. Therefore, the manufacturer-led one-to-many sequential game is a complete information dynamic game system. With the deepening of the supply chain greening, the game is played repeatedly. As the game evolves, the system will continue to optimize and improve until the Pareto optimality is achieved. The manufacturer
takes the lead in implementing a green investment, and the supplier
chooses to cooperate. The profit
of the manufacturer is the revenue of the product minus the processing cost of the product, the purchase cost of the material
and
, and the R&D cost
. The profit
of the supplier
, is the revenue of main material
minus the raw material cost and the raw material processing cost. The profit
of the supplier
, is the revenue of auxiliary material
minus the raw material cost and raw material processing cost. At this point, the profit
of the supplier
, in the original supply chain, is the revenue of the material
minus the raw material cost, and the raw material processing cost. The functions are as follows:
The manufacturer
takes the lead in implementing a green investment. If the supplier
chooses not to cooperate, the manufacturer
achieves cooperation with the supplier
. Then, the profit
of the manufacturer
, is the revenue of the products minus the processing cost of the product, the additional procurement cost, the procurement cost of the materials
and
, and the R&D cost
. The profit
of the supplier
is the revenue of the main material
minus the raw material cost and raw material processing cost. The profit
of the supplier
, is the revenue of the auxiliary material
minus the raw material cost and raw material processing cost. At this point, the profit
of the supplier
, is the revenue of the material
minus the raw material cost, the raw material processing cost and the additional sales cost. The functions are as follows:
The manufacturer
takes the lead in implementing a green investment and fails to reach cooperation with the supplier
after refused by the supplier
. Then the manufacturer
returns to cooperate with the original supplier
. Thus, the profit
of the manufacturer
is the revenue of the product minus the product processing cost, the procurement cost of the materials
and
, the additional processing cost and the R&D cost
. The profit
of the supplier
is the revenue of the main material
minus the raw material cost and raw material processing cost. The profit
of the supplier
, is the revenue of the auxiliary material
minus the raw material cost and raw material processing cost. At this point, the profit
of the supplier
is the revenue of the main material
minus the raw material cost and the raw material processing cost before green investment. The functions are as follows:
5. Conclusions
The textile and apparel industry in China is at a critical stage of green upgrading. The fulfillment of GSCM is a dynamic game process with complete information. Faced with the constraints imposed by different strategic choices from different stakeholders, stakeholders need to make scientific and rational decisions to address the main issues in the green process. Based on the reality of the textile and apparel industry, this study develops a one-to-three sequential GSC game model, in which the manufacturer is the leader. Through game analysis, the game equilibrium price and equilibrium conditions of the GSC are defined, which provides the strategic space for all parties to participate in the greening process and especially help the GSC leader to make managerial decision to promote greening. Our game analysis makes the following specific contributions to the existing literature.
(1) We find that the equilibrium price of the GSC game is and there are three possible equilibrium states under this price. In a manufacturer-led sequential game, the manufacturer has the right to bid first. The game equilibrium price can be achieved under the condition of the manufacturer’s first bid. At this price, the manufacturer has the maximum expected benefits, and one of the three game equilibrium states, i.e., , , and , can be reached. We obtain the strategic boundary of each equilibrium state. In a real scenario with known data conditions, it is not difficult to deduce the final game equilibrium based on the results of our model.
(2) If the manufacturer intends to cooperate with a specific supplier at the price of , this equilibrium can be reached by adjusting the supplier’s cost conditions to meet its decision boundaries. For example, in the first round of the game, to promote the supplier to select the cooperation strategy, the manufacturer can partly bear the processing cost () of the green material for the supplier, which can thus increase the supplier’s expected return to meet the critical condition for cooperation (as described in Proposition 1).
(3) If the manufacturer intends to maximize the supplier’s willingness to cooperate, the supplier may be allowed to take the lead in bidding. This situation usually occurs at the initial stage when the manufacturer pushes the greening of the supply chain. We assume that the suppliers could take the lead in bidding and obtain equilibrium prices and , as well as possible equilibrium states and equilibrium conditions. This result provides useful guidance to effectively encourage suppliers to participate in GSC.
(4) The influence of complementary suppliers on the decision-making of the main material supplier cannot be ignored. The strategy of adjusting the purchase price can encourage complementary suppliers to support greening. We consider the complementary supplier of auxiliary materials in this study, analyze the optimal expected benefits of the complementary supplier, and obtain the optimal supply price , which helps for interpreting the behavior of such suppliers.
In summary, each stakeholder has the best behavior strategy in the GSC game. There must be differences between these optimal strategies. Controlling the differences within the acceptable range of all the players is the key to achieving the equilibrium of cooperative games. Quantifying these differences and defining the scope of regulation acceptable to all parties is the focus of this study.
The limitation of this study is that the scenarios and conditions considered are still not comprehensive. First, we only consider the GSC game model under the complete information and does not consider the case of incomplete information. Second, we assume the ex-factory price of the product as the retail price and have not considered the impact of the retailer on the supply chain pricing. In addition, this game is only carried out within the supply chain, without considering the situation where external stakeholders, i.e. local governments, central government and consumers, have not achieved a balanced interest. Third, if the government still adopts the environmental policy of “who pollutes who governs” and shifts from “punishment-based” to “subsidy-based” in policy measures, the government will subsidize SMEs directly and it will be unclear what types of the game equilibrium of the GSC can be achieved. Fourth, future research needs to conduct numerical analysis with actual manufacturer and supplier behaviors to clearly indicate the conditions of the different types of equilibrium, which will test the model and help practitioners better understand the strategies they should select in a real scenario. Finally, as different countries implement different environment-protection policies and initiatives, it will be interesting to further evaluate how our model might fit different policy settings in different countries.